Abstract
This paper aims at comparing the use of different software environments for the study of a simple unreinforced masonry building through nonlinear static analyses. The presented results are part of a wider research project conducted within the ReLUIS consortium, and specifically within a research task whose purpose is providing practitioners with results and tools for an aware employment of commercial software packages for modelling masonry structures. In this study one of the benchmark structures of the research program is analysed; a two-story building characterized by rigid horizontal diaphragms, considering different configurations in terms of openings arrangements and effectiveness of ring beams, is subjected to seismic load conditions. Software packages considering two- and three- dimensional structural models are employed, and the obtained results are compared in terms of capacity curves and collapse mechanisms. One of the critical aspects on the basic assumptions made by software in terms of way to apply the horizontal loads is further investigated. In addition, the role of the shear strength is analysed correlating the mechanical properties to be adopted with micro- and macro- models. The considered models present very different features, and the analogies and differences obtained in the results are critically interpreted in view of the different hypotheses made by the software tools in terms of modelling strategies and adopted constitutive laws.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The employment of sophisticated approaches for modelling masonry structures has been growing in the last decades hand in hand with the availability of computational technologies. However, although refined and reliable tools are at hand also in engineering practice, the use of advanced software has to be supported by high-level expertise for a correct interpretation of the outcome and to avoid getting unrealistic results, even in presence of clear prescriptions of the national codes.
Recent trends of the research in the field of numerical modelling of masonry structures pushed on one side on detailed models, mainly based on continuous (Page 1978; Gambarotta and Lagomarsino 1997; Pegon and Anthoine 1997; Lourenço et al. 1998a) or discontinuous (Lourenço and Rots 1997a; Macorini and Izzuddin 2011) Finite Element (FE) approaches, and on simplified ones, based on mono- (Magenes and Della Fontana 1998; Kappos et al. 2002; Penna et al. 2014) or bi- (D'Asdia and Viskovic 1995; Casolo and Peña 2007; Caliò et al. 2012) dimensional models, on the other. Some authors also proposed hybrid strategies based on the combination of finite and discrete numerical models (Smoljanović et al. 2015). All these tools supported the exploration of the nonlinear behaviour of masonry structures, mainly through static analyses. In some cases, especially for the out-of-plane analysis of masonry walls, although several models are able to simulate the nonlinear response of entire structures (Pantò et al. 2017), other fast tools based on limit analysis are commonly adopted for the evaluation of the collapse load multiplier. Within this context local analyses employing rigid block approaches (Giresini et al. 2019; Giresini 2017; Casapulla et al. 2019) are usually preferred, even though other more complex strategies based on homogenization techniques (Milani et al. 2006) were also proposed. Attempts to compare different models were rarely done in the literature (Marques and Lourenço 2011; Quagliarini et al. 2017), as well as reviews of numerical models of masonry structures (Lourenço 2002; D'Altri et al. 2019a).
Despite the wide variety of methods for the analysis of masonry structures in the scientific literature, and the corresponding implemented software environments available for practitioners, their uncritical or unguided use may easily lead to wrong results. For the latter reason, a research program started on 2014 and still ongoing, within the ReLUIS project by the Italian Department of Civil Protection, is being conducted. This paper is part of a specific work package of the project, whose main goal is providing guidelines for practitioners for an aware use of software tools. For this reason, several research units from Italian universities contributed to the simulation of the nonlinear response of numerous benchmark structures adopting different numerical tools for the simulation of their nonlinear response, comparing the basic assumptions and the results, and finally trying to clarify how critically analyse the outcome of a numerical simulation and to provide a general methodology for approaching the nonlinear analysis of masonry structures.
The studied benchmark structures range from single panels (D’Altri et al. 2021), studied for different boundary conditions, axial load and aspect ratios, to real 3D buildings, such as a school located in Visso (Italy) heavily damaged by the seismic sequence that struck the central Italy in 2016 (Ottonelli et al. 2021; Castellazzi et al. 2021), that is modelled and investigated. A summary of the goals of this coordinated research can be found in Cattari and Magenes (2021), which also describes all the analysed benchmark structures, studied by means of different software packages. This paper is focused on a simple but three-dimensional masonry building. Although the considered case study can be hardly considered as realistic, its simplicity allows studying several aspects often taken for granted (way to apply loads, connections between orthogonal walls, flange effect) in the use of software and sometimes considered of negligible influence for the global response of the structure. The considered case study is investigated in Manzini et al. (2020) considering Equivalent Frame (EF) models only, and in this paper considering software which employ continuous (Smith 2009) and discontinuous (Mazzoni et al. 2006) Finite Element (FE) models, a Discrete Macro-Element Model (DMEM) (Caliò et al. 2009), and a limit analysis approach (Chiozzi et al. 2017). Such models present very different features and the corresponding software tools are often based on different basic assumptions, here duly highlighted. Several configurations of the case study are investigated, considering different arrangements of the openings and structural details assumptions. The results, even in presence of such different models, can be considered in reasonable agreement, and the unavoidable scatters are interpreted in light of the different assumptions of the software environments. A further investigation is made to clarify the role of the adopted mechanical properties to simulate the diagonal shear behaviour, which is governed by different parameters and constitutive laws according to the considered modelling strategy. In addition, the way to apply the horizontal load is further investigated with ad hoc analyses and identifying its influence on the response of the structure.
2 Brief description of the benchmark case study
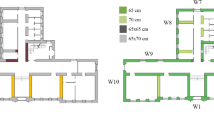
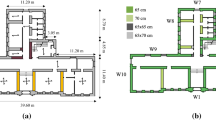
The structure investigated in this paper is a simple two-story masonry structure, with rigid floors and regular opening arrangement; the plan is rectangular and four only perimeter walls (with thickness 25 cm) are present. A comprehensive description of the benchmark structure, addressed as BS4, can be found in (Cattari and Magenes (2021); Manzini et al. (2020)), where several configurations are also introduced, considering different openings disposals and assuming different hypotheses in the structural details. In Fig. 1 the three considered plan schemes (P1 P2 and P3) of the structure are depicted; in particular, in addition to the blind wall adopted for the transversal walls, three other wall schemes are considered, namely A- and B-type for the longitudinal walls and C-type which replaces one of the blind transversal walls in the configuration P3, Fig. 1a. A-type wall is symmetric and includes two door-openings at the base level and two windows at the second one, B-type wall is unsymmetric and includes a window for each level, C-type wall is symmetric with a window per level. The reference plan configuration (P1) includes A-type and blind walls for the longitudinal and transversal walls, respectively. In configurations P2 and P3 the longitudinal rear wall is of B-type, and in the latter case the left transversal wall is further replaced with a C-type wall, Fig. 1b. With regard to the structural details, four different assumptions have been considered. Specifically, the reference hypotheses, in the following addressed with the letter B, are the absence of a ring beam combined with an axial coupling of the spandrels (simulated with the presence of tie rods with cross area equal to 314 mm2) at the floor levels. Configurations C and D differ for the presence of ring beams (with cross Sect. 25 × 25 cm with top and bottom rebars corresponding to 2ϕ16) at the floor levels. The ring beams section is associated to a reinforced concrete material and infinitely stiff sections (“shear type” hypothesis) for configurations C and D, respectively. An additional configuration, addressed with letter A, is based on the hypothesis of negligible tensile strength at the spandrels (the so called “weak spandrel-strong pier” hypothesis); however, the latter configuration is investigated only in Manzini et al. (2020) where EF models are adopted. On the contrary, in the present study only bi-and three-dimensional models are adopted, which cannot uncouple the axial and flexural behaviours, and therefore configuration A is not studied. According to the research program, 7 of the total 12 possible configurations had to be investigated, as shown in Table 1, where configuration BS4_P1/C is in this paper also included although not present in the original research program.
The numerical models are subjected to seismic nonlinear analyses with force distribution proportional to the masses along the longitudinal direction. The provided mechanical properties are reported in Table 2, together with other additional data.
It is worth mentioning a redundance in the mechanical properties provided for the simulation of the diagonal shear behaviour due to different modelling approaches here adopted; to this purpose the following considerations can be made:
-
The shear strength τo is a comprehensive parameter usually employed in the case of simplified macro-models.
-
In the case of discontinuous models, the simulation of the diagonal shear behaviour is quite complex, since it is the outcome of the combination of geometric (lb/hb) and mechanical (ftb) properties at the units level as well as of parameters governing the sliding among blocks (fvo and μ) and the mortar tensile strength (ftm).
-
In the case of FE macro-models, the shear behaviour cannot be uncoupled from the flexural one since both are governed by a uniaxial constitutive law (usually accounting for an equivalent tensile strength).
3 Adopted software tools
The benchmark structure described in the previous paragraph is studied with different software packages, which have in common the adoption of two- or three- dimensional models. It is worth noting that the adopted models exhibit very different features in terms of adopted constitutive laws, modelling strategies and basic assumptions of the software environments.
Despite its simplicity, this benchmark structure arises criticisms in the hypotheses assumed by the various software platforms, in terms of three-dimensional behaviour due to the flange effect associated to the connection of orthogonal walls and to the possibility of accounting for the out-of-plane response of the walls. An additional aspect here considered is the way the software tools apply the horizontal loads (concentrated at the floor levels or distributed along the whole building height). In order to reduce the scatter of the results and to limit the arbitrariness of the implementation of the numerical models, whenever possible these aspects have been aligned, although in some cases this was not possible due to basic hypotheses of the different software environments.
The four modelling approaches, briefly recalled in the following subsections and addressed with letters from A to D, include a discrete macro-element approach based on a mechanical scheme, a continuous and a discontinuous FE model approaches; in addition, a further strategy based on limit analysis is employed. The two adopted FE approaches are based on different strategies (models B and C belong to the discontinuous and continuous approaches, respectively), thus covering a wide although not exhaustive range of possible strategies and safeguarding the heterogeneity of the adopted tools. In the description of the models, after an introduction of the main characteristics of each approach, the consistence of the numerical models with the information on the case study provided in Sect. 2 is discussed, highlighting the aspects that can be rigorously followed and those which require simplifications or different assumptions. Then, in Sect. 4, after comparing some basic consistency checks among the models (e.g. the total mass of the structure), the results of the performed nonlinear simulations are reported and compared in terms of capacity curves and damage patterns.
Among the adopted software environments, model A is the most practically oriented tool employed in this study. However, both advanced tools based on nonlinear FE models and simplified methodologies, such as the limit analysis approach might be of help. Rigorous models (such as models B and C), although not easily applicable for engineering practice, can be adopted as reference models to calibrate simpler modelling strategies or when the use of the simplified approaches is prevented, that is in the case of complex buildings where their basic hypotheses are not satisfied. On the other hand, the employment of tools based on kinematic analysis (as for the case of model D), although not providing information on the global ductility and on the cyclic behaviour of structures, can be seen as a fast tool to obtain information on the global resistance, or to crosscheck the results obtained with other more advanced strategies.
It is worth noting that the adopted tools offer a partial view of possible approaches to simulate the nonlinear behaviour of masonry structures. To this purpose it should be mentioned that significant advances in the masonry material modelling have been made in the last decades. Some models were also implemented in software packages devoted both to the engineering practice (Lourenço et al. 1997,1998b; Lourenço and Rots 1997b) and for advanced academic investigations (Macorini and Izzuddin 2011).
3.1 Model A
The Discrete Macro-Element Method (Caddemi et al. 2017) (DMEM) is a modelling strategy based on a simple mechanical scheme that, in its original configuration, is able to simulate the main in-plane collapse mechanisms of a masonry wall subjected to vertical and horizontal loads, namely rocking diagonal cracking and sliding failure modes, Fig. 2.
Simulation of the main in-plane failure mechanisms of a masonry portion by means of the macro-element: a flexural failure; b shear-diagonal failure; and c shear sliding failure (Caliò et al. 2012)
Each element is a hinged quadrilateral with two diagonal nonlinear links which govern the diagonal shear behaviour, Fig. 3a. The diagonal links can reproduce a nonlinear behaviour which accounts for the effect associated to the confinement action of the adjacent elements according to Mohr–Coulomb or Turnsek and Cacovic (Turnsek and Cacovic 1971) domains. It is worth mentioning that, although some recent studies on the orthotropic diagonal shear behaviour are available in the literature (Casolo et al. 2019), here the adopted criterion is based on an isotropic constitutive behaviour, irrespectively of the masonry texture.
Calibration of the nonlinear links of the element: a diagonal and b flexural links (Caliò et al. 2012)
Nonlinear discrete interfaces rule the interaction among contiguous elements, and the calibration of the links is based on a fibre approach as sketched in Fig. 3b. A non-symmetric elasto-plastic behaviour with limited ductility is usually adopted. It is worth mentioning that, even in presence of an elastic-perfectly plastic behaviour of the transversal links, a smoothed nonlinear behaviour can be retrieved in terms of capacity curve, since the links progressively yield. Although more complex constitutive behaviours can be adopted for the considered model (as already made in Cannizzaro and Lourenço (2017); Chácara et al. 2018)), here the simplest constitutive laws have been assumed in accordance with the adopted standards (NTC 2018). According to such standards the simplified constitutive laws should be able to roughly retrieve the results obtained with advanced tools (see for example the adoption of a reduced compressive strength, 0.85*fm, to account for the softening branch of the compressive behaviour of masonry). To this purpose, relating a simplified model fully consistent with the code prescriptions (model A) with more advanced tools based on nonlinear FE strategies (models B and C), is one of the goals of this study.
One of the main advantages of this approach is the limited needed computational effort with respect to nonlinear FE approaches (each element possesses four degrees of freedom and can simulate the nonlinear behaviour of an entire masonry panel). For the latter reason, it can be still considered a simplified approach; however, its spatiality allows overcoming some drawbacks common to other simplified approaches. Precisely, each element can interact along all the four edges with other elements or with a contouring frame for modelling mixed reinforced concrete- (or steel-) masonry structures (Caliò et al. 2008). In addition, it allows a geometry modelling consistent with the actual geometry of a wall, even in presence of irregular openings and does not need the introduction of any rigid zone. Finally, the occurrence of combined failure mechanisms can be caught and the extension to the three-dimensional behaviour, also in presence of curved geometry (Caddemi et al. 2014; 2015), was achieved by introducing three additional out-of-plane degrees of freedom and conveniently extending the calibration procedures.
In this paper, the plane model is employed, i.e. no out-of-plane stiffness or resistance of the walls is accounted for, considering the interaction between the masonry panels and the ring beams. The slabs are rigid diaphragms, and a perfect vertical constraint is introduced between orthogonal walls. The mechanical properties adopted in the numerical simulations are fully consistent with those reported in Table 2. For sake of completeness the set of adopted mechanical parameters is reported in Table 3 with reference to the three possible in-plane failure mechanisms of a masonry panel and adopting a specific weight equal to w = 17.5 kN/m3. Regarding the flexural behaviour, the tensile strength ft is assumed equal to the mortar strength ftm, see Table 2, and unlimited tensile and compressive ductility is hypothesised; the ultimate diagonal shear drift γu is set equal to 0.4%. The material is considered isotropic and the sliding mechanism is inhibited. A sensitivity analysis to investigate the role of the shear strength τo and relate it to the mechanical parameters adopted by the other models is reported in Sect. 4.2.
As a final remark, all the checks relative to the ultimate flexural drift as well as that of the base shear reduction, which are commonly specified by the codes, are disabled to perform the numerical simulations. With regard to the reinforced concrete ring beams, a lumped plasticity approach is used, evaluating the plastic hinge properties according to the geometric and mechanical data reported in Table 2.
3.2 Model B
Model B uses the d+ d− tension/compression damage model based on the continuous model put forward by (Cervera et al. 1995), (Faria et al. 1998), (Wu et al. 2006), and further refined by (Petracca et al. 2017a, 2017b, 2016) to correctly reproduce the nonlinear shear response of masonry walls and to control the effect of dilatancy.
The advantage of micromodelling is obtaining a different response from the masonry wall in tension and compression, and at the same time, being able to describe unilateral effect crack closure correctly.
The bi-dissipative damage model defines the effective stress tensor, σeff:
where σeff is the effective stress tensor, \({\overline{\sigma }}^{ + }\) and \({\overline{\sigma }}^{ - }\) are the positive and negative parts of the effective stress tensor σeff (elastic part), d+ and d− are, respectively, the tension and compression damage indices and they influence the positive and negative parts of the effective stress tensor σeff (inelastic part). The compressive and tensile damage thresholds are calculated as:
Once the damage thresholds have been assessed, damage indices d+ e d− can be evaluated by means of two equivalent uniaxial laws where the degrading section is governed by the values assumed by the compressive Gc and tensile Gt fracture energies (Fig. 4).
The mechanical properties for masonry compression strength fm brick tensile strength ftb and mortar tensile strength ftm used in the simulations are shown in Table 2; tensile fracture energy Gt and compression fracture energy Gc were obtained with numerical calibration.
The mortar elastic modulus was evaluated as follows (Lourenço et al. 1998b):
where Em is the adjusted elastic modulus of the mortar, Eb is the elastic modulus of the brick, E is the elastic modulus of the masonry, hm is the joint thickness and hb is the heigh of the brick.
Table 4 shows the parameters adopted for the study case.
With the aforementioned parameters, the evaluated Young’s modulus of the mortar is about 346 MPa.
Table 5 shows the mechanical properties, tensile fracture energy Gt and compression fracture energy Gc used for the bricks and mortar. The fracture energies were calibrated using experimental data. Precisely, the numerical capacity and ductility were calibrated with experimental data available on masonry piers and spandrels by changing the unknown parameters such as fracture energies and residual strength, as also done in D’Altri et al. (2021).
3.3 Model C
Within this modelling framework, masonry nonlinear behaviour is supposed through a homogeneous isotropic plastic-damaging 3D continuum. Such plastic-damage model, firstly developed by Lee and Fenves (Lee and Fenves 1998), hypothesizes independent tensile and compressive behaviours ruled by tensile damage (0 ≤ dt < 1) and compressive damage (0 ≤ dc < 1) variables. Thus, the uniaxial stress–strain curves can be described by:
where σt is the uniaxial tensile stress, σc is the uniaxial compressive stress, E is masonry Young’s modulus, εt and εc are the uniaxial tensile and compressive strains, respectively, and εtp and εcp are the uniaxial tensile and compressive plastic strains, respectively (Fig. 5). Consequently, the uniaxial stress–strain curves shown in Fig. 5 represent the main input for the model mechanical characterization. Although the model was originally proposed for concrete like material, here it is adapted for masonry; despite the model is based on the assumption of isotropic mechanical behaviour, by properly tuning the model parameters it is possible to deal with the description of consistent (reliable) masonry global failure modes for simple or complex geometry. The masonry mechanical properties for Model C used in this study are collected in Table 6. Material parameter are set owing to the calibration done for the benchmark panel: setting the shear moduli and Poisson’s ratio to compute the Young’s moduli for the stiffness calibration; tuning the uniaxial tensile behaviour to better fit target analytical strength domains, see (D’Altri et al. 2021) for further details.
In order to manage dilatancy in the material behaviour and to govern the plastic strain rate, a nonassociative flow rule is supposed through a Drucker-Prager type plastic potential. Such potential is described by the angle of dilatancy ψ, supposed equal to 10° according to Mirmiran and Shahawy (1997), and a smoothing constant ϵ supposed equal to 0.1 according to (Milani et al. (2017); D'Altri et al. (2019b)). A multiple-hardening Drucker-Prager type surface is supposed as yield surface, described by fb0 / fc0, i.e. the ratio between the biaxial fb0 and uniaxial fc0 compressive strengths herein supposed fb0 / fc0 = 1.16 (Lubliner et al. 1989), and a shape parameter ρ which represents the ratio of the second stress invariant on the tensile meridian to that on the compressive meridian at primary yield, herein supposed ρ = 2/3 (Lubliner et al. 1989).
Within this study, the 3D continuum which represents masonry is discretized by means of 4-nodes tetrahedral linear FEs, with representative size 0.4 m. In case of presence of reinforced concrete floor beams, the same type of FEs is used to account for these beams (so obtaining a conforming mesh), and linear elastic behaviour is supposed for floor beams. In order to run pushover analyses and to account for possible global softening behaviour, a quasi-static direct-integration implicit dynamic algorithm has been utilized (D'Altri et al. 2019b). Accordingly, this algorithm allows the simulation of quasi-static behaviours, in which inertia is only introduced to regularize unstable responses.
3.4 Model D
The adopted method, first presented in Chiozzi et al. (2017), is based on a kinematic limit analysis applied to a model composed of very few rigid elements in which the initial discretization is iteratively adjusted to minimize the kinematic load multiplier. A masonry building is initially represented through a reduced number of 2D rectangular NURBS (Non-Uniform Rational Bezier Spline) plate elements. Macro-blocks are derived by assigning a thickness value to each plate element. Each one is considered as an infinitely rigid and infinitely resistant body, hence no elastic parameters are required and its kinematics is described in terms of the three degrees of freedom of the centroid. The internal dissipation is allowed only on the common boundaries between adjacent blocks, where interface elements are defined. Therefore, interfaces represent possible fracture lines. The amount of internal dissipation is computed by defining a 3D limit domain and assuming a rigid-plastic behavior. The limit domain is defined in terms of tensile strength (ft = ftm), compression strength (fc = fm), cohesion (τ0), and friction angle (φ = arctan(μ)) and represents a Mohr–Coulomb criterion with tension cut-off and linear cap in compression (see Fig. 6). In the model of the two-storeys masonry building the values reported in Table 2 have been maintained, i.e. tensile strength of 0.04 MPa, compression strength 6.2 MPa, shear resistance in absence of normal stress equal to 0.163 MPa, tangent of the friction angle 0.58, in addition to the specific weight equal to 17.5 kN/m3. For sake of simplicity, and to maintain a comparison with other models, an isotropic behavior has been considered. However, an orthotropic behavior could be taken into account by defining the 3D limit domain as a function of the inclination angle of the interface (a similar simplified procedure was followed in Tiberti et al. (2020)).
By applying a standard kinematic limit analysis procedure, which can be summarized into a linear programming (LP) problem, a load multiplier and a mechanism are derived. This mechanism is defined in terms of a discontinuous velocity field, where velocity jumps occur at the interfaces according to an associative flow rule.
where \(\lambda\) is the load multiplier, \({\dot{\mathbf{u}}}\) represents the discontinuous velocity field, \({\dot{\mathbf{\lambda }}}\) are the non-negative plastic multipliers at interfaces, \({\mathbf{c}}\) is the vector representing the amount of internal dissipation, \({\mathbf{f}}_{d}\) and \({\mathbf{f}}_{L}\) are respectively the vectors of dead- (permanent) and live-loads, and finally \({\mathbf{A}}\) and \({\mathbf{B}}\) are the matrices for the imposition of the compatibility constraints (i.e. the associative flow rule).
It is worth noting that, within this kinematic approach, it is easy to impose constraints aimed to avoid velocity jumps (i.e. the opening of cracks from a physical point of view) in some parts of the structure. In this model, cracks have been forced to remain closed in correspondence of the concrete edgings to reproduce the condition of rigid edgings, avoid local failures (such as the overturning of a single wall), and guarantee the box behavior.
The presented LP problem allows to obtain a mechanism which takes place starting from the interfaces of the initial mesh. However, the use of a very low number of blocks makes this result highly mesh-dependent, with the consequence to represent incorrect collapse mechanisms related to kinematic load multiplier far higher than the real collapse multiplier. Therefore, a mesh adaptation procedure is applied. The initial mesh is iteratively adjusted by modifying the elements’ shape until interfaces coincide with the real fracture lines. With this aim, a meta-heuristic approach based on a Genetic Algorithm (Haupt and Haupt 1998) (GA) is adopted. Mesh modifications are even facilitated in models realized through the NURBS geometry, in which subdividing of moving operations can be conducted in easy way. The collapse load multiplier and the collapse mechanism are so identified. Some recent works related to this method can be found in (Tiberti et al. 2020; Grillanda et al. 2019,2020).
Finally, it has to be pointed out that the obtained mechanism is always affected by the dilatancy effects deriving from the associative behavior in shear. When shear failures occur, velocity jumps are observed along both the tangential and the normal direction according to the associative flow rule. The dilatancy angle implicitly considered is equal to the friction angle. To avoid dilatancy effects and obtain pure-sliding failures in shear, a non-associative behavior can be reproduced. This requires the conversion of Eq. 8 into a Sequential Linear Programming in which, at each iteration, the limit domain on each point is modified into a fictitious domain with constant shear resistance increased according to the Mohr–Coulomb frictional law. For a detailed dissertation about this numerical strategy, we refer to Grillanda et al. (2021). In order to better compare the limit analysis result with those provided through the other methods, a non-associative behavior with zero-dilatancy has been assigned to the present model.
4 Results
This section reports the results of the numerical simulations conducted on the different configurations adopting the models described in the previous Sect. 3. The summary of the analyzed configurations with the adopted models is reported in Table 7.
After a critical comparison of the obtained results reported in Sect. 4.1, a sensitivity analysis with respect to the shear strength to be adopted with software A is reported in Sect. 4.2, aiming at justifying and interpreting some of the discrepancies observed among the models with the adoption of the reference values of the mechanical parameters; then, the influence of the way to apply the horizontal forces is further investigated in subsection 4.3, namely comparing the results of the nonlinear analyses when the horizontal loads are applied at the floor levels only or along the whole height of the building. The latter aspect was investigated considering the software packages C and D. For the reference results reported in Sect. 4.1 the load assignment with the latter software environments is considered as concentrated at the floor levels.
A cross check among the models consisted in the total mass of the structure, which was evaluated for the configurations without and with ring beams in 100.28 t and 102.09 t, respectively.
4.1 Comparisons of the results obtained with the different software packages
This section reports the results of the nonlinear static analyses. For each of the analysed configurations, in Figs. 7, 8, 9, 10, 11, the capacity curves and the damage patterns of the employed software packages are reported. No cracked state, that considers a reduction of the elasticity moduli, is accounted for in the numerical simulations, since all the structural models (except model D which is employed in the field of limit analysis) consider a progressive damage and stiffness degradation. The pushover curves are reported in terms of base shear vs horizontal displacement of the centre of gravity of the top floor.
For a better interpretation of the damage pattern, it should be considered that each software has different representations. Software A reports damage indicators at the panel scale, namely red and yellow lines along the edges of the panel, which are associated with tensile and compressive yielding, respectively, whereas the ‘X’ in the centre of the panel indicates the achieving of the yielding of the diagonal links (or their rupture if the ‘X’ is inscribed in a square). Software B and C report a colour map as a function of a damage parameter ranging from 0 to 1, whereas software D represents the collapse mechanism with a decomposition of the structure in blocks.
In the case of configurations BS4_P1/B (Fig. 7), BS4_P1/C (Fig. 8) and BS4_P2/B (Fig. 9) only the first two software packages were employed. The collapse mechanism mainly involves in all these configurations the crisis of both piers and spandrels, mainly at the first level and partially at the second one. The presence of the ring beams tends to preserve the spandrels from damaging and to concentrate the failure at the piers, which is confirmed by both the modelling approaches. Regarding the failure mode, both models show the occurrence of diagonal shear cracking in the spandrels, whereas some differences are encountered in the damage patterns of the piers. Specifically, software A exhibits rocking at the first level; on the other hand, software B mainly shows combined failure modes for all the piers at the base level. When the damage involves the piers at the second level the damage pattern is always of rocking type for both software.
The two approaches lead to different results in terms of global resistance and damage pattern (particularly for the piers of the first level); on the other hand, very close initial stiffnesses are observed for all the three configurations. Therefore, it can be stated that the contribution of the out-of-plane stiffness does not play a crucial role in the initial response of the structure. In terms of post-peak behaviour, software B shows a gradual decrease of the strength, whereas software A has different behaviours according to the encountered failure mode, namely a gradual loss of resistance for configuration BS4_P1/B associated to the achieving of the ultimate shear drift in the spandrels, no decrease for configuration BS4_P1/C where the failure mode is of rocking type and no check is activated to limit the flexural rotation of the panels, and with a sudden large loss of resistance for configuration BS4_P2/B due to the achieving of the ultimate shear drift in the pier at the first level of the rear longitudinal wall (which is followed by the complete loss of the carried load).
The results obtained for configuration BS4_P2/C, Fig. 10, for which software C is also employed, confirm that the presence of ring beams increases the resistance of the building with respect to configuration BS4/P2_B (as also for configuration BS4_P1/C with respect to BS4_P1/B). In terms of initial stiffness, the three models provide a similar outcome. In terms of resistance, software A and C provide similar peak loads, whereas software B shows a lower peak load, which can find a justification in the role of the shear strength as better shown in Sect. 4.2. The two FE models agree in terms of smoothed loss of resistance in the post-peak phase, in contrast with the sudden loss of strength associated to the diagonal behaviour of the model employed in software A.
In the same graph a grey band, corresponding to the envelope of the results obtained in Manzini et al. (2020) with EF models for the same configuration of the building, is reported; although the peak resistance scatter embeds the corresponding values obtained with software A and B, a major discrepancy with respect to the models employed in the present study is encountered in terms of initial stiffness. It is worth noting that the initial stiffness, as also explained in Castellazzi et al. (2021), are set according to a conventional degradation in the case of EF models (assuming a coefficient of reduction of the elastic stiffness equal to 0.5), and considering a progressive degradation associated to the evolution of damage for all the models adopted in this study. Therefore, the difference in terms of initial stiffness can be justified with the different assumptions in terms of elastic mechanical properties and are consistent with the results obtained at the real building scale in Castellazzi et al. (2021). In addition, the EF models show a higher scatter in terms of initial stiffness with respect to the models here employed, for which the discrepancy is basically negligible.
In terms of collapse mechanism, the damage mainly involves the piers at the first floor with combined rocking-diagonal shear mode for all the three models; in addition, the two FE models (software B and C) show a slight involvement of the spandrels at the second level. The opening of a plastic hinge in the ring beam of the front longitudinal wall is observed with software A.
In the case of configuration BS4_P2/D, Fig. 11, where the rotations at the floor levels are blocked (“shear-type” hypothesis), the results obtained with software A and limit analysis (software D) are compared. The resistance in the two cases is quite similar (482.6 kN vs 547.5 kN) and, as expected, software D shows a higher resistance than software A since the resistance of all the elements involved in the collapse mechanism is activated at the same time. A major agreement of the two approaches is encountered in terms of failure mode, being involved in both cases the masonry piers at the first elevation with combined rocking-diagonal shear mechanisms.
4.2 Calibration of the shear strength adopted in the macro-modelling strategy
The role of the shear strength is investigated in this section through a sensitivity analysis conducted with software A. The diagonal shear behaviour is governed by independent parameters according to the considered modelling strategy. In particular, for the discrete macro-model adopted by software A, which requires the adoption of a shear strength τo (the yielding dominium type and the ultimate drift), and for the FE model employed in software C, requiring an equivalent tensile strength (and a corresponding fracture energy), a uniaxial constitutive law is enough to completely characterize the diagonal shear behaviour of the masonry. On the other hand, such a behaviour is the outcome of a set of parameters and constitutive laws for the detailed modelling approach implemented in software B, as better specified in Sect. 2. The reference parameters adopted to perform the numerical simulations in Sect.4.1 can therefore lead to apparent mismatching results (in terms of global resistance and failure mechanism) if the adopted mechanical parameters are not correlated to each other. In addition, all the models but model B (for which an orthotropic behaviour is retrieved through the meso-scale texture) are characterized by an isotropic behaviour, which has been shown to have limits in the simulation of the diagonal shear behaviour (Casolo et al. 2019). With regard to the diagonal shear behaviour, there are still open issues related to the post-peak behaviour. One of the aspects is related to the constant ultimate shear drift usually adopted by the codes (NTC 2018) (typically 0.4%), irrespectively of the acting confinement action, which is in contrast with the experimental tests (Morandi et al. 2018) and advanced numerical simulations (D’Altri et al. 2021).
To provide a justification of the obtained results, a sensitivity analysis with respect to the shear strength τo, was performed with software A. Five values of shear strength are considered in addition to the reference one τo = 0.163 MPa, namely 0.04; 0.06; 0.085; 0.11; 0.135 MPa (being 0.04 equal to the tensile strength of the mortar ftm). The results in terms of capacity curves and damage pattern of the front longitudinal wall, are summarized in the following Figs. 12, 13, 14, 15, 16.
Regarding the global resistance it can be noticed that, as expected, as the shear strength reduces, the global resistance diminishes. The best match with the micro-modelling approach of software B is encountered in correspondence of a shear strength τo equal to 0.085 MPa in the configurations for which the comparison was possible, Figs. 12, 13, 14, 15.
As a further confirm of the crucial role played by the shear strength, the failure mechanisms obtained by software A and B tend to get more similar to each other. As the shear strength of the panels diminishes, the damage pattern of the piers at the first level (in particular the central one) tends to shift to a combined rocking-diagonal shear failure mode, Figs. 13, 14, 15, which is consistent with the collapse mode obtained with software B.
In Figs. 12b, 14b it can be noticed how the reduction of the shear strength changes the collapse mechanism at the second level from the rocking of the piers towards the diagonal shear failure of the spandrels. Similar considerations can be made for all the analysed cases. Although not investigating the mechanical parameters governing the post-peak behaviour, the latter aspect plays a role in the failure mechanisms obtained with model A; precisely, the adoption of a fixed ultimate shear drift γu = 0.4% for the diagonal shear behaviour leads to comparable levels of the global ductility, even considering different values of the shear strength, when the collapse mechanism is of shear diagonal type (both in the case of piers of spandrels). The latter aspect is clear in Fig. 12 where a drop in the global resistance is observed at around 10 mm for values of the shear strength τo equal to 0.04, 0.06, 0.085, 0.11 and 0.135 MPa, whereas in the case of τo = 0.163 MPa, the damage evolution is partially shifted towards the rocking failure, thus delaying the occurrence of diagonal shear collapse mode.
The obtained results are due to the independency of the shear strength τo from the set of parameters (lb/hb, ftb, fvo, μ, ftm) that characterize the diagonal shear behaviour in software B. Specific calibration processes of the micro-modelling strategy, as that adopted in D’Altri et al. (2021) at the panel scale, could be employed at the scale of buildings to obtain an improved match of the results.
The same considerations hold also for configuration BS4_P2/D, for which the shear strength directly influences the global resistance of the building, thus demonstrating the predominating role of the diagonal shear behaviour in the nonlinear response of this benchmark structure.
4.3 Assessment of different load assignment modes
The application of loads follows, in general, conventional assumptions about the load pattern geometry (first mode triangular shape, uniform proportional to mass locations) and to its summarized reduction within the modelling definitions. In order to evaluate the effect of different load assignment modes, two different investigations are performed considering model C and D.
In the case of model C a parametric study based upon the wall thickness variation by considering the application of load to floor level (concentrated) or by distributing the application over nodes (distributed) is proposed. To push the comparison, for the proposed benchmark we consider a wide range of wall dimensions: thickness of 10, 25, 40 and 70 cm are considered. Results are provided in Fig. 17 in terms of pushover curves for uniform and triangular load patterns, respectively. Loads are computed proportionally to dead load, and base shear increases according to the thickness variation, then, in order to provide information about the thickness influence we track the difference between the pushover curve obtained for concentrated and distributed load respectively. For lower thickness the difference between the two load assignment modes is negligible, while, for increasing values of thickness an increasing gap between base shear values is evident. This increasing gap is more pronounced for uniform than for triangular load path application.
This aspect is also highlighted in Table 8, which shows the percentage variations of the maximum base shear in the two cases considered, which reach the maximum (27.5%) in the case of a "uniform" distribution applied to the thickness 70 cm.
However, it can be observed that when the method of applying the horizontal load to the structure varies, the crack pattern does not vary significantly, as shown in Table 9.
The analysis of the two-storeys masonry building through adaptive NURBS limit analysis (model D) is also presented. The NURBS model is composed of two surfaces for each perimeter wall (one per storey). Additional surfaces have been inserted to model the concrete edgings. In particular, an equivalent specific weight has been assigned to the longitudinal edgings to take into account the load given by the supported floors.
A horizontal load has been applied along the longitudinal direction. Similarly to the previous cases, two horizontal load conditions have been considered, the first one constituted by pointed loads applied at the floor levels and the second one with a distributed load proportional to masses.
The initial mesh was defined by subdividing the two longitudinal and the two transversal walls respectively into 3 × 4 and 3 × 1 rectangular elements. The surfaces assigned to the longitudinal edgings have been subdivided into 4 × 1 elements to maintain the correspondence between elements’ vertices. However, as previously mentioned, velocity jumps along interfaces between adjacent edging-elements have been imposed null to reproduce the condition of rigid edgings and avoid local failures. This initial mesh can be adjusted through a total of 82 parameters, representing the allowed movements of elements’ vertices. For both the load cases, a population of 80 individuals and a maximum number of 200 generations have been used within the Genetic Algorithm. Results are presented in Fig. 18.
The optimized collapse mechanism and the associated base shear values are shown. The most evident damage is observed at the first storey, where both flexural openings and sliding cracks affected all four perimeter walls. As regards both the base shear and the collapse configurations, a good agreement is observed with the previous numerical methods. Moreover, it can be noted that the first load case, i.e. composed of pointed load at the floor levels, provided a lower base shear value in comparison with the second one. This result confirms the previous considerations in this subsection.
5 Conclusions
This paper analyses one of the benchmark structures proposed within the research task “URM nonlinear modelling—Benchmark project”, part of the wider ReLUIS projects funded by the Italian Department of Civil Protection and conducted starting from 2014 by several teams of Italian Universities. The goal of the work package consists in critical comparisons and cross validation among software tools available for professional engineers and further proposal under investigation in the academic context. The project is focused on the study of simple structures exhibiting recurring and clearly identifiable features, thus providing reference results in terms of seismic assessment and bringing to light common issues in the use of commercial software environments and highlighting the differences in their basic assumptions.
In particular, the case study here analysed is a two-story masonry building with rigid diaphragms, modelled considering different openings disposals and structural details (e.g. accounting for the presence of ring beams or assuming the ‘shear-type’ hypothesis), on which nonlinear static analyses were conducted. Four software packages employing two- and three-dimensional models were used, each of them implementing a specific modelling approach, namely a simplified two-dimensional mechanical-based model, a detailed discontinuous FE model, a continuous FE model, and a new approach based on a limit analysis strategy. The numerical methods under investigation are characterized by very different computational burden and modelling strategies. Namely three models consider a macro-scale discretization and one a detailed nonlinear FE approach. The obtained results exhibit a significant scatter between the meso-scale modelling, that implicitly incorporate the orthotropic nature of the masonry media, and the other isotropic modelling strategies performed at the macro-scale. This aspect needs to be further investigated since most of the modelling strategies currently adopted by practitioners do not take into account this feature. Some software needs the introduction of material data difficult to obtain via in-situ experimental tests (e.g. fracture energy) or require the introduction of a considerable amount of parameters generally not available for practical applications, as in the case of the meso-scale approach.
Aiming at providing a numerical interpretation of the scatter in the overall resistances obtained with the different software packages, a sensitivity analysis with respect to the shear strength is performed, showing that the Discrete Macro-Element and the discontinuous FE model provide similar results in terms of resistance and failure mechanisms once the diagonal shear behaviour is basically equivalent although characterized by different parameters. Such aspects lead to warmly encouraging a careful modelling of the diagonal shear behaviour irrespectively of the adopted numerical model and corresponding software tool adopted. Finally, the way to apply horizontal loads, which is a possible source of uncertainty in the numerical modelling, is investigated; loads concentrated at the floor level and distributed along the whole height of the building consistently with the actual mass distribution are considered, showing that the first option may lead to a significant underestimation of the bearing capacity of the structure.
Data availability
The whole results of the research activity “URM nonlinear modelling—Benchmark project” are collected in a scientific report (in Italian) downloadable from www.reluis.it. In the Annex to Cattari and Magenes 2020 a data sheet reports all the input data necessary to reproduce the structures considered in this paper by third parties. The English version of the document can be found at https://static-content.springer.com/esm/art%3A10.1007%2Fs10518-021-01078-0/MediaObjects/10518_2021_1078_MOESM1_ESM.pdf
References
Caddemi S, Caliò I, Cannizzaro F, Pantò B (2017) New frontiers on seismic modeling of masonry structures. Frontiers in Built Environment 3:39
Caddemi S., Caliò, I., Cannizzaro, F., Pantò, B. The seismic assessment of historical masonry structures (2014) Civil-Comp Proceedings, 106.
Caddemi S, Caliò I, Cannizzaro F, Occhipinti G, Pantò B (2015) A parsimonious discrete model for the seismic assessment of monumental structures. Civil Comp Proceed
Caliò I, Marletta M, Pantò B (2012) A new discrete element model for the evaluation of the seismic behaviour of unreinforced masonry buildings. Eng Struct 40:327–338
Caliò I, Cannizzaro F, D'Amore E, Marletta M, Pantò B (2008) A new discrete-element approach for the assessment of the seismic resistance of composite reinforced concrete-masonry buildings. AIP Conf Proc 1020 (PART 1):832–839
Caliò I, Cannizzaro F, Marletta M, Pantò B (2009). 3DMacro, Il software per le murature (3D computer program for the seismic assessment of masonry buildings), Gruppo Sismica s.r.l., Catania, Italy, Release 3.0, March 2014 (www.3dmacro.it)
Cannizzaro F, Lourenço, PB (2017) Simulation of shake table tests on out-of-plane masonry buildings. part (vi): discrete element approach. Int J Archit Herit 11(1):125–142
Casapulla C, Giresini L, Argiento LU, Maione A (2019) Non-linear static and dynamic analysis of rocking masonry corners using rigid macro-block modelling. Int J Struct Stab Dy 19(11):1950137
Casolo S, Peña F (2007) Rigid element model for in-plane dynamics of masonry walls considering hysteretic behaviour and damage. Earthq Eng Struct Dyn 36:1029–1048
Casolo S, Biolzi L, Carvelli V, Barbieri G (2019) Testing masonry blockwork panels for orthotropic shear strength. Constr Build Mater 214:74–92
Castellazzi G, Pantò B, Occhipinti G, Talledo DA, Berto L, Camata G (2021) A comparative study on a complex URM building part ii: issues on modelling and seismic analysis through continuum and discrete-macroelement. Models Bull Earthquake Eng. https://doi.org/10.1007/s10518-021-01147-4
Cattari S, Magenes G (2021) Benchmarking the software packages to model and assess the seismic response of URM existing buildings through nonlinear analyses. Bull Earthquake Eng. https://doi.org/10.1007/s10518-021-01078-0
Cervera M, Oliver J, Faria R (1995) Seismic evaluation of concrete dams via continuum damage model. Earthq Eng Struct Dyn 24(9):1225–1245
Chácara C, Cannizzaro F, Pantò B, Caliò I, Lourenço PB (2018) Assessment of the dynamic response of unreinforced masonry structures using a macroelement modeling approach. Earthq Eng Struct D 47(12):2426–2446
Chiozzi A, Milani G, Tralli A (2017) A genetic algorithm NURBS-based new approach for fast kinematic limit analysis of masonry vaults. Comput Struct 182:87–204
D’Altri AM, Cannizzaro F, Petracca M, Talledo DA (2021) Nonlinear modelling of the seismic response of masonry structures: calibration strategies. Bull Earthquake Eng. https://doi.org/10.1007/s10518-021-01104-1
D’Altri AM, Messali F, Rots J, Castellazzi G, de Miranda S (2019b) A damaging block-based model for the analysis of the cyclic behaviour of full-scale masonry structures. Eng Fract Mech 209:423–448
D'Altri AM, Sarhosis V, Milani G, Rots J, Cattari S, Lagomarsino S, Sacco E, Tralli A, Castellazzi G, de Miranda S (2019) Chapter 1—A review of numerical models for masonry structures, Editor(s): Bahman Ghiassi, Gabriele Milani, In Woodhead Publishing Series in Civil and Structural Engineering, Numerical Modeling of Masonry and Historical Structures, Woodhead Publishing, Pages 3-53
D’Asdia P, Viskovic A (1995) Analyses of a masonry wall subjected to horizontal actions on its plane, employing a non-linear procedure using changing shape finite elements. Trans Modell Comput Simul 10:519–526
Faria R, Oliver J, Cervera M (1998) A strain-based plastic viscous-damage model for massive concrete structures. Int J Solids Struct 35(14):1533–1558
Gambarotta L, Lagomarsino S (1997) Damage models for the seismic response of brick masonry shear walls. Part II: the continuum model and its applications 2. Earthq Eng Struct Dyn 26(4):441–462
Giresini L (2017) Design strategy for the rocking stability of horizontally restrained masonry walls. COMPDYN 2017 6th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, M. Papadrakakis, M. Fragiadakis (eds.) Rhodes Island, Greece, 15–17 June 2017
Giresini L, Solarino F, Paganelli O, Oliveira DV, Froli M (2019) One-Sided rocking analysis of corner mechanisms in masonry structures: Influence of geometry, energy dissipation, boundary conditions. Soil Dyn Earthq Eng 123:357–370
Grillanda N, Valente M, Milani G (2020) ANUB-Aggregates: a fully automatic NURBS-based software for advanced local failure analyses of historical masonry aggregates. B Earthq Eng 18:3935–3961
Grillanda N, Chiozzi A, Milani G, Tralli A (2019) Collapse behavior of masonry domes under seismic loads: an adaptive NURBS kinematic limit analysis approach. Eng Struct 200:109517
Grillanda N, Chiozzi A, Milani G, Tralli A (2021) Tilting plane tests for the ultimate shear capacity evaluation for dry joint masonry panels. Part II: Numerical analyses. Eng Struct 228:111460
Haupt RL, Haupt SE (1998) Practical Genetic Algorithms. John Wiley & Sons, New York
Kappos AJ, Penelis GG, Drakopoulos CG (2002) Evaluation of simplified models for lateral load analysis of unreinforced masonry buildings. J Struct Eng 128:890–897
Lee J, Fenves GL (1998) Plastic-damage model for cyclic loading of concrete structures. J Eng Mech 124(8):892–900
Lourenço PB (2002) Computations on historic masonry structures. Prog Struct Eng Mat 4(3):301–319
Lourenço PB, Rots JG (1997a) Multisurface interface model for analysis of masonry structures. J Eng Mech 123(7):660–668
Lourenço PB, Rots JG (1997b) A multi-surface interface model for the analysis of masonry structures. J Struct Eng ASCE 123(7):660–668
Lourenço PB, de Borst R, Rots JG (1997) A plane stress softening plasticity model for orthotropic materials. Int J Num Meth Eng 40:4033–4057
Lourenço PB, Rots JG, Blaauwendraad J (1998a) Continuum model for masonry: parameter estimation and validation. J Struct Eng 124(6):642–652
Lourenço PB, Rots JG, Blaauwendraad J (1998b) Continuum model for masonry: parameter estimation and validation. J Struct Eng ASCE 124(6):642–652
Lubliner J, Oliver J, Oller S, Onate E (1989) A plastic-damage model for concrete. Int J Solids Struct 25(3):299–326
Macorini L, Izzuddin BA (2011) A non-linear interface element for 3D mesoscale analysis of brick-masonry structures. Int J Numer Meth Eng 85:1584–1608
Magenes G, Della Fontana A (1998) Simplified non-linear seismic analysis of masonry buildings. Proc British Masonry Society 8:190–195
Manzini CF, Ottonelli D, Degli Abbati S et al. (2021) Modelling the seismic response of a 2-storey URM benchmark case study: comparison among different equivalent frame models. Bull Earthquake Eng. https://doi.org/10.1007/s10518-021-01173-2
Marques R, Lourenço PB (2011) Possibilities and comparison of structural component models for the seismic assessment of modern unreinforced masonry buildings. Comput Struct 89:2079–2091
Mazzoni S, McKenna F, Scott MH, Fenves GL (2006) OpenSees command language manual. Pacific Earthquake Engineering Research (PEER) Center 264
Milani G, Lourenço PB, Tralli A (2006) Homogenization approach for the limit analysis of out-of-plane loaded masonry walls. J Struct Eng 132(10):1650–1663
Milani G, Valente M, Alessandri C (2017) The narthex of the church of the nativity in Bethlehem: a non-linear finite element approach to predict the structural damage. Comput Struct 207:3–18
Mirmiran A, Shahawy M (1997) Dilation characteristics of confined concrete. Mech Cohes-Frict Mat 2(3):237–249
Morandi P, Albanesi L, Graziotti F, Li Piani T, Penna A, Magenes G (2018) Development of a dataset on the in-plane experimental response of URM piers with bricks and blocks. Constr Build Mater 190:593–611
NTC (2018) Italian Technical Code, Decreto Ministeriale 17/1/2018. Aggiornamento delle Norme tecniche per le costruzioni. Ministry of Infrastructures and Transportation, G.U. n.42 of 20/2/2018 (in Italian)
Ottonelli D, Cattari S, Marano C, Manzini CF, Calderoni B (2021) A comparative study on a complex URM building: sensitivity of the seismic response to different modelling options in the equivalent frame models. Bull Earthquake Eng. https://doi.org/10.1007/s10518-021-01128-7
Page AW (1978) Finite element model for masonry. ASCE J Struct Div 104:1267–1285
Pantò B, Cannizzaro F, Caliò I, Lourenço PB (2017) Numerical and experimental validation of a 3D macro-model for the in-plane and out-of-plane behaviour of unreinforced masonry walls. Int J Archit Herit 11(7):946–964
Pegon P, Anthoine A (1997) Numerical strategies for solving continuum damage problems with softening: application to the homogenization of Masonry. Comput Struct 64(1–4):623–642
Penna A, Lagomarsino S, Galasco A (2014) A nonlinear macroelement model for the seismic analysis of masonry buildings. Earthq Eng Struct Dyn 43:159–179
Petracca M, Pelà L, Rossi R, Oller S, Camata G, Spacone E (2016) Regularization of first order computational homogenization for multiscale analysis of masonry structures. Computat Mech 57(2):257–276
Petracca M, Pelà L, Rossi R, Zaghi S, Camata G, Spacone E (2017a) Micro-scale continuous and discrete numerical models for nonlinear analysis of masonry shear walls. Constr Build Mater 149:296–314
Petracca M, Pelà L, Rossi R, Oller S, Camata G, Spacone E (2017b) Multiscale computational first order homogenization of thick shells for the analysis of out-of-plane loaded masonry walls. Comput Method App M 315:273–301
Quagliarini E, Maracchini G, Clementi F (2017) Uses and limits of the equivalent frame model on existing unreinforced masonry buildings for assessing their seismic risk: a review. J Build Eng 10:166–182
Smith M (2009) ABAQUS/Standard User's Manual, Version 6.9. Dassault Systèmes Simulia Corp, Providence, RI
Smoljanović H, Nikolić Ž, Živaljić N (2015) A combined finite-discrete numerical model for analysis of masonry structures. Eng Fract Mech 136:1–14
Tiberti S, Grillanda N, Milani G, Mallardo V (2020) A genetic algorithm adaptive homogeneous approach for evaluating settlement-induced cracks in masonry walls. Eng Struct 221: 111073
Turnsek V, Cacovic F (1971) Some experimental result on the strength of brick masonry walls. 2nd International Brick Masonry Conference. UK: Stoke-on-Trent
Wu J, Li J, Faria R (2006) An energy release rate-based plastic-damage model for concrete. Int J Solids Struct 43(3):583–612
Acknowledgements
The authors acknowledge the financial contribution to the research provided by the Italian Network of Seismic Laboratories (RELUIS), in the frame of the 2014-2017 RELUIS III Project (Topic: Masonry Structures; Coord. Proff. Sergio Lagomarsino, Guido Magenes, Claudio Modena). Moreover, the authors acknowledge the whole research group that participated to this activity from 2014 to 2016: UNIGE-c (Coord. S. Cattari); UNIPV (Coord. Prof. G. Magenes); UNI-CH: (Coord. Proff. E. Spacone and G. Camata); UNICT-a: (Coord. Prof. I. Caliò); UNINA-b/d (Coord. Proff. B. Calderoni and A. De Luca); UNINA-c (Coord. Proff. C. Casapulla and F. Portioli); UNIRM3 (Coord. Prof. G. De Felice).
Funding
Open access funding provided by Università degli Studi di Catania within the CRUI-CARE Agreement. The research activity “URM nonlinear modelling—Benchmark project”, whose results are partly presented in this paper, did not receive any grant from funding agencies in the public, commercial or not-for-profit sectors that may gain or lose financially through publication of this work.
Author information
Authors and Affiliations
Contributions
All authors contributed to the modelling and the analysis of the considered benchmark case study. The comparison of the numerical results and the first draft of the manuscript were handled by Francesco Cannizzaro. All authors participated in the review of the document and read and approved the final manuscript.
Corresponding author
Ethics declarations
Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cannizzaro, F., Castellazzi, G., Grillanda, N. et al. Modelling the nonlinear static response of a 2-storey URM benchmark case study: comparison among different modelling strategies using two- and three-dimensional elements. Bull Earthquake Eng 20, 2085–2114 (2022). https://doi.org/10.1007/s10518-021-01183-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10518-021-01183-0