Abstract
All around the world, non-engineered masonry constructions (NECs) typically have high vulnerability to seismic ground motion, resulting in heavy damage and severe casualties after earthquakes. Even though a number of computational strategies have been developed for seismic analysis of unreinforced masonry structures, a few studies have focussed on NECs located in developing countries. In this paper, different modelling options for finite element analysis of non-engineered masonry buildings are investigated. The goal of the study was to identify the modelling option with the best trade-off between computational burden and accuracy of results, in view of seismic risk assessment of NECs at regional scale. Based on the experimental behaviour of a single-storey structure representative of Indian non-engineered masonry buildings, the output of seismic response analysis of refined 3D models in ANSYS was compared to that of a simplified model based on 2D, nonlinear, layered shell elements in SAP2000. The numerical-experimental comparison was carried out under incremental static lateral loading, whereas nonlinear time history analysis was performed to investigate the dynamic performance of the case-study structure. Analysis results show that the simplified model can be a computationally efficient modelling option for both nonlinear static and dynamic analyses, particularly in case of force-based approaches for design and assessment of base isolation systems aimed at the large-scale seismic vulnerability mitigation of NECs.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Despite the developments in structural engineering and construction industry, a large number of non-engineered constructions (NECs) still exists in many parts of the world. These buildings are mostly constructed with locally available materials such as stones, bricks or adobe, including monuments and heritage buildings in high-seismicity regions. Examples of NECs are load-bearing masonry wall buildings, stud-wall and brick-nogged timber constructions, and composite constructions consisting of load-bearing masonry columns/walls in combination with tie-columns and tie-beams made of reinforced concrete (RC), steel or wood. These buildings are constructed based on the experience and traditional knowledge of local masons without any intervention by qualified architects and engineers, resulting in high vulnerability to earthquakes. This is due to the low strength of materials, poor structural detailing and lack of seismic design, thus demanding higher levels of seismic protection (see e.g.: Arya et al. 2014; Feng et al. 2011; Boen 2006; Naseer et al. 2010; So and Spence 2013; Wu et al. 2013). Nonetheless, people in many developing countries still prefer living in such constructions due to their low cost, ease of construction, and cultural connections to local traditions.
In addition to residential buildings, non-engineered masonry structures found across the world also include historical constructions such as palaces, churches, bell towers, and temples, as well as industrial structures such as chimneys (Valente and Milani 2019; Minghini et al. 2014; Formisano et al. 2018). Since these structures are highly prone to seismic damage, over the years, several earthquakes caused the destruction of historical heritage constructions (Parisi and Augenti 2013a). Thus, seismic assessment of non-engineered masonry structures as attempted in the present study can help to reduce vulnerability of historical heritage. Since the aim of the present study is mainly focussed on the reduction of seismic risk connected to non-engineered dwelling units, a simple box-type URM building from rural areas of developing nations is selected as prototype.
Unreinforced masonry (URM) buildings are one of the most recurrent types of NECs where masonry units often consist of either burnt clay bricks or concrete blocks, which are usually connected to each other with mud/lime/cement sand mortar (Arya 2000; Chaudhary 2014; IS1905 1987, 1993). The roof or floor of such buildings are commonly constructed using RC, timber or steel joist metal deck with concrete topping and precast concrete planks. Such a structural system is mostly observed in both historic and modern constructions located in developing countries (Chaudhary 2014). Based on damage observations after recent earthquakes, these buildings tend to develop deep cracks due to excessive tensile/shear stresses and undergo significant damage or even collapse under moderate earthquakes (Arya et al. 2014). Thus, a deeper understanding of their structural behaviour is necessary to reduce seismic vulnerability (Coburn and Spence 2003). In order to run nonlinear dynamic analysis and develop fragility curves for a large class of buildings, an efficiently accurate numerical modelling strategy must be developed, as done in the literature for more general mechanical systems (see e.g.: Vaiana et al. 2019,2021).
In this respect, the orthotropic and softening behaviour of masonry, together with its low tensile strength and non-associated friction properties, would require refined finite element (FE) models with huge computational demand and need for experienced users. Other numerical strategies such as the applied element method (AEM) are becoming attractive alternative solutions for NECs compared to FEM, allowing realistic simulations that account for the discrete nature of masonry in this type of masonry structures. According to Adhikari and D’Ayala (2020), the use of 3D applied elements can provide an accurate prediction of both stiffness degradation and ductility for stone in mud mortar masonry buildings located in Nepal, allowing the random shape of stone units to be considered in the modelling procedure. AEM solutions also include the simulation of masonry fragmentation and out-of-plane collapse mechanisms, which often occur in NECs (e.g. in building corners). More specifically, the use of triangular meshing and clustering to generate irregular elements that simulate the random shape of rubble stone units was found to be an appropriate strategy to account for the randomness of the units in those masonry fabrics. AEM was also recently used to assess the seismic fragility of existing non-engineered confined masonry school buildings located in India (Parammal Vatteri and D’Ayala 2021), ensuring a high degree of accuracy in the prediction of the discrete behaviour of two types of interfaces, i.e. mortar-to-brick and brickwork-to-concrete confining element.
Nevertheless, orthotropic FE modelling of masonry elements and other advanced numerical strategies call for several material parameters that are not always available in the literature. This problem can be overcome through simplified FE models, especially when the aim of the study is more oriented towards the prediction of the overall nonlinear response of the building rather than its detailed local behaviour (Choudhury et al. 2015). The two main FE modelling approaches for masonry structures are referred to as micro-modelling and macro-modelling (Lourenço 1997, 2000; Lourenço and Rots 1997). In micro-models, the bricks and mortar are modelled with distinct material properties and connected to each other using interface/contact elements. This technique is capable of reproducing the exact behaviour of the masonry, but it demands high computational effort (see e.g.: Giambanco et al. 2001; Lourenço et al. 2007; Caporale et al. 2014). In the macro-modelling technique, masonry is modelled as a homogeneous material with equivalent mechanical properties (see e.g.: Rots 1991; Gambarotta and Lagomarsino 1997; Calderini and Lagomarsino 2008; Illampas et al. 2014; Parisi et al. 2019). This technique is more practical due to its memory efficient processing and user-friendly mesh generation (Mahini 2015). The major complication associated with this approach is the identification of equivalent mechanical properties of the masonry. Next to the modelling approaches of masonry structures, the cracks can be represented based on either discrete crack models or smeared crack models. In discrete crack models, the cracks are modelled as displacement discontinuities across the outline of the finite element, imposing restrictions in the crack propagation. In smeared crack models, the displacement discontinuity is spread across the finite element of the continuous model. This helps in obtaining a crack pattern which enables a better understanding on masonry behaviour (Menin et al. 2009).
As far as non-engineered masonry buildings located in developing countries are concerned, a few experimental investigations and some numerical studies have been carried out (see e.g.: Choudhury et al. 2015; Das et al. 2016; Ip et al. 2018). Detailed three-dimensional (3D) analysis of masonry buildings using isoparametric elements in ANSYS (Mahini 2015) and concrete damage plasticity model (Habieb et al. 2018) demonstrated acceptable accuracy in predicting the peak load and lateral deformation of non-engineered masonry buildings. However, such models need calibration of several material properties. Nonlinear time history analyses (NLTHAs) of historical masonry buildings developed using Drucker–Prager model with Willam–Warnke failure criteria in ANSYS effectively simulated the tensile strength of the masonry (Betti et al. 2015; Pauletta et al. 2018). Thuyet et al. (2018) assessed the vulnerability of a base-isolated masonry building that was modelled using nonlinear layered shell elements with isotropic material properties in SAP2000 (Computers and Structures 2020). Even though that study showed a satisfactory computational efficiency of nonlinear layered shell elements, the nonlinear response to cyclic lateral loading has not been investigated so far.
Recent initiatives have been taken in developing countries to promote the construction of affordable houses in earthquake-prone regions and rural areas such as the Earthquake Housing Reconstruction Project (EHRP) by the World Bank in Nepal and “Housing for all” scheme launched by the Indian government (Tiwari and Rao 2016; PMAYMIS 2015). In view of this, comprehensive studies on the global behaviour of NECs are necessary to support their seismic design and retrofit. Since the cost associated with experimental investigation on real-scale NECs would be high, a large number of sufficiently accurate FE analyses would be preliminarily required. In this perspective, the development of FE modelling approaches with a reduced set of parameters and less computational effort can aid in the seismic design of NECs. The target model should be capable of providing accurate results under both nonlinear static and time history analysis. Thus, a comparative assessment between numerical models properly calibrated on experimental data is the prime requirement for the optimization of the analysis.
This study is part of a research project for the application of low-cost seismic isolation systems to NECs. In order to run nonlinear dynamic analysis and develop fragility curves for a large class of buildings, an efficiently accurate numerical modelling strategy must be developed. Recently, Losanno et al. (2020) and Calabrese et al. (2019) demonstrated that fibre reinforced elastomeric isolators (FREIs) could be a convenient option for base isolation of residential buildings in developing countries. FREIs have been extensively investigated under both preliminary characterization and shaking table tests, demonstrating a good performance in comparison with conventional steel reinforced isolators and thus representing a low-cost technology for NECs (Ravichandran 2020).
This paper aims at identifying a set of suitable macro-modelling approaches for seismic assessment of NECs using the commercial packages ANSYS (APDL 2015) and SAP2000 (Computers and Structures 2020). A comparative assessment of five macro-modelling approaches using different finite elements and material models is presented. Three-dimensional macro-models were developed in ANSYS using solid elements and a simplified, two-dimensional (2D) shell element model was developed in SAP2000. FE analysis of a benchmark URM building with available experimental and numerical data (Shahzada et al. 2012; Choudhury et al. 2015) is developed using the proposed models to compare their accuracy and computational burden in case of a real-scale structure. The benchmark structure was developed by Shahzada et al. (2012) considering a typical URM building in the city of Abottabad, Pakistan. After that models on experimental lateral pushover behaviour were calibrated, nonlinear time history analysis under two natural records was performed to predict the seismic response of the selected buildings. The novelty of this study is thus the selection of the best modelling options for seismic assessment of the case-study NECs at territorial scale, as a key information for their potential strengthening or base isolation.
2 Benchmark Masonry Building—Case Study
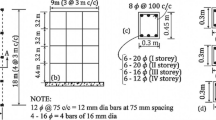
The benchmark structure is a single-story URM building reported by Shahzada et al. (2012) with plan dimensions 4.115 × 3.505 m2, built with 0.228-m-thick walls as shown in Fig. 1. The building is provided with 0.152-m-thick RC lintel beams above the openings to improve the structural capacity under vertical loads. The RC roof slab is 0.152-m-thick, above which parapet walls are provided with 0.343 m thickness and 0.914 m height. In addition, a 0.25-m-thick sand layer was also placed on the roof slab. The base of the building was bolted tightly to the floor during the tests. Experimental studies were carried on the building by applying quasi-static horizontal loading to the wall without opening (out-of-plane East wall) using a load cell up to failure (X direction in Fig. 1). The displacements were measured at the centre of the RC slab on the opposite wall (out-of-plane West wall). The force–displacement curves (pushover curves) and damage patterns were reported. The available material properties of the building from the experimental studies are listed in Table 1.
Details of URM building prototype (Shahzada et al. 2012)
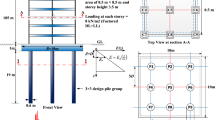
The lateral load was applied to the URM building using a hydraulic jack attached to a strong wall and the roof slab of the URM building, as shown in Fig. 2. During the test, the URM building was subjected to increasing reverse displacement cycles at the roof level, with each displacement cycle repeated three times. The damage to the building observed at the end of the test is shown in Sect. 4.3.
Experimental test set-up of URM building (Shahzada et al. 2012)
Choudhury et al. (2015) carried out numerical studies on the same building using commercial codes such as STRAND 7, ABAQUS and SAP2000. The experimental pushover curve was used for calibrating the proposed numerical models. In STRAND 7, the masonry was modelled by assuming Mohr–Coulomb failure criterion with associated flow rule, which reflects the main features of the masonry. An elastic perfectly-plastic (EPP) material behaviour was adopted despite its inability in reproducing the post-peak softening of masonry. This approach is consistent with code provisions such as those of the Italian building code (NTC 2018), which allows performing EPP modelling (Milani et al. 2009). Friction angle of 30° and cohesion value of 0.15 MPa were assumed. In ABAQUS, concrete damage-plasticity (CDP) material model was used for masonry with 10° dilation angle and 1.16 biaxial to uniaxial compressive strength ratio. This model—which has been widely adopted for masonry in the literature—allows different strength and damage parameters in tension and compression. Smoothed Drucker–Prager failure criterion was used to predict the failure of the masonry. It is agreed that the CDP model is one of the suitable material models for masonry. Despite the well-known advantages of the model, it requires additional masonry material properties (e.g. biaxial to uniaxial compressive strength ratio, eccentricity, viscosity, dilation angle) that are not readily available in the literature. This makes the model calibration tedious, further calling for additional random variables in the uncertainty modelling during fragility analysis. Hence, the model is not considered in the present study.
In SAP2000, Choudhury et al. (2015) proposed an equivalent frame (EF) approach by implementing plastic hinges. This simulates the failure of the masonry piers and spandrels under shear and flexure, mainly referring to their in-plane strength and stiffness contributions. A finite element approach suggested by Milani et al. (2009) was used to determine the ultimate shear and moment capacity of each structural element. RC elements were assumed to exhibit elastic behaviour considering their higher strength in comparison with masonry. The maximum lateral load capacity obtained from the experimental data was 99.50 kN and the accuracy of the FE models were improved with further analyses by varying the mechanical properties. The comparison between experimental and numerical pushover curves from the literature is shown in Fig. 3. Numerical and experimental analyses of a similar prototype was also carried out by Choudhury et al. (2020) who presented two FE modelling approaches using concrete damage plasticity model and a two-step homogenization model. The second approach was found to predict the exact behaviour of the masonry along with damage pattern in comparison with the first approach. Due to modelling complexities associated with this two-step strategy using homogenization approach, such methodology was not attempted in the present study.
The equivalent frame method is one of the most commonly used simplified modelling approaches for masonry structures, where each load-bearing wall with openings is idealised into a nonlinear frame. Several studies presented the application of this approach for masonry buildings, but notable issues and uncertainties associated with this simplified technique cannot be ignored. Penelis (2006) carried out pushover analysis of URM buildings using the EF approach. Lagomarsino et al. (2013) presented the EF solution for the implementation of the equivalent frame model in the TREMURI software analysis program for nonlinear static analysis of masonry buildings. Plastic hinges are typically assigned to the EF model (Quagliarini et al. 2017), using parameters that need to be carefully managed in non-engineered masonry buildings. In addition, the 50% reduction of the initial stiffness parameters to account for the panel cracked condition highly affects the global initial stiffness, ultimate displacement and acceleration of the equivalent system (Bracchi et al. 2015). This is confirmed in Fig. 3 by also including the EF model by Choudhury et al. (2015). Therefore, the simplified approach using nonlinear shell elements is considered in this study as an attractive alternative solution to EF models, ensuring a moderate computational effort.
Though developed models reproduced the nonlinear static behaviour of masonry with good accuracy, their ability to simulate the nonlinear dynamic response of the URM building to seismic input was not investigated. In addition, nonlinear analysis based on EPP modelling of masonry can only be carried out in STRAND 7 and it also disregards the non-associativity of masonry in shear and softening. ABAQUS model with CDP model is probably one of the most effective approaches requiring significant computational effort and experienced users, especially while analysing the performance of large structures. The numerical model developed in SAP2000 can be handled even by users with medium computational experience. However, this approach approximates the actual geometry with structural elements such as spandrels and piers, which works reasonably well only for regular walls with openings. Indeed, the identification of the geometry of the EF model may become rather ambiguous or questionable when the openings are irregularly arranged in the building (Parisi and Augenti 2013b). As mentioned earlier, it can be clearly seen that the EF model developed in SAP2000 underestimates the lateral stiffness of the building. The definition of nonlinear hinges and the load-carrying capacities of the individual masonry macro-elements (piers and spandrels) based on formulations recommended by code regulations may not link well with the actual experimental behaviour and 3D numerical models (Choudhury et al. 2015). This involves high computational time in the pre-processing phase, where each masonry element is extracted from the masonry building and both shear and flexural hinges have to be defined. Also, while analysing the structure with additional strengthening elements like steel bands, modified shear-displacement and moment-rotation curves have to be evaluated through proper modelling.
3 Numerical Macro-Modelling Options Selected in This Study
In a macro-modelling approach, the masonry units and mortar are smeared out in the continuum, which makes the model computationally less expensive in view of NLTHA at the building scale. As refined mechanical models are associated with the identification of a large number of material parameters and degrees of freedom (DOFs), the nonlinear behaviour of the masonry is represented by combining plastic behaviour with the smeared crack approach. Based on the smeared cracking constitutive law, the stiffness of the finite elements is modified due to crushing and cracking. However, this simplicity restricts the model from predicting some failure modes of the masonry including the failure in mortar joints, but the model can simulate the global response of the structure with acceptable accuracy (Mahini 2015). Since the modelling of orthotropic behaviour of masonry needs additional parameters that are not always available, this type of isotropic model is commonly accepted in the literature by properly tuning material parameters. More specifically, tensile and shear properties should be properly calibrated to fit the masonry behaviour, which is usually less affected by compression strength especially in case of URM buildings due to poor quality of materials (Choudhury et al. 2015).
In the present study, five alternative modelling approaches are discussed using different types of finite element and material models in ANSYS and SAP2000 software packages, as listed in Table 2. SOLID65 and SOLID185 elements were used in ANSYS, whereas nonlinear layered shell elements were used in SAP2000. The study is mainly focussed on the identification of suitable modelling approach for nonlinear time history analyses of URM building in view of fragility analysis. Along with the reduced computational time, an additional criterion considered in the selection of modelling approaches is the requirement of a limited number of masonry material parameters and the easier development of numerical models using commercial software. Considering the possibility to model the masonry behaviour through solid elements in ANSYS, different modelling approaches were identified using that finite element analysis program.
The selection of modelling approaches was initiated with the use of the commonly adopted EPP model with Drucker–Prager (DP) yield criterion and Willam–Warnke failure criterion, due to its proven effectiveness in simulating the tensile strength of masonry (Betti et al. 2015; Pauletta et al. 2018). Next, the modelling approach was further developed using different hardening rules (isotropic and kinematic hardening), while using the same type of finite element. Further, higher order 3D element SOLID185 was used with the same hardening rule and failure criterion to check the effectiveness of the model in reproducing the masonry behaviour. Even though the above-mentioned 3D numerical modelling approaches are capable of producing acceptable results, the computational time remains a major disadvantage when it comes for the large number of analyses required for fragility studies. Hence, a simplified numerical modelling approach using shell elements in SAP2000 was finally attempted to assess its accuracy and computational efficiency.
In order to reproduce the exact nonlinear behaviour of the masonry including quasi-brittle behaviour, additional material properties and detailed micro-modelling strategies would be necessary. For example, additional parameters such as orthotropy ratio, eccentricity, viscosity, dilation angle and the ratio between the distance from the hydrostatic axis of the maximum compression and tension are required in the most commonly used concrete damage plasticity model. Since this study is aimed at identifying a simplified modelling approach for nonlinear analysis of masonry structures with reduced number of material properties, plastic laws with different hardening rules were considered. Furthermore, the same strategy had also been proven to be suitable for modelling the behaviour of quasi-brittle materials like concrete, stone masonry, and brick masonry (ANSYS 2015; Pauletta et al. 2018).
Ultimate tensile and compressive strengths were mainly required to define the failure surface in addition to other parameters for the specific approaches. Models 1 to 5 were tested under both static and dynamic loading in order to provide an exhaustive comparison of numerical efficiency and provide useful comments on the applicability to large-scale seismic fragility analysis of NECs. In Table 2, \(f_{c}\) is the uniaxial compressive strength of masonry, \(f_{t}\) is the uniaxial tensile strength of masonry, \(\beta_{c}\) is the shear transfer coefficient for closed cracks, \(\beta_{t}\) is the shear transfer coefficient for open cracks, c is cohesion (i.e. shear strength at zero confining stress), \(\varphi\) is the friction angle, and ψ is the dilatancy angle. It is further noted that the orthotropic behaviour of masonry was not considered because of the lack of experimental data on the case-study masonry to properly calibrate required parameters. This motivated a macro-modelling of masonry as an isotropic material. Besides, either perfectly brittle or multilinear stress–strain laws with tension cut-off were used in ANSYS models to provide a simplified modelling approach with reduced number of parameters (Milani and Tralli 2011; Bertolesi et al. 2016). A trilinear stress–strain curve in tension was assigned to SAP2000 model, reducing convergence issues that arise during early stages of the analysis.
Based on the studies on masonry buildings in developing countries such as India (Singh et al. 2013; Sarkar et al. 2015; Kadam et al. 2020; Choudhury et al. 2020), Nepal (Habieb et al. 2018; Giordano et al. 2020), Pakistan (Shahzada et al. 2012) and Iran (Bhakshi and Karimi 2008) as available in the literature, the compressive strength (\(f_{c}\)) of masonry varies from 2.0 MPa to 6.0 MPa, tensile strength varies from 0.04\(f_{c}\) to 0.12\(f_{c}\), and shear strength varies from 0.02\(f_{c}\) to 0.07\(f_{c}\). A wide variation is observed in the elastic modulus of the masonry in developing countries, ranging from 400 to 2200 MPa. The mass density of masonry varies from 1400 kg/m3 to 1900 kg/m3. The material properties from Shahzada et al. (2012) were used in the present study in order to compare the available experimental results with numerical results.
3.1 Model Case 1
Model case 1 was based on the use of SOLID65, which is a solid element (Fig. 4a) defined by eight nodes with three translational DOFs in the nodal x, y, and z directions at each node. That type of finite element was adopted in previous studies to simulate the mechanical behaviour of quasi-brittle materials such as masonry (Pauletta et al. 2018; Betti et al. 2015). As summarised in Table 2, model case 1 was based upon the assumption of a simplified EPP behaviour in compression (Fig. 4b), a linear elastic-perfectly brittle (EPB) behaviour in tension (Fig. 4c), and Willam–Warnke failure criterion with linear tension cut-off (Fig. 4d). This allowed modelling both cracking in tension and crushing in compression, assuming that the yield surface does not change with progressive crushing.
Model case 1: a SOLID65 element; b EPP stress–strain diagram in compression; c EPB stress–strain diagram in tension; d Willam–Warnke failure domain in principal stress plane (ANSYS 2015)
Masonry failure was predicted through Willam–Warnke failure criterion (Willam 1975), where the failure surface is defined through ultimate uniaxial tensile strength, ultimate uniaxial compressive strength, ultimate biaxial compressive strength \(\left( {f_{cb} } \right)\), and ultimate compressive strengths for a state of biaxial and uniaxial compression superimposed on hydrostatic stress state \(\left( {f_{1} , f_{2} } \right)\). Nonetheless, the Willam–Warnke failure surface can be built in ANSYS only using uniaxial tensile and compressive strengths, so other parameters were assumed to be \(f_{cb} = 1.2 f_{c}\), \(f_{1} = 1.45f_{c}\), and \(f_{2} = 1.725f_{c}\) (Willam 1975; ANSYS 2015). Shear behaviour is controlled by two shear transfer coefficients that describe the possibility of shear sliding across the crack face. Typical shear transfer coefficients range from 0 to 1, with 0 representing a smooth crack (complete loss of shear transfer) and 1 representing a rough crack (no loss of shear transfer). This specification can be made for both closed and open cracks. The shear transfer coefficient for open crack (\(\beta_{t}\)) represents the shear strength reduction factor for the subsequent loads that induce sliding across the crack face. The shear transfer coefficient for closed crack (\(\beta_{c}\)) corresponds to the transfer of compressive stress normal to the crack plane, across the crack. These values were chosen by preliminary investigation on the numerical models under study to obtain the best fitting with experimental data. The value of \(\beta_{t}\) ranges from 0.05 to 0.5 for brick masonry. \(\beta_{c}\) values greater than 0.70 were usually adopted for adobe and brick prisms in the literature (Mahini 2015).
Even though the material behaviour is assumed linear elastic prior to failure, plasticity may be combined with the material properties to provide nonlinear behaviour before failure. Drucker–Prager criterion is used to define yield surface, assuming a non-associative flow rule (i.e. plastic potential, which determines the direction of plastic straining, is not equal to the yield function) so that plastic strains do not occur in a direction normal to the yield surface. When a yield criterion is used along with a failure criterion, the yield surface must lie within the failure surface, otherwise no yielding will occur. Drucker–Prager model, which is a smoothed version of Mohr–Coulomb surface, is defined using cohesion \(\left( c \right)\), friction angle \(\left( \varphi \right)\) and dilation angle \(\left( \psi \right)\).
Despite the availability of well-known modelling approaches using constitutive models with softening behaviour, the above-mentioned simplified approach was also used in previous studies because it requires a limited number of material properties (Pauletta et al. 2018). By contrast, constitutive models with softening behaviour were used in model cases 3 to 5, as described below. In this respect, post-peak softening in tension, compression and shear provides a realistic simulation of the quasi-brittle mechanical behaviour of masonry.
3.2 Model Case 2
In model case 2, SOLID65 elements were used with different behavioural rules. The macroscopic mechanical behaviour of masonry was modelled through a nonlinear stress–strain law with post-peak perfect plasticity in compression (Fig. 5a) and an EPB relationship in tension (Fig. 5b). Failure and direction of plastic straining was respectively defined via the Willam–Warnke failure criterion with tension cut-off and associative flow rule (i.e. plastic potential equal to yield function, resulting in plastic strains perpendicular to failure surface). It is noted that the compressive stress–strain law was directly implemented, assuming a multi-linear pre-peak isotropic hardening (Fig. 5c) rather than Drucker–Prager yield criterion (as in model case 1). That isotropic hardening rule was just used to describe the pre-peak micro-cracking in compression, which actually produces a nonlinear behaviour of masonry before peak compressive strength is reached, as highlighted in previous studies (e.g. Augenti and Parisi 2010). In that stage of mechanical behaviour, the isotropic hardening rule establishes a uniform increase in the size of the yield surface and results in a progressively increasing yield stress up to ultimate uniaxial compressive strength. This type of hardening can model the material behaviour under monotonic loading and elastic unloading, but the model does not give good results in the analysis of structures that experience additional plastic deformation after a load reversal from a plastic state (ANSYS 2015). The multi-linear isotropic hardening was described using stress–strain points, as shown in Fig. 5c.
Model case 2: a Nonlinear stress–strain diagram in compression; b EPB diagram in tension; c multi-linear isotropic hardening model (ANSYS 2015)
The uniaxial compressive stress–strain curve of the masonry shown in Fig. 5a was developed based on the material properties reported by Shahzada et al. (2012), in accordance with the analytical stress–strain model developed by Kaushik et al. (2007). These latter researchers reported that such a generalized analytical model is more suitable for typical masonry used in the Indian construction industry. The parabolic stress–strain curve was expressed in terms of non-dimensional stresses and strains as follows (Kaushik et al. 2007):
where: \(f_{m}\) is the compressive stress of masonry; \(\varepsilon_{m}\) is the compressive strain of masonry; \(f_{m}^{^{\prime}}\) is the ultimate compressive strength of masonry (i.e. \(f_{m}^{^{\prime}}\) = 3.02 MPa according to Table 1); and \(\varepsilon_{m}^{^{\prime}}\) is the corresponding peak strain. This latter property was obtained through the following equation:
where: \(f_{j}\) is the compressive strength of mortar and \(E_{m}\) is the Young’s modulus of masonry, i.e. \(E_{m}\) = 1227 MPa in Table 1 (Kaushik et al. 2007).
The other material properties required in the FE model were estimated based on the values available in the literature (Choudhury et al. 2015; Pauletta et al. 2018) and given in Table 1, along with sensitivity analysis through nonlinear pushover analysis of the masonry building in order to reproduce the experimental data with reasonable accuracy. Indeed, additional masonry material properties such as tensile strength and shear strength were derived through sensitivity analysis, which consisted in pushover analysis under varying those parameters in the ranges suggested by Choudhury et al. (2015). Sensitivity analysis highlighted that the peak resistance of the URM building significantly reduces as tensile strength decreases from 0.17 MPa to 0.11 MPa and as shear strength decreases from 0.15 MPa to 0.10 MPa in a pure Mohr–Coulomb failure criterion. A good agreement with the experimental pushover curve was found when tensile and shear strengths were set to 0.16 MPa and 0.145 MPa, respectively. The output of that numerical calibration consisted of the following data: uniaxial tensile strength equal to 0.16 MPa; Poisson’s ratio equal to 0.25; shear transfer coefficients for open and closed crack equal to 0.4 and 0.99, respectively.
3.3 Model Case 3
In model case 3, the mechanical behaviour of masonry was modelled via a nonlinear stress–strain relationship with post-peak softening in compression (Fig. 6a) and a multi-linear stress–strain diagram in tension (Fig. 6b). The former diagram was developed based on the material properties of the benchmark building, making use of a multi-linear kinematic hardening with Von Mises yield criterion and associative flow rule (Fig. 6c) to describe pre-peak nonlinear behaviour in compression. Kinematic hardening leads to a shift in the yield surface in stress space during plastic deformation, also simulating the plastic strain build-up during cyclic loading. Softening in tension was modelled by a sudden drop after the attainment of peak tensile strength and a linear softening up to zero stress. To that aim, a tension crack factor \(\left( {T_{c} = 0.2} \right)\) was included in the Willam–Warnke failure surface. The tension crack factor acts as a multiplier for stress relaxation and was thus calibrated based on pushover analysis of the case-study building. This modelling approach (with suitable modifications in the analysis parameters) can reproduce the softening behaviour of masonry, avoiding convergence issues to some extent. By contrast, the use of Tc did not significantly improve the results and convergence issues in previous model cases 1 and 2, so it was ignored therein. Except from the compressive stress–strain curve shown in Fig. 6a, other material properties used in the modelling were similar to those mentioned in model case 2.
Model case 3: a Nonlinear stress–strain diagram in compression; b multi-linear stress–strain diagram in tension; c multi-linear kinematic hardening model (ANSYS 2015)
3.4 Model Case 4
Such a model case was based on the use of SOLID185 element (Fig. 7), which is another type of finite element recommended for 3D modelling of structures. This element can be characterised by different types of mechanical behaviour, including plasticity, hyper-elasticity, stress stiffening, creep, large deflection, and large strain capabilities. Though SOLID65 element is very commonly used in masonry modelling due to its ability to represent cracks, it has been catalogued as a legacy element by ANSYS. Thus, high-order 3D elements like SOLID185 are being used in the recent numerical modelling of quasi-brittle materials such as concrete and masonry (see e.g.: Hawileh et al. 2010; Gisbert et al. 2018; Shrestha and Bhandari 2020).
SOILD185 element used in model case 4 (ANSYS 2015)
In the present study, the nonlinear behaviour of masonry in compression was modelled using the nonlinear stress–strain diagram with post-peak softening depicted in Fig. 6a, whereas the tensile constitutive behaviour was assumed to be elastic-perfectly brittle as shown in Fig. 5b. Pre-peak nonlinear behaviour in compression was defined using the multi-linear kinematic kinematic hardening model (Fig. 6c), similarly to model case 3. Nonetheless, in ANSYS, the Willam–Warnke failure criterion cannot be combined with SOLID185 element, so failure was defined by means of maximum stresses and strains in tension, compression and shear.
3.5 Model Case 5
For the aim of comparison and searching for a simplified approach, a 2D model in SAP2000 with nonlinear layered shell elements was used. Under this approach, several shell layers in the thickness direction with different constitutive law can be defined to simulate the nonlinear behaviour of the masonry. These layers are kinematically connected according to the Reissner–Mindlin assumption that the normal to the reference surface (axis 3 in Fig. 8) does not change its own direction after deformation. The material behaviour is integrated at finite number of points in the thickness direction of each layer and the use of excessive number of thickness integration points increases the analysis time. In addition, the material angle can also be defined to represent the material axes with respect to the element axes for modelling orthotropic materials. For each layer, three membrane stress components \(\left( {\sigma_{11} ,\sigma_{22} ,\sigma_{12} } \right)\) shown in Fig. 8 can be considered as linear, nonlinear, or inactive. In this macro-modelling approach, masonry is considered as an isotropic material and thus the material angle in each layer is taken as zero. For the first layer that defines the normal stress–strain behaviour of the masonry, \(\sigma_{12}\) is considered as inactive. Similarly, for the second layer which corresponds to the shear behaviour of masonry, \(\sigma_{11}\) and \(\sigma_{22}\) are considered as inactive.
Model case 5 using SAP2000: a Stress components of shell element; b Quadrilateral shell element (SAP2000 2020)
In the present study, two stress–strain curves corresponding to normal stress (compression and tension) and shear stress were used to represent the nonlinear behaviour of masonry using a two layered shell element (Thuyet et al. 2018; Valente and Milani 2016). The maximum compressive, tensile and shear strengths of the masonry obtained from the calibration of ANSYS models were used also in SAP2000 model. The tensile strength of the masonry was taken as 0.16 MPa and corresponding behaviour was defined based on the relationship suggested by Akhaveissy and Milani (2013). Mohr–Coulomb failure criterion with associative flow rule was used for representing the shear behaviour of masonry, which has major influence on seismic performance of masonry buildings in the north-eastern zone of India. Cohesion was taken as 0.145 MPa and friction was ignored in order to match the load-carrying capacity obtained from experimental results (Thuyet et al. 2018). The shear and tensile stress–strain curves used in the model are shown in Fig. 9a and b. The compressive stress–strain curve used in this model is similar to that of model case 3, as shown in Fig. 6a. The RC elements were assumed as linear elastic.
4 Numerical Simulation of the Case-Study Building
4.1 Detailed FE Modelling in ANSYS and Simplified FE Modelling in SAP2000
In order to assess the effectiveness of the modelling approaches for the analysis of real-scale structures, numerical models of the benchmark building were developed. The bottom nodes of the building were constrained in all three DOFs. RC lintel beams and roof were also modelled using solid elements with linear elastic behaviour. The additional mass from 0.25-m-thick sand layer on the roof top was modelled using MASS21 element, which is a point element with six DOFs. The mass element was constrained to the top nodes of the slab. The FE model of fixed-base masonry building developed in ANSYS is shown in Fig. 10a. The mesh size of the FE model was determined through detailed sensitivity analysis to match the experimental data. Mesh size of 0.114 m (half of the wall thickness) was found to be adequate through a preliminary convergence analysis, so the model was meshed with 10,801 elements and 18,636 nodes.
In SAP2000, the masonry building was modelled using nonlinear layered shell elements with a rigid diaphragm constraint at the roof level. Assuming the same mesh size of ANSYS model for subsequent comparison, the model was meshed with 5184 shell elements and 5337 joints. The developed simplified masonry building model in SAP2000 is shown in Fig. 10b.
4.2 Modal Analysis
Modal analysis on both ANSYS and SAP2000 models was carried out preliminarily. A difference lower than 5% in predictions of fundamental frequency and participating mass ratio of translational deformation modes along both X and Y directions is found, remarking a good agreement of models in simulating the initial stiffness of the building. A slightly higher variation (8%) is obtained under the first torsional mode. The output of modal analyses for the first three vibration modes is outlined in Table 3.
4.3 Numerical-Experimental Comparison Based on Pushover Analysis
4.3.1 Monotonic Loading
The seismic capacity of the building models was then assessed through pushover analysis, which was carried out by imposing a monotonically increasing displacement at the roof level along X direction. The response of the building models is compared with the experimental data from Shahzada et al. (2012) in Fig. 11. In the experimental study reported in the literature, the masonry building reached its peak lateral resistance of 99.5 kN at an inter-storey drift of 0.23% (corresponding to a lateral displacement equal to 7.89 mm). The maximum load-carrying and displacement capacities of the building obtained from ANSYS and SAP2000 models are given in Table 4.
The model cases 1 (Drucker–Prager) and 2 (isotropic hardening) overestimated the maximum load-carrying capacity of the building by 5.20% and 15.70%, respectively. The results from model case 3 (kinematic hardening) are found to be in good agreement with the experimental data but the solution is found to be not converging at 9.14 mm (corresponding to an inter-storey drift of 0.27%), thus underestimating the lateral displacement capacity in the post-peak softening range. Model case 4 with SOLID185 elements provided a hardening behaviour with a maximum load-carrying capacity approximately seven times higher at 20 mm, thus being inaccurate and making it impossible to plot the curve in Fig. 11. The initial stiffness and the load–displacement curve have a good match with other results only up to 1.20 mm (0.035% inter-storey drift) with corresponding load-carrying capacity of 73 kN. Hence, this approach is not considered further in the comparison of results. Even though higher order SOLID185 element is being increasingly used in the modelling of masonry buildings, the discrepancy of this modelling approach in reproducing the nonlinear behaviour of the URM building shows that additional refined parameters are necessary to define the plastic flow and failure criterion accurately. Further improvement of this modelling approach is being studied by these authors.
The SAP2000 model provides satisfactory results in terms of peak force and corresponding displacement even if not including any softening branch, thus underestimating the ultimate displacement capacity. It is also noted that the simplified model also allows the best reproduction of the pre-peak rising branch of the load–displacement curve. Sensitivity analysis was conducted in all cases to understand the influence of different mechanical properties on the response of the FE models. Based on relevant outcomes, it is found that the maximum load-carrying capacity of the building is highly affected by tensile strength in model cases 2 to 5. In the case of model case 1, the peak resistance of the building increases with the increase in masonry shear strength.
The final damage pattern from the experimental observation (see Fig. 12a) was compared with the FE results. The crack patterns in the in-plane North wall obtained from ANSYS are shown in Fig. 12b, c and d. According to experimental observations, the North and South walls of the building suffered more damage in comparison with the out-of-plane walls. Piers in the North wall developed both vertical and flexural cracks. Vertical cracks were also observed at the intersection of the in-plane and out-of-plane walls from the numerical results of model cases 2 and 3, almost identical to the experimental results. According to Sorace and Terenzi (2011) and Pauletta et al. (2018), if the tensile stress limit is reached in at least two main directions of the element quadrature point, damage becomes visible on the surface of the wall. The elements in the piers of the North and South walls were subjected to this condition, so they developed excessive cracks.
Numerical versus experimental final crack patterns: a Experimental cracks (Shahzada et al. 2012); b Model case 1 (ANSYS-S65/Drucker–Prager); c Model case 2 (ANSYS-S65/isotropic hardening); d Model case 3 (ANSYS-S65/Kinematic hardening)
All models well predicted the occurrence of diagonal cracks starting from opening corners, as well as horizontal cracks at the base of left-hand side pier. Both types of cracks highlight the flexural behaviour of that pier, which had the highest effective height (see e.g. Parisi and Augenti 2013b and Lagomarsino et al. 2013, for such a parameter that can play a key role in other modelling approaches and seismic behaviour of masonry buildings). The crack patterns obtained from the experimental studies corresponds to the final damage pattern at 0.48% inter-storey drift. In case of numerical results, pushover analysis stopped at smaller deformation levels, i.e. an inter-storey drift equal to 0.27%, due to convergence issues. However, the crack pattern observed from the numerical models in terms of vertical cracks near the intersection of walls and near the openings is similar to the crack initiation reported from the experimental tests.
Maximum equivalent stresses are found to be concentrated near the opening corners, due to higher stiffness of the RC elements. This trend was also confirmed by SAP2000 model (Fig. 13) where convergence issues were due to excessive tensile stresses developed in the in-plane masonry walls. The maximum tensile stress is also concentrated at the base of the pier (highlighted in the figure). The same behaviour was observed in the numerical simulations carried out by Choudhury et al. (2015). The horizontal tensile strains at the peak load-carrying capacity of the URM building model in SAP2000, i.e. 0.19% inter-storey drift ratio, are shown in Fig. 13b. Excessive tensile strain close to 0.10% (i.e. maximum value in Fig. 9a) can be observed close to the upper left of the door opening in the in-plane North wall. Due to convergence issues, the SAP2000 model was not able to reproduce the behaviour of URM building beyond the peak load-carrying capacity. Excessive tensile strains are observed close to the openings of the URM buildings, similar to the crack initiation mentioned during the experimental study. The same trend can also be seen in the numerical results obtained from ANSYS models.
4.3.2 Cyclic Loading
In order to compare the hysteretic behaviour under static cyclic loading, the SAP2000 numerical model was subjected to increasing reverse displacement cycles, repeating each displacement amplitude three times according to the experimental protocol adopted by Shahzada et al. (2012). A set of continuous nonlinear static analyses with increasing displacement was carried out. The force–displacement behaviour of the URM building under numerical model and the backbone of the experimental results are compared in Fig. 14. The shape of the numerical hysteresis loops is larger than their experimental counterparts with predominant shear behaviour where nonlinearity is observed almost from the beginning of the test. Due to convergence issues in the SAP2000 model, the cyclic analysis stopped at the same level of displacement reached under monotonic loading, i.e. inter-storey drift ratio equal to 0.19%.
Equivalent viscous damping obtained from numerical results ranges from 13% to 18%, whereas the same parameter reported from the experimental study varies between 5.8% and 7.8%. The numerical model overestimates the damping capacity of the URM building due to limited effect of the pinching phenomenon. Similar values of damping to those obtained from SAP2000 model are reported in the studies performed on URM walls (i.e. 7.7% to 39.5%) by Zimmermann et al. (2012). Furthermore, displacement capacity and damping values obtained in SAP2000 from cyclic loading and NLTHA are consistent with each other.
As a major advantage of SOLID65 ANSYS models (i.e. from model case 1 to 3), the cracking pattern is captured and displacement capacity estimated with higher accuracy, even if the only model accounting for softening (i.e. model case 3) experienced convergence issues at earlier stage. Apart from SOLID185 model (i.e. model case 4) resulting inaccurate to capture both softening and maximum load capacity, the simplified model in SAP2000 (i.e. model case 5) demonstrated satisfactory response until peak load thus being useful in case softening has not to be investigated. This can be the case if a base isolation system is provided and internal stresses are significantly reduced within the masonry being the subject of a research project by the authors of this paper.
With proper limitations, the modelling approaches considered in the present study (except the model case 4) can be effective in modelling the pushover response of the selected URM buildings under proper calibration of mechanical properties. The same models are considered in subsequent section under time history analyses for a further comparison and to predict the nonlinear dynamic response under seismic input with incremental intensity.
4.4 Numerical Prediction of Nonlinear Dynamic Response
The current section is aimed at predicting the numerical response of the benchmark building under dynamic loading. Even if dynamic response had not been experimentally tested, numerical investigation could provide relevant suggestions on the expected behaviour due to properly calibrated nonlinear parameters according to pushover results. It is well known that shaking table tests of real-scale prototype buildings would require large facilities (see e.g. Mendes et al. 2014; Magenes et al. 2014; Meoni et al. 2019) thus making experimental data not always available for different types of masonry buildings, particularly those representative of NECs. In order to assess the different performance of proposed models through NLTHA, nonlinear direct integration transient analyses were carried out using Hilber-Hughes-Taylor (HHT) algorithm (Hilber et al. 1977), with a time step of 0.01 s. HHT algorithm was selected due to its unconditional stability. Classical Rayleigh formulation was considered for damping and 4% damping ratio was adopted based on the literature (Betti et al. 2015). The time integration algorithm and the corresponding parameters were maintained the same in both the software packages for the sake of comparison.
NLTHA was performed along X direction under two ground motions assumed to be representative of the seismic hazard in Himalayan regions where a relevant number of NECs can be found. Two strong earthquakes which occurred in Bhuj and Nepal were considered. Bhuj earthquake occurred in 2001 with moment magnitude Mw = 7.9, causing extensive damage to buildings and loss of life. The Bhuj earthquake occurred along the Allah Bund fault and resulted in huge uplift of the ground surface. Bhuj town in the Kutch district of Gujarat state was reported as the epicentre of the earthquake. The large magnitude of the earthquake combined with the poor construction quality in that seismically active region (Zone V according to Indian building code IS 1893 code) had contributed to the destruction of more than 300,000 buildings (BIS 2002). Due to very few recording stations in the area, the only strong motion record was measured in Ahmedabad with a peak ground acceleration (PGA) of 0.11g, 260 km away from the epicentre (Madabhushi and Haigh 2005). Though there is no record available from the Bhuj area, the PGA of the earthquake in the epicentral area would have been higher considering the magnitude of the earthquake. The acceleration time history measured in Ahmedabad and corresponding Fourier amplitude frequency content are shown in Fig. 15a. The other large earthquake with Mw = 7.8 considered in this study occurred along the Himalayan thrust fault in central Nepal in 2015. The earthquake was caused by the collision between the Indian and Eurasian plates. The epicentre was near the Gorkha region and the only record available close to the region was at Kathmandu, 80 km from the epicentre (Takai et al. 2016). The recorded acceleration time history is characterised by PGA = 0.13g (Fig. 15b). The earthquake ground motion data were collected from the strong-motion virtual data centre (VDC) developed at the University of California Santa Barbara (COSMOS 2014).
According to IS 1893 (BIS 2002), the seismic zone factor for Zone V (very severe seismic intensity) is 0.36, meaning PGA = 0.36g. This latter acceleration reflects the actual PGA considering the maximum considered earthquake (MCE), while it is reduced by a factor of 2 for the design basis earthquake (DBE) that establishes a moderate intensity level. As the PGA for the available seismic records is less than DBE level, NLTHA was carried out by scaling selected records to investigate nonlinear behaviour and trigger any collapse mechanism in the building. Accordingly, seismic response analysis of the benchmark building was run by also scaling the maximum acceleration to 0.36g and 0.5g. Three different earthquake record sets corresponding to original ground motions (set 1) and scaled ground motion records with PGA = 0.36g (set 2) and PGA = 0.5g (set 3) were used (Table 5).
4.4.1 Nonlinear Dynamic Response to Set 1 (Unscaled) Ground Motions
NLTHA results for the original (unscaled) ground motions recorded during Bhuj and Nepal earthquakes are summarized in Table 6. To estimate the hysteretic damping of the building, the equivalent viscous damping ratio was calculated for the loading cycle corresponding to the maximum displacement response (Chopra 1995; Shahzada et al. 2012). The same procedure was used in previous experimental studies on URM structural systems (see e.g. Parisi et al. 2014). The results obtained from model cases 1 and 2 (i.e. Drucker–Prager and isotropic hardening, respectively) exactly match with each other under earthquakes and computational time is very similar. According to pushover analysis results, the base shear predictions from model cases 1 and 2 are higher compared to other cases. Loss of convergence was found occurring in model case 3 (kinematic hardening) under both earthquakes due to excessive distortion of finite elements, even if the base shear demand (i.e. 29.42 kN; see Table 6) was approximately 30% of the peak resisting base shear measured during quasi-static testing (i.e. 99.50 kN; see Table 4). According to pushover curves in Fig. 11, that level of base shear was expected to be associated with a linear elastic behaviour of the building. Due to the early termination of the kinematic hardening model analyses at 41.7 s in Bhuj earthquake and 29.4 s in Nepal earthquake, the top acceleration values are 28% and 46% less than DP model under Bhuj and Nepal earthquakes, respectively. This highlights some computational issues related to the implementation of model case 3 for NLTHA, thus making it unsuitable for further comparison in dynamic load conditions. The results from SAP2000 layered shell element model tend to slightly underestimate the response of the building, both in terms of base shear and inter-storey drift. Stress concentrations were only observed close to the openings and lintels. The difference in the masonry behaviour obtained from different modelling approaches can be attributed to the combination of type of finite element alongside hardening laws. Further, plastic deformation developed in the elements during load reversal can also be seen as a major parameter for the variation of the results between model cases 2 and 3 (Park et al. 1987).
As the DP model is one of the most acknowledged models in the literature (see e.g.: Choudhury et al. 2015; Pauletta et al. 2018), corresponding results in terms of base shear and inter-storey drift are considered for comparison with model cases 2 and 5 under Bhuj earthquake in Fig. 16. Model case 3 is not included in the comparisons due to its early termination of time history analyses. A similar pattern between different approaches is observed under Nepal earthquake as seen from Fig. 17. Severe damage to the building is not observed since the response is almost linear elastic and calculated damping values are consistently lower than 5%. In case of SAP2000 model, results show a consistent pattern with ANSYS models. In addition, the reduced numerical burden of SAP2000 model to less than half computational time with no convergence issues is a relevant outcome when comparing the different strategies for seismic performance assessment of NECs at a large scale.
4.4.2 Nonlinear Dynamic Response to Set 2 Ground Motions (PGA = 0.36g)
NLTHA results with PGA = 0.36g are listed in Table 7. Because of the excessive deformation due to increased PGA, loss of convergence was found to be occurring in all model cases developed in ANSYS. In case of Bhuj (Nepal) earthquake, the analysis stopped due to excessive deformation of elements at 46.8 s (29.4 s) and 38 s (29.4 s) in ANSYS model cases with DP (model case 1) and isotropic hardening (model case 3), respectively. A significant variation in the NLTHA results is observed due to variation in the duration of the records. The converged solution with reduced computational effort of the SAP2000 model is confirmed as a major advantage. The output of NLTHA on SAP2000 model is consistent with experimental behaviour in terms of maximum base shear and corresponding inter-storey drift. Differently, ANSYS models under Nepal earthquake experienced larger base shear, evidencing peak inter-storey drift values (0.049%–0.064%) significantly lower than experimentally found under both earthquakes.
The simplified SAP2000 model was able to capture the nonlinear behaviour of the masonry building at excessive deformation with inter-storey drift value greater than 0.1%, which is defined as moderate damage level by Calvi (1999) and Shahzada et al. (2012). An increase in hysteretic damping is observed in all the modelling approaches when compared to Set 1 even if significantly higher values are obtained in SAP2000, i.e. up to 21.2% and 16.6% for Bhuj and Nepal earthquake, respectively. In such a context, previous studies reported that the increase in damping may occur after masonry cracking due to the reduction in elastic modulus as compared to the uncracked behaviour (Elmenshawi et al. 2010). Further, a large variation in damping of URM buildings can be seen from the values reported in the literature. Benedetti et al. (1998) estimated the initial damping ratio associated with the fundamental mode of vibration for brick masonry buildings as 6% to 10% and for stone masonry buildings about 10%. Studies on unreinforced brick masonry walls reported a damping ratio of 13% according to cyclic in-plane shear-compression tests (Magenes and Calvi 1997; Santa-Maria et al. 2004). Shear behaviour of masonry walls involves higher values of damping compared to flexural behaviour for the same inter-storey drift. Parisi (2016) assumed equivalent damping ratios of 10% and 15% for flexural and shear failure modes of URM walls, respectively, in a direct displacement-based approach for URM buildings with box-type seismic response. However, these values tend to change with respect to the loading pattern, intensity of loading and, in case of experimental assessment, testing conditions. Despite the uncertainties associated with the damping value of URM structures, literature suggests 10% for most of the cases (Magenes and Calvi 1997). Though the damping curves developed for masonry walls may not be valid for a masonry building, the global damping of a masonry building can be evaluated by the weighted average based on the energy dissipated by several structural elements (Priestley et al. 2007). Hence, these reference values can be considered suitable for the benchmark URM building, which is a simple single storey box-type structure.
Shahzada et al. (2012) reported damping ratios of 5.7% to 7.8% for the benchmark URM building tested under quasi static loading. A slight increase in damping value was also identified beyond a storey drift of 0.15%. Further the experimental curves are characterized by the pinching phenomenon which tends to reduce the dissipated hysteretic energy, the latter in turn affecting the overall damping capacity. The disagreement between the damping values estimated by SAP2000 with the experimental results can be attributed to larger hysteretic curves in addition to dynamic loading type.
The graphical comparison of NLTHA results is shown in Figs. 18 and 19, where a good agreement in the trend is found until the analysis stops in ANSYS models. The damage in the in-plane walls was comparatively higher than out-of-plane walls in both ANSYS and SAP2000 models detected by cracking and stress/strain patterns, respectively. Diagonal cracking in the masonry was observed close to the openings and lintels. The crack progression near the openings was well reproduced by the ANSYS DP and isotropic hardening models, compared to the kinematic hardening model. In case of SAP2000 model, high horizontal tensile strains were observed near the openings.
4.4.3 Nonlinear Dynamic Response to Set 3 Ground Motions (PGA = 0.5g)
NLTHA of the benchmark building was further carried out with records scaled up to PGA = 0.5g and the results are listed in Table 8. Due to the significant increase in the ground acceleration, significant damage in the URM building is observed under all modelling approaches, which resulted in the excessive deformation and cracking (numerical collapse of the model). Loss of convergence had occurred in all cases including SAP2000 simplified model.
As for Set 2 ground motions, maximum inter-storey drift and damping values for ANSYS models tend to be lower than SAP2000. A maximum damping value of approximately 25% was found in SAP2000 under Bhuj earthquake, whereas the analysis stopped earlier due to large plastic excursion under Nepal earthquake. The comparison of hysteresis curves from different modelling approaches are shown in Figs. 20 and 21.
Results of Set 3 confirmed that SAP2000 tends to overestimate the URM damping capacity due to excessively large enclosed area during hysteretic cycles, practically neglecting any pinching phenomenon that can occur in cracked elements. Even if maximum inter-storey drift values are consistent with experimental capacity, higher damping values would underestimate the plastic demand in SAP2000, and this must be properly taken into account in case large plastic deformations are expected. In a similar way, even if damping values are in accordance with the ones reported in the literature, ANSYS models would provide a significantly lower displacement capacity due to numerical instability.
Diagonal crack patterns were observed close to the openings in ANSYS DP and isotropic hardening models, similar to what observed under Set 2 ground motions with PGA = 0.36g.
The maximum vertical compressive stress developed in the FE models is around 20% of the corresponding strength under both earthquakes, which shows that the damage associated with excessive distortion of elements is not due to crushing. On the other hand, the horizontal and vertical tensile stresses developed in the URM building reach the ultimate strength. These regions close to the door and window openings in the in-plane North and South walls developed diagonal cracks according to a flexural failure mode. The analysis stops with the slight widening of the diagonal cracks in the ANSYS FE models (Fig. 22). Though the cracking cannot be captured from the SAP2000 model, the increased tensile stresses together with the loss of convergence confirm the severe damage to the URM building (Fig. 23).
The crack pattern obtained using ANSYS DP model under set 3A Bhuj earthquake at the end of NLTHA is shown in Fig. 22 and a similar pattern is also obtained from the isotropic hardening model. Initial cracking and crack progression stages are observed in the in-plane walls. The final cracks occur in the out-of-plane West wall before termination of analysis. The model was not able to capture the final crack pattern ‘3’ in the in-plane walls due to convergence issues.
Based on the results obtained from ANSYS models, damage to the out-of-plane walls and formation of vertical cracks at the corners of the building do not occur at the initial stage of cracking. Horizontal cracks are observed at both the base and lintel levels of the piers, initially in the in-plane North wall. Diagonal cracks close to the corners of the opening are also observed. In ANSYS crack pattern, small circles will appear where the material is cracked and small octagons when it is crushed (ANSYS 2015). The cross section of these cracks is circular in the crack plane, indicating the absence of crushing. Similar to the North wall, diagonal cracks close to opening corners and horizontal cracks at the lintel and sill levels are also observed in the in-plane South wall. The horizontal cracks at the base of the in-plane walls progressed further with time, resulting in a continuous horizontal crack at the base of out-of-plane West wall. That out-of-plane damage induced excessive deformation and the analysis stopped indicating the severe damage or collapse of the building.
The results obtained from the simplified SAP2000 model indicate a maximum horizontal compressive stress of 0.53 MPa (17.6% of compressive strength) close to the lintels in the in-plane South wall. Furthermore, the maximum vertical compressive stress developed in the URM building is 0.7 MPa, which is only about 23% of the corresponding strength. This clearly shows that the predicted damage to the URM building is associated with the tensile stress concentration and excessive tensile strain. The lack of crushing at pier toes is a direct consequence of the models’ partial or total inability to follow the post-peak softening behaviour of the benchmark building, as evidenced by the numerical-experimental comparison under quasi-static loading. Nonetheless, this is not a major drawback of the selected models in view of their force-based seismic assessment before and after the implementation of base isolation systems. This was the aim of another study by the same research group (Losanno et al. 2021).
The tensile stress developed at the lintel and sill levels in the in-plane walls tend to reach the maximum tensile strength of the masonry. Those regions of stress concentration are highlighted in the horizontal stress distribution shown in Fig. 23a and b. The location of tensile stress concentration is similar to the location of cracks observed in the initial stages of damage from ANSYS FE models. However, the damage in out-of-plane wall is not observed in the SAP2000 model. In addition to the stress concentrations close to the lintel, large tensile strains are also observed in the piers of the in-plane walls as shown in Fig. 23c and d. The formation of horizontal cracks is also expected to be coupled with the activation of a sliding shear failure, in agreement with the higher energy dissipation and displacement capacity of the URM building.
5 Conclusions
The present study was carried out within a research programme for seismic risk mitigation of non-engineered constructions through low-cost base isolation. In view of seismic risk assessment of as-built, fixed-base NECs, this paper has presented a comparative assessment of different macro-models for nonlinear seismic analysis of non-engineered masonry buildings located in developing countries. Five alternative modelling approaches with different types of finite elements and material models were considered, including four detailed 3D models developed in ANSYS APDL and a simplified nonlinear layered shell element model developed in SAP2000. The developed numerical models were selected with due consideration to the number of mechanical properties required for a macro-model approach, in order to reduce the computational work.
A masonry building tested by other researchers was assumed as a case study and was analysed according to the selected models with both pushover and NLTHA. The material properties not available in the literature were suitably calibrated to reproduce the experimental behaviour available from the literature, particularly the initial stiffness and peak base shear under incremental static lateral loading. All models confirmed the prime dependence of maximum load-carrying capacity on either shear (DP model) or tensile strength (models 2 to 5), which are usually significantly lower for NECs than other masonry structures.
The 3D modelling of the benchmark building based on SOLID65 finite elements with kinematic hardening rule provided good accuracy in predicting the peak load capacity and limited softening in case of pushover analysis. Nonetheless, such a modelling approach failed during NLTHA even under natural (unscaled) strong ground motions. The modelling approaches with DP and SOLID65 isotropic finite elements were found to overestimate the maximum load-carrying capacity of the building. NLTHA results have shown an adequate performance of the alternative FE models under natural earthquake records with PGA between 0.11g and 0.13g. However, convergence issues started occurring during the analysis with higher acceleration levels. Unconverged solutions have been found, indicating excessive crack patterns occurring between 0.05% and 0.06% inter-storey drift under scaled earthquake records with PGA = 0.36g.
In case of shell layered element model in SAP2000, the modelling phase is remarkably facilitated due to use of 2D shell elements and a reduced number of mechanical parameters for nonlinear behaviour of masonry. Pushover analysis results have been found to be in good agreement with experimental data in terms of both peak base shear and corresponding displacement, even if no softening was provided with lower ultimate displacement capacity. In case of NLTHA, the performance of that structural model appears to be more promising than 3D FE models even if a damping overestimate could be obtained under stronger input motions. The analysis stopped only under the scaled earthquake with PGA = 0.5g probably due to structural failure rather than numerical issues. Maximum inter-storey drift and stress distribution are deemed representative of significant damage under earthquake excitation. Even if a direct comparison with experimental shaking tests is not available from the literature, peak values of base shear and inter-storey drift derived through NLTHA are consistent with pushover results and contribute to validate numerical results. An additional advantage of SAP2000 model relies upon its computational time, which is significantly lower than 3D models. ANSYS model’s potential under NLTHA is strongly limited due to excessive cracking when cracks tend to spread more than a certain limit even under lower intensity ground motion. This would prevent the possibility to assess the effective seismic capacity of non-engineered masonry buildings under incremental dynamic analysis without convergence issues.
The displacement capacity of SAP2000 model obtained under earthquake excitation sets 3A and 3B is approximately 0.145% and 0.087%, respectively, which is lower than that predicted under static loading (i.e. 0.19%). NLTHA of ANSYS models highlighted a maximum deformation that is only a small fraction (around 10% to 20%) of maximum values predicted through pushover analysis. In both cases, i.e. SAP2000 and ANSYS, even if peak shear force is consistent with experimental and pushover results, a limited displacement capacity is achieved so that possibility to accurately predict ultimate displacement through numerical models remains questionable without experimental dynamic test. If moderate plastic deformations of the URM building are expected, e.g. in case of base-isolated configuration, the SAP2000 model strategy could provide a suitable solution.
Even if a direct comparison with experimental shaking tests is not available from the literature, peak values of base shear derived through NLTHA are consistent with pushover results whereas inter-storey drift values are slightly lower. Numerical models under NLTHA demonstrated lower displacement capacity in comparison to static analysis especially in case of ANSYS models. Further research needs to be carried out in order to improve the numerical accuracy in the prediction of displacement capacity unless limited ductility demand is considered as in the case of base-isolated URM buildings.
In view of these considerations, the simplified SAP model represents a trade-off between accuracy of results and numerical burden with significant advantage in the modelling process. Thus, this simplified model can be used to run nonlinear seismic analysis for developing fragility curves of NECs. Even if SAP2000 does not provide results in terms of cracking pattern, it is also important to note that this approach is capable of providing stress distributions in the wall panels. This finally helps in both tracking damage and designing proper seismic strengthening techniques including low-cost base isolation. This also shows that the ANSYS models considered in the study are not suitable for predicting the masonry behaviour up to failure, especially for capturing displacement capacity.
The next step of this study is the development of fragility curves for different geometries (e.g. number of storeys, plan area, wall and opening distribution, material properties, etc.) of common housing units in developing regions. To achieve this goal, the modelling strategy in SAP2000 with nonlinear shell layered elements could be implemented for a huge number of numerical simulations. In this perspective, the authors of this paper will assume a number of case studies to be numerically investigated under the following different conditions: (1) the conventional, fixed-base building configuration with limited seismic capacity due to low-strength masonry and poor detailing; and (2) the novel, base-isolated building configuration with improved performance thanks to low-cost isolators. For this reason, the partial inability of some models to follow the post-peak softening of the building structure (associated with crack propagation throughout masonry) and to accurately estimate effective damping is not a main drawback in order to investigate the overall seismic capacity with limited internal stress in case of base isolation. At the same time, in case of severe damage the model would be capable to provide internal stress concentrations and numerical instability due to loss of convergence.
References
Adhikari RK, D’Ayala D (2020) 2015 Nepal earthquake: seismic performance and post-earthquake reconstruction of stone in mud mortar masonry buildings. Bull Earthq Eng 18(8):3863–3896
Akhaveissy AH, Milani G (2013) Pushover analysis of large scale unreinforced masonry structures by means of a fully 2D non-linear model. Constr Build Mater 41:276–295
ANSYS (2015) Mechanical APDL material reference. ANSYS Inc
APDL, A. M. 16.2 [Computer software] (2015) ANSYS, Canonsburg, PA
Arya AS (2000) Non-engineered construction in developing countries-an approach toward earthquake risk prediction. Bull N Z Soc Earthq Eng 33(3):187–208
Arya AS, Boen T, Ishiyama Y (2014) Guidelines for earthquake resistant non-engineered construction. UNESCO
Augenti N, Parisi F (2010) Constitutive models for tuff masonry under uniaxial compression. J Mater Civ Eng 22(11):1102–1111
Bakhshi A, Karimi K (2008) Performance evaluation of masonry buildings using a probabilistic approach. Scientia Iranica 15(3):295–307
Benedetti D, Carydis P, Pezzoli P (1998) Shaking table tests on 24 simple masonry buildings. Earthquake Eng Struct Dynam 27(1):67–90
Bertolesi E, Milani G, Lourenço PB (2016) Implementation and validation of a total displacement non-linear homogenization approach for in-plane loaded masonry. Comput Struct 176:13–33
Betti M, Galano L, Vignoli A (2015) Time-history seismic analysis of masonry buildings: a comparison between two non-linear modelling approaches. Buildings 5(2):597–621
BIS (2002) IS 1893 (Part 1): Indian standard criteria for earthquake resistant design of structures. Bureau of Indian Standards, New Delhi
Boen T (2006) Yogya earthquake 27 May 2006: structural damage report. EERI
Bracchi S, Rota M, Penna A, Magenes G (2015) Consideration of modelling uncertainties in the seismic assessment of masonry buildings by equivalent-frame approach. Bull Earthq Eng 13(11):3423–3448
Calabrese A, Losanno D, Spizzuoco M, Strano S, Terzo M (2019) Recycled rubber fiber reinforced bearings (RR-FRBs) as base isolators for residential buildings in developing countries: the demonstration building of Pasir Badak, Indonesia. Eng Struct 192:126–144
Calderini C, Lagomarsino S (2008) Continuum model for in-plane anisotropic inelastic behavior of masonry. J Struct Eng 134(2):209–220
Calvi GM (1999) A displacement-based approach for vulnerability evaluation of classes of buildings. J Earthq Eng 3(3):411–438
Caporale A, Parisi F, Asprone D, Luciano R, Prota A (2014) Micromechanical analysis of adobe masonry as two-component composite: influence of bond and loading schemes. Compos Struct 112:254–263
Chaudhary MTA (2014) Seismic vulnerability mitigation of non-engineered buildings. World Acad Sci Eng Technol Int J Civil Environ Struct Constr Architect Eng 8(4)
Chopra AK (1995) Dynamics of structures: theory and applications to earthquake engineering. Prentice Hall. Inc., Upper Saddle River, NJ
Choudhury T, Milani G, Kaushik HB (2015) Comprehensive numerical approaches for the design and safety assessment of masonry buildings retrofitted with steel bands in developing countries: the case of India. Constr Build Mater 85:227–246
Choudhury T, Milani G, Kaushik HB (2020) Experimental and numerical analyses of unreinforced masonry wall components and building. Constr Build Mater 257:119599
Coburn A, Spence R (2003) Earthquake protection. John Wiley & Sons
Computers & Structures, Inc. (CSI) (2009) SAP2000-Integrated software for structural analysis and design. Comput Struct
COSMOS (2014) Strong‐motion virtual data center. Global component of the Center for Engineering Strong Motion Data: https://strongmotioncenter.org/vdc/scripts/default.plx
Das A, Deb SK, Dutta A (2016) Comparison of numerical and experimental seismic responses of FREI-supported un-reinforced brick masonry model building. J Earthq Eng 20(8):1239–1262
Elmenshawi A, Sorour M, Mufti A, Jaeger LG, Shrive N (2010) Damping mechanisms and damping ratios in vibrating unreinforced stone masonry. Eng Struct 32(10):3269–3278
Feng Y, Yi D, Bi Q (2011) Seismic design analysis of the country masonry school buildings in the meizoseismal area. Earthq Eng Eng Vib 10(3):359
Formisano A, Vaiano G, Fabbrocino F, Milani G (2018) Seismic vulnerability of Italian masonry churches: the case of the Nativity of Blessed Virgin Mary in Stellata of Bondeno. J Build Eng 20:179–200
Gambarotta L, Lagomarsino S (1997) Damage models for the seismic response of brick masonry shear walls. Part I: the mortar joint model and its applications. Earthq Eng Struct Dyn 26(4): 423–439
Giambanco G, Rizzo S, Spallino R (2001) Numerical analysis of masonry structures via interface models. Comput Methods Appl Mech Eng 190(49–50):6493–6511
Giordano N, De Luca F, Sextos A (2020) Analytical fragility curves for masonry school building portfolios in Nepal. Bull Earthq Eng 19:1121–1150
Gisbert JI, Bru D, Gonzalez A, Ivorra S (2018) Masonry micromodels using high order 3D elements. Proc Struct Integ 11:428–435
Habieb AB, Milani G, Tavio T (2018) Two-step advanced numerical approach for the design of low-cost unbonded fiber reinforced elastomeric seismic isolation systems in new masonry buildings. Eng Fail Anal 90:380–396
Hawileh RA, Rahman A, Tabatabai H (2010) Nonlinear finite element analysis and modeling of a precast hybrid beam–column connection subjected to cyclic loads. Appl Math Model 34(9):2562–2583
Hilber HM, Hughes TJ, Taylor RL (1977) Improved numerical dissipation for time integration algorithms in structural dynamics. Earthq Eng Struct Dyn 5(3):283–292
Illampas R, Charmpis DC, Ioannou I (2014) Laboratory testing and finite element simulation of the structural response of an adobe masonry building under horizontal loading. Eng Struct 80:362–376
Ip K, Dizhur D, Sorrentino L, Masia M, Griffith M, Ingham J (2018) Critical review of numerical modelling techniques for seismic response of complex URM buildings. In: Proceedings of 10th Australasian Masonry Conference, 11–14 February 2018, Sydney, Australia
IS13828 (1993) Improving earthquake resistance of low strength masonry buildings: guidelines. Bureau of Indian Standards
IS1905. (1987). Indian standard code of practice for structural use of unreinforced masonry. Bureau of Indian Standards
Kadam SB, Singh Y, Bing L (2020) Seismic fragility reduction of an unreinforced masonry school building through retrofit using ferrocement overlay. Earthq Eng Eng Vib 19:397–412
Kaushik HB, Rai DC, Jain SK (2007) Uniaxial compressive stress–strain model for clay brick masonry. Curr Sci 497–501
Lagomarsino S, Penna A, Galasco A, Cattari S (2013) TREMURI program: an equivalent frame model for the nonlinear seismic analysis of masonry buildings. Eng Struct 56:1787–1799
Losanno D, Calabrese A, Madera-Sierra IE, Spizzuoco M, Marulanda J, Thomson P, Serino G (2020) Recycled versus natural-rubber fiber-reinforced bearings for base isolation: review of the experimental findings. J Earthq Eng 1–20
Losanno D, Ravichandran N, Parisi F, Calabrese A, Serino G (2021) Seismic performance of a Low-Cost base isolation system for unreinforced brick Masonry buildings in developing countries. Soil Dyn Earthq Eng 141:106501
Lourenço, P. B. (1997). Computational strategies for masonry structures. PhD Thesis, Delft University of Technology, The Netherlands.
Lourenço PB (2000) Anisotropic softening model for masonry plates and shells. J Struct Eng 126(9):1008–1016
Lourenço PB, Rots JG (1997) Multisurface interface model for analysis of masonry structures. J Eng Mech 123(7):660–668
Lourenço PB, Milani G, Tralli A, Zucchini A (2007) Analysis of masonry structures: review of and recent trends in homogenization techniques. Can J Civ Eng 34(11):1443–1457
Madabhushi SPG, Haigh SK (2005) The Bhuj, India earthquake of 26th January 2001: a field report by EEFIT. Earthquake Engineering Field Investigation Team, Institution of Structural Engineers, London, UK
Magenes G, Calvi GM (1997) In-plane seismic response of brick masonry walls. Earthq Eng Struct Dyn 26(11):1091–1112
Magenes G, Penna A, Senaldi IE, Rota M, Galasco A (2014) Shaking table test of a strengthened full-scale stone masonry building with flexible diaphragms. Int J Arch Herit 8(3):349–375
Mahini SS (2015) Smeared crack material modelling for the nonlinear analysis of CFRP-strengthened historical brick vaults with adobe piers. Constr Build Mater 74:201–218
Mendes N, Lourenço PB, Campos-Costa A (2014) Shaking table testing of an existing masonry building: assessment and improvement of the seismic performance. Earthq Eng Struct Dyn 43:247–266
Menin RG, Trautwein LM, Bittencourt TN (2009) Smeared crack models for reinforced concrete beams by finite element method. RIEM-IBRACON Struct Mater J 2(2):167–182
Meoni A, D’Alessandro A, Cavalagli N, Gioffré M, Ubertini F (2019) Shaking table tests on a masonry building monitored using smart bricks: damage detection and localization. Earthq Eng Struct Dyn 248:910–928
Milani G, Tralli A (2011) Simple SQP approach for out-of-plane loaded homogenized brickwork panels, accounting for softening. Comput Struct 89(1–2):201–215
Milani G, Beyer K, Dazio A (2009) Upper bound limit analysis of meso-mechanical spandrel models for the pushover analysis of 2D masonry frames. Eng Struct 31(11):2696–2710
Minghini F, Milani G, Tralli A (2014) Seismic risk assessment of a 50 m high masonry chimney using advanced analysis techniques. Eng Struct 69:255–270
Naseer A, Khan AN, Hussain Z, Ali Q (2010) Observed seismic behavior of buildings in northern Pakistan during the 2005 Kashmir earthquake. Earthq Spectra 26(2):425–449
NTC (2018) DM 17.01.2018: Aggiornamento delle norme tecniche per le costruzioni. Ministero delle Infrastrutture e dei Trasporti (Gazzetta Ufficiale Supplemento ordinario n.8, 20.02.2018, Serie generale n.42), Rome, Italy
Parammal Vatteri A, D’Ayala D (2021) Classification and seismic fragility assessment of confined masonry school buildings. Bull Earthq Eng 19:2213–2263
Parisi F (2016). Seismic design of box-type unreinforced masonry buildings through direct displacement-based approach. Open Constr Build Technol J 10(1):293-311
Parisi F, Augenti N (2013a) Earthquake damages to cultural heritage constructions and simplified assessment of artworks. Eng Fail Anal 34:735–760
Parisi F, Augenti N (2013b) Seismic capacity of irregular unreinforced masonry walls with openings. Earthq Eng Struct Dyn 42(1):101–121
Parisi F, Augenti N, Prota A (2014) Implications of the spandrel type on the lateral behavior of unreinforced masonry walls. Earthq Eng Struct Dyn 43(12):1867–1887
Parisi F, Balestrieri C, Varum H (2019) Nonlinear finite element model for traditional adobe masonry. Constr Build Mater 223:450–462
Park YJ, Ang AH, Wen YK (1987) Damage-limiting aseismic design of buildings. Earthq Spectra 3(1):1–26
Pauletta M, Di Luca D, Russo E, Fumo C (2018) Seismic rehabilitation of cultural heritage masonry buildings with unbonded fiber reinforced elastomeric isolators (U-FREIs)—a case of study. J Cult Herit 32:84–97
Penelis GG (2006) An efficient approach for pushover analysis of unreinforced masonry (URM) structures. J Earthq Eng 10(03):359–379
PMAYMIS, Pradhan Mantri Awas Yojana (Urban)-PMAY (U) (2015) Ministry of Housing and Urban Affairs, Government of India 2015: https://pmaymis.gov.in/#
Priestley MJN, Calvi GM, Kowalsky MJ (2007) Displacement-based seismic design of structures. IUSS Press, Pavia
Quagliarini E, Maracchini G, Clementi F (2017) Uses and limits of the equivalent frame model on existing unreinforced masonry buildings for assessing their seismic risk: a review. J Build Eng 10:166–182
Ravichandran N (2020) A comparative study of phenomenological hysteretic models with application to recycled rubber-fibre reinforced bearings. J Vibroeng 22(8):1798–1813
Rots JG (1991) Numerical simulation of cracking in structural masonry. Heron 36(2):49–63
Santa-Maria H, Duarte G, Garib A (2004) Experimental investigation of masonry panels externally strengthened with CFRP laminates and fabric subjected to in-plane shear load. In: Proceedings of 8th US national conference on earthquake engineering. San Francisco, USA, Paper (No. 1042)
SAP2000, C. S. I. (2020) Analysis reference manual. Computers and Structures Inc, Berkley, California, USA
Sarkar A, Halder L, Sharma RP (2015) Seismic damage evaluation of unreinforced masonry buildings in high seismic zone using the nonlinear static method. In Advances in structural engineering. Springer, New Delhi, pp 1039–1053
Shahzada K, Khan AN, Elnashai AS, Ashraf M, Javed M, Naseer A, Alam B (2012) Experimental seismic performance evaluation of unreinforced brick masonry buildings. Earthq Spectra 28(3):1269–1290
Shrestha JK, Bhandari S (2020) A model for in-plane capacity of multi-leaf stone masonry walls. J Eng 2020:4028675
Singh Y, Lang DH, Prasad JSR, Deoliya R (2013) An analytical study on the seismic vulnerability of masonry buildings in India. J Earthq Eng 17(3):399–422
So E, Spence R (2013) Estimating shaking-induced casualties and building damage for global earthquake events: a proposed modelling approach. Bull Earthq Eng 11(1):347–363
Sorace S, Terenzi G (2011) Analisi sismica di edifici storici in muratura mediante modelli globalmente non lineari. In: Workshop on design for rehabilitation of masonry structures. Edizioni Polistampa Firenze, pp 302–313
Takai N, Shigefuji M, Rajaure S, Bijukchhen S, Ichiyanagi M, Dhital MR, Sasatani T (2016) Strong ground motion in the Kathmandu Valley during the 2015 Gorkha, Nepal, earthquake. Earth Planets Space 68(1):1–8
Thuyet VN, Deb SK, Dutta A (2018) Mitigation of seismic vulnerability of prototype low-rise masonry building using U-FREIs. J Perform Constr Facil 32(2):04017136
Tiwari P, Rao J (2016) Housing markets and housing policies in India. Asian Development Bank Institute, ADBI Working Paper 565, Tokyo
Vaiana N, Sessa S, Marmo F, Rosati L (2019) Nonlinear dynamic analysis of hysteretic mechanical systems by combining a novel rate-independent model and an explicit time integration method. Nonlinear Dyn 98(4):2879–2901
Vaiana N, Losanno D, Ravichandran N (2021) A novel family of multiple springs models suitable for biaxial rate-independent hysteretic behavior. Comput Struct 244:106403
Valente M, Milani G (2016) Non-linear dynamic and static analyses on eight historical masonry towers in the North-East of Italy. Eng Struct 114:241–270
Valente M, Milani G (2019) Damage assessment and collapse investigation of three historical masonry palaces under seismic actions. Eng Fail Anal 98:10–37
Willam KJ (1975) Constitutive model for the triaxial behaviour of concrete. Proc Intl Assoc Bridge Structl Eng 19:1–30
Wu F, Li G, Li HN, Jia JQ (2013) Strength and stress–strain characteristics of traditional adobe block and masonry. Mater Struct 46(9):1449–1457
Zimmermann T, Strauss A, Bergmeister K (2012). Energy dissipation and stiffness identification of unreinforced masonry. In: Proceedings of 15th international brick and block masonry conference, 3–6 June 2012, Florianópolis, Brazil
Acknowledgements
This study was carried out in the framework of Programme STAR (2017 LO-CO-ISO project), which is financially supported by University of Naples Federico II and Compagnia di San Paolo.
Funding
Open access funding provided by Università degli Studi di Napoli Federico II within the CRUI-CARE Agreement. This study was funded by University of Naples Federico II and Compagnia di San Paolo through 2017 STAR Programme.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ravichandran, N., Losanno, D. & Parisi, F. Comparative assessment of finite element macro-modelling approaches for seismic analysis of non-engineered masonry constructions. Bull Earthquake Eng 19, 5565–5607 (2021). https://doi.org/10.1007/s10518-021-01180-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10518-021-01180-3