Fragility estimation for global building classes using analysis of the Cambridge earthquake damage database (CEQID)

Abstract

This paper describes CEQID, a database of earthquake damage and casualty data assembled since the 1980s based on post-earthquake damage surveys conducted by a range of research groups. Following 2017–2019 updates, the database contains damage data for more than five million individual buildings in over 1000 survey locations following 79 severely damaging earthquakes worldwide. The building damage data for five broadly defined masonry and reinforced concrete building classes has been assembled and a uniform set of six damage levels assigned. Using estimated peak ground acceleration (PGA) for each survey location based on USGS Shakemap data, a set of lognormal fragility curves has been developed to estimate the probability of exceedance of each damage level for each class, and separate fragility curves for each of five geographical regions are presented. A revised set of fragility curves has also been prepared in which the bias in the curve resulting from the uncertainty in the ground motion parameter has been removed. The uncertainty in the fragility curves is evaluated and discussed and the curves are compared with those from other studies. A resistance index for each class of building is developed and cross-regional comparisons using this resistance index are presented.

1 Introduction

Reliable earthquake loss estimates depend on developing an understanding of building structures’ performance in each earthquake-risk country, whether for real-time impact notifications, insurance catastrophe modelling or mitigation planning. Sufficiently detailed data on building performance in past earthquakes can be used to develop fragility functions for the building classes found in each country or region, and also to estimate the uncertainty in those fragility functions. Although in recent years there has been a tendency to depend on calculated fragility functions, for most areas of the world there is currently insufficient knowledge of the structural materials and building techniques used in the building stock for fragility estimates to be reliably based on calculations of structural performance. Even where calculated fragility functions can be used, the parameters used, and the uncertainties assumed, need to be calibrated against observed damage. Thus the compilation of damage databases, and the comparison of damage with either observed or estimated ground motion at the same locations, remains a vital activity to support earthquake loss estimation studies.

Since the 1980s, the Department of Architecture at the University of Cambridge in association with Cambridge Architectural Research Ltd. has been assembling data on building performance in earthquakes, and on the associated casualties. And since 2007, this data has been made widely available through an online GIS database, the Cambridge Earthquake Impact Database (CEQID, www.ceqid.org). Between 2017 and 2020, a major upgrade of this database was carried out, providing many additional earthquake damage and casualty surveys, and streamlining the analysis capabilities associated with the database.

In a single expandable and web-accessible database, CEQID assembles summary information on worldwide post-earthquake building damage surveys which have been carried out since the 1980s, and some older survey data. Currently it contains data on the performance of more than 5 million individual buildings in 1003 survey locations following 79 separate earthquakes.

An important aspect of CEQID not found in other such databases is that it includes cross-event analytical tools enabling data from different events affecting similar building types to be assembled. This facilitates derivation of fragility relationships for any chosen ground motion parameter, for a given class of building, and for particular countries or regions.

The paper describes the organisation of the database, and summarises the data available in it, showing how it varies by country, region and building type. It discusses how problems in developing fragility relationships from data in which both building typologies and damage states are defined in a variety of different ways were addressed. It presents a statistical analysis of the data available for five broad classes of buildings: Weak Masonry (WM); Unreinforced Masonry (URM); and Reinforced Concrete Frame classes according to level of earthquake-resistant design Low or absent, Medium and High (RCFL, RCFM and RCFH respectively) across different regions of the world.

The paper then presents new fragility curves for five classes of damage against peak ground acceleration derived from USGS Shakemap data (www.usgs.gov/shakemap), assuming a lognormal distribution, for each of these building classes in the global dataset and for particular defined regions. For each class it also develops a set of resistance indices applicable to the different regions. In developing the fragility curves, it applies a newly developed approach to the removal of the bias in the fragility curve resulting from the uncertainty in the ground motion used. The paper examines the uncertainty in the fragility curves and compares the resulting curves with those derived from other studies.

2 CEQID: description of the database

Geographic open data repositories are an important source of updated data in different fields of activities. In the field of Earthquake Engineering, there are several open data repositories which offer available data very useful for multiple applications in seismic risk studies. The Copernicus Emergency Management Service (https://emergency.copernicus.eu/) and the PAGER System (https://earthquake.usgs.gov/data/pager/) (Jaiswal and Wald 2008) provides estimates of location and ground motion, damage and fatalities within hours after significant earthquakes worldwide; the World Housing Encyclopaedia (www.world-housing.net) is designed to assist in improving global construction practices; and the Global Earthquake Model (GEM) (https://www.globalquakemodel.org/gem) provides the basis for developing a set of earthquake data and models for use worldwide (Silva et al. 2020).

CEQID currently contains data for 79 events. For each event in CEQID, information about the earthquake including the date, time, depth and the location of the epicentre, all derived from the USGS Shakemap archive are reported. For each event there are one or multiple studies from different organisations or academic institutions. These include reports from the Earthquake Engineering Field Investigation Team (EEFIT), the Earthquake Engineering Research Institute (EERI) and Geotechnical Extreme Events Reconnaissance (GEER), as well as data from the Global Earthquake Model (GEM) Earthquake Consequences Database, and academic papers. For each study used, CEQID identifies the data source, and tables are provided defining the different building classes and the different damage levels (Tables 1 and 2).

Table 1 Example of data provided in CEQID for the 2016 Central Italy earthquake. Definition of damage levels used.

Table 2 Example of data provided in CEQID for the 2016 Central Italy earthquake, Definition of building classes used

Each study may include multiple surveys in different locations. For each survey location the web page will include information on the distance to the epicentre, intensity, peak ground acceleration (PGA) and peak ground velocity (PGV) derived from the USGS Shakemap archives (Wald et al. 2008) and the USGS global Vs30 map, which enables the ground motion parameters to be estimated using a GIS mapping system.

For each survey location the database also, as its primary purpose, provides information about building damage level and/or casualty levels. When entering the survey in the database, the definitions within each study are used to define the building types and damage levels, which then creates a table, known as a damage matrix (such as Table 3) where the number of buildings within each category are defined e.g. number of buildings with ‘damage grade 2’ constructed from a ‘reinforced concrete frame’. Casualty data, where available, are similarly recorded.

Table 3 Examples of data provided in CEQID for the 2016 Central Italy earthquake, Damage matrices for 5 locations showing numbers of buildings of each class in each damage level (including undamaged buildings)

The format of the primary data and amount of detail varies depending on the study. In most studies there are tables with a breakdown of different building types and then the number of buildings in each damage level, as in Table 3. In other surveys, studies may provide a graphical representation, such as a pie chart, of damage levels and buildings types, and the data inserted into CEQID has been extracted from that. Alternatively, a map may be provided with pin points for buildings, their construction type and damage level and overall figures calculated. As there is a large variation in the damage scales and the classification of the building stock used in different studies ‘superclasses’ have been assigned to allow for cross event analysis, this is explained further in Sect. 3.3.

A number of earlier papers have described CEQID and presented analyses based on the assembled data (So and Spence 2013), Polidoro and Spence (2015). This paper is the first to be based on the 2020 CEQID upgrade, and the first to attempt a regional analysis of the data.

3 Analysis of the data

3.1 Geographical Information mapping system

A complete set of earthquake data was downloaded from the CEQID platform to create an extensive database. Data has been standardized in order to create a Geographical Information System (GIS) and conduct a global scale spatial analysis. In seismic risk studies, it is important to define the hazard and vulnerability. These two main variables alongside the exposure provide fatality and economic loss impact (Coburn and Spence 2002). On the CEQID platform these two variables are obtained through the earthquake magnitude and the building classes. Building damage and casualties can also be obtained. In addition, other relevant information including the percentage of the number of buildings collapsed in a location, provide an insight into the earthquake resistant design level of the buildings or the year of occurrence of the event as a sign of the seismic activity in the area.

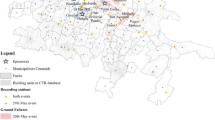
Examples of the global maps generated are shown in Fig. 1a and b. Figure 1a shows the location of each event in the database, and the average percentage of buildings in the damage surveys which collapsed. Figure 1b shows the magnitude of each event in the database, and, country by country, the proportion of the total recorded deaths in the complete CEQID database. The countries with the greatest number of casualties recorded in the database are China, Pakistan, Iran and Indonesia, which is broadly consistent with the global distribution of casualties over the 20th century (Coburn and Spence 2002).

Fig. 1

a spatial distribution of the percentage of buildings collapsed by event; b spatial distribution of the percentage of casualties of total CEQID data

3.2 Identification of building classes grouping by countries

The different countries with data in the CEQID database have been merged into five regions to account for differing construction techniques and materials of each region. The five regions are: Asia, Australasia, Latin America, Europe and the Middle East. New Zealand and Australia are grouped together under the region Australasia. For the present analysis neither the USA nor Japan are included in the regional groupings defined.

Table 4 shows the countries included in each of the defined regions. The Asian region contains the greatest number, with 6 countries and 11 separate events. In Europe there are 5 affected countries, with 20 earthquakes reflecting (especially in Italy) a more active programme of gathering post-event damage data. There are also 4 Middle Eastern countries (8 events) and 2 Latin American countries (2 events) represented in the database.

Table 4 Countries and number of events in each region

Table 5 shows the uneven distribution of building type in seven overarching building classes defined in CEQID accounting for 259,742 buildings: weak masonry (26%), unreinforced masonry (31%), reinforced concrete, with different levels of earthquake resistant design (42.2%%), timber (0.7%) and steel (0.1%).

Table 5 Number of buildings of the different building types and relation between building type of CEQID in the events shown in Table 2

However, as shown in Fig. 2 this distribution varies significantly depending on the country and region. A regional breakdown, as shown in Fig. 2, is therefore more appropriate as data within the database is dominated by some regions. In Latin America, the entirety of the building stock documented is reinforced concrete, representing 63% of all reinforced concrete buildings in CEQID, while in Europe the majority of the buildings are either weak or unreinforced masonry, representing 97 and 94% respectively of all buildings of those classes within the database.

Fig. 2

distribution of the buildings and building types in the five regions

The distribution also varies significantly for the countries within the different regions. Using European countries as an example, weak masonry buildings have only been classified in two of the five countries, Greece and Italy, with 95% of the documented weak masonry buildings in CEQID being in Italy. For reinforced concrete, buildings are documented in four European countries with the following distributions: Greece (50%), Italy (44%), Spain (5%) and Romania (0.3%).

This skewed distribution in the data is important to acknowledge as it results in an uneven representation of the global building stock at risk. Assembly and analysis of more data in the future is essential to provide a better representation.

3.3 Cross-event damage analysis: definitions of “superclasses”

The different studies in CEQID give various descriptions of the stages of damage. These definitions are grouped according to the classes defined in the EMS-98 scale (Grünthal 1998) to obtain damage “superclasses”: DS0, DS1, DS2, DS3, DS4 and DS5. The damage state descriptions are as follows: DS0—No damage; DS1—Negligible to slight damage (no structural damage, slight non-structural damage); DS2—Moderate damage (slight structural damage, moderate non-structural damage); DS3—Substantial to heavy damage (moderate structural damage, heavy non-structural damage); DS4—Very heavy damage (heavy structural damage, very heavy non-structural damage) and DS5—Destruction (very heavy structural damage).

For many of the studies, the damage classes used were already defined using the EMS-98 classes defined above. However, in some other cases, a six-point damage scale was used, though using slightly different linguistic definitions which were considered sufficiently close for the EMS-98 classes to be used as equivalent. In a few cases, notably a number of Italian earthquakes, a nine-point damage scale was used, requiring some damage classes to be grouped together to create the required six-point scale. In a few other cases less than 6 damage grades were defined, and judgements were needed to divide the data points in one or more of the classes, using information used in the original data source.

4 Lognormal fragility functions

Empirical fragility functions derive from damage observed in past earthquakes. Fragility functions express the probability of damage to a class of structures as a function of the ground motion excitation causing that damage. Empirical fragility functions are assumed to be applicable to future events affecting the same class of buildings. Empirical fragility functions thus take into account damage scales, structure classes and ground motion. The functional form of the relationship between the measure of ground motion and probability of damage also has to be considered.

For the present study, the damage scale used is that proposed in Sect. 3.3). Peak ground acceleration (PGA) obtained from the USGS shakemap archives (Wald et al. 2008), was chosen to characterize the ground motion. The relationship between PGA and probability of damage is represented with a cumulative lognormal relationship, as nowadays very widely adopted (Kappos et al. 2006; Polidoro and Spence 2015). A lognormal fragility function assumes that the logarithm of the PGA at which a building gets damaged is normally distributed, with mean value here defined as ln µ and standard deviation σ. Equation (1) defines the fragility function of the building class and is entirely defined by the two parameters µ and σ.

$$P_{K} \left( {{\text{PGA}}} \right) = ~\Phi \left( {\frac{{~\ln {\text{PGA}}_{e} - ~\ln \mu }}{\sigma }} \right)$$

(1)

where P_K(PGA) is the probability of exceedance of damage state K at the given PGA, and Φ is the standard normal cumulative distribution function. The parameter µ is the median PGA at which damage occurs, or, in terms of damage, the 50th percentile damage state probability. In this study “binned” CEQID data, explained in more detail in Sect. 4.1, is used to determine this lognormal distribution, using a least squares regression procedure.

4.1 Bin creation

For each building class, data was grouped into 10 ranges of PGA: < 0.1 g; 0.1 to 0.15 g; 0.15 to 0.2 g; 0.2 to 0.25 g; 0.25 to 0.3 g; 0.3 to 0.35 g; 0.35 to 0.4 g; 0.4 to 0.5 g; 0.5 to 0.6 g; 0.6 to 0.7 g. For data points in each bin, the mean value of the probability of exceedance of each damage state was evaluated. This value was calculated by weighting the probability of exceedance of each damage state with the number of surveys observed in each event belonging to that range. In all the regions there are more buildings damaged with intermediate values of PGA, 0.25 to 0.5 g. For lower values, (PGA < 0.1 g) and higher values (PGA > 0.5 g), the number of damaged buildings are fewer.

4.2 Fragility curves for building typologies

Five damage states were considered ranging from slight (DS1) to complete damage (DS5). An important feature of the resulting cumulative lognormal fragility curves for different damage states is that they must not cross each other, since that would imply probability of exceedance of a higher damage state larger than that for a lower damage state, which is not possible. This requires that the σ values for each damage state for any building class are the same, and the regression is carried out with this requirement. Three different values of σ (for masonry 0.8, 0.6 and 0.4) were used across all the damage states, and the σ value for which the dispersion of the data was the smallest was selected,

Table 6 shows the fragility parameters µ and σ for the 5 building classes defined in Sect. 3. In general the highest values of µ for all buildings classes and damage states are in Europe. For certain damage states, shown with an asterisk, there is very limited data. For RCFM and RCFH in Europe, data is almost exclusively from one event (The Lefkada, Greece event of 2003), and the building type classification is uncertain.

Table 6 Parameters (μ and σ) of the lognormal fragility curves for the five regions and across all regions in the different building classes

5 Unbiasing the regression curves

As reported elsewhere (Ader et al 2018; Ioannou, et al 2015), fragility curves derived from data in which the PGA is uncertain, for example in the USGS Shakemap values used here, have larger variances (σ) than the “true” curve which would be derived from the actual PGA at the location of the survey. This problem has been addressed by Ader et al (2018), who have presented a process for removing this bias and estimating an unbiased fragility curve. The Ader process has been adopted here to estimate the parameters of the unbiased fragility curve.

The parameters used are defined as follows:

• σ_est is the estimate of the variance of the lognormal fragility distribution derived from the original data points.

• σ is the unbiased estimate of the variance of the lognormal fragility distribution

• σ_PGA is the uncertainty in the ln(PGA), based on the ground motion prediction equation used.

• σ_D is the standard deviation of the ln(PGA) of the data points projected onto the original estimated fragility curve by minimising the distance between the data point and the curve.

The value of σ can be estimated from the following relationship:

$$\frac{{\sigma _{{{\text{est}}}} }}{\sigma } = ~\sqrt {1 + \lambda ^{2} \frac{{\sigma _{{{\text{PGA}}}} ^{2} }}{{\sigma _{D} ^{2} }}~}$$

(2)

where the parameter λ² is found (Ader et al. 2018) to have the approximate value of 1.66.

As Ader et al. (2018) point out, to be rigorous σ_D should be estimated by projecting the data points onto the true fragility curve rather than the original biased fragility curve. Thus, a better estimate of σ can be found by iteratively updating the value of σ_D and the resulting unbiased fragility curve. In this study only two iterations were used as it was found that further iterations made no significant difference given the data uncertainties.

The value of σ_PGA to be used derives from data given by Worden et al (2012) describing the Shakemap archive. Its value depends not just on the ground motion prediction equation used, but also on whether any observed ground motion data was available. Although for some locations in the Shakemap archive σ_PGA varies from 0.4 to 0.7, for the vast majority of the Shakemap dataset σ_PGA = 0.5, and this value has been adopted here.

In this study the value of σ_est was found by a least squares regression process as described earlier. The projected points were found by finding the distance from the data point to the nearest point on the regression curve using Excel’s Solver routine.

The calculation of the unbiased σ as described above was carried out for the DS1 fragility curves for the 5 building classes, and the σ values for DS1 were then used for the fragility curves for all damage states, for the reasons explained in Sect. 4.2 above. The values of µ for each damage state were then determined using least squares regression based on the revised σ.

For each of the five regions, the values of the unbiased σ, and associated values of µ for each building class and each damage state are given in Table 7. The resulting lognormal fragility curves for building class RCFL in each region are shown in Fig. 3. It is important to note that only in Europe were all the 5 classes represented in the available data.

Table 7 Parameters (μ and σ) of the unbiased fragility curves for the five regions and across all regions in the different building classes

Fig. 3

Lognormal fragility curves for building class RCFL in each region and all regions

6 Analysis and discussion

6.1 Damage Index

To analyse the damage and make comparisons between different regions and building classes, a damage index (DI) is defined combining the damage across all the damage states.

The damage index (DI) is defined here as:

$${\text{DI}} = (\mathop \sum \limits_{{K = 0}}^{5} P\left[ {D = K} \right].K)~/5~$$

(3)

where DI is the damage index for a set of buildings, K = 0,1,2,3,4,5 are the 6 damage states and P[D = K] represents the probability of occurrence of a certain damage state, K

Figure 4 shows the average lognormal relationship of the damage index to ground motion (PGA) for two of the largest classes of buildings in the dataset, weak masonry (WM) and unreinforced masonry (URM), with different curves plotted for the different regions where data is available, and an average curve for the CEQID dataset as a whole.

Fig. 4

Relationship of Damage Index (DI) to peak ground acceleration (PGA) for buildings of classes WM (weak masonry), and URM (unreinforced masonry), comparing performance of these classes in the different regions and for the all regions database as a whole

For both building classes, it can be seen that the damage in countries in the Asia and the Middle East regions is higher than the all regions average, while that in Europe and Australasia (URM only) is lower than the average. For these two classes the regional differences are very significant. The differences may to some extent be due to variations in the way in which the building classes have been defined in the different regions, but a large part of the difference is the result of standards of building, in particular the absence of effective building regulations and building control in most Asian and Middle Eastern countries, particularly in rural areas, where most of the earthquake damage has occurred (Spence and So 2021).

6.2 Resistance index

To facilitate comparison between the fragility of different classes of building region by region, a Resistance Index (RI) has been defined. The resistance index for a class of building is defined as the PGA value corresponding to a damage index (DI) of 50% using the average relationship of PGA to damage index. Thus, a high resistance index implies better resistance to earthquake ground shaking.

Table 8 shows the value of the resistant index for the three most common building classes in each of the 5 regions and for the all regions database as a whole. The chart in Fig. 5 plots these values to show the relationships graphically. The relationship between the resistance index for the three classes is the same for all regions, WM having the lowest, and RCFL the highest of the three. The data again show the higher than average resistance index for Europe and Australasia (and also Latin America), where only RCFL is represented, slightly lower than average for Middle East, and significantly lower for Asia, reflecting the regional differences already noted. The resistance index is potentially a useful tool for loss estimation and loss modelling, and also to help prioritisation strategies for retrofit or replacement of existing buildings.

Table 8 Resistance Index by region for buildings in classes WM, URM and RCFL

Fig. 5

Resistance Index for the three most common building classes in each of the 5 regions and all regions

6.3 Comparison with existing fragility curves

Validation of the fragility functions can be done by comparison with independent post-earthquake observations (Orsini 1999; Rossetto et al. 2013; Spence et al. 2003). In other studies the validation consists of a comparison with functions constructed for similar asset types by the same or other authors (Yamaguchi and Yamazaki 2000; Colombi et al. 2008; Elefthiadou and Karabinis 2011).

In this study post-earthquake survey damage data for buildings has been represented into parametric probability distribution in different regions, using a lognormal distribution of observed damage against PGA. According to various research teams (Haselton et al. 2011; Lazar and Dolšek 2014; Martins and Silva 2020), for regular buildings, the σ values for the complete damage state should vary between 0.30 and 0.8. In this study the unbiased σ values obtained are σ = 0.6 for WM and URM and σ = 0.5 for RCFL, RCFM and RCFH, which is within this range.

To compare the fragility curves obtained with recent empirical fragility models (Rosti et al. 2020), fragility functions for masonry classes, in terms of damage index, were analysed. The correlation between the typologies of this study and Rosti et al. (2020) was completed by grouping together structure types that would be expected to behave similarly during a seismic event. The plotted curves for the different typologies are shown in Fig. 6. Although the slopes of the curves are different, in the range of PGA 0.3–0.8, the curve of this study covers the probability of exceedance of damage index with all the typologies compared.

Fig. 6

Comparison of CEQID relationship of damage index with curves of Rosti et al. (2020) for European weak masonry (WM) and for European unreinforced masonry (URM)

6.4 Analysis of uncertainty

The assessment of the uncertainty in the fragility curves requires a comparison between the estimates and observed damage (Ioannou 2012). This study was carried out by analysing the standard deviation of the observed damage and the residuals between the estimates and observed damage. The standard deviation describes the dispersion of the observed damages data in the different events and for ranges of PGA (bins). Table 9 shows for the building typology URM the amount of data in the different regions in each bin of pga and the standard deviation of the different damage states. There is a greater amount of data in bins where PGA is less than 0.3 g. For these bins, in the majority of the cases, in DS1 and DS2, the dispersion in the data is bigger than in DS3, DS4 and DS5.

Table 9 Standard deviation of observed damage in bins of PGA in different regions for the building typology URM

For testing the randomness of the data, we analyse the residuals. In this study there are no biases in the residuals (trends) or a non-constant dispersion (variance) for the different regional groups and damage states. The residuals for the building typology URM in damage state DS1 are shown in Fig. 7.

Fig. 7

Residuals for the building typology URM in damage state DS1

7 Conclusion

This study has described the development of empirical fragility curves derived from the Cambridge Earthquake Impact Database (CEQID). The fragility models developed within this study are derived from a robust database, with 79 earthquake events and 259,742 buildings, from the 1980s to 2016. CEQID is a compilation of data on building performance in earthquakes in various countries or regions, which has been described in detail.

The initial step in the analysis was to group countries into regions taking into account construction techniques and materials. The output of the study included five regions: Asia, Australasia, Latin America, Europe and the Middle East with five broadly-defined building classes: weak masonry (WM), unreinforced masonry (URM), reinforced concrete frame low-code, medium-code and high-code (RFCL, RFCM and RFCH). The outlined methodology defines damage in 6 damage classes consistent with the classes defined in the EMS-98 macroseismic scale (Grünthal et al. 1998). The new fragility curves within this study are based on peak ground acceleration derived from USGS Shakemap ground motion data. In developing the fragility curves, the study applies a recently developed approach to the removal of the bias in the fragility curve resulting from the uncertainty in the ground motion used.

A Resistance Index (RI) has been defined to facilitate comparison between the fragility of different classes of building region by region. The RI enables a comparison of fragility for different building classes, where higher values indicate a better behaviour of the building class in that region. In all the regions, the higher values obtained are for reinforced concrete and the lowest for weak masonry (WM), with unreinforced masonry (URM) having intermediate values. Europe and Australasia have the best behaviour in all the typologies.

Consideration was given to the validation and assessment of the uncertainty in the fragility curves proposed in this study. To this end, the fragility curves were compared with studies in the literature. European fragility curves were compared with a recent empirical model (Rosti et al. 2020), obtaining a reasonable agreement for WM and URM curves. Comparison with additional published fragility curves will be possible following an anticipated further analysis of this data against spectral acceleration values appropriate to each building class.

To assess the uncertainty, the standard deviation of the observed damage and the residuals between the estimates and observed damage were analysed. The standard deviation of the fragility curves shows that in DS1 and DS2 the dispersion in the data is bigger than in DS3, DS4 and DS5. The analysis showed that there are no biases in the residuals (trends) or a non-constant dispersion (variance) for the different regional groups and damage states.

The authors consider that, while calculated fragility is increasingly used in loss assessment, empirical approaches to fragility will continue to be important, both to validate other approaches and to show the real dispersion of damage data. To enable empirical fragility curves to be updated, post-event damage data must continue to be assembled and archived, and made freely available to users. New methods of data acquisition using remote sensing will become increasingly important (Stone 2017), and standardised methods of archiving and analysis appropriate to such data will need to be developed.