Modelling the seismic response of a 2-storey URM benchmark case study: comparison among different equivalent frame models

Abstract

The paper presents the comparison of the results of non-linear static analyses performed with different software based on the equivalent frame (EF) modelling approach on a simple two-story unreinforced masonry building with rigid diaphragms. This study is part of a wider research activity carried out in the framework of the Italian Network of Seismic Laboratories (ReLUIS) projects, funded by the Italian Department of Civil Protection. Different configurations have been considered varying the layout of the openings on the bearing walls and the structural details. The EF models have been defined adopting as much as possible common assumptions, in order to reduce the epistemic modelling uncertainties and to facilitate the interpretation of the differences in the results obtained by the software. The comparison involved different aspects: the global scale response, in terms of capacity curves, the predicted damage pattern as well as checks at the local scale, in terms of distribution of the generalized forces. Moreover, in order to assess the reliability of the obtained results, the numerical predictions have been compared to an analytical upper bound reference solution. Finally, the sensitivity of the numerical response to the criterion adopted for the EF idealization of masonry walls has been investigated.

1 Introduction

The use of computer programs is nowadays a common practical resource for researchers and professional engineers. In fact, software packages are useful, if not quite indispensable, both for the design of new structures and for the assessment of existing ones. The problem of their reliability and correct use is therefore more and more recognized by associations and codes, representing a critical issue for the correctness of the obtained numerical results. As an example, the Italian Technical Code (NTC 2018) makes explicit reference to the need of verifying the reliability and suitability of the software adopted, as well as the correctness of the achieved results.

In the specific field of masonry buildings, in the last decades the Equivalent Frame (EF) modelling approach has achieved great success, both at research level and for practice engineering aims, due to its simplicity of implementation and computational efficiency with respect to the Finite Element (FE) approach, even for non-linear analyses. Indeed, at present, many commercial software for the analysis of masonry buildings adopt this approach, such as ANDILWall (Manzini et al. 2006), PRO_SAM (Manzini et al. 2019), 3Muri (Lagomarsino et al. 2013), Aedes.PCM (Spacone and Camata 2007). Moreover, the EF approach can be effectively implemented in general purpose software packages directly by analysts, as for example in SAP2000 (e.g. by Kappos et al. 2002; Salonikios et al. 2003; Pasticier et al. 2008). The wide availability of EF model-based computer programs results in a huge variety of options, but also in a potential scattering of achievable results (e.g. Mendes et al. 2017; Esposito et al. 2019; Parisse et al. 2021), especially when analysts adopt the default settings, without proper knowledge of the software features and experience in the modelling approach.

Only few comparative studies are available in the literature on this topic (e.g. Marques and Lourenço 2011 and 2014; Betti et al. 2014; Calderoni et al. 2015; De Falco et al. 2017; Aşıkoğlu et al. 2020); moreover, they are often not conclusive in quantifying the uncertainty associated to the software-to-software variability. In order to fill this gap, a wide research program has been carried out starting from 2014 by several Italian Universities involved in the Italian Network of Seismic Laboratories (ReLUIS) projects, funded by the Italian Department of Civil Protection. In such a project, hereinafter named as “URM nonlinear modelling - Benchmark project” (Cattari and Magenes 2021), different benchmark case studies of increasing complexity have been designed and analysed using a large set of software packages based on various modelling approaches.

Within this context, the paper presents the comparative study carried out on the benchmark structure BS4, a single-unit two-story unreinforced masonry (URM) building with rigid diaphragms. In particular, the results of non-linear static analyses performed with seven commercial software based on the EF approach are presented, while Cannizzaro et al. (2021) treats the same topic with reference to software packages employing different FE modelling strategies using either two- or three-dimensional elements.

Though BS4 is a case study significantly easier than the structures practitioners usually deal with, its analysis is certainly useful to focus on specific issues related to the seismic assessment of masonry buildings, providing information about the role on the actual response of a series of effects that affect the action redistribution among the bearing walls. For example, it highlights the role of the axial load variation on the flexural and shear strength of masonry piers, the effects of the interaction between piers and spandrels and of the presence of tensile resistant elements coupled to the latter. Moreover, 3D analysis allows to study the effects of the stress redistribution in the presence of intersecting walls with significantly different stiffness (i.e. the so called “flange” effect) as well of torsional effects.

The main objective of this study is to quantify the dispersion of the numerical results achievable using different software when adopting shared modelling assumptions. This choice reflected the will to reduce the epistemic uncertainties and the influences of the arbitrariness of analysts, which would have produced a higher scattering of results (as highlighted in other studies, e.g. that discussed in Parisse et al. 2021), in order to facilitate the interpretation of the differences in the results obtained by the software.

After a description of the considered benchmark case study (Sect. 2), the paper presents in detail the software packages used to perform the analyses and the shared modelling and analysis assumptions (Sect. 3) and the standardized criteria adopted for the comparison of the numerical results (Sect. 4). The analytical procedure for the evaluation of a reference upper bound solution is hence illustrated (Sect. 5), followed by a comprehensive discussion of the obtained numerical data (Sects. 6, 7), in terms of model mass, initial distribution and variation during the analysis of the normal forces, local and global capacity curves, equivalent bi-linear curves, damage prediction and comparison of the numerical response with the analytical reference solution. Finally, a parametric study on the sensitivity of the results to the adopted EF idealization is reported in Sect. 8.

The set of data herein reported (integrated by those illustrated in Cattari and Magenes 2021), on the one hand, allows the replication by other researchers and analysts of the investigated structures and, on the other hand, may represents a useful reference for the comparison of the results achievable with other software. In this way, it is expected that the presented topics will constitute a useful contribution for both professional engineers and the scientific community.

2 Description of the benchmark case study

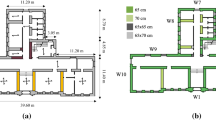
BS4 is a single-unit two-story URM building with rigid diaphragms, inspired by a full-scale brick masonry structure subjected to static cyclic tests carried out at the University of Pavia in mid 1990s (Calvi and Magenes 1994; Magenes et al. 1995). The prototype was characterized by a rectangular plan of 6.0 × 4.4 m² and only four perimeter walls with thickness of 0.25 m and a total height of 6.44 m. Starting from this geometry, different configurations have been defined, by varying the opening pattern on the walls and some structural details concerning the pier-spandrel interaction.

With regard to the opening pattern, two geometries have been considered for the longitudinal walls, hereinafter referred to as I-type and II-type and illustrated in Fig. 1a. A symmetrical plan configuration and an asymmetrical one, named respectively as BS4_P1 and BS4_P2 in Fig. 1b, have been then defined, assembling the I-type and II-type walls in different ways and coupling them to blind transversal walls.

Fig. 1

Geometry of the considered benchmark case study: a masonry walls; b plan configurations (measures in cm)

It should be noted that in Fig. 1a, as well as in all the following Figs., the I-type and II-type walls are represented so that, with reference to the analyses performed in the positive X-direction, reported in Fig. 1b, the “upstream” piers (i.e. the panels at the loading side) are shown on the left side of both the walls.

Different structural details have been considered, in order to estimate the sensitivity of the numerical response to the variation of the effectiveness of the pier-spandrel interaction:

• case A: masonry spandrels not coupled to any tensile resistant element (configuration aimed to promote a “weak spandrel-strong pier” behaviour type);

• case B: masonry spandrels coupled to ϕ20 mm steel tie rods at each storey level;

• case C: presence of 0.25 × 0.25 m² reinforced concrete (RC) ring beams at each storey level with four ϕ16 mm longitudinal rebars and ϕ10 mm stirrups at 200 mm spacing;

• case D: starting from case C, the further condition of fixed rotations at each storey level has been imposed (“shear type” idealization).

Whereas in the case of BS4_P1 only the comparison between “weak spandrels” and spandrels coupled to steel tie rods has been considered, in the case of the more realistic non-symmetric plan configuration BS4_P2 the study of the effectiveness of the pier-spandrel interaction has been further deepened, by varying the typology of the tensile resistant elements coupled to the masonry beams and the boundary conditions. Table 1 summarizes the six analysed structural configurations, obtained combining the considered plan configurations and structural details.

Table 1 Identification of the considered structural configurations

The values of the mechanical properties assumed for materials are reported in Table 2.

Table 2 Mechanical properties of materials

In particular, the parameters of the masonry have been derived from the results of experimental tests performed by Anthoine et al. (1995) on piers characterized by a masonry typology consistent with that of the brickwork prototype inspiring BS4.

The shear strength of the masonry piers has been calculated according to the diagonal cracking criterion by Turnšek and Čačovič (1971) with the modification introduced in Turnšek and Sheppard (1980). The flexural strength of the panels has been evaluated through the criterion commonly proposed in the codes (e.g. CEN 2005; NTC 2018), neglecting the tensile strength of the material and assuming an equivalent rectangular stress block at the compressed toe.

As regards the masonry spandrels, two different approaches have been considered, depending on whether the axial forces are known or unknown from the analysis (e.g. as proposed in NTC 2018). In the former case, the spandrels are treated like piers, whereas in the latter the contribution of the spandrels to the global response can only be considered if a strut-and-tie mechanism can develop (i.e. a tension member must be present).

The effective strength of the elements has been computed as the minimum between the shear and the flexural strengths.

The ultimate deformation limit for the masonry piers and spandrels has been assumed equal to 0.4% and to 0.6% in case of shear and flexural failure mode, respectively. These values are consistent with the results of in-plane cyclic tests on unreinforced masonry piers, carried out within different research projects, available in the literature (e.g. Morandi et al. 2018).

Finally, it should be noted here that the adopted strength formulations and deformation limits are as valid as others, based on different code provisions and/or experimental reference data, as the aim of this study is independent of the starting assumptions, as long as they are plausible, shared and consistently applied by the various software used in the research. The same considerations apply in general to all the adopted modelling and analysis hypotheses, described in detail in Sect. 3.

3 Adopted software packages and modelling and analysis criteria

Within the “URM nonlinear modelling – Benchmark project”, BS4 has been modelled and analysed with a large set of software, adopting different modelling strategies. In this paper, the attention is focused on the results of non-linear static analyses performed on the configurations described in Sect. 2 with seven different software packages, all belonging to the EF approach. Although not exhaustive, the set of adopted software reflects the tools nowadays available in Italy; moreover, many are also used at international level.

Six of the software describe the response of the structural elements through non-linear frame elements with “zero-length” lumped plasticity, adopting bi-linear elastic perfectly plastic constitutive laws with a limitation of the maximum displacement:

• 3Muri (2016, release 10.0.1), developed by Lagomarsino et al. (2013) and distributed by S.T.A. DATA;

• Aedes.PCM (2017), based on the hinge formulation proposed in Spacone and Camata 2007 and distributed by Aedes;

• ANDILWall (release 3.1.0.0) and Pro_SAM (2020, release 20.7.0) (both the software are based on the SAM-II solver developed by Magenes et al. 2006; the former, used in the first years of the project, nowadays is no longer in distribution and has been replaced by the latter, distributed by 2Si);

• CDSWin OpenSees (2016), distributed by STS;

• MIDAS Gen (2017), distributed by MIDAS Information Technology Co.;

• SAP2000 (2016, release 18), distributed by Computers and Structures Inc.

Finally, a fiber model proposed in Spacone et al. (1996) and implemented in one of the above-cited software (MIDAS Gen 2017) has been adopted.

Figure 2 depicts 3D views of the EF models generated by the software, with reference to structure BS4_P2 as an example. It is noted that the geometric configurations of cases B and D correspond to those of cases A and C, respectively.

Fig. 2

3D views of the EF models generated with each adopted software

Since the purpose of this study is not to express a judgment on the reliability of the adopted software, an anonymous reference system has been adopted. In particular, random colours and tags (from SW1 to SW7) have been associated to the software packages, so as not to make identifiable the specific software in the discussion of the issues posed in the paper.

Non-linear static analyses have been performed assuming a “uniform” pattern of the lateral loads, acting in the positive X-direction (see Fig. 1). In particular, at each storey level the lateral load has been applied at the centre of the masses, considering no accidental transversal eccentricity. This choice is justified by the fact that in other studies (e.g. see Annex B to CNR-DT 212/2013 2014) the “uniform” pattern often resulted more consistent with the activation of seismic inertial forces in a strong non-linear phase. Moreover, in the case of two-storey buildings, like the considered one, no significant differences are expected from the application of the “uniform” and the “modal” patterns (e.g. Cattari et al. 2018).

The EF models have been defined adopting as much as possible common assumptions, described in detail below. When relevant, the solutions adopted by the software to manage some specific modelling aspects are also reported.

The same EF idealization of the considered structures, based on the criterion proposed by Lagomarsino et al. (2013), has been shared. With reference to the geometrical configuration BS4_P2 as an example, Fig. 3 depicts the adopted dimensions and numbering of masonry piers and spandrel. As shown in Fig. 3a, the longitudinal walls have been named W1-II and W3-I, while the transverse ones have been named W2 and W4. It should be noted that, in the definition of the dimensions of the masonry piers, as reported in Fig. 3b, the length of each corner element in W1-II and W3-I and of the panels in W2 and W4 has been reduced of half of the thickness of each intersecting wall, compared to the corresponding value resulting from Fig. 1. This was done in order to not overestimate the masonry resisting area.

Fig. 3

Geometrical configuration BS4_P2: identification of the longitudinal (in red) and transverse (in blue) walls (a) and of the masonry elements constituting each wall (S: spandrel; P: Pier) (b)

In the EF models where the presence of RC ring beams has been considered (cases C and D), the effective length of each RC beam, in all cases modelled as an inelastic frame element, has been assumed equal to the opening width for the evaluation of the stiffness and of the degree of constrain provided to the spandrels. Actually, the EF models in Fig. 2 only differ for the graphical representation criteria adopted by the software: whereas some show the deformable part, others sketch the total length of the RC beam elements. The mass has been instead unanimously assumed to be distributed along the whole perimeter of the structure.

Floors have been assumed as supported by the longitudinal walls and a total permanent floor load equal to 10 kN/m² has been considered at each storey level. The same distribution of the floor loads among the masonry piers of the longitudinal walls has been shared, based on proper assumptions on the tributary areas. Only in the case of SW7, 10% of the floor load has been attributed to each of the transverse walls to account for the possible redistribution of the axial load in the intersecting piers due to the “flange” effect when assuming a good connection between the masonry elements; furthermore, this redistribution has been kept constant during the analysis.

All the adopted software consider masses and gravity loads concentrated in the end-joints of the masonry piers, neglecting any torsional contribution in the single element.

Diaphragms have been assumed as infinitely stiff in their plane. When the software (SW1, SW4, SW5 and SW6) don’t directly manage this option through a kinematic condition, it has been conventionally assumed to model the diaphragms as RC slabs with 0.2 m thickness.

A perfect coupling between intersecting walls has been assumed. This condition is managed through different solutions by the software (see Cattari and Magenes 2021 for further details): perfect kinematic coupling of the vertical displacement of the piers constituting the flanged wall (SW1); rigid-link elements (SW2, SW3 and SW6) or equivalent beam elements with properly calibrated bending and axial stiffness (SW4 and SW5) connecting at each storey level the end-nodes of the piers. Finally, in SW7 a modification of the cross-section properties of each pier has been considered, assuming a “T” or “L” section with a length of the flange equal to a maximum of the half length of the incident panel.

In this study, the out-of-plane stiffness and strength contributions of the piers to the overall response of the structure have been neglected, having been judged as not particularly significant, given the reduced thickness of the masonry of BS4 (equal to 0.25 m). Indeed, all the software, except SW1, consider by default these contributions in the calculation: thus, in these cases, to be consistent with the aforementioned hypothesis, internal releases in the out-of-plane direction have been introduced at the end-joints of masonry piers. Within the “URM nonlinear modelling - Benchmark project”, the influence of the walls’ out-of-plane contribution has been investigated with reference to other BSs, characterized by higher thickness of masonry walls (Ottonelli et al. 2021). Moreover, the issue of the evaluation of URM walls’ out-of-plane behaviour and of its interaction with the in-plane response is still little investigated in the case of load-bearing masonry walls (e.g. Donà et al. 2020; Vanin et al. 2020; Kollerathu and Menon 2017; Cattari et al. 2021a) whereas, in recent years, it has been more extensively deepened in the case of masonry infills (e.g. Milanesi et al. 2021; da Porto et al. 2020; Ricci et al. 2018).

The effects of cracking have been considered. Whereas SW4 is capable to evaluate step-by-step the progressing stiffness degradation, in all the other software the flexural and shear stiffness contributions of each element have been conventionally assumed equal to one-half of the corresponding values in uncracked conditions and kept constant during the analysis, consistently with the provisions of the European Codes (e.g. CEN 2005 and NTC 2018). Depending on the software, this reduction is applied either to the cross-section moments of inertia and shear areas or to the elastic moduli of materials; the latter are reported in Table 2.

The evaluation of the displacement capacity of structural elements, to be compared to the adopted ultimate deformation limits, is based in the software on different formulations: in terms of drift computed by deducting the rotations contribution at the end sections (SW1), of drift computed by considering only the horizontal displacement contribution (SW3, SW4, SW5 and SW6) or of chord-rotation (SW2); in SW7, a threshold is assigned directly to the component of plastic rotation.

Unlike all the other adopted software, SW2 assumes in the damage assessment that, after the achievement of a failure condition in a non-linear element at a certain step of analysis, re-entry into the strength domain is possible if at a subsequent step the stress value becomes again lower than the corresponding strength. Hence, to the aim of the comparison with the results obtained by the other software, in this study the damage prediction for SW2 has been defined recording for each element the first occurrence of any failure mode, regardless of whether or not it is followed by a return to the safe domain.

Finally, it is stressed that in the EF models of structures BS4_P1/A and BS4_P2/A, the masonry spandrels have been modelled with SW4 and SW7 as axially rigid connecting rods, unlike all the other software, in which they have been considered as inelastic frame elements. This choice is justified by the assumption that, in the absence of any coupled tensile resistant element, the flexural strength of the spandrels is negligible when other resistance contributions are not considered, such as those due to the mechanical interlocking activated in the end-sections through the overlap of the masonry units.

4 Standardized criteria for the comparison of the numerical results

The global response of numerical models of URM buildings is clearly influenced by various aspects (Cattari et al. 2021a) such as the modelling assumptions, the implemented constitutive laws, the adopted strength criteria and the sensibility of the linear/non-linear transition phase of the structural elements to parameters governing the numerical convergence (e.g. tolerance, maximum number of iterations, etc.). Given the complexity of such a problem, a unique and rigorous reference solution cannot be evaluated. However, it is possible to adopt analytical tools aimed at avoiding gross errors resulting from a wrong input of the model parameters into the software, such as the check of the consistency of the total mass, and a methodological approach for the critical interpretation of the obtained results. In particular, after a brief general overview on the numerical response of the EF models (Sect. 6.1), the results of the performed analyses have been compared in terms of:

• total model mass (Sect. 6.2);

• normal stress acting at the base section of the masonry piers at the ground level of the EF models after the application of the dead loads (Sect. 6.3);

• variation of the axial load at the base of the masonry panels at the ground level deriving from the application of the lateral loads (Sect. 6.4);

• force–displacement (pushover) curves representative of the global response of the structure (Sect. 6.5);

• parameters defining the corresponding equivalent bilinear curves (i.e. the equivalent stiffness, K_s, the yielding equivalent base shear, V_y, and the ultimate displacement, d_u, as defined in MIT 2019), assumed as representative of the numerical response and hereinafter referred to as SRPs (Structural Response Parameters, Sect. 6.6).

For each of the above-listed parameters, the scattering of results has been evaluated in terms of percentage change with respect to an average reference value, calculated as the mean value across all the software, not being possible to differentiate the level of reliability of each one. An analytical solution has been also evaluated on the hypothesis of “shear-type” behaviour of the EF models (Sect. 5), constituting an upper bound for the numerical response, at least relating to the maximum base shear and to the stiffness of the walls and of the structure. The comparison of this reference solution to the results of the numerical analyses performed on BS4_P2/D has been also considered (Sect. 7).

The whole procedure is summarized in Fig. 4, which also illustrates the anonymous reference system adopted for the presentation of the obtained numerical results.

Fig. 4

(adapted from Cattari and Magenes 2021)

Exemplification of the procedure adopted for: a conversion of the pushover curve into an equivalent bilinear curve (as defined in MIT 2019); b computation of the average values of the SRPs (K_s, V_y, d_u); c computation, for each software, of the scatter with respect to the average values of the SRPs

Finally, the failure mechanism predicted by the software for each structural element and the damage distribution in the walls have been checked at the step of the analysis corresponding to the maximum top displacement (Sect. 6.7), adopting a colour map to represent the damage state of the elements, as shown in Fig. 5.

Fig. 5

Adopted criterion for the comparison of the damage distribution: a Example of damage pattern in a wall obtained by a software; b Legend of failure mechanisms: E: Elastic; F-p: Flexural-plastic; F–c: Flexural-collapse; DC-p: Diagonal Cracking-plastic; DC-c: Diagonal Cracking-collapse; T: Tension; C–c: Compression-collapse

5 Analytic upper bound reference solution

Although BS4 is inspired by a full-scale brickwork prototype, the purpose of this study is not to compare the results of the performed numerical analyses with the actual experimental response. In this regard, it is noted that the adopted modelling assumptions introduce some simplifications and dissimilarities in the EF idealization with respect to the characteristics of the real building.

However, an analytical reference solution for the evaluation of the reliability of the numerical results has been defined, through the estimation of upper bound values for the parameters characterizing the capacity curve (i.e. the elastic stiffness, the maximum base shear and the ultimate displacement) under the hypothesis of “shear-type” behaviour.

The simplified assumption of restrained nodal rotations at each storey, commonly adopted as a consequence of the hypothesis of infinite flexural rigidity of the coupling beams, makes the solution independent from the interaction between masonry piers and spandrels. In this case, in fact, the static scheme of panels is known a priori, being the point of contraflexure at half height of the elements. This further hypothesis clearly represents an ideal constraint condition which, on the one hand, allows for some considerable simplifications in the analytical calculation of the above-mentioned quantities and, on the other hand, leads to an overestimation of their values, which can therefore be adopted to define upper bounds of acceptability of the numerical solution.

The procedure can be applied either considering the response of the structure as a whole or referring to each storey or wall separately.

The only kinematic unknowns of the problem are the horizontal displacements at the storey levels; moreover, as the analysis evolves, the normal stress in the masonry panels is invariant, with respect to the application of the gravitational loads only. Consequently, the problem can be solved once the storey stiffness and the distribution of the applied horizontal forces are known.

In order to obtain a more realistic estimate, for the reasons explained below, the procedure uses some of the results produced by the software:

• Normal stress distribution in masonry piers after the application of the dead loads. The axial load in piers depends on the redistribution effects deriving from the role of both the “frame” and the “flange” effects. The former is responsible of the variation of normal forces in the piers of a masonry wall, which tends to partly balance the overturning moment induced by the applied horizontal forces with the resultant torque. The latter produces the variation of the strength and displacement capacity of an in-plane loaded pier in the presence of an intersecting panel, due to the interlocking between the masonry units. For this reason, the hand calculation, generally simply based on proper assumptions on the tributary areas, can only provide an approximate estimate of the actual normal stress in the panels.

• Storey horizontal forces distribution among the masonry piers at each level in elastic conditions. This calculation, quite simple for perfectly symmetrical structural configurations, is certainly more complex for systems with elements of different stiffness and characterized by significant eccentricity between the storey mass and stiffness centroids. The complexity even increases in the more general case of EF models where floor slabs are not regarded as infinitely rigid and which therefore explicitly take into account the loads redistribution carried out by floor diaphragms. It is therefore considered more reliable to determine the distribution of the storey horizontal forces in elastic conditions from the shear values in masonry piers obtained by the software before the first damage occurs (for example, at the application of the first increment of the lateral forces).

The total elastic stiffness at each storey of the structure is computed as the sum of the contributions of the corresponding masonry piers, evaluated according to the Timoshenko beam theory (Timoshenko and Gere 1972). In analogy with the hypotheses adopted in the definition of the EF models, a reduction factor equal to 0.5 of the gross stiffness is adopted in order to take into account the effects of cracking. Furthermore, the sole contribution of stiffness and strength in the main plane of the masonry piers of the longitudinal walls is considered in the calculation. The correctness of the slope of the elastic branch of the numerical capacity curve (i.e. the predicted elastic stiffness) may be checked by evaluating from the analysis the shear distribution among the masonry piers at a loading step preceding the occurrence of the first damage in the structure. In particular, the sum of the inter-storey displacements, evaluated by dividing each storey total shear by the corresponding analytical stiffness, can be compared to the top displacement resulting from the analysis.

As regards the maximum base shear, it is assumed that at each storey the achievement of the maximum strength occurs simultaneously in all masonry piers. On the basis of this simplified hypothesis, the maximum storey shear is simply calculated as the sum of the strengths of the panels. The obtained value obviously represents a higher limitation for the numerical prediction. The evaluation of the strength of each element requires the knowledge of the applied normal stress which, as discussed above, is assumed from the first step of the analysis. In particular, the effective strength is assumed as the minimum value resulting from the adopted shear and flexural strength formulations. Furthermore, these data are also useful to check the consistency between the damage pattern obtained by the software and the one analytically predicted.

The deformation capacity of each masonry panel is evaluated on the basis of its geometry, of the expected critical failure mechanism and of the corresponding assumed deformation limit. It is here recalled that, in ideal “shear-type” behaviour, with blocked end rotations of masonry piers, deformation capacity values evaluated in terms of chord-rotation and drift perfectly match. The comparison of the calculated limit for each panel to the numerical displacement predicted by the software, in particular at the step of analysis corresponding to the maximum displacement at the top of the structure, represents a further check of the correctness of the numerical results. Finally, the ultimate displacement capacity of the structure can be evaluated as the lowest displacement capacity of the masonry piers belonging to the level where the “soft-storey” condition is activated (i.e. where a sufficient number of plastic hinges at the end-joints of the piers is activated to generate a mechanism).

6 Discussion of results

For sake of brevity, this Section only presents the results of the analyses carried out on the geometrical configuration BS4_P2, more affected than BS4_P1 by the stress redistribution effects between walls W1 and W3, due to its asymmetric plan. Moreover, more emphasis is put in particular on cases A and C, while only some comments are reported from cases B and D to confirm some general trends found in the obtained results. However, it may be stated that the considerations reported in the following in general also apply to BS4_P1.

6.1 General overview on the numerical response of EF models

Figure 6 reports, for SW1 as an example and for the four considered configurations of the masonry spandrels, the global capacity curves of BS4_P2 and the local capacity curves of wall W3-I in BS4_P1 and BS4_P2.

Fig. 6

Variation in the numerical response obtained by SW1 for different configurations of masonry spandrels: a global capacity curves of BS4_P2; b Capacity curves of wall W3-I of structures BS4_P1 and BS4_P2

As shown in Fig. 6a, both the global stiffness and the maximum base shear of the structure gradually increase passing from case A to case D, whereas the maximum displacement capacity is progressively reduced. A similar trend in the global response has been generally obtained by all the software, as results from the comparison of the graphs reported in Fig. 7. Yet, in some limited cases (SW5 and SW7), a less marked difference has been obtained between the responses of structures BS4_P2/B (steel tie rods coupled to masonry spandrels) and BS4_P2/C (RC ring beams at each floor level of the building).

Fig. 7

Global capacity curves of BS4_P2 obtained by the EF software for different configurations of masonry spandrels

Figure 6b allows further checks on the consistency of the numerical response of wall W3. Since in BS4_P1 and BS4_P2 this wall is characterized by the same geometric configuration (I-type, see Fig. 1), similar responses are expected under the same assumptions on the structural details. Actually, the capacity curves obtained from BS4_P1/A and BS4_P2/A and the ones from BS4_P1/B and BS4_P2/B are mutually consistent, in particular with respect to the initial stiffness. Some discrepancies, especially on the maximum base shear, can be justified by taking into account the different variation of the normal force distribution in the masonry piers of wall W3-I due to its coupling with different configurations of wall W1 (I-type in BS4_P1 and II-type in BS4_P2).

6.2 Scatter in total model mass

In order to verify the consistency among the numerical EF models, the total mass evaluated by each software has been compared with the result of the manual calculation. This latter value, assumed as a reference, has been computed on the basis of the geometrical, mechanical and load data reported in Sect. 2. Table 3 summarizes the mass contributions evaluated for structures BS4_P2/A and BS4_P2/C. In particular, the self-weight of masonry piers and spandrels have been evaluated assuming masonry continuous from the base to the top of the structure in the case of BS4_P2/A and interrupted at each floor level by the RC ring beams in the case of BS4_P2/C. Please note that BS4_P2/B and BS4_P2/D are characterized by the same geometrical configurations and, therefore, by the same total mass of BS4_P2/A and BS4_P2/C, respectively.

Table 3 Analytical calculation of the mass contributions (in [t]) for structures BS4_P2/A and BS4_P2/C

The data presented in Table 4 show, for all the software, an excellent consistency of the numerical estimate with the manual calculation, with a maximum percentage variation lower than 0.5% and 4.5% in the case of BS4_P2/A and BS4_P2/C, respectively.

Table 4 Total mass (M) estimated by the software and corresponding percentage variation on the reference value (ΔM)

The slightly greater scattering found in the case of BS4_P2/C can be justified by the different approaches adopted by the various software in the evaluation of the geometric dimensions of masonry piers and spandrels in the presence of RC ring beams at the floor level, which in some cases may cause the interpenetration of elements and consequently the overestimation of the total mass. From Table 4, it results that only the mass estimation of SW2 and SW7 is based on the same hypotheses adopted in the manual calculation, whereas all the other results are affected by the cited interpenetration of elements assumed by the software (under this latter hypothesis, the total mass resulting from the manual calculation would be equal to 107.6 t).

6.3 Scatter in normal forces from dead loads

A further check involved the comparison among the normal forces at the base section of the masonry piers at the ground level after the application of the gravity loads. During the analysis, the redistribution of the dead loads applied to the structure among these elements may occur at each storey:

• Between different walls, as a consequence of the difference in their flexural stiffness and of the role played by the floor diaphragms in coupling the walls. These aspects, differently from the following ones, clearly influence the axial load redistribution only in the presence of lateral forces acting on the structure and have no effect at the first step of analysis, corresponding to the application of the gravity loads.

• Between the elements belonging to a given wall, as a consequence of the “frame” effect that occurs in the wall. This depends on the features of the spandrels and on the different degree of coupling they can provide to the piers, also for the presence of tension elements coupled to them (such as steel tie rods and, mainly, RC ring beams, the latter being characterized by a greater flexural stiffness with respect to the former).

• Between the elements located at the intersection of two orthogonal walls, as a result of the coupling between the walls, for example guaranteed by the mechanical interlocking effect in the intersection area due to the overlap of the masonry units. The software handle this effect in different ways, allowing in some cases to vary the degree of coupling (see Cattari et al. 2021a for further detail on this aspect). In particular, in all the EF models here considered, the condition of effective (“perfect”) interlocking between the walls has been assumed, producing the so-called “flange” effect. Yet, in case of SW7, unlike all the other cases, the redistribution of the axial loads between the intersecting masonry piers has been fixed initially and kept constant during the analysis.

Figure 8 shows the percentage variation of the initial axial load in each pier of BS4_P2/A and BS4_P2/C predicted by the different software, with respect to the average reference values calculated according to the above introduced criterion. It should be stressed that the results of SW7 have been excluded from this check and have not been considered in the evaluation of the reference values, since, due to the aforementioned reason, in this case they depend on the analyst’s arbitrariness more than on the intrinsic modelling approach adopted by the software.

Fig. 8

Scatter of the normal force values at the base section of the masonry piers at the ground level of structures BS4_P2/A and BS4_P2/C resulting after the dead load application

As can be seen from Fig. 8, the detected scattering in almost every case is lower than 10%. Since the out-of-plane contributions of the masonry piers have been neglected in the definition of the EF models, the global response of the structures in governed by the panels belonging to walls W1-II and W3-I. Focusing on these elements, the following considerations arise.

On pier P15 (i.e. the central element of wall W3-I not coupled to any orthogonal panel) the differences among the software with very few exceptions decrease from about 5% to less than 2.5%, passing from BS4_P2/C to BS4_P2/A. While BS4_P2/A is characterized by “weak” spandrels, not able to guarantee a significant coupling effect between the masonry piers, in BS4_P2/C, due to the presence of the RC ring beams, the masonry spandrels are more resistant (even characterized by the same stiffness) and affect in a more significant way the stress redistribution between the piers in the wall. The differences detected may therefore be attributable to modest dissimilarities in the handling of the “frame” effects by the software.

With reference to BS4_P2/A, the most significant differences among the software in the elements of walls W1-II and W3-I are recorded on piers P04, P14 and P16, all coupled to squat masonry panels belonging to the transverse walls W2 and W4 and therefore influenced by the “flange” effect. The dispersion in the predicted results may be ascribable to the different solutions adopted by the software to manage the adopted condition of perfect coupling between intersecting panels. The greater variability detected for P04, P14 and P16 with respect to pier P05 (all “corner” elements), can be explained by the fact that, since the first three elements are slenderer and have a lower axial stiffness than the latter, they are much more affected by the stress redistribution effects.

In the case of BS4_P2/C, in general a greater scattering in the corner elements is found, attributable to the interaction between the “flange” and the “frame” effects.

It is important to stress that the masonry element which most affects the global response of BS4_P2 is pier P05, which carries almost a 60% of the total base shear. Since for this element the scattering of the axial load at the base section obtained by the software is lower than 10%, it is reasonable to expect that the aforementioned scattering in the other piers at the ground level should have a very limited influence on the global response.

As to piers P08 and P20, the detected variability again mainly results from the cited dissimilarities in the handling of the “flange” effects by the software.

6.4 Variation of normal forces in piers of wall W3-I

Figure 9 shows the predicted variation of the normal forces in the masonry piers at the ground level of wall W3-I (P14, P15 and P16) of BS_P2/A and BS_P2/C, deriving from the application of the lateral loads. For the same reason reported in previous Sect. 6.3, the results of SW7 have not been considered also in this check.

Fig. 9

Structures BS4_P2/A and BS4_P2/C: variation of the normal force at the base section of the piers of wall W3-I (d_W3-I: total displacement at the top of the wall)

In general, a quite good agreement is observed in the results obtained by the software. Passing from BS4_P2/A to BS4_P2/C, in particular, a change is observed in the modality of variation of the axial load in the elements. Referring to BS4_P2/A, the corner elements P14 and P16 are subjected to an increase and to a decrease in the state of compression, respectively, whereas in the central pier P15 the normal force remains constant. On the contrary, in the case of BS4_P2/C the trend is reversed for P14 and P16 and a modest decrease of the axial load in P15 is observed.

With reference to the loading direction, piers P14 and P16 are located on the “upstream” and on the “downstream” sides of the wall, respectively. The variation of the normal force in the two masonry elements (as well in the central pier P15) in BS4_P2/C is therefore consistent with the “frame” effect, due to the coupling between the piers provided by the spandrels, in turn coupled to the RC ring beams. Vice versa, the “frame” effect cannot be generated in BS4_P2/A, due to the modest coupling offered by the “weak” spandrels (starting from the first step of the analysis, if they are simply modelled as connecting rods, or after the sudden plasticization due to combined compression and bending failure, if they are modelled as inelastic beam elements). In this case, the variation of the axial load in the two corner piers is attributable to the “flange” effect, generated by the interaction of these elements with the squat panels belonging to the intersecting side walls. Actually, by evaluating the overall normal forces acting on the masonry panels on the “upstream” side (P14, P20 and P04) and on those on the “downstream” side (P16, P08 and P05) of BS4_P2/A, it can be observed that, as expected, the resultant loads do not undergo any change during the analysis. This result is illustrated and compared to the corresponding calculation carried out on BS4_P2/C in Fig. 10, with reference only to some of the adopted software.

Fig. 10

Variation of the overall normal forces acting on the masonry piers on the “upstream” side (P14, P20 and P04) and on those on the “downstream” side (P16, P08 and P05) of structures BS4_P2/A and BS4_P2/C

6.5 Comparison of global pushover curves

Figure 11 reports, for each of the considered configurations of the masonry spandrels, the comparison among the global capacity curves of BS4_P2 obtained with the different software. An increasing agreement in the numerical prediction of the global response can be observed passing from BS4_P2/A to BS4_P2/D, in terms of initial stiffness, maximum strength and maximum displacement capacity. The possible causes of the obtained dispersion on the numerical results are discussed in detail in following Sect. 6.6.

Fig. 11

Comparison of the numerical results obtained by the software in terms of global capacity curves

In the case of SW5, the dot reported on the curve indicates the step of the analysis corresponding to the activation in the EF model of a plastic hinge associated to the flexural failure of pier P05. The reaching of this condition in cases BS4_P2/A, BS4_P2/B and BS4_P2/C has been explicitly indicated, since it has been ascertained that in this software, unlike all the other cases, the axial load and the bending moment become independent in the elements after the activation of the plastic hinge (i.e. the flexural strength is no longer consistently evaluated and remains constant as the axial load changes during the analysis). Although the global response seems not to be significantly affected by this issue, with respect to the results of the other software (see Fig. 11, especially in case BS4_P2/C), since element P05 as discussed above balances itself a significant part of the storey horizontal forces, SW5 has been considered as not reliable after the attainment of this condition and has been neglected in the computation of SRPs.

6.6 Scatter in equivalent bi-linear curve parameters

From the data of the equivalent bi-linear curves corresponding to the global capacity curves obtained by the software, the scattering of the SRPs K_s, V_y, d_u has been calculated. It should be stressed that, with reference to BS4_P2/A, BS4_P2/B and BS4_P2/C, the results obtained by SW5 were not considered in the calculation of the reference values for V_y and d_u for the above discussed reasons, regarding the inconsistent evolution of the plastic hinge.

As shown in Fig. 12, the dispersion on the SRPs generally tends to progressively decrease passing from BS4_P2/A (lower than 30%, except for few cases) to BS4_P2/C, to settle on an order of 5% (even lower, in some cases) for BS4_P2/D. Moreover, it is observed that BS4_P2/A is the most sensitive to the algorithms and the solutions implemented in the software and to the adopted modelling assumptions. Some of the aspects which mainly affect the numerical response may be traced back to:

Fig. 12

Percentage variation on the average reference value of the parameters describing the equivalent bi-linear curve

• The possibility for the software to calculate the actual normal force acting on the spandrels and to consistently evaluate their flexural and shear strengths at each step of the analysis. Regarding this issue, it is reminded that, as an example, the Italian Technical Code (NTC 2018) allows two alternative approaches in the definition of the failure criteria to be adopted for these elements, depending on whether the normal force is known from the analysis or not. The numerical result hence deeply depends on the criterion for the modelling of the diaphragms (infinitely rigid or with a finite stiffness in their plane) and on the strength formulation for masonry spandrels adopted by the software.

• The effects of the interaction between masonry panels and diaphragms, when the latter are explicitly modelled. For example, the setting of an excessively high value of axial stiffness for diaphragms may cause the same effect due to the coupling to spandrels of tensile resisting elements, even in case these latter are not included in the EF model.

• In the fiber approach, the possibility to define the tensile strength law of the masonry allows a more accurate evaluation of the behaviour of piers and spandrels; yet, it also represents another source of variability, not being of simple determination.

With reference to BS4_P2/A, the scattering greater than 50% of K_s detected in the case of SW4 is due to the different way in which this specific software considers the stiffness degradation (see Sect. 3). Though the calculation hypothesis of SW4 is certainly more refined than the other software, the resulting value of K_s is associated with the greater detected dispersion, since the adopted reference value (assumed equal to the average of the results of all the software) is affected by the simplified assumption which most of them are based on.

As far as d_u is concerned, the higher scattering of the results (in general within 20%, except for few cases) when referring to BS4_P2/A, BS4_P2/B and BS4_P2/C, compared to BS4_P2/D, is ascribable to some discrepancies regarding the failure mechanisms predicted by the software for specific masonry panels and to the adoption of different formulations of the displacement capacity, in terms of either element drift or chord-rotation (Cattari and Magenes 2021). In particular, the software predictions match very well for BS4_P2/D, since the cited differences in the calculation of the displacement capacity in this case do not play any role, being the rotations blocked at the end-joints of masonry piers.

6.7 Comparison of damage patterns

Figure 13 illustrates the damage pattern predicted by the software for the masonry elements of walls W1-II and W3-I of BS4_P2/A and BS4_P2/C at the step of the analysis corresponding to the maximum top displacement. It should be noted that, in some cases, spandrel S01 of wall W1-II has not been modelled (being defined between fixed nodes) for analyst’s choice or for the intrinsic modelling approach of the software. It is also recalled that, in the EF model of BS4_P2/A generated with both SW4 and SW7, the spandrels have been simply modelled as axially rigid rods connecting the masonry piers; in the performed analyses, therefore, the evolution of the damage in these elements has not been evaluated.

Fig. 13

Comparison of the damage pattern corresponding to the ultimate displacement predicted by the software for walls W1-II and W3-I of structures BS4_P2/A and BS4_P2/C

A quite good agreement in the damage predictions is observed in the case of BS4_P2/A, with a prevailing flexural response of the elements. This is consistent with the fact that the masonry piers are generally subjected to low compression rates, corresponding to the region of the strength domain governed by this failure mode. The differences in the predicted plastic or collapsed damage condition may be ascribable only to the different formulations adopted by the software for the calculation of the displacement capacity. In the case of SW2, the failure in traction of the corner piers P16 and P18 on the “downstream” side of wall W3-I is attributable to the “flange effect” and to the interaction with the squat panels belonging to the transverse wall W2, as already discussed in Sect. 6.4.

Although a prevailing flexural failure mode of the masonry elements is also found in BS4_P2/C, most significant differences in the results occur in this case, in particular with regard to pier P05. To explain this, Fig. 14a reports the whole domain of this element, considering, in the case of flexural failure, three different static schemes: “cantilever”, “fixed–fixed” and an “intermediate” condition, representative of the state of the pier in the configurations A (“weak” spandrels), D (“shear type”) and C (presence of RC beams), respectively. The latter condition has been obtained by considering the actual shear span of the element resulting from the EF models after the first steps of the analysis (“elastic response”). In this way, referring to BS4_P2/C, the “intermediate” and the “cantilever” static schemes define the limit conditions for the numerical response of pier P05 which, starting from the former, moves to the latter due to the progressive damage occurring in the spandrels. The shear domain of the element, related to the diagonal cracking failure mechanism, is also reported.

Fig. 14

Strength domain of pier P05: a whole domain; b initial part of the domain, with indication of the initial average value (N_DL), corresponding to the application of the gravity loads, and of the maximum range of variation of the axial load during the analysis detected by the software

In Fig. 14b a magnification of the initial part of the domain is shown, on which the following significant values of the axial load in the element are reported:

• the value N_DL at the step of application to the structure of the dead loads (continuous vertical black line), evaluated by averaging the numerical results of both BS4_P2/A and BS4_P2/C obtained by all the software;

• the minimum and the maximum values resulting from the analyses (dashed vertical black lines), evaluated by averaging the obtained numerical results of BS4_P2/A and of BS4_P2/C, respectively.

As regard these latter two limit values, it is noted that pier P05 is subjected to a significant progressive reduction of the axial load in the case of BS4_P2/A, for the same reasons reported in Sect. 6.4 with reference to pier P16. On the contrary, in the case of BS4_P2/C a slight increase in the axial load is followed by an equivalent decrease, due to the change in the interaction of this element with the other piers (influenced by both the “frame” and the “flange” effects), as a consequence of the damage evolution in the structure.

Considering the domains in the range of variation of the normal force, it is observed that the shear and the flexural strength values are very close, when the boundary conditions of the panel are of the ideal “fixed–fixed” or of the “intermediate” type (as in the case of BS4_P2/C, where masonry spandrels are coupled to RC ring beams). Hence, even small differences among the software in terms of the predicted value of the axial load can easily justify the activation of different prevailing failure modes in the element (flexural or shear). On the contrary, when the static scheme tends to the “cantilever” type (as in the case of BS4_P2/A, where “weak” spandrels are not able to guarantee a significant coupling effect between the masonry piers of the wall), a flexural failure would be expected.

Finally, as regards the failure in compression of the masonry spandrels of BS4_P2/C predicted by SW4, it has been ascertained that it is attributable to unexpected axial forces in these elements, resulting from the assumptions adopted by the analyst in defining the model in order to properly reproduce the shared wall configuration of Fig. 3b (in particular, the imposition of vertical offsets with respect to the storey levels).

7 Comparison with analytical reference solution

The analytical procedure for the evaluation of an upper bound solution described in Sect. 5 has been applied to BS4_P2/D, by adopting as reference the axial and shear force distributions in the masonry piers (when still in elastic conditions) resulting from the analysis performed with SW2 in the positive X-direction (Fig. 1). Below, the results of each step of the calculation are compared with the numerical results of SW2. Finally, the obtained analytical solution is also compared to the wall capacity curves resulting from the analyses performed with all the software.

Table 5 collects the values of the geometric parameters of the masonry piers of walls W1-II and W3-I (see Fig. 3 for the element numbering) and the corresponding elastic stiffness k.

Table 5 Analytical calculation of the storey stiffness of walls W1-II and W3-I of BS4_P2/D

Table 6 presents the comparison between the analytical estimate of the total displacement of walls W1-II and W3-I at each storey level and the values obtained from SW2, with reference to the step of the analysis corresponding to the occurrence of the first damage in the structure (Elastic Limit State, ELS). For each wall, V_SW2|ELS is the total storey shear distribution at the considered step assumed from the numerical results, F is the corresponding distribution of the applied horizontal forces, k is the total storey stiffness (evaluated as the sum of the stiffness contributions of the masonry piers, reported in previous Table 5), Δu and u are the calculated inter-storey and storey displacements, respectively, and u_SW2 is the corresponding numerical result. This latter perfectly matches with the analytical estimate at each storey.

Table 6 Analytical calculation of the displacement at ELS at each storey of walls W1-II and W3-I and comparison with the numerical result

The total equivalent elastic stiffness k_eq of each wall can be evaluated by dividing the total base shear at ELS by the corresponding total top displacement (bold values in Table 6). It results 84,766 kN/m and 43,373 kN/m for walls W1-II and W3-I, respectively.

Figure 15 sketches the damage pattern predicted by SW2 at the last step of the analysis, corresponding to the exceeding of the limit total shear degradation (20% of the maximum force, in accordance with NTC 2018). All the masonry piers at the base of walls W1-II and W3-I have reached the damage condition. In particular, piers P04 (W1-II) and P14, P15 and P16 (W3-I) are affected by a flexural failure mode, whereas pier P05 (W1-I) is damaged by shear and has reached the corresponding limit deformation. Under these conditions, the total shear at the base of each wall can be computed as the sum of the shear strengths of the masonry piers at the first level.

Fig. 15

Damage pattern of walls W1-II and W3-I predicted by SW2 at the last step of the analysis

Table 7 summarizes for each panel the flexural M_R,F and the shear V_R,DC strength values, the corresponding effective strength value V_R and the predicted critic failure mechanism (F: flexural and DC: diagonal cracking) resulting from the analytical calculation, based on the applied normal stress N_SW2 assumed from the results of the numerical analysis. For the computation of V_R,F (i.e. the shear strength corresponding to M_R,F), the shear span has been assumed equal to half of the element effective height, consistently with the “shear-type” hypothesis. Table 7 also reports the displacement capacity Δu_max of each masonry panel, evaluated as a function of the effective height and of the conventional deformation limit assumed for the expected failure mode.

Table 7 Analytical calculation of the shear strength and prediction of the failure mechanism (F flexural, DC diagonal cracking shear modes) and of the displacement capacity for the masonry piers of walls W1-II and W3-I

The maximum base shear, evaluated as the sum of the maximum strength of the masonry piers at the first level (bold values in Table 7), is equal to 362.9 kN for wall W1-II and to 157.1 kN for wall W3-I. The corresponding total top displacement in elastic conditions (i.e. assuming no damage occurs in the masonry elements and referring to the total equivalent elastic stiffness k_eq of the walls) is equal to 4.3 mm and 3.6 mm, respectively.

As results from Fig. 16, the numerical prediction (continuous black line) perfectly matches with the analytical estimate of the response of the walls (dashed black lines), in terms of both elastic stiffness and maximum base shear. In the graphs, ELS has been identified on the capacity curves by means of a black dot, corresponding to the bold values of total base shear and top displacement reported in Table 6 for each wall. In particular, the first damage occurs in a pier of W3-I; this justifies the reduction in the slope of the capacity curve of this wall, since the contribution of the damaged element is neglected in the calculation from that step on, whereas the response of W1-II is still elastic.

Fig. 16

Capacity curves of walls W1-II and W3-I: comparison between the numerical response obtained by SW2 and the analytical prediction in terms of elastic stiffness and maximum base shear

Table 8 illustrates the comparison between the predicted displacement capacity at each level of the walls and the corresponding maximum value obtained by SW2. At the last step of the analysis, wall W1-II reaches at the ground level its ultimate displacement capacity (corresponding to that of pier P05), with a perfect match between the numerical and the analytical predictions.

Table 8 Comparison between the analytical inter-storey displacement capacity at each storey of walls W1-II and W3-I and the corresponding maximum inter-storey displacement obtained by SW2

Finally, with reference only to some of the adopted software (since not in all cases the single wall response can be obtained), in Fig. 17 the analytical solution is compared to the wall capacity curves resulting from the performed analyses. Though the procedure has not been applied to each software and the reference solution is based on the results of SW2, a quite good match results for almost all cases. Few minor differences mainly involve the predicted maximum strength and are attributable to the abovementioned scattering of the normal stress distribution in the masonry piers. This is in line with the agreement in the prediction of the global response of BS4_P2/D obtained by the software, resulting from Fig. 11.

Fig. 17

Capacity curves of walls W1-II and W3-I of BS4_P2/D: comparison between the numerical response obtained by some of the adopted software and the analytical prediction in terms of elastic stiffness and maximum base shear

8 Sensitivity to the adopted EF idealization of walls

In the EF idealization, the definition of the element geometry actually represents a critical issue. Indeed, since seismic codes do not provide specific and standardized indications, it represents a first source of uncertainty and a potential cause for differences on the obtained results (Camilletti 2019; Cattari et al. 2021a, b; Ottonelli et al. 2021). The criteria commonly used to define the EF models mainly depend on the opening pattern, consistently with the earthquake damage observation, that shows in most cases a concentration of damage in the masonry portions located between the openings aligned in the horizontal and vertical direction. This idealization, rather simple in case of openings of the same size and perfectly aligned, becomes more arbitrary in presence of misalignments. Various criteria are available in the literature, based on different principles, especially for what concerns the determination of the pier effective height. Some derive from the observation of experimental results (Moon et al. 2006; Yi et al. 2006) or of post-earthquake damage (Augenti 2006), others result instead from numerical studies and comparisons with more accurate FE simulations and are already implemented in computer programs (Dolce 1991; Lagomarsino et al. 2013).

This Section presents the results of further investigations conducted with SW1 on BS4_P2/C, in order to evaluate the influence on the numerical response of different possible assumptions on the pier effective height. Non-linear static analyses have been performed both in the positive and in the negative X-directions (Fig. 1), assuming a “uniform” pattern of the lateral loads.

8.1 Adopted EF geometries and sensitivity at the global scale

Since the openings of walls W1-II and W3-I are perfectly aligned at the two storeys, no specific uncertainties are present in the identification of the geometry of the spandrels, for which the criterion proposed in Lagomarsino et al. (2013) has been adopted in all cases.

Regarding the determination of the pier effective height, the criteria by Dolce (1991), Augenti (2006) and Moon et al. (2006) have been considered, in addition to the one by Lagomarsino et al. (2013) adopted for the definition of the EF geometric configurations analysed in the main part of the study (Fig. 3). It is recalled that the criteria suggested in Augenti (2006) and in Moon et al. (2006) take into account the dependency of the pier effective height to the loading orientation; therefore, for each of these latter cases two different EF models are considered, depending on the direction of the performed analysis.

The adopted EF idealizations of walls W1-II and W3-I are sketched in Fig. 18 and in Fig. 19, respectively. Quite significant differences in the effective height of the piers and, consequently, in the extension of the rigid nodes can be observed, clearly affecting the final deformability of the considered walls.

Fig. 18

EF idealization of wall W1-II according to the criteria adopted for the definition of the pier effective height

Fig. 19

EF idealization of wall W3-I according to the criteria adopted for the definition of the pier effective height

Figure 20 shows the comparison of the obtained results in terms of global capacity curve, considering both the positive and the negative X-directions of analysis. The different effective heights of masonry piers significantly influence the numerical response, producing not negligible differences in terms of stiffness, strength and displacement capacity.

Fig. 20

Global pushover curves corresponding to the different adopted criteria for the EF idealization: positive (a) and negative (b) X-direction of analysis

In order to quantify the dispersion associated to the obtained results, for each considered criterion the scattering of the SRPs characterizing the equivalent bi-linear curve with respect to a reference value has been computed. The latter has been assumed as the average among the results provided by the software adopted for the analyses presented in previous Sect. 6 (hereinafter referred to as “benchmark solution”).

The obtained results, illustrated in Fig. 21, confirm that the dispersion on the key structural parameters is not negligible. Since the sensitivity to the criterion adopted for the definition of the geometrical dimensions of the EF structural elements has been investigated only by SW1, it is worth noting that the presented scatter also includes the intrinsic model uncertainty related to the choice of the software to use (i.e. that responsible for the initial scattering of the SW1 data with respect to the “benchmark solution”, as highlighted in Fig. 12).

Fig. 21

Scatter with respect to the “benchmark solution” of the SRPs associated to the equivalent bi-linear curves (K_s, V_y and d_u): positive (a) and negative (b) X-direction of analysis

In particular, Fig. 21 shows that the criteria by Augenti (2006) and by Dolce (1991) are the ones characterized by the highest scattering with respect to the “benchmark solution”, especially concerning the initial stiffness and the ultimate displacement capacity.

The criterion by Augenti (2006) predicts a higher stiffness and a lower displacement capacity than the other ones in both directions of analysis (Fig. 20), whereas the opposite trend occurs in the EF model by Dolce (1991). These results can be explained by considering that the former EF idealization tends to produce rather squat piers with extended rigid nodes, especially in the case of wall W1-II, whereas the latter leads in general to quite slender piers, characterized by higher effective heights (see Figs. 18, 19). Consequently, the walls defined according to Dolce (1991) are characterized by a higher deformability, that actually corresponds to a reduction of the global stiffness and to a higher displacement capacity. This latter result is attributable to two different reasons:

• rather slender panels are usually affected by a ductile flexural failure mode, which is associated to higher drift thresholds, unlike squat panels that tend to undergo shear failure;

• since masonry panels fail when they reach fixed values of the ultimate limit drift, the higher is their effective height, the higher is the displacement capacity.

8.2 Sensitivity at the local scale

Figures 22 and 23 show, respectively, the comparison of the capacity curves of walls W1-II and W3-I obtained by adopting the different considered EF idealization criteria and the predicted damage patterns at the step of the analysis corresponding to the maximum top displacement. For sake of an example, the results only refer to the negative X-direction of analysis, where the most significant differences are detected.

Fig. 22

Capacity curves of walls W1-II (a) and W3-I (b) corresponding to the different adopted EF idealization criteria: negative X-direction of analysis

Fig. 23

Damage pattern in walls W1-II and W3-I corresponding to the maximum top displacement (negative X-direction of analysis) predicted by the considered EF models

A quite significant dispersion in the obtained numerical prediction for both the walls can be observed in Fig. 22, especially with reference to the one corresponding to the criterion by Dolce (1991). In this case, the capacity curves are characterized by a displacement capacity much higher than the others. This is consistent with the damage prediction, detected in Fig. 23, which is more spread and involves the piers at both levels of the structure.

As regards wall W1-II, its response is clearly mainly governed by pier P05, characterized by very different effective height values depending on the applied criteria. On the contrary, with reference to wall W3-I, the effective height of the masonry piers is almost similar in all the considered EF models, apart from a few discrepancies mainly regarding the corner elements. Moreover, the structural response of this wall is mainly governed by the central pier at the ground floor (P15, carrying almost 60% of the base shear of the whole wall), which is characterized by the same geometry in all the considered EF idealizations, with the only exception of the one by Dolce (1991), where its effective height is slightly higher.

As can be seen in Fig. 23, the collapse of the structure is due to the flexural failure of the piers at the ground floor in wall W3-I in all the cases. This is explained by the fact that (as already reported in Sect. 6.7) the piers are subjected in general to low compression rates, corresponding to the region of the strength domain governed by this failure mode. Moreover, in all the considered EF models the spandrels are still elastic, since the presence of the coupled RC ring beams allows a significant strength level in these masonry elements.

In order to check these results, with regard to pier P05 as an example, Fig. 24 reports for each of the considered EF idealization criteria a magnification of the initial part of the diagonal cracking (DC) and flexural (F) strength domains, in the range of variation of the axial load of the element. Since the negative X-direction of analysis is considered, due to the “frame” effect affecting wall W1-II, the element is subjected to a progressive reduction of the normal force, from the value associated to the application of the dead loads (N_DL) up to a minimum value (N_min). In the definition of the domain associated to the flexural failure mode, an “intermediate” boundary condition has been considered, obtained as already explained in Sect. 6.7 by adopting in the calculation the actual shear span characterizing the element in the first steps of the analysis. This assumption is justified by the fact that, at the end of the analysis, in all the considered EF models the spandrels are still elastic, since the presence of the coupled RC ring beams allows a significant strength level in these masonry elements. Only in the case of Augenti (2006), a “cantilever” boundary condition has been assumed by limiting the shear span, which resulted higher than the effective height of the panel, to this latter value. It is also worth noting that whereas the flexural domain changes as a consequence of the different effective height, the shear domain is the same for each considered EF idealization. This is due to the fact that in the diagonal cracking failure criterion the geometry comes into play only through a coefficient related to the aspect-ratio of the element, in any case not to be assumed lower than 1. Since, despite the variations in its effective height, the aspect-ratio of pier P05 remains below 1 in all cases, its shear strength is invariant with respect to the adopted EF idealization criterion.

Fig. 24

Magnification of the strength domains of pier P05 for the different adopted EF idealization criteria in the range of variation of the axial load resulting from the performed numerical analyses

As shown in Fig. 24, in Lagomarsino et al. (2013), Moon et al. (2006) and Dolce (1991) the flexural strength results to be lower than the shear strength in the whole range of variation of the axial load, justifying the prediction of a flexural failure mode. Only for Augenti (2006) a shear failure mode is expected. It is also noted that, given that in this case P05 is subjected to a higher compression level, with respect to the other considered EF models, its strength is also higher; this can explain why the element is still in an elastic phase at the end of the analysis.

9 Conclusions

The paper presents a comparative study, developed in the framework of the Italian Network of Seismic Laboratories (ReLUIS) projects, aimed to quantify the dispersion of the numerical results achievable using different software packages. In particular, the attention is focused on the results of non-linear static analyses performed with seven commercial software based on the EF modelling approach on a simple two-story URM building with rigid diaphragms. In order to reduce the epistemic uncertainties and the influences of the arbitrariness of analysts on the obtained results, shared modelling assumptions have been adopted.

The methodological approach adopted for the critical evaluation of the results (involving checks both at the global and at the local scales) is presented in detail, together with the description of the case study and of the adopted analysis and modelling hypotheses. The set of collected data (integrated by those illustrated in Cattari and Magenes 2021), on the one hand, allows the replication by other researchers and analysts of the investigated structures and, on the other hand, represents a reference for the comparison of the results achievable with other software. Moreover, although not exhaustive, the set of software adopted in this study reflects the tools nowadays available in Italy and many are also used at international level. In this way, it is expected that the presented topics will constitute a useful contribution for both professional engineers and the scientific community.

A very good agreement in the numerical predictions has been obtained when assuming the “shear-type” idealization, while an increasing scattering has been found by progressively reducing the effectiveness of the pier-spandrel interaction up to the limit case of “weak” spandrels. The possible reasons for the achieved dispersion of results have been critically discussed in the paper through an in-depth analysis on the features of the different software and the way some specific modelling issues are managed, just to mention a few: the adopted solutions for the modelling of “weak” spandrels, the infinite in-plane stiffness of diaphragms, the perfect coupling between intersecting walls, the stiffness degradation and the displacement capacity of structural elements.

The presented results highlight the importance of the analyst’s awareness of the critical issues involved in the modelling process of masonry buildings, when using commercial computer programs available for their seismic analysis and assessment, and knowledge of the features of the adopted software, for the purposes of the proper definition of the EF model and of the critical evaluation of the obtained results.

Finally, since seismic codes do not prescribe standardized criteria to be adopted for the definition of the geometry of the structural elements in the EF models, the paper also investigates the influence on the numerical response of different assumptions on the pier effective height, based on some criteria available in the literature. The reported results clearly highlight how the EF idealization to be used in the modelling process represents a significant source of uncertainty and a potential cause of not negligible differences on the obtained numerical results. Moreover, it can actually significantly affect the outcomes of the seismic verifications of masonry buildings which, according to the current building codes, are performed on the global pushover curves resulting from the non-linear static analysis.