Multi-level performance-based design optimisation of steel frames with nonlinear viscous dampers

Abstract

This paper presents a practical multi-level performance-based optimisation method of nonlinear viscous dampers (NVDs) for seismic retrofit of existing substandard steel frames. A Maxwell model is adopted to simulate the behaviour of the combined damper-supporting brace system, with a fractional power-law force–velocity relationship for the NVDs, while a distributed-plasticity fibre-based section approach is used to model the beam-column members thus incorporating the nonlinearity of the parent steel frame in the design process. The optimum height-wise distribution of the damping coefficients of NVDs satisfying given performance requirements is identified via a uniform damage distribution (UDD) design philosophy. The efficiency of the proposed multi-level performance-based design optimisation is illustrated through nonlinear time-history analysis of 3-, 7- and 12-storey steel frames under both artificial and natural spectrum-compatible earthquakes. Sensitivity analysis is performed to investigate the effects of initial height-wise damping distribution, convergence factor and uncertainty in design ground-motion prediction on the optimisation strategy. The efficiency of the final optimum design solution is also investigated by using drift-based, velocity-based, and energy-based UDD approaches to identify the most efficient performance index parameter for optimisation purposes. It is found that regardless of the selected performance parameter, the optimum damping distribution identified by the proposed methodology leads to frames exhibiting lower maximum inter-storey drift, local damage (maximum plastic rotation) and global damage index compared to an equal-cost uniform damping distribution. However, using drift-based UDD approach generally results in a better seismic performance. It is shown that the proposed UDD optimisation method can be efficiently used to satisfy multiple performance objectives at different intensity levels of the earthquake excitation, in line with performance-based design recommendations of current seismic codes. The proposed method is easy to implement for practical design purposes and represents a simple yet efficient tool for optimum seismic retrofit of steel frames with NVDs.

1 Introduction

Fluid viscous dampers are among the most widely used passive energy dissipation systems for seismic performance enhancement of new structures as well as seismic retrofit of existing substandard structures (Soong and Dargush 1997; Christopoulos and Filiatrault 2006). Within a piston-cylinder device, the translational motion of a piston rod pushes a silicone oil to pass from one chamber to another through small orifices (Constantinou and Symans 1992). This dashpot-like mechanism produces conversion of kinetic energy of the piston rod into heat, thus generating energy dissipation. Initially conceived for military purposes, these dampers were then extensively used in the earthquake engineering field since 1990s (Soong and Spencer 2002). Some inherent advantages of these dampers for civil engineering applications are the generation of velocity-dependent forces that are, consequently, out of phase with peak displacements, the possibility of introducing supplemental energy dissipation in a structure without considerably modifying its stiffness properties (unlike other devices like viscoelastic or hysteretic dampers (Apostolakis and Dargush 2010)), the low sensitivity over a wide range of frequencies and the relatively large strokes and forces that can be obtained (Housner et al. 1997). Previous experimental and numerical studies demonstrated that fluid viscous dampers, when suitably sized and placed, absorb a major portion of the input energy from an earthquake, thereby reducing structural damage under severe earthquakes (Lee and Taylor 2001; Sorace and Terenzi 2009; Dong et al. 2016).

The seismic performance of a structure with added viscous dampers is strictly related to the selection of an appropriate size (generally expressed in terms of damping coefficient) and placement of the devices. Therefore, the optimum design of viscous dampers has attracted increasing attention from both researchers and practitioners in the last decades. Among the most popular approaches, heuristic methods like the sequential search algorithm (Zhang and Soong 1992) and its subsequent simplifications (Lopez Garcia 2001) and extensions (Wu et al. 1997; Lopez Garcia and Soong 2002; Aguirre et al. 2013), gradient-based optimisation methods like the incremental inverse problem approach (Takewaki 1997) and subsequent extensions (Takewaki et al. 1999; Fujita et al. 2010; Takewaki 2009; Aydin et al. 2007; Ayding 2012), the fully stressed analysis/redesign procedure (Levy and Lavan 2006), evolutionary approaches like genetic algorithms (Singh and Moreschi 2002; Movaffaghi and Friberg 2006; Lavan and Dargush 2009; Silvestri and Trombetti 2007; Apostolakis 2020), multi-step design methods (Martinez-Rodrigo and Romero 2003; Silvestri et al. 2010; Palermo et al. 2018), direct displacement-based design procedures (Lin et al. 2003; Sullivan et al. 2012; Moradpour and Dehestani 2019) and stochastic-based approaches (Di Paola and Navarra 2009; Gidaris and Taflanidis 2015; Tubaldi and Kougioumtzoglou 2015; De Domenico and Ricciardi 2019) have been utilised. Addionally, nowadays metaheuristics are emerged as very efficient algorithms for tackling complex optimization problems (Fattahi and Gholizadeh 2019; Hassanzadeh and Gholizadeh 2019; Ghaderi and Gholizadeh 2021). Some studies also compared different damper distributions in view of the resulting seismic performance (Hwang et al. 2013; Whittle et al. 2012; Aguirre et al. 2013; Del Gobbo et al. 2018b). A recent review paper by De Domenico et al. (2019) summarised and classified most of the above-mentioned approaches. This brief overview demonstrates the lively and increasing interest of the scientific community towards the development of efficient and practical optimum design procedures of viscous dampers.

Most of the above-mentioned design methodologies, including the very recent ones (Cetin et al. 2019; Pollini 2020), assumed, for simplification purposes, a linear elastic behaviour of the parent frame along with a linear behaviour of the viscous dampers, with a resisting force linearly proportional to the relative velocity at their two terminals (Del Gobbo et al. 2018a). However, the actual constitutive behaviour of the viscous dampers, especially for the devices available in the market, is more realistically described by a nonlinear power law force–velocity relationship (Seleemah and Constantinou 1997), with power factor $\alpha$ typically falling in the interval [0.1–0.5]. Using nonlinear viscous dampers (NVDs) has certain advantages over linear viscous dampers, mainly due to the considerable reduction of damper forces for achieving a comparable seismic performance (Martinez-Rodrigo and Romero 2003; Pekcan et al. 1999; Lin and Chopra 2002; Tubaldi et al. 2014; Dall’Asta et al. 2016). As an example, within a reliability-based design framework, Altieri et al. (2018) demonstrated that reducing $\alpha$ from 1.0 (linear case) to 0.3 leads to a reduction of the sum of the damper forces by 30% for a target failure probability of 10% in 50 years. Since high damper forces have important implications on the overall retrofitting cost, manufacturers generally strive for achieving such a nonlinear power law behaviour in their products, sometimes also by introducing a relief mechanism to limit the maximum developed forces (Adachi et al. 2013). Additionally, conventional structures are expected to exceed their elastic thresholds under severe earthquake excitations. While this is certainly true under the maximum considered earthquake (MCE) (2% probability of exceedance during the structure lifetime), for existing substandard structures in need of seismic retrofit, the nonlinear phenomena may be significant also under the design basis earthquake (DBE) (10% probability of exceedance). Thus, the structural nonlinear behaviour cannot be neglected in a reliable performance-based optimum design of NVDs (Attard 2007; Cimellaro et al. 2009; Akehashi and Takewaki 2019; Idels and Lavan 2021). This is confirmed, in a broader context, by pertinent recent references in the area of performance-based design and optimization of energy dissipation devices (Alavi et al. 2021; Dehghani et al. 2021; Fathizadeh et al. 2020, 2021; Mohammadi et al. 2021). Using a linear frame assumption in these cases could lead to an underestimated structural response and, in turn, to an unconservative damping distribution violating the design constraints (Pollini et al. 2018). This highlights the need for the development of practical design methodologies of dampers fully incorporating the inherent nonlinear behaviour of both the damping devices and the structural frame within a performance-based design framework (Terenzi et al. 2020).

This study aims to develop a simple yet efficient performance-based design optimisation methodology of NVDs for seismic retrofit of existing substandard steel frames. The proposed methodology is able to identify the best height-wise distribution of damping coefficients to satisfy given performance requirements with low computational effort, based on the concept of uniform damage distribution (UDD) (Moghaddam and Hajirasouliha 2008; Hajirasouliha et al. 2012). According to this design philosophy, the damping coefficients at different storey levels are updated using an iterative process until an almost uniform height-wise distribution of a predefined performance index (e.g., maximum inter-storey drift) is attained. In this manner, the energy dissipation capacity of the NVDs is fully exploited, and therefore the structural elements will exhibit minimum damage by satisfying all the design constraints. The application of the proposed low-cost optimisation methodology is illustrated through design examples on 3, 7 and 12-storey steel frames under both artificial spectrum-compatible records and natural earthquakes. The efficiency of the optimum design solutions is assessed both at the local (maximum plastic rotation) and global (overall damage index) level. It should be noted that while the UDD concept has been previously adopted for optimum design of viscous dampers (Levy and Lavan 2006), that study was limited to simplified yielding shear frames with linear dampers, which may not represent the actual behaviour of typical multi-storey steel frames. The main contributions of this research can be summarized as follows:

• A modified UDD optimisation method is adopted, for the first time, for optimum seismic design of non-linear multi-storey steel frames equipped with NVDs under a specific design spectrum. The reliability of the method is investigated by using different initial damping distributions, convergence factors and number of selected design records.

• A simple method is proposed to take into account the effect of equivalent damper stiffness, as a function of damping coefficient, in the optimisation process. Ignoring this effect may lead to inaccurate designs in practical applications.

• By using drift-based, velocity-based, and energy-based optimisation approaches, the most efficient performance index parameter is identified for optimum design of NVDs leading to the best seismic performance.

• The proposed UDD optimisation method is further developed to satisfy multiple performance objectives at different intensity levels of the earthquake excitation, in line with performance-based design recommendations of current seismic codes (FEMA-356 2000; ASCE/SEI Standard 41-17 2017; CEN Eurocode 8 2004).

2 Modelling and assumptions

2.1 Reference steel frames

To show the efficiency of the proposed optimisation method, three substandard moment-resisting steel frames with 3, 7 and 12 storeys are considered, as illustrated in Fig. 1. The dead and live loads for intermediate storeys are assumed to be $5.0$ and $2.5\,{\text{kN}}/{\text{m}}^{2}$, while for the roof level they are reduced to $3.5$ and $1.0\,{\text{kN/m}}^{2}$, respectively. To represent substandard frames in high-seismic regions, the bare frames are designed for gravity loads and horizontal loads calculated from the Eurocode 8 (CEN Eurocode 8 2004) design spectrum for low seismic activity areas (peak ground acceleration (PGA) equal to $0.15\,{\text{g}}$) using ground type C (shear wave velocity 180- 360 m/s) and behaviour factor $q = 2.0$. By assuming regularity in plan and in elevation, nonlinear time-history analyses (NTHAs) are performed with reference to planar models of the structures as per EC8 §4.2.3 (CEN Eurocode 8 2004). Steel S275 (nominal yield strength equal to $275\,{\text{MPa}}$) with a strain-hardening ratio equal to $1\%$ is considered for beams and columns. The steel sections resulting from the design are reported in Fig. 1. Wide flange profiles of HEA type are adopted for beams, while square hollow sections are used for columns (e.g., the nomenclature $180\, \times \,17.5$ indicates a square section with side $180\,{\text{mm}}$ and thickness $17.5\,{\text{mm}}$).

Fig. 1

Details the reference steel frames equipped with nonlinear viscous dampers

The frames are modelled using the finite element software OpenSees (McKenna et al. 2006). Both beam and column members are modelled with a distributed-plasticity approach, using force-based nonlinear elements (“nonlinearBeamColumn”) with five Gauss–Lobatto integration points per element. According to the recommendations by Kostic and Filippou (2012), beam sections (wide flange) and column sections (hollow square tube) are discretized using 40 fibres and 52 fibres, respectively. P-Delta effects are taken into account in the analyses. The inherent damping of the frame is modelled using Rayleigh damping ratio equal to $5\%$ for the first mode and for the mode associated with a cumulative mass participation exceeding 95% (Moghaddam and Hajirasouliha 2008). It is worth noting that, although lower damping ratios are often adopted for steel frames (e.g. $2\%$), the value of $5\%$ is chosen to match the target EC8 design spectrum (described in Sect. 3.1) in line with other literature studies (Del Gobbo et al. 2018a, b; D'Aniello et al. 2013; Karamanci and Lignos 2014). The Newmark constant average acceleration scheme is used for the time integration of the equations of motion. The frames are then strengthened with diagonal dissipative braces equipped with NVDs and implemented in their middle bay according to the sketches in Fig. 1. Modelling details of NVDs and their supporting braces are given in the next subsection.

2.2 Nonlinear viscous damper-brace modelling

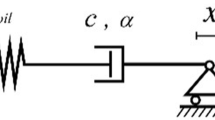
Viscous dampers are widely utilized in practice for the seismic retrofit of existing substandard structures. They are typically installed through supporting braces connecting two subsequent storeys along the building height, according to an “inter-storey installation scheme”. By isolating a damper-brace element as in Fig. 2, the constitutive behaviour of a fluid viscous damper can be described by a Maxwell model comprising a linear spring (of stiffness coefficient $k_{d}$) representing the fluid compressibility (Singh et al. 2003), and a nonlinear dashpot exhibiting a fractional power-law force–velocity relationship (Seleemah and Constantinou 1997)

$$F_{d} = c_{d} ~\left| {\dot{u}_{d} } \right|^{\alpha } \text{sgn} \left( {\dot{u}_{d} } \right)~$$

(1)

Fig. 2

Nonlinear viscous damper-brace system and its idealized mechanical representation

where $c_{d}$ is the damping coefficient; $\dot{u}_{d}$ is the relative velocity between the two terminals of the device projected along the axis of the damper (in this case coinciding with the inter-storey velocity multiplied with $\cos \theta$, where $\theta = \arctan \left( {H/L} \right)~$ is the angle of the brace with respect to the horizontal axis); $\alpha$ is a velocity exponent related to the hydraulic circuit used, which is responsible for the power-law-type nonlinearity ($\alpha$ ranges from 0.1 to 0.5 for devices commonly available in the market; $\alpha = 1$ for ideal linear viscous damper); and ${\text{sgn}}\left( \cdot \right)$ denotes the signum function. In Fig. 2 the Maxwell element representing the NVD is placed in series with another spring representing the brace stiffness $k_{b}$.

Previous experimental studies demonstrated that the flexibility of the brace might influence the mechanical behaviour of the damper-brace system (Akcelyan et al. 2016). The ratio between the damper force and the supporting brace stiffness plays an important role in this case. The optimisation of the dissipative brace with NVD aims at identifying the set of parameters $k_{b} ,k_{d} ,c_{d}$ (while $\alpha$ is generally fixed in the design). To simplify the design process, the stiffness properties of the damper and the supporting brace can be related to the optimum damping coefficient of the NVD through some reasonable assumptions. Building on a previous work by Pollini et al. (2018) but following slightly different derivations, a simplified analytical procedure is here developed. The damper and brace stiffness are represented by two springs in series as shown in Fig. 2. Therefore, the equivalent spring stiffness $k_{{eq}}$ can be calculated as follows:

$$\frac{1}{{k_{{eq}} }} = \frac{1}{{k_{b} }} + \frac{1}{{k_{d} }}~~ \Rightarrow ~~k_{{eq}} = \frac{{k_{b} \cdot k_{d} }}{{k_{b} + k_{d} }}$$

(2)

The total elongation of the dissipative brace is the sum of the elongation of the supporting brace $u_{b}$ and that of the NVD $u_{d}$

$$u_{{{\text{tot}}}} = u_{b} + u_{d}$$

(3)

and its time derivative is

$$\dot{u}_{{{\text{tot}}}} = \dot{u}_{b} + \dot{u}_{d}$$

(4)

The damper-brace element is then assumed to undergo an imposed sinusoidal motion $\delta _{d} \left( t \right) = \delta _{{d,0}} \sin \bar{\omega }t$, with amplitude $\delta _{{d,0}} = \delta _{0} \cos \theta$ and frequency $\bar{\omega }$ equal to the first natural frequency of the structure. $\delta _{0}$ is the maximum inter-storey displacement experienced by the structure at the considered storey level (it may be calculated from the analysis or set as a target value in the design procedure of the dampers). Since the maximum total elongation of the damper-brace system coincides with $\delta _{{d,0}}$, the maximum elongation of the damper can be calculated from Eq. (3)

$$u_{d}^{{{\text{max}}}} ~ = u_{{{\text{tot}}}}^{{{\text{max}}}} - u_{b}^{{{\text{max}}}} = \delta _{{d,0}} - u_{b}^{{{\text{max}}}}$$

(5)

and its time derivative

$$\dot{u}_{d}^{{{\text{max}}}} ~ = \dot{u}_{{{\text{tot}}}}^{{{\text{max}}}} - \dot{u}_{b}^{{{\text{max}}}} = \bar{\omega } \cdot \delta _{{d,0}} - u_{b}^{{{\text{max}}}}$$

(6)

Let $F$ be the reaction force of the damper-brace system (unknown). Since Eq. (6) is valid at each time step $dt$, one can write:

$$\dot{u}_{d} = \frac{{u_{d} }}{{dt}} = \frac{{F/k_{d} }}{{dt}};~~~\dot{u}_{b} = \frac{{u_{b} }}{{dt}} = \frac{{F/k_{b} }}{{dt}}~~~ \Rightarrow ~~\frac{{\dot{u}_{d} }}{{\dot{u}_{b} }} = \frac{{k_{b} }}{{k_{d} }}~~~ \Rightarrow ~~\dot{u}_{b} = \frac{{k_{d} }}{{k_{b} }}\dot{u}_{d}$$

(7)

By substituting (7) back into (4) and solving for $\dot{u}_{d}$, the following equation is obtained:

$$\dot{u}_{d} = \dot{u}_{{{\text{tot}}}} - \frac{{k_{d} }}{{k_{b} }}\dot{u}_{d} ~~ \Rightarrow ~~\dot{u}_{d} = \frac{{\dot{u}_{{{\text{tot}}}} }}{{\left( {1 + \frac{{k_{d} }}{{k_{b} }}} \right)}}$$

(8)

Consequently, the maximum velocity at the two ends of the damper can be expressed as follows:

$$\dot{u}_{d}^{{{\text{max}}}} = \frac{{\dot{u}_{{{\text{tot}}}}^{{{\text{max}}}} }}{{\left( {1 + \frac{{k_{d} }}{{k_{b} }}} \right)}} = \frac{{\bar{\omega } \cdot \delta _{{d,0}} }}{{\left( {1 + \frac{{k_{d} }}{{k_{b} }}} \right)}}$$

(9)

The ratio $\frac{{k_{d} }}{{k_{b} }}$ appearing in Eq. (9) can be expressed in terms of the equivalent stiffness in Eq. (2)

$$\frac{{k_{d} }}{{k_{b} }} = \frac{{k_{{eq}} }}{{k_{b} - k_{{eq}} }}$$

(10)

Combining Eqs. (9) and (10) leads to:

$$\dot{u}_{d}^{{{\text{max}}}} = \frac{{\bar{\omega } \cdot \delta _{{d,0}} }}{{\left( {1 + \frac{{k_{{eq}} }}{{k_{b} - k_{{eq}} }}} \right)}}$$

(11)

In a design process, the axial stiffness of the brace $k_{b}$ can be easily calculated as follows:

$$k_{b} = \frac{{E_{s} A_{b} }}{{L_{b} }}$$

(12)

where $E_{s}$ is the Young’s modulus of steel, $L_{b} = \sqrt {L^{2} + H^{2} }$ is the brace length and $A_{b}$ is the area of the brace cross-section, assumed large enough to avoid yielding. Note that the assumption of a linear spring $k_{b}$ for the brace in the mechanical model of Fig. 2 is justified only if the brace does not yield. Therefore, the equivalent stiffness of the damper-brace system $k_{{eq}}$ can be obtained as the maximum force of the damper-brace system $F_{{{\text{max}}}}$ divided by the total deformability of the damper-brace system:

$$k_{{eq}} = \frac{{F_{{{\text{max}}}} }}{{u_{b} + u_{d} }} = \frac{{c_{d} \left| {\dot{u}_{d}^{{{\text{max}}}} } \right|^{\alpha } }}{{u_{{{\text{tot}}}} }}$$

(13)

Introducing the ratio $\rho = k_{{eq}} /c_{d}$, the previous relation can be re-written as follows:

$$\frac{{\left| {\dot{u}_{d}^{{{\text{max}}}} } \right|^{\alpha } }}{{u_{{{\text{tot}}}} }} = \frac{{k_{{eq}} }}{{c_{d} }} = \rho ;~~~~~\dot{u}_{d}^{{{\text{max}}}} = \left( {u_{{{\text{tot}}}} \cdot \rho } \right)^{{\frac{1}{\alpha }}}$$

(14)

The value $u_{{{\text{tot}}}}$ in (13)–(14) can be considered as a known term in the design procedure, based on some reasonable assumptions. Following the assumptions in Pollini et al. (2018) and applying them to a brace length $L_{b} = 5.94\,\,{\text{m}}$ and steel grade S275 (relevant to the frames considered in this study and shown in Fig. 1) the calculation leads to $u_{{{\text{tot}}}} = 10.8\,\,{\text{mm}}$. Therefore, by introducing (12) and (14) in Eq. (11) a nonlinear (implicit) equation in terms of $\rho$ is obtained.

$$\rho = \frac{1}{{u_{{{\text{tot}}}} }} \cdot \left( {\bar{\omega } \cdot \delta _{{d,0}} /\left( {1 + \frac{{c_{d} \cdot \rho }}{{\frac{{E_{s} A_{b} }}{{L_{b} }} - c_{d} \cdot \rho }}} \right)} \right)^{\alpha } \quad ~ \Rightarrow \quad ~k_{{eq}} = \rho \cdot c_{d}$$

(15)

Based on these derivations, the equivalent stiffness of the damper-brace system can be easily calculated based on the target maximum inter-storey drift using the nonlinear Eq. (15).

The derived formulation shows similarity to the procedure proposed by Pollini et al. (2018) with two minor differences: (1) Unlike the Pollini et al. (2018) method, the formulation of the present paper does not need any iterative harmonic time-history analysis, which can considerably reduce the computational costs; (2) The value of $\rho$ obtained by Eq. (15) depends upon both $c_{d}$ and $\alpha$, whereas the ratio $\rho$ obtained by Pollini et al. (2018) ignores the influence of $c_{d}$. For illustration purposes, the ratio $\rho$ is plotted in Fig. 3 for two inter-storey drift ratios $\delta _{0} /H$ and a fundamental period of the frame equal to 1 s. It is shown that the ratio $\rho$ is strongly influenced by the velocity exponent $\alpha$ and moderately influenced by the damping coefficient $c_{d}$. Also, it is found that $\rho$ slightly increases with increasing the displacement demand of the frame.

Fig. 3

Value of the ratio $\rho$ for two inter-storey drift ratios

In the NTHAs performed in OpenSees (McKenna et al. 2006), NVDs are modelled through “twoNodeLink” elements with a “ViscousDamper” material that implements a Maxwell model (linear spring and nonlinear dashpot in series). The $K parameter of the ViscousDamper material is set as $k_{{eq}} = \rho \cdot c_{d}$, with $\rho$ being calculated according to Eq. (15), thus incorporating both damper stiffness and brace stiffness. The damper forces are obtained by using the element recorder localForce in the twoNodeLink elements. In this paper, damper limit states [typically associated with the exceedance of a maximum stroke limit by the piston during severe earthquakes (Miyamoto et al. 2010)] are not considered in the model. This simplification is also supported by the fact that dampers currently available in the market can be manufactured to have extended strokes, up to $\pm \,900\,\,{\text{mm}}$ (Taylor Devices inc. 2020), so that dampers’ limit states are generally avoided, even under very large drifts.

3 Performance-based optimisation for a code-based design spectrum

3.1 Design spectrum and selected excitation records

To calculate the seismic design loads for practical engineering purposes, a code-based response spectrum, representing the seismic hazard of the selected region, is considered. Therefore, in this study a method is proposed for optimum design of multi-storey steel frames equipped with NVDs under a specific design spectrum. Here, it is assumed that the site of interest is located in a high seismicity region represented by the EC8 elastic design response spectrum with PGA = 0.4 g and ground type C. To illustrate the design methodology and to assess the seismic performance of the structures equipped with NVDs, fifteen natural records are considered as listed in Table 1. These records are selected from the Pacific Earthquake Engineering Research Center (PEER) ground motion database (2020) (records 1–8) and from the SIMBAD database (Smerzini et al. 2014) within the software REXEL v. 3.5 (Iervolino et al. 2010) (records 9–15). These records are selected such that their mean response spectrum is close to the EC8 design spectrum in a wide range of natural periods covering the fundamental periods of the three steel frames as shown in Fig. 4.

Table 1 Selected natural ground motion records

Fig. 4

EC8 response spectrum and acceleration spectra of natural (top) and artificial (bottom) records

To ensure spectrum compatibility to a target spectrum, natural records are generally scaled in amplitude. Nevertheless, in this work the selected records are unscaled (as-recorded) ground motion acceleration time histories, meaning that no scaling factors are preliminarily applied. Although no scaling procedure is adopted, the spectrum compatibility conditions were checked for the selected (unscaled records) as recommended in seismic codes (e.g., ASCE/SEI Standard 41-17 2017; CEN Eurocode 8 2004). As can be seen in Fig. 5, in the range of periods $0.2T - 1.5T$ (where $T$ is the fundamental period of the structure) it is verified that the spectrum ordinates are comprised within a $\pm \,10\%$ tolerance with respect to the target design spectrum (considering the period of the three-story frame $T_{3}$ as the lower bound and the period of the twelve-story frame $T_{{12}}$ as the upper bound). Based on the generally good agreement observed (with little discrepancies only near the end of the spectrum plateaux), the selected records can be reasonably considered as spectrum-compatible records for practical design and seismic performance assessment purposes.

Fig. 5

Spectrum matching assessment vs target spectrum for natural (top) and artificial (bottom) records

Additionally, a set of six artificial records fully compatible with the EC8 response spectrum are generated through the TARSCTHS software, which is the acronym for “Target acceleration spectra compatible time histories” and was developed at the State University of New York at Buffalo (Papageorgiou et al. 2002). The code TARSCTHS is the implementation of the method described in Deodatis (1996) and uses non-stationary stochastic vector processes to generate artificial records compatible with a target response spectrum. The iterative scheme is applied in frequency domain where the phase angles of the desired motion are randomly generated ground motion scaling in time domain. Although the response spectra of all the six generated artificial records compare very well with the selected target spectrum (as depicted in Fig. 4), each of the records has its own random specifications. Similar to the natural records, the spectrum compatibility conditions are verified for the selected artificial records in the range of periods $0.2T - 1.5T$, as shown in Fig. 5. In the remainder of the paper, the design of NVDs is carried out under either the six artificial records or just one of the six simulated artificial records (SIM01) in order to ascertain whether, and to what extent, the latter approach can be adopted for simplification purposes. Finally, it is worth noting that these records (and the corresponding EC8 target spectrum) represent the DBE level. In the multi-level performance-based design methodology, the MCE records are obtained by scaling these artificial records to PGA = 0.56 g (scaling factor 1.4).

3.2 Uniform damage distribution design philosophy

The design methodology used in this study is based on the concept of uniform damage distribution (UDD). During severe earthquakes it is expected that the deformation demand of a frame structure is not uniform. Hence, if the damping coefficients of NVDs are increased in those storey levels experiencing higher level of damage and, conversely, are decreased in those storey levels undergoing less deformation demand, a status of uniform deformation demand is eventually achieved. According to this design philosophy, the energy dissipation capacity of the NVDs is fully exploited because underused dampers are reduced in size (or eliminated at all) to accomplish certain performance requirements at the minimum cost.

In this paper, the deformation demand is related to the inter-storey drift ratio ${{\Delta }} = \delta /H$ because of its widely accepted physical role to quantify damage in both structural and non-structural components. However, any other (local or global) damage index can be easily used in the proposed method as will be explained in the following sections. The deformation demand is computed through NTHAs performed in OpenSees and interfaced with an external subroutine, written in MATLAB environment (MATLAB R 2018a), that controls the iterative updating of the damper parameters. Throughout the remainder of the paper it is assumed that the velocity exponent of the dampers is equal to $\alpha = 0.3$ at all the storey levels (Altieri et al. 2018), and the optimisation is focused on the determination of the damping coefficients only. In particular, the following sequential formula is implemented in the MATLAB script:

$$c_{{d,i}}^{{n + 1}} = c_{{d,i}}^{n} \times \left( {\frac{{{{\Delta }}_{{{\text{max}},i}}^{n} }}{{{{\Delta }}_{{{\text{target}}}} }}~} \right)^{\gamma }$$

(16)

where ${{\Delta }}_{{{\text{max}},i}}^{n}$ and ${{\Delta }}_{{{\text{target}}}}$ are the maximum inter-storey drift ratio at the ith storey computed at the nth iteration and the target inter-storey drift ratio, respectively; $\gamma$ is a scalar parameter that influences the convergence rate and, in turn, the computational cost of the procedure; and $c_{{d,i}}^{n}$ and $c_{{d,i}}^{{n + 1}}$ represent the damping coefficients of the NVDs installed at the i^th storey at two subsequent iterations $n$ and $n + 1$. Using Eq. (16) in an iterative process will eventually lead to a uniform profile of inter-storey drifts that is as close as possible to the target value ${{\Delta }}_{{{\text{target}}}}$ at every storey level. Therefore, the sequential updating is carried on until the difference between the coefficient of variation (CoV) values of inter-storey drifts at two subsequent iterations is lower than a certain threshold.

The value of ${{\Delta }}_{{{\text{target}}}}$ significantly affects the final design parameters of the NVDs, and in this paper this value is assumed equal to $1.5\%$ and $2.0\%$ for DBE and MCE, according to FEMA recommendations for life safety (LS) and collapse prevention (CP) performance levels in braced steel frames (FEMA-356 2000), respectively.

3.3 Effect of initial damping distribution

For any optimisation method, it is important to assess to which extent the choice of the initial damping distribution (within a range considered “reasonable” from an engineering point of view) affects the final design solution, in the sense of potentially leading to a local optimum solution. The effect of the initial damping distribution is investigated here by considering three uniform damping distributions as initial choice in the iterative procedure. The first distribution is defined by damping coefficients $c_{{d,i}} = c_{{d0}}$, where $c_{{d0}}$ is the minimum value for which all the inter-storey drifts are lower than (or at least equal to) ${{\Delta }}_{{{\text{target}}}}$. In other words, $c_{{d0}}$ is the minimum damping coefficient of a uniform damping distribution that can reach the target performance level. The other two initial uniform distributions are $c_{{d,i}} = 0.3 \times c_{{d0}}$ and $c_{{d,i}} = 3 \times c_{{d0}}$, thus including an under-estimated distribution and an over-estimated distribution compared to the minimum damping distribution. For simplicity, the results are related to one arbitrary artificial record (SIM01), but similar conclusions can be drawn under any other artificial or natural record.

In Fig. 6 the total damping coefficient ${{\Sigma }}_{i}^{N} c_{{d,i}}$ (with $N$ the number of storeys) is plotted with increasing number of iterations for the 7-storey and 12-storey steel frames. It is noted that the sum of damping coefficients is obviously different in the first few steps of the procedure, as there are significant discrepancies between the damping coefficients using different initial design assumptions as described above. Nevertheless, as the iterations proceed, the damping coefficients are adjusted (either increased or decreased) to converge toward the same final distribution. This is clearly noted in the bottom part of Fig. 6 showing the optimum damping distribution obtained after just 20 iterations (with a convergence factor $\gamma = 2.0$), which indicates that the final solution is reasonably independent from the initial distribution of damping coefficients in the optimisation methodology. Indeed, apart from minor differences noted at the lower storey levels related to the relatively low number of iterations performed, practically the same final damping distribution is obtained for the three initial design assumptions. Obviously, using an appropriate initial damping distribution (along with a reasonable value of the convergence factor $\gamma$) can speed up the convergence rate of the procedure towards the final solution. In the next subsection, the influence of the convergence factor is discussed.

Fig. 6

Variation of total damping coefficient (top) and height-wise damping distribution after 20 iterations (bottom) for different initial damping distribution assumptions

3.4 Effect of convergence factor

The computational cost of the proposed optimisation procedure is strongly affected by the convergence factor $\gamma$. Small values of $\gamma$ always lead to a converged solution but may imply a high number of iterations to reach convergence. On the other hand, while large values of $\gamma$ aims at speeding up the convergence rate, very large values of $\gamma$ may be counterproductive because they may generate significant fluctuations. Therefore, it is necessary to identify a reasonable interval of variation of $\gamma$ for ensuring computational efficiency without implying fluctuations as the iterations proceed. Comprehensive sensitivity analyses were carried out on the three considered steel frames under several earthquakes (both natural and artificial). Here, a limited set of results pertinent to the 7-storey and 12-storey frames under one arbitrary artificial record (SIM01) are illustrated for the sake of brevity. In particular, in Fig. 7-top the CoV of the maximum drift ratio ${{\Delta }}_{{{\text{max}}}}$ (calculated as standard deviation divided by average of ${{\Delta }}_{{{\text{max}}}}$ across the storey levels) is plotted during the optimisation process for $\gamma$ values equal to 0.2, 0.5, 1.0, 2.0, 4.0, and 5.0, starting from a uniform damping distribution $c_{{d,i}} = c_{{d0}}$ as defined in the previous subsection. The same calculations are repeated for $c_{{d,i}} = 0.3 \times c_{{d0}}$ and $c_{{d,i}} = 3 \times c_{{d0}}$ and qualitatively similar results are obtained, so the same considerations apply. It is observed that for values of $\gamma$ lower than 0.2 the convergence can be very slow, whereas as $\gamma$ increases from low values up to $\gamma = 2.0$, the speed of convergence increases without any significant fluctuation. Note that the CoV of ${{\Delta }}_{{{\text{max}}}}$ generally decreases monotonically as the iterations proceed. Additionally, for larger values of $\gamma$ the proposed methodology may not convergence to the optimum design solution as confirmed by the trend of the CoV of ${{\Delta }}_{{{\text{max}}}}$ for $\gamma = 4.0$ in the 12-storey frame and for $\gamma = 5.0$ for both the 7- and 12-storey frames.

Fig. 7

Coefficient of variation (CoV) of maximum drift ratio ${{\Delta }}_{{{\text{max}}}}$ as iterations proceed (top) and height-wise distribution of ${{\Delta }}_{{{\text{max}}}}$ at selected iterations for $\gamma =2.0$ (middle) and $\gamma =5.0$ (bottom)

The height-wise distribution of ${{\Delta }}_{{{\text{max}}}}$ at selected iterations for $\gamma = 2.0$ (Fig. 7-middle) reveals that as the iterations proceed, the damping coefficients are decreased at some storey levels (e.g. for the dampers at the top storey) in order to eventually reach a profile of uniform maximum drift ratios approaching the target drift ratio ${{\Delta }}_{{{\text{target}}}} = 1.5\%$. The final solution at convergence is indeed associated with the lowest possible value of the CoV of ${{\Delta }}_{{{\text{max}}}}$, in line with the UDD design philosophy. Note that the choice of $\gamma = 2.0$ makes it possible to obtain a reasonable drift profile close to the final solution after just 5 iterations.

The results indicate that some storeys do not need dampers to comply with the selected performance requirement (e.g. the first storey in the 7-storey frame and the first three storeys in the 12-storey frame). This is consistent with the height-wise damping distribution shown in Fig. 6-bottom. The value of ${{\Delta }}_{{{\text{max}}}}$ in these storeys is in fact lower than ${{\Delta }}_{{{\text{target}}}}$ even by placing no damper. On the contrary, by inspection of the height-wise distribution of ${{\Delta }}_{{{\text{max}}}}$ at selected iterations for $\gamma = 5.0$ (Fig. 7-bottom) it is clearly seen that the procedure is not able to reach convergence with this higher value of the convergence factor. Indeed, the maximum drift ratios initially fluctuate around the target value and may also move away from it as the iterations proceed (e.g. in the 7-storey frame). These results confirm that values $\gamma > 4.0$ are not recommended as they may lead to fluctuations and may hinder the convergence of the procedure.

These obtained results are critically analysed in relationship to previous indications from the literature. Levy and Lavan (2006) suggested a value $\gamma = 1/5 = 0.2~$ for nonlinear shear yielding frames equipped with viscous dampers, which seems to be quite low in relationship to the results obtained in this paper. Hajirasouliha and Pilakoutas (2012) proposed a convergence factor between 0.1 and 0.2 for optimum strength distribution of shear building structures to achieve a UDD; Mohammad et al. (2019) recommended a convergence factor of 1.2 for steel frames equipped with buckling restrained brace dampers; Nabid et al. (2018) proposed a factor of 0.2–0.5 for reinforced concrete (RC) frames with friction dampers. Based on this sensitivity analysis, it seems that a reasonable factor for non-linear steel frames equipped with NVDs to achieve convergence without fluctuations is, in general, between 1.0 and 2.0. Therefore, all the following numerical analyses in this study will be performed using $\gamma$ equal to 2.0.

It is worth noting that the proposed approach requires only a few iterations/nonlinear analyses (generally 10–15) to achieve convergence and to identify the optimal design solution. This is a major advantage compared to evolutionary algorithms, which are certainly more accurate in exploring the entire search space but also more computationally expensive due to the large number of iterations involved. In previous studies (Mohammadi et al. 2019; Nabid et al. 2020) it was demonstrated that the proposed UDD approach leads to optimum design solutions of comparable accuracy to genetic algorithms using thousands of iterations, thus showing high computational efficiency and simplicity.

3.5 Sensitivity to the selected earthquake record

The seismic design of structures is influenced by the inherent uncertainty in the selected earthquake ground-motion. Consequently, the optimum damping distribution may also change from one record to another based on the characteristics of the design earthquake. However, this effect is generally reduced (but not eliminated) when code-based spectrum-compatible earthquakes are utilised. An obvious design criterion to capture the record-to-record variability would be to consider the mean damping distribution obtained for a set of earthquakes. To investigate the effects of the chosen design earthquake on the resulting optimum damping distribution, four alternatives are compared and their performance in terms of maximum drift ratios is analysed. As a first choice, the uniform damping distribution is considered as a benchmark solution because of practicality reasons. The second distribution is obtained by applying the optimisation methodology to a single artificial spectrum-compatible record (arbitrarily selected, e.g. SIM01) and optimising the damping coefficients under this record individually (SIM01 distribution). The third distribution is obtained as mean of the six optimum damping distributions relevant to each of the six artificial records (mean artificial optimum). In a similar manner, the fourth distribution is obtained as mean of the fifteen optimum damping distributions relevant to each of the fifteen natural records (mean natural optimum). For comparison purposes, the four damping distributions are defined such that they share the same total damping coefficient ${{\Sigma }}c_{{d,i}} = {{\Sigma }}_{{{\text{target}}}}$. In other words, the damping coefficients found via Eq. (16) are scaled, at each iteration, according to the following formula:

$$\left[ {c_{{d,i}}^{{n + 1}} } \right]_{{{\text{scaled}}}} = c_{{d,i}}^{{n + 1}} \times \left( {\frac{{{{\Sigma }}_{{{\text{target}}}} }}{{{{\Sigma }}_{i}^{N} c_{{d,i}}^{{n + 1}} ~}}} \right)$$

(17)

In this way, the sum of the damping coefficients at all storeys remains unchanged at each iteration and for every distribution considered. Since the suite of the six artificial records is the one that approaches the EC8 design spectrum more closely, the value ${{\Sigma }}_{{{\text{target}}}}$ is assumed to be the total damping coefficient of the mean artificial optimum distribution.

It is shown in Fig. 8 that for the 3- and 7-storey frame the damping distribution obtained by considering just one artificial record (SIM01 distribution) is quite similar to that obtained under a set of spectrum-compatible records (mean artificial and mean natural optimum distribution). It is implicit that optimising the damping distribution based on just one earthquake would be much more convenient than using a set of records, in terms of both computational effort and simplification purposes. The corresponding height-wise profiles of ${{\Delta }}_{{{\text{max}}}}$ shown in the bottom part of Fig. 8 (average results under six artificial records) confirm that the use of a single artificial spectrum-compatible record generally leads to acceptable results for short-to-medium rise structures in the proposed performance-based design methodology. For these two frames, the optimum distributions (regardless of the class of earthquake records considered) generally lead to lower maximum drift ratios than the equal-cost uniform damping distribution. On the other hand, for taller buildings (e.g. the 12-storey frame) the number of design variables increases and the response may be affected by higher-mode effects that are triggered to a different extent depending on the excitation record. Consequently, using a single record may lead to slightly inaccurate results for a design spectrum-based methodology. This implies that for the optimum design of tall buildings equipped with NVDs, the use of a set of records is generally recommended.

Fig. 8

Sensitivity to the selected earthquake record: comparison between different damping distributions (top) and related height-wise distribution of ${{\Delta }}_{{{\text{max}}}}$, average results under six artificial records (bottom)

It is worth noting that the mean spectrum of the six artificial records and of the fifteen natural records both exhibit a good agreement with the EC8 design spectrum. It is shown in Fig. 8 that for all the three frames the mean artificial and mean natural optimum distributions are reasonably comparable, which confirms that there is generally a unique optimum design solution under a specific design spectrum.

4 Efficiency of the optimum solution under natural records

4.1 Local and global damage index

The efficiency of the optimum design solution is analysed by NTHAs of the steel frames under the selected fifteen natural records in Table 1 whose mean pseudo-acceleration response spectrum is close to the EC8 design spectrum as illustrated in Fig. 4. The seismic performance is assessed through the calculation of local and global damage indices. The local damage is quantified by the value of the maximum plastic rotation $\theta _{p}^{{{\text{max}}}}$ attained in the beam and column elements of the steel frame. Note that $\theta _{p}^{{{\text{max}}}}$ is recognized as a key performance parameter of structural steel components in current seismic regulations like ASCE/SEI 41-17 (2017). The global damage is quantified by a general damage index proposed by Powell and Allahabadi (1988):

$$D_{i} = \left( {\frac{{\delta _{c} - \delta _{t} }}{{\delta _{u} - \delta _{t} }}} \right)^{m}$$

(18)

where $\delta _{c}$, $\delta _{t}$ and $\delta _{u}$ are the calculated, threshold and ultimate values of the generic damage parameter $\delta$, respectively, and $m$ is an exponent controlling the relationship between the damage index and the damage parameter. In this study, the inter-storey inelastic deformation is assumed as the basic damage parameter. The factor $m$ is assumed to be 1.5, which is consistent with a low-cycle fatigue approach as suggested by Krawinkler and Zohrei (1983). The cumulative damage index at the ith storey $D_{i}$ ranges from 0 (undamaged) to 1 (severely damaged). In this study, the threshold damage parameter is represented by the nominal yield deformation of the ith storey $\delta _{{yi}}$ (Nabid et al. 2018; Moghaddam et al. 2005). The global damage of the structure is computed as weighted average of cumulative damage indexes in (18) at the various storey levels, with weights represented by the dissipated energy at the ith storey $W_{{pi}}$, that is

$$D_{g} = \frac{{\mathop \sum \nolimits_{{i = 1}}^{N} D_{i} \cdot W_{{pi}} }}{{\mathop \sum \nolimits_{{i = 1}}^{N} W_{{pi}} }}$$

(19)

with $N$ the total number of storeys. Assuming that the dissipated energy corresponding to each storey level is proportional to the damage in that storey level, the global damage formula in (19) is simplified as follows (Nabid et al. 2018; Moghaddam et al. 2005):

$$D_{g} = \frac{{\mathop \sum \nolimits_{{j = 1}}^{N} D_{i}^{2} }}{{\mathop \sum \nolimits_{{j = 1}}^{N} D_{i} }}$$

(20)

The nominal yield deformation of the ith storey $\delta _{{yi}}$ is calculated through a pushover analysis of the bare frame (without NVDs) under constant gravity loads and assuming a monotonically increasing lateral load applied at the ith storey only, while keeping all the nodes below the ith storey fixed. This load pattern minimises the uncertainties related to the assumption of a pre-determined load pattern (e.g. uniform or triangular) as it is specifically focused on the inter-storey force and deformation of the ith storey. The lateral load is increased in displacement-controlled mode until a maximum drift ratio equal to $\delta _{{{\text{max}}}} /H = 5\%$ (corresponding to collapse prevention performance level for steel moment resisting frames (FEMA-356 2000)) is achieved. For the identification of the $\delta _{{yi}}$ value, an equivalent bilinear elastoplastic relationship with hardening under an equal-energy assumption is adopted according to current seismic regulations (FEMA-356 2000; CEN Eurocode 8 2004). An illustrative example of the calculation procedure of $\delta _{{yi}}$ for three arbitrary storey levels of the 7-storey steel frame is illustrated in Fig. 9.

Fig. 9

Determination of nominal yield deformation via pushover analysis

4.2 Seismic performance assessment

Figure 10 compares the local damage index (in terms of maximum plastic rotation $\theta _{p}^{{{\text{max}}}}$), global damage index, maximum base shear and maximum absolute floor acceleration of the 3-, 7- and 12-storey steel frames equipped with three different distributions of NVDs, namely uniform, SIM01 distribution and mean artificial optimum, the latter simply called “optimum”. The three distributions have the same cost in terms of sum of damping coefficients, so the differences of the seismic performance are uniquely ascribed to the different placement of the dampers. The histograms report the average value of the response quantity under the selected fifteen natural records in a normalized fashion, i.e. divided by the corresponding response parameter in the bare frame (without NVDs), and the superimposed error bars indicate the corresponding standard deviation. In general, by using NVDs significant reductions in both the local and global damage indices are achieved, up to 70% and 90%, respectively. Among the three damper distributions, it is noted that the SIM01 distribution (i.e. optimisation under a single artificial spectrum-compatible record) is associated with a comparable seismic performance to the optimum distribution for low to medium-rise structures (3- and 7-storey frames). Instead, for the 12-storey frame the damage reduction of the SIM01 distribution is slightly lower than the optimum distribution and, considering the standard deviation, of comparable order of the uniform distribution. As already observed in subsection 0 for artificial records, these results confirm the conclusion that a set of records is recommended for high-rise buildings, while a single record can be practically adopted in low to medium-rise buildings for simplification purposes.

Fig. 10

Seismic performance assessment, average results (plus standard deviation) under fifteen natural records

The large standard deviation observed in the damage histograms is consistent with the wide range of frequency contents and amplitudes of the fifteen individual (unscaled) natural records (see Fig. 4). It should be mentioned that similar trends of damage are obtained under artificial records (here not shown for brevity) but with a considerably lower standard deviation than natural records. The results, on average, suggest that the optimum UDD solution is more efficient in reducing the structural damage of the frames compared to an equal-cost uniform distribution, with up to 40% reductions in terms of local and global damage indices. On the other hand, the response in terms of base shear and floor absolute acceleration is rather comparable with negligible differences among the three damping distributions, which is reasonable considering the same total damping coefficient.

It is worth noting that in this study the optimum damping distribution is identified by using the artificial records and then the seismic performance is assessed under the set of independent natural records. While the two classes of records share, on average, a similar mean response spectrum (close to the EC8 design spectrum), they have different random acceleration vibration characteristics. In Fig. 11, the height-wise average profiles of ${{\Delta }}_{{{\text{max}}}}$ under the set of fifteen natural records are shown. It is noted that the proposed optimisation methodology based on the concept of UDD leads to less concentrated drifts than an equal-cost uniform damping distribution. Indeed, the drift profiles tend to be close to the value of ${{\Delta }}_{{{\text{target}}}}$ at all the storey levels (except the first storey in the 7-storey frame and the first three storeys in the 12-storey frame that do not need dampers at all). The drift target was more closely approached under the artificial records, whereas in the case of natural records there was a wider range of variability due to the frequency contents of each earthquake. Nevertheless, there are only small discrepancies in the value of ${{\Delta }}_{{{\text{max}}}}$ compared to ${{\Delta}}_{\text{target}}$ (less than $\pm 10\,{\%}$ of differences), which is reasonable considering the nonlinearity of the frame behaviour, the inherent uncertainties associated with the natural records and the fact that an independent set of records (different from the artificial records used for the design) is considered. These discrepancies are generally covered by appropriate safety factors in the seismic design process. The overall trend observed for natural records is consistent with that previously observed for artificial records. As an example, it is shown that using one record (SIM01 distribution) is an acceptable simplification to obtain a reasonable damping distribution for the 7-storey frame but it may be unsatisfactory when a high number of storeys is involved as in the case of the 12-storey frame. In these cases, using a group of records is recommended.

Fig. 11

Maximum drift profiles, average results under fifteen natural records

It is shown in Fig. 10 that the addition of dampers slightly increased the base shear compared to the bare frame, in the order to 10–15% for the considered distributions. It should be noted that the presence of NVDs may also increase the axial force in the columns, which may require supplemental strengthening of foundations and columns in view of capacity design principles (Karavasilis 2016). Generally, the most critical columns are those located near the supporting braces where the dampers are installed. To investigate this effect, the axial force-bending moment interaction diagrams of the middle-bay columns (near the supporting braces) for two representative storey levels of the 7-storey frame are illustrated in Fig. 12. According to §6.2.9 Eurocode 3 (CEN Eurocode 3 2005), for class 1 sections the design plastic moment resistance, reduced due to the axial force ${N}_{\text{Ed}}$, is:

$$M_{{{\text{N,Rd}}}} = M_{{{\text{pl,Rd}}}} \left[ {1 - \left( {\frac{{N_{{{\text{Ed}}}} }}{{N_{{{\text{pl,Rd}}}} }}} \right)^{2} } \right]$$

(21)

where ${M}_{\text{pl,Rd}}$ is the design resistance for pure bending and $N_{{{\text{pl,Rd}}}}$ is the design resistance for uniform compression (calculated with an appropriate reduction factor depending on the non-dimensional slenderness to account for buckling). The interaction diagram given by Eq. (21) is plotted in Fig. 12 along with the characteristic points (average maximum value of the axial force-bending moment combination from the NTHAs under the fifteen natural records) relevant to the bare frame and the frame equipped with NVDs according to both uniform and optimum distributions.

Fig. 12

Axial force-bending moment interaction diagram of steel columns adjacent to the supporting brace at the 2nd and 4th storey of the 7-storey steel frame, average peak results under fifteen natural records

As expected, the results in Fig. 12 confirm that the 7-storey bare frame was under-designed with respect to the considered earthquake intensity level (PGA = 0.4 g), and thus the maximum combination of axial force-bending moment experienced by the column cross-section exceeded the corresponding design resistance combination. Although the overall seismic performance of the frames with NVDs improves in terms of both global and local damage indices, it should be noted that there is no guarantee that the frames with supplemental dampers satisfy all the cross-section ultimate limit states verifications unless these conditions are explicitly considered in the performance-based optimisation methodology. It can be seen that, in general, the addition of dampers slightly increases the axial force in the columns (here in the order of 10–15%, similar to the base shear results shown above) but also concurrently reduces the bending moment compared to the bare frame due to a reduced inter-storey shear deformation. For the representative cases analysed in Fig. 12, it is noted that the uniform distribution leads to higher values of axial force and bending moment than the optimum distribution. Therefore, the optimum distribution is associated with a higher safety margin compared to the uniform distribution in relationship to the interaction diagram. Similar results were observed for the other structures considered in this study.

Although in general the seismic performance depends on a range of design parameters such as number of storeys, amplitude and frequency content of the earthquake excitation, mechanical and geometrical characteristics of the parent structure, topology of damper installation, which are only partly investigated in these examples, the outcomes of this investigation demonstrate the proposed optimisation method leads to more efficient design solution (with a lower and less concentrated structural damage) than a conventional equal-cost uniform damping distribution.

5 Optimisation based on alternative performance parameters

5.1 Velocity-based optimisation

The expression (16) underlying the proposed UDD design philosophy is general and can be applied to any other relevant response parameter. Although a uniform height-wise distribution of maximum drift seems a reasonable design target addressing both structural and non-structural damage, for comparison purposes it is of interest to explore alternative variants of the UDD methodology based on other response quantities. As an example, maximum damper forces $F_{{{\text{d,max}}}}$ can be considered as a measure to assess the efficiency of a damper distribution as well as to estimate the upfront damper cost in the seismic retrofit process. Fitting a curve of some commercial viscous dampers available in the market, Gidaris and Taflanidis (2015) proposed the following approximate formula to estimate the upfront damper cost at storey level j:

$${\text{Upfront}}\,{\text{Damper}}\,{\text{Cost}}_{j} [\$ ] = 96.88 \times \left( {F_{{dj,\max ~}} ~[kN]} \right)^{{0.607}}$$

(22)

Despite the approximate nature of Eq. (22), this simplified formula is used here for comparison purposes only. Some studies (e.g., Hwang et al. 2013; Del Gobbo et al. 2018b) suggested to assess the damper placement efficiency by computing the ratio between the maximum damper force $F_{{dj,\max }}$ and the corresponding damping coefficients ${c}_{d,j}$ at each storey level. This ratio represents a measure of the engagement of the damper in terms of energy dissipation. If linear viscous dampers were used ($\alpha =1$), this ratio would be equal to the peak relative velocity at the two terminals of the device, which is in turn related to the peak inter-storey velocity (apart from minor vertical movements). For NVDs ($\alpha <1$ as in this paper), however, this ratio is proportional (not equal) to the peak relative velocity. Based on these motivations, to obtain a more uniform height-wise distribution of peak inter-storey velocity, the damping coefficients of the NVDs can be redistributed according to the following formula:

$$c_{{d,i}}^{{n + 1}} = c_{{d,i}}^{n} \times \left( {\frac{{v_{{\max ,i}}^{n} }}{{v_{{\max ,\text{ave}}}^{n} }}~} \right)^{\gamma }$$

(23)

where $v_{{\max ,i}}^{n}$ and $v_{{\max ,{\text{ave}}}}^{n}$ represent the maximum inter-storey velocity at the ith storey computed at the nth iteration and the average peak inter-storey velocity at all storeys at the same iteration, respectively. In addition to the previous motivations justifying the appropriateness of a velocity-based optimisation to promote a uniform engagement of the damper in terms of energy dissipation, it should be noted that for some specific industrial facilities and equipment, the mitigation of the maximum velocity response of the structure could be more important than maximum displacement. Similar to the drift-based procedure, the sequential updating is carried on until the difference between the CoV values of inter-storey velocity at two subsequent iterations is lower than a certain threshold.

5.2 Energy-based optimisation

The primary aim of the dampers is to absorb and dissipate a major portion of the input energy from an earthquake. In line with other studies from the literature (De Domenico and Ricciardi 2019; Sorace and Terenzi 2008), the efficiency of a damper optimisation methodology can be assessed based on energy dissipation criteria. An energy based UDD methodology was recently adopted by Nabid et al. (2020) for the optimisation of friction dampers in RC structures. In the quoted study, the slip forces of friction dampers were redistributed with the aim to obtain a more uniform height-wise distribution of energy dissipation capacity under a design earthquake. Based on a similar concept, the damping coefficients of the NVDs can be redistributed according to the following formula:

$$c_{{d,i}}^{{n + 1}} = c_{{d,i}}^{n} \times \left( {\frac{{E_{{d,i}}^{n} }}{{E_{{d,{\text{ave}}}}^{n} }}~} \right)^{\gamma }$$

(24)

where ${E}_{d,i}^{n}$ represents the energy dissipated by the viscous damper at the ith storey computed at the nth iteration, and $E_{{{\text{d,ave}}}}^{{\text{n}}}$ is the average energy dissipation by all dampers in the structure at the same iteration. Expression (24) aims at increasing the size of the dampers that dissipate more and reducing the size of the dampers that are less efficient in terms of energy dissipation. The energy balance equations of a structure equipped with NVDs can be expressed in the following form (Uang and Bertero 1990):

$$E_{k} + E_{\xi } + E_{d} + \underbrace {{E_{s} + E_{h} }}_{{E_{a} }} = E_{i}$$

(25)

where ${E}_{k}$ is the kinetic energy, ${E}_{\xi }$ is the damping energy of the structure (due to inherent damping, like Rayleigh damping), ${E}_{d}$ is the energy dissipated by the NVDs, ${E}_{a}$ is the absorbed energy, which is composed of recoverable elastic strain ${E}_{s}$ and irrecoverable hysteretic energy ${E}_{h}$, and ${E}_{i}$ is the input energy. An efficient distribution of dampers from an energy-based perspective aims at maximizing ${E}_{d}$ for a given input energy ${E}_{i}$, thus implying a reduction of both hysteretic energy ${E}_{h}$ and damping energy ${E}_{\xi }$ (the vibrational energy ${E}_{k}+{E}_{s}$ is nonzero only in the transient phase and is completely recovered at the end of the seismic excitation). Based on these concepts, the following energy dissipation index (${\text{EDI}}$) can be adopted to quantify the efficiency of the dampers in dissipating the largest possible amount of input energy (De Domenico et al. 2019):

$${\text{EDI}} = \frac{{E_{d} }}{{E_{d} + E_{\xi } + E_{h} }}$$

(26)

with $0< {\text{EDI}} <1$. Due to their cumulative nature, the terms in Eq. (26) are evaluated at the end of the earthquake excitation. The larger the ${\text{EDI}}$, the more effective the damper distribution in terms of energy dissipation. Considering the concept of UDD, the application of Eq. (24) is expected to lead to an increase in the ${\text{EDI}}$ value representing more efficiently in terms of energy dissipation. Since the target of the optimisation is to obtain the maximum possible energy dissipation in the dampers (relative to the input energy), the ${\text{EDI}}$ value is monitored at each iteration and the sequential procedure given by Eq. (24) stops as soon as ${\text{EDI}}$ reaches its peak value. Similar to the drift-based and the velocity-based procedures, only a few iterations are generally sufficient to obtain the maximum ${\text{EDI}}$ value.

5.3 Results and discussion

Figure 13 shows the height-wise distribution of the damping coefficients and the related seismic performance of the 7-storey frame equipped with NVDs designed according to the drift-based (Eq. 16), velocity-based (Eq. 23), energy-based (Eq. 24) UDD methodology, as well as according to a uniform distribution pattern. For comparison purposes, in the UDD methodology the constrained expression (17) is applied so that all the four damping distributions have the same sum of damping coefficients. It can be observed that the height-wise distribution of the peak damper forces ${F}_{d, {\text{max}} }$ is considerably different for the four distributions, with differences up to 250%. The efficiency ratio ${F}_{d,\mathrm{m}\mathrm{a}\mathrm{x}}/{c}_{d}$ is also plotted in Fig. 13 (bottom-left), along with the corresponding CoV of the values along the building height. This parameter can demonstrate the efficiency of the dampers at different storey levels. It is clearly noted that velocity-based and energy-based distributions produce more uniform trends of the efficiency ratio, with lower CoV (5.9% and 5.2%) than drift-based and uniform distributions (8.1% and 8.7%). This is consistent with the nature of the UDD design philosophy that, in the velocity-based and energy-based cases, attempts to make the energy dissipation engagement of all the NVDs more uniform.

Fig. 13

Comparison of damping distributions and seismic performance for alternative design parameters in the UDD optimisation methodology, average results under six artificial records for the 7-storey steel frame

As reasonably expected, the CoV of drifts is significantly lower for the drift-based UDD methodology that is aimed at producing a uniform drift profile. In particular, the CoV of the drifts is clearly reduced (more than halved, from 29.4 to 12.0%) in the drift-based distribution compared to the uniform distribution having the same sum of damping coefficients. Figure 13 also plots the trend of the maximum floor acceleration, which is an important parameter for the seismic protection of non-structural components and acceleration-sensitive equipment (Mohsenian et al. 2019). Although the differences in terms of $\mathrm{a}\mathrm{c}{\mathrm{c}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ are not particularly marked, a better trend is observed for the energy-based distribution, while the drift distribution leads to relatively higher top-floor acceleration.

To comparatively assess the seismic performance of the four analysed damper distributions from energy-balance perspectives, in Fig. 14 the different energy contributions defined in Eq. (25) are plotted under the SIM01 record. As expected, the energy-based distribution leads to the highest value of the $\mathrm{E}\mathrm{D}\mathrm{I}$, whereby the energy dissipated by the NVDs is increased in comparison to the absorbed energy of the structure. The drift-based distribution also leads to a good energy dissipation behaviour (comparable to the energy-based), whereas a lower value of the $\mathrm{E}\mathrm{D}\mathrm{I}$ is obtained for the uniform distribution. This is because dampers that are distributed uniformly are not fully efficient in terms of energy dissipation. It is worth noting that the input energy is reasonably comparable in the four systems, but the way in which this energy is distributed is different depending on the damper distributions. It is interesting to discuss two cases, namely energy-based and uniform distribution. For the energy-based distribution a large amount of input energy is dissipated by the NVDs, while the absorbed energy is relatively low. In contrast, in the uniform distribution the energy dissipated by the dampers is lower and, hence, the absorbed energy (and the energy dissipated by the inherent damping mechanisms in the structure) is increased accordingly. This produces a higher damage in the beam and column members of the steel frame. This different energy dissipation behaviour of the two discussed distributions is confirmed by the force–displacement loops of the dampers at various storey levels plotted in Fig. 15. It is clearly seen that the area of the hysteretic loops is higher in the energy-based distribution, which directly affects the ${E}_{d}$ value in Fig. 14 and, in turn, the $\mathrm{E}\mathrm{D}\mathrm{I}$.

Fig. 14

Time history of energy contributions under SIM01 record for the 7-storey steel frame equipped with NVDs according to different damper distributions

Fig. 15

Force displacement loops under SIM01 record of NVDs in the 7-storey frame according to energy-based (left) and uniform (right) distribution

The average value of $\mathrm{E}\mathrm{D}\mathrm{I}$ under six artificial records along with the average of other relevant parameters including global damage ${D}_{g}$, maximum plastic rotation ${\theta }_{p}^{\mathrm{m}\mathrm{a}\mathrm{x}}$, first-mode supplemental damping ratio of NVDs ${\xi }_{d1}$ [calculated through the energy method proposed by Ramirez et al. (2001)] and upfront damper cost are listed in Table 2. In general, the three UDD alternatives are better than the uniform distribution with minor differences depending on the performance parameter considered. The energy dissipation efficiency is comparable in the drift-based and energy-based distributions, and relatively lower for the velocity-based distribution. The drift-based distribution is characterized by the lowest global damage, the lowest maximum plastic rotation, and the highest damping ratio. Also, the drift-based and velocity-based distributions are associated with the lowest upfront damper cost. Overall, these results confirm the adequacy of using drift for optimum design of viscous dampers.

Table 2 Performance parameters for different damper distributions (average results under six artificial records)

6 Multi-level UDD optimisation method

Current seismic codes (FEMA-356 2000; ASCE/SEI Standard 41-17 2017; CEN Eurocode 8 2004) prescribe different performance objectives depending on the probability of occurrence (return period) of the earthquake excitation. Indeed, different structural performance levels, related to the value of a specific response parameter like maximum inter-storey drift or maximum plastic rotation, are considered for different levels of the seismic input. Motivated by the results discussed in the previous section, drift is assumed as the main performance parameter. The optimisation procedure discussed in the previous sections for a single performance objective is extended here to deal with multiple performance objectives. A simple and conservative manner to achieve this task is to consider a generalized variant of the sequential formula (16) that is modified as follows:

$$c_{{d,i}}^{{n + 1}} = c_{{d,i}}^{n} \times \max \left[ {\left( {\frac{{\Delta _{{\max ,i}}^{{n,I}} }}{{\Delta _{{{\text{target}}}}^{{\text{I}}} }}~} \right);\left( {\frac{{\Delta _{{\max ,i}}^{{n,{\text{II}}}} }}{{\Delta _{{{\text{target}}}}^{{{\text{II}}}} }}~} \right); \ldots ;\left( {\frac{{\Delta _{{\max ,i}}^{{n,K}} }}{{\Delta _{{{\text{target}}}}^{K} }}~} \right)} \right]^{\gamma }$$

(27)

where ${{\Delta }}_{\text{max},i}^{n,K}$ and $\Delta _{{{\text{target}}}}^{{\text{K}}}$ denote the maximum and target inter-storey drift ratio for the ith storey, nth iteration, and related to Kth performance objective, respectively, with $K = {\text{I}},{\text{II}}, \ldots$ covering different performance levels.

The efficiency of the proposed multi-level performance-based optimisation methodology is demonstrated by applying the procedure to the same steel reference frames analysed above but considering two performance objectives, namely: I = LS performance level under DBE (10% probability of exceedance during the structure lifetime) and II = CP performance level under MCE (2% probability of exceedance). This approach is common for most ordinary buildings. In this paper, DBE is defined by the EC8 design response spectrum with ${\text{PGA}} = 0.4\,{\text{g}}$, while it is assumed that MCE is obtained by scaling the PGA of the DBE with a factor 1.4 (${\text{PGA}} = 0.56\,{\text{g}}$). The target drift ratio is assumed equal to $\Delta _{{{\text{target}}}}^{{\text{I}}} = 1.5\%$ and $\Delta _{{{\text{target}}}}^{{{\text{II}}}} = 2.0\%$ for DBE and MCE, respectively, according to FEMA recommendations for LS and CP performance levels in braced steel frames (FEMA-356 2000), respectively.

Figure 16 compares the height-wise distribution of $\Delta _{{\max }}$ for the optimisation methodology applied in its single-level and multi-level variants. It is shown that the multi-level design procedure satisfies both performance objectives for all the three frames. In contrast, the single-level design procedure violates the performance objective under MCE for the 3- and 7-storey frames in a pronounced way, and for the 12-storey frame in a less marked manner. As observed in Fig. 16, it is not easy to anticipate which intensity level of the seismic excitation (DBE or MCE) is more critical in the design. The adoption of the sequential formula (27) in the design process is able to incorporate different performance objectives simultaneously, and overcomes conventional trial and error procedures that typically involve design optimisation under a certain level of the earthquake and subsequent verification under other levels.

Fig. 16

Height-wise distribution of $\Delta _{{\max }}$ for single-level and multi-level optimisation methodology, average results under six artificial records corresponding to DBE and MCE

The efficiency of the proposed multi-level optimisation methodology is also investigated via incremental dynamic analysis (IDA) under the set of six artificial spectrum-compatible records for different earthquake intensity levels. Figure 17 illustrates the global damage index of the three steel frames without dampers (bare frames) and with three different distributions of NVDs, namely uniform (equal-cost) distribution, single-level optimum and multi-level optimum. The PGA levels range from 0.05 to 0.8 g, thus covering low and moderate serviceability earthquakes up to very exceptional events with extremely high intensity. The results in Fig. 17 show that the global damage associated with the multi-level optimum distribution of NVDs is always less than both uniform and single-level optimum distribution at all PGA levels. It is noted that the global damage associated with the single-level design is relatively high for the 3-storey frame, and the seismic performance at high intensity levels (say PGA > 0.6 g) is even worse than the equal-cost uniform distribution. This is because the design under the DBE level leads to a low value of damping coefficient at the first storey. However, this first storey is relatively weak and suffers from high localised damage for increasing earthquake intensity levels. Since the uniform distribution provides a higher damping coefficient at the first storey compared to the single-level optimum design (cf. for instance Fig. 8), the associated global damage is lower. However, in general, the efficiency of the uniform damping distribution is reduced at higher intensity levels compared to the single-level and multi-level optimum solutions (this is evident in both the 7- and 12-storey frame). This is reasonable since using the same damping coefficient at all storey levels generally leads to a non-uniform distribution of lateral displacement demand and, consequently, to a localised damage concentrated at weaker storeys (soft-storey behaviour), especially marked under high-intensity earthquakes. This soft-storey behaviour is effectively mitigated by the proposed UDD multi-level optimum design methodology.

Fig. 17

Incremental dynamic analysis (IDA), global damage of the bare frame compared to frames equipped with NVDs designed according to different methodologies, average results under six artificial records

7 Conclusions

In this paper, a practical multi-level performance-based optimisation method of nonlinear viscous dampers (NVDs) for seismic retrofit of existing substandard steel frames is presented. A fractional power-law force–velocity relationship is used for the dampers, while the supporting brace stiffness and the damper axial stiffness are incorporated via a Maxwell model, and the nonlinearity of the structure is modelled through a distributed-plasticity fibre-based section approach. The method is based on the uniform damage distribution (UDD) design philosophy applied within an iterative scheme, and its efficiency is illustrated through examples on 3-, 7- and 12-storey substandard steel frames under both artificial and natural earthquakes that are compatible with the EC8 design response spectrum.

The main findings of this research work can be summarised as follows:

• The proposed method is easy to implement for nonlinear structures, requires few iterations to converge and is not affected by the initial design solution. It has been demonstrated that the convergence factors currently adopted in the literature are rather conservative and may be slightly increased to reduce the computational effort by speeding up the convergence rate without implying any fluctuation in the design solution.

• For a design spectrum-based methodology, the proposed optimum design procedure can be further simplified by using a single artificial spectrum-compatible record, which leads to acceptable results for short-to-medium rise structures. However, for taller buildings the use of a set of spectrum-compatible records is generally recommended.

• The optimum UDD solution (corresponding to a reasonable added damping ratio of around 15%) produces, on average, up to 30% and 40% reductions in terms of maximum plastic rotation and global damage index compared to the equal-cost uniform distribution. It is shown that by using a relatively low added damping ratio, the efficiency of the solution in mitigating the structural damage avoids overstressing the columns adjacent to the supporting braces, which is an important design requirement in view of capacity design principles.

• The efficiency of alternative performance parameters is comparatively investigated, by using drift-based, velocity-based, and energy-based UDD optimisation approaches. The analysis of a wide range of response indicators (including global damage ${D}_{g}$, maximum plastic rotation ${\theta }_{p}^{\mathrm{m}\mathrm{a}\mathrm{x}}$, first-mode supplemental damping ratio $\xi _{{d1}}$ and upfront damper cost) confirms the adequacy of using drift as main performance parameter for optimum design of viscous dampers.

• In line with performance-based design recommendations of current seismic codes, the proposed multi-level UDD optimisation is able to satisfy multiple performance objectives at different intensity levels of the earthquake excitation, a goal that may not be effectively achieved by a single-level design procedure. The proposed method is easy to implement for practical design purposes, prevents localised damage at higher earthquake intensity levels, and overcomes conventional trial and error procedures that typically involve design optimisation under a certain level of the earthquake and subsequent verification under other levels.

• It should be noted that the proposed multi-level UDD optimisation method is general and can be easily adopted for optimum performance-based design of other energy dissipation systems. For future investigations, the method can be also further developed to satisfy multi-criteria optimization targets (e.g., minimising both maximum inter-storey drift and floor acceleration) using appropriate weighting factors.