Abstract
The paper presents the comparison of the results obtained on a masonry building by nonlinear static analysis using different software operating in the field of continuum and discrete-macroelement modeling. The structure is inspired by an actual building, the "P. Capuzi" school in Visso (Macerata, Italy), seriously damaged following the seismic events that affected Central Italy from August 2016 to January 2017. The activity described is part of a wider research program carried out by various units involved in the ReLUIS 2017/2108—Masonry Structures project and having as its object the analysis of benchmark structures for the evaluation of the reliability of software packages. The comparison of analysis was carried out in relation to: global parameters (concerning the dynamic properties, capacity curves and, equivalent bilinear curves), synthetic parameters of structural safety (such as, for example, the maximum acceleration compatible with the life safety limit state) and the response in terms of simulated damage. The results allow for some insights on the use of continuum and discrete-macroelement modeling, with respect to the dispersion of the results and on the potential repercussions in the professional field. This response was also analyzed considering different approaches for the application of loads.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The paper presents the work carried out by various research units about the analysis of benchmark structures for the evaluation of the reliability of software packages within the ReLUIS 2017/2018 project—Masonry Structures Project (Cattari et al. 2019; Cattari and Magenes 2021) that aims at the seismic analysis of unreinforced masonry buildings.
In particular, in this article, the results of the evaluations carried out through nonlinear static analysis on an actual case study, inspired by a real building the school "P. Capuzi" of Visso (Macerata, Italy), are shown. The case study represents the benchmark n.5 (BS5) analyzed in the research program (Cattari and Magenes 2021). This building dates back to the 30 s and was strengthened following the Umbria-Marche 1997 earthquake. Then it was severely damaged, mainly due to the in-plane response of the walls, by the seismic events that affected Central Italy in 2016/2017. The structure, now demolished because of the serious damage suffered, was the subject of a permanent seismic monitoring system by the Seismic Observatory of Structures (Dolce et al. 2017). The BS5 has been modeled with three software packages: two in the field of continuum modeling and one in the field of discrete-macroelement. In the following, owing to anonymous presentation and discussion of results the software will be named as SW8, SW9, SW10. Results will also refer to outcomes obtained within the companion paper, see (Ottonelli et al. 2021) about seven software operating in the field of equivalent frame modeling, available at the professional level, here named software of Group1 (in the following SWG1). Similarly, SW8, SW9, SW10 are named software of Group 2 (in the following SWG2).
The input data and some modeling choices were shared at an early stage by the researchers involved in order to limit the potential dispersion of the results and make the comparison more robust.
It is important to note that the reconstruction of the actual damage is an important feedback to carry out considerations on the reliability of the software used in predicting and capturing the damage mode activated or, more generally, the seismic response.
The synergy between the Part I and Part II of the present work allows for a critical comparison of the solutions that can be adopted in order to achieve consistent modeling of the same structure using different modeling strategies. The paper is organized as follows: in Sect. 2 the case study is presented, Sect. 3 describes the seismic response of the structure obtained, with the same modeling choices, from the different SWs in terms of masses, dynamic parameters, pushover curve, and damage modes for the different piers. Section 4 presents the results obtained for the calculation of bilinear equivalents with respect to the modeling techniques used in the present work. Section 5 describes the repercussions on seismic assessment, implemented by evaluating the ultimate capacity of the structure in terms of peak ground acceleration (PGA), considering the sensitivity to different SWs and modeling contributions.
2 Brief description of the benchmark case study and modelling hypotheses adopted
A brief description of the case study is reported here, but the interested reader is addressed also to the Part I paper (Ottonelli et al. 2021) for further details.
The BS5 structure was selected as a benchmark since it possesses interesting features: (i) regular distribution of openings; (ii) the availability of a detailed reconstruction of the damage; (iii) the structure experienced a prevalent global response with damage concentrated mainly in piers.
The severe damage experienced by the structure, also caused by damage accumulation, led to the activation of a tilting mechanism in a very limited portion of the building. It worth mentioning that the structure was provided by a permanent monitoring system by the Seismic Observatory of Structures (Dolce et al. 2017) and was the subject of other research as part of ReLUIS projects funded by the Department of Civil Protection (ReLuis—Task 4.1 Workgroup (2018)). The building is characterized by an irregular "T" shape and possesses load-bearing unreinforced masonry and rigid floors organized into two levels plus an attic floor and an underground part.
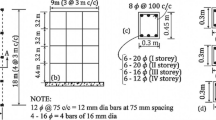
The walls are made mainly of stone masonry whose properties are presented in the companion paper Part I (Ottonelli et al. 2021) and whose collocation is briefly recalled in Fig. 1. Within the Masonry Structures Project (Cattari and Magenes 2021; Calderoni et al.) two hypotheses have been analyzed for the benchmark structure BS5 in order to investigate the dispersion of the results provided by the different software due to the variation of different structural configurations recurring in existing buildings:
-
BS5/A: absence of tensile strength elements coupled to the spandrels, to simulate a so-called weak spandrel behavior.
-
BS5/C: spandrels coupled to tensile strength elements (reinforced concrete ring beams).
In the present paper, only the BS5/C case will be addressed and discussed. In particular, in-situ investigations revealed a full-thickness reinforced concrete ring beam, so the most plausible modeling hypothesis is that the spandrels interrupt at the level of the ring beam forming under- and over-window elements.
To push the comparison of the results collected in both the companions’ papers Part I (Ottonelli et al. 2021) and Part II, and in order to reduce the dispersion of the results, the following common assumptions hold for both the studies:
-
The geometrical data (such as the wall thicknesses, as synthetically reported in Fig. 1 for the ground floor);
-
The distribution and values of the floor loads, including that of the roof, considered only as an equivalent additional load and not through the explicit modeling of every single structural element;
-
The mechanical properties of all materials.
For the sake of paper length, the material properties are summarized into the companion paper only (see Table 1) along with the comprehensive description of the cracking pattern and pictures of the building collected after each one of the multiple seismic events that allow for the precise inspection of cracking pattern evolution due by the accumulation of subsequent damage.
This aspect is of fundamental importance in the following when we aim at being comparing this cracking pattern with the outcome of the present modeling: we will make use of the conventional push-over analysis to study the structural behavior and not of the nonlinear dynamic analysis could be more appropriate for the comparison of modeled and real cracking patterns. Moreover, the application of push-over analysis, due to its intrinsic conventionality, is not straightforward when dealing with continuum modeling and requires assumptions that can have a decisive impact on the results, such as the selection of the element type, the choice of convergence criteria, the definition of the load history and the method of load application (Degli Abbati et al. 2019; D’Altri et al. 2020).
The following software have been used in this study:
-
SIMULIA ABAQUS 6.14 distributed by Dassault Systemes, where masonry nonlinear behavior is modeled using a homogeneous isotropic plastic-damaging continuum. This model hypothesizes independent tensile and compressive behaviors ruled by tensile damage (0 ≤ dt < 1) and compressive damage (0 ≤ dc < 1) variables. The masonry wall panels are modeled with three-dimensional four-nodes tetrahedral finite elements, using standard integration rule, with representative size 0.4 m, see (Degli Abbati et al. 2019). In the case of the presence of reinforced concrete floor beams, the same type of element is used to account for these beams (so obtaining a conforming mesh), and linear elastic behavior is supposed for floor beams, see Fig. 2a, b);
-
MIDAS FEA 2016 Ver. 1.1, distributed by MIDAS Information Technology Co. where masonry nonlinear behavior is modeled using the Total Strain Crack Model, assuming a fixed reference system for the cracked element called the fixed crack model. The masonry wall panels are modeled with four-nodes two-dimensional shell finite elements, based on the discrete Kirchhoff–Mindlin formulation, using standard integration rule, with representative size 0.25 m. In the case of the presence of reinforced concrete floor beams, the same type of element is used to account for these beams (so obtaining a conforming mesh), and linear elastic behavior is supposed for floor beams, see Fig. 2c, d.
-
3DMacro Ver. 4.7, distributed by Gruppo Sismica, works for plane discrete elements and adopts a macro-element formulation in which the different failure modes are managed by different types of nonlinear springs. The panels are described by discrete two-dimensional elements, see Fig. 2e, f. The coupling of incident walls is managed through appropriate "corner elements", characterized by rigid prismatic elements connected via interfaces (which can be calibrated by the user) to other connected elements. The floors can be modeled as orthotropic slabs or, alternatively, adopting the ideal solution of infinite stiffness. The program also allows for the out-of-plane contribution of stiffness and panel strength. The convergence algorithm used in nonlinear analyzes is an event-to-event strategy.
Mesh definition has been carried on aiming at the lower computational cost (but avoiding mesh dependencies issues) and considering that the main objective of the numerical analysis is to simulate the in-plane response. Then, a preliminary mesh calibration and checking were conducted for each software according to their modeling assumption (ABAQUS, Standard User's Manual, Version 6.18 2018; Midas 2016; Caliò et al. 2005).
The calibration of the mechanical parameters of the material is the preliminary step necessary to establish a correspondence between the parameters of the material and the behavior of the element (the scale at which the checks are usually carried out).
In general, the parameters that usually can be calibrated are the elastic modulus of the material, the compressive strength, the tensile strength since these values affect the stiffness, strength, and ultimate deformation of the material. It worth remembering here that, all the three software, have been prior tuned and calibrated to reproduce simple conventional benchmark results, see D'Altri et al. (2021). The interested reader is addressed to D'Altri et al. (2021) where a simple and practitioner-friendly calibration strategy to consistently link target panel-scale mechanical properties (that can be found in national standards) to model material-scale mechanical properties is presented. Then, in the following, the assumption made for the modeling of the structures follow these preliminary setting. The interested reader could get some further complementary information in the following references (Lee and Fenves 1998; ABAQUS, Standard User's Manual, Version 6.18 2018; Castellazzi et al. 2018; D'Altri et al. 2019; Mirmiran and Shahawy 1997; Milani et al. 2018; Vecchio and Collins 1986; Selby and Vecchio 1997; Midas 2016; Caliò et al. 2005, 2012).
The structural models of the BS5 are illustrated in Fig. 2 for the above-mentioned software along with the association of the specific software package, but no further specification will be addressed in the following sections to link the computed results to their software, and comments and discussion will preserve the anonymous illustration.
The geometrical representation of the vertical structure is here driven by the sole geometry of the building without introducing specific simplification of the structure (i.e., dimension of the opening), whether the effective length of the walls is accounted for models that employ conventional representation of the floor thickness.
Some general simplifications are also considered for all the software and reflect the assumptions made for the research activity of the "URM nonlinear modeling—Benchmark project", including that of neglecting the explicit modeling of the roof and of the basement floor which also involved only a minor part of the floor plan.
3 Sensitivity of results to different software packages with standardized modeling assumptions
In this section, the sensitivity of the numerical modeling is studied with respect to some specific modeling assumption that could affect the characterization of the structural dynamic behavior of the BS5 benchmark. To extend the comparison to results provided in the companion paper (Ottonelli et al. 2021), the same parameters are used here:
-
The total mass of the building;
-
The periods, participant masses, and modal shapes obtained from the modal analysis;
-
The global pushover curves and the synthetic parameters that unequivocally define the equivalent bilinear of those curve (i.e. the stiffness \({K}_{s}\), the base shear \({V}_{y}\), and the ultimate displacement \({d}_{u}\));
-
The cracking pattern and the damage corresponding to the ultimate displacement capacity (\({d}_{u}\)) evaluated on the pushover curves have been also compared with the actual one that occurred in the “P. Capuzi” school.
For a comprehensive description of the input parameters please refer to the Annex—BS Input Data reported in Cattari and Magenes (2021).
3.1 Masses and dynamic properties comparison
A comparison of the structural dynamic behavior provided by the software programs is discussed here by means of modal analysis. For this purpose, the (i) effective masses, (ii) periods, and (iii) shape modes of the first three modes are compared and discussed. The discussion is also including the results reported in Part I by means, where applicable, of the averaged result. As anticipated, the structural model steams from the geometry definitions, then, if modeling simplification is introduced, the computed volume of the structure will lead to possible differences in the mass definition.
Table 1 reports the total mass estimated by the three SWs and the percentage variation with respect to the reference value obtained from the hand calculation, along with the description of the contributions associated with the gravity loads transmitted by the floors, those of the load-bearing walls, those of the ring beams, etc. In the table, the item “attic masonry” refers to the contribution offered by the portions of masonry walls composing the attic, including roofing elements, whose contribution has been modeled as equivalent mass. The mass variation computed using the reference value, manually computed, produces very small errors confined at \(1\mathrm{\%}\), [for equivalent frame software the error is confined in general below \(5\mathrm{\%}\), see Ottonelli et al. (2021)].
Despite this little variation, it worth noting that, the calculation of the dynamic properties will depend on the effective mass distribution consequent of the discretization procedure. Then, considering the mesh reported in Fig. 2, it is possible to note that, owing to different modeling approaches, the software will produce then different mass distribution. With this in mind, in order to compare the dynamic properties computed by the different software modes are extracted and analyzed, and then a comparison is carried out on similar modes with similar participating masses. The overall inspection of mode shape reveals that the first three significant modes, with the highest participation masses, can be compared in terms of eigenvalues and eigenvectors, namely X, Y, and X–Y in the following sections. This comparison, carried out by means of global modes, is justified since the structure examined is characterized by very rigid slabs, which are, therefore, able to effectively couple the walls. The modal analyses eigenvectors show a flexural–torsional vibration mode (identified by the "X–Y" subscripts, characterized by significant percentages of activated participation mass along both X and Y) and two vibration modes of a predominantly translational type (identified by the "X" and "Y" subscripts, respectively).
Table 2 summarizes the participation mass values associated with the three modes estimated by each software.
It worth mentioning that modal analyses on equivalent frame models are generally carried out by adopting cracked stiffness values, (applying a reduction coefficient of 0.5). For this reason, in this paper, the analyses were run considering both cracked-stiffness and uncracked-stiffness for macro-element and continuum modeling, respectively.
Then Table 3 also reports the reference value obtained for each of the three modes considered, assessed as the average of the software estimates for each of the two groups (SWG1 and SWG2), as they operate under the same modeling approach.
It is observed that the periods of "Y" and "X–Y" modes, in the uncracked case, are rather close together, while the periods of the two modes, that can be classified as translational in "X" and "Y", are more dissimilar.
Figure 3a illustrates the percentage changes relative to the reference averaged value of the modes in X, Y, and X–Y that are in general confined below (5%) showing a very good agreement. Moreover, the comparison of some eigenvectors components, by means of the conventional reconstruction of mode shape, is very good between the estimates offered by the equivalent frame models, continuum and macro-element models as illustrated by the overlapping plot reported in Fig. 3b–d.
3.2 Global pushover curve comparison
Nonlinear static analyses were conducted in the main X and Y directions, considering both positive and negative directions of seismic action, without considering the effect of additional accidental eccentricity. In fact, the present research activity is mainly focused on the comparison of results obtained by models that employ different modeling techniques and analysis methods but the same initial assumptions and boundary conditions. For this reason, although the irregular plan of the building would suggest further interesting investigations on the use of other horizontal load patterns or more refined nonlinear static procedures able to better account for the higher and torsional modes (Azizi-Bondarabadi et al. 2019), these issues are not discussed here. Thus, also in performing the nonlinear static analyses and representing the results, the research units adopted common hypotheses on the load pattern, the displacement plotted in the pushover curves, and the choice of the control node (close as much as possible to the barycenter of masses).
Two different distributions of lateral forces are considered: proportional to the mass distribution (uniform) and to the distribution of the product of the masses for the relative elevations (inverse triangle).
Therefore, eight global pushover analyses are performed whose curves are illustrated in Figs. 4 and 5 for uniform and triangular load distribution, respectively. The curve comparison is carried out including the equivalent frame model results (SWG1) summarized by envelope results of the pushover curves for each load distribution. Some details in terms of panel stiffness and strength definition are discussed in the following to push the comparison.
3.2.1 Panels stiffness definition
For an existing building, in general, the initial stiffness is set according to the two usual strategies:
-
Conventional degradation: assuming a restrictive elastic stiffness coefficient equal to 0.5 for the full reactant sections (usually for frame models).
-
Progressive degradation: due to the evolution of the spread of damage and to different degrees depending on the damage mode activated in the panels (compression-bending or shear).
Continuum modeling of masonry supposes a homogeneous isotropic material idealization, whether macro-element modeling is based on the separation of the possible failure mechanisms of masonry (i.e., flexural, diagonal cracking, and sliding modes), being each of them governed by a different set of links of the model (D'Altri et al. 2021).
In the present paper, dealing with an isotropic continuum, the well-known relationship G = E/2(1 + ν) links the 3 elastic constants, i.e., Young’s modulus (E), Poisson’s coefficient (ν), and shear modulus (G). However, masonry shows an anisotropic response also in terms of stiffness. Accordingly, values of E and G experimentally measured or suggested in standards for masonry panels would often lead, in an isotropic model, to unrealistic values of ν (which is typically included within the range 0.15–0.25 for masonry). Here, following the stiffness calibration strategy adopted for isotropic models in D'Altri et al. (2021), for all the models we consider a realistic value of ν, typically 0.2. Accordingly, the value of G is herein assumed equal to the target shear modulus (e.g., G = 580 MPa as from Table 1 in Ottonelli et al. 2021) and the value of E is computed for the isotropic model. Furthermore, for the macro-element model, the suggested value of Young’s modulus is not modified to account for the cracked conditions, as often done in the case of equivalent frame models, since the loss of lateral stiffness associated with the rocking mechanism is gradual and associated with the progressive plasticization of the nonlinear links that belong to the interfaces.
It can be observed that in some cases the pushover curves do not show a clear post-peak response. In those cases, it is necessary to adopt different criteria for defining maximum load capacity and displacement capacity to compute effectively the bilinear equivalent curves.
Figures 4 and 5, owing to a productive comparison of software, we propose two stiffness configurations for the macro-element model: same parameters as for the continuum models (SW10*); reducing the shear modulus by a factor 2 (SW10). As reported in D'Altri et al. (2021), unlike the continuous models, the macro-element allows defining separately the parameters that characterize the shear and bending behavior. Once the elastic Young’s modulus E was determined based on the shear modulus and Poisson’s ratio values, the model was analyzed even in the presence of a 50% reduction in the modulus G in order to evaluate the response considering a cracked state. The above is due to the use of an elastic–plastic shear bond assigned to two diagonal springs (D'Altri et al. 2021) which are not sufficient to simulate the degradation of stiffness. On the other hand, the bending behavior is linked to discrete interfaces of non-linear links so that, even in the presence of an elastic–plastic bond, the progression of damage along the aforementioned interfaces does not require a reduction of E.
3.2.2 Strength panel definition
Following the calibration procedures proposed in D'Altri et al. (2021) for continuum modeling, the target panel strength is deduced by standard well-known analytical strength criteria (Cannizzaro et al.): strength characterization is basically governed by the definition of the tensile and compressive uniaxial stress–strain curves. Uniaxial compressive strength is here assumed equal to the target masonry compressive strength, while compressive strain values are defined according to the available literature.
Together with the shear stiffness value G, for the macro-element model, we select two values of the masonry friction coefficient. Respectively the use of the value 0.3 for which the response is close to that of the equivalent frame models (Ottonelli et al. 2021), although lower than the peak values of the continuous models. For this reason, an increase of the parameter up to the value of 0.5 was adopted with a consequent increase in peak values and a better overlap on the results of the continuous models.
4 Calculation of bilinear equivalent curves
The calculation of the bilinear equivalent curves are presented and discussed, with respect to X and Y directions, for uniform distribution of load for the sake of paper length.
In some cases, the adoption of continuous models with nonlinear material can lead to shear-displacement curves without a marked softening branch. This aspect does not usually allow to clearly identify the ultimate displacement with respect to a criterion based on the base shear decay. In order to overcome that we adopt a different criterion that controls the structure’s ultimate displacement instead.
In particular, following the direction of the standards, the panel drift is computed and controlled for a significant number of masonry piers. It worth mentioning that this is an ex-post operation for continuum models and requires specific extraction of data based on the custom selection of reference sections.
Then, the construction of the bilinear equivalent curves is based on three parameters: the stiffness K, the shear Vy at yielding, and the ultimate displacement du. These parameters are computed using the pushover curves by means of the following common criteria:
-
Stiffness K was assessed by imposing the intersection of the equivalent bilinear curve to the point of the pushover curve corresponding to the base shear equal to 70% of the maximum value.
-
Ultimate displacement du was identified at 20% decay of the base shear from the maximum value; this level of displacement is assumed to be representative of the Ultimate condition.
-
Base shear at yield Vy was determined by imposing the equality of the areas under the original pushover curve and of the bilinear curve until the ultimate displacement.
Figures 6 and 7 show the computed bilinear curves where results for the macro-element model are reported using both the configuration about the definition of stiffness and strength of the panel.
Table 4 reports the mean values conventionally adopted to compare the three parameters that define the equivalent bilinear curves (derived from the data presented in Sect. 3.2 according to the criteria illustrated in Sect. 3.1).
To foster the comparison between SWG1 and SWG2 software results in Figs. 8 and 9 the percentage variation of parameters is computed and illustrated with respect to the averaged quantities provided by SWG1 for X and Y directions, respectively. This choice is done for comparison purposes only since no judgment of reliability is reported or discussed. With this in mind, we track that: (i) stiffness (K): the percentage variations relative to the reference value reach 140%; the percentage variations relative to their average (i.e. average of SWG2) reach 22% if SW10 is disregarded, whether it is limited to a maximum of 16% for SWG1.
The significant difference between the results obtained from the two groups of models is due to the different stiffness degradation, as previously illustrated. (ii) overall base shear (Vy): the percentage variations relative to the reference value reach 39%; the percentage variations relative to their average reach 9% if SW10 is disregarded, whether it is limited to a maximum of 16% for SWG1. (iii) Ultimate displacement (du): the percentage variations relative to the reference value reach 71%; the percentage variations relative to their average reach 23% if SW10 is disregarded, whether it is limited to a maximum of 42% for SWG1.
4.1 Cracking pattern comparison
The availability of an accurate survey of the crack extension represents a precious and rare reference to validate the adopted structural models. Then, the comparison of results is also provided by means of cracking pattern comparison using the “uniform” load pattern, for both the X and the Y directions and the positive and negative verse of the lateral forces. The data on the damage, that relates only to the severity and not on the failure mode (as in the companion paper Part I), has been post-processed for both the continuum element software to match the general criteria adopted in the “URM nonlinear modeling—Benchmark project” introduced in Cattari and Magenes (2021).
In relation to the structural response exhibited by the building, it is important to underline that the structure has been subjected to a sequence of seismic events starting from August 2016, with widespread damage to several walls. Then, the seismic sequence, caused a progressive worsening of the damage, including an out-of-plane overturning collapse of a portion of a perimetral wall. The resulting overall damage can then be classified as an incipient collapse, with extremely limited residual capacity to withstand horizontal actions, so the cracking pattern comparison could be done using the simulated damage for the ultimate displacement condition (based on the ultimate drift) highlighted in Figs. 4 and 5.
It must be pointed out that, this comparison aims at highlighting possible matching between software than a real one-to-one comparison with the real damage since the conventional pushover analysis results could not capture what a more accurate representation of the seismic response can be obtained with non-linear dynamic analysis and recorded accelerograms as base input boundary conditions.
Nonetheless, the comparison is useful for verifying whether the global damage mode envisaged by the software is in any case consistent with that which actually occurred.
In this regard, dealing with pushover analysis, it becomes necessary to assess the validity of the proposed criteria, based on the ultimate drift of a significant number of masonry piers, also by comparison with the cracking patterns and failure modes experienced by the real structure, see Fig. 10.
Further difficulties may arise when post-processing the results for comparison with the equivalent frame models regarding the rendering of the damaged framework at different analysis steps, intended as severity and type of damage suffered. In fact, continuous models can often obtain very detailed information (position and width of cracks, location of damaged portions in each wall panel, etc.), which are generally not easily unambiguously comparable with simplified damage frameworks obtainable using equivalent frame models.
In Figs. 11, 12, and 13 the real cracking pattern is compared with the simulated cracking pattern produced by the software in terms of damage, plastic strain, or failure modes for walls W8–W10, W1, and W3–W5–W7–W9 respectively.
In general, a good coherence is observed between the global damage mode and that foreseen by most software: an overall response characterized by a more severe concentration of damage to ground floor with prevalence, for masonry walls, of activation of the shear damage mode by cracking diagonal at ground floor and, limited to some walls, with pressure flexion at first floor, and, for the spandrels, response shear for diagonal cracking. Moreover, these results are also in agreement with that of the software of Group1 (described in the companion paper). Among all it is interesting the comparison we can carry out about wall W10, which is characterized by a very squat pier coupled to a very slender one: Group1 software predicted a concentration of the damage at the ground floor with mostly diagonal cracking shear failure mode predictions for the squat element, while flexural failure mode unanimous prediction for the slender one. Group2 software results also suggest a diagonal cracking shear failure mode and flexural failure mode for the squat and slender piers, respectively.
5 Sensitivity to different modeling assumptions on the global response
5.1 Contribution of the load application method
The numerical response of the structure summarized by means of the pushover curve could change significantly if the external load is applied following different conventional modes of application. Conventionally, regardless of the load patterns (i.e., triangular or uniform) load could be applied uniformly over the structure (condensing masses to each node of the mesh) or concentrating its action at floor levels (condensing level by level at the floor mid-plane). Note that the second choice is usually employed for equivalent frame models. It has been proven that this aspect of more pronounced when the wall ratio thickness to height tends to increase, see also Cannizzaro et al.
The BS5 is characterized by thick walls of 65 cm of the thickness of average, then it worth assessing whether the different choice could lead to significantly different results.
The analyses were completed using the software programs from among those considered in the context of the study presented in the general document, which allows for the application of concentrated or distributed actions. The same mechanical properties and hypotheses for modeling the structure’s geometry described in Sect. 3.1 are adopted here.
A horizontal load distribution proportional to the masses, assuming a positively directed seismic action in the X direction, without accounting for the effects of accidental eccentricity, was applied to the structure. Obtained push-over curves provide similar outcomes then, owing to the anonymous illustration we report only one representative set of pushover curves for Distributed and Lumped Loads as illustrated in Fig. 14. It is evident how the pushover curve obtained for the distributed load pattern, is characterized by peak load substantially higher with respect to the one obtained using concentrated load. Specifically, we register a general increase of up to 22% of the maximum load when moving from lumped actions to distributed actions at floor level for all the employed software.
Therefore, the use of concentrated actions at floor level in pushover analyses of buildings with significantly thick walls can lead to the underestimation of the structure’s capacity, compared to the use of distributed horizontal actions. However, this effect favors safety, so the use of horizontal actions concentrated at the floor level appears to be an acceptable simplification in the pushover analysis of masonry buildings, although, as the thickness of masonry piers increases, the capacity of the structure is gradually underestimated.
5.2 Maximum acceleration calculation compatible with various limit states
The comparison of the maximum acceleration (PGA) is carried out for different performance levels (PL): (i) \({PGA}_{Vy}\) at yield point of the equivalent bilinear curve and (ii) \({PGA}_{du}\) at the ultimate displacement computed for pushover curves. Considering the uniform distribution only.
As previously established, the N2 method was used for the evaluation of PGA. According to that method, the differences that play a role in the final calculations of the PGASL are:
-
the differences of the parameters (Fy,K, du) that define the equivalent bilinear form; the differences of the conversion factors of system SDOF(Γ,m*), which allow the conversion of the global base shear and the stiffness in system yield acceleration (Ay = Fy /Γm*) and in period T*.
-
The final value is also affected by the assumed value for TC (the period separating the spectrum regions at constant acceleration and velocity) and its relationship to T*.
The result is useful to illustrate how differences in the representation of the nonlinear response of the structure can affect the final safety assessment. The following parameters have been adopted to calculate the spectral form: (i) S = 1.52; (ii) TC = 0.714; (iii) Fo = 2.363. Figure 15 shows the relationship obtained for T*/ TC. In each case, the relationship between T*/ TC was less than 1; thus, the calculation of the expected seismic demand is made with reference to the region with maximum response spectrum amplification.
For the calculation of Γ (Fig. 16), for the SWG2 (i.e. SW8, SW9 and SW10) there are no differences between the different distribution of forces adopted. This is consistent with the assumption that this modal participation factor is calculated by most of the software with reference to the eigenvector form corresponding to the first mode (approximated, where appropriate, with the deformation resulting from the application of a system of forces proportional to the distribution of the product of the nodal masses for their dimensions on the modeled structure in the elastic field,) regardless of the forces applied in the nonlinear static analysis. This assumption, as highlighted in the companion paper, is not adopted by all the SWG1, because for two of them a unitary value of Γ is assumed as default in case of uniform load pattern.
Figures 17, 18, and 19 show values in different software with varying force distributions applied and differentiated analysis directions (X and Y, positive and negative) for M*, ΓM, and q* respectively.
Finally, Figs. 20 and 21 show the PGA and percentage variations obtained: it is worth noting that the percentage variation is assessed according to the reference values obtained by the SWG1 on a conventional and purely comparative basis. The percentage variations reach a maximum of 48%, and with a mean (considering the four analyses treated) of about 10% for PGA—Vy; and up to a maximum of 30%, and with a mean (considering the four analyses treated) of about 11% for PGA—du.
6 Conclusions
The paper presents the comparison of the results obtained on a masonry building by nonlinear static analysis using different software operating in the field of continuum and discrete-macroelement modeling. The activity described is part of a research carried out by several research teams involved in the “URM nonlinear modeling—Benchmark project” on the benchmark structure BS5, inspired by the “P. Capuzi” school in Visso (MC, Italy), seriously damaged following the seismic events that affected Central Italy in 2016/2017. The benchmark structure has been selected in order to explore the influence of modeling approaches adopted by different software at both research and professional levels by means of nonlinear static analyses Although not exhaustive, three commercial software were considered and compared. Furthermore, the results are compared with the outcomes obtained from equivalent frame models reported in the companion paper (Part I). The comparison of analyses was carried out in relation to: global parameters (concerning the dynamic properties, capacity curves, and equivalent bilinear curves), synthetic parameters of structural safety (such as, for example, the maximum acceleration compatible with the performance levels), and the response in terms of simulated damage.
The computed dynamic properties are affected by very small errors in general and the comparison, carried out by means of the conventional reconstruction of mode shape, is very good between the estimates offered by the Part I and II software.
Nonlinear static analyses, conducted in the main X and Y directions for both positive and negative directions of seismic action, highlighted a substantial difference between group one and group two software in the estimation of the base shear and ultimate displacement despite the used calibration procedures. This aspect is mainly due to the different stiffness degradation.
The availability of an accurate survey of the crack extension has been used to further validate the adopted structural models. A good coherence is generally observed between the global damage mode and that foreseen by most software with a more severe concentration of damage to the ground floor.
The results allow for some insights on the use of continuum and discrete-macroelement modeling, with respect to the dispersion of the results and on the potential repercussions in the professional field. This response was also analyzed considering different methods for the application of loads. With respect to the comparative study reported in the companion paper Part I the results confirm that the dispersion achievable when different software packages are used is not completely negligible, especially when comparing different modeling techniques although it is generally contained within acceptable ranges when the consistency of the modeling assumptions are ensured.
Availability of data and material
The benchmark structure analyzed in the paper (BS5) can be replicated by other researchers and analysts thanks to the input data provided in the paper made by Cattari and Magenes (2021) as supplementary electronic material (Annex I—Benchmark Structures Input Data). Some additional data support the findings of this study are available from the corresponding author upon reasonable request.
References
ABAQUS/Standard User's Manual Version 6.18 (2018) Dassault Systemes Simulia Corp, United States
Azizi-Bondarabadi H, Mendes N, Lourenco PB (2019) Higher mode effects in pushover analysis of irregular masonry buildings. J Earthq Eng. https://doi.org/10.1080/13632469.2019.1579770
Cattari S, Calderoni B, Caliò I, Camata G, de Miranda S, Magenes G, Milani G, Saetta A, Nonlinear modelling of the seismic response of masonry structures: critical aspects in engineering practice. Submitted to Bulletin of Earthquake Engineering, SI on URM nonlinear modelling-Benchmark project (under review)
Caliò I, Marletta M, Pantò B (2005) A simplified model for the evaluation of the seismic behavior of masonry buildings. In: Proceedings of the 10th international conference on civil, structural and environmental engineering computing, Civil-Comp 2005, pp 1–17. https://doi.org/10.4203/ccp.81.195
Caliò I, Marletta M, Pantò B (2012) A new discrete element model for the evaluation of the seismic behavior of unreinforced masonry buildings. Eng Struct 40:327–338
Cannizzaro F, Pantò B, Castellazzi G, Petracca M, Grillanda N. Modelling the nonlinear static response of a 2-storey URM benchmark case study: Comparison among different modelling strategies using two- and three-dimensional elements, Bull Earthq Eng, SI on URM nonlinear modelling—Benchmark Project, (under review)
Castellazzi G, D’Altri AM, de Miranda S, Chiozzi A, Tralli A (2018) Numerical insights on the seismic behavior of a non-isolated historical masonry tower. Bull Earthq Eng 16(2):933–961
Cattari S, Magenes G (2021) Benchmarking the software packages to model and assess the seismic response of URM existing buildings through nonlinear analyses. Bull Earthq Eng. https://doi.org/10.1007/s10518-021-01078-0
Cattari S, Ottonelli D, Degli Abbati S, Magenes G, Manzini CF, Morandi P, Spacone E, Camata G, Marano C, Caliò I, Pantò B, Cannizzaro F, Occhipinti G, Calderoni B, Cordasco EA, de Miranda S, Castellazzi G, D'Altri AM, Saetta A, Talledo DA, Berto L (2019) Uso dei codici di calcolo per l'analisi sismica non lineare di edifici in muratura: confronto dei risultati ottenuti con diversi software su un caso studio reale. In: Proc. XVIII ANIDIS, Ascoli Piceno, Italy
D’Altri AM, Messali F, Rots J, Castellazzi G, de Miranda S (2019) A damaging block- based model for the analysis of the cyclic behavior of full-scale masonry structures. Eng Fract Mech 209:423–448
D’Altri AM, Sarhosis V, Milani G et al (2020) Modeling strategies for the computational analysis of unreinforced masonry structures: review and classification. Arch Comput Methods Eng 27:1153–1185. https://doi.org/10.1007/s11831-019-09351-x
D’Altri AM, Cannizzaro F, Petracca M, Talledo DA (2021) Nonlinear modelling of masonry structures: calibration strategies. Bull Earthq Eng. https://doi.org/10.1007/s10518-021-01104-1
Degli Abbati S, D’Altri AM, Ottonelli D, de Miranda S, Lagomarsino S et al (2019) Seismic assessment of interacting structural units in complex historic masonry constructions by nonlinear static analyses. Comput Struct 213:51–71
Dolce M, Nicoletti M, De Sortis A, Marchesini S, Spina D, Talanas F (2017) Osservatorio sismico delle strutture: the Italian structural seismic monitoring network. Bull Earthq Eng 15(2):621–641
Lee J, Fenves GL (1998) Plastic-damage model for cyclic loading of concrete structures. J Eng Mech 124(8):892–900
Midas FEA 2016 v1.1 - Build: Nov. 06, 2018 (2016) Nonlinear and detail FE analysis system for civil structures. Midas Information Technology Co. Ltd
Milani G, Valente M, Alessandri C (2018) The narthex of the church of the nativity in Bethlehem: a non-linear finite element approach to predict the structural damage. Comput Struct 207(3):18
Mirmiran A, Shahawy M (1997) Dilation characteristics of confined concrete. Mech Cohes Frict Mater 2(3):237–249
Ottonelli D, Manzini C, Marano C, Cordasco EA, Cattari S (2021) A comparative study on a complex URM building. Part I: sensitivity of the seismic response to different modelling options in the equivalent frame models. Bull Earthq Eng. https://doi.org/10.1007/s10518-021-01128-7
Selby RG, Vecchio FJ (1997) A constitutive model for analysis of reinforced concrete solids. Can J Civ Eng 24(3):460–470
Vecchio FJ, Collins MP (1986) Modified compression-field theory for reinforced concrete elements subjected to shear. J Am Concr Inst 83(2):219–231
Acknowledgements
The study presented in the paper was developed within the research activities carried out in the frame of the 2014–2018 ReLUIS Project (Topic: Masonry Structures; Coord. Proff. Sergio Lagomarsino, Guido Magenes, Claudio Modena, Francesca da Porto) and of the 2019–2021 ReLUIS Project—WP10 "Code contributions relating to existing masonry structures" (Coord. Guido Magenes). The projects are funded by the Italian Department of Civil Protection. Moreover, the Authors acknowledge the following members of research teams (RT) that participated to the analyses of the benchmark structure illustrated in this paper or in his companion paper: UniPV RT (University of Pavia: Coord. Guido Magenes, Participants: Paolo Morandi); UniCH RT (University of Chieti-Pescara; Coord. Prof. Guido Camata); UniCT RT (University of Catania—Coord. Prof. Ivo Caliò; Participants: Francesco Canizzaro, Giuseppe Occhipinti, Bartolomeo Pantò); UniNA RT (University Federico II of Naples—Coord. Prof. Bruno Calderoni); UniBO RT (University of Bologna—Coord. Prof. Stefano de Miranda—Participants: Giovanni Castellazzi, Antonio Maria D’Altri); POLIMI RT (Polytechnic of Milan—Coord. Prof. Gabriele Milani); IUAV RT (University of Venice—Coord. Prof. Anna Saetta; Participants: Luisa Berto, Diego Alejandro Talledo).
Funding
Open access funding provided by Alma Mater Studiorum - Università di Bologna within the CRUI-CARE Agreement. The research activity “URM nonlinear modelling—Benchmark project”, whose methodology and benchmark structures proposed, are presented in this paper, did not receive any grant from funding agencies in the public, commercial or not-for-profit sectors that may gain or lose financially through publication of this work.
Author information
Authors and Affiliations
Contributions
GC: interpretation of results, writing—review, conceptualization, supervision; numerical analyses, data curation, writing—original draft, methodology, comparisons of results made by the research teams; BP: numerical analyses, data curation, writing—original draft, methodology, comparisons of results made by the research teams,; GO: numerical analyses, data curation, writing—original draft, methodology, comparisons of results made by the research teams; DT: numerical analyses, data curation, writing—original draft, writing—review, methodology, comparisons of results made by the research teams; LB: numerical analyses, data curation, writing—original draft, writing—review, methodology, comparisons of results made by the research teams; GC: numerical analyses, data curation, writing—original draft, methodology.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Castellazzi, G., Pantò, B., Occhipinti, G. et al. A comparative study on a complex URM building: part II—issues on modelling and seismic analysis through continuum and discrete-macroelement models. Bull Earthquake Eng 20, 2159–2185 (2022). https://doi.org/10.1007/s10518-021-01147-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10518-021-01147-4