Simulation of building damage distribution in downtown Mashiki, Kumamoto, Japan caused by the 2016 Kumamoto earthquake based on site-specific ground motions and nonlinear structural analyses

Abstract

Most of the buildings damaged by the mainshock of the 2016 Kumamoto earthquake were concentrated in downtown Mashiki in Kumamoto Prefecture, Japan. We obtained 1D subsurface velocity structures at 535 grid points covering this area based on 57 identified velocity models, used the linear and equivalent linear analyses to obtain site-specific ground motions, and generated detailed distribution maps of the peak ground acceleration and velocity in Mashiki. We determined the construction period of every individual building in the target area corresponding to updates to the Japanese building codes. Finally, we estimated the damage probability by the nonlinear response model of wooden structures with different ages. The distribution map of the estimated damage probabilities was similar to the map of the damage ratios from a field survey, and moderate damage was estimated in the northwest where no damage survey was conducted. We found that both the detailed site amplification and the construction period of wooden houses are important factors for evaluating the seismic risk of wooden structures.

1 Introduction

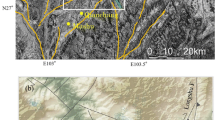
The 2016 Kumamoto earthquake sequence included two major earthquakes, both epicenters were located in Kumamoto, Japan. According to the Japan Meteorological Agency (JMA), the first strong earthquake occurred at 21:26 Japan standard time (JST) on April 14 (12:26 coordinated universal time, UTC) and had a magnitude of 6.5 on the JMA magnitude scale (M_JMA), which converts to a moment magnitude (M_W) of 6.2. Its focal depth was 11 km, and the highest JMA seismic intensity of VII was recorded in downtown Mashiki. The second strong earthquake occurred at 01:25 JST on April 16, 2016 (16:25 UTC on April 15, 2016). The reported M_JMA was 7.3 (M_W = 7.0) and the focal depth was 12 km. The highest JMA seismic intensity of VII was also recorded in Mashiki (Sugino et al. 2016; Asano and Iwata 2016; Yamanaka et al. 2016; Nagao et al. 2017; Yamada et al. 2017; Kawase et al. 2017; Yamazaki et al. 2018; Sun et al. 2020). Hereafter, we refer to the 6.5 M_JMA earthquake on April 14, 2016 as the foreshock and the 7.3 M_JMA earthquake on April 16, 2016 as the mainshock. Three strong-motion stations were established at Mashiki: KMMH16 (station of NIED KiK-net), KMMP58 (Mashiki Town Hall station), and Bunkakaikan (Mashiki Community Hall station), their locations are shown in Fig. 1. The inset shows the locations of downtown Mashiki and the epicenter locations of the two earthquakes on the Kyushu Island (NIED 2020; Sun et al. 2020).

Fig. 1

Building damage ratios obtained through a field survey of downtown Mashiki (NILIM and BRI 2016). The damage ratio of each cell = (the number of ≥ D4 damaged buildings in a cell)/(the total building number in a cell). 2016 and 2018 microtremor observation sites are marked by blue triangles and red rectangles, respectively. The three strong-motion stations at Mashiki are marked by large purple stars (Sun et al. 2020). Site K (black star in the northeast) is the location where a borehole was drilled by Arai (2017) and Shingaki et al. (2017); it is very close to the NIED KiK-net site KMMH16. The inset shows the earthquake mechanism information of the foreshock and mainshock; the colors of the earthquake symbols represent the depths of the centroid moment tensor (CMT) solution, 17 and 11 km (NIED 2020)

Downtown Mashiki is located in the east of Kumamoto City, Japan, which was heavily damaged by the mainshock. After the mainshock, the Architectural Institute of Japan (AIJ) performed a field survey to estimate the building damage, as shown in Fig. 1 (NILIM and BRI 2016). The damage survey followed the building damage scale which includes seven damage grades, from D0 (no damage) to D6 (full collapsed), as referring to the Damage Scale #4 in Fig. 3. The damage ratio of each cell in Fig. 1 is the ratio between the total number of buildings with ≥ D4 damage and the total number of buildings in a cell (damage levels were referred to the Damage Scale #4 in Fig. 3). D4 means the building occurs pancake-like collapse, loss of connectivity of beam and column, or interlayer deformation (Takai and Okada 2001). Most of the heavily damaged buildings appeared in the area between the local road No. 28 and the Akitsu River (Kawase et al. 2017). Unfortunately, Fig. 1 does not depict the building damage in the northwest. Then, Yamada et al. (2017) estimated the building damage distribution in Mashiki by the aerial photo analysis departed before, after, and during the interval of the foreshock and mainshock. Moya et al. (2018) discussed the building damage in the south part of Mashiki using the empirical fragility functions. Yamazaki studied the relationship between the building damage ratio and the building construction period in Mashiki (Yamazaki et al. 2018). In this study, we want to simulate the building damage distribution in Mashiki and figure out the damage distribution of houses in the northwestern area, considering the building construction periods by using the nonlinear dynamic analysis of wooden houses (Yoshida et al. 2004; Nagato and Kawase 2004).

Estimating building damage based on the local strong ground motions is crucial for urban disaster prevention. An accurate prediction of seismic damage to buildings on a regional scale is important for modern city planning and post-earthquake rescue, which will help to mitigate direct/indirect seismic losses (Hori 2011; Lu et al. 2014). Currently, existing approaches for seismic damage evaluation of buildings on a regional scale mainly include the damage probability matrix method (e.g., Ulrich et al. 2014; Rojahn et al. 1985; Yakut et al. 2006; Polese et al. 2015; Palanci and Senel 2019; Del Gaudio et al. 2020), the spectrum method (Jalayer et al. 2010; FEMA 2012), and methods based on time history analysis (e.g., Nagato and Kawase 2002, 2004; Yoshida et al. 2004; Benavent-Climent et al. 2014; Lu and Guan 2017; Brunelli et al. 2020). After the 1995 Hyogo-ken Nanbu Earthquake (hereafter Kobe earthquake), several researchers statistically analyzed the damage survey data to study the relationship between the structural characteristics and building damage ratios (e.g., Hayashi et al. 2000; Murao and Yamazaki 2000; Miyakoshi 2002). Also, other researchers attempted to determine the relationship between the peak ground acceleration (PGA) or peak ground velocity (PGV) and the building damage ratio and established empirical vulnerability functions for different building types (e.g., Hayashi et al. 1997; Murao and Yamazaki 2000, 2002; Yamaguchi and Yamazaki 2000). However, these methods could not precisely evaluate the damage probability (DP) to every building in an area. For more quantitative prediction it would be better to build numerical-models of structures based on the seismic response analyses for wooden and reinforced concrete (RC) buildings in the heavily damaged area during the previous earthquakes.

Nagato and Kawase (2004) developed a seismic response analysis model (i.e., Nagato–Kawase model) for multi-story structures, based on the building damage statistics for the Kobe city after the 1995 Kobe earthquake. They successfully reproduced the damage belt in Kobe after the disaster, based on the estimated ground motions (Kawase 1996). This work established a standard model of the common two-story wooden houses in the Kobe area associated with the Japanese building code. Further, because the Japanese building codes were improved in 1950, 1971, and 1981 in terms of the seismic performance of buildings for design forces, Yoshida et al. (2004) enhanced the standard model of Japanese wooden houses to consider four construction periods (i.e. Yoshida model) before 1950, 1951–1970, 1971–1981, and after 1982. Thus, the local ground motions and construction period should be considered when estimating the damage to wooden houses.

In this study, we evaluate the damage probabilities of wooden houses in Mashiki which were caused by the 2016 Kumamoto earthquakes by considering the construction period and estimated strong ground motions. We also attempt to estimate the building DP distribution in the northwestern part, where no systematic survey was conducted during the AIJ survey. We have previously identified subsurface velocity structures for this area (Sun et al. 2020). However, as the precondition, we need a more spatially dense sampling of ground responses to delineate a detailed map that corresponds to the damage survey. The construction period of every building in this area is also needed to be determined.

2 Data preparation and methodology

2.1 Statistical analysis of wooden houses and building damage scales used in Japan

A statistical analysis of the damage to wooden houses obtained from the AIJ survey report was depicted in Fig. 2. The buildings were classified into six categories based on the main construction material: wooden structure, steel structure, RC structure, hybrid structure, others, and unknown (NILIM and BRI 2016). For the hybrid structure, the main building material varied between different floors; for example, RC or steel was used in the first floor of the building, whereas wood was on the second floor. The other structures used steel or other materials in certain parts of the building. In total, the AIJ surveyed 2,340 buildings: 1,955 wooden, 276 steel, 52 RC, 32 hybrid, 21 other, and 4 unknown. Thus, most of the buildings in this area were wooden (83.5%). Because Japan updated the seismic code for buildings in June 1981, we separated the AIJ survey results as before and after 1981 in Fig. 2. Furthermore, D0–D6 indicate the damage grade according to the damage scale used by the AIJ (Okada and Takai 1999; Takai and Okada 2001; NILIM and BRI 2016). Figure 3 defines different damage scales and their comparison to each other for each damage grade. The meanings of each damage grade for the 2016 Mashiki building damage survey followed Damage Scale #4 in Fig. 3 (Okada and Takai 1999; Takai and Okada 2001).

Fig. 2

Statistical analysis of the damage to the wooden houses (NILIM and BRI 2016). The x-axis denotes the construction period, and the y-axis denotes the damage grade used in the AIJ survey and the corresponding damage index. The number inside the parentheses is the building number of the respective category

Fig. 3

Four damage scale standards and damage index used in Japan. Damage Scale #1 is the European Macroseismic Scale 1998 (Grunthal 1998). Damage Scale #2 is the AIJ 1987 standard. Damage Scale #3 is used in the Yoshida model. Damage Scale #4 was used for the AIJ survey after the 2016 Kumamoto earthquake. This figure is edited based on the results of Takai and Okada (2001)

Most of the wooden houses in Mashiki were built after 1981, and the damage grades of approximately 27% of wooden houses were ≥ D4 (Fig. 2). The DP of wooden houses might be correlated with the construction period, as more than two-thirds of heavily damaged wooden houses (≥ D4) were built before 1981, while wooden houses built after 1981 showed a better seismic performance. Houses with ≥ D4 damage made up 46% (351/770) of buildings built before 1981 while only 15% (176/1185) of the buildings were built after 1981.

2.2 Microtremor observation and identified subsurface velocity structures

We performed the microtremor observations at 86 sites in the heavily damaged area in 2016 and 2018, with the locations shown in Fig. 1. We then generated 57 one-dimensional (1D) subsurface velocity structures for this area (Sun et al. 2020). Table 1 presents the identified velocity models at KMMH16 and KMMP58 (Town Hall site).

Table 1 Identified subsurface velocity structures of KMMH16 and KMMP58

The relationship between the shear strain and shear modulus reduction ratio (γ–G/G_max) and between the shear strain and damping ratio (γ–h) for shallow layers were previously obtained at site K (Fig. 1), where Arai (2017) and Shingaki et al. (2017) conducted triaxial tests of borehole soil materials. For horizontal motions at the seismological bedrock (V_s > 3000 m/s), Nagashima and Kawase (2018) estimated the seismic bedrock motions at KMMH16 during the mainshock by using the diffused field concept for earthquakes (Kawase et al. 2011; Nagashima et al. 2017). Figure 4 shows the acceleration time histories of the calculated bedrock input. We assumed that the same input was incident to the seismological bedrock of all soil columns for the site response analyses (Sun et al. 2020).

Fig. 4

Estimated horizontal seismic bedrock motions obtained from Nagashima and Kawase (2018): a Time-domain accelerations and b Fourier spectra. The solid and dashed lines denote the estimated EW and NS components, respectively

Based on these results, we estimated the seismic ground motions at KMMH16 during the mainshock by using the linear and equivalent linear analysis (LA and ELA) methods (Yoshida and Iai 1998; Yoshida 2014). In Mashiki, we obtained the ground accelerations for the mainshock at KMMP58 and the ground and borehole accelerations (underground 252 m) for the mainshock at KMMH16. Figures 5 and 6 show the comparisons of the estimated and observed ground motions at KMMH16 for the east–west (EW) and north–south (NS) components, respectively. The horizontal strong ground motions at KMMH16 were simulated well. The linear soil responses produced much larger accelerations than observed. According to these results, consideration of soil nonlinearity in the ground response analysis is found to be necessary when we compare linear and equivalent linear analysis.

Fig. 5

Dynamic responses of KMMH16 subsurface velocity structure for EW component (Sun et al. 2020). a, b Estimated accelerations and velocities at the ground surface with LA and ELA, which were compared with observations at KMMH16 during the mainshock, respectively. c, d Estimated Fourier spectra and acceleration response spectra, respectively. The dotted, dashed, and solid lines denote the LA, ELA, and observation results, respectively

Fig. 6

Dynamic responses of KMMH16 for the NS component. The dotted, dashed, and solid lines are same as those in Fig. 5 but for the NS component

2.3 Nonlinear response models of wooden buildings

Nagato and Kawase constructed a model for estimating the damage probabilities of a group of buildings in an area, including wooden, RC, and steel structures (Nagato and Kawase 2004). They calculated the observed damage ratios (ODRs) based on statistical data for Kobe after the 1995 Kobe earthquake. They also established building models by referring to the Japanese building code (except for wooden houses, for which the dependence on the construction period was not obtained). Subsequently, they analyzed the seismic responses of the building models and obtained the calculated damage ratios (CDRs, the CDR is a value of the calculated DP of a building) by assuming log-normal distributions of the yield capacities. They compared the ODRs and CDRs, modified the strength of the building model, and performed the analysis until the deviation between the ODRs and CDRs was sufficiently small. Finally, they established the Nagato–Kawase model, which was applied to successfully reproduce the special building damage belt caused by the 1995 Kobe earthquake. Nagato and Kawase (2004) used multi-degree-of-freedom models with non-linear springs for their seismic response analysis model. They assumed that RC buildings are characterized by the degrading trilinear hysteresis type (D-tri type) of nonlinear springs (e.g., Fukada 1969; Otani 1981; Nagato and Kawase 2004), as shown in Fig. 7. In particular, Japanese wooden houses were estimated to be twice as strong on average, compared to the building standard.

Fig. 7

An example of nonlinear behavior of assumed D-tri type. The horizontal axis is the story drift angle, and the vertical axis is the shear force coefficient (Nagato and Kawase 2004)

Nagato and Kawase (2004) found that the reproduced strong-motion synthetics of Matsushima and Kawase (2000) are sufficient to reproduce observed severe damages in Kobe because the possibility of the heavy damage and collapse is primarily controlled by the strength of the velocity input. This is because the maximum deformation of a building in the nonlinear regime is correlated with the potential energy that the structural system should absorb. Under such a relatively low-frequency (but with high peak ground velocity) input, we would not see a strong correlation between the building’s deformation and its resonant frequency. This is because the resonant frequency of a building is a parameter in the linear regime so that it will correlate only with a small deformation for a small input (less than 1/100 in terms of the story drift angle), referring to the results of capacity demand diagram by Chopra and Goel (1999). Additionally, inelastic response of a building with a higher resonant frequency would result in the same level of response in the inelastic regime (i.e., the potential-energy regime). Then, Kawase and Masuda (2004) applied this model to predict the building damage in the Yatsushiro City, Japan.

Yoshida et al. (2004) followed the construction procedure of the Nagato–Kawase model and updated the parameters related to the Japanese building codes during four construction periods to analyze the dynamic response of the standard models, for a more detailed damage estimation of Japanese wooden houses. They used 24 representative models for the two-floor wooden houses of different strengths. For the first floor, eight representative strength factors relative to the standard strength and the existing ratio were used. These eight strength factors are shown in Fig. 8. For the second floor, they used a ratio between the structural wall sufficiency rate (i.e. a ratio between the existing structural wall quantity and necessary structural wall quantity) of the second and first stories, which are 1.0, 1.5, and 2.0 (Yoshida et al. 2004; Nagato and Kawase 2004), respectively. The strength of the standard wooden model was defined by the necessary structural wall quantity for a wooden house according to the Japanese building code. Figure 9 shows three types of nonlinear factors for the standard model used in the Yoshida model. Parameters of the standard wooden house in the Yoshida model are listed in Tables 2 and 3. Furthermore, ${\gamma }_{t}^{\mathrm{1,2}}$ and ${\gamma }_{t}^{\mathrm{1,3}}$ denote the stiffness ratio of 2nd stiffness/1st stiffness and 3rd stiffness/1st stiffness for the tri-linear type model, respectively.${\gamma }_{s}^{\mathrm{1,2}}$,${\gamma }_{s}^{\mathrm{1,3}}$, and ${\gamma }_{s}^{1,R}$ denote the stiffness ratio of 2nd stiffness/1st stiffness, 3rd stiffness/1st stiffness, and returning stiffness/1st stiffness for the slip type model, respectively. The necessary structural wall quantity is satisfied when the base shear coefficient is 0.2 and the angle of deformation is 1/120 rad. (Kawase and Masuda 2004; Yoshida et al. 2004; Nagato and Kawase 2004). They also set a parameter α, which is the ratio between the structural strength of a wooden house for a specific construction period and that of the standard wooden model, as given in Table 4 (Yoshida et al. 2004, 2005). Then, the strength of a model is the product of α and the standard strength. As for the estimated DP by Yoshida model, we calculate the sum of the log-normal existing ratios of heavily damaged models after the analysis, the total percentage of damaged models among 24 models is obtained as the DP of the site. They successfully expanded the Nagato–Kawase model to consider different construction periods because they used the damage statistics for tax evaluation by municipal governments which requires the construction period of each house. The database of building damage to make the Yoshida model was following the Damage Scale #3 in Fig. 3.

Fig. 8

Log-normal distribution of existing probability with different strength coefficients (normalized strength with respect to the average) for the two-floor wooden house of Yoshida model (Yoshida et al. 2004; Nagato and Kawase 2004)

Fig. 9

Nonlinear factors of the standard model in Yoshida model (Yoshida et al. 2004), with three types of relationships between the story drift angle and base shear ratio

Table 2 Weights and heights of two floors of the standard model used in Yoshida model

Table 3 Stiffness ratios of two types of nonlinear factors for standard model used in Yoshida model

Table 4 Parameter α for every construction period in Yoshida model

Furthermore, 24 models with different strengths were defined for the nonlinear analysis when the construction period of the building was identified. Figure 10 presents the predominant frequencies of the 24 models used for four different construction periods. After the nonlinear analysis, the DP of the input seismic waveform is calculated as the sum of the existing ratios of the models (Fig. 8) that exceed the damage criterion among 24 models. Please note that the first and second frequencies are varying as a function of construction age and the strength variation with the log-normal distribution of existence. This is so because we set the same yield deformation angle to be 1/120 for all the models. The higher the yield strength is, the higher the stiffness in the linear regime. The actual measured fundamental peak frequencies of wooden houses in Japan are distributed in the same range of 2–10 Hz. According to the above-mentioned descriptions, the Yoshida model was built in 2005 for wooden houses in Kobe, based on the same estimated ground motions up to 1.75 Hz by Matsushima and Kawase (2000). Again, despite of much higher resonant frequencies of actual wooden houses in Japan, the estimated ground motions had sufficient power to create heavy damages or collapses. Therefore, in this study, it is better to filter the estimated ground motions by the high-cut (1–2 Hz) filter when applying the Yoshida model.

Fig. 10

Two predominant frequencies of 24 models during four construction periods. Circles and triangles denote the first and second fundamental frequencies of the models, respectively

2.4 Investigation of construction periods

According to the Yoshida model, the construction period is an important parameter for determining the average yield strength of the wooden houses (Yoshida et al. 2004). The model considers four construction periods: before 1950, 1951–1970, 1971–1981, and after 1982. Thus, it was required to obtain the construction period of each building in the target area.

After the mainshock, Yamazaki et al. (2018) performed a statistical analysis of the building ages for the entire Mashiki. However, they did not provide details on the construction period for every building. Note that our target area is the central part of the entire Mashiki town. Yamada et al. (2017) determined the building construction period for every building in the target area related to the date when the aerial photos of the Geospatial Information Authority of Japan (GSI) in Mashiki were obtained. Moya et al. (2018) reported their building construction period results for the southern area between road No. 28 and Akitsu river. However, these results did not define construction period the same way as the Yoshida model; hence, their data could not be used directly in this study. We obtained the building ages for the AIJ surveyed area in Mashiki. However, the AIJ survey only covered the area shown in Fig. 1, without including the northwestern part. In addition, the AIJ classified building ages as either before 1981 or after 1982, and thus, this information alone (Fig. 1) was insufficient for our study. We needed to generate a database of wooden houses in the target area corresponding to the construction period as defined by the Yoshida model.

We used the following steps to determine the construction period of the target area corresponding to the Yoshida model:

• (1) We obtained the coordinates of all building centroids in the target area by referring to OpenStreetMap (OSM).

• (2) We determined the building construction periods by referring to Yamada et al. (2017). They had investigated construction periods as before 1967, 1968–1975, 1976–1981, 1982–1986, 1987–1997, 1998–2008, and after 2008. These results were obtained through an analysis of aerial photos shared by the Geospatial Information Authority of Japan (GSI). We then re-investigated the construction periods of our target area as before 1967, 1967–1981, and after 1982.

• (3) We used the geographical coordinates of buildings in the AIJ survey with a construction period after 1982. All the buildings were located within the heavy blue dashed line shown in Fig. 11. We checked all these buildings and corrected any information contradicting the AIJ survey data.

• (4) For buildings with construction periods before 1967, we compared their locations with aerial photos captured in 1947 and 1956 (GSI). For buildings with a 1967–1981 construction period, we re-checked their locations in aerial photos captured in 1964 and 1975 (GSI). After this step, we obtained the database of construction period as before 1947, 1947–1956, 1956–1967, 1967–1975, 1975–1981, and after 1981

• (5) We compared our results with Moya et al. (Moya et al. 2018) to correct and confirm the database for buildings between Road No.28 and Akitsu River in Mashiki. Then, we built a database for the actual construction period of each building in Mashiki.

• (6) According to the Yoshida model, 1951, 1971, and 1981 are important transitions for construction periods. Because we could not obtain aerial photos captured exactly in 1951 and 1971, we assumed construction periods for the database to correspond with the construction periods used in the Yoshida model, as given in Table 5. Finally, we obtained a distribution map of the construction periods for the target area following the same standards as those used in the Yoshida model, as shown in Fig. 11.

Fig. 11

obtained from OpenStreetMap

Definition of the construction periods for all buildings in the target area. The black, blue, and yellow dashed lines denote the heavily damaged area, AIJ field survey area, and northwestern part not surveyed by the AIJ, respectively. The three stars mark the strong motion stations, as in Fig. 1. The dark red, red, yellow, and green dots mark buildings built before 1950, during 1951–1970, during 1971–1981, and after 1982, respectively. The background was

Table 5 Comparison between real construction periods and those used in the Yoshida model

We compare the statistical analysis results of building construction periods of our database with those of Yamazaki et al. (2018), as depicted in Fig. 12. The overall matching was satisfactory. We had a slightly lower percentage of buildings constructed before 1950 than Yamazaki et al. because we counted buildings based on an aerial photo that was captured in 1947, so we were missing 3 years. We had a larger percentage of buildings constructed during 1951–1970 because this period included buildings constructed during 1947–1975. We had a slightly larger percentage of buildings constructed before 1950 and during 1951–1970 than Yamazaki et al. This may be because the number of older buildings built before 1970 in the target area was slightly more than that of the entire downtown Mashiki. For buildings built after 1982, our result was close to those of Yamazaki et al.

Fig. 12

Statistical analysis of construction periods. The blue and orange columns denote our results and those of Yamazaki et al. (2018), respectively

3 Research steps

With the necessary introduction above, our research process is clear. First, we observed the microtremor in the target area. Second, we identified 57 1D subsurface velocity structures of this area. Third, we obtained 535 1D subsurface velocity structures in this area. Fourth, we obtained the ground motions by the ELA. Finally, we estimated the building DPs through the Yoshida model. The detailed workflow is illustrated in Fig. 13.

Fig. 13

Workflow of this study

4 Results

4.1 Interpolated subsurface velocity structures

Based on the 57 1D subsurface velocity structures, we generated a 30 × 30 grid along the horizontal plane of each subsurface layer for the target area (each grid has an area of approximately 47 m × 47 m) by using the linear interpolation method for a 3D space (Barber et al. 1996; Virtanen et al. 2020). Finally, we obtained 535 velocity structures for Mashiki. The upper 8 layers (from ground to the engineering bedrock) are shown in Fig. 14. Shallow subsurface structures in the southwest are deeper than other areas.

Fig. 14

Grid model of the identified velocity structures in the target area. Each colored surface represents the boundary between two subsurface layers. The shading indicates the difference in layer depth (darker means deeper). Each grid has a size of approximately 47 m × 47 m from the top view. Please note that the vertical axis is exaggerated approximately 10 times with respect to the horizontal distance

4.2 Dynamic response analyses of subsurface velocity structures at 535 sites

We followed the basic procedure of the ground motion simulation scheme as in previous research (Sun et al. 2020) but analyzed the ground response with considerably denser sampling locations. We estimated the ground motions during the mainshock for these 535 grid points by employing the ELA (Yoshida and Iai 1998; Yoshida 2001). Figure 15 depicts the distribution maps of the estimated PGAs and PGVs according to the ELA. Although we previously summarized the distribution of the estimated PGAs and PGVs of the 57 microtremor sites (Sun et al. 2020), Fig. 15 has a more detailed spatial resolution, especially in the large PGA/PGV distributed area. A close relationship was not obtained between the PGA and building damage distribution at Maishiki (Fig. 1); however, the PGV distribution of the ELA showed a close relationship with the building damage distribution from the AIJ survey. Moreover, the seismic response was clearly stronger for the EW component than for the NS component. This is primarily because the amplitude of the EW component had a larger amplitude than the amplitude of the NS component for the seismic bedrock waves in the intermediate (~ 1 Hz) frequency range.

Fig. 15

Estimated PGA and PGV distribution maps. PGA distributions for the a EW and b NS components with the ELA. PGV distributions for the c EW and d NS components with the ELA. The triangles mark the 57 microtremor observation sites. The stars mark the three strong-motion stations. The blue dashed line denotes the boundary of the heavily damaged area shown in Fig. 1. GMT5 interpolation function was used

Because most of the wooden houses in Mashiki were two-story structures, we used the two-story wooden model of Yoshida model for analyzing the target area. We applied the Newmark–β analysis method, with β = 0.25 and a time increment Δt = 0.005 s. Instantaneous stiffness proportional-type damping was applied with a damping ratio of 5%. For the standard model constructed according to the Japanese building code, the mass of the first floor was set to 15.88 tons and that of the second floor was 11.52 tons. Both floors were set to a height of 2.9 m. A log-normal distribution was assumed with the standard deviation based on the measured resonant frequency distribution of wooden houses. Because the damage ratios shown in Fig. 1 are those for damage grades of D4 and higher, we set the damage criterion for the nonlinear building response analysis to a story drift angle of greater than 1/30 rad. This threshold was used by Yoshida et al. (2004) to represent the total damage grade in the survey for property tax evaluation; this should be similar to a damage grade of D4 or higher, although it is not an exact match.

The average yield capacities of the Nagato–Kawase model and Yoshida model, were obtained by using synthetic seismograms of the ground surface in Kobe, that was simulated by the 3D finite difference method for a frequency range of up to 1.75 Hz (Kawase et al. 2000). Thus, we apply a high-cut filter of 1–2 Hz to the estimated strong motions of the ground surface at Mashiki. Even though we filter high-frequency components from the input waves, the damage still occurs because the structural period will be prolonged owing to the strong nonlinearity of the model. Figures 16 and 17 show representative results for the dynamic response analysis of a wooden house model with a weaker yield strength (construction period of 1971–1981, strength coefficient factor of the first and second floors respectively are 0.29648 and 0.59296) among the 24 representative models. The filtered estimated ground motions at KMMH16 were applied to this model. The maximum story drift angles of the EW and NS components were 16.7% and 3.8% rad, respectively. Full damage was considered to occur because both were greater than 1/30 rad (3.33%). Table 6 lists the maximum response accelerations, velocities, and displacements of the ground floor (0F), first floor (1F), and second floor (2F) with the EW and NS components.

Fig. 16

Dynamic response of the damaged model for a two-floor wooden house. Story drift angles for a EW and b NS components in the time domain. Hysteresis curves for c EW and d NS components. The red and green lines (solid and dashed) denote the results of the first and second floors, respectively

Fig. 17

Response accelerations of the damage model for the a EW and b NS components. Response velocities of the c EW and d NS components. The black, red, and green lines denote the results of the ground, first, and second floor, respectively. Figures 14 and 15 show the response results of the same model

Table 6 Maximum response accelerations, velocities, and displacements of the ground floor (0F), first floor (1F), and second floor (2F) of a building model

By applying the filtered ground motions and setting different construction periods in Yoshida model, we estimated the DPs for four construction periods at every grid point with the two-floor standard wooden model. The DPs corresponding to the construction periods of before 1950, 1951–1970, 1971–1981, and after 1982 are designated as DP₉₅₀, DP₉₇₀, DP₉₈₀, and DP₉₉₀, respectively. We created distribution maps of these DPs through ELA. Figure 18 presents the estimated DP distributions of Mashiki for the four construction periods with the estimated ground motions by ELA.

Fig. 18

Estimated damage probability distribution maps of wooden buildings from different construction periods according to the Yoshida model, based on the estimated horizontal ground motions using the ELA: a DP₉₅₀, b DP₉₇₀, c DP₉₈₀, and d DP₉₉₀. The other markers and lines have the same meanings as in Fig. 15

Based on the statistical analysis of buildings in Mashiki by Yamazaki et al. (2018), we calculated the composite DP (DP_COM) of each grid point by considering the building percentages of different construction periods, using Eq. (1).

$$ DP_{COM} = Per_{950} \times DP_{950} + Per_{970} \times DP_{970} + Per_{980} \times DP_{980} + Per_{990} \times DP_{990} $$

(1)

where Per₉₅₀, Per₉₇₀, Per₉₈₀, and Per₉₉₀ are the existing percentages of buildings in the corresponding square cell with construction periods before 1950, 1951–1970, 1971–1981, and after 1982, respectively. Figure 19 shows the distribution map of DP_COM based on the estimated ground motions from ELA.

Fig. 19

Distribution maps of the composite damage probabilities of the ELA. The markers and lines have the same meanings as in Fig. 15

After obtaining the DPs for four different construction periods at every grid point, we calculated the DP of each building. Within a 30 × 30 grid, each wooden house is surrounded by four grid points, as shown in Fig. 20. The distance between a grid point and a wooden house was denoted as Dis(i) (House1–grid point). In other words, a building is affected by the estimated ground motions at the four surrounding grid points. Then, we defined an influence coefficient (IC) related to the distance between the building and four grid points, as shown in Eq. (2). We used IC to calculate the DP of every building with Eq. (3). For example, if House1 is one building as shown in Fig. 11 with a construction period after 1982, then DP(B2)₉₉₀, DP(B3)₉₉₀, DP(C2)₉₉₀, and DP(C3)₉₉₀ are the damage ratio of B2, B3, C2, and C3 respectively, with a construction period of after 1982 (Fig. 18d). By considering IC(B2), IC(B3), IC(C2), and IC(C3) of the four grid points, we could obtain the damage ratio of this building with Eq. (3).

$$ Power \left( i \right) = \frac{1}{Dis\left( i \right)}; IC\left( i \right) = \frac{Power\left( i \right)}{{\mathop \sum \nolimits_{i = 1}^{4} Power\left( i \right)}} $$

(2)

where, Power(i) denotes the inverse of each distance, and IC(i) represents the influence coefficient of each grid point.

$$ DP_{building} = \mathop \sum \limits_{i = 1}^{4} IC\left( i \right) \times DP\left( i \right)_{period} $$

(3)

where, DP_building denotes the DP of the target building, and DP(i)_period is the estimated DP of the four surrounding grid points with the same construction period as the target building.

Fig. 20

Schematic map of locations of wooden houses and surrounding grid points. A1–E5 are the grid points corresponding to the grids shown in Fig. 11. The small circles are the building locations (unit: m)

Although we estimated the DP of every building in the target area, we cannot present these results because it is the private information of the relevant house owner. To compare the estimated damage of houses with the AIJ survey results, we created a new grid similar to the AIJ survey and calculated the averaged DP of each cell (DP_cell) with Eq. (4). Figure 21 is the distribution map of DP_cell.

$$ DP_{cell} = \frac{{\mathop \sum \nolimits_{i = 1}^{N} DP\left( i \right)_{building} }}{N} $$

(4)

where, N is the number of buildings located in the cell, and DP(i)_building is the estimated DP of each building in the cell. The size of the new grid is approximately equal to that used in the AIJ survey results (Fig. 1).

Fig. 21

Averaged damage probability of each cell based on the estimated ground motions of the ELA. The green, yellow, orange, red, and dark red colors denote damage probabilities of 0–15%, 15–25%, 25–50%, 50–75%, and greater than 75%, respectively. The other markers and lines have the same meanings as in Fig. 1

5 Discussion

Figure 18 indicates that most of the houses which were constructed before 1950 and during 1951–1970 had a high DP during the mainshock. Buildings built during 1971–1981 and after 1982 showed a better seismic performance than the older ones. Figure 19 shows that the damage grades of the DP_COM distribution map correspond to those for DP₉₈₀ and DP₉₉₀. The estimated DP distribution shows a close correlation with the estimated PGV distribution (Fig. 18c and d). This is because building damage requires large deformation and therefore a large amount of energy, as shown in Fig. 16. Thus, PGV is the controlling ground motion index for structural damage in Mashiki because the input energy is proportional to the square of PGV.

Figure 21 indicates that most of the large DPs were located in the south Mashiki, and the overall pattern were similar to the AIJ damage survey. Moreover, the estimated DPs in the northwestern area of Mashiki were not negligible. In the southwestern part near Akitsu River as well as the northeastern part, several cells with large DPs in Fig. 21 were located outside the heavily damaged cells in Fig. 1. One explanation is that some of the buildings in these cells were actually steel or RC structures, whereas we assumed all buildings to be two-floor wooden structures. Another more plausible reason is that most of the buildings in these cells were built after 2000 and did not have the same yield strength as that specified for the construction period after 1982 because the Japanese building code for wooden structures was updated in 2000. In addition, we did not consider soil liquefaction in the southwestern part near the Akitsu River. Further study is needed of a nonlinear effective stress analysis of soil columns. Moreover, the number of buildings in each cell was different as shown in Fig. 1. The observed damage ratio of a cell will be strongly affected by the building number when the building number of the cell is small. This is a reason why there are so many cells with no damage in the observed ratio distribution in Fig. 1. If the expected damage ratio of a cell was less than say 25% and the existing number of buildings was less than four, it will be highly probable to have no damage at the cell. Furthermore, the estimated ratio of heavy damage tended to be slightly greater than the AIJ survey results for the lightly damaged cells (DP < 25%), while the results were opposite for heavily damaged cells (DP > 75%). This is because the Yoshida model was developed based on the damage to wooden houses after the 1995 Kobe earthquake (Okada and Takai 1999; Takai and Okada 2001) for property tax evaluation by the municipal government (Damage Scale #3 in Fig. 3), the AIJ survey used the Damage Scale #4 to evaluate building damage in Mashiki. The damage grades used to construct the Yoshida model construction were interpreted to correspond to D1–D2, D3, and D4–D6, but it is difficult to prove the appropriateness of the correspondence. These differences explain the estimated damage probabilities and AIJ survey results. Although the results in Fig. 21 do not perfectly match the survey results for every cell in Fig. 1, they indicate that the Yoshida model can be used to estimate the building damage probabilities in Mashiki. Further improvement is needed to consider the construction period after 2000.

Figure 22 shows the overall comparison between the AIJ investigated DRs and estimated DPs of the AIJ survey cells with or without using the high-cut 1.0–2.0 Hz filter. Even though the estimated DPs without using filter, generating a slightly better match to the AIJ DR in the heavy damage grade (DR > 50%) than the case of 1.0–2.0 Hz high-cut filter, they do not close to the AIJ DRs in the slight and moderate damage grades (DR < 50%). In contrast, results from the 1.0–2.0 Hz high-cut filter show results close to the AIJ DR in the slight and moderate damage grades, while they were underestimated in the heavy damage grades (DR > 50%). According to the AIJ DR, 74% of the investigated cells were slightly and middle damaged, which emphasizes the good match in the slight and middle damage grades, which is more expected. Figure 23 presents the absolute difference between the estimated DP with 1.0–2.0 Hz high-cut filter and the middle value of the AIJ DR range in each cell. The difference of 83% cells is less than 35%, whereas only several cells have a very large difference. Thus, applying the 1.0–2.0 Hz high-cut filter to estimated ground motions was applicable to estimate DP in Mashiki. Considering the Yoshida model was built based on the building data of Kobe city, and most of the large DPs were found in the older buildings (before 1970), the seismic performance of older buildings in Mashiki was worse than that of Kobe buildings, while that of the Mashiki young buildings was similar to the Kobe young buildings.

Fig. 22

Comparisons of estimated DPs for five cases and observed damage ratios. Grey dot with error bar denote the AIJ investigated damage ratios in 400 cells, recall that the cell locations were show in Fig. 1, in which the damage ratio ranges are 0%, 0  –25%, 25%–50%, 50%–75%, and 75%–100%. The red rectangles denote the final averaged DP of each cell from the response of estimated ground motions by the 1.0−2.0 Hz high-cut filter; Similarly, the yellow crosses denote the averaged DP of each cell which is analyzed from the response of estimated ground motions by using the no filtered waveforms

Fig. 23

Distribution map of difference between estimated DP and AIJ survey DR. Other markers are the same as in Fig. 21

Figure 24 shows the comparison between estimated DPs by using the local strong ground motions of each building and the interpolation method from four grid points as shown in Fig. 20. It is obvious to find that two estimated DPs at most sites were similar. Moreover, it is really time-consuming to analyze the site response by LA and ELA and continue estimating the DP by nonlinear analysis for more than 3000 buildings in Mashiki. These results indicate the proposed four-point-interpolation method for the DP estimation is sufficiently accurate and efficient.

Fig. 24

Estimated DPs by two methods. Blue columns denote the estimated DPs by using the estimated strong ground motions of every building, orange columns denote the estimated DPs by the interpolation method from four grid sites (as Fig. 20 shown). a, b, c, and d denote the results of buildings in Cell 331, Cell 394, Cell 530, and Cell 796, which are shown in Fig. 21. The horizontal and vertical axes denote the building ID and estimated DP, respectively

6 Conclusion

In this study, we estimated the detailed ground motions of Mashiki during the mainshock of the 2016 Kumamoto earthquakes through the equivalent linear ground response analysis of 1D soil columns from the seismological bedrock to the ground surface. We also estimated the building damage probabilities through nonlinear dynamic response analysis of wooden houses. We evaluated the site responses based on velocity models at the 535 grid points, determined the construction periods, and estimated the building DP for each wooden house in Mashiki. The whole study was begun from the microtremor observation which is a very convenient research tool. Based on the field data of buildings, the seismic risk of buildings could be inferred. Before an earthquake, this method can be used to guide how to retrofit local buildings. After an earthquake, this method can be used to quickly estimate the damage ratios of the near-source buildings for immediate action of rescue and recovery.

Our main conclusions and finding are as follows:

• 1. The estimated spatial PGV distribution of the EW component by ELA was similar to that of the building damage distribution in the AIJ survey. In addition, the estimated PGAs and PGVs of the EW component were considerably stronger than those of the NS component. The analytical results for the 535 1D subsurface velocity structures have a more detailed resolution (~ 47 m × 47 m grid) than the previous work. The 535 estimated ground motions provided the conditions for analyzing the dynamic response of every building.

• 2. We determined the construction period for every building in the target area with our research method. The total percentage of the older buildings (constructed before 1950 and during 1951–1970) in the central Mashiki was slightly greater than that of another survey for all the Mashiki buildings.

• 3. The estimated DPs indicated heavily damage to older buildings (constructed before 1950 and during 1951–1970). The estimated DP distribution of each new cell (Fig. 21) generally matched the DP distribution of the AIJ survey, although our study underestimated the heavy damaged buildings. Moreover, in the northwestern part where the AIJ survey did not cover, we found that non-negligible damage probabilities would have been caused by the mainshock. In several cells in the northwestern and southwestern parts, the DPs were clearly found to be greater than those of the AIJ survey. This may be because the buildings were not wooden, or newly built (after the building code was modified 2000); both factors were not considered in this study. Soil liquefaction may also have caused a smaller amount of damage to houses in the area near Akitsu River. We will study these aspects further in the future.

• 4. The results indicate that the presented building damage evaluation method can be used to estimate the DP distributions of other areas as long as the necessary building information is obtained in a similar manner. We believe that the detailed estimated ground motions can serve as a basis for dynamic analyses of structures for quantitative damage prediction. This method allows the building responses of a target area to be estimated precisely. We emphasize that the construction period of buildings and the soil conditions must be considered when evaluating the safety of a building.

7 Data and resources

JMA research data can be accessed at https://www.jma.go.jp/jma/indexe.html (last accessed November 2020). NIED KiK-net strong motions can be accessed at https://www.kyoshin.bosai.go.jp/ (last accessed November 2020). NIED F-net earthquake mechanism information can be accessed at: http://www.fnet.bosai.go.jp/event/search. php?LANG = en (last accessed November 2020). The quick report of the 2016 Kumamoto Earthquake by National Institute for Land and Infrastructure Management (NILIM), and Building Research Institute (2016) can be found at https://www.kenken.go.jp/japanese/contents/publications/data/173/index.html (in Japanese, last accessed November 2020). “DYNEQ” software was downloaded at https://www.kiso.co.jp/yoshida/yoshida/computercodes/english/ (last accessed March 2021). Several figures were generated using the QGIS3 software and GMT5 software, which can be found at https://www.qgis.org/en/site/ (last accessed November 2020) and http://gmt.soest.hawaii.edu/projects/gmt (last accessed November 2020), respectively. Several figures were generated using Python3 together with scientific packages such as Numpy, Scipy, Pandas, Matplotlib, Seaborn, and Pillow.