Abstract
Pulse-wave propagation velocity and resonance frequency measured in civil engineering structures are both related to structural design. Monitoring their variation following seismic strong shaking provides information about the immediate building capacity. Joint-interpretation of frequency and velocity variation requires a better understanding of the processes controlling seismic structural health. In this study, we analysed 8 years of earthquake data recorded by the vertical array installed in the Te Puni building in Wellington, New Zealand, as part of the GeoNet building instrumentation programme. Co-seismic variations of pulse wave velocity and fundamental frequency are analysed and interpreted through a Timoshenko beam-like building model. This study shows that even though no structural damage was visually reported over the considered time of monitoring, co- and post-seismic variation of both parameters’ values are observed for almost all earthquakes, including a permanent shift following strong ground shaking. Variations of pulse-wave velocity and resonance frequency are cross-interpreted in terms of the building model. They reflect a time variant building response, correlated with the seismic loading. In addition, time delay of the pulse-wave velocity as a function of the building height provides relevant information on the location of the changes and confirms the efficient cross-interpretation of both methods for seismic Structural Health monitoring.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Earthquakes are responsible for some of the most catastrophic and costly damages to civil engineering structures. Rapid and objective structural damage assessment, through visual and detailed inspections is usually lengthy and difficult. Making this process faster and more precise is one of the goals of Seismic Structural Health Monitoring (S2HM, Limongelli et al. 2019), which can be defined as a process of implementing a damage identification strategy for large variety of infrastructures including buildings (Farrar and Worden 2006), with specific application to post-earthquake case. S2HM involves long-term implementation of observation strategy using continuous or/and temporary and periodical measurements, identification of the damage-sensitive features and statistical analysis of those features in order to estimate the current state of a structure and its safety or operability (Limongelli et al. 2019).
Snieder and Safak (2006) pioneered seismic interferometry by deconvolution (SIbyD) to estimate the dynamic properties of a structure. SIbyD had since been applied to earthquake data (e.g. Kohler et al. 2007, 2018; Todorovska and Trifunac 2008; Newton and Snieder 2012; Wen and Kalkan 2017; Michel and Guéguen 2018; Guéguen et al. 2019) and ambient vibrations (e.g. Prieto et al. 2010; Nakata and Snieder 2014; Mordret et al. 2017). Structural earthquake response recorded by sensors is a combination of (1) the ground input shaking into the structure, (2) the coupling of the building with the ground (i.e. soil-structure interaction SSI), and (3) the mechanical properties of the building. The deconvolution of the signals from a vertical array of sensors distributed at very floor of a building, allows separating the building response from the input earthquake shaking and from the SSI.
The relationship between wave velocity and resonance frequency proposed by Snieder and Safak (2006) was based on pure-shear beam model assumption. However, many actual buildings do not in principle behave in a pure shear response. The Timoshenko beam model, initially proposed by Boutin et al. (2005), applied to real-cases buildings by Ebrahimian and Todorovska (2014) and Perrault et al. (2013), and later applied by Michel and Guéguen (2018) and Guéguen et al. (2019) for SIbyD interpretation, is a fairly effective beam-like building model that includes bending effect in terms of cross-interpretation of velocity and fundamental frequency. For a proper interpretation of the structural response with SIbyD, Michel and Guéguen (2018) proposed a correction factor to take into account shear-to-bending ratio in the frequency-to-velocity relationships, assuming a stationary response at low level of deformation. However, several studies (e.g., Clinton et al., 2006; Michel and Guéguen, 2010; Astorga et al. 2018, 2019) reported the co-seismic shift to the lower values of the building resonant frequency as well as over long seismic sequences. This raises the question of the invariant nature of the frequency-to-velocity relationship over these two-time scales, and its effect on the interpretation of the behaviour of the structures.
The main aim of this study is to improve our understanding of the dynamic response of buildings to earthquake shaking, in particular we focus on the interpretation of wave propagation pattern in presence of seismic damage. We take advantage of an instrumented New Zealand structure having experienced strong earthquake shaking over eight years to confirm the significance of SIbyD method for S2HM. In addition, related to S2HM activity, post-earthquake evaluation of the building state is crucial for building safety management. In this study, earthquake data are considered for studying the structural changes during earthquake using seismic interferometry-based method. We first present the earthquake data used in this study, the building structural characteristics and seismic array. We then describe the methods used for the analysis, explaining briefly seismic interferometry by deconvolution, building transfer function and Timoshenko beam model. In the following section, we present our results, focusing on changes in structural parameters over time and as a function of seismic loads. Finally, we present the conclusions of this study.
2 Building description and seismic array
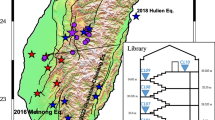
The building of interest (Fig. 1) is the Victoria University Wellington Student Accommodation Te Puni Apartments building (VUWB building), part of the GeoNet monitoring programme in New Zealand (station code: VUWB) (Uma et al. 2010). The Te Puni building is a complex of three buildings of five, ten and eleven storeys (Fig. 1a). Two 14 m long structural steel truss link bridges span between the Tower and Edge buildings. Gravity loads are supported at each end by independent structural steel SHS columns. A central pin connection at the end of each span allows for transverse loads to be braced by the adjoining buildings, while allowing for longitudinal movement via a slotted bolted connection. Base shear is resisted by a number of fixed-head bored concrete piles. The seismic array is located in the 37 m high tower, in the middle part of VUWB (in rectangle in Fig. 1a). This is a high-rise (according to Hazus classification, FEMA 2020) and relatively light structure built in 2009. Design of the Te Puni building follows a ‘Damage Avoidance Design (DAD)’ philosophy. The DAD system featured coupled Concentrically Braced Frames (CBF) with prestressed Ringfeder Springs transversely between columns and foundations and Sliding Hinge Joints (SHJ) between columns and beams in the longitudinal direction (Gledhill et al. 2008). The coupled CBF’s behave similarly to a coupled shear wall and is effectively a “steel shear wall”. The longitudinal bracing consists of steel moment resisting frames with sliding hinge joints at beam and column joints, and, additionally, vertical sliding hinge joints for column base protection. SHJs are essentially semi-rigid beam column connections and they are suitable for moderate ductility, high rotation applications (Gledhill et al. 2008; Uma et al. 2010). The building is situated on a hillside at the university’s Kelburn Campus in Wellington. According to the New Zealand Standard for Structural Design Actions (NZ 1170.5:2004), VUWB is situated on class B-rock, equivalent to class A/B in the Eurocode 8 (EC8) (Khose et al. 2012), around 1 km from the Wellington active fault. The site condition consists of highly weathered greywacke rock overlaid with a softer soil lens (Uma et al. 2010). Due to the fairly stiff site conditions, substantial site effects and soil-structure interaction (SSI) during earthquakes are not expected (Uma et al. 2010; Gledhill et al. 2008). Unfortunately, there were no free field station located close to the building to capture potential SSI.
View of the Te Puni Apartments building and its instrumentation. a VUWB building cross section (Architectus 2019). The middle part in the rectangle is the instrumented "Tower" building analysed in this study. b Side view (top) and plan view (bottom) of the building seismic array with the location of the accelerometers. Dimensions on the drawing are in meters. Y and X correspond to longitudinal and transverse direction of the building, respectively
Since 2010, the building has been permanently instrumented with CUSP-M sensors distributed at several levels, connected with the CUSP-M central recording unit through Ethernet cables (Fig. 1b). CUSP-M accelerographs use tri-axial MEMs silicon sensors, and the full technical description is provided by the Canterbury seismic instruments website (http://www.csi.net.nz/index.php/general/products/) and illustrated in Uma et al. (2011). The whole instrumentation consists of 12 seismic sensors and 5 LVDT (Linear Variable Differential Transformer) instruments, a wind sensor at the roof to monitor wind parameters (speed, direction) and a GPS for time synchronization. All seismic sensors are tri-axial strong motion accelerometers mounted at various levels with data-logger sampling frequency 200 Hz. For the need of this study we used only data from eight vertically aligned sensors in the central part of the building (sensors 1–8 Fig. 1b). We consider Y axis (along longer side of the building) as the longitudinal direction, and X axis (along shorter side) as transverse. The azimuth of the Y axis is 23°. In this paper we consider only earthquake data in relation to the S2HM objectives of this study.
3 Data
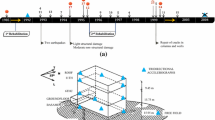
Since the start of the instrumentation programme in 2010, raw data has been stored at GNS Science (New Zealand Crown Research Institute). In this study, we analysed data from July 2010 to March 2018, including multiple sequences of moderate to strong earthquakes (Fig. 2). A first selection was performed based on estimation of the signal to noise ratio from accelerometer recordings. Once selected, data was cross-validated with the GeoNet earthquake catalogue, and, finally, a total of 208 recordings make up the dataset used in this study, represented on map in Fig. 2a. The magnitude of selected earthquakes ranges from 2.4 to 7.2 with epicentral distances from 8.6 to 630 km (Fig. 2b) and depths from 5 to 241 km, corresponding to maximal acceleration recorded at the building top (Peak Top Acceleration PTA) ranging from about 3 × 10–4 to 2 × 10−1 g.
Description of the dataset. a Location of the earthquakes selected for this study. The white square represents the location of the Te Puni building and the black crosses the earthquake epicentres. b Magnitude versus epicentral distance for the selected events. Grey scale corresponds to the peak top acceleration (PTA) value recorded in the transverse direction. c PTA for both directions versus structural drift for the selected events
We divided data in five periods (Table 1) in order to monitor changes during major earthquakes sequences (P2 and P4), and in-between (P1, P3 and P5). The second sequence (P2) contains the Cook Strait (M 6.5) earthquake on 21.07.2013, which was followed by Lake Grassmere (M 6.6) on 16.08.2013 and many strong aftershocks. The fourth sequence (P4) is the aftershocks sequence of the M7.8 Kaikoura earthquake (13.11.2016). Due to the temporary breakdown of the device, the Kaikoura main shock and early aftershocks were not recorded.
Figure 3 presents an example of the observed waveforms and their Fourier transform corresponding to the Cook Strait earthquake (M 6.5) on 21.07.2013. This earthquake produced the greatest acceleration at the top of the building in our dataset (PTA equal to 0.2 g in longitudinal direction).
Time histories of accelerometer data were processed following Boore’s recommendations (Boore 2005; Boore and Bommer 2005), including mean and trend removal. The resonance frequency of the building (Fig. 4) was first roughly estimated by computing the mean Fourier transform (FT) of the ten early weak motion recordings that corresponds to about 5% of the dataset, and picking the frequency corresponding to the maximum amplitude of the FT considered as fundamental resonance frequency. The resonance frequencies are estimated to oscillate around 1.56 Hz and 1.44 Hz in the transverse and longitudinal direction, respectively. This information is used to define the frequency band considered in the rest of the manuscript. In addition, structural design and the spectral response of the building may suggest the presence of torsion (rotation around vertical axis), as suggested by the double peak in the transverse direction (and lesser in the longitudinal). The torsional motion of the building response could be as a result of several components (e.g., static eccentricity related to the design, accidental related to the rotational seismic ground motion, with nonlinear aspects, etc.), that would require a full and extensive analysis in further studies (Guéguen et al. 2021; Guéguen and Astorga. 2021). This point will not be discussed more herein.
Fourier transform (FT) of the early weak motion data recorded at the top of the Te Puni building. Thin grey lines: Fourier transform of unfiltered signals from ten early events. Thick black line: corresponding average of Fourier transforms. Peak for transverse direction is around 1.59 Hz and for longitudinal around 1.44 Hz. The considered frequency bands are in between the grey vertical lines. Most of the energy for both directions is distributed between 0.5 and 10 Hz
The structural drift corresponding to data from our dataset is calculated as the relative displacement between bottom and top sensors divided by the inter-sensor distance (33.3 m). Acceleration waveforms are integrated twice and filtered with 4-th order Butterworth filter between 0.5 and 3.5 Hz for transverse component and 0.5 and 2.9 Hz for longitudinal (vertical lines in Fig. 4). In this way, the study focuses on the first mode in both directions, considering its high modal participation. Average structural drift values range from 5 × 10–5% to 0.2%. Figure 2c shows the distribution of the average structural drift values versus PTA, representing at the first order the experimental strain–stress curve of this building. A bilinear curve is observed, with a first segment up to PTA = 3 × 10–4 g for a structural drift of about 10–4%, followed by a second linear curve up to PTA = 2 × 10–1 g. Assuming a conventional yield deformation value for such steel-frame structure of about 10–3% (FEMA 2020), the dataset should contain post-yield data, without, however, a beginning of the plastic behaviour generally considered for these deformation values, as reported in-situ.
4 Methodology used
Seismic interferometry by deconvolution method (SIbyD), popularized by Snieder and Safak (2006), provides a wave propagation model for the building, removing the effect of seismic ground motion by considering the sensor of the last floor as a reference for deconvolution. Time delay of the pulse between sensors gives the pulse-wave velocity, considering an equivalent homogenous medium. For the analysis of the velocity changes in the Te Puni building, recordings were band-pass filtered using Butterworth filter with cut-off frequencies of 0.5 and 10 Hz where the seismic energy is concentrated (Fig. 4). Deconvolution was performed using water-level regularisation technique (Clayton and Wiggins 1976) as follows:
with wl water-level value set to 10%, h(t) the impulse response between the sensors, Yi(f) the Fourier transform of the output signal recorded by i-th sensor in the vertical array, and X(f) the Fourier transform of the reference signal. FT−1 indicates inverse Fourier transform. In this study, X(f) refers to the recordings at the top floor. The deconvolution by the top sensor provides a clear up- and down-going pulse wave (Fig. 5a) to assess time delays of the pulse travel time (Δt), by picking the time of the maxima of the deconvolved traces in time. Pulse-wave velocity (β) is calculated as follows:
with H the inter-station distance (Fig. 5b). Under pure shear assumption, Snieder and Safak (2006) linked the observed velocity with the resonance frequency f of the building, as follows:
Example of the SIbyD derived from acceleration time-history considering Cook Strait earthquake (M 6.5). a Interferogram in the transverse and longitudinal directions b Principle of time delay assessment in SIbyD. Data filtered between 0.5 and 10 Hz. c Comparison of BTF and Fourier transform of acceleration signal from sensor 8. Data filtered between 0.5 and 3.5 Hz for transverse component and 0.5 and 2.9 Hz for longitudinal
SIbyD was applied to each pair of recordings in both directions contained in the dataset. The deconvolved traces were resampled 2 times for a better accuracy of the time delay. First, we consider the whole time delay between top and bottom sensors to get information on the variation of the global building properties, in relation to the resonance frequency. Second, we applied SIbyD to all sensors (1–8) for locating the level along the building height with the maximum contribution to the observed changes.
In the Fourier domain (Fig. 5c), the FT of the top recording is also compared to the building transfer function (BTF) of the Te Puni building, for all earthquakes in our dataset. According to Chandra and Guéguen (2017), BTF refers at the first order to the structure response removing the soil structure interaction effects and the FT to the soil-structure system. BTF is computed using Eq. 1 without performing FT−1 with X(f) that refers to the signal from sensor 1 and Y(f) to the signal from sensor 8. All signals were filtered with the 4-th order Butterworth filter with cut-off frequencies 0.5–3.5 Hz for transverse component and 0.5–2.9 Hz for longitudinal, to focus on the fundamental frequencies of the structure. Very slight differences are observed between BTF and Fourier transform (Fig. 5c) that suggests a very slight contribution of the soil-structure interaction in the whole response of the structure, in coherence with the stiff-rock site condition of the building.
For a large number of existing buildings with different design and typology, the shear beam model (Eq. 3) is not always appropriate (Michel and Guéguen 2018). Boutin et al. (2005) proposed a model based on the Timoshenko beam theory, which takes into account shear and bending behaviour of the structure, neglecting the rotation inertia. Based on Jensen (1983), they introduced a dimensionless parameter C to evaluate behaviour of the structure as follows:
where L is the length of the beam, EI is the bending stiffness, K = kGAG is the shear stiffness with A the cross section of the beam, G the shear modulus of equivalent medium and kG the shear adjustment factor depending on the shape of the cross section of the beam and reflecting the non-uniform distribution of shear stress and shear strain over the section (Cowper 1966). 2L/π characterises the dispersive nature of the beam. For pure bending, C tends to 0 and for pure shear C tends to + ∞. Michel and Guéguen (2018) linked the resonance frequencies with the shear wave velocity cS and dimensionless parameter C by introducing the correction factor χ(C) as follows:
where fj is the jth resonance frequency of the beam and k1j are roots of the wave equation of the Timoshenko beam (see Michel and Guéguen 2018 for details). Michel and Guéguen (2018) introduced the correction factor χ(C) to account for bending effect, that depends only on the dimensionless parameter C as follows:
χ(C) for pure shear behaviour tends to 1 and degenerates Eq. 6 into Eq. 3. In this study, χ(C) is considered as the proxy of the structural behaviour used for monitoring the co-seismic and the long-term variation of the response. In practice, C coefficient is assessed based on the ratio of the two first modes frequencies extracted from BTF (Michel and Guéguen 2018) computed for each event contained in the dataset, as follows:
The second mode frequency is obtained by filtering data using 4-th order Butterworth filter with cut-off frequencies 2.5–6 Hz for transverse component and 2.5–5 Hz for longitudinal, defined on Fig. 4. A Konno-Ohmachi smoothing window (b = 30) is applied in order to facilitate the picking of the second frequency to avoid artefacts.
5 Velocity monitoring results
Figure 6 presents the variations of the velocity β obtained by SIbyD (Eq. 2) between top and bottom sensors. Figure 6a presents variation of β as a function of structural drift. The results in Fig. 6b present the variation of velocity in time and show a step-like decrease of the velocity values right after each earthquake in both directions, with a significant drop in period P2. Mean velocity values, standard deviations and coefficients of variation for each sequence for both directions are listed in Table 2.
Time variation of the wave propagation velocity: a as a function of calculated drift. Error bars represent the average (white circles) and standard deviation (vertical lines) computed by bins of 16 events sorted by increasing drift value. Blue lines are semi-log fits to the data defined with the equation in the top part of the plots. b as a function of time. Horizontal dashed lines correspond to average velocity value calculated for periods P1, P3 and P5 defined in Table 2. Vertical lines are the limits of period considered. For both: Colour scale corresponds to PTA
Both transverse and longitudinal components show the decrease of velocity correlated with increased loading (PTA or/and drift). The slope of decrease in lin-log scale (Fig. 6a) has greater value for transverse direction than for longitudinal. Mean values of velocity (± standard deviation) for 16 subsequent earthquakes are given in Fig. 6a. For the smallest values of drift in the transverse direction, velocity is stabilised around 229 ± 12 m/s for drift between 1.54 × 10–4 and 2.94 × 10–4%. For the larger values, we observe a constant decrease up to drift value larger than 10–1%, i.e. for post-yield behaviour with expected structural damage. For the longitudinal direction, the mean values of each 16 events show stable decrease of mean velocity with increasing drift. In addition, the scattering of the velocity values is larger for the transverse direction that reflects different structural response for two directions. The wave velocity variation also depends on the time period of the data considered. Figure 6b and Table 2 show the shift of the mean velocity from 243.03 ± 9.28 m/s in P1 to 213.92 ± 9.79 m/s in P5 that corresponds to average shift of 12% in transverse direction. In longitudinal, the decrease of the mean velocity is slightly smaller of about 11% from 192.07 ± 9.09 m/s in P1 to 170.30 ± 11.33 m/s in P5. Step-like drops of co-seismic velocity are observed for high PTA connected with the sequences of strong earthquakes. During the Cook Strait sequence (P2), the average velocity dropped by 10% in transverse and 14% in longitudinal direction. The lowest velocity was observed for Lake Grassmere earthquake (P2), with β in transverse direction shifted to 162.44 m/s that corresponds to 33% decrease in comparison to average velocity from period P1. In longitudinal direction, for the same event, velocity shifts to 121.09 m/s, that is equivalent to 37% decrease (comparing to P1). In period P4, the velocity drops could have had even greater values for the Kaikoura earthquake, which was not recorded. In this period, the average velocity dropped by 10% in transverse and 9% in longitudinal direction in comparison to the previous period P3.
In addition, for a given PTA value, the velocity shift varies also according to the period considered. Astrorga et al. (2018) reported that considering permanently instrumented building in Japan, coefficients of variation of the velocity decrease in time, as a consequence of the structural degradation of the structural elements. This is not the case in our study, same coefficient of variation being observed for period P1, P3 and P5 (Table 2). For periods following the strongest earthquakes (for periods P2 and P4, immediately after the Cook Strait and Kaikoura main shocks), a recovery of velocity values is observed, already reported for other buildings by Astorga et al. (2018, 2019) as a consequence of the slow dynamic consequences, that produce larger coefficient of variation. Note also that for about the same PTA values, coefficient of variation during P2 is much larger than for period P4, that may reflect the cumulative internal degradation process as reported by Astorga et al. (2018, 2019). The monitoring of the velocity changes in permanent monitored building may then reveal relevant information about the structural dynamics of existing structures, providing insights about physical processes acting in structural elements. Actually, Astorga et al. (2018, 2019) linked the decrease of the coefficient of variation and the post-earthquakes recovery of the elastic properties to a proxy of the structural state of buildings that could be implemented for S2HM.
6 Frequency-to-velocity monitoring
According to Guéguen et al. (2019), frequency and velocity are correlated to the nature of the structure behaviour, characterized by the beam-like structure response using the Timoshenko model (Eq. 5). Figure 7 presents the fundamental frequency (BTF frequency) in the same way as velocity (Fig. 6). At the first order, same variations are observed for velocity and frequency that confirms the close relationship between these two parameters, also confirmed by the same tendency for coefficients of variation over time. Figure 7a presents the variation of frequency as a function of drift and Fig. 7b as a function of time. We observe anti-correlated values of frequency versus PTA; a progressive decrease of frequency in time with step-like drop during Cook Strait sequence (P2); a reduction of dispersion of frequency values over time. Frequency values in longitudinal direction are more scattered than in transverse. Mean velocity values, standard deviations and coefficients of variation for each period for both components are listed in Table 3.
Same as Fig. 6 for frequency computed by BTF. Data are filtered between 0.5 and 3.5 Hz and 0.5 and 2.9 Hz for transverse and longitudinal components, respectively
In the transverse direction the mean frequency drops from 1.54 ± 0.07 Hz in period P1 to 1.42 ± 0.06 Hz in period P5, what corresponds to 8% decrease of the fundamental frequency, i.e. in the same order of magnitude of 12% for velocity. In the longitudinal direction, the fundamental frequency shifts from 1.42 ± 0.09 Hz in period P1 to 1.23 ± 0.08 Hz in P5, what corresponds to 13% reduction. However, the coefficients of variation are smaller for transverse direction than for longitudinal.
The step-like variations of fundamental frequency are also observed for events with the highest PTA values. This is clearly visible during the Cook Strait sequence (P2), where average frequency in transverse direction decreases to 1.41 ± 0.11 Hz, what indicates 8% reduction, and in longitudinal direction to 1.19 ± 0.14 Hz, what is equivalent to 16% reduction, which corresponds to a fairly significant reduction in relation to structural integrity. In the transverse direction, the minimal fundamental frequency, 1.13 Hz, is observed during the Cook Strait earthquake, corresponding to a 27% co-seismic reduction compared to the average value in period P1. In the longitudinal direction, the minimal fundamental frequency is observed for Lake Grassmere earthquake, i.e. 0.81 Hz corresponding to a 42% co-seismic reduction in comparison to the mean value in period P1. It is certain that the mainshock of Kaikoura earthquake could have caused an even greater decrease of the fundamental frequency. As for velocity, co-seismic variations of resonance frequency associated with slow dynamics process provide relevant information for S2HM, as suggested by Astorga et al. (2018, 2019).
Based on the Timoshenko beam model, the variation over time and according to structural drift of the correction factor χ(C) is shown in Fig. 8 and Table 4.
Same as Fig. 6 for χ(C) coefficient
We observe different structural behaviour in both directions. For the transverse direction, χ(C) is scattered and does not show one clear value, indicating a modification of the structural response according to the loading. Over time, even though the variation of χ(C) between events is significant, the average is decreasing insignificantly, with the total reduction of correction factor around 4%. We did not observe significant drop of mean value in period P2, although this period is characterised by the biggest dispersion of the data. The total average of all χ(C) values is around 0.77 ± 0.08, i.e. with a significant contribution of bending.
For the longitudinal direction, the χ(C) values are oscillating around 1, corresponding to pure shear behaviour, with an average value of 0.94 ± 0.08. During periods P1 to P4, the correction factor drops below 1, but after the Kaikoura earthquake, χ(C) stabilises close to 1 and we do not observe any more dispersion of χ(C) results. In this direction, we do not observe clear correlation between χ(C) and loading and the post-earthquake process characterized by the recovery of the frequency and velocity does not exist for χ(C). When compared to frequency and velocity, this observation enforces the fact that slow dynamics properties observed in civil engineering structure (Astorga et al. 2018, 2019) must reflect more the macroscopic properties of the structural elements, than the permanent damage of the structure. This confirms the relevance of this observation for structural health assessment. This is also confirmed by the lack of any structural damage reported in-situ over the monitoring period. However, Fig. 8a shows clear correlation of the decrease of χ(C) with increased loading, reflecting the co-seismic variability of the beam-like model: the frequency-to-velocity relationship is then not stable with the loading that provides dispersion and misinterpretation of the velocity values in terms of behaviour.
7 Location of the changes
The distribution of sensors installed at nearly every level allow us to identify the floors that have contributed most to the parameter changes (Picozzi et al. 2011; Nakata et al. 2013). In this study, we compared pulse wave velocity between sequence P1 and P5, considering the mean interferograms obtained by stacking all events in both specific periods. The differences of time delay between P1 and P5 are shown in Fig. 9a, converted into absolute difference with respect to the top sensor along the building height in Fig. 9b.
Location of damage along the Te Puni building height. a Stacked deconvolved traces from periods P1 and P5 in transverse and longitudinal direction at each instrumented story in the building derived from acceleration time-history. b Converted time delays of the pulse wave propagation reported along the building height with respect to the top sensor. Horizontal dashed lines correspond to the levels with accelerometers
Deconvolution of signals recorded by sensor 7 shows zero-time delay difference between P1 and P5 in transverse and longitudinal directions, because of its location close to the reference top sensor. Note also that in the transverse direction, the separation of up-going and down-going waves is not possible, because of the faster wave velocity in this direction, with more bending effect.
Figure 9a clearly shows that the overall shape of interferograms remains the same between periods P1 and P5 for both directions. In this study, we focus only on the up-going wave time delay, as a similar observation is being reported for the down-going part. We observe delay appearing in the lower part of the building, starting from sensor 6. In the transverse direction, differences are the largest between sensors 5 and 4 and constant from sensors 4 to 1. In this direction, time delay reported along the building height (Fig. 9b) change slopes significantly between sensors 4 and 5, and to a lesser degree between sensors 5 and 6. Below sensor 4, the slopes of the time delay in period P1 and P5 are similar, that reflects the stability over time of the structural elements between these two periods. In the longitudinal direction, differences start from sensor 5 followed by a relatively constant increase from sensors 5 to 1 confirmed in Fig. 9b. Indeed, between sensors 6 and 4, the slope of the time delay in P5 is largest than in P1 that reflects the location of the biggest changes between P1 and P5. Below sensor 4, slight differences are observed, as a consequence of uniform slight structural changes in the lower part of the building.
8 Discussions
Through the analysis of pulse propagation velocity and fundamental frequency of the Te Puni building seismic array we were able to detect changes in seismic parameters. Because velocity and frequency are directly related to the stiffness of the structure, they are both showing variations over time and with loading. After the 2013 Grassmere earthquake, no clear damage was reported by engineers (personal comment from Aurecon NZ lead engineers). However, the significant variation observed for fundamental frequency (up to 42%) or velocity (up to 37%) during co-seismic shaking of let us suppose a non elastic response of the structure. Permanent monitoring of building provides then an efficient tool for even slight damage detection, as also confirmed by Guéguen and Tiganescu (2018) in previous study.
Our results show also that both parameters, even though they are related to the structural stiffness, do not evolve in the exact same way, with slight differences observed over time or with the loading. Average velocity over time drops by 12% in transverse and by 11% in longitudinal, and average frequency 8% in transverse and 13% in longitudinal direction. This observation indicates different sensitivity of both parameters to the changes in time. Figure 10 presents normalised velocity and frequency values as a function of drift. Both parameters present strong anti-correlation with drift. The semi-log fit of the velocity data is similar for both components, but for frequency, results from longitudinal direction show higher sensitivity to the increase of loading than for transverse. The slope of the decrease of frequency is lower for transverse direction (2.9%) than for longitudinal direction (4.7%). Differences between sensitivity of parameters in both directions might be related to the presence of sliding hinge joints in one direction, which are essentially a semi rigid beam column connection.
Results from correction factor χ(C) calculations are coherent with the design of the building. We observe shear behaviour of the structure in longitudinal direction and influence of bending in transverse. It is worth noting the co-seismic change of the correction factor values as function of the seismic loading. In transverse direction, we notice slight decrease of the average value of χ(C) in time and anti-correlation with PTA values. In contrast, results from longitudinal direction do not show correlation with the loading and the average value is clearly oscillating around 1. A possible explanation for this observation might have been related to the presence of sliding hinge joints, which activate for certain level of shaking. Shaking from the Kaikoura earthquake, which was not recorded by the Te Puni building seismic array, might have triggered the earthquake resistant mechanism moving the structural response into pure shear. However, these were not activated as the joints have a small guide bolt to centre the connections, and these shear off when the load levels reach a certain level. According to Michel and Guéguen (2018), estimation of C parameter, and consequently evaluation of correction factor χ(C), could be influenced by SSI effect (even slight), the effect of bending or non-linear elastic effects. Because Te Puni building is located on rock, the soil-structure interaction (SSI) effects can be expected as negligible in the whole response of the structure. The dispersion of the χ(C) in longitudinal direction in periods P1-P4 might be then caused by non-linear elastic effects, confirming the co-seismic variation of the beam-like building response and then the co-seismic demand.
To illustrate, Fig. 11 presents comparison frequencies extracted from BTF and resonance frequencies calculated from the Timoshenko correction factor χ(C). We observe clear differences between the two directions. In transverse direction (Fig. 11a) TB frequencies for lower χ(C) tend to underestimate the frequencies values comparing to the BTF results. With increase of χ(C) up to ∼0.9 we observe results closer to the reference 1:1 line. For the largest values of χ(C) (close to 1), TB values overestimate the BTF values, illustrating the modification of the structural response. On the contrary, in longitudinal direction (Fig. 11b), there is a good agreement between frequencies evaluated using both methods: the linear fit of the data is almost 1:1 with a small shift. Figure 11b shows that TB frequencies with lower correction factor χ(C) underestimate the BTF frequencies. TB frequencies with χ(C)≈1 (i.e. pure shear behaviour) present the best fit with the BTF frequencies. Because resonance frequency of Timoshenko beam model (TB) is directly related to the wave propagation velocity in the equivalent homogenous medium and the considered beam-like model, differences between small and high values of χ(C) reflect structural response variation in term of velocity. Even though in longitudinal direction we expected a pure-shear behaviour based on the design of the structure, lower χ(C) clearly indicate this is a bending dominated system.
Comparison of frequencies from BTF and Timoshenko beam model (TB) with χ(C), calculated using Eq. 6. Dashed grey line presents reference 1:1 line. Black lines are representation of linear fit of the data defined by the equations in the top left corners of the plots
The clear differences between both components are strongly connected with the design of the structure, but this cannot fully explain all the observed behaviours. Both models, TB and BTF, are based on the assumption of the fixed base conditions, but our results suggest that they are representing different behaviour. This observation was also reported in Chandra and Guéguen (2017). We also noticed there are clear changes of the structural behaviour as a function of loading, even for moderate earthquakes.
Based on the analysis of changes in time delay of the pulse wave propagation in the building, the variation of the velocity over time can be clearly located. As other researchers suggested (e.g. Kohler et al. 2018), detection of the velocity-based variation might indicate the location of the potential damage. In this study, changes of the time delay are located at sensors 4 and 5 and only sensor 5 in transverse and longitudinal direction, respectively, corresponding to a change of the floor design, i.e. irregularity in elevation where the seismic stresses may be the highest. The fourth floor, which contains the cafeteria and services areas, is a large open space in contrast to all other floors which are heavily partitioned into many student rooms, and therefore structurally stiffer.
The same analysis revealed that even though there were no structural damage visually reported by the engineers after any of the events from our dataset (even after the Kaikoura earthquake), in this study, changes in the non-structural elements (e.g. partitioning walls) but also in structural elements of the Te Puni building could explain velocity changes, confirmed by the post-sequence stability of χ(C) values.
9 Conclusions
In this paper, we analysed seismic data from the actual Te Puni building, designed with innovative damage avoidance features, and we studied its response to 208 earthquakes recorded over eight years. We analysed variations of wave propagation velocity and fundamental frequency as proxies of structural health, due to their direct relation with the structural stiffness. Our study revealed, that even though no structural damage was observed in the analysed period of time, the decrease of both parameters is strongly correlated with the increase of seismic loading and we observe permanent decrease in time. Based on comparison of the above two parameters, we found that their sensitivity differs even if they are related to the same feature, which reflects their different sensitivity to seismic loading, boundary conditions (e.g., soil-structure interaction) and the evolution of the overall response of the structure on different time scales (co-seismic or long-term).
Thanks to the adjustment of beam-like model to the structure, we observed changes in the χ(C) values in our dataset. Although correlation with loading is not clear for longitudinal direction, we observed that in the transverse direction, there is a trend of decreased χ(C) with increasing loading, reflecting a non-linear-like behaviour of the equivalent beam-like model. According to Michel and Guéguen (2018), parameter C, and therefore χ(C), depends on the contribution of the bending, non-linear behaviour effects or/and soil-structure interaction effects. Our results showed that for the longitudinal direction, χ(C) is not stable with seismic loading (and then over time). Under the assumption of no SSI, this observation could be explained either by non-linear elasticity effects or changes in the shear-to-bending ratio over time, according to the state of the building.
By comparing frequencies from building transfer function approach and Timoshenko beam model approach, we found quite good agreement for the longitudinal direction (i.e. shear case with χ(C)≃1). For lower values of χ(C) corresponding to lower seismic loading, TB model tends to underestimate frequencies values in comparison to BTF frequencies. For the transverse direction, where more bending effects are observed, the agreement between BTF and TB is poor for χ(C) below ∼0.85 and above ∼0.95. This observation indicates that the direct relationship between frequency and velocity, which is the basis for the interpretation of velocity by the SIbyD method, is not invariable over time and reflects the evolution of the behaviour of the structure as a function of time and seismic loading.
With instrumentation at almost each floor it is possible to localise the area in the building where changes in wave propagation time delay are the most significant. In our case, SIbyD was sensitive enough to detect the change in the design of the Te Puni building and indicate clearly the floor with lower structural stiffness (large open space, less partition walls) concentrating the most the seismic stress. Interferograms provides the detection and location of the changes that could be related to possible non-structural earthquake damage. Combining frequency and velocity, a better interpretation on the amount of the changes is expected, and then the structural health, once the interpretation of the velocity change related to nonlinear mechanisms and structural response variation improved.
Data availability
Analyzed data was provided by GNS Science.
Code availability
The codes used for this study are available from the corresponding author on reasonable request.
References
Architectus (2019). Te Puni Village, Victoria University of Wellington. http://architectus.co.nz/en/projects/te-puni-village-victoria-university-wellington
Astorga AL, Guéguen P, Kashima T (2018) Nonlinear elasticity observed in buildings during a long sequence of earthquakes. Bull Seismol Soc Am 108(3A):1185–1198
Astorga AL, Guéguen P, Rivière J, Kashima T, Johnson PA (2019) Recovery of the resonance frequency of buildings following strong seismic deformation as a proxy for structural health. Struct Health Monit 18(5–6):1966–1981
Boore DM (2005) On pads and filters: processing strong-motion data. Bull Seismol Soc Am 95(2):745–750
Boore DM, Bommer JJ (2005) Processing of strong-motion accelerograms: needs, options and consequences. Soil Dyn Earthq Eng 10:93–115
Boutin C, Hans S, Ibraim E, Roussillon P (2005) In situ experiments and seismic analysis of existing buildings. Part II: seismic integrity threshold. Earthq Eng Struct Dyn 34(12):1531–1546
Chandra J, Guéguen P (2017) Nonlinear response of soil-structure systems using dynamic centrifuge experiments. J Earthq Eng 23(10):1719–1741
Clayton RW, Wiggins RA (1976) Source shape estimation and deconvolution of teleseismic bodywaves. Geophys J Int 47(1):151–177
Clinton JF, Bradford SC, Heaton TH, Favela J (2006) The observed wander of the natural frequencies in a structure. Bull Seismol Soc Am 96(1):237–257
Cowper GR (1966) The shear coefficient in Timoshenko’s beam theory. J Appl Mech 33(2):335–340
Ebrahimian M, Todorovska M (2014) Wave propagation in a Timoshenko beam building model. J Eng Mech 140(5):04014018
Farrar CR, Worden K (2006) An introduction to structural health monitoring. Philos Trans R Soc A Math Phys Eng Sci 365(1851):303–315
FEMA (2020). Multi-hazard loss estimation methodology - Earthquake Model, Hazus®–MH 2.1 technical manual. Department of Homeland Security. Federal Emergency Management Agency. Mitigation Divi-sion.Washington, D.C. (last access: https://www.fema.gov/sites/default/files/2020-09/fema_hazus_earthquake-model_technical-manual_2.1.pdf)
Gledhill SM, Sidwell GK, Bell DK (2008) The damage avoidance design of tall steel frame buildings - Fairlie Terrace Student Accommodation Project, Victoria University of Wellington. 2008 NZSEE Conference, Paper Number 63
Guéguen P, Mercerat DE, Alarcon F (2019) Parametric study on the interpretation of wave velocity obtained by seismic interferometry in beam-like buildings. Bull Seismol Soc Am 109(5):1829–1842
Guéguen P, Tiganescu A (2018) Consideration of the effects of air temperature on structural health monitoring through traffic light-based decision-making tools. Shock Vib 2018:1–12
Guéguen P, Guattari F, Aubert C, Laudat T (2021) Comparing direct observation of torsion with array-derived rotation in civil engineering structures. Sensors 21(1):142
Guéguen P, Astorga A (2021) The torsional response of civil engineering structures during earthquake from an observational point of view. Sensors 21(2):342
Jensen J (1983) On the shear coefficient in Tmoshenko’s beam theory. J Sound Vib 84(4):621–635
Khose VN, Singh Y, Lang DH (2012) A comparative study of design base shear for RC buildings in selected seismic design codes. Earthq Spectra 28(3):1047–1070
Kohler MD, Allam A, Massari A, Lin F-C (2018) Detection of building damage using Helmholtz tomography. Bull Seismol Soc Am 108(5A):2565–2579
Kohler MD, Heaton TH, Bradford SC (2007) Propagating waves in the steel, moment-frame factor building recorded during earthquakes. Bull Seismol Soc Am 97(4):1334–1345
Limongelli M, Dolce M, Spina D, Guéguen P, Langlais M, Wolinieck D, Maufroy E, Karakostas C, Lekidis V, Morfidis K, Salonikios T, Rovithis E, Makra K, Masciotta M, Lourenço P (2019) S2HM in some European countries. Seismic structural health monitoring. Springer, Cham, pp 303–343
Michel C, Guéguen P (2010) Time-Frequency analysis of small frequency variations in civil engineering structures under weak and strong motions using a reassignment method. Struct Health Monit 9(2):159–171
Michel C, Guéguen P (2018) Interpretation of the velocity measured in buildings by seismic interferometry based on Timoshenko beam theory under weak and moderate motion. Soil Dyn Earthq Eng 10:131–142
Mordret A, Sun H, Prieto GA, Toksöz MN, Büyüköztürk O (2017) Continuous monitoring of high-rise buildings using seismic interferometry. Bull Seismol Soc Am 107(6):2759–2773
Nakata N, Snieder R (2014) Monitoring a building using deconvolution interferometry. II: ambient-vibration analysis. Bull Seismol Soc Am 104(1):204–213
Nakata N, Snieder R, Kuroda S, Ito S, Aizawa T, Kunimi T (2013) Monitoring a building using deconvolution interferometry. I: earthquake-data analysis. Bull Seismol Soc Am 103(3):1662–1678
Newton C, Snieder R (2012) Estimating intrinsic attenuation of a building using deconvolution interferometry and time reversal. Bull Seismol Soc Am 102(5):2200–2208
Perrault M, Guéguen P, Aldea A, Demetriu S (2013) Using experimental data to reduce the single-building sigma of fragility curves: case study of the BRD tower in Bucharest, Romania. Earthq Eng Eng Vib 12:643–658
Picozzi M, Parolai S, Mucciarelli M, Milkereit C, Bindi D, Ditommaso R, Vona M, Gallipoli MR, Zschau J (2011) Interferometric analysis of strong ground motion for structural health monitoring: the example of the L’Aquila, Italy, seismic sequence of 2009. Bull Seismol Soc Am 101(2):635–651
Prieto GA, Lawrence JF, Chung AI, Kohler MD (2010) Impulse response of civil structures from ambient noise analysis. Bull Seismol Soc Am 100(5A):2322–2328
Snieder R, Safak E (2006) Extracting the building response using seismic interferometry: theory and application to the Millikan library in Pasadena, California. Bull Seismol Soc Am 96(2):586–598
Todorovska MI, Trifunac MD (2008) Impulse response analysis of the Van Nuys 7-storey hotel during 11 earthquakes and earthquake damage detection. Struct Control Health Monit 15(1):90–116
Uma SR, Cousins WJ, Young J (2010) Seismic instrumentation in Victoria University Wellington student accommodation building. GNS Science Report, 2010/30
Uma SR, King A, Cousins J, Gledhill K (2011) The GeoNet building instrumentation programme. Bull N Z Soc Earthq Eng 44(1):53–63
Wen W, Kalkan E (2017) System identification based on deconvolution and cross correlation: an application to a 20-story instrumented building in Anchorage, Alaska. Bull Seismol Soc Am 107(2):718–740
Acknowledgements
The authors would like to acknowledge John Young from GeoNet for his time and for providing us information and comments, which has been a great help in understanding instrumentation of the Te Puni building. A.M.S. would like to thank The New Zealand France Friendship Fund for the travel support and GNS Science for hosting during stay in New Zealand. P.G. would like to thank LabEx OSUG@2020 (Investissements d’avenir-ANR10LABX56).
Funding
Open access funding provided by Università degli Studi di Trieste within the CRUI-CARE Agreement. This work is part of the URBASIS program (H2020-MSCA-ITN-2018, grant number 813137). This work was supported by the Real-time earthquake rIsk reduction for a reSilient Europe (RISE) project, funded by the EU Horizon 2020 program under Grant Agreement Number 821115.
Author information
Authors and Affiliations
Contributions
Conceptualization, all authors; methodology, P.G. and C.H.; validation, all authors; formal analysis, all authors.; data processing and validation, AMS.; writing—original draft preparation, AMS; writing—review and editing, PG, CH, AMS. All authors have read and agreed to the published version of the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors have no conflicts of interest to declare that are relevant to the content of this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Skłodowska, A.M., Holden, C., Guéguen, P. et al. Structural change detection applying long-term seismic interferometry by deconvolution method to a modern civil engineering structure (New Zealand). Bull Earthquake Eng 19, 3551–3569 (2021). https://doi.org/10.1007/s10518-021-01110-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10518-021-01110-3