Classification and seismic fragility assessment of confined masonry school buildings

Abstract

School buildings being a critical social infrastructure, assessment of their seismic behaviour is of utmost importance in ensuring safe schooling facilities in locations of high seismicity. This study presents two important aspects in analysing any existing building stock for seismic behaviour: the development of an appropriate taxonomy system and an appropriate analytical method to conduct fragility assessment. A detailed desk study of existing schools’ databases and tailored field investigation in Guwahati, Assam, situated in India’s highest seismic zone, reveal that the majority of school buildings can be categorised within the confined masonry (CM) typology. This study discusses first, the addition to the World Bank promoted Global Library of School Infrastructure taxonomy of the specific category relating to CM as to include the buildings under study, which are non-engineered CM buildings with flexible roofs. Identifying the density of confinement and quality of connections as critical parameters for the seismic response of these buildings, varying seismic design levels are defined in relation to these indicators. Secondly, the paper presents an approach for carrying out nonlinear static pushover analysis of these buildings with flexible diaphragms and elaborates on the criteria adopted for determining the performance drift limits in buildings with varying levels of seismic design. Numerical analysis for the capacity assessment of selected index buildings is carried out using a commercial software that enables nonlinear extreme loading analysis. Different failure mechanisms as a function of the level of confinement are identified and the performance range for three damage states for three index buildings is obtained by using the N2 method. The study shows the influence of both choices of performance indicators and intensity measure on the resulting fragility functions. Given the consistency of the educational building stock in Guwahati, the results can be used for investment on retrofit decision making at regional level.

1 Introduction

1.1 Background

Confined masonry (CM) is a structural system formed of unreinforced masonry panels confined by lightly reinforced concrete elements at all intersections and periphery. This typology is found to have superior seismic performance compared to unreinforced masonry (Tomaževiˇc and Weiss 2010; Chourasia et al. 2016), mainly due to improved ductility provided by the confining elements. First reported in use after the 1908 Messina earthquake, Italy, this construction practice has been in existence in Chile and Columbia since 1930′s and in Mexico since 1940′s (Brzev and Perez-Gavilan 2014). It is an alternative to costlier reinforced concrete (RC) frame with brick infills construction, which has performed poorly in past earthquakes if not built properly (Jain et al. 2001; Brzev 2007). Observation after multiple earthquakes in Chile and Peru have highlighted the superior performance of CM structurers compared to other forms of masonry construction, while also signalling limitations and failure mechanisms of this typology under seismic action (Meli et al. 2011; Astroza et al. 2012). Guidelines for the construction of CM buildings are available internationally and in countries where this construction practice is well established and encouraged (NCh2123 1997; NTC-M 2004; Meli et al. 2011).

A significant amount of experimental (San Bartolomé et al. 1992; Alcocer et al. 2004a; Zavala et al. 2004; San Bartolome et al. 2012; Quiroz et al. 2014; Chourasia et al. 2016; Singhal and Rai 2016);, analytical (Tomaževič and Klemenc 1997a; Tomaževič 1999; Marques and Lourenço 2013; Yekrangnia et al. 2017; Erberik et al. 2019) and numerical (Nucera et al. 2012; Torrisi et al. 2012; Lang and Benzoni 2014; Marques and Lourenço 2014) research has been carried out to investigate the behaviour of CM walls and buildings. These studies mostly focus on in-plane (IP) behaviour of CM walls and global behaviour of CM buildings. A number of factors influence the mechanism that governs the overall behaviour of CM buildings. These include level of confinement, component material properties, level of vertical stress on the wall, geometry of the wall, type of floor and slab diaphragms, connection between wall and diaphragm elements etc. For individual walls subjected to horizontal loading, IP shear failure occurs in the form of either diagonal cracking or shear sliding, whereas flexural failure manifests as cracks at the tension end of the wall in bending. The most common failure mechanism observed in CM buildings with rigid diaphragms and global behaviour is the in-plane shear failure of walls, characterised by diagonal X shaped cracks (Meli et al. 2011). Out-of-plane (OOP) mechanisms are also observed in CM walls, predominantly in buildings with flexible diaphragms, where walls may overturn locally with more pronounced effects in upper floors (Meli et al. 2011). OOP failure can be observed as plate failure, by bending in vertical and/or horizontal directions, depending on the relative spacing between horizontal and vertical confinements of the wall’s panels (Matthews et al. 2007). These mechanisms result in failure of CM walls by forming horizontal and vertical cracks, respectively. Literature on detailed OOP behaviour of CM walls is relatively sparse, compared to the study of IP behaviour (Varela-Rivera et al., 2011; Singhal and Rai 2016; Noor-e-khuda, Dhanasekar and Thambiratnam, 2016).

Most of the building-level experimental research were carried out with rigid diaphragms (e.g. Alcocer et al. 2004a; Tomaževiˇc and Weiss 2010; Tomaževič and Klemenc 1997b) or developed in such a way that the predominant failure mode is through IP mechanisms. Effect of flexible diaphragms has been investigated by experimental and numerical approaches mainly for unreinforced and unconfined masonry (URM) buildings (Magenes et al. 2014; Sathiparan 2016; Nakamura et al. 2017), while specific studies on CM typology are rare. These studies on unconfined masonry typologies confirm the prominance of OOP failure mechanisms, which can be avoided by improving strength and stiffness of the diaphragm and its connection to the walls.

Varela-Rivera et al. (2011) conducted one of the few experimental studies focusing on OOP capacity of CM walls with varying confinement conditions by applying uniform out-of-plane pressure. The results show that walls confined on four edges and on three edges exhibit similar behaviour. These experiments show the capability of confining element to provide sufficient stiffness and strength to act as a support, so that analytical models based on yield line theory were able to predict maximum OOP capacity (as uniform lateral pressure) reasonably well. Tests were carried out by Singhal and Rai (2016) on CM wall panels with varying levels of toothing, confinement and openings. The testing procedure comprised successive IP and OOP loading until the collapse of the wall occurs, to capture the bidirectional behaviour of CM. It was concluded that unlike infill walls, OOP capacity of CM walls are not significantly affected due to prior IP damage.

Although evidence is available that well-built CM buildings can survive high magnitude earthquakes with modest damage, severe damage and collapse are reported when design and construction quality are compromised (Brzev 2007). Damage has been reported to non-engineered or partially confined masonry buildings in countries where this typology is prevalent, such as Chile, Mexico, Indonesia, Columbia, El Salvador etc. Experimental studies on non-engineered and low quality confined masonry walls (Narafu et al. 2012) and building models (Quiun 2011) are reported to assess their available seismic capacity and to study techniques that can improve their performance. OOP mechanisms become critical in buildings with insufficient connection at the interface between masonry and tie-columns (by means of toothing or dowel bars), inadequate confinement around wall panels and at intersections by means of horizontal and vertical RC members, large unconfined openings, slender walls and flexible roof diaphragms. Hausler et al. (2014) identified OOP failure by overturning of gable end as common in single storey CM buildings with flexible roofs in Indonesia. Even in well-confined masonry buildings with flexible roofs, OOP failure has been observed by Astroza et al. (2012). While analysing such building stock, close attention shall be given to their OOP capacity and failure mechanisms along with global in-plane capacity.

Undoubtedly, CM is a potential construction practice for cost-effective and seismically reliable masonry buildings in developing countries, especially for critical infrastructure such as schools. In India, a country with regions of high seismicity, CM construction practice is included in the recent update of the National Building Code NBC (NBC 2016) and other technical guidelines (Chourasia 2017). Some older masonry school buildings in parts of India exhibit significant similarities with the engineered confined masonry typology, while also showing critical deviation from national standards. This study examines some school buildings in Guwahati that belong to this category. This could be attributed to the fact that no dedicated section in a national code for CM was available until 2016, and construction was mainly guided by recommendations for improving seismic performance of load bearing masonry structures by providing seismic bands or corner reinforcements or both (IS4326 1993; IS1893 2002; IS13935 2009). Since they do have certain features of CM typology, they respond to seismic loading differently with respect to unreinforced and unconfined masonry structures. The closest reference in India, are the recommendations of existing Indian code for seismic resistant design and construction of buildings (IS4326 1993) and seismic repair and strengthening of maosnry buildings (IS13935 2009), as discussed in detail in Sect. 3.1. However, these structrewures with flexible roofs, instead of vertical reinforcement bars, have vertical RC tie-columns, which, combined with horizontal bands brings them closer to confined masonry seismic response. Hence, this study classifies them as confined masonry typology, regardless of the original intent of their design and proceeds to identify their features and seismic capacity under this consideration, recognising that they exhibit diverse levels of confinement. The objective of the study is to recognize the features of these non-engineered CM buildings that belong to CM typology, and quantify the available seismic capacity due to the presence of the RC confining elements. In the process, the study also addresses the seismic assessment of buildings with flexible diaphragms.

Similar school typologies, with variable level of confinement, deviating from engineering standards, are present in several other countries worldwide, as discussed in Sect. 3.2.1. Such form of construction is considered advantageous due to the seismic improvement on simple load bearing masonry, relatively low skill set requirements and favourable cost compared with other solutions. Due to these circumstances, it is essential to classify and assess the specific seismic fragility of existing non-engineered and partially confined masonry buildings. To achieve this, a review of existing classification systems to determine index buildings; and of analytical seismic fragility assessment through numerical modelling, suitable for application to CM school buildings, are presented in the next two subsections, respectively.

1.2 Classification systems

Classification of precise typology helps in providing a basis for numerical modelling and performing dynamic analysis to assess vulnerability (Lang et al. 2018). Well-developed taxonomy systems identify buildings with similar behaviour under the type of loading considered. Globally applicable (Coburn and Spence 2002; Jaiswal and Wald 2008; Brzev et al. 2013) and regionally relevant (ATC13 1985; Grünthal 1998; FEMA 2015) taxonomy systems are available in literature. Such systems commonly classify buildings based on construction materials, structural load bearing system, design and construction quality, building height and other factors assumed to determine their response to lateral loading. For example, the widely used ATC 13 (1985) and the follow up FEMA P-154 (revised in 2015) cover up to 36 mainly engineered structural types designed to specific standard. The PAGER inventory database (Jaiswal and Wald 2008) was instrumental in extending building classification to structures which were not engineered, hence tackling the weakest buildings in any building stock worldwide. A comprehensive procedure was followed to harmonize different databases and extrapolate for missing inventory information, which is then used for quick estimation of post-event casualty and damage (Jaiswal et al. 2011). The Global Earthquake Model platform (Brzev et al. 2013) classifies buildings based on attributes varying from generic to more specific features that affect their seismic performance. This system identifies primary and secondary parameters and a taxonomy string is assigned to each building considering 13 attributes. The advantage of such system is its ability to classify buildings from surveys with different level of information, from the more generic to the more detailed, while maintaining the relation to different levels. For buildings in the Indian subcontinent, two frameworks are available paying specific attention to features of regional building typologies: the NDMA (2013) providing a typology catalogue for predominant construction types in India, and Lang et al. (2018).

It is often required to have specialised taxonomy systems for different occupancy classes of buildings due to their inherent differences in structural and architectural features that determine their seismic response. The present study focuses on school buildings due to their critical role in creating safe learning spaces and reducing vulnerability of young children in the event of an earthquake. Several past events have highlighted the vulnerability of school buildings to earthquakes, such as Spitak earthquake (1988), Chi-Chi earthquake (1999), Wenchuan earthquake (2008) and Kashmir earthquake (2005) (UN 2009). In India, more than 15,000 school buildings were damaged in 2001 Bhuj earthquake of which 1884 buildings collapsed with over 1000 casualties (Bhakuni 2005; Pathak 2014). Classification of school buildings needs to be addressed through a dedicated taxonomy system, because of their special features that increase their seismic vulnerability (Rodgers 2012). The Global Library of School Infrastructure (GLOSI), is such a system dedicated to school building stock that is developed as part of Global Program for Safer Schools (Adhikari et al. 2018; World Bank 2019; D’Ayala et al. 2020). This system follows the GEM typology classification approach of assigning alphanumeric strings pertaining to a set of attributes that are relevant to school building typologies. Although the GLOSI system addresses load bearing masonry school buildings, a well-developed section for confined masonry typology is yet to be developed. Hence, this paper proposes to adopt GLOSI system as the base to develop a fitting classification system for the buildings in this study and to include more granularity to CM typology in general.

1.3 Analytical Fragility assessment

In the absence of empirical data, the analytical approach to fragility assessment is the preferred choice, also due to its simplicity in defining a direct relationship between the characteristics of index buildings, structural response to seismic action and damage effects (D’Ayala 2013). Analytical fragility functions have been developed specifically for CM buildings in various countries in the last decade (Ahmad et al. 2012; Lovon et al. 2013; Ranjbaran and Hosseini 2014; Ranjbaran and Kiyani 2015; Said et al. 2016; Erberik et al. 2019). These studies differ in their approaches in generating a numerical or analytical CM model, capacity assessment, definition of damage limits and fragility derivation. As can be observed in these studies, detailed fragility assessment often involve statistical treatment of performance points, obtained through nonlinear analysis of CM models using a selected set of ground motions.

Ahmad et al. (2012) used equivalent frame model and nonlinear time history analysis for capacity assessment, to derive fragility curves based on deformation limits and damage scale chosen from Tomaževiˇc and Weiss (2010) and FEMA 2003. Fragility curves were derived against intensity measures (IM) in terms of peak ground acceleration (PGA) and spectral acceleration (Sa(T₁)). The study showed up to 50% reduction in seismic capacity of typical Pakistani CM buildings when low quality materials is used, although they could withstand shaking intensity up to 0.4 g PGA without collapse.

Nonlinear dynamic analysis on CM models generated based on analytically derived backbone curves was carried out by Ranjbaran and Hosseini (2012, 2014), to derive lognormal fragility curves. A range of structural parameters was considered in this study to investigate their influence on the seismic behaviour. Ranjbaran and Kiyani (2015) further developed a simplified approach for fragility and performance assessment of CM structures based on comparison of displacement demand and capacity of an equivalent single degree of freedom (SDOF) system characterised by bilinear force–displacement response. Analytical structural models were used by Lovon et al. (2013) and Erberik et al. (2019), for capacity formulation, following which the former employed the displacement-based earthquake loss assessment DBELA methodology (Silva et al. 2013), while the latter applied the capacity spectrum method (CSM- Freeman 1998). Finite element modelling of CM walls and incremental displacement cyclic load was also applied for capacity and direct fragility assessment by Said et al. (2016) as the cumulative distribution of demand parameters.

The studies reported above use the assumptions of in-plane failure mechanism and presence of rigid diaphragms. Fragility functions for the out-of-plane failure of confined masonry is not reported. While a range of options for capacity and fragility estimation have been reviewed, other reliable fragility assessment methods such as N2 method (Fajfar 2000), FRACAS (Rossetto et al. 2016) etc., have not been applied in the context of CM.

The present study analyses existing non-engineered confined masonry school buildings in Guwahati, Assam, a city in the highest seismic zone in India, for their seismic capacity and fragility. Most of these buildings were built as part of Sarba Siksha Abhiyan, during last 30 years (Pathak 2014). Unlike engineered CM buildings, buildings observed in Guwahati do not have the specific features such as toothing or dowel bars at the RC-masonry interfaces. In some buildings, the correct sequence of construction is followed, i.e. masonry is erected before casting RC elements, which provides certain level of improved connectivity at the junctions between perpendicular walls. These buildings also have varying levels of horizontal and vertical confinement. Such features enhance their seismic performance to various degrees compared to URM buildings, although they may not satisfy all the criteria for engineered CM buildings, such as confinement around openings. These buildings have flexible diaphragms, which can make them vulnerable to lateral action by dominating OOP failure mechanisms. Due to the nature of school buildings, a tailored methodology to analyse non-engineered or partially confined masonry buildings is presented in Sect. 2, applicable across the world. Section 3 explains the modes of data collection of school buildings from the case study location, and their classification within a global taxonomy system, specific for schools. The paper proposes to use numerical analysis of index buildings using the applied element method, which is suitable for extreme analysis of masonry structures, as discussed in Sect. 4. Definition of performance limit states is an important challenge in analysing these buildings, due to their non-typical failure patterns. These are arrived through further review of literature and numerical analysis. Performance points are derived through N2 method using a set of scaled ground motions. Finally, fragility curves as lognormal cumulative functions for three performance levels are derived by piece-wise regression of performance points, with PGA and Sa(T₁) as intensity measures, as discussed in Sect. 5.

2 Methodology

The approach of this paper towards the development of a classification system and methodology for fragility assessment is achieved in three stages (Fig. 1). The first step is to develop a robust classification system, so that suitable representative or index buildings (IBs) can be identified in the sample of building stock studied. The process of developing a taxonomy for seismic assessment of CM typology, is based on the GLOSI system (World Bank 2019) considering the critical parameters as they emerge from guidelines for the design of confined masonry structure. As shown in Sect. 1, current taxonomies only assign one generic class to CM, without further distinction. Therefore, the review of critical parameters from construction practices worldwide, together with the detailed survey of a sample of buildings from the case studies will be used to identify the parameters and their attributes defining alphanumeric strings as a signature for each building in the sample and grouping the buildings with similar signature to identify index buildings.

Fig. 1

Flowchart illustrating methodology of the paper

The second step entails to assess the seismic capacity of the index building. A suitable procedure should be identified that allows obtaining robust assessment with the level of data that can be obtained for these levels of assessment, while ensuring that the non-linear response of the composite masonry-concrete is accurately reproduced. To this end, an applied element method (AEM) based software, Extreme Loading for Structures (ELS) (ASI 2018), is used in this study. AEM is a numerical modelling technique that can predict to a high degree of accuracy, the discrete behaviour of the interface mortar to brick and brickwork to concrete confining element (Mayorca and Meguro 2003; Pandey and Meguro 2004). Selected index buildings are analysed using a particular non-linear static pushover approach, whereby the load is applied as monotonically increasing ground acceleration. The numerical analysis enables study of failure mechanisms of buildings with flexible roofs and partial confinement. As a result, capacity curves are generated using suitable engineering demand parameters that capture the behaviour.

Finally, fragility curves from idealised capacity curves are generated for three performance levels considered. Drift limits corresponding to the performance levels of each index building are identified from the evolution of damage as observed from the numerical models. The OOP failure drifts and global IP failure drifts obtained with the models are calibrated by comparison with values available in literature. The set of ground motions provided by FEMA P695 is used with scaling to generate performance points using the N2 method (Fajfar 2000), and to derive fragility curves based on least square regression (D’Ayala et al. 2015). It is shown that the fragility assessment for this type of buildings is particularly sensitive to both the determination of the representative capacity curve and to the choice of IM.

3 From data collection to taxonomy and index buildings

The school building stock under study is in Guwahati, India, situated in seismic hazard zone V, according to Indian Standard 1893 (IS1893 2002). The region has witnessed several earthquakes in the past, including two great quakes (M_w > 8) in 1897 and 1950 (Jain 1998; Murty 2005) and over 20 large earthquakes (8 > M_w > 7) (Bora et al. 2014). Zone V suggests a MSK intensity of IX and above, and expected PGA of 0.18 g and 0.36 g for the design basis earthquake (475 year return period) and the Maximum Considered Earthquake (2475 year return period) respectively (Menon et al. 2010). Some in-depth studies suggest seismicity to the region even higher than the level assumed by IS 1893 (Nath and Thingbaijam 2012). In the present study, data collection of school building stock in Guwahati is carried out in two stages: a desk study of existing school inventory database (Pathak 2014) and a field survey. The analysis of the data identifies confined masonry structures as prevalent in the school building stock. Their characteristics, compared with standardised confined masonry, highlights the need for a systematic classification, currently missing in literature, and the consistent choice of index buildings, that can be used for analytical fragility and vulnerability studies.

3.1 Data collection

A survey database of school buildings in Guwahati city (Pathak 2014) was published in 2014 after a survey conducted by Assam State Disaster Management Authority (ASDMA) and Assam Engineering College (AEC). The objective was to assess multi-hazard (earthquake, flood, fire and wind) vulnerability of school infrastructure and to identify retrofitting strategies to reduce their vulnerability. Guwahati city accounts for more than 500 government schools’ compounds mainly in masonry buildings, some of which aged 100 years and over (Fig. 2). There are also about 200 private schools, mostly built as 3–4 storey RC frame buildings. The former were found poorer in structural aspects and maintenance status, rendering them as the more vulnerable category. It is a fact that majority of the low and middle- income population depends on free education provided by government schools. Hence, this study focuses only on government school buildings, which collectively accounted for 793 building blocks. The survey in 2014 classified about 60% of the building blocks as confined masonry, while acknowledging that detailed inspection and understanding of the construction process are required to qualify these classroom buildings as fully confined masonry buildings. The database desk study reviewed information on location, site conditions, main structural system, number of stories and non-structural vulnerable components, provided by photographs and condition reports. The CM buildings identified were single-storey with a wall thickness of up to 125 mm. Detailed structural information such as locations and size of confining elements of the CM buildings was not provided by the database, and therefore a field survey was organised to understand the construction process to qualify them as fully confined masonry buildings.

Fig. 2

Location of case study and some sample school buildings in Guwahati

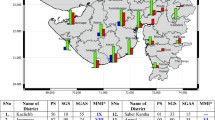
A representative sample of 50 school compounds from the population of 521 Government schools is selected for a field survey, (see Fig. 2), resulting in 151 building blocks being visually inspected. A comparison of the distribution of different structural systems in the population and the field survey sample (Table 1) shows good representation of the population.

Table 1 Distribution of major structural systems in the population and survey sample of school buildings

The CM buildings as reported in the 2014 database and surveyed for this study have RC tie-columns at corners and at regular intervals along long walls. RC tie bands are observed at plinth and lintel levels; however, they lack confinement around openings and RC band at roof level in most cases. A comparison is made with their features with typical recommendations for CM buildings, to reveal the extent of compliance of these buildings to this typology, based on visually observable information. Table 2 compares the details of a typical building surveyed with the provisions in the EERI Guideline 2011 (Meli et al. 2011) and the National Building Code of India (NBC 2016) (henceforth abbreviated as EERI-11 and NBC-16 respectively). As mentioned in the introduction, these buildings were not intentionally built to satisfy these conditions, as no Indian standard recommendation for CM construction was available at the time of their construction. Even then, it can be seen that most of the boxes are checked for the dimensional requirements suggested by both guidelines. However, some critical features are not compliant:

• 1. Confinement around openings The typical building has large openings, with confinement only on one side in the form of a lintel band. This does not ensure a confined masonry action of the wall according to both EERI-11 and NBC-16, and results in insufficient wall density in the longitudinal direction of the buildings.

• 2. Tie-band at roof level As the building under consideration has a flexible roof diaphragm, tie-band at roof level is necessary according to both the EERI-11 and NBC-16. The tie-band, and horizontal bracing, as suggested by NBC, are required to ensure load redistribution between out-of-plane and in-plane walls.

• 3. Spacing of cross walls The building has unconstrained longitudinal walls in the absence of cross walls at required spacing. Even with the presence of intermediate tie-columns, this feature can increase vulnerability to out-of-plane deformations and failure in buildings with flexible diaphragms.

Table 2 Comparison of index building with EERI (Meli et al. 2011) and NBC (NBC 2016) guidelines for CM

A comparison of the features of this typical building is also made with existing seismic code of the time, i.e. IS4326-1993, to understand the level of compliance of these typologies. Provisions of IS4326-1993 for masonry buildings include RC horizontal bands and vertical reinforcement bars at designated locations. In buildings with walls thinner than 200 mm, IS4326-1993also recommends to provide tie-columns at intervals of not more than 1500 mm, instead of vertical reinforcement bars. It was observed that the buildings under study partially conformed to this code, while deviating in aspects such as spacing of vertical tie-columns, provision of vertical reinforcement and strengthening/confinement around openings. Horizontal band at roof level is another feature recommended by IS 4326–1993, which is largely missing, but observed in some of the buildings, as discussed further in Sect. 3.2.3 in relation to seismic design level. In the words of SK Jain (Jain 2004): ‘India on the one hand has design and construction firms that can compete internationally; on the other hand the country has no system to control poor quality design and construction of ordinary buildings’. This remains an area of challenge in the construction industry in the country, even though school buildings are considered as structures worth of special attention. A strong motivation of this study is the awareness that buildings partially code-compliant tend to be more vulnerable, and such vulnerability might go undetected as they are associated to code-compliant buildings, which are expected to be safe for the seismic hazard in the region.

Hence, it can be concluded that the surveyed school buildings in Guwahati generally classified under the category of CM, exhibit a varied level of confinement and might have different levels of performance under lateral loading compared to building designed as per code requirements. This paper acknowledges them as a variant of CM typology. Therefore, the development of a taxonomy apt to classify them appropriately within this typology, and the assessment of their available seismic performance, become critical in risk assessment and development of strengthening strategies. In the present study, non-linear seismic analyses are conducted with the specific objective of determining the difference in performance depending on the presence of these elements and of accurately capturing their influence through realistic modelling.

3.2 Taxonomy for confined masonry

The intent of this section is to identify specific parameters and indicators of confined masonry school buildings that characterise their seismic performance, while considering the possibilities of deviation from standards as mentioned in the previous section, in order to develop a taxonomy string for individual buildings. The framework developed for the GLOSI system (D’Ayala et al. 2020) is adopted to determine the specific parameters and their attributes useful to fully define the variability observed in CM. The GLOSI system follows a three-tier approach, whereby three primary parameters characterize a generic building typology and nine secondary parameters define specific index buildings, within the typology. While the primary parameters are directly observable features from databases, photographs etc., secondary parameters have to be collected through field surveys. Intrinsic parameters in tier 3 are associated with mechanical characterisation and details of local construction practice, which are to be obtained for complete assessment of a building stock. Confined masonry (CM) is one of the six main structural types identified in the GLOSI Taxonomy system, others being adobe (A), unconfined/unreinforced masonry or ordinary masonry (UCM-URM or OM), reinforced masonry (RM), light steel frame with load bearing masonry walls (SFM) and RC frame (RC).

The scope of the taxonomy discussed herein is limited to masonry panels composed of rectangular blocks in mortar, confined by RC confining elements. The term “rectangular blocks” is used here as a commonly used terminology in masonry construction, to include both bricks and blocks that are rectangular in plan and elevation. It is noted that other forms of traditional construction practices may be included in the broad definition of CM, such as masonry confined by wooden elements for example (Rai et al. 2014), which are not considered under this taxonomy. The basic distinction of CM from other load bearing masonry (LBM) typologies being the confinement of masonry panels in RC elements on all four sides, it is a minimum requirement for classifying a building into CM typology. Masonry buildings with walls not satisfying this minimum confinement (explained further in Sect. 3.2.3) shall be treated as unconfined/ unreinforced masonry (URM/UCM) as per GLOSI system.

As a technology initially developed on site, and not through detailed theoretical and experimental investigations, most guidelines for construction of CM follow prescriptive or empirical approaches. A broad review of CM construction practice in various countries and their construction guidelines was carried out to understand common and varying aspects of this typology. National construction codes are available for CM in countries such as Mexico (NTC-M 2004), Peru (E.070 2006), Chile (NCh2123 1997), Colombia (NSR102010) etc. Most of the international guidelines such as seismic design guide for low rise CM buildings by Earthquake Engineering Research Institute-EERI (Meli et al. 2011) and several national codes address construction of residential buildings in CM typology. Nonetheless, confined masonry is being increasingly used for construction of school buildings in high seismic regions such as Ecuador, Indonesia, Iran, Pakistan and India, with significant variance. Therefore, a clear taxonomy and comprehensive vulnerability assessment of such typologies is necessary to ensure their safety and upgrade, where necessary. The present document sets out the specific parameters and their attributes for the classification of CM school buildings globally, in line with the GLOSI system. It then applies the taxonomy to the case study of school buildings in Guwahati, India (Pathak 2014).

Section 3.2.1 describes the main structural systems within the CM broader class of buildings observed in various parts of the world. The taxonomy parameters for the typology CM1, as per the GLOSI system are described in Sect. 3.2.2, with special attention to seismic design level, wall panel length and wall opening size which are defined differently from general LBM typology in GLOSI.

3.2.1 Main structural systems

The primary structural typology of CM in GLOSI taxonomy is subdivided into four categories based on a review of CM construction in various countries, such as Chile, Mexico, El Salvador, Cambodia, Indonesia, Iran, Pakistan, India etc. The classification is based on the primary materials of the masonry fabric and the presence of elements of reinforced masonry in combination with the confinement. Attribute’s notations of these categories are listed in Table 3, followed by a more detailed description, of each type.

Table 3 CM structural systems in the modified taxonomy system

3.2.1.1 CM1

These are unreinforced masonry panels made of rectangular blocks (kiln clay solid bricks, hollow clay units, multi-perforated clay bricks, concrete solid & hollow blocks, autoclaved cellular concrete blocks etc.) in cement or lime mortar, with RC confining elements around the panels. Reinforcement in the walls are concentrated only in the confining elements. This is the most common CM typology found around the world—Chile, Mexico, El Salvador, Cambodia, Indonesia, Iran, Pakistan, India etc. (Brzev 2007; Yekrangnia et al. 2020; Ahmad et al. 2012; Jain et al. 2014). Some examples are shown in Fig. 3.

Fig. 3

CM1 type confined masonry buildings from around the world

3.2.1.2 CM2

These CM buildings are also called combined and confined masonry construction, where alternating courses of concrete block and clay bricks panels are confined with RC elements. It is a common practice in central Mexico. Three courses of clay bricks alternate with a course of concrete blocks in the most common arrangement of this construction. This construction gained popularity during reconstruction after Tecoman earthquake in 2003, because of cost savings and reduced time in construction, while also resulting in aesthetic appearance due to the contrast in colours (Tena-Colunga et al. 2010). It is used for residential as well as industrial construction such as warehouses (Fig. 4a.)

Fig. 4

CM2, CM3 and CM4 type confined masonry construction

3.2.1.3 CM3

Shear strength of masonry walls, including those of CM is sometimes improved by horizontal bed reinforcement. National codes such as the Mexico code NTC-M 2002 provides calculations of the contribution of this reinforcement to wall shear strength (Alcocer et al. 2003). CM3 refers to such rectangular block masonry panels with bed reinforcement of steel wires or wire meshes embedded in mortar joints and anchored at the wall edges or in the intermediate tie-columns (Fig. 4b). Similar bed reinforcement is also provided to improve out-of-plane capacity of CM buildings with flexible roof, in Indonesia (Hausler et al. 2014).

3.2.1.4 CM4

This is a hybrid masonry construction with confined masonry in one direction of the building and reinforced masonry or reinforced concrete walls in the other direction. It is used throughout Chile (Moroni et al. 2003) for housing up to 4 storeys (Fig. 4c). However, this type of CM buildings has exhibited structural damage and poor performance in past earthquakes. Although this is a hybrid typology, it is considered within this taxonomy for CM, as it partially exhibits properties of CM.

The focus of the present study is on the main structural system CM1, and the specific attributes that characterise the 12 remaining parameters of the taxonomy string. Many of the attributes are still relevant and applicable to the other main structural systems; however, value ranges for the attributes might differ.

3.2.2 Parameters for CM1 GLOSI taxonomy classification

The attributes of the parameters of the GLOSI taxonomy classification are chosen in agreement EERI-11 and NBC-16, while their attributes are determined with reference to site observations related specifically to schools. Other national codes are also referred wherever necessary. The variability of CM construction is taken into consideration while defining the parameters and the ranges of attributes, so that the taxonomy is able to classify them appropriately. By scoring the attributes of these parameters, each school building can be assigned a string, which encodes its seismic vulnerability. Three of the twelve parameters, namely seismic design level, wall opening size and wall panel length, are specifically characteristic and particularly critical for the response of CM buildings, hence the criteria for selecting their range are discussed in detail. The remaining nine parameters as defined for LBM in the GLOSI system can be attributed to CM typologies without change. These are included in the description of attributes in Table 4.

Table 4 Definition of attributes of parameters for CM in line with GLOSI taxonomy

3.2.3 Seismic design level

Seismic design level of CM buildings can be identified by three main features: (1) the density and distribution of vertical and horizontal confining elements, (2) the quality of connections between structural elements (3) the wall density in two orthogonal directions. A criterion based on these features is introduced in GLOSI to classify the seismic design level of CM buildings into four levels namely, Poor Design, Low Design, Medium Design and High Design. The three parameters and criteria for each design level are chosen such that deficiencies of non-engineered or partially confined masonry practices are accommodated in the taxonomy, in addition to code-compliant CM construction around the world. The attributes of these features influence the design level of CM buildings, as explained below.

Feature 1—minimum required confinement (MRC) A ‘minimum required confinement’ is defined as the presence of plinth band, lintel/roof band, corner tie-columns and intermediate tie-columns at spacing not exceeding the limits for vertical confining elements provided by EERI-11 and relevant national guideline. Details of the spacing of vertical elements is explained in Sect. 3.2.4. This criterion checks whether the building under consideration can be essentially included within the CM typology, by ensuring confinement around all four sides of main structural masonry panels. In many of the non-engineered CM construction, this criteria comes as a decisive factor in identifying the typology, and the design level. Absence of MRC suggests that the building is not confined masonry, and presence of additional confinement over and above MRC suggests that the building has a better design level, conditioned also on the other two criteria.

Feature 2—good connections Good connection between masonry panels and the tie-columns is considered a basic feature of confined masonry (Meli et al. 2011). It is recommended to provide toothing (leaving staggered ends) at the ends of masonry panels before casting RC tie-columns to achieve good connection. If provision of toothing is not possible for any reason, dowel bars can be used at this intersection to provide similar levels of connection. In the absence of both toothing and dowel bars, at least the sequence of construction should be such that the RC elements are cast after erecting the masonry panels, because this ensures a friction interface and some level of interlocking of concrete and brickwork/blockwork. This kind of connection between masonry panel and confining elements, achieved through correct sequence of construction, is recommended for seismic-resistant masonry construction, even when toothing is not specified (for example, national guidelines of Argentina and Algeria—Meli et al. 2011). Similarly, the toothing is not common in some other countries such as Indonesia where CM construction is practiced with correct sequence. After experiencing damages in the 2004 earthquake sequences, dowel bars have been introduced in newly built CM buildings in Indonesia (Hausler et al. 2014). For the sake of this taxonomy, adherence to correct sequence of construction (Fig. 5a) is considered to provide good connection between masonry and tie-columns, even if toothing is not intentionally provided.

Fig. 5

Connection at tie-column-masonry interfaces: a Correct sequence of construction in El-Salvador (Yoshimura et al. 2004), b Rough interfaces indicating good connection- India, c Smooth interface indicating poor connection- India, d Failure at tie-column connection in Iran (Yekrangnia and Mahdizadeh 2009)

Toothing alone cannot save the CM walls from failing, as it is meaningless without good quality of construction and good connection between horizontal and vertical tie elements, as was frequently observed in Iranian CM buildings, which failed in past earthquakes (Fig. 5d). Hence, the quality of connection between structural elements, i.e. between masonry and tie-columns, between horizontal and vertical confining elements and between the roof and walls, becomes a factor that decides the level of seismic design of CM. A good connection between the elements depends on the quality of materials and workmanship in addition to good detailing. This feature is often difficult to observe in existing buildings with plaster finish. However, some distinction can be noticed during visual survey on unplastered walls as shown in Fig. 5b, c, and inference on good connections can be made from general quality of materials and construction.

Feature 3—wall density (WD) Wall density is the ratio of area of walls in any one direction to the plan area of the building. EERI-11 recommends wall density ranging from 1 to 5% and from 1.5 to 9.5% for single and double storeys, respectively, depending on construction materials, soil type and seismic hazard zone. The complete range of recommended values from EERI-11 are copied in Table 5:

$${\text{Wall}}\,{\text{density}},\,WD = \frac{{A_{w} }}{{A_{p} }}$$

(1)

where $A_{w}$ is the area of cross section of all walls in one direction of the building, and $A_{p}$ is the floor plan area of the building.

Table 5 Recommended values of minimum wall density, (

Wall panels with large unconfined openings shall be excluded from the wall density calculation, while if the openings are confined, the panels on either side of the opening can be included. Note that an opening with area larger than 10% of the wall panel is considered as large opening, as further explained in Sect. 3.2.5. This condition for calculating wall density is explained in Fig. 6, as adapted from EERI-11. The criteria based on area of opening also suggests that horizontal and vertical dimensions of the openings should be no more than 1/3rd of the corresponding dimensions of the wall panel. Wall panels with small openings can be included in the calculation, but with due reduction in panel length to account for the opening size, depending on the position of the opening on the panel. Having sufficient wall density in both directions ensures the design is adequate, however, this alone will not be a sufficient criterion, as this does not ensure confinement of all wall panels in both directions, and hence the definition of typology will also depend on the density of confinement. In school buildings, it is required to have larger than usual spacing between cross walls, and large openings for ventilation purposes. In such cases, adequate wall density may still be achieved by increasing the thickness of walls and providing full confinement around large openings.

Fig. 6

Taken from EERI-11)

Masonry wall with a large opening: a an unconfined panel, as the opening is not framed by concrete elements—to be disregarded in wall density calculations, b Confined—the two confined wall panels on each side of the opening can be considered in the wall density calculations, A_op: Area of opening and t: thickness of wall, (

Based on the status of these three features, the first three seismic design levels of CM building can be determined as shown in the decision diagram in Fig. 7. The MRC being the decisive criteria for classifying a building as CM, absence of MRC leads to the building being classified as URM/UCM. The presence or absence of good connections and adequacy or inadequacy of wall density in both principal directions of the building decide the design levels among PD, LD and MD. The forth design level, i.e. High Design (HD) relies on the building having all the three features over and above the minimum prescribed levels. For example, the building should have proper toothing/dowel bars and good connection between all structural elements, more confinement than MRC and wall density greater than the minimum recommended values as per Table 5. Additional confinement could be in the form of horizontal bands around sill level, lintel band in addition to a roof band and full confinement around openings. In the case of buildings with flexible roof, a rigid roof band and horizontal bracing at roof level are required for the building to be considered to have HD.

Fig. 7

Criteria for deciding seismic design level of CM

It is indeed difficult to obtain features of reinforcement of RC confining elements when conducting visual survey, except in the rare case where structural drawings are available for the study or unless NDT equipment is available. In this context, it is by default assumed that these elements have minimum required longitudinal and transverse reinforcement as per EERI-11 or the relevant regional standard. Therefore, the reinforcement density is not included as a criterion for the classification system. This is also in line with the approach of the GLOSI taxonomy used for RC frame structures, whereby the typology is determined based on the layout and relative stiffness of the RC elements. However, for CM typologies, it is recommended to check the adequacy of reinforcement detailing of the confining elements as per the relevant guidelines before assigning high seismic design (HD) level. This is particularly important as the capacity of RC elements become critical in deciding the building capacity if other factors are in expected standard, as in the case of HD. In short, a fully confined masonry building complying with all requirements can be labelled as HD.

3.2.4 Wall panel length

In CM buildings, the wall panel length is determined by the spacing of tie-columns. It is important to limit the panel length to avoid out-of-plane failure mechanisms. Based on the minimum criterion as per NBC-16, the span of half-brick thick walls (100–110 mm thick) between confining columns lesser than 3 m is considered as Short Panel (SP) and more than 3 m is considered as long panel (LP). In full-brick thick walls (200–220 mm thick), the critical panel length for the classification is 4 m. In this case, the NBC-16 criterion is chosen over EERI-11 criterion, as it is more conservative. Different national codes vary in their recommendation of maximum spacing of tie-columns that define the panel length: the Peruvian code recommends 5 m spacing while the Chilean code permits up to 6 m. Other codes and guidelines in countries such as Mexico, Columbia and Indonesia restrict spacing to 4 m. Hence, the criterion chosen for panel length is in line with several national codes for full-brick thick walls. A greater density of vertical confinement will not directly affect architectural and use requirements. It is recognised that it will increase the cost of construction, although only marginally, while it will considerably reduce damage and ensure immediate occupancy, as it controls lateral drift and cracking.

In addition to the spacing of tie-columns, spacing of cross walls is also an important criterion that influences the out-of-plane failure mechanism, especially in buildings with flexible diaphragms when the confining elements are very slender. In such cases, the confinement alone may be inadequate to provide sufficient stiffness against out-of-plane bending of the wall. EERI-11 suggests the same spacing for cross walls as that of tie-columns, however, this might be impractical in the case of school buildings (4.5 m in high seismic areas and 6 m in moderately seismic areas). Hence, for the taxonomy, wall panel length is conditioned on the spacing of tie-columns, as prescribed above, rather than on the spacing of cross walls. Adequacy of cross walls in a building is however implicitly considered through the definition of wall density that decides the level of seismic design, as explained previously in Sect. 3.2.3.

3.2.5 Wall opening size

Within confined wall panels, the width of vertical masonry piers plays an important role in the lateral load resisting system and it is reduced by the presence of openings. Yáñez et al. (2004) have shown that openings with up to 10% area of the wall do not affect the lateral capacity significantly. This is reflected in the EERI-11, which neglects the contribution to the wall density of panels with unconfined opening larger than 10%. Various national codes give different thresholds of opening sizes beyond which confinement is necessary on both sides of the opening, in order to overcome the capacity reduction due to that opening. For example, Colombian code suggests that an area of opening (Aop) up to 35% of wall area (L*h) is acceptable without confinement, while the Chile code recommends confinement on both sides of openings larger than 5% of wall area. Peru code suggests the length of opening to be within half the length of the wall panel and recommends confinement around (presumably all of) them. Mexican code recommends confinement if the horizontal or vertical dimension of the opening exceeds a quarter of the length of the wall, or 600 mm. This would be less than 10% of area of wall for a typical 4mx3m wall. In recent CM construction in Indonesia, confinement is recommended around openings larger than 2.5 m² (BuildChange 2006) which is about 20% of the wall area for a 4mx3m wall. However, large openings on the front wall is a prominent feature in older buildings in Indonesia. UNESCO guidelines for school buildings in Iran (Ghaidan 2002) also suggests confinement around openings larger than 2.5 m². Even when such recommendations exist in most countries, this feature is largely absent in non-engineered CM buildings, leading to heavy seismic damage (Brzev et al. 2010), a few cases are illustrated in Fig. 8.

Fig. 8

Confining openings in CM walls

For the purpose of this taxonomy, an unconfined combined area of openings less than 10% of the wall panel can be considered as small opening (SO), and can be left unconfined without any reduction in masonry capacity. Along with the criteria based on area, horizontal and vertical dimensions of the openings shall be limited to no more than 1/3^rd of the corresponding dimensions of the wall panel. Nonetheless, in school buildings it is often required to have openings larger than 10% of the wall area for lighting and ventilation purposes. Hence, to recognise the positive effect of confinement around openings, large openings are classified into two subclasses: large opening with confinement (LOC) and large opening with no confinement (LON), as illustrated in Fig. 6. For the case of school buildings in CM typology, LOC is often the preferred option as SO is not practical.

3.3 Definition of index buildings

In the seismic fragility assessment of a building stock, it is important to define representative buildings for each typology in the population. An index building represents all the buildings in the population having chosen specific attributes for the parameters of interest, which influence their seismic performance. This assumption allows to infer seismic performance of the whole population by detailed numerical modelling and analysis of only the chosen index buildings. As a result, there is enormous savings of time and resources.

The taxonomy developed for CM school buildings in the previous section is applied to all the buildings surveyed in Guwahati and index buildings are identified by grouping similar strings together, as listed in Table 6. It can be inferred that all of them are single storey buildings made of rectangular blocks in cement mortar and have flexible roof. They have horizontal RC confinement at least at plinth and lintel levels and vertical RC confining elements are placed within a spacing of 4 m. They have inadequate wall density, long wall panels, large wall openings and flexible foundation. They are structures with no visible retrofitting to improve capacity and they all have some form of vulnerable non-structural components such as falling objects, false ceiling etc. Structural health condition and status of pounding risk are ignored at this stage for identifying index buildings, as their influence can be reflected by modifying analysis settings and varying material strength values for the same buildings. The varying structural parameters that distinguish the index buildings are the seismic design level and the plan irregularity. Seismic design levels vary from poor to medium levels. Six index buildings are thus identified as shown in Table 6 and Fig. 9, with their frequency in the survey sample, and extrapolated approximate frequency in the population of school compounds in Guwahati. Horizontal irregularity is the only distinguishing parameter between the pair IB1 and IB4. The same applies for the pairs IB2 and IB5 and IB3 and IB6.

Table 6 CM Index buildings identified in the school building stock in Guwahati

Fig. 9

Representative buildings in the sample for each of the index buildings: IB1, IB2 and IB3 have simple rectangular plans, while IB4, IB5 and IB6 have irregular plan shape. Other parameters of the IB4-IB6 correspond to IB1-IB3, respectively

Sample plan shapes of the regular and irregular single unit blocks are shown in Fig. 10. These are sometimes composed in blocks of multiple units. This study identifies the single unit block as the index building for the detailed non-linear analysis conducted in Sect. 4. The first three index buildings with no plan irregularity are numerically analysed for illustrating the influence of seismic design level on seismic capacity assessment and fragility assessment.

Fig. 10

Sample plan of the index buildings a with regular plan, b with irregular plan (Dimensions in meter)

4 Seismic capacity assessment using AEM-based numerical analysis

According to the workflow devised in the methodology section, assessment of the seismic capacity of the CM school buildings is accomplished by using nonlinear numerical modelling aimed at obtaining capacity curves and the definition of performance levels reflecting the damaging process and the specific failure modes observed. The specific choices made in this study, in relation to each of these steps are discussed in the following in the context of diverse strategies available in literature and their limitations.

4.1 Numerical modelling and capacity assessment

Modelling approaches for confined masonry buildings need to be able to simulate the interaction not only between brick/blocks and mortar but also between them and the concrete confining elements. Micro-models using discrete elements developed for CM modelling were found to successfully capture initial stiffness, peak strength, stiffness degradation and energy dissipation (Lang and Benzoni 2014). Multiscale models consider the individual properties of units and mortar, which are then homogenized to obtain a macro model whereas macro models are built on the constitutive laws for the masonry material, without distinguishing the blocks and mortar (Addessi et al. 2014). Noor-e-khuda et al. (2016) used explicit FE modelling to simulate out-of-plane behaviour of CM walls using layered shell elements, which could satisfactorily capture maximum lateral capacity and displacement characteristics.

The most commonly used macro-element model for URM is the equivalent frame model (EFM) (Petrovčič and Kilar 2013; Quagliarini et al. 2017). This approach was extended to model CM buildings by Nucera et al. (2012), using 2 dimensional macro-elements for masonry panels and non-linear frame elements with lumped plasticity for RC members such as columns and beams, and non-linear interface elements for panel-frame interfaces. This technique is able to show failure mechanisms such as diagonal shear cracking, compression and tension failure of masonry panel. EFM was employed for CM modelling by Ahmad et al. (2012) by idealising masonry walls as one dimensional beam-column elements and considering only the diagonal shear mechanism of failure. Strut and Tie Model (STM) was attempted for CM wall modelling with openings by (Ghaisas et al. 2017), although with significant limitations such as capability for only linear-elastic analysis and allowing moment transfer at beam-column joints, which is not the case in CM. Quiroz et al. (2014), also investigated the applicability of this method to modelling of CM buildings.

Most of the analysis on CM buildings reviewed above assume a shear dominated-global failure mode because of rigid diaphragms. Modelling and analysis of masonry buildings with flexible diaphragms is very limited for confined masonry. A study of influence of diaphragm flexibility modelling on masonry analysis (Kollerathu and Menon 2017) revealed that (1) models based on EFM consistently gives non-conservative results as they do not account for the OOP response, (2) FE modelling is able to capture the influence of OOP action in reducing global capacity, while being computationally expensive. The study warns against macro-modelling approaches, especially when the OOP effects are not accounted for, and suggests the use of dis-continuum modelling such as discrete element method to reduce computational effort in global analysis of masonry buildings.

The applied element method (AEM) (Guragain et al. 2003; Mayorca and Meguro 2003; Pandey and Meguro 2004; Christy et al. 2018, Adhikari and D'Aayla 2020) combines the beneficial aspects of finite and discrete element modelling approaches, allowing simulation of structural behaviour from early elastic stages until final collapse. In this approach, a masonry structure is discretised to elements representing the bricks and these are connected through a set of normal and shear springs, distributed along the element edges (Fig. 11). These springs capture the stresses and deformations due to loading of the volume of material of the elements that they connect. This approach does not require predefining failure modes as the cracking can occur on load progression by failure of any spring governed either by stress-based or strain-based criteria. When the applied stresses exceed the material capacity, cracks known as ‘open cracks’ are formed. Depending on the type of loading, open cracks either continue developing (under monotonous loading) or close (under cyclic loading/load reversal). The ultimate deformation capacity in tension is defined by a so-called “separation strain”. When the open cracks are large enough so that the resultant strain in the springs between two adjacent elements exceed the separation strain, the elements are disconnected and the springs become inactive. After this instance, the springs do not become active again, even under load reversal, which means a ‘permanent or separation crack’ is formed. If the separated elements do come in contact afterwards, they behave like two rigid bodies in contact.

Fig. 11

Discretisation and connectivity of elements in AEM model

In this study, the real configuration of the confined masonry walls, is generated in ELS, an AEM based software for numerical modelling and analysis of structures. It is assumed that cracks develop through the mortar joints, and not the brick elements. Under combined normal and shear stresses, the masonry material follows a Mohr–Coulomb envelop with tension cut off. After cracking in the mortar, the model incorporates residual shear strength unless the cracked surface is subjected to normal tensile stress, in which case, residual shear strength available due to roughness of the crack surface is neglected. Validation of the ELS models of CM walls with respect to experimental studies and analytical formulations for stiffness and strength by Tomaževič and Klemenc (1997a) was presented in Vatteri and D’Ayala (2019). Further modelling details are discussed in the following section.

4.1.1 Model details

The index buildings IB1, IB2 and IB3, are modelled on ELS as shown in Fig. 12. Although there is variability in length of classroom blocks, all geometric features are considered the same for the three index buildings, as the focus of numerical analysis is to study the influence of seismic design levels on the seismic behaviour. These parameters are referred to as Tier 3 parameters in the GLOSI approach. The buildings have a wall thickness of 110 mm and an average total height of 3.5 m. As majority of the blocks with regular plans for which the data was available had an average length and width in the ranges of 7–10 m and of 4.6–6 m respectively, a plan dimension of 8 m × 5 m is chosen for the index buildings. Similarly, distribution and sizes of openings are considered the same for all the index buildings to avoid the change in behaviour due to change in the geometry of openings. The confining column’s dimensions, 150 mm × 150 mm, and confining bands’ dimensions, 150 mm × 100 mm, are also based on typical dimensions observed on site. The difference between the three index buildings lies in the seismic design level, which, as seen in Sect. 3 and Table 4, is a function of the presence of minimum required confinement, quality of connection and wall density. IB1 has poor design level, meaning buildings represented by IB1 do not have good connection/toothing but have MRC, i.e. tie bands at plinth and lintel levels and tie-columns spaced to less than 3 m and at wall intersections. IB2 has low design level, owing to the fact that buildings in this category have toothing and MRC, but inadequate wall density. Considering index buildings with and without toothing while being similar in all other aspects takes care of the ambiguity in deciding the presence of toothing or dowel bars through visual survey as mentioned before. Finally, IB3 represents buildings of medium design level, owing to presence of toothing and confinement greater than, MRC, i.e. additional tie bands at sill level and at roof level. Buildings satisfying all design requirements of CM, such as confinement around large openings and horizontal bracing at the roof level where flexible diaphragm sits, were not observed during the survey. Hence, no index building shows high design level in this study.

Fig. 12

ELS model for a Index Building 1 b Index Building 2 (toothing at the tie-column-masonry interfaces represented by yellow lines) and c Index Building 3

The effect of toothing or correct sequence of construction is accounted in the model by the choice of material parameters assigned to the springs representing the interface between the RC tie-columns and the masonry wall panels. When there is no toothing (or the masonry panel is built after erecting the tie-columns), the connection between tie-column and masonry panel is achieved by filling the gap with mortar. Whereas when there is toothing (or the tie-columns are cast after the masonry panel is built), the gaps are filled with concrete, this having higher tensile and bond strength than the mortar. Hence, in the numerical model, the interface is modelled with the properties of the mortar for the former case, and with the properties of the concrete in the latter case. Although the light roof truss system is altogether neglected in the numerical models (considered as flexible diaphragm), its weight is directly applied to the walls, to determine the state of stress–strain associated with gravity loads. It is noted that the limited stiffness provided by the roof truss and purlins system could have a modest influence on coupling of parallel walls, but insufficient information could be obtained as to the detailed connection between trusses, purlins and masonry. The door and window frames are also neglected, as their confining action cannot be easily assessed. Uncertainty in the material properties, workmanship and current material conditions, although recognised as relevant in determining the scatter in building response, are not reported in this study.

The properties of the materials used in the numerical model (Table 7) are gathered from Choudhury and Pathak (2014) and Kaushik et al. (2007) as suitably applicable to the building stock in Guwahati.

Table 7 Material properties used for modelling of CM buildings

Determination of failure modes.

Non-linear static pushover analysis whereby a monotonically increasing lateral load is applied to the structure until a target displacement is reached, is found suitable for analysis of CM structures with rigid diaphragms (Marques and Lourenço 2013). As it is assumed that the roof systems of the index buildings provide no diaphragm action in resisting lateral loads, this creates some modelling and analysis challenges, when estimating the global lateral capacity of the structures. Indeed, absence of a rigid diaphragm removes the possibility of using a default control node for pushover analysis, and does not guarantee integrated action between the in-plane (IP) and out-of-plane (OOP) walls. In such structures with flexible diaphragms, the total base shear versus average displacement of four corners at roof level is the strategy often used to produce capacity diagrams (Betti et al. 2014), as they lack global box-like behaviour and the lack of interaction between IP and OOP loaded walls is very significant in their collapse behaviour.

In order to overcome the difficulty of not having a suitable control node to perform pushover analysis on CM index buildings with flexible roofs, this paper proposes a slightly different approach. Instead of applying force or displacement on the structure, ground acceleration is applied in a monotonically increasing manner (see also Ferreira and D´Ayala 2012; Adhikari and D’Ayala 2020). This approach is similar to a non-linear time history analysis, with loading monotonically increasing with time, providing a distribution of forces along the height of the building homogenous to its mass distribution and causing the same type of response as a pushover analysis.

The specific failure mechanisms significantly influence the seismic capacity of masonry buildings (D'Ayala 2005, Magenes and Morandi, 2008). A global mechanism or storey mechanism develops when there is effective connection between wall-wall and walls-roof intersections. In such cases, building resists the lateral load mainly by the in-plane resistance of the walls (Magenes 2006; Ahmad and Ali 2017), by effectively controlling the out-of-plane deflections. In the absence of adequate connection between orthogonal walls and of RC beams/ring beams connecting walls to floors, masonry buildings are found to exhibit collapse of portion or complete walls due to out-of-plane overturning (D'Ayala and Speranza 2003; Magenes 2006; D’Ayala and Paganoni 2011). The overturning may develop by a combination of horizontal and vertical out-of-plane flexure depending on the slenderness ratios and edge constraints (Matthews et al. 2007). If connections with orthogonal walls are strong, the out-of-plane failure might involve a portion of in-plane walls (D’Ayala and Speranza 2003), nonetheless OOP collapse might be triggered without significant damage to in-plane walls (Restrepo-Velez and Magenes, 2009; Ahmad and Ali, 2017).

The buildings in this study, with different confinement densities and flexible diaphragms, exhibit two distinct failure mechanisms, as shown in Fig. 13. The numerical analysis of IB1 with poor connection shows that irrespective of the direction of loading, cantilevering dominated OOP failure of the portion of walls above the lintel determines the ultimate capacity of the system, even though the IP walls stand practically undamaged (Fig. 13 a and b). This happens for low level of seismic input, without mobilising the capacity of the IP CM walls, as it is evident from separation of the OOP walls from the corner tie-columns and the lack of distributed cracking within the masonry fabric.

Fig. 13

Exaggerated deflections (10 times) at failure when loaded in X and Y directions- black marks showing open (minor) cracks and red marks showing separated (major) cracks

In IB2 with good connection and the same level of confinement as IB1, although the cantilevering OOP failure still governs the collapse of wall portions above lintel, the flexural horizontal OOP resisting mechanism develops, thanks to the better connectivity with the confining elements and failure occurs for higher levels of loading. In the numerical modelling, the collapse stage shows the formation of significant separation cracks, in both sets of walls, as indicated by red marks in Fig. 13 c and d, and the formation of shear cracks in the in-plane walls.

In the case of IB3, the confinement, which includes an RC band at the top of the wall, is adequate in providing full participation of the two sets of walls in either direction of loading. The crack pattern obtained shows that damage is well distributed on both IP and OOP walls, allowing improved ductility for the whole system, while preventing local failure. The global behaviour is more evident for loading in the X direction (IB3X) (Fig. 13e), and the collapse is governed by IP diagonal shear mechanism. For loading in the Y direction (Fig. 13f), although the near global engagement of the walls is avoiding local failure, a horizontal OOP failure can be observed due to high length to thickness (L/t) ratio of long unconstrained walls.

Figure 13 also illustrates significant differences in behaviour in the two orthogonal directions for IB3, with loading in Y (transverse) direction displaying a more flexible and weaker behaviour, compared to the response for loading in X (longitudinal) direction. This difference can be attributed to the different level of confinement of the gable walls, well confined and solid, compared to the longitudinal walls, with openings and longer free length of inflection. As IB3 has better confinement, the capacity of the building depends on the effectiveness of transfer of horizontal action from the OOP walls to the IP walls. This is better achieved in the X direction than in the Y direction of loading, owing to the lower stiffness of the long walls causing larger deformation and nonlinearity at lower levels of loads. Therefore, although the IP gable walls take the load transfer indicating global behaviour, the deflection at mid-span of the long walls governs the ultimate failure, which occurs at a lower average drift compared to that in X direction of loading. This response also identifies the limitations of the confining action of column ties in the OOP response, when they are not associated with either stiff diaphragm or the presence of transversal internal bearing walls, which can act as bracing.

The participation of IP and OOP walls in resisting lateral loads can be observed in terms of their deflections increased with increasing loading increments as shown in Fig. 14, when loaded until failure in the X direction. The time step corresponding to the failure mode development depicted in Fig. 13 are marked with red lines. In IB1, a clear separation has occurred at the failure threshold identified, although the remaining OOP walls have further displacement capacity before collapse. Similarly, in the case of Y direction loading, the failure of portion of long walls above lintel is localised to the two end panels, hence not mobilising all of the OOP wall capacity. In the case of IB2 and IB3, failure thresholds identified match with the point of collapse of OOP wall.

Fig. 14

IP, OOP and average displacements at top of walls with loading steps

Figure 14 also shows the top displacement of the walls computed as the average of maximum displacements of individual walls in the direction of loading. The average displacement is significantly lower than the maximum displacement of the OOP walls, which solely govern the failure criteria in IB1 and IB2, and to a lesser but not negligible extent in IB3. It can be concluded that either a single node displacement or the average top displacement, as suggested by other authors, is not the correct representation of the meaningful engineering demand parameter (EDP) for these buildings. This observation illustrates the importance of the choice and location of one or more EDPs and hence one or more capacity curves for a robust representation of the seismic fragility of structures with flexible diaphragms, and the development of partial collapse mechanisms. The implications of these observations for the determination of capacity curves and performance thresholds for these building types are presented in the next two sections.

Determination of capacity curves.

The choice of appropriate EDP being a critical step in deriving fragility curves, based on the discussion in the previous section, two measures are used. The objective is to determine which one best capture the effect of OOP local failure mechanisms accounting for the overall capacity of the buildings with flexible diaphragms, in terms of both strength and ductility capacity. In all cases, the analysis is terminated when the system reaches the failure stage as defined above and shown in Fig. 13. Since both approaches consider the total base shear capacity, the element under scrutiny is the displacement capacity.

The first approach is the conventional method of considering the average top displacement or drift and total resisted base shear to generate capacity curves (named CCavg in the following). This corresponds to roof level displacement in buildings with rigid diaphragms showing global behaviour (Tomaževiˇc and Weiss 2010; Chourasia et al. 2016). It is also applied in the case of buildings with flexible diaphragms (eg: Betti et al. 2014; Magenes et al. 2014), and it is admissible when the connections between orthogonal walls are strong. Figures 13, 14 highlight that the average displacement at roof level might be misleading when assessing actual displacement capacity of these buildings, especially those with governing OOP failure mechanisms. In order to capture the actual displacement capacity of OOP walls, while accounting for the overall strength capacity of the three index buildings in a comparable manner, a second approach to the generation of capacity curves (CCmax) is considered. In this approach, the EDP is taken as the maximum top drift among all walls, resulting in taking the drift of the OOP walls as representative of the global behaviour.

Capacity curves obtained for the three index buildings through CCavg approach, in the two orthogonal directions are presented in Fig. 15a, while Fig. 15b shows the same obtained through CCmax approach. The top drift is calculated with respect to average total height of the building. The base shear is represented as a ratio of weight of the building, giving a Base Shear Coefficient (BSC). The ultimate strength capacity values for the three index buildings prove the critical role of connections between masonry and confining elements and their density as shown in.

Fig. 15

Comparison of capacity curves for the three index buildings a CCavg approach b CCmax approach

Table 8. The capacity curves presented in Fig. 15a illustrate increasing strength and displacement capacities of the index buildings with increasing levels of seismic design, as expected. With an increase in ultimate strength for IB3 of at least 80% and 200%, and in global ductility of at least 50% and 230%, compared to IB2 and IB1, respectively, outlining the critical role of the nature of connection at masonry-tie-column interface or toothing, when confinement is insufficient, and of standard levels of confinement. Flexible behaviour of long walls compared to the gable walls in IB3 as previously discussed, is reflected in the capacity curves of IB3Y and IB3X. The decreasing portion of capacity curve beyond the ultimate capacity is not captured in this analysis, mainly because a force-based pushover is conducted to derive the capacity curves. It is worth noting that the capacity curves for IB1 and IB2 are terminated before arriving at a plateau, because in-plane walls in these buildings continue to resist lateral load beyond the level of loading identified as failure, based on local mechanism. Hence, there is an increasing trend to the total base shear resisted by the building. However, any additional capacity available through the in-plane walls is neglected as per the definition of failure.

Table 8 Lateral strength and displacement capacity by CCavg and CCmax approaches

With reference to the curves obtained with the CCmax approach, it is shown that the IB2 in X loading direction has significantly higher displacement capacity compared to the Y direction, highlighting the critical relevance of this second set of capacity curves. Such displacement capacity is now comparable to IB3. As shown in.

Table 8, the CCmax approach better captures the full capacity associated to mechanisms where global failure is determined by a single set of walls, such as in IB1X, IB1Y and IB2X, whereby the ultimate maximum displacement is 2–2.5 times larger than the average ultimate displacement. As a result of this interpretation of the results, it can be seen that, for IB1, the critical wall’s ultimate displacement is close to the half-wall-thickness criterion, indicating their behaviour as URM walls without edge constraints due to the absence of toothing. Even in cases where there is better integrated action, such as IB2Y, IB3X and IB3Y, the local ultimate displacement is about 1.5 times that of the average computed with the first method. This highlights that ductility per-se’ is not the issue in these buildings without diaphragm actions, as much as the differences in stiffness between the two sets of walls. As heavier, stiffer roof might not necessarily be the answer to the problem, alternative forms of bracing and stiffening, might be a more effective remedy.

4.2 Definition of performance levels, drift limits and idealised capacity curve

Three structural performance levels are considered in this study, commonly adopted in the context of seismic evaluation of structures (ASCE41-17 2017), namely Immediate Occupancy (IO), Life Safety (LS) and Collapse Prevention (CP). In the Indian context, the National Code for seismic evaluation and retrofit of masonry structures (IS13935 2009) defines damageability degrees, which can be correlated to expected seismic performance when combined with seismic hazard zone and building type. IO, LS and CP performance levels can be broadly linked to damageability grades designated as moderate damage, substantial to heavy damage and very heavy damage respectively. Most of the literature on experimental studies on masonry walls and buildings (such as Tomaževič and Klemenc 1997a, b) identify on the capacity curve three physical behaviour thresholds, namely, the point of first significant cracking ${(\Delta }_{1})$, maximum attained strength capacity ${(\Delta }_{2})$ and near collapse ${(\Delta }_{3})$. The crack limit- i.e. onset of masonry cracking—can be correlated to serviceability of the structure (Alcocer et al. 2004b; Tomaževiˇc and Weiss 2010), which in turn can be identified as the immediate occupancy level in terms of performance. The other two limits are correlated to life safety and collapse prevention, respectively, in this study.

The two issues that arise in defining the values of drift corresponding to each of the performance levels, are: (1) the actual values corresponding to out-of-plane and in-plane behaviour most appropriate for confined masonry response; and (2) which of the capacity curves derivation approach, discussed in the previous section should be used to represent the structural behaviour of the three index buildings. In answer to the first issue, performance limits reported in the literature are reviewed before setting out drift limits for the index buildings based on the extent of damage observed in the analysis, corresponding to the damage definitions of the performance levels. In answer to the second issue, since IB1 and IB2 have predominantly local failure, the drift limits are identified considering the capacity curves derived with the CCmax approach, while the corresponding drift limits for IB3 will be considered using the CCavg approach.

Table 9 summarises the threshold values of displacements or drift as obtained from literature for the performance of walls subjected to OOP failure. Some of the data has been manipulated in order to derive equivalent drift limits at the three performance threshold defined above. It should be noted that only Varela-Rivera et al., (2011) provided data directly obtained from testing of CM walls in out-of-plane flexure. Other authors, (eg Ferreira et al. 2015, Simsir et al. 2004) have highlighted the substantial drift capacity associated with rocking of LBM walls, in the order of 3.4%, well above the limits usually found in standards, while Griffith et al. (2003) measured ultimate displacements corresponding to 5% drift for walls without overburden. In agreement with these observations Doherty et al. (2002) suggest the ultimate displacement at collapse should be taken as 2/3^rd of the wall thickness.

Table 9 OOP Displacement (Drift) Limits for load bearing masonry walls

Therefore, considering that the OOP walls in IB1 and IB2 behave largely as partially constrained cantilevers, whose level of horizontal maximum deflection depends on the effect of the horizontal confinement provided by the RC tie-columns, which act as stiff supports as part of the in-plane walls, the value in Table 9 can be used as a base reference for the index buildings under this study.

Conversely, there has been considerable research on CM building models with rigid diaphragms, which exhibit global in-plane failure mechanisms. Drift limits reported by some of the experimental studies (Alcocer et al. a, 2004b; Tomaževiˇc and Weiss 2010; Chourasia et al. 2016 etc.), corresponding to the three performance levels are reported in Table 10. Chourasia et al. (2016), experimentally determined drift value of 1.8% corresponding to a ductility of 5.75 based on the idealisation of the bilinear capacity curve obtained. Alcocer et al. (2004b, a) recommended conservative drift limits for confined masonry based on experiments, considering the need for repairing masonry structure after moderate-to-severe event. Zavala et al. (2004) proposed experimentally determined performance thresholds for CM designed and built as per Peruvian standards, including torsional effects.

Comparison of Tables 9 and 10 shows clearly the disparity in drift values for the same performance thresholds, between the two sets of structural response and therefore the need to keep these into account when evaluating the fragility of confined masonry structures with flexible diaphragms.

Table 10 In-plane global drift limits reported in Literature for Confined Masonry

The threshold points separating the three performance levels are identified on the capacity curves in Fig. 16, considering the corresponding damage description given in literature and standards. IO is identified at the formation of flexural cracks on the OOP walls in the ELS model, as these are the first to form in all cases and provide a significant change in initial stiffness. The LS threshold point corresponds to the formation of major open crack in ELS and wall panels disconnecting from the confining elements or developing significant cracking, while sustaining the applied acceleration. Finally, the incipient collapse point is identified by a significant distribution of major cracks developing into a mechanism, either local or global. Although the analysis might be progressing beyond this point, the curve is truncated at this point. Table 11 gives the values of performance drift limits identified at IO, LS and CP levels with respect to both capacity curves derivation approaches and direct comparison with the ranges identified in Tables 9 and 10. Only in the case of IB3X under CCavg approach (indicating global behaviour) the values of drift limits fall within the range of all performance levels considered for global behaviour of confined masonry buildings. Drift limits of IB3Y show an intermediate state between both the mechanisms. In the case of IB2, the drift limits fall well within the ranges corresponding to OOP mechanism, in both directions. Similarly, drift limits of IB1 appear closer to the range for OOP behaviour computed by CCmax. It is noticed that the rotation of overturning wall occurs about the lintel band in IB1, whereas it is about the plinth band (at the base of the wall) in the other two IBs. If the drift values are calculated based on the height of wall above lintel, the performance drift levels for IB1 becomes well within the limits of local mechanism at all performance levels, as provided in brackets in the table below. However, the drift calculation is based on the overall height of the building for the rest of the calculations, in order to maintain consistency in the analysis and comparison between the three IBs. Considering the predominant individual mechanisms observed in each building, i.e. local OOP failure in IB1 and IB2 represented by CCmax approach and near-global failure in IB3 represented by CCavg approach, corresponding values are italicized.

Fig. 16

Capacity curves and bilinear idealization for a IB1, b IB2 and c IB3 in X and Y directions along with performance limits identified-a and b using CCmax approach and c using CCavg approach

Table 11 Performance drift levels identified for the three IBs as percentage of total height

A third issue that arise in deriving performance points and fragility functions is the idealisation of the capacity curves. As seen from Fig. 15 the capacity curves obtained do not have a clear point that can be identified as yielding threshold separating the strength capacity from the displacement capacity, hence a bilinear conventional elastic-perfectly plastic curve is not the correct solution. A better idealisation is provided by considering a bilinear curve with a post elastic hardening slope (FEMA_356 2000). The capacity curves obtained with the two approaches discussed in Sect. 4.1 are idealised to an acceptable level of accuracy, giving an error ε ≤  1% when comparing the areas under the curves. Figure 16 presents the capacity curves obtained through CCmax approach for IB1 and IB2, and CCavg approach for IB3 for each of the index buildings in both X and Y directions, along with the identified performance thresholds and their bilinear idealization.

The period of the buildings and initial stiffness are obtained from the idealised capacity curves. Referring to the two approaches CCavg and CCmax, these values are as presented in Table 12. Similar to Table 11, the period and stiffness values corresponding to the predominant individual mechanisms are italicized. Considering that the fundamental period of well-confined 1 storey masonry buildings falls in the range of 0.16 to 0.18 (Nema and Basu 2019), only IB3X shows a comparable fundamental period, whereas the other two buildings’ periods range between 0.25 and 0.31, according to the CCmax representation.

Table 12 Time period and stiffness from idealised capacity curves

5 Seismic fragility assessment

The fragility assessment represents the last step in the methodology to determine the seismic response of these school buildings. Among various methods of deriving fragility functions, the N2 method (Fajfar 2000) incorporated in EC8 is adapted here by using idealised capacity curves from a non-linear static pushover analysis against natural response spectra in the acceleration-displacement response spectral space (ADRS) to identify performance points as coordinates of IM and EDP. Single storey index buildings in this study are assumed to be single degree of freedom systems while applying the N2 method.

In order to derive fragility curves without being specific to site seismicity, the response spectra of the far-field ground motion record suite provided by FEMA P 695 (FEMA_P6952009) are used in this study, thereby including record-to-record variability. This suite of ground motions are scaled (Ahmad et al. 2012; Ranjbaran and Hosseini 2012) with PGA values ranging from 0.02 to 2 g for IB1 and 0.02 g to 4 g for IB2 and IB3, so that sufficient data points are obtained for fitting lognormal fragility curves corresponding to all the performance levels considered. A discussion on the limitations of using ground motion scaling, well documented in literature and acknowledged, is beyond the scope of this study (Jalayer et al. 2017).

In this study, two IMs are considered to obtain fragility functions, the Peak Ground Acceleration (PGA) and the Spectral acceleration at the fundamental period of the structure (Sa(T₁)). PGA based analysis gives a measure of fragility independent of the structural properties, and is particularly relevant to define the response of masonry walls subjected to OOP failure because, as discussed in Sect. 4, rocking is predominant on elastic deformation (Giordano et al. 2020). Previous fragility studies of CM buildings are almost entirely based on PGA (Erberik, 2008; Ranjbaran and Hosseini, 2014; Ranjbaran and Kiyani, 2015; Erberik, Citiloglu and Erkoseoglu, 2019). On the other hand, fragility analysis based on Sa(T₁) focuses on the response caused by the maximum amplification in the elastic range of the structure and its corresponding fragility. Sa(T₁) is recommended for structures whose response is dominated by the first mode (Adhikari and D’Ayala 2020) and fragility function for CM buildings with Sa (at specified period) as IM are reported by Ahmad et al. (2012) and Lovon et al. (2013).

Point clouds are generated for the three index buildings and for both IMs under CCavg and CCmax approaches to generate fragility curves following the least square error method (D’Ayala et al. 2015) that assumes a lognormal relationship between EDP and IM as given in Eq. 1:

$$ P\left( {PL > PL_{i} / IM} \right) = {\Phi }\left( {\frac{\ln IM - \ln \alpha }{\beta }} \right) $$

(1)

where $P{L}_{i}$ are the performance levels in terms of the EDPs considered, $\Phi$ is the standard normal cumulative function, $\alpha$ and $\beta$ are the median and standard deviation of the lognormal cumulative distribution representing the fragility function. The least square error method involves estimation of these parameters of lognormal distribution through range-wise linear regression with respect to the performance levels defined. The sample of performance points obtained for IB1, following the CCavg and CCmax approaches in transverse direction are shown in Fig. 17 for both IMs considered, along with the performance drift limits identified for this case (refer to Table 11 for IB1Y).

Fig. 17

Performance points obtained for IB1Y following CCavg approach with a IM as PGA and b IM as Sa(T₁) and CCmax approach c IM as PGA and d IM as Sa(T₁)

Fragility curves generated for the three IBs in two directions of loading using the CCavg approach are presented in Fig. 18. The capacity of the buildings consistently improve in the longitudinal direction (solid lines) with increasing seismic design features. In the transverse direction (dashed lines) an exception is represented by IB3-Y having higher fragility than IB2-Y. This occurs because while the same drift limits apply to IB2-Y and IB3-Y at IO level as given in Table 11, IB3-Y shows lower initial stiffness than IB2Y as noted in Table 12, this being a result of the idealisation approach adopted to minimise differences in total energy, between actual and idealised capacity curves. Therefore, the apparently contradictory results for the IO limit, which depends on the initial stiffness, despite the presence of improved confinement in IB3. However, this is not the case at LS and CP performance levels, and the curves reflect better performance of IB3 compared to IB2, although not as significantly as in the X direction.

Fig. 18

Comparison between fragility curves of three IBs at IO, LS and CP performance levels based on CCavg approach

Fragility curves of the three IBs as per CCmax approach are compared in the same manner in Fig. 19. The observation in the previous case is true in this case as well. While other cases exhibit consistent improvement in performance with increasing design level, IB3Y shows weaker performance than IB2Y at IO level. In this case, both the parameters mentioned before – defined IO drift limit and initial stiffness – of IB3Y are lower than those of IB2Y. These results show the sensitivity of fragility curves on the idealisation approach, especially at the IO performance level.

Fig. 19

Comparison between fragility curves of three IBs at IO, LS and CP performance levels based on CCmax approach

Fragility curves obtained through both approaches compare similarly in the two coordinate directions of loading for individual buildings. It can be noted that IB1X and IB1Y curves are very similar at all performance levels, while IB2 and IB3 are clearly more vulnerable in the transverse direction. This is due to the fact that IB1 showed local OOP mechanisms at relatively low seismic hazard intensity, irrespective of the loading direction. IB2 and IB3 have improved connections or/and confinement that enhances their seismic response in the X direction better than in the Y direction. The unconstrained long walls remain the decisive feature that dictates the performance of these CM buildings with low and medium design levels. This result indicates that better confinement alone cannot guarantee superior performance. Cross walls or a stiffer diaphragm would be necessary to improve the overall capacity and global behaviour of IB3, notwithstanding the presence of a band at roof level. As the cross walls would compromise the intended use of the space, appropriate stiffening of the roof structure becomes critical.

The probability of exceedance of each performance level for the CCavg and CCmax approaches at the PGA level of maximum considered earthquake (MCE), i.e. 0.36 g is presented in Table 13. The fragility curves derived for each IB with either approach are directly compared in Fig. 20, with a vertical black line marking PGA at MCE. The CCavg approach suggests that at this hazard intensity there is about 99% chance for IB1 to exceed IO level, whereas IB2 and IB3 have 74% and 90% chance of exceeding this level, in either one direction, respectively. CCmax approach gives corresponding values as 94%, 60% and 75%, indicating the the CCavg approach yields slightly conservative results for fragility at IO level. This is true for other performance levels in the case of IB1 and IB2 in both loading directions and for IB3Y. Significant improvement is observed for the collapse prevention level in IB2X with CCmax approach compared to CCavg approach, reflecting the increase in ductility observed with respect to the capacity curves presented in Fig. 15a, b. IB3X shows very similar results for fragility with both approaches, due to the near-global behaviour. The results illustrate the influence of the two EDPs chosen in determining the fragility curves for buildings with flexible diaphragms and predominantly local failure mechanisms.

Table 13 Probability of exceedance of performance levels at PGA corresponding to maximum considered earthquake at the case study location

Fig. 20

Comparison of fragility curves derived by CCavg and CCmax approaches-with PGA as IM

Following the same procedure, fragility curves generated using Sa(T₁) as the IM are presented in Fig. 21. Vertical lines mark the demand spectral acceleration at fundamental period corresponding to the MCE, for the three IBs. All IBs have periods within the range corresponding to constant spectral acceleration of 0.9 g in zone V as per the design acceleration spectrum of IS 1893, irrespective of the choice of soil type. Probabilities of exceedance of performance levels corresponding to this spectral acceleration are shown in Table 14. Comparison with corresponding values of Table 13 suggests that the fragility curves with Sa(T₁) as the IM predict slightly higher probabilities of exceeding individual performance levels in most cases. Similar to the case with PGA as IM, CCavg approach consistently produces conservative results compared to CCmax approach. The curves for the two different approaches at LS and CP levels show some overlap in IB3X, as CCmax yields higher dispersion (β), although ultimately providing lower fragility at higher hazard intensity. Overall, it can be concluded that for both choices of IM, CCmax approach results in lower fragility, as it considers larger displacement capacity at the same base shear. Median and dispersion (β) of the fragility curves derived with PGA and Sa(T₁) as IMs are presented in Tables 15 and 16. It can be seen that for both IMs, results of dispersion are comparable at all performance levels under both approaches, not indicating a consistent superior performance by either IM.

Fig. 21

Comparison of fragility curves derived by CCavg and CCmax approaches- with Sa(T₁) as IM

Table 14 Probability of exceedance of performance levels at Sa(T₁) corresponding to maximum considered earthquake at the case study location

Table 15 Mean and standard deviation of fragility curves with PGA as IM

Table 16 Mean and standard deviation of fragility curves with Sa(T₁) as IM

Conclusion

The paper addresses three fundamental steps for determining seismic vulnerability assessment of large building stocks, aimed at decision making to reduce risk: classification, capacity assessment and fragility assessment. The objects of the study are non-engineered confined masonry school buildings, with specific reference to the educational building stock in Guwahati city, Assam, India. The study recognizes them as a variant of confined masonry typology and proceeds to assess their available seismic capacity due to the presence of RC confining elements. A taxonomy system for classification of the CM building stock is derived, using the GLOSI approach, with focus on four parameters, namely main structural system, design level, opening size and panel size. The level of confinement density, a critical factor determining the seismic performance of these buildings, is incorporated into the taxonomy through the definition of seismic design levels, by reference to international Guidelines. This parameter allows to effectively record the deviation from recommendations of CM Guidelines found in the buildings under study, and to correctly account for their influence on seismic response.

Three index buildings thus identified by applying the taxonomy to the sample in the case study are seismically assessed using an AEM based platform. The complexity of modelling CM buildings with flexible diaphragms and performing a non-linear static pushover analysis using a monotonically increasing ground acceleration are discussed. Two approaches, CCavg and CCmax, are introduced to derive capacity and fragility curves to account for the variability in the failure mechanisms of the three IBs observed, one based on average top drift and the other based on maximum (OOP) top drift. Comparison between the two approaches in two perpendicular directions of loading are carried out for all the buildings, which revealed the improvement in box-like behaviour, ultimate capacity and displacement capacity with increasing levels of seismic design, i.e. confinement density and quality of connections or toothing.

The results broadly confirm the observation of failure mechanisms of the three IBs, i.e. IB1 and IB2 exhibiting local OOP failure in both X and Y directions while IB3 exhibiting a near global behaviour, more evident in X direction. IB1 with no toothing and minimum required confinement is very close to a URM building, with highly localised response. Better confined buildings, IB2 and IB3 are found to be weaker in the Y direction of loading, due to the high flexibility of long walls, whereby the lintel and roof band alone, with no cross walls and rigid diaphragms, are not sufficient, to generate an effective box action. This is explicitly included in the taxonomy string as an indicator of vulnerability. Although IB3 in X direction shows significant improvement in capacities and global behaviour, improvement in the overall performance is limited due to the out-of-plane deflections of the longitudinal walls, as confirmed by the fragility curves under both CCavg and CCmax approaches. This is a critical issue as school buildings need large classrooms and hence longer wall panels unrestrained by cross walls. Nonetheless, good connections and level of confinement, i.e. the seismic design level, has a definitive influence on the seismic fragility of the buildings. At the PGA level of maximum considered earthquake (MCE), IB2 and IB3 have negligible possibility of collapse, while IB1 has 35% probability of exceeding the collapse prevention threshold as per CCmax approach. All the IBs have considerably high probability of exceeding immediate occupancy threshold in the weaker direction of loading, indicating the need for strengthening to ensure schools remain functional in the event of MCE magnitude. The analysis thus illustrates the available capacity of these buildings with partially confined masonry panels with varying levels of deficiencies as compared to CM Standards, and hence validate their classification as per the proposed taxonomy.

The analysis highlights the uncertainty that can be expected in fragility curves by having different assumptions based on different EDPs for deriving capacity curves and different choices of IMs for generating fragility curves. This is particularly critical in the case of existing buildings with flexible diaphragms, and variable failure mechanisms. It is concluded that for buildings with predominantly OOP failure mechanisms, the CCmax approach is able to capture the available displacement capacity better than CCavg and provide a more realistic assessment of fragility against both PGA and Sa(T₁) as IM. Both IMs considered are suitable for deriving fragility curves with comparable dispersion around median values. Sa(T₁) is found to give slightly higher probabilities of exceedance of performance levels than PGA, at comparable hazard levels.

Results of the fragility analysis presented in this paper are used as inputs to a broader Bayesian network based framework, for decision making on retrofitting needs for the school infrastructure in Guwahati city. The analysis could be further improved by considering available stiffness of the flexible diaphragms and incorporating uncertainty in material characteristics. However, the methodology established here can reliably be used for seismic assessment and derivation of fragility curves for existing confined masonry school buildings, not just in India, but also in several Asian and Latin American countries, especially when they are non-engineered and exhibit variations from international standards.