Inelastic displacement ratios for non-structural components in steel framed structures under forward-directivity near-fault strong-ground motion

Abstract

This paper describes a detailed numerical investigation into the inelastic displacement ratios of non-structural components mounted within multi-storey steel framed buildings and subjected to ground motions with forward-directivity features which are typical of near-fault events. The study is carried out using detailed multi-degree-of-freedom models of 54 primary steel buildings with different structural characteristics. In conjunction with this, 80 secondary non-structural elements are modelled as single-degree-of-freedom systems and placed at every floor within the primary framed structures, then subsequently analysed through extensive dynamic analysis. The influence of ground motions with forward-directivity effects on the mean response of the inelastic displacement ratios of non-structural components are compared to the results obtained from a reference set of strong-ground motion records representing far-field events. It is shown that the mean demand under near-fault records can be over twice as large as that due to far-fault counterparts, particularly for non-structural components with periods of vibration lower than the fundamental period of the primary building. Based on the results, a prediction model for estimating the inelastic displacement ratios of non-structural components is calibrated for far-field records and near-fault records with directivity features. The model is valid for a wide range of secondary non-structural periods and primary building fundamental periods, as well as for various levels of inelasticity induced within the secondary non-structural elements.

1 Introduction

The seismic performance of non-structural components (NSCs) plays a key role in the quantification of economic losses in the aftermath of earthquakes, and the related cost could even surpass that of the full replacement of a collapsed building (Filiatrault et al. 2002). One possible approach for improving the design of NSCs is to consider their nonlinear response, hence enabling the adoption of reduction factors (F_p) to the applied lateral inertia forces. According to ASCE 7–10 (2016), typical values for F_p range from 1.0 to 12 for non-structural elements. The lower ranges are typically used for mechanical and electrical equipment, while the higher values are usually associated with ‘high-deformability elements’, such as piping and ductwork. Another approach for the design of acceleration-sensitive NSCs in structures involves the use of bracing elements that act as fuses during severe earthquake ground motions (Miranda et al. 2018; Kazantzi et al. 2020a, b). These approaches make the behaviour less dependent on the NSC typology (i.e., flexible or rigid) and its nonlinear performance, and readily suit the development of engineering tools that facilitate the design of such components including inelastic displacement ratios of NSCs (Obando and Lopez-Garcia 2018).

The idea of allowing NSCs to deform into the inelastic range is rather simple yet powerful, since it enables a rational reduction of the unusually large forces controlling their design. This concept has been widely used in the seismic design of secondary structures. For instance (Miranda et al. 2018; Kazantzi et al. 2020a), showed that by enabling modest nonlinear behaviour (e.g., ductility demand of 2.0 alongside 2% viscous damping) for NSCs in a building, the design force can be reduced by up to five times. In line with these observations, Anajafi et al. (2020) showed that by a slight levels of inelasticity in NSCs, not only are significant reductions observed in their seismic forces but also in their displacement demands. These findings are particularly valid for the peak values of elastic floor response spectra, which take place near the predominant periods of a building. On the other hand, Obando and Lopez-Garcia (2018) suggested a single expression for the estimation of inelastic displacement ratios for NSCs based on the floor acceleration response of 8 elastic multi degree-of-freedom systems (MDOF) subjected to far-field like artificial records. It was shown that for NSCs with a period tuned to the fundamental period of the building, the actual inelastic displacement is lower than that attained by an equivalent elastic system, if designed to behave inelastically. Significant displacement amplification was also reported for NSCs with fundamental periods lower than that of the building (i.e., short spectral region). Overall, there are various merits for using ductile NSCs to reduce the design lateral forces, particularly considering the deficiencies in current simplified methods, as discussed further below.

The characterisation of NSCs that are sensitive to floor acceleration in buildings has been examined in a number of previous studies. In an early investigation, Penzien and Chopra (1965) highlighted the large amplifications in the acceleration of a non-structural appendage placed on top of a multi-storey building. Up to 9 times higher forces were estimated in the NSCs with respect to the forces in the structure when their fundamental periods were tuned (i.e. at resonance). This led to the recommendation of designing NSCs with a fundamental period that differs considerably from that of the primary building and preferably its significant higher modes. Since then, several efforts have been made to understand the key features that govern the seismic demand in NSCs. Available studies can be grouped into 4 main categories: (i) elastic NSCs mounted within an elastic building (Filiatrault et al. 2004; Miranda and Taghavi 2005; Reinoso and Miranda 2005; Rodriguez et al. 2002; Medina et al. 2006; Petrone et al. 2016), (ii) elastic NSCs within an inelastic building (Medina et al. 2006; Petrone et al. 2016; Ray-Chaudhuri and Hutchinson 2011; Ray-Chaudhuri and Villaverde 2008; Sankaranarayanan and Medina 2007; Wieser et al. 2013; Adam and Furtmüller 2008; Wang et al. 2014; Fathali and Lizundia 2011; Anajafi and Medina 2018; Sewell et al. 1986), (iii) inelastic NSCs within an elastic building (Obando and Lopez-Garcia 2018), and (iv) inelastic NSCs in an inelastic building. Additionally, recent studies have considered the actual floor motions of instrumented buildings to study the performance of inelastic NSCs (Kazantzi et al. 2020a, b), overcoming the uncertainties introduced by numerical models of the structural systems.

The above discussed studies have led to findings upon which there is general agreement, while there are other aspects that still require further assessment. In general, there is agreement regarding the deficiencies and limitations of simplified equivalent static methods in current North American (ASCE, SEI 2016) and European (CEN 2005a) seismic provisions to estimate the design forces of NSCs. In these provisions, the peak acceleration of the NSC solely depends on the vertical location and flexibility of the NSC, in addition to the peak ground acceleration (PGA) (Anajafi and Medina 2018). Accordingly, key parameters such as the periods of vibration of the building (Miranda and Taghavi 2005), the period of vibration of the NSCs (Sankaranarayanan and Medina 2007), and the type of lateral-load resisting system, are overlooked (Taghavi and Miranda 2012). There is also consensus regarding the effects of ductility in the primary structure, such as the reduction of floor acceleration when the NSC period of vibration is tuned to the fundamental period of the primary structure (Petrone et al. 2016; Sankaranarayanan and Medina 2007; Sewell et al. 1986).

The assumption of using linear-elastic buildings to assess and control the demand imposed on NSCs has been justified based on the following: (i) although modern building are designed to behave inelastically under strong ground motion, in most cases they experience severe earthquakes without sustaining significant damage, (ii) in buildings sustaining severe structural damage, the performance of NSCs becomes secondary, and (iii) in undamaged buildings the potential downtime is due to the performance of NSCs (Obando and Lopez-Garcia 2018). However, one key area of disagreement has been related to the magnitude of floor response spectral ordinates in the primary structure due to inelastic behaviour, which suggests the need for reviewing the linear-elastic modelling assumption. In particular, Flores et al. (2015) observed a reduction in the amplitude of floor response spectral ordinates when the primary building behaved inelastically, with respect to it elastic counterpart. This observation seems to contradict other results available in the literature (e.g. Rodriguez et al. 2002; Ray-Chaudhuri and Villaverde 2008; Sankaranarayanan and Medina 2007). Hence, the impact of nonlinear behaviour in the primary structure on the response of NSCs needs to be considered to assess the extent of this effect.

In this study, the seismic behaviour of inelastic NSCs, mounted within steel moment-resisting frames, is investigated through the determination of inelastic displacement ratios (IDRs), when subjected to floor accelerations. The IDR is recognised as a powerful yet simple approach to estimate the peak inelastic seismic response of structures based on the results of linear elastic analysis (Miranda 2000; Applied Technology Council 2005; FEMA-440 2003). The extension of this method, as proposed in this study, to examine the inelastic response of NSCs within inelastic structures enables the detailed characterisation of the behaviour using nonlinear time-history analysis. This overcomes the limitation of studying the NSCs response only in resonance with the primary structure. To enable this, a large set of 54 code-compliant (CEN 2005a, b) moment resisting frames are subjected to 3 suites of actual strong-motion data from: (i) far-field records and (ii) near-field records with no velocity pulses and (iii) near-field records with velocity pulses or forward-directivity features. The time-history floor response accelerations are recorded in all floors to undertake the subsequent IDR assessment for the NSCs. Based on the results, a model to predict the mean IDR in NSCs is proposed and calibrated for the specific cases of ground motions with far-field characteristics and near-field with forward-directivity effects.

2 Methodology

The use of inelastic displacement ratios to estimate the maximum expected inelastic displacement of a structural system, based only on the peak response of an equivalent elastic system under a ground motion excitation, is well documented in the literature (e.g., Miranda 2000; Chopra and Chintanapakdee 2004). This concept has played a fundamental role in seismic assessment guidelines for existing buildings, such as in the ‘coefficient method’ to estimate peak roof inelastic displacements (Miranda 2000). Only recently, however, has this approach been extended in order to estimate inelastic peak displacements in NSCs mounted on the floors of multi-storey buildings (e.g., Obando and Lopez-Garcia 2018). Herein, a similar approach is adopted and extended to study the effect produced by supporting structures that undergo low levels of inelasticity. In addition, the effect of near-field strong-motion records, with and without directivity effects, is also examined.

The inelastic displacement ratio of NSCs is defined in this paper as C_R and expressed as follows:

$$C_{R} = \frac{{\Delta_{inelastic} }}{{\Delta_{elastic} }}$$

(1)

where $\Delta_{{{\text{elastic}}}}$ is the absolute maximum displacement response of an elastic SDOF, fully defined by T and ${\upxi }$, which correspond to the period of vibration and damping ratio, respectively. $\Delta_{{{\text{inelastic}}}}$ is the absolute maximum displacement of an inelastic SDOF, fully defined by T, ${\upxi }$, and R, noting that R is the strength reduction factor, used in order to induce different levels of lateral strength demand. The yield capacity of the inelastic system is defined by the absolute maximum displacement of the elastic counterpart (i.e., $\Delta_{{{\text{elastic}}}}$) divided by R (i.e., constant strength approach). In other words, once the elastic peak of the lateral deformation of a NSC is known, usually through simple analysis such as elastic floor displacement response spectrum, the expected inelastic peak can be readily computed using the inelastic displacement ratio as shown in Eq. (1).

2.1 Supporting structures

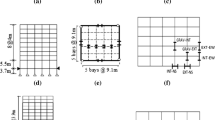
The NSCs considered in this study are mounted within a large set of 54 steel moment-resisting frames, which comply with the guidelines of EC8 (CEN 2005a) and EC3 (CEN 2005b). The frames were designed to represent typical low-to-medium rise European structures, using different realistic seismic scenarios at the design stage, such as peak ground acceleration, soil type, and seismic loads. The combination of these input design parameters resulted in a set of buildings with diverse structural properties. Figure 1a shows a plan view along with a series of elevations of the typical structural system, which consists of three lateral resisting moment frames in one plan direction, whereas braced systems provide lateral load resistance in the orthogonal direction. Figure 1b shows the distribution of key structural properties within the frame set, such as the fundamental period T₁ which ranges from 0.40 s to 1.91 s, the global lateral stiffness ${\uptau } = {\text{T}}_{1} /{\text{N}}_{{\text{s}}}$ where N_s is the number of stories, and the plasticity resistance ratio α (defined as α_u/α₁ in EC8). The frames are clustered according to the number of stories, and referred to as Set A, B, C, and D, for buildings with 3, 5, 7, and 9 stories, respectively.

Fig. 1

(Left) Structural configuration of the frames: a typical plan view, b–e schematic elevation of the 4 building sets considered (standard notation for beams and columns is illustrated in c, d, respectively). f–h Distributions of relevant structural properties considered in the study, groups defined by the number of stories

Due to the symmetry and regularity of the structural systems, the moment-resisting frames are modelled as plane frames (i.e., 2D). The numerical model was implemented in OpenSees (Mazzoni et al. 2006), following a lumped plasticity approach for beams and columns, which are characterised by a combination of elastic and zero-length elements. The behaviour of the zero-length elements or idealised plastic hinges, is defined by the Ibarra-Medina-Krawinkler model (Ibarra et al. 2005) and the subsequent calibration carried out by Lignos and Krawinkler (2011). The structural characteristics (e.g., steel member sizes) and modelling details of buildings (e.g., panel zones, damping model, steel properties) are not included herein for the sake of conciseness, but details can be found elsewhere (Bravo-Haro et al. 2018).

2.2 Strong-motion records

One of the main objectives of this study is to assess the differences in the inelastic displacement ratios (or C_R) of NSCs when the primary structure is subjected to different sets of strong-motion recordings: far-field (FF), near-field without velocity pulses (NF), and near-field with velocity pulses (NFP). To this end, the suite of ground motion records proposed in FEMA P-695 (ATC-63 Project Report 2008) are considered herein. The FF set consists of 44 records from 22 events, whereas the NF set is comprised of 56 records from 28 events, with both horizontal direction components used, amounting to a total of 100 strong motion records. Within the NF set, half of the recordings (i.e., 26) exhibit velocity pulses, according to typical pulse-like classifications (ATC-63 Project Report 2008). Figure 2a shows a tripartite median response spectrum for the three sets of records. Two metrics are used to characterise the ground motion records, namely the mean period T_m (Rathje et al. 1998) and the predominant period T_g of ground motion (Miranda and Ruiz-Garcia 2002). The latter corresponds to the period at which a 5%-damped velocity response spectrum reaches its peak, and was chosen to characterise the behaviour of near-fault pulse-like records, since it is readily computed. Ruiz-Garcia (2011) suggested that T_g is an appropriate metric to characterise the frequency content of NF records with velocity pulses due to directivity effects. Figure 2b shows T_m and T_g across the ground motion records. A detailed description of the strong-motion recordings can be found in FEMA P-695 (ATC-63 Project Report 2008).

Fig. 2

a (Top) Tripartite median and dispersion response spectrum for near-fault records with forward-directivity features; (bottom) Combined tripartite median response spectrum of the three sets of records, and b Distributions of ground motion metrics, T_m and T_g used to characterise the content of frequency and dominant pulses: (top) NFP (middle) NF, and (bottom) FF

2.3 Analysis procedures

• (i) Time-history analysis of the MDOF supporting frame systems subjected to the 100 strong-motion records, scaled to both levels of structural performance, namely elastic (i.e., R_str = 1) and inelastic (i.e., R_str = 2). The scaling factors of ground motions are defined as follows:

  $$SF = R_{str} \cdot \frac{{V_{1} }}{{S_{a} \left( {T_{1} } \right)m\gamma_{1} }}$$

  (2)

  where V₁ is the base shear of the building corresponding to formation of the first plastic hinge based on pushover analysis; m is the seismic mass; ${\upgamma }_{1}$ is the effective mass participation ratio of the first vibration mode. The full time-history acceleration response was recorded at every floor of the building. A total of 10,800 analyses were carried out.

• (ii) Time history analysis of the elastic SDOF systems subjected to the previously recorded floor time-history accelerations. A total of 80 SDOF oscillators were considered, whose period of vibration ranges from 0.05 s to 4.0 s. This range corresponds to that of the period of vibration of the NSCs in this study, referred to as T. The hysteretic behaviour corresponds to an elastic-perfectly plastic system, with a damping ratio of 0.05. The absolute maximum elastic displacement was recorded. A total of 384,000 analyses were carried out.

• (iii) Time history analysis of the inelastic SDOF subjected to the previously recorded floor time-history acceleration, for 5 levels of lateral strength demand (i.e., R_nsc = 2, 3, 4, 5, and 6). The yield capacity of the inelastic SDOF was calculated based on the maximum displacement recorded in the previous step divided by the non-structural strength reduction factor R_nsc. The absolute maximum inelastic displacement was recorded. A total of 1,920,000 analyses were carried out.

• (iv) The inelastic displacement ratio C_R of the NSCs modelled as SDOF systems was computed for every oscillator (i.e., using Eq. 1), at every floor, for every strong-motion recording, as the ratio of the maximum inelastic displacement to the maximum elastic displacement. A total sample of 33,631,200 values of C_R was obtained for the subsequent statistical assessment.

3 Characteristics of non-structural inelastic displacement ratios

3.1 Displacement response spectra of NSC

Before examining the inelastic displacement ratios (C_R) for non-structural components (NSC), it is useful to illustrate and discuss their elastic and inelastic response characteristics. Firstly, the displacement response spectra (S_d) of typical NSCs across the floors of the supporting structures are considered. Figure 3 shows the median displacement response spectra for the 9-storey structure (D14) subjected to the FF set of ground motion records whilst remaining elastic (i.e., R_str = 1). The lowest panel shows the displacement response spectra under the ground acceleration normalised by the mean period of the ground-motion record T_m. In the upper panels, the NSC displacement response spectra are normalised by the fundamental period of the supporting structure, where the vertical lines indicate the normalised first period of the building T₁ (i.e. T/T₁ = 1) and the normalised second period T₂ (i.e. T₂/T₁). The first observation is the presence of apparent peaks, tuned to the periods of vibration of the structure, on the NSC response spectra regardless of the floor level location of the NSC, and the attenuation of these peaks as the NSC strength reduction factor (R_nsc) increases (i.e., higher inelastic demand). This dominant influence from the predominant periods of the supporting structure has been shown by Obando and Lopez-Garcia (2018) as a salient characteristic to understand the behaviour of the inelastic displacement ratios of NSC. In contrast, the ground floor displacement response spectra do not exhibit a dominant frequency effect when normalised by the mean period of the ground motion record, irrespective of the level of R_nsc (i.e., from bottom-left panel towards bottom-right). This is attributed to the filtering effect of the building response on the strong-ground motion wide-band spectra, resulting in floor narrow-band spectra modulated by the building vibration modes (Kazantzi et al. 2020b; Obando and Lopez-Garcia 2018).

Fig. 3

NSC displacement response spectra, for FF set of records and Structure D14 (T₁ = 1.91 s and T₂ = 0.65 s; T₂/T₁ = 0.34)

It is interesting to extend the discussion for a supporting structure undergoing modest inelasticity (i.e., R_str = 2), which could represent a more realistic situation. Figure 4 shows the same case as in Fig. 3 except that the levels of R_nsc are fixed while varying R_nsc. It is noticeable that for this level of induced inelastic demand in the supporting structure, the same observations made above with respect to the elastic supporting structure hold true. As expected, for a given level of R_nsc, a higher displacement demand occurs as R_str increases and, importantly, the difference in the demand increases with T/T₁ particularly for T/T₁ > 1, with the spectral response maintaining a largely similar spectral shape.

Fig. 4

NSC displacement response spectra, for FF set of records and Structure D14 (T₁ = 1.91 s and T₂ = 0.65 s; T₂/T₁ = 0.34)

3.2 C _R for NSC in elastic supporting structures

In order to examine the general trends of the inelastic displacement ratios (C_R) for NSCs, the case of elastic supporting structures (i.e. R_str = 1) is firstly considered, under the influence of the FF and NF sets of ground-motion records. Firstly, Fig. 5 shows the mean value of C_R for 2 selected structures with different number of floors. Each line represents a constant value of R_nsc, and C_R is plotted against the NSC period T normalized by the fundamental period of the building (T/T₁). The characteristics of NSC C_R shown in the plots are representative of the typical behaviour exhibited by the set of frames considered in this study, not only for FF ground motion records, but also for NF ground motions records as discussed in more detail in subsequent sections. A first observation is that, even if maximum NSC displacements are usually attained at roof level (e.g., Fig. 3), the roof inelastic displacement ratio does not necessarily exceed their counterpart at floor levels. Moreover, it reaches a global minimum when tuned to the characteristic period of vibration T₁. Secondly, and in close agreement with the findings of Obando and Lopez-Garcia (2018), for NSCs with periods lower than T₁, C_R increases as T decreases, usually finding local minima in the short region of T/T₁. These local minima, depending on the floor level, might be controlled by the higher modes of vibration of the supporting building. Such effect can be observed more clearly by inspecting the response of NSCs solely placed at the roof of the same buildings considered in Fig. 5. This is shown in Fig. 6 in which the mean response of C_R is shown versus the vibration period of NSC (T). The most salient characteristic in the response of either structure is that the valleys of C_R are controlled by the vibration modes of the building. Near T₁, C_R is lower than 1.0 at a global minimum, hence the maximum lateral deformation of the inelastic NSC is lower than the peak of the corresponding elastic system. Near T₂, a local minimum is observed, breaking the trend of C_R increasing as T decreases. A similar effect of the predominant periods on the response of C_R was also observed by Ruiz-García and Miranda (2006) in the inelastic displacement ratios of primary systems in soft soil sites. Secondly, it can be seen in Fig. 5, that for NSC with periods of vibration higher than T₁, (i.e., T/T1 > 1.5) the well-known equal displacement rule (i.e., C_R = 1), originally proposed by Veletsos and Newmark (1960; Veletsos et al. 1965), does on average hold true, especially if the variability in the estimation of C_R is taken into account as discussed below (e.g., see Fig. 9).

Fig. 5

Mean $C_{R}$ trend at all floors versus T/T₁ for R_str = 1: (a) Frame B03 (for R_nsc = 4), and Frame D01 (for R_nsc = 6. FF set of records

Fig. 6

Mean C_R trend at roof level versus T for R_str = 1 and all levels of R_nsc a Frame C07. b Frame D14. NF set of records

The influence of R_nsc is assessed by examining C_R for the roof level of a randomly selected structure C01 (i.e., 7-storey). Figure 7a shows the response when the elastic supporting structure is subjected to the FF set of records. In general, it can be observed that C_R for NSC increases with the lateral strength ratio, as reported in Obando and Lopez-Garcia (2018), while the observations drawn above regarding the characteristics of C_R across the spectral region remain valid. In addition, the indicative influence of the strong-motion characteristics on C_R is illustrated in Fig. 7b, by adding the results corresponding to the set of NFP records. Most noticeable is the likeness of the trend exhibited by C_R across all normalized periods. In the tuned central region (i.e. T/T₁ = 1) and higher spectral region (i.e., T > T₁), the ordinates of C_R are comparable. In contrast, in the short spectral region (T < T₁) the magnitude of C_R is amplified when the supporting systems is subjected to NFP records. These observations offer the first insights into the inelastic displacement ratios of NSCs due to the action of ground motion records with velocity pulse. This suggests that, as in the case of floor acceleration responses controlled by the natural periods of the supporting systems, the frequency content of the ground-motion records is less relevant (e.g., either T_m or T_p). Additionally, further to the previous remark on the “equal displacement rule” in the long period ratio region ($T/T_{1} > 1.5$), it can be observed in Fig. 7a and b that as ${\text{R}}_{{{\text{nsc}}}}$ increases there is more deviation from unity, however and on average, peak inelastic displacement of the NSC are close to the peak elastic displacement. In order to quantify these near-field effects on the ordinates of C_R, Fig. 8 shows the NFP-to-FF and NF-to-FF mean C_R ratios, respectively, for the same building considered in Fig. 7. Incidentally, as a result of the definition of C_R, this ratio also represents the difference in absolute magnitudes of lateral inelastic displacements of the NSC due to NFP or NF with respect to the FF set of records. It can be seen that the effects of near-field records on the response of C_R are more predominant in the short $T/T_{1}$ region where, irrespective of R_nsc, significant C_R amplifications are observed especially in the case of NFP-to-FF (Fig. 8a). Conversely, in the mid- and long $T/T_{1}$ region, the near-field effect is not significant given that the C_R ratio oscillates steadily around unity. In other words, in the short $T/T_{1}$ region, the effect of NFP records cannot be neglected, regardless of the level of R_nsc.

Fig. 7

Mean C_R at roof level as a function of T/T₁ for different levels of R_nsc for Structure C01: a FF records and b NFP records

Fig. 8

Mean C_R ratios versus for different levels of R_nsc for Structure C01: a NFP to FF and b NF to FF

To examine the variability in the estimation of C_R, the coefficients of variation (COV) of C_R are depicted in Fig. 9. As in the case of inelastic displacement ratios for primary structures (e.g., Miranda 2000; Ruiz-García and Miranda 2006), dispersion is not uniform and is dependent on $R_{nsc}$ and the spectral regions separated by ${\text{T}}/{\text{T}}_{1} = 1$. In particular, for NSCs with periods higher than ${\text{T}}_{1}$ the dispersion increases with $R_{nsc}$ and the ordinates are relatively low, comparable to the levels of dispersion observed in inelastic displacement ratios for primary structures (Ruiz-Garcia 2011; Ruiz-García and Miranda 2006). Importantly, in the shorter spectral region, for NSC periods lower than ${\text{T}}_{1}$, the magnitude of the dispersion is larger. This larger variability means that the prediction of C_R for NSCs in this spectral region is comparatively less reliable. Moreover, there seems to be a slight reduction in the dispersion for periods of vibration near $T_{1}$ and $T_{2}$, in contrast to the findings of Ruiz-García and Miranda (2006) for inelastic displacement ratios of primary structures in soft soil sites.

Fig. 9

Dispersion of C_R as a function of T/T₁ for different levels of R_nsc at roof level for Structure C02: a FF and b NFP

3.3 C _R for NSC in inelastic supporting structures

The influence of incursion of the supporting structure into the inelastic range is still a matter of debate in available literature. For instance, Flores et al. (2015) recently showed that in the case of special steel moment resisting frames, lower ordinates are achieved in the floor response spectrum or peak floor acceleration when the buildings exhibits inelastic response (i.e., compared to elastic behaviour). However, the opposite has been observed in other studies (e.g. Ray-Chaudhuri and Villaverde 2008). These open issues, and considering that NSC performance is pertinent when no or limited structural damage occurs in the supporting structure, have restricted the attention given to assessing IDR for NSCs mounted within buildings exhibiting inelastic response.

To observe the effects of inelastic demand in the primary structure on $C_{R}$ for NSCs$,$ Fig. 10 shows the mean trend of $C_{R}$ determined at the roof level using all of the 7-storey frames in Set C (i.e., 16 structures, 7-storey). A first key observation is that the differences are concentrated in the shorter spectral region, where ${\text{T}} \le {\text{T}}_{1}$. In this region, $C_{R}$ reduces as the supporting building undergoes inelastic response; however, this reduction is less significant for higher levels of ${\text{R}}_{{{\text{str}}}}$. Secondly, it is notable that when in resonance (e.g., ${\text{T}} = {\text{T}}_{1}$) tuned to the first or even the second period of vibration of the supporting structure, there is negligible difference in the ordinates of $C_{R}$, with a slight trend reversal, namely that $C_{R}$ increases in the case of ${\text{R}}_{{{\text{str}}}} = 2$, with respect to the elastic case.

Fig. 10

Mean inelastic displacement ratios at roof level as a function of T/T₁ for different levels of lateral strength; Considering Set C subjected to NF: a R_nsc = 2, b R_nsc = 2, c R_nsc = 4, and d R_nsc = 6

3.4 Influence of strong-motion characteristics on $C_{R}$

Representative trends of the observed effects of strong-motion characteristics are shown in this section. For this purpose, the mean trend of $C_{R}$ computed at the roof level using all of the 9-storey frames in Set D (i.e., 15 structures) is presented. Figure 11 shows the computed mean $C_{R}$ ordinates due to the effect of the three sets of strong-motion records, three levels of ${\text{R}}_{{{\text{nsc}}}}$, solely for the elastic case of supporting systems (i.e., ${\text{R}}_{{{\text{str}}}}$ = 1). The first observation is that there are no distinguishable differences between the trends of $C_{R}$ for FF and NF records. Secondly, $C_{R}$ increases significantly in the shorter spectral region due to the effect of near-fault records with velocity pulses. Thirdly, this differential increment increases as ${\text{R}}_{{{\text{nsc}}}}$ increases, and it is noticeable that the shape of $C_{R}$ remains similar but shifted upwards due to the amplification. In the case of ${\text{R}}_{{{\text{nsc}}}} = 6$, the maximum amplification of $C_{R}$ due to NFP is 36% higher than the FF or NF counterparts.

Fig. 11

Mean C_R ratios at roof level as a function of T/T₁; Considering Set D and (Elastic). a R_nsc = 2, b R_nsc = 2, c R_nsc = 4, and d R_nsc = 6

4 Quantification of NF effects

4.1 Assessment of mean $C_{R}$ ratios

In this section, the influence of forward-directivity effects on $C_{R}$ for NSCs is explicitly quantified and statistically assessed. This is firstly examined through the comparison of the tendencies for mean $C_{R}$ ratios under FF and NF excitations. Secondly, a series of hypothesis tests are conducted to examine if the differences observed in the mean demand of $C_{R}$ under NF records are statistically significant, when contrasted with that under FF records.

Figure 12a shows the mean and dispersion of $C_{R}$ ratio at the roof of a structure for NF records to FF counterparts, for a given R_nsc of 4.0. On the other hand, Fig. 12b shows solely the mean of $C_{R}$ ratio for all considered levels of R_nsc. Firstly, it is worth recalling that for two given buildings (i.e., different $T_{1}$), and irrespective of the set of records, the range of $T/T_{1}$ does not coincide and hence is not readily comparable. To overcome this and compute the mean and dispersion, a linear interpolation was used, enabling the comparison of $C_{R}$ at discrete equidistant values of $T/T_{1}$ with a delta step of $0.05$. Secondly, it can be observed that in this comparison where all buildings are included, there are three clear spectral regions. In the short region of $T/T_{1}$ a clear amplification of the demand of $C_{R}$ is seen due to the effect of NF records, with an increase of 30–40%, and without a discernible trend with respect to $R_{nsc}$. The central region, not necessarily demarcated in its lower end by $T/T_{1}$ of 1.0, thus ranging from 0.5 to 1.7, where similar responses are computed through a flat line around 1.0 for all values of $R_{nsc}$. Interestingly, in the long spectral region, a reduction of the mean demand of $C_{R}$ is observed, since values below 1.0 occur, with larger reduction of up to 20% for higher $R_{nsc}$; in other words, the mean demand of $C_{R}$ is higher due to the effect of FF records. The latter behaviour has been previously observed in the computation of structural inelastic displacement ratios (e.g., Ruiz-Garcia 2011). Furthermore, Fig. 13 shows the same type of results but comparing the mean ratio of $C_{R}$ between records with forward-directivity effect and the set of FF records. The more significant effect of NFP on the mean demand of $C_{R}$ is evident when contrasted with the FF case. This effect divides the behaviour of $C_{R}$ ratio into two spectral regions, enlarging the short-mid span of $T/T_{1}$ where the ratio is higher than 1.0, approximately up to $T/T_{1} \approx 2$, and exhibiting up to twice as much $C_{R}$ mean demand because of records with forward-directivity effect. Moreover, in this region, it is clear that $C_{R}$ ratio increases with $R_{nsc}$. In the case of $T/T_{1} > 2$, the same reversibility is observed, where $C_{R}$ ratio is below 1.0, and tends to saturate around 0.9 regardless of the level of.

Fig. 12

Mean C_R ratios versus (NF to FF) across the entire set of buildings for R_str = 1: a Mean and dispersion for R_nsc = 4, and b Mean C_R ratios for various R_nsc

Fig. 13

Mean C_R ratios versus (NFP to FF) across the entire set of buildings for R_nsc = 1: a Mean and dispersion for R_nsc = 4, and b Mean for various R_nsc

To understand further the behaviour of C_R ratio and taking advantage of the large family of buildings considered in this study, 3 bins of 18 buildings are defined based on their fundamental period of vibration. The results are shown in Fig. 14 for each bin of group corresponding to, 0.39 s ≤ 1 ≤ 0.94 s, 0.95 s ≤ 1 ≤ 1.11 s, and 1.14 s ≤ 1 ≤ 1.87 s, and in Fig. 12a–c, respectively. The first observation is that for the three bins, the same global trend is seen for the mean value of C_R ratio. For < 1.0, the ratio increases as the normalised period decreases and its absolute value increases with. When > 1.0 the ratio flattens out for all levels of and extends below 1.0 – as noted before – for levels of larger than about 2, the latter being valid for bins 2 and 3. There are however clear differences between the various bins. For example, the first bin of short-period buildings (i.e., stiffer systems) shows a mean C_R whose ordinates are larger than 1.0 across the whole span of normalised periods, with the mean C_R demand due to NFP being always higher across all NSCs. All in all, it was observed that the mean values of C_R ratio oscillates from about 2.3 to 0.8 across. Therefore, it is useful to assess when these differences are statistically significant, a characteristic that is uniquely dependent on the sample size, distribution, and level of dispersion of C_R datasets under consideration. To this end, hypothesis tests are carried out as described below.

Fig. 14

Mean C_R ratios versus (NFP to FF) across the entire set of buildings for R_nsc = 1. a Bin 1: 0.30 ≤ T₁ ≤ 0.94, b Bin 2: 0.95 ≤ T₁ ≤ 1.11 and c Bin 3: 1.14 ≤ T₁ ≤ 1.84

4.2 Hypothesis tests on mean C _R response

In this sub-section, a series of hypothesis tests are conducted to assess if the differences observed in the mean demand of C_R due to the action of FF and NF records, are statistically significant. These effects were quantified and discussed above through the computation of the mean C_R ratio. If pulse effects present in NF records have no influence, the median demand of C_R should be similar to the median demand imposed by a record set without pulse effects, which in this study corresponds to the FF records set. Among the statistical tests available (e.g., t-test and Wilcoxon-test), the Z-score method proposed by Zhou et el. (1997) was chosen for comparing the means of two independent log-normally distributed samples. This is a likelihood test that requires knowledge of the parametric distributions of the data. If both samples of interest are distributed as log-normal, the logarithm of the outcomes (i.e., data points) are normally distributed, such that:

$$\log X_{i} \sim N\left( {\mu_{1} ,\sigma_{1}^{2} } \right),\;\log Y_{i} \sim N\left( {\mu_{2} ,\sigma_{2}^{2} } \right)$$

(3)

and whose corresponding means are M₁ and M₂ respectively. Hence, the null hypothesis of both mean responses being virtually equal is represented as:

$$H_{0} :M_{1} = M_{2}$$

(4)

To accept or reject the null hypothesis, a significance level $\alpha$ is defined, which is the probability of rejecting it (i.e., wrongly), given that the null hypothesis was in fact correct. In this case, the estimators for $\mu_{1}$ and $\mu_{2}$ are defined as follows:

$$\hat{\mu }_{1} = \frac{1}{{n_{1} }}\mathop \sum \limits_{i = 1}^{{n_{1} }} \log X_{i} ,\;\hat{\mu }_{2} = \frac{1}{{n_{2} }}\mathop \sum \limits_{i = 1}^{{n_{2} }} \log Y_{i}$$

(5)

and the unbiased estimators of $\sigma_{1}^{2}$ and $\sigma_{2}^{2}$ are defined by:

$$S_{1}^{2} = \frac{1}{{n_{1} - 1}}\mathop \sum \limits_{i = 1}^{{n_{1} }} \left( {\log X_{i} - \hat{\mu }_{1} } \right)^{2} ,\;S_{2}^{2} = \frac{1}{{n_{2} - 1}}\mathop \sum \limits_{i = 1}^{{n_{2} }} \left( {\log Y_{i} - \hat{\mu }_{2} } \right)^{2}$$

(6)

Since the null hypothesis $H_{0} :M_{1} = M_{2}$ is equivalent to testing $\mu_{1} + \left( {1/2} \right)\sigma_{1}^{2} = \mu_{2} + \left( {1/2} \right)\sigma_{2}^{2}$, due to the innate relationship between a normal and a log-normal distribution. Thus, a test can be derived from $\log \hat{M}_{1} - \log \hat{M}_{2}$, where $\log \hat{M}_{k} = \hat{\mu }_{k} + S_{k}^{2} /2$. Given that $\hat{\mu }_{k}$ and $S_{k}^{2}$ are independent, $\hat{\mu }_{k} \sim N\left( {\mu _{k} ,\sigma _{k}^{2} /n_{k} } \right)$ and $\left( {n_{k} - 1} \right)S_{k}^{2} /\sigma _{k}^{2} \sim {\rm X}^{2}$ with $(n_{k} - 1)$ degrees of freedom, this results in:

$${\text{var}} \left( {\hat{\mu }_{2} + \left( \frac{1}{2} \right)S_{2}^{2} - \hat{\mu }_{1} - \left( \frac{1}{2} \right)S_{1}^{2} } \right) = \frac{{\sigma_{1}^{2} }}{{n_{1} }} + \frac{{\sigma_{2}^{4} }}{{2\left( {n_{2} - 1} \right)}} + \frac{{\sigma_{2}^{2} }}{{n_{2} }} + \frac{{\sigma_{1}^{4} }}{{2\left( {n_{1} - 1} \right)}}$$

(7)

and by replacing $\sigma_{k}^{2}$ by the unbiased estimator $S_{k}^{2}$ (see Eq. 6), the Z-score test is obtained, whose distribution is approximately normal under $H_{0}$ when $n_{1}$ and $n_{2}$ are large, as follows:

$$Z = \frac{{\hat{\mu }_{2} - \hat{\mu }_{1} + \left( {1/2} \right)\left( {S_{2}^{2} - S_{1}^{2} } \right)}}{{\sqrt {\frac{{S_{1}^{2} }}{{n_{1} }} + \frac{{S_{2}^{2} }}{{n_{2} }}} + \left( {1/2} \right)\left( {\frac{{S_{1}^{4} }}{{n_{1} - 1}} + \frac{{S_{2}^{4} }}{{n_{2} - 1}}} \right)}}$$

(8)

Given that the null hypothesis and the Z-score are defined, the statistical tests can be conducted. Naturally, the next step is to define the C_R datasets to be tested. The C_R response of the NSCs on the roof of each building was selected to perform the tests, for a given structural period T of each SDOF NSC (i.e., 80 oscillators) as shown in Fig. 15. Importantly, the normalised version of T (i.e., T/T₁) that was shown to be better at characterising the behaviour of C_R might be indistinctly used here unaffecting the results of the test, as is the same for both NSCs roof responses. Subsequently, a significance level equal to “” is considered, which for a normal distribution corresponds to 0.0455 or approximately 5%. In other words, to accept the null hypothesis that postulates that a pair of set means are virtually identical, the Z-score has to be lower than 2.0. If this is higher than 2.0, the null hypothesis is rejected, meaning that at the 5% significance level, the difference between the means is statistically significant, leading to the conclusion that NF with or without directivity effect is significant. It is important to restate that for a given level of relative strength demand, both at building level (i.e., R_nsc = 1,2) and NSC level (i.e., R_nsc = 1…6), the ground motion records of the 2 sets of records under consideration are scaled based on the yield to induce the same S_a level.

Fig. 15

Representative full C_R response versus T of the NSC components on the roof of a given building. Solid-dotted lines correspond to mean C_R values for a given period T, whose sample distributions are schematically shown for an arbitrarily selected period of 2.4 s

Figure 16 shows the resulting Z-score of the statistical test conducted on the same case shown in Fig. 15, which is presented versus the structural period of the NSC. In this particular case, it is clear that in the short spectral region (shaded in the figure) where T < T₁, the null hypothesis is rejected in most NSC cases. The same is observed in the longer spectral region, for between 2.5 s and 3.5 s. These observations confirm the important T-dependant behaviour, particularly the forced dynamic response in the short-spectral region (i.e., T < T₁), hence the need to separately assess the behaviour of the inelastic displacement ratio across spectral regions. However, the rate of cases where the null hypothesis is rejected, amongst the full range of 80 structural periods, can be used to gain insight into the statistically significant influence of NF excitations with or without velocity pulses, over the entire set of buildings and relative strength levels of demand. For instance, the case shown in Fig. 16 has a global null hypothesis rejection rate of 47.5%, derived from the total number of rejections across T, that reaches 38 in this case (filled out in the figure), over the total amount of structural systems, which amounts to 80. Similarly, a local null hypothesis rejection rate of the short period can be estimated, as the ratio of rejections in the shaded region (which varies per each building) to the total number of NSCs below T₁, that in this particular case amounts to 80%.

Fig. 16

Results of the Z-score test for to the case shown in Fig. 15. The dashed lines demarcate the significance level, corresponding to approximately normal distribution of Z under H₀

In the following, results of null hypothesis rejection rates are presented, among the FF set and NF with and without directivity effects. The first conducted test is between the FF record set and the NF set. The results are shown in Fig. 17 in terms of the global rate, for every structural building (i.e., 54 steel frames) sorted by their fundamental period T₁ and every levels of lateral demand imposed on the NSCs mounted only on the roof of the buildings. The first observation is the virtually zero value of the global rejection rate for the elastic case of NSCs, when R_nsc = 1, across all buildings, confirming the practically identical response of C_R under both sets of records. These correspond to the black dots at the bottom of the plot for the zero ordinate. Secondly, the overall global rate is always lower than 50%, implying that the statistically significant difference in the mean of the C_R demand is neither constant nor governing along the whole range of NSC vibration periods T (see Fig. 16), for a particular building at a given level of NSC lateral demand. Thirdly, the global rate seems to increase modestly for higher levels of R_nsc, indicating that C_R central tendencies are significantly different, from a statistical viewpoint. This is coupled with the fact that as R_nsc increases, the dispersion of both lognormal distributions examined augment as well.

Fig. 17

Global rate for Z-score among FF and NF record sets, R_str = 1 and significance level = 5%

It is noticeable that the behaviour of the global rate is not uniform either across the structural periods or R_nsc—see for example the case of buildings with periods within 1.20 s to 1.50 s, where the rate of null hypothesis rejection is considerably higher than the group of more flexible systems immediately next to it on the right-hand side (i.e., 1.50 s < T₁ < 1.90 s). Considering the tests conducted between the FF and the NFP set, shown in Fig. 18, similar trends are observed but with an increase in the statistically significant differences among the means of C_R between the sets, as expected. Hence the same observations noted above apply in this case. By focussing only to the short spectral region by means of the local rate, it can be seen in Fig. 19 that the difference between the means of C_R is remarkably larger, even reaching 100% in the case of buildings with short periods. In other words, the differences among C_R means are statistically significant for all NSC elements whose period of vibration T are shorter than the building fundamental period T₁. Overall, the differences in the mean C_R are statistically significant, across all the range of primary structures especially in the case of short period systems, and are evident even for the lowest level of relative lateral strength imposed on the NSCs (i.e., R_nsc = 2).

Fig. 18

Global rate for Z-score among FF and NFP record sets, R_str = 1 and significance level = 5%

Fig. 19

Local rate for Z-score among FF and NFP record sets, R_str = 1 and significance level = 5%

5 Prediction of C _R for NSCs considering forward-directivity effects

In this section, an expression to estimate the mean expected value of C_R due to the effects of FF and NFP records is presented. The main observed effect of near-fault records with velocity pulses on the behaviour of C_R – in contrast to the influence of FF records –, is a significant amplification in the demand of C_R for the short spectral range (i.e., $T/T_{1} \le 1.0$). This observation is valid over the whole set of 54 structural buildings considered in the study, being slightly more pronounced in the case of buildings with longer structural periods (e.g., see Fig. 14). An overall larger demand on the mean expected value of $C_{R}$ was also observed across the normalised spectral region, being most apparent in the case of buildings with short fundamental periods; in other words, even for NSCs with vibration period T longer than the building fundamental period T₁, the mean demand of $C_{R}$ due to NF records with velocity pulses is larger. Nonetheless, the global shape of $C_{R}$ vesus $T/T_{1}$ is virtually the same irrespective of the set of records. Hence, the functional form shown in Eq. 9 is adopted, as proposed in (Ruiz-García and Miranda 2006) to predict C_R for primary structures built on soft soil sites. The functional form of this expression is particularly suitable for the observed trend of C_R, as it can capture the reduction (or valleys) of C_R near the predominant periods of vibration of the building. As in the original study, separate nonlinear regressions were conducted for each level of R_nsc, for a more accurate assessment. This dedicated treatment per level of relative strength demand can be found in the literature for the closely related assessment of structural inelastic displacement ratios (e.g., Ruiz-Garcia 2011) for estimating roof displacements. The resulting coefficients are given in Tables 1 and 2 for FF and NFP sets, respectively, along with the coefficients defining the 95% confidence intervals and fitting error. The non-linear least-square regressions were conducted using the mean trend for C_R upon the elastic response (i.e., R_nsc = 1) of the whole set of 54 buildings for only the roof response. A comparison of the fitted model and mean C_R of the observed data is shown in Figs. 20a and b, 21 for NFP records at R_nsc = 2.0 and R_nsc = 3.0, respectively.

$$\begin{aligned} C_{R} \left( {\frac{T}{{T_{1} }},R_{nsc} ,\overline{a}} \right) = & a_{1} + \left( {R_{nsc} - 1} \right)\left[ {\frac{1}{{a_{2} \cdot \left( {\frac{T}{{T_{1} }}} \right)^{2} }}} \right] + a_{3} \cdot \left( {T/T_{1} } \right) \cdot exp\left[ { - 4.5 \cdot \left\{ {\left( {\ln (\frac{T}{{T_{1} }} - 0.05} \right)} \right\}^{2} } \right] \\ & \quad + a_{4} \cdot \left( {\frac{T}{{T_{1} }}} \right) \cdot exp\left[ {a_{5} \cdot \left\{ \ln \left ( {\frac{T}{{T_{1}}} + 0.67} \right ) \right\}^{2}} \right] \\ \end{aligned}$$

(9)

Table 1 Coefficients for Eq. (9) calibrated for FF records

Table 2 Coefficients for Eq. (9) calibrated for NFP records

Fig. 20

Comparison of for roof level of the entire set of buildings to those obtained by Eq. (9) and coefficients given in Table 2 for NFP set: a R_nsc = 0.2; and b R_nsc = 3.0

Fig. 21

Comparison of regression (Eq. 9) and Table 1) obtained in this study versus existing expressions for buildings: a 5-storey B02, and b 7-storey C07

The effectiveness of Eq. (9) is illustrated below through a series of individual responses for selected buildings at various levels of R_nsc. Firstly, for FF records, Fig. 21 shows 2 different buildings whose fundamental period ${T}_{1}$ and relative lateral strength demand of the NSCs ${R}_{nsc}$ are displayed in each sub-figure. The expression proposed by Obando and Lopez-García (2018), is included for comparison, noting that this expression was deduced from a database consisting of structural buildings with modal damping ratios of $2\%$ (steel structures) and $5\%$ (RC structures), and a set of far-field like ground motions records (without pulse effects). As can be seen, the most salient difference between the models is that Eq. (9) captures the reduction of ${C}_{R}$ near the predominant periods of the buildings. Although in the study described herein only $2\%$ damping was assumed for the steel frames, the expression developed in (Obando and Lopez-Garcia 2018) predicts relatively well the mean trend of ${C}_{R}$ across $T/{T}_{1}$ except around ${T}_{1}$ and ${T}_{2}$ of the buildings where it conservatively over-estimates ${C}_{R}$. Secondly, for NFP records, Fig. 22 presents a comparison of the predictions from Eq. (9) in conjunction with the coefficients reported in Table 2 for two 9-storey buildings from the set under study, for R_nsc = 4.0 and R_nsc = 5.0, respectively. As in the case of FF, the calibrated model captures the general mean of C_R for the roof of the two randomly selected buildings.

Fig. 22

Comparison of regression (Eq. (9) and Table 2) obtained in this study for buildings: a 9-storey D0, and b 9-storey D13

The functional form of Eq. (9) offers a good estimation of the mean C_R across T/T1, especially near (i.e. tuned) the predominant modes of vibration of the primary structure, as discussed above. This accurate prediction of C_R at tuned periods is particularly useful, as this is usually the most critical case of a roof-mounted NSC. However, practical as it may be for the assessment of existing structures, the design of light NSCs whose vibration periods are identical to the fundamental periods should be avoided, as noted by Penzien and Chopra (1965) more than 50 years ago: “to greatly reduce the seismic forces in an appendage, it should be designed so that its period of vibration differs considerably from the first mode of vibration of the building and also does not coincide with other building modes”. Finally, it is recommended to use the proposed equation within the scope it was developed for, namely for primary systems behaving elastically (i.e., R_nsc = 1), fundamental periods $T_{1}$ ranging from 0.39 to 1.87 s, and levels of relative lateral strength R_nsc ranging from 2 to 6. The results obtained in the case of R_nsc = 2 will be considered further in future studies, along with larger levels of lateral strength demand.

6 Conclusions

This investigation examined the inelastic behaviour of non-structural components (NSCs) mounted within multi-storey steel framed buildings, through the determination of inelastic displacement ratios (C_R). Particular attention was given to the effects of near-fault strong-motion with forward-directivity effects, which are commonly characterized by the presence of velocity pulses. For this purpose, a large pool of 54 primary structural systems was considered, in conjunction with 80 secondary non-structural systems mounted across all floors, resulting in a wide range of structural properties and primary-secondary structure combinations. The strong-motion input corresponded to real earthquake data classified into two sets of near-fault records, with and without forward-directivity effects, in addition to a reference set characteristic of far-fault records.

Existing observations with respect to the general trends of C_R of NSCs based on artificial FF records were shown to hold true when considering the effects of NF recordings with directivity effect. The most salient conclusion being that the floor acceleration demand that controls the behaviour of NSCs, upon which the C_R are computed, is strongly modulated by the periods of vibration of the supporting structure, irrespective of the frequency content of the ground motion. Hence, the influence of near-fault records with forward-directivity effects on the mean demand of C_R of NSCs, is expressed mostly as an increase in the magnitude of the inelastic displacement ratio. This is most perceptible in the case of short period primary structures and NSCs with periods of vibration (T) shorter than that of the fundamental period of the primary structure (T₁). In the short normalised spectral region, where $T/T_{1} < 0.75$, the effect of ground motions with velocity pulses on the mean demand of C_R increases as T decreases, and reduces as the relative lateral strength demand increases. In this region, the mean demand of C_R imposed by NF records can be more than twice the demand due to FF records. The hypothesis tests revealed that in this same region, the differences in the mean response of C_R can be statistically significant even from the lowest level of relative lateral strength demand considered, namely R_nsc = 2. Furthermore, if the supporting primary buildings undergo modest inelastic demands (i.e., R_nsc = 2), although higher absolute floor displacement are reached, lower C_R ordinates are observed mostly in the short spectral region of normalised periods (i.e., T/T₁ < 1). Additionally, it was observed that in the long spectral region (i.e., T/T₁ > 1.5), on average, the peak inelastic displacement of the NSCs are close to the peak elastic displacement.

Finally, using the results obtained in this investigation, a functional form was calibrated to estimate the mean response of C_R due to the action of FF and NFP strong-motion records on the elastic response of the primary buildings (i.e., R_nsc = 1). To increase the accuracy of the model, different sets of coefficients were introduced for each individual level of R_nsc considered in the study. The model was generally shown to provide reliable estimates for the mean inelastic displacement ratios of NSCs, throughout the normalised spectral region considered (i.e., T/T₁), particularly when the period of the NSC is near the first or second period of vibration of the primary structure.