Abstract
In this paper, empirical fragility curves for reinforced concrete buildings are derived, based on post-earthquake damage data collected in the aftermath of earthquakes occurred in Italy in the period 1976–2012. These data, made available through an online platform called Da.D.O., provide information on building position, building characteristics and damage detected on different structural components. A critical review of this huge amount of data is carried out to guarantee the consistency among all the considered databases. Then, an in-depth analysis of the degree of completeness of the survey campaign is made, aiming at the identification of the Municipalities subjected to a partial survey campaign, which are discarded from fragility analysis. At the end of this stage, only the Irpinia 1980 and L’Aquila 2009 databases are considered for further elaborations, as fully complying with these criteria. The resulting database is then integrated with non-inspected buildings sited in less affected areas (assumed undamaged), to account for the negative evidence of damage. The PGA evaluated from the shakemaps of the Italian National Institute of Geophysics and Volcanology (INGV) and a metric based on six damage levels according to EMS-98 are used for fragility analysis. The damage levels are obtained from observed damage collected during post-earthquake inspections through existing conversion rules, considering damage to vertical structures and infills/partitions. The maximum damage level observed on vertical structures and infills/partitions is then associated to the whole building. Fragility curves for two vulnerability classes, C2 and D, further subdivided into three classes of building height, are obtained from those derived for specific structural typologies (identified based on building height and type of design), using their frequency of occurrence at national level as weights.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Earthquakes are one of the most devastating natural disasters, potentially producing the destruction of the physical environment, the interruption of the economic and social activities, causing thousands of dead, injured and homeless. Although the events with a destructive potential are quite rare compared with other natural disasters, being characterized by a low probability of occurrence, their consequences are catastrophic and can affect even large areas for a long time.
Dolce et al. (2019a) estimate that the earthquakes with magnitude between 5.5 and 6.9 occurred in Italy from 1976 to 2012 caused monetary losses for over €150 billion, due to recovery and reconstruction costs. Such consequences can be certainly justified by the moderate-to-high seismic hazard of Italy, but also by the significant exposure, with a high housing density and an extremely high artistic, monumental and economic value. An additional factor is the significant vulnerability of the existing building stock, since most constructions were designed before modern seismic codes were enforced, even completely neglecting seismic actions and accounting for gravity loads only, in case they were built prior to the first seismic classification of the Municipality.
For these reasons, the evaluation of seismic risk in Italy has a strategic role, not only for the safety of citizens, but also for the definition of policies for seismic risk reduction and the allocation of funds for seismic upgrading of public and private buildings.
Several studies (e.g. Lucantoni et al. 2001; Di Pasquale et al. 2005; Crowley et al. 2009; Bernardini et al. 2010; Rota et al. 2011; Silva et al. 2018; NDCP 2018; Dolce et al. 2019b; Del Gaudio et al. 2020) proposed approaches for the evaluation of seismic risk of Italy at the regional/national scale. These approaches rely on mechanical or empirical models to evaluate the seismic vulnerability of the existing building stock and on census data to evaluate the exposure, either for building units (i.e. 14th or 15th General Census of Population and Dwellings–ISTAT 2001 or ISTAT 2011), or for dwelling units (i.e. 13th General Census of Population and Dwellings–ISTAT 1991). Generally speaking, analytical methods make use of numerical models of building prototypes, to simulate their behaviour under seismic actions. Several approaches were proposed in the literature to derive analytical fragility curves for reinforced concrete buildings, either relying on simplified mechanics-based procedures (e.g. Cosenza et al. 2005), capacity spectrum methods (e.g. Iervolino et al. 2007; Del Gaudio et al. 2015), simplified Incremental Dynamic Analysis (e.g. Del Gaudio et al. 2016, 2018), or on displacement-based methods (e.g. Calvi 1999; Crowley et al. 2004; Borzi et al. 2008).
On the other hand, empirical methods are based on the availability of post-earthquake data, providing a realistic estimate of the damage suffered by buildings during past seismic events. Nevertheless, the selection and refinement of empirical data require accurate processing, to avoid bias in further statistical elaborations or to homogenize data collected in different surveys. Among the empirical approaches developed in Italy for reinforced concrete buildings, some are based on the definition of Damage Probability Matrices (DPMs) (e.g. Braga et al. 1982; Dolce et al. 2003; Zuccaro and Cacace 2015; Rosti et al. 2018), others provide fragility curves (e.g. Sabetta et al. 1998; Lagomarsino and Giovinazzi 2006; Rota et al. 2008; Del Gaudio et al. 2017).
This study derives empirical fragility curves for reinforced concrete buildings, by taking advantage of a huge amount of post-earthquake data (more than 300,000 residential buildings), collected in the aftermath of the Italian earthquakes occurred in the period 1976–2012 and available in the online platform Da.D.O. (Dolce et al. 2019a). A comprehensive revision of all the datasets was initially done, to guarantee the consistency of data. A completeness analysis was carried out, with the aim of removing unreliable and biased subsets of data, with a number of building inspections lower than a predefined percentage of the total number of residential buildings, evaluated from census data. Only the Irpinia 1980 and L’Aquila 2009 databases are considered for further elaborations, as fully complying with the abovementioned criteria. The resulting database is then integrated with non-inspected buildings, located in less affected areas, assumed to be undamaged. Buildings sited in non-surveyed or partially-surveyed (completeness ratio lower than 0.1) municipalities were assumed undamaged, to account for the negative evidence of damage in municipalities characterized by lower shaking intensities. The number of buildings in these municipalities was retrieved from National census data.
Fragility analysis was then carried out by considering the peak ground acceleration (PGA) to characterize seismic input at the buildings’ location. Five damage states were defined in accordance with the EMS-98 classification, accounting for damage on both structural and non-structural building components.
Lognormal fragility curves were firstly obtained for different building typologies, identified based on building height and design level (i.e. buildings designed for gravity or seismic loads). They were then used to characterize the seismic fragility of two vulnerability classes, through a refining process based on the frequency of occurrence of each structural typology at the national level, evaluated from census data. In particular, the two considered vulnerability classes of decreasing vulnerability, C2 and D, are defined according to the Italian National Seismic Risk Platform, IRMA (http://irma.eucentre.it/irma/web/home, Borzi et al. 2020b). Vulnerability class C2 includes RC buildings designed for both gravity and lateral loads according to outdated (pre-1981) seismic prescriptions. Vulnerability class D refers to RC constructions designed according to more recent (post-1981) seismic codes. These curves represent the propensity to damage of the RC building stock at the national level.
The presented empirical model was used, together with others (i.e. Borzi et al. 2020a; Donà et al. 2020; Lagomarsino et al. 2020; Rosti et al. 2020a; Zuccaro et al. 2020) for assessing seismic risk in Italy (NDCP 2018; Dolce et al. 2019b, 2020; Masi et al. 2020), by using the IRMA platform.
2 Description of post-earthquake damage data collected after the recent Italian earthquakes
In this study, empirical fragility curves were derived by taking advantage of the huge amount of data released by the Italian National Department of Civil Protection (DPC) in the online platform Da.D.O. (Dolce et al. 2019a). DPC manages all the phases concerning damage and usability assessment after earthquakes occurred nationwide since Friuli 1976, with a substantial support from Regions, Provinces, Municipalities, Firemen, National Chambers of Engineers, Architects and Surveyors and National Research Council (Dolce and Goretti 2015). Post-earthquake inspections aim at evaluating buildings’ immediate occupancy and their structural safety in case of aftershocks, together with the main characteristics affecting seismic vulnerability and information on the observed seismic damage. Thus, information on building position, metrical data (e.g. number of storeys, interstorey height, storey area and construction age), typological characteristics and information on damage detected on different building components are collected during the surveys.
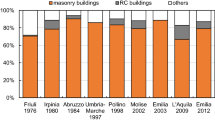
The online platform Da.D.O. collects data for nine seismic events (i.e. Friuli 1976; Irpinia 1980; Abruzzo 1984; Umbria-Marche 1997; Pollino 1998; Molise 2002; Emilia 2003; L’Aquila 2009; Emilia 2012), occurred in Italy in the period 1976–2012, with magnitude between 5.5 and 6.9 (see Fig. 1a), which caused monetary losses for over 150 billion of euros, due to recovery and reconstruction (Dolce et al. 2019a). The whole database counts about 320,000 ordinary buildings (see Fig. 1b), constituted by approximately 78% of masonry buildings, 8% of RC buildings and 14% of other structural typologies. In this study, only RC buildings are investigated, consisting of approximately 24,000 records. It is worth noting that the majority of this sample (about 67%) refers to two datasets only (i.e. Irpinia 1980; L’Aquila 2009), as highlighted in Fig. 1b.
The availability of such a considerable amount of empirical data represents an unprecedented opportunity for its invaluable contribution to the improvement of seismic vulnerability assessment of existing buildings. Nonetheless, the huge amount of data and the use of different survey forms, prompted the DPC to fulfill, with the support of the EUCENTRE Foundation, a comprehensive and thorough harmonization process, in order to make data more recognizable, understandable and mutually comparable, before publishing them in the Da.D.O. platform.
3 Ground motion characterization
In this study, PGA was used to characterize the ground motion intensity at each building’s location. Although alternative seismic intensity measures could be employed (e.g. Rosti et al. 2020b), the adoption of PGA allows for consistency with the national seismic risk platform (Borzi et al. 2020b), where the official national seismic hazard model MPS04 in terms of PGA (Stucchi et al. 2004, 2011) is implemented, thus making the proposed fragility model easily usable for territorial seismic risk applications.
PGA values at each building’s location were obtained from the shakemaps published by INGV soon after the earthquake’s occurrence. The latter follow the methodology reported in Michelini et al. (2008), implementing the software package ShakeMap®, originally developed by the U. S. Geological Survey Earthquake Hazards Program (Wald et al. 2006). This methodology combines the real measurements, provided by the INGV broadband and the Italian Strong Motion Network (Rete Accelerometrica Nazionale, RAN), and the results of Ground Motion Prediction Equations (GMPEs) obtained for a coarse, uniformly spaced grid of points. Different GMPEs are used, depending on the magnitude of the event and the considered region. Site amplification factors are also used based on a nationwide 1:100,000 geological map, calibrated against the average shear wave velocity of the top 30 m of the subsurface profile (VS30), obtaining the amplitude of shaking at the ground surface level. The availability of shakemaps is guaranteed for events occurred after 2008, with the addition of some of the major earthquakes (i.e. Irpinia 1980) reported in Michelini et al. (2008). It is worth noting that INGV also releases maps incorporating the uncertainties of ground motion estimates, which could be accounted for in the fragility analysis (e.g. Rosti et al. 2020b). Nevertheless, as uncertainty maps are available for the events occurred after 2008 only (i.e. not for the Irpinia 1980 event), the uncertainty on the shakemap estimates was not considered, to ensure consistency between the databases.
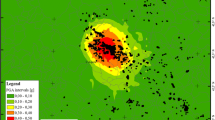
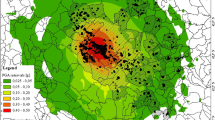
Figure 2 shows the PGA shakemaps of the 23rd November 1980 Irpinia, the 6th April 2009 L’Aquila and 20th May 2012 Emilia earthquakes.
Shakemap for the November 23rd, 1980 Irpinia earthquake (a) from Michelini et al. (2008), shakemap for the April 6th, 2009 L’Aquila earthquake (b) and for the May, 20th 2012 Emilia earthquake (c) published by INGV
4 Review of post-eartquake data and analysis of damage data in light of the EMS-98 classification
This section presents a critical review of the data available from the online platform Da.D.O. (Dolce et al. 2019a). This analysis aims at verifying the availability of data for the considered structural typology, at guaranteeing the consistency among all damage databases and then at checking their survey-completeness through a two-step procedure based on census data, allowing to obtain an unbiased database.
Firstly, the original Da.D.O. database has been carefully analyzed and filtered as a function of building use and structural typology, thereby removing all the structures characterized by exclusive uses different from residential and also by a vertical loadbearing structure different from moment resisting frames (MRF), i.e. structural walls or mixed structures. The Umbria-Marche 1997 and the Emilia 2003 databases were completely discarded, being characterized by a negligible percentage of RC buildings (less than 1% of the total). Both the Friuli 1976 and the Abruzzo 1984 databases were discarded because they do not provide any information on damage to infills/partitions. As a matter of fact, damage to infills/partitions and its consequence in terms of monetary losses represent a significant percentage of those of the whole building (Dolce and Goretti 2015; Del Gaudio et al. 2019b; De Risi et al. 2019; Del Vecchio et al. 2020).
The survey-completeness of the post-earthquake damage data was then checked, with reference to the remaining seismic events. To this aim, a completeness ratio (CR), given by the ratio of the number of inspected buildings in each municipality and the total number of residential buildings from census data (ISTAT 2001), was calculated. The CR gives a measure of the completeness of the survey for a given Municipality: the higher the CR is, the higher the number of building inspections compared to the total number of buildings is and vice-versa. In case of low CR values in less affected areas, the representativeness of the sample could be strongly compromised, since the few inspections are not randomly carried out, but generally limited to damaged buildings only, improperly disregarding those undamaged. To avoid biases in the fragility assessment, a completeness threshold was set, below which the considered sample was discarded. In this study, a completeness threshold equal to 90% was used to identify fully-inspected municipalities, whereas past studies (e.g. Sabetta et al. 1998; Goretti and Di Pasquale 2004; Rota et al. 2008) adopted lower thresholds, ranging between 60 and 80%. Following this analysis, the Pollino (1998), Molise (2002) and Emilia (2012) databases were excluded, as the inspections were made only upon the owner’s request, resulting in very low CR values for all the Municipalities.
All the 41 Municipalities of the Irpinia (1980) dataset were completely surveyed (Braga et al. 1982), whereas, for the L’Aquila dataset, only 36 Municipalities (8206 RC buildings) near the epicentre resulted as fully-inspected.
RC buildings in the municipalities of the L’Aquila dataset which were not completely surveyed correspond approximately to 20% of the total and were not considered. Moreover, only buildings with associated PGA value larger than 0.06 g (i.e. 2414 out of 3935) were considered for consistency with the Irpinia dataset, whose data refer to the same minimum PGA threshold.
It is worth noting that the considered datasets (Irpinia 1980; L’Aquila 2009) are representative of both RC buildings designed for gravity loads only and for seismic loads as well. As a matter of fact, the design type can be determined by simply comparing the construction age of each building with that of the first seismic classification of the municipality where it is located. Almost all buildings of the Irpinia 1980 dataset dated back to before the year of seismic classification, which took place with Ministerial Decree 7/3/1981, thus resulting all designed for gravity loads only. Contrarily, almost all buildings of the L’Aquila dataset were constructed after the year of seismic classification of the belonging municipalities, which took place with Royal Law n.573 1915, thus resulting all seismically designed.
Figure 3 shows the distributions of the number of storeys and age of construction for the two considered datasets. About 50% of the buildings of the Irpinia dataset, does not report any information on the construction age, whereas 20% was built before 1971 and 30% thereafter. On the other hand, about 35% of buildings of L’Aquila dataset was built before 1981, whereas the remaining 65% thereafter. Buildings in the L’Aquila dataset are generally taller than those of the Irpinia one: in fact, the former has a modal value equal to 3, the latter equal to 2.
A further treatment of the considered building stock deals with the addition of non-surveyed buildings located in low-PGA areas and hence accounting for the negative evidence of damage (e.g. Karababa and Pomonis 2010). This integration was carried out by assuming that buildings located in the non-surveyed and in the partially-surveyed Municipalities (with CR lower than 10%) of the low-PGA area can be considered undamaged. The number of these buildings was evaluated from ISTAT 2001 census data and resulted in a total of 37,861 RC buildings sited in the 176 non-surveyed municipalities and 14,641 RC constructions located in the 49 partially-surveyed Municipalities (with CR lower than 10%), see Fig. 4.
Besides metrical and typological data, post-earthquake survey forms collect information on the observed seismic damage detected during the inspection. In the framework of seismic vulnerability assessment, damage data collected using different forms need to be homogenized to obtain a uniformly merged dataset. To this aim, damage conversion rules, inspired by conventional criteria, are used to convert the damage description of the survey form into discrete levels of damage.
Several institutions produced, over the years, different versions of damage conversion rules, including the one of the Applied Technology Council (ATC-13 1985 and ATC-40 1996), of the Federal Emergency Management Agency (FEMA273 1997 and HAZUS 1999, 2012), of the Structural Engineers Association of California (Vision-2000 1995) and of the Architectural Institute of Japan (ALl 1995). Afterwards, Rossetto and Elnashai (2003) provided a homogenized version of damage scale for reinforced concrete buildings, starting from the results of the above studies.
Then, the European Macroseismic Scale, EMS-98, introduced in Grünthal et al. (1998) and forthwith become the reference scale for intensity classification of earthquakes in the European context, provided classification schemes, separately for RC and masonry buildings, associating the damage pattern experienced by several structural components to six global damage grades. These classification schemes represent a benchmark for damage description of inspection forms used in Italy in the aftermath of an earthquake (Baggio et al. 2007).
In this work, post-earthquake damage data collected after the Irpinia 1980 and L’Aquila 2009 earthquakes are employed to derive empirical fragility curves for RC buildings. Two different inspection forms were used after the two events. The “Irpinia 1980” form grades the seismic damage observed on different building components on eight damage levels (from no damage, L1, to collapse, L8). Braga et al. (1982) reports the first version of damage conversion rules related to the “Irpinia 1980” inspection form. In particular, it provides a useful table, describing the progressive damage observed on each structural component, both in qualitative (cracks, crushing, disconnections) and quantitative terms (< 0.2 width crack; < 1 mm width crack; etc), as a function of the eight damage levels, as well as an association rule between the aforementioned damage levels and the six damage levels of the Medvedev Sponheuer Karnik (MSK) scale.
The “AeDES 06/2008” form, used for the L’Aquila post-earthquake surveys, adopts a metrics based on four damage levels (D0-Null; D1-Slight; D2-D3-Medium-severe; D4-D5-Very heavy), representing condensed damage grades of the EMS-98. Thus, it results quite simple to switch from the damage description of the AeDES survey form to the EMS-98 damage grades, by adopting, for example, the damage conversion rule proposed by Rota et al. (2008).
These damage conversion rules (both for the Irpinia and the AeDES 06/2008 forms) deal with damage to vertical structures only. Lately, Del Gaudio et al. (2017) and Rosti et al. (2018) proposed to integrate existing damage conversion rules, by also including damage to infills/partitions, recognizing their strong impact on damage estimation and resulting losses, as highlighted by recent studies (e.g. Dolce and Goretti 2015; Del Gaudio et al. 2016).
In this study, the damage conversion scheme reported in Table 1 was used to determine the global damage level of each building (DSi), as a function of the maximum damage levels attained by vertical structures and infills/partitions, unlike other studies (Zucconi et al. 2017; De Martino et al. 2017) considering a weighted average of the damage observed on different components. The damage rules employed for the vertical structure are consistent with Braga et al. (1982) and Dolce et al. (2019a), in case of the Irpinia, and with Rota et al. (2008), in case of the L’Aquila dataset. The damage relations used for infills/partitions are instead consistent with Del Gaudio et al. (2017).
It has to be noted that Table 1 reports a different damage classification for infills/partitions and vertical structures for both (Irpinia 1980; L’Aquila 2009) survey forms (2nd to 5th columns). This circumstance is consistent with the classification suggested by EMS-98, where damage to infills is generally heavier than that to vertical components. In fact, as already highlighted in Del Gaudio et al. (2020), the failure of infill panels implies a substantial to heavy damage grade (i.e. Grade 3) for the building, whereas damage to structural components could be up to heavy (large cracks in structural elements with compression failure of concrete and fracture of rebars, bond failure of beam reinforced bars, tilting of columns) or even less severe. Accordingly, as an example, observation of Table 1 referring to L’Aquila damage data shows that, in case of a building with collapsed partitions (D4-D5) but moderately damaged vertical structure (D2-D3), the building is not considered collapsed, as damage to partitions would be graded as DS3, whereas damage to the vertical structure may be graded as DS2/DS3. The global damage level assigned to that building would thus be DS3.
5 Derivation of empirical fragility curves
In this section, the statistical model and fitting procedure adopted for the derivation of empirical fragility curves are discussed. Lognormal fragility curves, considering five damage states consistent with the EMS-98 classification, are derived for building typologies, identified based on the building height and type of design, and then for two vulnerability classes, C2 and D, of decreasing vulnerability. These fragility curves, together with those of the three vulnerability classes, A, B and C1, representative of masonry buildings, derived in Rosti et al. (2020a) through a similar approach with the one presented herein, can be used to fully characterize seismic risk in Italy in a comprehensive approach.
5.1 Fitting procedure and fragility curves for building typologies
Seismic vulnerability was represented in terms of fragility curves, providing a continuous relationship between the selected ground motion intensity measure and the probability of reaching or exceeding the different damage states. To this aim, a statistical model was fitted to observational data points through a suitable fitting procedure. The cumulative lognormal distribution was selected among several possibilities, such as the exponential (e.g. Rossetto and Elnashai 2003; Del Gaudio et al. 2017, 2019a; Rosti et al. 2020c) or normal (e.g. Spence et al. 1992; Karababa and Pomonis 2010) distributions. This choice was mainly dictated by the need of deriving fragility functions consistent with the main characteristics of the Italian national seismic risk platform (Borzi et al. 2020b), where the proposed fragility model was then implemented. Furthermore, it is recognized that the lognormal model is widely employed in existing seismic fragility studies (e.g. Rota et al. 2008; Rossetto et al. 2013; Del Gaudio et al. 2017).
The ground motion range, expressed in terms of PGA, was subdivided into equally-spaced bins of 0.05 g. Based on the cumulative lognormal distribution, the probability of reaching or exceeding a given damage level was expressed as:
where Φ[·] is the cumulative standard normal distribution, θi is median PGA value of the fragility curve associated with damage level DSi and β is the logarithmic standard deviation. To avoid intersecting fragility functions, a constant value of dispersion (β) was adopted for each set of fragility functions (e.g. Lallemant et al. 2015).
In line with other literature studies (e.g. Charvet et al. 2014; Macabuag et al. 2016; Rosti et al. 2020a), the repartition of buildings in the different damage states, for a given PGA, was described by the multinomial distribution. The number of building nij undergoing damage state DSi at the jth PGA threshold was hence approximated as:
where nDS is the number of damage states, Nj is the total number of buildings in the jth PGA bin and P(ds = DSi|PGAj) is the conditional probability of occurrence of DSi, given by:
For a given building class, fragility curves were fitted simultaneously to empirical data points by maximising the logarithm of the likelihood:
where θ and β are the optimal parameters, corresponding to the median and logarithmic standard deviation values, respectively.
With the statistical model and fitting procedure described above, empirical fragility curves were derived for different building typologies, identified based on building height (low-rise (L)-1-2 storeys; medium-rise (M)-3-4 storeys; high-rise (H)-more than 4 storeys) and considering three levels of design (i.e. buildings designed for gravity loads only, for seismic loads pre-1981 and for seismic loads post-1981). The level of design for each building was deduced by comparing its construction age with the year of first seismic classification of the Municipality where it was sited. Figure 5 shows the number and percentage of buildings in the considered database, subdivided as a function of the number of storeys and design level. These data were then used to derive empirical fragility curves (Fig. 6).
Empirically-derived fragility curves depicted in Fig. 6 show a clear reduction of seismic fragility with the building code evolution. It is worth noting that buildings designed for gravity loads only were mostly included in the Irpinia 1980 dataset, whereas buildings with effective seismic design were in the L’Aquila 2009 dataset only. In fact, a clear hierarchy was observed, with increasing damage for buildings designed for gravity loads only, for seismic loads pre-1981 or for seismic loads post-1981, respectively. For a given level of design, it can be also observed that seismic fragility increases with the building height. Median PGA (θ) and logarithmic standard deviation (β) values, defining typological fragility curves, are reported in Table 2.
5.2 Fragility curves for vulnerability classes
For large-scale seismic risk applications through the Italian national platform, the previously derived typological fragility functions need to be combined with the main building attributes from the national building census (i.e. construction material, construction age and number of storeys). Two vulnerability classes of decreasing vulnerability (i.e. C2 and D) were defined. Vulnerability class C2 includes RC buildings designed for both gravity and seismic (pre-1981) loads. On the other side, vulnerability class D refers to RC constructions with seismic design post-1981. Each vulnerability class was further refined based on the building height (i.e. low-rise-L; medium-rise-M; high-rise-H).
To account for the actual representativeness of the predefined building typologies at the national level, fragility curves for vulnerability classes were derived by weighting typological fragility curves based on their frequency of occurrence. The composition of each vulnerability class in terms of building typologies was evaluated by statistically elaborating national building census data (Fig. 7).
Resulting fragility curves for vulnerability classes and building height are depicted in Fig. 8, showing an increase of seismic vulnerability with building height and, as expected, a reduction of seismic vulnerability from class C2 to D, for a given building height. For each vulnerability class, Table 3 collects the parameters (i.e. median PGA values and logarithmic standard deviation value) of the cumulative lognormal fragility functions.
These curves obviously differ from those reported in Fig. 6, reflecting the different composition of the vulnerability classes in terms of data included in the database, with respect to data according to the national census. In particular, the comparison of Figs. 5 and 7 highlights the different proportions of buildings with a given number of storeys within each class of height and design level.
6 Conclusions
Empirical fragility curves for residential RC buildings are derived by statistically processing Italian post-earthquake damage data, collected after the Irpinia (1980) and L’Aquila (2009) seismic events. Considering the issue represented by the use of data from incomplete post-earthquake field surveys, a careful analysis of empirical damage data is first carried out on a larger number of post-earthquake databases, leading to the selection of the considered dataset. A reliable damage dataset is obtained through a two-step procedure, firstly identifying the municipalities completely surveyed and then including undamaged buildings sited in the less affected areas, to account for the negative evidence of damage.
The peak ground acceleration, estimated from shakemaps, is selected for characterizing the ground motion severity at the building locations. Existing damage conversion rules are used to convert the damage description reported in the post-earthquake survey forms into the discrete damage levels of the EMS-98 and a global damage level, accounting for both structural and non-structural damage, is then assigned to each inspected building.
Empirical fragility curves are derived for specific building typologies, identified based on three classes of building height (i.e. low-rise 1–2 storeys, medium-rise 3–4 storeys, high-rise buildings ≥ 5 storeys) and type of design (i.e. gravity loads, seismic loads pre-1981 and post-1981). To this aim, the cumulative lognormal distribution is employed to describe the probability of reaching or exceeding the different damage levels, as a function of the selected seismic intensity measure.
The availability of fragility curves, which could be easily combined with the building attributes considered by national census data, could be handier for large scale seismic risk applications. To this end, fragility curves are derived for two vulnerability classes and three classes of building height, by weighting the typological fragility curves, based on their representativeness (i.e. frequency of occurrence) evaluated at the national scale.
The proposed fragility model complies with the framework of the Italian national seismic risk platform (Borzi et al. 2020b) and it was used, together with other vulnerability models (i.e. Borzi et al. 2020a; Donà et al. 2020; Lagomarsino et al. 2020; Rosti et al. 2020a; Zuccaro et al. 2020), for national seismic risk assessment (NDPC 2018; Dolce et al. 2019b, 2020; Masi et al. 2020).
The results reported in this paper, i.e. parameters of the fragility functions derived for both building typologies and vulnerability classes, could be used for evaluating seismic vulnerability and risk in other regions with similar seismotectonic characteristics and building inventory.
Future developments of the work could envisage the derivation of fragility curves using different intensity measures, for example based on spectral ordinates, which could be more representative and better correlated with physical damage. The possibility of integrating additional post-earthquake damage data will be also explored, whenever both shakemaps and reliable survey data would be made available.
References
Applied Technology Council Report ATC-13 (1985) Earthquake damage evaluation data for California. Palo Alto
Applied Technology Council Report ATC-40 (1996) Seismic evaluation and retrofit of concrete buildings. Redwood City
Architectural Institute of Japan (1995) Preliminary report of the 1995 Hyogoken-Nanbu Earthquake, (English edition). Tokyo, April
Baggio C, Bernardini A, Colozza R, Coppari S, Corazza L, Della Bella M, Di Pasquale G, Dolce M, Goretti A, Martinelli A, Orsini G, Papa F, Zuccaro G (2007) Field manual for post-earthquake damage and safety assessment and short term countermeasures. In: Pinto A, Taucer F (eds) Translation from Italian: Goretti A, Rota M, JRC Scientific and Technical Reports, EUR 22868 EN-2007
Bernardini A, Lagomarsino S, Mannella A, Martinelli A, Milano L, Parodi S, Coolen F, Oberguggenberger M, Troffaes M (2010) Forecasting seismic damage scenarios of residential buildings from rough inventories: a case-study in the Abruzzo Region (Italy). Part O J Risk Reliab 224(4):279–296
Borzi B, Pinho R, Crowley H (2008) Simplified pushover-based vulnerability analysis for large scale assessment of RC buildings. Eng Struct 30(3):804–820
Borzi B, Faravelli M, Di Meo A (2020a) Application of the SP-BELA methodology to RC residential buildings in Italy to produce seismic risk maps for the national risk assessment. Bull Earthq Eng. https://doi.org/10.1007/s10518-020-00953-6
Borzi B, Onida M, Faravelli M, Polli D, Pagano M, Quaroni D, Cantoni A, Speranza E, Moroni C (2020b) IRMA platform for the calculation of damages and risks of Italian residential buildings. Bull Earthq Eng. https://doi.org/10.1007/s10518-020-00924-x
Braga F, Dolce M, Liberatore D (1982) A statistical study on damaged buildings and an ensuing review of the MSK-76 scale. In: Proceedings of the 7th European conference on earthquake engineering, Athens, Greece, pp 431–450
Calvi GM (1999) A displacement-based approach for vulnerability evaluation of classes of buildings. J Earthq Eng 3(3):411–438
Charvet I, Ioannou I, Rossetto T, Suppasri A, Imamura F (2014) Empirical fragility assessment of buildings affected by the 2011 Great East Japan tsunami using improved statistical models. Nat Hazards 73:951–973
Cosenza E, Manfredi G, Polese M, Verderame GM (2005) A multi-level approach to the capacity assessment of existing RC buildings. J Earthq Eng 9(1):1–22
Crowley H, Pinho R, Bommer JJ (2004) A probabilistic displacement-based vulnerability assessment procedure for earthquake loss estimation. Bull Earthq Eng 2(2):173–219
Crowley H, Colombi M, Borzi B, Faravelli M, Onida M, Lopez M, Polli D, Meroni F, Pinho R (2009) A comparison of seismic risk maps for Italy. Bull Earthq Eng 7(1):149–180
De Martino G, Di Ludovico M, Prota A, Moroni C, Manfredi G, Dolce M (2017) Estimation of repair costs for RC and masonry residential buildings based on damage data collected by post-earthquake visual inspection. Bull Earthq Eng 15(4):1681–1706
De Risi MT, Del Gaudio C, Verderame GM (2019) Evaluation of repair costs for masonry infills in RC buildings from observed damage data: the case-study of the 2009 L’Aquila earthquake. Buildings 9(5):122. https://doi.org/10.3390/buildings9050122
Del Gaudio C, Ricci P, Verderame GM, Manfredi G (2015) Development and urban-scale application of a simplified method for seismic fragility assessment of RC buildings. Eng Struct 91:40–57. https://doi.org/10.1016/j.engstruct.2015.01.031
Del Gaudio C, Ricci P, Verderame GM, Manfredi G (2016) Observed and predicted earthquake damage scenarios: the case study of Pettino (L’Aquila) after the 6th April 2009 event. Bull Earthq Eng 14:2643–2678. https://doi.org/10.1007/s10518-016-9919-2
Del Gaudio C, De Martino G, Di Ludovico M, Manfredi G, Prota A, Ricci P, Verderame GM (2017) Empirical fragility curves from damage data on RC buildings after the 2009 L’Aquila earthquake. B Earthq Eng 15:1425–1450. https://doi.org/10.1007/s10518-016-0026-1
Del Gaudio C, Ricci P, Verderame GM (2018) A class-oriented mechanical approach for seismic damage assessment of RC buildings subjected to the 2009 L’Aquila earthquake. Bull Earthq Eng 16(10):4581–4605. https://doi.org/10.1007/s10518-018-0365-1
Del Gaudio C, De Martino G, Di Ludovico M, Manfredi G, Prota A, Ricci P, Verderame GM (2019a) Empirical fragility curves for masonry buildings after the 2009 L’Aquila, Italy, earthquake. Bull Earthq Eng. https://doi.org/10.1007/s10518-019-00683-4
Del Gaudio C, De Risi MT, Ricci P, Verderame GM (2019b) Empirical drift-fragility functions and loss estimation for infills in reinforced concrete frames under seismic loading. Bull Earthq Eng 17(3):1285–1330
Del Gaudio C, Di Ludovico M, Polese M, Manfredi G, Prota A, Ricci P, Verderame GM (2020) Seismic fragility for Italian RC buildings based on damage data of the last 50 years. Bull Earthq Eng 18(5):2023–2059. https://doi.org/10.1007/s10518-020-00890-4
Del Vecchio C, Di Ludovico M, Prota A (2020) Repair costs of RC building components: from actual data analysis to calibrated consequence functions. Earthq Spectra 36(1):353–377
Di Pasquale G, Orsini G, Romeo RW (2005) New Developments in Seismic Risk Assessment in Italy. Bull Earthq Eng 3:101–128
Dolce M, Goretti A (2015) Building damage assessment after the 2009 Abruzzi earthquake. Bull Earthq Eng 13(8):2241–2264
Dolce M, Masi A, Marino M, Vona M (2003) Earthquake damage scenarios of the building stock of Potenza (Southern Italy) including site effects. Bull Earthq Eng 1(1):115–140
Dolce M, Speranza E, Giordano F, Borzi B, Bocchi F, Conte C, Di Meo A, Faravelli M, Pascale V (2019a) Observed damage database of past Italian earthquakes: the Da.D.O. WebGIS. Bollettino di Geofisica Teorica ed Applicata 60(2):141–164
Dolce M, Borzi B, da Porto F, Faravelli M, Lagomarsino S, Magenes G, Moroni C, Penna A, Prota A, Speranza E, Zuccaro G, Verderame GM (2019b) Seismic risk maps for the Italian territory. In: XVIII Italian conference on earthquake engineering (ANIDIS). Ascoli Piceno (Italy), 15–19 September 2019. (in Italian)
Dolce M, Prota A, … , (2020) Seismic Risk Assessment of residential buildings in Italy: methodology overview and main results. Bull Earthq Eng (In peer review at time of publishing this article)
Donà M, Carpanese P, Follador V, Sbrogiò L, da Porto F (2020) Mechanics-based fragility curves for Italian residential URM buildings. Bull Earthq Eng. https://doi.org/10.1007/s10518-020-00928-7
Federal Emergency Management Agency (1997) NEHRP Guidelines for seismic rehabilitation of buildings. Federal Emergency Management Agency Report: FEMA 273. Washington D.C.
Federal Emergency Management Agency (1999) HAZUS user and technical manuals. Federal Emergency Management Agency Report: HAZUS 1999, Washington D.C., Vol 7
Federal Emergency Management Agency (FEMA) (2012) Hazus-MH 2.1 Technical Manual: Earthquake Model
Goretti A, Di Pasquale G (2004) Building inspection and damage data for the 2002 Molise, Italy, earthquake. Earthq Spectra 20(S1):S167–S190
Grünthal G, Musson RMW, Schwarz J, Stucchi M (1998) European Macroseismic Scale. Cahiers du Centre Européen de Géodynamique et de Séismologie, vol 15-European Macroseismic Scale 1998. European Center for Geodynamics and Seismology, Luxembourg
Iervolino I, Manfredi G, Polese M, Verderame GM, Fabbrocino G (2007) Seismic risk of R.C. building classes. Eng Struct 29(5):813–820
Karababa FS, Pomonis A (2010) Damage data analysis and vulnerability estimation following the August 14, 2003 Lefkada Island, Greece, Earthquake. B Earthq Eng 9:1015–1046
Lagomarsino S, Giovinazzi S (2006) Macroseismic and mechanical models for the vulnerability assessment of current buildings. Bull Earthq Eng 4(4):415–443
Lagomarsino S, Cattari S, Ottonelli D (2020) Macroseismic fragility curves for Italian residential URM buildings calibrated by observed damage. Bull Earthq Eng (In peer review at time of publishing this article)
Lallemant D, Kiremidjian A, Burton H (2015) Statistical procedures for developing earthquake damage fragility curves. Earthq Eng Struct Dyn 44:1373–1389
Lucantoni A, Bosi V, Bramerini F, De Marco R, Lo Presti T, Naso G, Sabetta F (2001) Seismic risk in Italy. Ingegneria Sismica 1:5–36 (in Italian)
Macabuag J, Rossetto T, Ioannou I, Suppasri A, Sugawara D, Adriano B, Imamura F, Eames I, Koshimura S (2016) A proposed methodology for deriving tsunami fragility functions for buildings using optimum intensity measures. Nat Hazards 84(2):1257–1285
Masi A, Lagomarsino S, Dolce M et al (2020) Towards the updated 2020 Seismic Risk Assessment: definitions and developments. Bull Earthq Eng 5:977
Michelini A, Faenza L, Lauciani V, Malagnini L (2008) ShakeMap implementation in Italy. Seismol Res Lett 79:688–697
Ministerial Decree 7/3/1981. Declaration of seismic zones for Basilicata, Campania and Puglia Regions (in Italian)
National Department of Civil Protection (NDCP, ed., 2018) National risk assessment: overview of the potential major disasters in Italy http://www.protezionecivile.gov.it/documents/20182/823803/Documento+sulla+Valutazione+nazionale+dei+rischi/57f337fd-a421-4cb0-b04c-234b61997a2f
R.D.L. (1915) n. 573 Regio Decreto Legge “Norme tecniche ed igieniche da osservarsi per i lavori edilizi nelle località colpite dal terremoto del 13/01/1915”. Gazzetta ufficiale 11/05/1915, p 117
Rossetto T, Elnashai A (2003) Derivation of vulnerability functions for European-type RC structures based on observational data. Eng Struct 25(10):1241–1263
Rossetto T, Ioannou I, Grant DN (2013) Existing empirical fragility and vulnerability functions: compendium and guide for selection. GEM Technical Report 2013-X, GEM Foundation, Pavia, Italy
Rosti A, Rota M, Penna A (2018) Damage classification and derivation of damage probability matrices from L’Aquila (2009) post-earthquake survey data. B Earthq Eng 16(9):3687–3720
Rosti A, Rota M, Penna A (2020a) Empirical fragility curves for Italian URM buildings. Bull Earthq Eng. https://doi.org/10.1007/s10518-020-00845-9
Rosti A, Rota M, Penna A (2020b) Influence of seismic input characterisation on empirical damage probability matrices for the 2009 L’Aquila event. Soil Dyn Earthq Eng 128:105870. https://doi.org/10.1016/j.soildyn.2019.105870
Rosti A, Del Gaudio C, Di Ludovico M, Magenes G, Penna A, Polese M, Prota A, Ricci P, Rota M, Verderame GM (2020c) Empirical vulnerability curves for Italian residential buildings. Boll Geofis Teor Appl 61(3):357–374
Rota M, Penna A, Strobbia CL (2008) Processing Italian damage data to derive typological fragility curves. Soil Dyn Earthq Eng 28:933–947
Rota M, Penna A, Strobbia C, Magenes G (2011) Typological seismic risk maps for Italy. Earthq Spectra 27(3):907–926
Sabetta F, Goretti A, Lucantoni A (1998). Empirical fragility curves from damage surveys and estimated strong ground motion. In: Proceedings of the 11th European conference on earthquake engineering, Paris, France, pp 1–11
Silva V, Amo-Oduro D, Calderon A, Dabbeek J, Despotaki V, Martins L, Rao A, Simionato M, Viganò D, Yepes C, Acevedo A, Horspool N, Crowley H, Jaiswal K, Journeay M, Pittore M (2018). Global Earthquake Model (GEM) Seismic Risk Map (version 2018.1). https://doi.org/10.13117/gem-global-seismic-risk-map-2018.1
Spence RJS, Coburn AW, Pomonis A (1992). Correlation of ground motion with building damage: The definition of a new damage-based seismic intensity scale, Proceedings of 10th World Conference on Earthquake Engineering, Balkema, Rotterdam
Structural Engineering Association of California (SEAOC) (1995) Vision 2000. Seismology Committee, Structural Engineering Association of California, CA
Stucchi M, Akinci A, Faccioli E, Gasperini P, Malagnini L, Meletti C, Montaldo V, Valensise G (2004). Mappa di Pericolosità sismica del territorio Nazionale http://zonesismiche.mi.ingv.it/documenti/rapportoconclusivo.pdf
Stucchi M, Meletti C, Montaldo V, Crowley H, Calvi GM, Boschi E (2011) Seismic hazard assessment (2003–2009) for the Italian building code. Bull Seismol Soc Am 101(4):1885–1911
Wald DJ, Worden CB, Quitoriano V, Pankow KL (2006) ShakeMap manual, technical manual, users guide, and software guide. http://pubs.usgs.gov/tm/2005/12A01/pdf/508TM12-A1.pdf
Zuccaro G, Cacace F (2015) Seismic vulnerability assessment based on typological characteristics. The first level procedure “SAVE”. Soil Dyn Earthq Eng 69:262–269
Zuccaro G et al (2020) Empirical fragility curves for Italian masonry buildings: evolution of the vulnerability model from DPM to curves as a function of acceleration. Bull Earthq Eng 6:137
Zucconi M, Sorrentino L, Ferlito R (2017) Principal component analysis for a seismic usability model of unreinforced masonry buildings. Soil Dyn Earthq Eng 96:64–75
Acknowledgements
This work was carried out under the financial support of the Italian Department of Civil Protection within the ReLUIS-DPC 2014-2018 project. This support is gratefully acknowledged.
Funding
Open access funding provided by Università degli Studi di Napoli Federico II within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rosti, A., Del Gaudio, C., Rota, M. et al. Empirical fragility curves for Italian residential RC buildings. Bull Earthquake Eng 19, 3165–3183 (2021). https://doi.org/10.1007/s10518-020-00971-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10518-020-00971-4