Abstract
With the increased number of multi-storey buildings in seismic areas, research efforts have been focused on developing earthquake resilient systems, such as low-damage techniques based on the combination of post-tensioning and dissipating devices. This paper describes the experimental study performed on a 3-storey post-tensioned timber framed (Pres-Lam) building equipped with energy dissipating systems. The testing project consisted of three phases adopting different configurations of the experimental model: (1) post-tensioning to beam-column joints only, (2) post-tensioning and dissipative rocking mechanisms and (3) post-tensioning and dissipative braces. The main objective of this paper is to experimentally investigate on the seismic response of a large-scale specimen with dissipative braces located in high seismic area, considering construction details similar to those adopted in practical applications. During the experimental campaign, the test frame was subjected to more than one hundred ground motions considering a set of seven spectra-compatible earthquakes at increasing intensity levels. The dissipating bracing system with external replaceable hysteretic dampers improves the seismic resilience of multi-storey Pres-Lam buildings, showing inter-storey drift comparable to those with rocking walls, with full recentring capability and without structural damages or post-tensioning losses through seismic tests.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The traditional seismic design is based on structural ductility, generally causing the development of excessive displacements that might lead to structural and non-structural damage after moderate or severe earthquakes (Di Cesare et al. 2014a). Recent advancement in earthquake engineering has led to the development of seismic resilient construction technologies that employ passive control systems to withstand strong earthquakes with limited structural damages (Ríos-García and Benavent-Climent 2020). A number of successful building projects utilizing mass-timber components is spreading in recent years thanks to their optimal strength-weight ratio, with important economic, social, environmental benefits and reduced construction time (Loss et al. 2018; Ugalde et al. 2019). Among the various structural low-damage solutions for medium and high-rise multi-storey timber buildings located in high seismic risk area, moment-resistant timber frame (Polocoșer et al. 2018), platform frame or cross laminated timber (CLT) constructions (Ceccotti et al. 2013; Van de Lindt et al. 2018; Masaeli et al. 2020; Chen et al. 2020) are emerging. Particular interest is being received worldwide by the post-tensioned timber (Pres-Lam) system, recognized as one of most effective solutions for achieving seismic-resilient and sustainable buildings.
The Pres-Lam concept was originally proposed at the University of Canterbury (UoC) in New Zealand (Palermo et al. 2005) and derives from the low-damage design of reinforced concrete structures (PREcast Seismic Structural System—PRESS) started by Priestley (1991). The technology used unbonded post-tensioned steel tendons or bars to join together structural members of timber frames or walls, creating a moment resisting connection (Buchanan et al. 2011). Due to the considerable stress induced in timber members by post-tensioning, the technology finds its application within engineered wood materials, such as laminated veneer lumber (LVL), glue-laminated timber (glulam), and cross-laminated timber (CLT). In high seismic areas the post-tensioning is usually combined with energy dissipating devices. Based on capacity design principles, the controlled rocking mechanisms of elastic post-tensioning provide self-centering action to eliminate residual drifts, while additional dissipative devices, such as replaceable steel fuses, increase the damping and reduce lateral displacements of multi-storey buildings.
Over the last years extensive experimental testing on the seismic performance of Pre-Lam frames, walls or a combination of these, has been performed and used in real building projects (Granello et al. 2020). Testing on post-tensioned beam-column joints with and without internal or external dissipative dampers showed that the systems were capable to sustain large drift demands with good re-centering capability and the addition of devices provided significant supplemental damping to the system (Palermo et al. 2005; Smith et al. 2014). Quasi static testing has been performed on Pres-Lam wall subassemblies, such as single LVL (Sarti et al. 2015a) and CLT walls (Ho et al. 2016) with elastoplastic dampers at the rocking interface, coupled walls with U-shaped flexural plates (UFP) dissipaters among them (Iqbal et al. 2017), single and coupled CLT rocking walls with UFP dissipaters (Ganey et al. 2017), coupled column-walls with UFPs (Sarti et al. 2015b). All experimental results showed a complete re-centering capability of post-tensioned walls, demonstrating the effectiveness of the system with dissipative dampers in minimizing the uplift forces on the floor with limited damages to the system. A few seismic tests on Pres-Lam building specimens have been performed in New Zealand (Newcombe et al. 2010), United States (Pei et al. 2019) and Italy (Di Cesare et al. 2017; Ponzo et al. 2019).
Newcombe et al. (2010) tested a 2/3-scale two-story LVL post-tensioned specimen by applying quasi-static loads. The structure was made of post-tensioned frames in one direction and post-tensioned walls in the other. The experimental results showed fully re-centering and no significant damage up to 2% of drift. Pei et al. (2019) conducted a full-scale shake table test of a two-story mass timber building with post-tensioned CLT rocking walls at the University of California San Diego. The results showed the resilience of CLT rocking-wall system with a heavy-timber gravity system up to the MCE and validated the low-damage characteristics of different key connection details. Moreover, it was observed that the natural period of these buildings is relatively long for the given building height and post-tensioning losses of about 8% were observed for large earthquakes. Stiffness and deformation are likely to control the design for taller building implementations. In both cases, the systems were essentially damage free up to 2% of drift, while drift values higher than 3% caused fractures of the rocking wall corners (Pei et al. 2019) or cracking in columns and slabs due to high stress concentration around dissipative anchorages (Newcombe et al. 2010).
Di Cesare et al. (2017) tested a 2/3 scale three-story post-tensioned frame specimen made of glulam timber, widely used in Europe, on the shake table at the University of Basilicata (UNIBAS, Italy) with and without supplemental dissipative rocking mechanisms. The dissipative-rocking impacts on the seismic response by increasing the equivalent viscous damping and reducing maximum drift of approximately 30%. No damage was observed on the main structural elements up to drift values of over 3%. The development of the Pres-Lam technology with additional dampers has led to the application of such systems in real building projects in many countries (Granello and Palermo 2020; Leyder et al. 2015; Kirstein et al. 2018).
In this study the resilient seismic performance of Pres-Lam buildings has been improved by coupling post-tensioned frame with dissipative bracing systems allowing a more flexible architectural configuration respect to heavy-timber gravity-framing systems combined with cross-laminated timber (CLT) walls or post-tensioned rocking walls. The dissipative bracing systems included dissipative devices able to dissipate large amounts of energy during a strong seismic event, significantly reducing the inter-storey drifts and regularizing also the structure (Ponzo et al. 2019), due to the additional stiffness and damping provided to the structural system. In case of moderate earthquakes, the system remained elastic until the fixed yielding level of damper was reached. The use of external dampers ensures that in case of eventual permanent damage after strong earthquakes, they can be replaced allowing the structure to remain operational, increasing the seismic resilience of the building.
Experimental testing and results of the 3-story post-tensioned timber frame specimen with dissipative bracing systems presented in this paper are part of an extensive experimental campaign performed at the structural laboratory of UNIBAS, in collaboration with UoC (Smith et al. 2014; Di Cesare et al. 2017), in which the bare post-tensioned frame was alternatively combined with two different form of energy dissipation. The structure was subjected to more than 100 tests considering a set of seven natural earthquakes, properly scaled at various peak ground acceleration in order to investigate from a Service Level Earthquake (SLE) to a Design Base Earthquake (DBE). The objective of the shaking table tests is to examine the seismic response of the braced post-tensioned frame at large-scale with connection details similar to those necessary for implementation in practice. For this aim, the experimental results of the braced frame in terms of inter-storey drifts, storey displacements and accelerations and base shear are compared with that of the bare post-tensioned frame with and without dissipative rocking.
2 Experimental testing
2.1 Experimental model and design configurations
The experimental specimen was a 3-D, 3-storey post-tensioned timber frame characterized by single bays in both directions. The geometry of the 2/3 scaled test specimen, 2 m inter-storey height and 4 m × 3 m in plant (Ponzo et al. 2012), was determined based on several aspects including the limitation of shake table available at the structural laboratory of the University of Basilicata. The testing frame realized using glulam grade GL32h (CNR-DT 206 2018) was post-tensioned in both directions with steel bars crossing at the beam-column joints. The flooring consisted of 150 mm thick solid timber panels. The columns of the building frame were continuous through the floor diaphragms. The prototype model was designed according to European code (UNI EN 1998-1 2013) for office use at first and second floors (live load of Q = 3 kPa) and considering a rooftop garden load (Q = 2 kPa). The seismic demand was characterized by a peak ground acceleration (PGA) of 0.44 g and a medium soil class. Observing the Cauchy-Froude similitude laws (Krawinkler and Moncarz 1981) suitable scale factors were applied to the prototype model. The additional masses due to scaling of dead load and live load were made up of concrete blocks and steel hold downs.
The dimensions of the structural elements, post-tensioning and dissipative devices were designed according to the displacement-based design procedure proposed by Priestley et al. (2007) and optimized for post-tensioned timber framed buildings with passive energy dissipation systems (Di Cesare et al. 2019a; Ponzo et al. 2019). The Modified Monolithic Beam Analogy (MMBA) procedure (Newcombe et al. 2008) was used for dimensioning the post-tensioned beam-column and column foundation connections. The resulting hysteretic response of the equivalent model is represented by the flag-shape behaviour (Fig. 1). The equivalent viscous damping ξeq for the displacement-based design (DBD) procedure could be estimated by Priestley et al. (2007) as the sum of the elastic viscous damping ξeq,v and the hysteretic viscous damping ξeq,h,v corrected by a reduction factor k in order to account for the random nature of seismic inputs.
The equivalent hysteretic viscous damping ξeq,h,v associated with the flag-shaped model is estimated as Eq. 2, where µ is the displacement ductility, r is the post-yield stiffness ratio and βF is the flag loop parameter which controls the global amount of energy dissipation provided to the system (Priestley and Grant 2005).
Three configurations were designed starting from a target lateral displacement Δd (or drift) and assuming ξeq,v = 2%, k = 0.85 and flag loop parameter βF of 0, 0.4 and 0.8 as a function of the amount of equivalent hysteretic viscous damping, as reported in detail in (Di Cesare et al. 2019a; Ponzo et al. 2019):
-
(i)
Bare post-tensioned frame (F), representing the free rocking condition with post-tensioning only without energy dissipation (βF = 0, see Fig. 1a), designed for a target drift of about 3%;
-
(ii)
Dissipative frame (DF), representing the bare frame (F) with additional dissipative rocking at the beam-column joints and at the column-foundation connections (βF = 0.4, see Fig. 1b), designed for a target drift of about 2%;
-
(iii)
Braced frame (BF), representing the bare frame (F) with dissipative braces (βF = 0.8, see Fig. 1c), designed for a target drift of 1.25%.
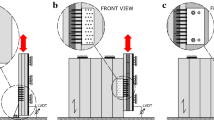
The installation of the test frame specimen was completed in a short period of time of 2 days by two workers (Fig. 2a). An overview of the bare post-tensioned frame model is shown in Fig. 2b. During the third testing phase two V-inverted braces composed by glulam grade GL24h (CNR-DT 206 2018) timber rods in series with hysteretic dampers were added to each storey of the test model (Fig. 2c). Table 1 summarizes the total mass of the braced test frame.
2.2 Testing apparatus
A plan and elevation view of the testing apparatus and the sensor location is shown in Fig. 3. The testing apparatus consisted of a single degree of freedom (in longitudinal direction) shaking table driven by an MTS dynamic actuator characterized by ±500 kN maximum load capacity of and ±250 mm stroke (Di Cesare et al. 2014b). The actuator has two cylindrical hinges and was fixed at the base of the shake table and pushed against a reaction wall. Three hydraulic pumps, each capable of a flow rate of 600 l/min, operated the actuator controlled by an inner load cell and temposonic linear displacement transducer. The shaking table consisted of a four-profile rail guides located under the columns, each composed by two carriages with a friction factor of less than 1%.
The seismic response of the frame was recorded by more than 50 acquisition channels. Different types of sensors were installed on the test frame, providing measurements of acceleration, displacement force and strain. A longitudinal, transversal and plan view of the instrumentation installed on the frame are shown in (Fig. 3). Fourteen horizontal and two vertical accelerometers were placed on different storey. The absolute horizontal displacements and rotations were measured directly by 7 displacement transducers connected from shake table to an external reference structure (Fig. 3). The tension loading of the post-tensioned bars in both directions was measured by 6 load cells, the gap opening due to the rocking motion was recorded by 3 potentiometers placed across 3 beam-column joints and 2 potentiometers at the base of 2 columns (see details in Fig. 4). Local force–displacement of the dissipative bracing systems were measured using a load cell and a potentiometer displacement transducer placed on all hysteretic dampers (see details in Fig. 6).
2.3 Hysteretic dampers and construction details
Figure 4 shows the construction details of the beam to column joints and of the column to shake table connections. The structural elements were characterized by 320 × 200 mm cross sections for columns, 305 × 200 mm and 240 × 200 mm for primary and secondary beams respectively. The beam-column joints (Fig. 4a) were composed by a single 26.5 mm diameter steel bar crossing the beam, with fy = 1050 N/mm2 yield strength and 170 kN/mm2 Young’s modulus, post-tensioned at 100 kN and 50 kN for the longitudinal and transversal direction, respectively. In order to protect the column face, thirty-six ϕ 8 mm screws, 80 mm long screws were installed in the column face adjacent to the beam and 30 screws were installed in contact with the post-tensioning backing plate. Vertical loads were transferred through a ϕ 76.1 mm steel tube which extends 66 mm from the beam and sits inside to the column. Twenty-two ϕ 8 mm 80 mm long screws were used to reinforce where the beam and the post-tensioning backing plate meet the column. The post-tensioning forces in both directions were recorded by 2 load cells located in a monitored joint for each storey (Fig. 3). The column base connection (Fig. 4b) was fitted with a steel shoe which was epoxied into the base of the column and was left free to rock on a base plate using four ϕ 20 mm bars of 300 mm length. Shear transfer was achieved using a ϕ 76.1 mm steel tube which extended 15 mm from the steel shoe and slotted into a cavity in the base plate.
Based on the DIS-CAM concept (Dolce et al. 2006), the hysteretic dissipative devices considered for dissipative rocking at the beam-column joints (DF configuration) and at the column-foundation connections (DF and BF configurations) consisted of steel angles created by milling down a certain section of the angles. As shown in Fig. 4 the steel angles dampers were attached to the structural elements by M16 bolts fixed to backing plates. Moreover, a reinforcement with ten ϕ 80 mm long screws was introduced in the contact zone between the plate and the column. In order to facilitate the attachment of steel angles devices, holes were drilled and tapped in the steel shoe. Figure 5 shows the scheme adopted for quasi-static testing on steel angles devices of S275 steel grade and the force–displacement response behaviour for two different geometrical configurations relevant to beam-column joints (L 100 × 10 × 80) and to column-foundation connections (L 100 × 8.5 × 160), respectively. A test sequence was performed applying two cycles at increasing amplitudes up to the 100% of the design displacement (Di Cesare et al. 2013).
Each dissipative brace was composed by two 160 mm × 180 mm V-inverted timber rods and hysteretic dampers consisted of two C60 steel grade U-shaped flexural plates (UFP) dampers working in parallel. UFP devices were selected as dampers in order to provide steady restraint in horizontal direction, to accommodate rotations and vertical displacements, i.e. do not transmit bending moments and vertical loads (UNI EN 15129 2018). Figure 6 shows the construction details of bracing connection to UFP and beam. The UFPs were developed by Kelly et al. (1972) to provide energy dissipation between structural walls and adjacent floors, and then successfully used for other applications (Baird et al. 2014; Braga et al. 2019). The timber rods were designed to behave elastically for an axial force greater than the yielding force of the UFPs fixed to the top and bottom flanges through four M10 bolts. The bottom flange was held to the top of rods through height ϕ 8 mm 120 mm long screws and twelve ϕ 16 dowels. In order to acquire the shear force of the braces, the top flange was connected under the beam through a load cell with a pinned connection. In order to avoid possible out-of-plane displacements of braces, safety stoppers were installed, by using steel rigid elements with slotted holes which accommodate free relative displacement (without friction) between the UFPs and the rigid support of about 2 mm along out-of-plane direction and 20 mm along in-plan direction.
Figure 7 shows the force–displacement behaviour of quasi-static characterization tests performed on couples of UFPs with different geometrical dimensions (named as UFP1, UFP2 and UFP3) installed to each storey of the braced frame (Di Cesare et al. 2019b).
The main characteristics of the steel yielding angles and UFPs hysteretic dampers, are reported in Table 2.
3 Experimental results
3.1 Dynamic characteristics
The dynamic properties of the experimental model for the three considered configurations and have been identified by dynamic characterization tests. Hammer impact and pink noise excitation sources have been performed for the Welch’s Power Spectral Density (PSD) estimation (Welch 1961). Figure 8 show the experimental results in terms of frequencies corresponding to the first and second vibration mode in the main direction for the braced frame BF (blue line), dissipative frame DF (red line) and bare frame F (black line). As the mass remained almost the same, this result highlight, as expected, a greater stiffness of the BF model respect to the DF and F ones, more evident for the second mode.
Numerical non-linear dynamic analyses were performed in order to reproduce the experimental results (Di Cesare et al. 2017). The modelling of the test frame based on the lumped plasticity approach and using elastic timber elements connected with non-linear links was implemented using finite element software (SAP2000 and OpenSees). All detected frequencies and the relevant modes were used to calibrate the numerical models. More details about numerical modelling and comparison between numerical analysis and experimental results are reported in Ponzo et al. (2018), Di Cesare et al. (2019c).
3.2 Seismic test results
3.2.1 Ground motions and testing program
The experimental campaign was performed using a set of seven natural earthquake records, selected from the European strong motion database. These spectra-compatible records were defined according to the current Eurocode (UNI EN 1998-1 2013) considering a peak ground acceleration PGA of 0.44 g and medium soil class in high seismic zone (Italy). To ensure consistency with the scale of the experimental model, all input accelerations were scaled down in duration by a factor of 1/ √(3/2).
The shake table testing program for all experimental configurations (bare frame F, dissipative frame DF and braced frame BF) for the three selected seismic inputs considered in this paper is summarized in Table 3. In Fig. 9 the spectra of ground motions and their average spectrum are compared with the elastic DBE spectrum. In case of bare frame (F) the PGA level was increased up to 75% because an imposed interlock of 3.5% of maximum inter-storey drift was reached, except for the weaker earthquake (ID code 1228).
3.2.2 Global seismic response
The global seismic response of shaking table tests performed on all model configurations for all selected seismic inputs are shown in Fig. 10 in terms of distribution along the building height of the maximum and mean values of key parameters: maximum inter-storey drift (MID), maximum storey displacement (MD) and acceleration (MA) and maximum columns shear force (MCF). As can be observed, the effect of the dissipating braces is clearly evidenced from the reduction of MID and MD values. Comparing the MID of the three configurations no significant variations of the mean values were observed up to 25% of PGA. It is worth noting that the dissipative devices become effective in reducing the drift respect to the bare frame F when the earthquake intensity exceeded a threshold value of 25% of PGA as a function of the yield strength of the dampers. In particular, for the BF model at 75% of PGA the values of MID and MD reduced of about 20% than DF model and of about 45% than F model, while MA values were similar for all configurations due to the additional damping of the dissipative bracing system. It is interesting to note that for the BF configuration the values of the MIDs at all stories were comparable (this means an optimal activation of the dampers) and the mean value of MID was about 1.5% at 100% of PGA, coherently with experimental results of Pres-Lam structures with rocking walls at the DBE level (Newcombe et al. 2010; Pei et al. 2019). This result further proved the reliability and robustness of the design procedure (design drift 1.25%) meeting the criteria for regularity in elevation required by code for buildings categorised as regular in elevation (Ponzo et al. 2019).
The MCF profiles highlighted that the introduction of dissipative bracing systems was effective in reducing the columns shear respect to DF and F configurations. The bare frame F and the dissipative rocking frame DF exhibited the highest values of MID and MA when subjected to the earthquake 535, characterized by high spectral values in comparison with those of the elastic design spectrum in the range of vibration periods of interest for the examined cases (T1 > 0.5 s). The earthquake 196 provided the highest response for the braced frame BF, this behaviour can be explained comparing the spectral acceleration corresponding to the fundamental vibration periods of the structure with damped braces (see Fig. 9).
The results of BF model under the seismic action having a larger probability of occurrence than the design seismic action (50% of PGA), showed that the “damage limitation requirement” was satisfied (UNI EN 1998-1 2013), limiting the average values of maximum inter-storey drift to MID < 0.75% (see mean BF of Fig. 10), in accordance with buildings having ductile non-structural elements. Considering the complete set of seismic inputs, including the earthquakes not reported in this study, the test specimen was subjected to over 30 tests for each model configuration increasing PGA levels (from 10% to 100%). During the complete set of ground motions at various intensities the post-tensioned bars were not re-tensioned, highlighting the capability of the building to withstand multiple consecutive strong earthquakes.
The maximum global base shear and corresponding mean values are shown in Fig. 11a for all configurations of selected seismic inputs at increasing PGA levels. The base shear is obtained by subtracting from the actuator force the contribution of the shake table due to its inertial mass (5kN) and frictional forces (friction coefficient less than 1%). As expected, the global base shear reached by the BF, evaluated as the sum of shear columns and braces, was greater than ones relevant to DF and F configurations.
The maximum and mean variation of post-tensioning force ΔPT are shown in Fig. 11b for all configurations at increasing PGA levels. The maximum percentage of variation of PT force, calculated as ΔPT = (PTmax − PTinitial)/100, was highest for the case of bare frame F model, with a mean value of ΔPT of about 50% at PGA of 75%. In case of BF model the mean value of ΔPT was almost 25% at PGA of 100%. Moreover, the post-tensioning loss due to seismic action, defined as the variation between the initial and the final value of the post-tensioning force recorded within the complete set of ground motion for each testing configuration, is negligible for the cases of bare post-tensioned frame (F model) and of braced frame (BF model). It is about 2% for the dissipative frame (DF model) configuration due to the strengthening effect of dissipative angles of the post-tensioned beam-column joints.
Figure 12 reports the time history of first storey drifts for all testing configurations, considering the seismic inputs at 25% and 75% of PGA level. The comparison confirmed a drift increasing of about 2 times of the maximum peak values for F and DF models respect the BF model. The recorded time histories highlighted that all configurations of the building frame were able to recentre with negligible residual drift even for large events.
3.2.3 Global hysteresis
The global building hysteresis in terms of base shear versus inter-storey drift for all testing configurations are shown in Figs. 13, 14 and 15 considering all selected seismic inputs at 25%, 75% and 100% of PGA levels, respectively. The hysteresis curves at low-level ground motions (PGA level of 25%, see Fig. 13) show that the frame responses of all configurations are nearly elastic.
In case of strong earthquakes (Figs. 14 and 15) the global flag shape hysteretic loop was more evident. As can be observed, the braced frame BF configuration was able to dissipate higher amount of energy through hysteretic damping for the strongest earthquake inputs (EQ 196 and EQ 535). In case of tests with earthquake EQ 535, from Figs. 14 and 15 is evident that the seismic response of the structure was drastically reduced in terms of drift amplitude with a slight increase of base shear when the dissipative bracing systems were used.
The braced model configuration BF permitted the highest value of PGA to be reached, without visible structural damage. The overall hysteretic energy dissipation is a reflection of many contributors, mainly including the yielding of hysteretic dampers and nonlinear geometric behaviour of rocking mechanisms of beam-column joints and of column-foundation connections.
In order to evaluate the effectiveness of the additional energy dissipation systems, the equivalent viscous damping of the three testing frame configurations was estimated. Figure 16a shows the acceleration-drift design spectra compared with the experimental values of maximum total drift versus the corresponding acceleration recorded during the selected tests.
Figure 16b shows the experimental damping values estimated from the global hysteretic behaviour of the DF and BF configurations for increasing ground motion intensities using the hysteretic area-based approach proposed by Jacobsen (1960), Priestley et al. (2007). Based on the concept of dissipated (EDiss) and stored (Esto) energy, the experimental damping ξexp was estimated as Eq. 3, where Ahyst represents the area of dissipated energy, F0 and u0 are the maximum force and displacement for the given hysteretic loop.
As can be observed in Fig. 16b, the mean value of the hysteretic experimental damping grows for increasing PGA levels. At 10% of PGA the hysteretic dampers were not yet activated and the experimental equivalent damping was almost the same for both configurations (ξexp ≅ 2.5%). At higher PGA levels the hysteretic experimental damping of BF was significantly higher than DF configuration. It was stable around 14% in BF configuration and around 6% in DF configuration. The trend of the experimental results of Fig. 16 was in line with the equivalent damping obtained by the design (6% of DF model; 12% of BF model) confirming the increase of strength and stiffness passing from bare frame F to dissipative frame DF and braced frame BF configurations.
3.2.4 Local hysteresis of dissipative braces
The local hysteresis of the UFP dampers at each storey of the braced frame BF are displayed in Figs. 17, 18 and 19 in terms of force–displacement behaviour for the selected ground motions at 25%, 75% and 100% of PGA levels, respectively.
As mentioned above, figures show that the UFP dampers were not fully activated at lower intensities (25% of PGA, Fig. 17) for all seismic inputs and were mobilized exhibiting an excellent dissipative capacity at higher PGA levels (75% of PGA, Fig. 18, and 100% of PGA, Fig. 19).
The UFPs at all stories (UFP1, UFP2 and UFP3) showed a stable hysteretic behaviour without degradation in strength and stiffness with similar maximum displacements. This response confirmed the uniform distribution of the maximum inter-storey drift (MID) along the building height (see Fig. 10), thus minimizing the possibility of concentration of excessive inelastic deformation and damage in a single storey or in localized regions. It is pointed out that the characteristics of hysteretic behaviour of UFPs obtained from the dynamic tests are consistent with the results obtained by the quasi-static cyclic tests performed on the mock-up devices (see Fig. 7).
4 Conclusions
In this paper, experimental dynamic testing on a 2/3 scaled, 3 storey post-tensioned timber frame building equipped with dissipative bracing systems has been investigated. The experimental test performed at the structural laboratory of the University of Basilicata represents a large-scale shake table testing performed on a glulam post-tensioned timber frame with hysteretic dissipative braces as additional earthquake resistant system. The testing of braced frame (BF) was part of an extensive shake table testing campaign, also including the bare post-tensioned frame (F) and dissipative rocking frame (DF) with steel angles placed at the beam-column and column foundation joints. All experimental results proved the robustness of the design procedure and pointed out the fundamental role of the dissipative bracing system in controlling the seismic vibrations improving the performance of the post-tensioned timber frame building. The following observations and conclusions can be drawn based on the comparison between the experimental test results of all model configurations.
-
1
The bracing system composed by V-inverted timber braces including external replaceable steel U-shaped flexural plates (UFP) dampers allowed of developing a resilient and more flexible architectural system for Pres-Lam buildings without changing the gravitational load distribution on beams and columns and reducing the influence on the post-tensioned beam-column joints.
-
2
The fundamental period of the braced frame BF is compliant with the building height, increasing stiffness and reducing deformation respect to F model and DF model. The dissipative bracing system significantly increased the equivalent viscous damping of the system to values of about 12% for earthquakes levels equal or higher than 50% of PGA, in good agreement with the design procedure.
-
3
The introduction of the dissipative bracing systems resulted in significant benefits on the overall seismic behaviour, reducing the maximum inter-storey drift and the columns shear force MCF, with a similar maximum storey acceleration MA and a slight increase of global base shear. In particular, the mean value of the maximum inter-storey drifts of the braced frame BF is < 0.75% at 50% of PGA level, compatible with ductile non-structural elements, and about 1.5% at 100% of PGA.
-
4
UFPs remained in elastic range at input levels lower than 25% of PGA and exhibited an excellent dissipative capacity when PGA level increased up to 75%. Local response of UFP dampers of the bracing system showed a stable hysteretic behaviour for all seismic inputs under a large number of deformation cycles up to ductility values higher than 4.
-
5
The global response of the braced model showed a flag-shaped hysteretic behaviour with a complete re-centering capability. The combination of Pres-Lam timber frame and dissipative bracing system has permitted to achieve a resilient seismic performance without observing structural damages or post-tensioning losses under repeated earthquakes.
References
Baird A, Smith T, Palermo A, Pampanin S (2014) Experimental and numerical study of U-shape flexural plate (UFP) dissipators. In: New Zealand society for earthquake engineering conference, Christchurch, New Zealand
Braga F, Laguardia R, Paolocci A, Gigliotti R (2019) Experimental tests on dissipative device based on U-shaped plates for seismic isolation systems. In: XVIII Convegno di Ingegneria Sismica, Associazione Nazionale di Ingegneria Sismica, Ascoli Piceno, Italy, pp 56–63
Buchanan AH, Palermo A, Carradine D, Pampanin S (2011) Post-tensioned timber frame buildings. Struct Eng 89(17):24–30
Ceccotti A, Sandhaas C, Okabe M, Yasumura M, Minowa C, Kawai N (2013) SOFIE project–3D shaking table test on a seven-storey full-scale cross-laminated timber building. Earthq Eng Struct Dyn 42(13):2003–2021
Chen Z, Popovski M, Iqbal A (2020) Structural performance of post-tensioned CLT shear walls with energy dissipators. J Struct Eng 146(4):04020035
CNR-DT 206 R1 (2018) Istruzioni per la Progettazione, l’Esecuzione ed il Controllo delle Strutture di Legno
Di Cesare A, Ponzo FC, Nigro D, Simonetti M, Smith T, Pampanin S (2013) Experimental testing and numerical analysis of steel angles as hysteretic energy dissipating systems. In: XV Convegno di Ingegneria Sismica, Associazione Nazionale di Ingegneria Sismica, Padova, Italy
Di Cesare A, Ponzo FC, Vona M, Dolce M, Masi A, Gallipoli MR, Mucciarelli M (2014a) Identification of the structural model and analysis of the global seismic behaviour of a RC damaged building. Soil Dyn Earthq Eng 65:131–141
Di Cesare A, Ponzo FC, Nigro D (2014b) Assessment of the performance of hysteretic energy dissipation bracing systems. Bull Earthq Eng 12(6):2777–2796
Di Cesare A, Ponzo FC, Nigro D, Pampanin S, Smith T (2017) Shaking table testing of post-tensioned timber frame building with passive energy dissipation systems. Bull Earthq Eng 15(10):4475–4498
Di Cesare A, Ponzo FC, Pampanin S, Smith T, Nigro D, Lamarucciola N (2019a) Displacement based design of post-tensioned timber framed buildings with dissipative rocking mechanism. Soil Dyn Earthq Eng 116:317–330
Di Cesare A, Ponzo FC, Lamarucciola N, Nigro D, Pampanin S (2019b) Dissipative bracing system for post-tensioned timber framed buildings: experimental testing of U-shape hysteretic dampers. Int J Earthq Eng 36(3):38–54
Di Cesare A, Ponzo FC, Lamarucciola N, Nigro D (2019c) Modelling of post-tensioned timber framed buildings with hysteretic bracing system: preliminary analysis. IOP Conf Ser Earth Environ Sci 233:022026. https://doi.org/10.1088/1755-1315/233/2/022026
Dolce M, Moroni C, Nigro D, Ponzo FC, Santarsiero G, Di Croce M, De Canio G, Ranieri N, Caponero M, Berardis S, Goretti A, Spina D, Lamonaca B, Marnetto R (2006) TREMA project experimental evaluation of the seismic performance of a R/C 1/4 scaled model upgraded with the DIS-CAM system. In: 2nd FIB Congress, Naples, Italy
Ganey R, Berman J, Akbas T, Loftus S, Daniel DJ, Sause R, Ricles J, Pei S, Lindt JVD, Blomgren HE (2017) Experimental investigation of self-centering cross-laminated timber walls. J Struct Eng 143(10):04017135. https://doi.org/10.1061/(ASCE)ST.1943-541X.0001877
Granello G, Palermo A (2020) Monitoring the dynamic properties of a Pres-Lam structure: the trimble navigation office. J Perform Constr Facil 34(1):04019087. https://doi.org/10.1061/(ASCE)CF.1943-5509.0001359
Granello G, Palermo A, Pampanin S, Pei S, van de Lindt J (2020) Pres-lam buildings: state-of-the-art. J Struct Eng 146(6):04020085. https://doi.org/10.1061/(ASCE)ST.1943-541X.0002603
Ho TX, Dao TN, Aaleti S, van de Lindt JW, Rammer DR (2016) Hybrid system of unbonded post-tensioned CLT panels and light-frame wood shear walls. J Struct Eng 143(2):04016171. https://doi.org/10.1061/(ASCE)ST.1943-541X.0001665
Iqbal A, Fragiacomo M, Pampanin S, Buchanan A (2017) Seismic resilience of plywood-coupled LVL wall panels. Eng Struct 167(1):750–759. https://doi.org/10.1016/j.engstruct.2017.09.053
Jacobsen LS (1960) Damping in composite structures. In: Proceedings of 2nd world conference on earthquake engineering, vol. 2, Science Council of Japan, Tokyo, pp 1029–1044
Kelly JM, Skinner RI, Heine AJ (1972) Mechanisms of energy absorption in special devices for use in earthquake resistant structures. Bull N Z Soc Earthq Eng 5:63–73
Kirstein A, Siracusa J, Smith T (2018) The new timber von Haast replacement building in Christchurch. In: Proceedings of, New Zealand society for earthquake engineering annual conference Auckland, New Zealand, University of Auckland
Krawinkler H, Moncarz PD (1981) Theory and application of experimental model analysis in earthquake engineering. Standford, CA: NASA STI/Recon technical report N 82
Leyder C, Wanninger F, Frangi A, Chatzi E (2015) Dynamic response of an innovative hybrid structure in hardwood. Proc Inst Civ Eng Constr Mater 168(3):132–143. https://doi.org/10.1680/coma.14.00043
Loss C, Tannert T, Tesfamariam S (2018) State-of-the-art review of displacement-based seismic design of timber buildings. Constr Build Mater 191:481–497
Masaeli M, Gilbert BP, Karampour H, Underhill ID, Lyu CH, Gunalan S (2020) Scaling effect on the moment and shear responses of three types of beam-to-column connectors used in mass timber buildings. Eng Struct 208:110329
Newcombe MP, Pampanin S, Buchanan A, Palermo A (2008) Seismic design of post-tensioned timber frames. In: 14th World conference in earthquake engineering, Beijing, China; p 8. (paper no. S12-008)
Newcombe MP, Pampanin S, Buchanan AH (2010) Global response of a two-storey Pres-Lam building. In: Proceedings of New Zealand society for earthquake engineering confernce Wellington, New Zealand: New Zealand Society for Earthquake Engineering
Palermo A, Pampanin S, Buchanan A, Newcombe M (2005) Seismic design of multi-storey buildings using laminated veneer lumber (LVL). In: Proceedings of New Zealand society for earthquake engineering conference Wairakei, New Zealand: New Zealand Society for Earthquake Engineering
Pei S, van de Lindt JW, Barbosa AR, Berman JW, McDonnell E, Dolan JD, Blomgren HE, Zimmerman RB, Huang D, Wichman S (2019) Experimental seismic response of a resilient 2-story mass-timber building with post-tensioned rocking walls. J Struct Eng 145(11):04019120
Polocoșer T, Leimcke J, Kasal B (2018) Report on the seismic performance of three-dimensional moment-resisting timber frames with frictional damping in beam-to-column connections. Adv Struct Eng 21(11):1652–1663
Ponzo FC, Smith T, Di Cesare A, Pampanin S, Carradine D, Nigro D (2012) Shaking table test of a multistorey post- Tensioned glulam building: design and construction. In: WCTE 2012, Auckland, New Zealand, vol 2, pp 44–52
Ponzo FC, Di Cesare A, Lamarucciola N (2018) Modelling of post-tensioned timber-framed buildings with seismic rocking mechanism at the column-foundation connections. Int J Comput Methods Exp Meas 5:966–978. https://doi.org/10.2495/CMEM-V5-N6-966-978
Ponzo FC, Di Cesare A, Lamarucciola N, Nigro D (2019) Seismic design and testing of post-tensioned timber buildings with dissipative bracing systems. Front Built Environ 5:104
Priestley NMJ (1991) Overview of the PRESSS research program. PCI J 36(4):50–57. https://doi.org/10.15554/pcij.07011991.50.57
Priestley MJN, Grant DN (2005) Viscous damping in seismic design and analysis. J Earthq Eng 9:229–255. https://doi.org/10.1142/S1363246905002365
Priestley MJN, Calvi GM, Kowalsky MJ (2007) Displacement-based seismic design of structures. IUSS Press, Pavia
Ríos-García G, Benavent-Climent A (2020) New rocking column with control of negative stiffness displacement range and its application to RC frames. Eng Struct 206:110133
Sarti F, Palermo A, Pampanin S (2015) Development and testing of an alternative dissipative post-tensioned rocking timber wall with boundary columns. J Struct Eng 142(4):E4015011. https://doi.org/10.1061/(ASCE)ST.1943-541X.0001390
Sarti F, Palermo A, Pampanin S (2016) Quasi-static cyclic testing of two-thirds scale unbonded posttensioned rocking dissipative timber walls. J Struct Eng 142(4):E4015005
Smith T, Ponzo FC, Di Cesare A, Pampanin S, Carradine D, Buchanan AH, Nigro D (2014) Post-tensioned Glulam Beam-column joints with advanced damping systems: testing and numerical analysis. J Earthq Eng 18(1):147–167
Ugalde D, Almazán JL, Santa MH, Guindos P (2019) Seismic protection technologies for timber structures: a review. Eur J Wood Wood Prod 77:173–194. https://doi.org/10.1007/s00107-019-01389-9
UNI EN 15129 (2018) Anti-seismic devices, CEN, European Committee for Standardization
UNI EN 1998-1 (2013) EUROCODE 8: design of structures for earthquake resistance—part 1: general rules, seismic actions and rules for buildings. European Committee for Standardization
Van de Lindt JW, Amini MO, Furley J, Pei S, Tamagnone G, Barbosa AR, Line P, Rammer D, Fragiacomo M (2018) Experimental seismic behavior of a two-story CLT platform building: shake table testing results. WCTE 2018, Center Seoul; 20–23 August, Seoul, South Korea
Welch PD (1961) A direct digital method of power spectrum estimation. IBM J Res Dev 5:141–156
Acknowledgements
The authors would like to acknowledge the DPC-RELUIS 2019-2021 Project for the financial support and Prof. Stefano Pampanin for his contribute to the research study.
Funding
Open access funding provided by Università degli Studi della Basilicata within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Di Cesare, A., Ponzo, F.C., Lamarucciola, N. et al. Experimental seismic response of a resilient 3-storey post-tensioned timber framed building with dissipative braces. Bull Earthquake Eng 18, 6825–6848 (2020). https://doi.org/10.1007/s10518-020-00969-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10518-020-00969-y