Magnetic damped links to reduce internal seismic pounding in base-isolated buildings

Abstract

A limited gap between closely spaced structural parts may induce internal pounding in seismically isolated structures, because of notable displacement at the level of the isolation system under severe earthquakes. A gap between a fixed-base elevator shaft and the surrounding building is presented here with reference to a reinforced concrete building located in the Sicilian town of Augusta. The building, comprising a basement and three storeys above the ground level, is seismically isolated at the top of rigid columns in the basement with a hybrid isolation system including elastomeric and sliding bearings, while a steel framed elevator shaft crosses the isolation level. Despite the gap, internal pounding may occur at all levels of the superstructure when the elevator with maximum load stops at the upper floors. To reduce structural pounding effects, a magnetic damped link (MDL) between adjacent corners of the elevator and the surrounding building is proposed. This is obtained as an in parallel combination of an eddy current damped link (ECDL) and an elastic helicoidal spring, and occupies less space than traditional passive dampers and transmits considerably less forces compared to a rigid link configuration. Specifically, an ECDL consists of an outer cylindrical copper tube, as conductor, and an inner tube, equipped with an array of axially magnetized and ring-shaped permanent magnets separated by iron pole pieces, as mover. The relative motion between conductor and magnets, during seismic loading, induces an eddy current producing electromagnetic damping. Given that viscoelastic linear behaviour can be hypothesized for the MDL, a simplified iterative design procedure of the ECDL is proposed, with optimization of the thickness and radius of the magnets, thereby enhancing magnetic flux and energy dissipation. The directionality of the near-fault ground motions is investigated through nonlinear seismic analysis, comparing no connection with four configurations of the interconnection: i.e., flexible and rigid elastic links, viscous and magnetic damped links.

1 Introduction

Seismic pounding between two or more of adjacent buildings, of differing dynamic properties and built in close proximity to one other as is often the case in urban settings, has been observed in past earthquakes and investigated in many works (e.g. Efraimiadou et al. 2013; Abdel Raheem et al. 2019). The potential for impact increases for base-isolated buildings, where large horizontal displacements of the superstructure are expected (Komodromos et al. 2007; Agarwal et al. 2007; Polycarpou and Komodromos 2010; Pant and Wijeyewickrema 2012). This may occur due to the fact that out-of-phase movements of independent units may lead to structural interaction during an earthquake (Maison and Kasai 1992). However, little attention has been paid to the internal pounding between a fixed-base elevator shaft and/or stairs crossing the isolation level and structural parts of the surrounding seismically isolated building (Mazza and Labernarda 2018). Previous studies showed that seismic pounding may lead to significant damage of the lighter structure (e.g. the elevator shaft), whereas the behaviour of the heavier structure (i.e. the main building) is only slightly influenced by collisions (Jankowski 2009). Up until now many pounding models between adjacent structures have been proposed, based on an impact force with linear or nonlinear stiffness and with or without energy dissipation (e.g. Anagnostopoulos and Spiliopoulos 1992; Jankowski 2005; Jankowski 2006; Kose and Abacioglu 2008; Rojas and Anderson 2012; Pratesi et al. 2014). Moreover, the high deformability of an isolated structure may lead to amplification in the pounding under anomalous ground motions like those recorded near-faults (Pant 2013; Mazza and Labernarda 2018), where considerable displacement is expected under long-duration and high-amplitude velocity pulses (Chioccarelli and Iervolino 2010). Seismic codes require a minimum gap between independent units of the same building, depending on maximum horizontal displacement of the two units at the corresponding level under the design basis (NTC18 2018) and/or maximum considered (EC8 Eurocode 2004) earthquakes. Moreover, some works have started to investigate spatial aspects of the structural pounding related to torsional vibrations of in-plan asymmetric buildings, inducing tangential forces that may develop due to friction (Mavronicola et al. 2017), and the incidence angle of the horizontal seismic loads (Mavronicola et al. 2020).

The simplest way to avoid or reduce internal pounding is to design a clear separation joint preventing pounding between the potentially colliding systems, but such a gap may well conflict with practical considerations that may make the creation of a sufficiently wide internal gap problematic. One alternative is to minimize the effect of pounding through decreasing lateral motion at the level of the isolation system with a self-stopping mechanism (Ismail 2014) or a passive gap damper (Rawlinson et al. 2015), but a substantial increase in the shear and drift demands of the superstructure represents the counterpart (Mazza and Vulcano 2009). In-phase motion of adjacent structures is expected with rigid links placed at critical locations (e.g. floor levels), but an increase of base shear on the stiffer structure and significant mutual forces are transmitted (Westermo 1989). Alternatively, bumper dampers made with polymers prove effective in shock absorbers, but they are activated when the gap is closed and generally increase the pounding times (He et al. 2018). In order to prevent mutual pounding under severe earthquakes, the idea of connecting two structures with different dynamic properties by using traditional passive devices was explored in the early 1970s, by using displacement-activated (e.g. friction, FR, and metallic-yielding, YL), velocity-activated (e.g. viscous, VS, and viscoelastic, VE) and motion-activated (e.g. tuned mass, TM, and tuned liquid, TL) dampers (Christopoulos and Filiatrault 2006; Jankowski and Mahmoud 2016). FR (Bhaskararao and Jangid 2006) and YL (Ni et al. 2001) dampers are characterized by a stable hysteretic behaviour independent of temperature and velocity of motion whose activation is triggered when preset stress levels are reached. These devices are generally manufactured from traditional materials and require little maintenance, representing a low cost and reliable solution for energy dissipation. On the other hand, VS (Xu et al. 1999; Zhang and Xu 1999; Licari et al. 2015; Tubaldi et al. 2014) and VE (Zu and Xu 2005; Kim et al. 2006) dampers have a higher cost, but are characterized by self-centring capability and are reusable after strong earthquakes. Finally, a shared tuned mass damper connected to adjacent buildings has been proposed to reduce both structural vibrations and the likelihood of seismic pounding, but with additional problems of tuning for the stiffness and damping properties (Abdullah et al. 2001). However, the space for damper installation between different subsystems of a same structure is generally very limited. A convenient and feasible strategy to overcome this is to install a magnetic damped link (MDL), representing one of the most recent developed vibration control systems which takes up less space than other types while allowing a damping of the same order as viscous dampers. This type produces an electromagnetic damping force by using an array of axially magnetized ring-shaped permanent magnets separated by iron pole pieces (Ebrahimi et al. 2008; Wang et al. 2012). Specifically, the movement of a magnet through a conducting material, without mechanical contact, causes eddy currents to flow in the conductor, with a resulting drag force through the resistance of the conductor proportional to the velocity similar to a viscous damper.

With the aim of studying the effects of damped links to reduce internal pounding, a recently constructed commercial building in the Sicilian town of Augusta (Italy) is considered as test structure for the numerical investigation (Athanasiou 2015). Specifically, an r.c. framed structure with rectangular plan, composed of a basement and three storeys above ground level, is seismically isolated with a hybrid system including sixteen elastomeric (i.e. High-Damping-Rubber Bearings, HDRBs) and sixteen sliding (i.e. Low-Friction-Sliding Bearings, LFSBs) bearings. An internal elevator shaft with a fixed-base steel frame crosses the isolation plane and emerges in the basement. In order to prevent mutual pounding of these parts under severe earthquakes, a major innovation is proposed in the form of a MDL at the floor levels, between adjacent corners of the elevator and surrounding building. Stiffness and damping properties of the MDL are first designed through an iterative procedure where minima floor displacements of the elevator are selected as performance targets. Optimization of the thickness and radius of the magnets, so as to enhance magnetic flux and energy dissipation, is carried out on the assumption of viscoelastic linear behaviour of the MDL. A seismic gap is also designed to verify the possibility of displacement of the steel structure and deformation of the isolation system, without internal pounding of the unconnected r.c. superstructure. To this end, the effectiveness of the Italian (NTC18 2018) and European (EC8 Eurocode 2004) seismic codes provisions is investigated, based on the assigned design gaps between independent units of a building expressed as function of maximum horizontal displacement of the two units at the same level. Coupling with links placed only at top level and at all levels is checked by means of nonlinear dynamic analysis of the said building considering the effect of seismic orientation, with reference to near-fault ground motions selected from the Pacific Earthquake Engineering Research center database (PEER 2014) and scaled in line with the design hypotheses adopted. Traditional interconnection, assuming flexible and rigid elastic links and viscous damped links, and no connection are also considered as a comparison.

2 Design of the seismically isolated benchmark building

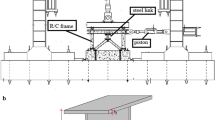
An r.c. commercial building located in the Sicilian town of Augusta (Italy), composed of a basement, two storeys above ground level and a penthouse, is considered as test structure (Fig. 1a). It is seismically isolated with a hybrid system including sixteen elastomeric (i.e. HDRBs) and sixteen sliding (i.e. LFSBs) isolators inserted at the top of rigid columns in the basement (Fig. 1b). R.c. floor slabs with thickness equal to 250 mm and hollow bricks are used for all storeys. The presence of the staircase, made of a 200 mm thick r.c. slab with a half landing configuration, and steel framed elevator core, crossing the isolation level, introduces some asymmetry with respect to the longitudinal direction (i.e. X axis) of the building plan (Fig. 1c, d). In-elevation and in-plan geometric dimensions of the building are shown in Fig. 1c, d, respectively. A reference life V_R = 75 years, corresponding to a nominal life V_N = 50 years and a coefficient of use C_u = 1.5 (i.e. functional class III), are considered in line with the former Italian seismic code (NTC08 2008) for the building site (i.e. longitude 15.2135°and latitude 37.2508°).

Fig. 1

R.c. framed building in the Sicilian town of Augusta, Italy (units in cm)

The design of the isolation system is carried out on the basis of the following assumptions for the horizontal seismic loads at the collapse prevention (CP) limit state: equivalent viscous damping of the isolation system ξ_H = 15%; high-risk seismic zone (peak ground acceleration on rock, a_g = 0.406 g); stiff subsoil (class B, with subsoil parameter S_S = 1.018); topographic class T1 (stratigraphic parameter S_T = 1); displacement demand d_dc = 270 mm. The fundamental vibration period of the seismically-isolated structure is equal to T_1H = 2.38 s (Oliveto et al. 2013), corresponding to a mass of the superstructure equal to 2400 ton and a horizontal stiffness of the isolation system of 16.45 kN/mm. The latter is divided between the sixteen HDRBs on the assumption that the stiffness contribution of the sixteen LFSBs is negligible. Type SI-N500/150 is selected for the HDRBs produced by FIP Industriale (FIP Industriale S.p.A. 2018), corresponding to normal rubber compound with a shear modulus G = 0.8 MPa, assuming the geometrical and mechanical properties shown in Table 1: i.e. external diameter of the isolator (D_b); total thickness of the rubber (t_r); primary (S₁) and secondary (S₂) shape factors; horizontal (ξ_H) and vertical (ξ_V) viscous damping ratios; horizontal (K_H0) and vertical (K_V0) stiffnesses at the shear deformation γ = 1; maximum vertical load (P_c) and displacement capacity (d_c) at the CP limit state. Two types of LFSBs produced by the same company are placed in the building plan depending on the maximum loading capacity (Fig. 1b): i.e. type 1, VM 200/600/600, and type 2, VM 150/600/600, where the first number represents the vertical load capacity in tons (P_c) and the other two the permitted longitudinal and transversal movements in mm (± d_c). Moreover, a dynamic-fast friction coefficient μ_fast = 1.7% is the outcome of a calibration process (Gesualdi et al. 2018). Further details on the design of the base-isolation system can be found in Oliveto et al. (2013).

Table 1 Geometrical and mechanical properties of the HDRBs (units in kN, mm and s)

The design of the superstructure is carried out at the ultimate life-safety (LS) limit state, under the corresponding horizontal seismic loads (i.e. a_g = 0.285 g and S_S = 1.136), assuming nearly elastic response (behaviour factor, q = 1.5). The vertical gravity loads applied to the first three levels consist of a dead-load q_dl = 6.75 kN/m² and a live-load q_ll = 3 kN/m², while q_dl = 5.65 kN/m² and q_ll = 1 kN/m² are assumed on the roof. Perimeter masonry infills without openings, corresponding to an additional dead load of 2.7 kN/m², are placed along the short façade of the building, at the second storey, and in the central bay of the long façade of the building, at the first and second storey, while additional masonry infills are also placed around the staircase. The characteristic values of the cylindrical compressive strength of concrete and yield strength of steel are 30 N/mm² and 450 N/mm², respectively. The length of the frame members is shown in Fig. 1, where cross-sections of columns (Fig. 1c) and beams (Fig. 1d) are also reported. Columns n. 4, 5, 28 and 29 (Fig. 1d) at the penthouse level have dimensions equal to those of the floor below (i.e. 50 × 50 cm²) while the remaining columns present a reduced section (i.e. 30 × 30 cm²).

The steel frame elevator shaft crosses the isolation plane and emerges in the basement where it is fixed-base and separated from the surrounding building by a gap (Fig. 2a). The elevator shaft is classified as non-dissipative (i.e. behaviour factor q = 1) and designed at the LS limit state. A dead load of 10 kN plus a live load of 10 kN, depending on the maximum number of persons allowed, are considered for the elevator. Moreover, a lightweight infill panel of the elevator shaft equal to 0.43 kN/m² is applied on three sides of its perimeter. For the elevator eight design scenarios are considered, assuming maximum (W_elev. = 20 kN) and minimum (i.e. empty, W_elev. = 10 kN) loads combined with four different vertical positions, corresponding to the basement (level -1 in Fig. 2b) and three floors above (levels 0, 1 and 2 shown in Fig. 2c–e). The elevator shaft is designed to fulfil the full operational [∆/h = 0.33%, defined as interstorey drift (Δ) normalized by the storey height (h)] and operational (∆/h = 0.5%) deformability limit states, under the corresponding horizontal seismic loads (FO: a_g = 0.056 g and S_S = 1.20; OP: a_g = 0.076 g and S_S = 1.20), and ultimate LS limit states for strength and buckling. Cross-sections of steel frame members are assumed constant along the height and ductile, in line with class 1 (i.e. double-T steel sections type HEA 120 for beams) and 2 (i.e. double-T steel sections type HEA 160 for columns, with principal axis oriented as shown in Fig. 2a) provided by the former Italian seismic code (NTC08 2008). Yield and ultimate strengths of 355 N/mm² and 510 N/mm² are assumed for the steel, respectively. Finally, the dynamic properties of the elevator shaft for different vertical positions of the elevator at maximum load are presented in Table 2: i.e. fundamental vibration periods (T_1,X and T_1,Y) and effective masses (m_e1,X and m_e1,Y) along the principal axes of the building plan.

Fig. 2

Steel framed elevator shaft of the Augusta building (units in cm)

Table 2 Dynamic properties of the steel framed elevator shaft

A three-spring-three-dashpot viscoelastic model is adopted for an HDRB, consisting of three different couples constituted of an elastic spring and a viscous dashpot connected in parallel along the horizontal (x and y) and vertical (z) axes of the global coordinate system. Specifically, coupled nonlinear elastic springs in the horizontal (F_K,x, F_K,y) and vertical (P_K) directions proportional to horizontal and vertical displacement (u_H,x, u_H,y and u_V), with a vertical displacement (${\text{u}}_{\text{V}}^{ *}$) taking into account the axial shortening or lengthening due to second order geometric effects, are assumed (Mazza and Labernarda 2018)

$$\left\{ \begin{aligned} F_{K,x} \hfill \\ F_{K,y} \hfill \\ \end{aligned} \right\} = \bar{K}_{H0} \cdot \left( {1 - \left( {\frac{P}{{P^{\prime}_{cr} }}} \right)^{2} } \right) \cdot \left\{ \begin{aligned} u_{H,x} \hfill \\ u_{H,y} \hfill \\ \end{aligned} \right\} = K_{H0} \cdot \left[ {0.337 + 0.663 \cdot e^{ - 4.64 \cdot \gamma } } \right] \cdot \left( {1 - \left( {\frac{P}{{P^{\prime}_{cr} }}} \right)^{2} } \right) \cdot \left\{ \begin{aligned} u_{H,x} \hfill \\ u_{H,y} \hfill \\ \end{aligned} \right\}$$

(1a)

$$P_{K} \text{ = }\bar{K}_{V0} \cdot u_{V}^{*} \cong \frac{{K_{V0} \cdot sgn\left( {u_{V} } \right)}}{{1 + 48 \cdot \left( {\frac{{\varvec{u}_{H} }}{{\pi \cdot D_{b} }}} \right)^{2} }} \cdot \left( {\left| {u_{V} } \right|-\frac{{16 \cdot \alpha_{b} }}{{\pi^{2} \cdot D_{b} \cdot S_{2} \cdot \alpha_{K0} }} \cdot \varvec{u}_{H}^{2} } \right)$$

(1b)

where α_K0(= K_V0/K_H0) is the nominal stiffness ratio, ${\text{P}}_{\text{cr}}^{'}$ is the reduced critical buckling load and α_b = h_b/t_r, h_b being the total height of the bearing and t_r the total thickness of the rubber. It is worth noting that the horizontal stiffness is characterized by significant variation when shear deformation (γ) is lower than 1 and is practically constant for γ values greater than 1.

On the other hand, taking into consideration that the equivalent viscous damping in the horizontal direction depends on the amplitude of the shear strain (Markou et al. 2017), the following uncoupled damping axial forces (F_C,x, F_C,y and P_C), proportional to the horizontal and vertical velocity (${\dot{\text{u}}}_{{{\text{H}},{\text{x}}}} ,$ ${\dot{\text{u}}}_{{{\text{H}},{\text{y}}}}$ and ${\dot{\text{u}}}_{\text{V}}$), are assumed

$$\left\{ \begin{aligned} F_{C,x} \hfill \\ F_{C,y} \hfill \\ \end{aligned} \right\} = \bar{C}_{H0} \cdot \left\{ \begin{aligned} \dot{u}_{H,x} \hfill \\ \dot{u}_{H,y} \hfill \\ \end{aligned} \right\} = C_{H0} \cdot \left[ {0.543 + 0.457 \cdot e^{ - 2.843 \cdot \gamma } } \right] \cdot \left\{ \begin{aligned} \dot{u}_{H,x} \hfill \\ \dot{u}_{H,y} \hfill \\ \end{aligned} \right\}$$

(2a)

$$P_{C} \text{ = }C_{V0} \cdot \dot{u}_{V} { \cong }\frac{{\xi_{V} \cdot K_{V1} \cdot T_{1V} }}{\pi } \cdot \dot{u}_{V}$$

(2b)

with significant differences for low horizontal displacements and almost the same values when γ > 1 are obtained (see Eq. 2a).

On the other hand, for the sliding bearings with low values of the friction coefficient (i.e. steel-PTFE low friction flat sliding bearings, LFSBs, corresponding to the types 1 and 2 shown in Fig. 1b), a simplified force–displacement behaviour in the horizontal directions is assumed. In particular, variable axial load (i.e. N = W±∆N, W being the weight of the superstructure and ∆N the additional axial load, positive when compressive, due to the overturning moment produced by the horizontal ground acceleration) and constant value of the friction coefficient (i.e. μ equal to the dynamic fast value μ_fast) are represented by a hysteretic model with biaxial interaction

$$\left\{ \begin{aligned} F_{x} \hfill \\ F_{y} \hfill \\ \end{aligned} \right\} = \mu_{fast} \cdot N \cdot \left\{ \begin{aligned} Z_{x} \hfill \\ Z_{y} \hfill \\ \end{aligned} \right\} = \mu_{fast} \cdot N \cdot \left\{ \begin{aligned} cos\theta \hfill \\ sin\theta \hfill \\ \end{aligned} \right\}, \, \theta = \arctan \left( {\frac{{F_{y} }}{{F_{x} }}} \right)$$

(3a)

where the dimensionless quantities Z_x and Z_y represent the biaxial interaction. Moreover, a gap element in the vertical direction takes into account that a FSB cannot resist tensile axial loads and is hence free to uplift when the variation of the axial load is large enough to produce its reversal from compression to tension

$$P = N \, \text{for} \, u_{V} \ge 0 \, \text{and} \, P = 0 \, \text{for} \, u_{V} < 0$$

(3b)

where the equivalent viscous damping in the vertical direction is neglected.

3 Design of the connection for mitigating internal pounding

A seismic gap (g_d) between the fixed-base elevator shaft (Es) and base-isolated surrounding building (Sb) is first designed on the basis of current Italian (NTC18 2018) and European (EC8 2004) seismic codes (Fig. 3a). Specifically, three different thresholds are evaluated as function of the lateral load resisting system (i.e. base-isolated or fixed-base structure), the LS (i.e. PGA_LS = 0.324 g) and CP (i.e. PGA_CP = 0.413 g) limit states and the elevator height (i.e. H = 14.06 m): i.e. sum of the horizontal top displacements of both systems at the LS limit state (i.e. g_d,NTC18 = 33 cm), no less than 2·H/100·a_g·S/g; square root of the sum of the squares of the maximum top horizontal displacements of both systems, at the LS (i.e. g_d,EC8.1 = 24 cm) and CP (i.e. g_d,EC8.2 = 35 cm) limit states. To ensure that the seismic gap is large enough to cope with sizeable horizontal displacements induced by strong earthquakes, the Es-Sb relative displacements are evaluated along the in-plan X (i.e. u_Es,i and u_Sb,i) and Y (i.e. v_Es,i and v_Sb,i) directions

$$g_{X,i} \left( t \right) = u_{Es,i} \left( t \right) - u_{Sb,i} \left( t \right), \, g_{Y,i} \left( t \right) = v_{Es,i} \left( t \right) - v_{Sb,i} \left( t \right) , {\text{ i}} = 1 - 4$$

(4)

with positive value when the coordinate of the Es corner is greater than that of the corresponding Sb corner (Fig. 3a).

Fig. 3

Internal gap between the fixed-base elevator shaft and base-isolated surrounding building

The problem of connecting two different subsystems of the same structure is examined for four types of connection between the four couples of corner joints at each floor level (Fig. 3c): i.e. flexible links (FLs); rigid links (RLs); viscous damped links (VDLs); magnetic damped links (MDLs). Once selected the type of connection, the model of coupling between the base-isolated Sb and fixed-base Es is made only at the top floor (case A, Fig. 4a) or at all floors (case B, Fig. 4b) along both the principal in-plan directions (i.e. X and Y), under the following assumptions: (1) mass, stiffness and damping of the Sb (m_Sb,j, k_Sb,j and c_Sb,j) and Es (m_Es,j, k_Es,j and c_Sb,j) and stiffness and damping of the connective links (k_L,j and c_L,j) can be varied along the height (j = 0–3); (2) viscous damping of the Sb is considered only at the isolation level (c_Sb,0), while the contribution of the superstructure is not considered; (3) assuming an equivalent viscous damping ratio ξ_Es,H = 2%, the Rayleigh approach is used to evaluate the viscous damping of the Es; (4) the Sb and Es are modelled as shear- (r.c.) and flexible-type (steel) plane frames, respectively; (5) floor elevations are the same for Sb and Es, without taking into account the extra head at top of the elevator shaft; (6) elevator with maximum load stops at the second level. The main properties of the surrounding building (Sb) and elevator shaft (Es) are reported in Table 3.

Fig. 4

Models of coupling between surrounding building (Sb) and elevator shaft (Es)

Table 3 Main properties of the model of coupling between Sb and Es

It should be noted that a tridiagonal stiffness matrix corresponds to Sb, with the same storey stiffness for the X and Y directions since all columns have a square section, while full stiffness and damping matrices of Es with different values along the principal axes are expected. Along each principal direction, the equation of motion of the coupled system subjected to a harmonic ground excitation, corresponding to the ground acceleration ü_g and the fundamental frequency of the elevator ω_Es,p (p ${ \in }$(X,Y)), can be written in matrix form as follows

$$\left[ M \right] \cdot \left\{ {\ddot{u}\left( t \right)} \right\}_{p} + \left[ C \right]_{p} \cdot \left\{ {\dot{u}\left( t \right)} \right\}_{p} + \left[ K \right]_{p} \cdot \left\{ {u\left( t \right)} \right\}_{p} = - \left[ M \right] \cdot \left\{ 1 \right\} \cdot \ddot{u}_{g} \cdot e^{{i\omega_{Es,p} t}} = - \left\{ Q \right\} \cdot e^{{i\omega_{Es,p} t}} , \, p \in (X,Y)$$

(5)

in which [M] is the diagonal mass matrix and [K]_p and [C]_p (p ${ \in }$(X,Y)) are the stiffness and damping full matrices, all having dimensions [8 × 8] because a static condensation of the number of degrees of freedom reduces the number of free displacement to eight (i.e. four horizontal displacements for Sb and Es, respectively)

$$\left[ M \right] = \left[ {\begin{array}{*{20}c} {\left[ {M_{Sb} } \right]} & {\left[ \text{0} \right]} \\ {\left[ \text{0} \right]} & {\left[ {M_{Es} } \right]} \\ \end{array} } \right]; \, \left[ C \right]_{p} = \left[ {\begin{array}{*{20}c} {\left[ {C_{Sb} } \right]} & {\left[ \text{0} \right]} \\ {\left[ \text{0} \right]} & {\left[ {C_{Es} } \right]} \\ \end{array} } \right]_{p} + \left[ {C_{link} } \right]_{p} ; \, \left[ K \right]_{p} = \left[ {\begin{array}{*{20}c} {\left[ {K_{Sb} } \right]} & {\left[ \text{0} \right]} \\ {\left[ \text{0} \right]} & {\left[ {K_{Es} } \right]} \\ \end{array} } \right]_{p} + \left[ {K_{link} } \right]_{p} , \, p \in (X,Y)$$

(6)

being [K_link]_p and [C_link]_p the sparse stiffness and damping matrices of the link elements

$$\left[ {K_{link} } \right]_{p} = \left[ {\begin{array}{*{20}c} {{\text{k}}_{\text{L0}} } & 0 & 0 & 0 & {-{\text{k}}_{\text{L0}} } & 0 & 0 & 0 \\ 0 & {{\text{k}}_{\text{L1}} } & 0 & 0 & 0 & {-{\text{k}}_{\text{L1}} } & 0 & 0 \\ 0 & 0 & {{\text{k}}_{\text{L2}} } & 0 & 0 & 0 & {-{\text{k}}_{\text{L2}} } & 0 \\ 0 & 0 & 0 & {{\text{k}}_{\text{L3}} } & 0 & 0 & 0 & {-{\text{k}}_{\text{L3}} } \\ {-{\text{k}}_{\text{L0}} } & 0 & 0 & 0 & {{\text{k}}_{\text{L0}} } & 0 & 0 & 0 \\ 0 & {-{\text{k}}_{\text{L1}} } & 0 & 0 & 0 & {{\text{k}}_{\text{L1}} } & 0 & 0 \\ 0 & 0 & {-{\text{k}}_{\text{L2}} } & 0 & 0 & 0 & {{\text{k}}_{\text{L2}} } & 0 \\ 0 & 0 & 0 & {-{\text{k}}_{\text{L3}} } & 0 & 0 & 0 & {{\text{k}}_{\text{L3}} } \\ \end{array} } \right]_{p} , \, p \in (X,Y)$$

(7)

$$\left[ {C_{link} } \right]_{p} = \left[ {\begin{array}{*{20}c} {{\text{c}}_{\text{L0}} } & 0 & 0 & 0 & {-{\text{c}}_{\text{L0}} } & 0 & 0 & 0 \\ 0 & {{\text{c}}_{\text{L1}} } & 0 & 0 & 0 & {-{\text{c}}_{\text{L1}} } & 0 & 0 \\ 0 & 0 & {{\text{c}}_{\text{L2}} } & 0 & 0 & 0 & {-{\text{c}}_{\text{L2}} } & 0 \\ 0 & 0 & 0 & {{\text{c}}_{\text{L3}} } & 0 & 0 & 0 & {-{\text{c}}_{\text{L3}} } \\ {-{\text{c}}_{\text{L0}} } & 0 & 0 & 0 & {{\text{c}}_{\text{L0}} } & 0 & 0 & 0 \\ 0 & {-{\text{c}}_{\text{L1}} } & 0 & 0 & 0 & {{\text{c}}_{\text{L1}} } & 0 & 0 \\ 0 & 0 & {-{\text{c}}_{\text{L2}} } & 0 & 0 & 0 & {{\text{c}}_{\text{L2}} } & 0 \\ 0 & 0 & 0 & {-{\text{c}}_{\text{L3}} } & 0 & 0 & 0 & {{\text{c}}_{\text{L3}} } \\ \end{array} } \right]_{p} , \, p \in (X,Y) \,$$

(8)

Then, the displacement vector is obtained as the real part of the closed-form solution

$$\left\{ u \right\}_{p} = \text{Re} \left\{ {\left\{ { - \omega_{Es,p}^{2} \cdot \left[ M \right] + i\omega_{Es,p} \cdot \left[ C \right]_{p} + \left[ K \right]_{p} } \right\}^{ - 1} \cdot \left\{ Q \right\}} \right\}, \, p \in (X,Y)$$

(9)

assuming the following expressions

$$\left\{ {u\left( t \right)} \right\}_{p} = q_{p} \cdot e^{{i\omega_{Es,p} t}} , \, \left\{ {\dot{u}\left( t \right)} \right\}_{p} = i\omega_{Es,p} \cdot q_{p} \cdot e^{{i\omega_{Es,p} t}} , \, \left\{ {\ddot{u}\left( t \right)} \right\}_{p} = -\omega_{Es,p}^{2} \cdot q_{p} \cdot e^{{i\omega_{Es,p} t}} , \, p \in (X,Y) \,$$

(10)

Many design procedures of dissipative links connecting adjacent structures are proposed in literature in order to optimize their placement and sizing in accordance with the minimization of suitable response quantities (Patel and Jangid 2013; Tubaldi 2015; Kandemir-Mazanoglu and Mazanoglu 2017; Gattulli et al. 2018). In this paper, a design procedure is proposed to evaluate the vertical distribution of stiffness (k_L,j, j = 0–3), with the objective of minimizing horizontal displacement of the elevator at all levels (u_i, i = 0–3). Firstly, each link is supposed to be elastic, introducing constraints on the motion of the coupled systems but providing no dissipation (i.e. [C_link]_p = [0]). A four-sweep-four-step iterative approach is implemented, where the first sweep starts (step 1) assigning a zero value of the stiffness to links of the first three levels (k_L,j = 0, j = 0–2), then searching the stiffness k*_L,3 that minimizes horizontal displacement of the elevator at that level. In the second step of the first sweep, starting from assigned values of stiffness at the first two (k_L,j = 0, j = 0–1) and last (k_L,3 = k*_L,3) levels, the stiffness k*_L,2 is evaluated so as to minimize the horizontal displacement at the second level. Once an initial value of stiffness is evaluated for the links at all levels (see step 4 of the first sweep), an iterative procedure is applied in which the k-th sweep consists of four steps each with the aim of evaluating stiffness by reducing the horizontal displacement at one level at a time, for fixed values of stiffness at the other levels. An upper bound value of the stiffness (i.e. k_L,lim = 400 kN/m) is assigned for all levels, so limiting geometric dimensions of the damped links to values compatible with seismic gap provisions imposed by Italian (NTC18 2018) and European (EC8 Eurocode 2004) code provisions (see numerical results). Note that the absolute minimum value of the horizontal displacement is searched for the elevator at all floor levels, varying the stiffness in the range 0–k_L,lim with a stiffness-step ∆k_L = k_L,lim/100 able to ensure that all relative minimum points are checked. Results of the iterative procedure, in terms of the horizontal displacement ratio (u_i/u_max, being u_max the maximum displacement of the iterative procedure selected from all levels), are shown in Fig. 5, with reference to both principal in-plan directions (Fig. 3). Note that maximum displacement (i.e. u_i/u_max = 1.0) is obtained to step four of the first sweep along both the principal in-plan directions (Fig. 5a). Moreover, gradual reduction of the ratio u_i/u_max occurs at all four levels proving the effectiveness of the iterative procedure (Fig. 5d). Finally, damping force of the dissipative links is evaluated based on a stiffness-proportional criterion, with equivalent viscous damping ratio ξ_DL = 25%. Stiffness and damping properties of the links are summarized in Table 4 (see case B).

Fig. 5

Results of the four-sweep-four step iterative design procedure of links

Table 4 Main properties of links (units in kN, m and s)

As an alternative solution, connection at only one floor level is assumed, using properties of the magnetic links previously evaluated (see case B of Table 4). To this end, maximum dimensionless displacement (u_i/u_max, being u_max the maximum floor displacement at step 4 of the fourth sweep) over the height of the building is plotted in Fig. 6, with reference to four different positions of the links (i.e. L_i, i = 0–3) along the X and Y directions. As can be observed, the optimal behaviour corresponds to link at the top level (see case A of Table 4).

Fig. 6

Results corresponding to link placed only at a floor level

4 Optimized design of the magnetic damped link

A sketch of the magnetic damped link (MDL), obtained as an in parallel combination of an eddy current damped link (ECDL) and an elastic helicoidal spring, is shown in Fig. 7. Specifically, the ECDL shown in Fig. 7a, b consists of an outer cylindrical tube, as conductor, and an array of axially magnetized ring-shaped permanent magnets, separated by iron pole pieces, as a mover (Ebrahimi et al. 2008). In detail, eddy currents are generated in the copper conductor following the relative motion from the magnets, where the direction of magnetization for each permanent magnet is indicated by bold arrows. It should be noted that these eddy currents produce an electromagnetic damping force proportional to the velocity of the conductor so that the ECDL acts as a viscous damper but with a significant improvement because it takes up less space.

Fig. 7

Sketch of a magnetic damped link (MDL) constituted of an in parallel combination of an eddy current damped link (ECDL) and an elastic helicoidal spring

An optimized design of the ECDL is carried out in order to ensure the highest damping force consistent with the lowest dimensions along the longitudinal axis of the damper. To this end, the equivalent damping constant is expressed as function of the pole thickness (t_p), the magnet thickness (t_m) and the inside r_in(= r_m + a_g, where r_m is the annular magnet radius and a_g is the air gap) and outside r_out(= r_in + t_c, where t_c is the conductor thickness) radii (Ebrahimi et al. 2009):

$$c_{L} = \sigma \cdot t_{p} \cdot \int\limits_{0}^{2\pi } {\int\limits_{{r_{in} }}^{{r_{out} }} {r \cdot B_{r}^{2} (r,z_{0} ) \cdot e^{{\frac{{ - (r - r_{in} )}}{{\delta_{p} }}}} dr \cdot d\theta } } ; \, z_{0} = \frac{{t_{p} + t_{m} }}{2}$$

(11)

where

$$\delta_{p} = \sqrt {\frac{1}{{\sigma_{c} \cdot f \cdot \pi \cdot \mu }}}$$

(12)

represents the penetration depth, defined as the depth above the internal conductor surface at which the current density decreases to 1/e of the initial value, which also depends on the conductivity (e.g. σ_c = 5.8 × 10⁷ S/m in the case of copper), the frequency of the alternating current (e.g. f = 1.2 Hz) and the absolute magnetic permeability of the conductor (e.g. μ = 1.25 × 10⁻⁶ H/m).

Moreover, the magnetic flux density at the distance (r, z₀) is calculated as:

$$B_{r} (r,z_{0} ) = 2 \cdot \left[ {B_{r} (r,z_{0} )\left| {_{{r_{m} ,t_{m} }} } \right. - B_{r} (r,z_{0} )\left| {_{{r_{r} ,t_{m} }} } \right.} \right]$$

(13)

with

$$B_{r} (r,z_{0} )\left| {_{{r_{m} ,t_{m} }} } \right. = \frac{{B_{res} }}{2\pi } \cdot \int\limits_{{{\raise0.7ex\hbox{${ - t_{m} }$} \!\mathord{\left/ {\vphantom {{ - t_{m} } 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}^{{{\raise0.7ex\hbox{${t_{m} }$} \!\mathord{\left/ {\vphantom {{t_{m} } 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} {\frac{{(z_{0} - z)}}{{r \cdot \left[ {(r_{m} + r)^{2} + (z_{0} - z)^{2} } \right]^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} }} \cdot \left[ { - K(k) + \frac{{r_{m}^{2} + r^{2} + (z_{0} - z)^{2} }}{{(r_{m} - r)^{2} + (z_{0} - z)^{2} }} \cdot E(k)} \right]} \cdot dz$$

(14a)

$$B_{r} (r,z_{0} )\left| {_{{r_{r} ,t_{m} }} } \right. = \frac{{B_{res} }}{2\pi } \cdot \int\limits_{{{\raise0.7ex\hbox{${ - t_{m} }$} \!\mathord{\left/ {\vphantom {{ - t_{m} } 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}^{{{\raise0.7ex\hbox{${t_{m} }$} \!\mathord{\left/ {\vphantom {{t_{m} } 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} {\frac{{(z_{0} - z)}}{{r \cdot \left[ {(r_{r} + r)^{2} + (z_{0} - z)^{2} } \right]^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} }} \cdot \left[ { - K(k) + \frac{{r_{r}^{2} + r^{2} + (z_{0} - z)^{2} }}{{(r_{r} - r)^{2} + (z_{0} - z)^{2} }} \cdot E(k)} \right]} \cdot dz$$

(14b)

being B_res the residual magnetization (e.g. B_res = 1.43 T when the Nd–Fe-B alloy is assumed for the magnet material) and assuming

$$K(k) = \int\limits_{0}^{{{\raise0.7ex\hbox{$\pi $} \!\mathord{\left/ {\vphantom {\pi 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} {\frac{1}{{\sqrt {1 - k^{2} \cdot sin^{2} (\theta )} }} \cdot d\theta } ; \, E(k) = \int\limits_{0}^{{{\raise0.7ex\hbox{$\pi $} \!\mathord{\left/ {\vphantom {\pi 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} {\sqrt {1 - k^{2} \cdot sin^{2} (\theta )} \cdot d\theta } ; \; k^{2} = 4r_{..} \cdot r \cdot \left[ {(r_{..} + r)^{2} + (z_{0} - z)^{2} } \right]^{ - 1} , { }r_{..} = r_{m} \left( {r_{r} } \right)$$

(15)

As a result, the variation of the normalized equivalent damping constant (c_L/c_L,max) in terms of the ratio α_cL(= t_c/δ_p) is plotted in Fig. 8a. As can be observed, the maximum value of the dimensionless ratio (i.e. c_L/c_L,max = 1) is obtained for α_cL ≥ 0.33–0.40, highlighting that for an assigned value of the penetration depth is useless to take a conductor thickness greater than 0.33δ_p–0.40δ_p. In a similar way, the outward magnetic flux from each pole

$$\varPhi_{L,1} \text{ = 2}\pi \cdot r_{m} \cdot t_{p} \cdot B_{r}$$

(16)

is expressed in Fig. 8b as a function of the normalized magnet thickness α_Φ(= t_m/(t_m + t_p)). This time, note that the maximum normalized flux (i.e. Φ₁/Φ_1,max = 1) is obtained at α_Φ = 0.55.

Fig. 8

Optimized design of the ECDL

At this point, it is possible to change the thickness (t_m) and radius (r_m) of the magnet, and consequently the pole thickness t_p, until the values of the viscous damping defined in the previous section (see Table 4) correspond to the optimal values of the ratios α_cL(= 0.33 at the first three levels and 0.40 in the basement) and α_Φ(= 0.55, at all levels). For the sake of brevity, only the main geometric parameters of the ECDLs are reported in Table 5a as a combination of maximum values along the X and Y directions: i.e. t_c, conductor thickness; t_m, magnet thickness; t_p, pole thickness; r_m, annular magnet radius; r_r, cylindrical rod radius; air gap, a_g; number of magnets (n_m) and poles (n_p).

Table 5 a. Main properties of the ECDLs (unit in mm). b. Main properties of the helicoidal springs (unit in mm)

On the other hand, the elastic axial stiffness of the helicoidal spring representing the restoring force of the MDL can be evaluated with the following expression (Bansal 2007)

$$k_{L} \text{ = }\frac{{d_{c}^{4} \cdot G}}{{8 \cdot D_{mw}^{3} \cdot N_{c} }}$$

(17)

where (Fig. 7c, d): D_mw is the mean diameter of the spring wire, evaluated considering an air gap of 2 mm from the interior ECDL; d_c is the diameter of a coil; N_c is the number of coils; G is the shear modulus of the harmonic steel (e.g. G = 80000 MPa for the A228 type). Afterwards, the length (L_Ls) when the spring is fully compressed (i.e. when it becomes solid and adjacent coils touch) is obtained as

$$L_{Ls} \text{ = }\left( {N_{c} + 2} \right) \cdot d_{c}$$

(18)

Finally, the total length of the spring (L_Lt) is evaluated imposing that the maximum shear stress (τ_L,max) is equal to the corresponding yielding value (e.g. τ_y = 1608 MPa for the A228 type):

$$\tau_{L,\hbox{max} } \text{ = }\frac{{k_{B} \cdot F_{L} \cdot 8D_{mw} }}{{\pi \cdot d_{c}^{3} }} = \tau_{y}$$

(19)

where

$$F_{L} \text{ = }k_{L} \cdot \left( {L_{Lt} - L_{Ls} } \right)$$

(20)

being the main geometric parameters of the elastic springs reported in Table 5b: i.e. D_mw, mean diameter of the helix; d_c and p_c, diameter and pitch of a coil; N_c, number of coils; k_B, Bergsträsser coefficient; L_Ls, spring length of a solid; L_Lt, total length of the helicoidal spring.

5 Numerical results

To investigate the effectiveness of different types of connection between surrounding building (Sb) and elevator shaft (Es) of the Augusta building to mitigate internal pounding, nonlinear dynamic analyses are carried out considering the horizontal components of seven near-fault (NF) earthquakes characterized by low-frequency content (PEER 2014). Regarding the scaling of the NF accelerograms, both horizontal components of all records are pooled together and the mean of the scaled elastic response spectra is verified be compatible with the design spectrum of current Italian seismic code (NTC18 2018) at the ultimate (collapse prevention, CP) limit state. In Table 6, the main data of the employed NF earthquakes are reported: i.e. seismic event (station), date, closest distance from fault (∆), magnitude (M_w), peak ground acceleration in the horizontal directions (PGA_H1 and PGA_H2) and corresponding scale factors (SF_H1 and SF_H2). This set of records is classified as pulse-like on the basis of the classification algorithm proposed in (Shahi and Baker 2014), which utilizes wavelet transform of both the horizontal components. The main results for two potential pulses of each ground motion are reported in Table 7: i.e. angle of orientation (α), in the clockwise direction from North, pulse period (T_P) and pulse indicator (PI, where PI > 0 corresponds to a pulse-type record).

Table 6 Details of the employed near-fault earthquakes (PEER 2014)

Table 7 Potential pulses of the employed near-fault earthquakes (Shahi and Baker 2014)

A large number of time-history analyses is carried out, using the 7 scaled pairs of orthogonal components rotated with respect to principal directions of the building plan, at different angles of incidence θ in the range 0°–360°, with a constant step of 15°. A home-made computer code, already proposed for the nonlinear seismic analysis of spatial structures (Mazza and Mazza 2012; Mazza 2014), is modified in order to enable relative motion between two independent structural parts, including the inelastic response of the Sb above the isolation level and the linearly-elastic response of the Es, connected at the floor levels. Flexible (FL) and rigid (RL) linear links are compared with viscous damped (VDL) and magnetic damped (MDL) links, assuming connection only at the top floor (case A) or at all floors (case B). Moreover, the three-degrees-of-freedom model of the HDRBs and the simplified model of the LFSBs, previously described, are adopted for the hybrid isolation system. For the sake of brevity, all results refer to the elevator at maximum load placed on level 1 of the superstructure, representing the most conservative assumption resulting from the four different vertical positions (i.e. the basement and three floors above).

First, polar plots of the maximum and mean internal pounding parameter (g) along the building height are plotted in Figs. 9 and 10 with reference to the X (i.e. g_X,max and g_X,mean) and Y (i.e. g_Y,max and g_Y,mean) directions, respectively. Specifically, the envelope of the results obtained for the four couples of opposite corner joints is evaluated referring to links without (i.e. FL and RL) and with (i.e. VLD and MDL) dissipation, in the case of connection at all levels (see configuration B shown in Fig. 4b). As a comparison, relative displacements of the Sb and Es are also evaluated in the original configuration without links.

Fig. 9

Maximum and mean internal pounding along the X direction, for different links at all floors (case B)

Fig. 10

Maximum and mean internal pounding along the Y direction, for different links at all floors (case B)

The size of the design gap between adjacent structures imposed by current Italian (NTC18) and European (EC8) seismic codes is also represented with dashed black lines. In particular, three different thresholds are evaluated: g_d,NTC18 = 33 cm, g_d,EC8.1 = 24 cm and g_d,EC8.2 = 35 cm.

As can be observed, the most evident effects are found along the Y direction (Fig. 10), where mean values of g_i for the original structure already fulfil the upper bound design gap imposed by EC8 (i.e. g_d,EC8.2) considerably exceeding the corresponding lower bound (i.e. g_d,EC8.1) while there are a few cases with values slightly above g_d,NTC18 (Fig. 10b). These results suggest a revision of the EC8.1 threshold and the addition of a specific threshold on the CP seismic gap for base-isolated structures currently non-existent in the NTC18. On the other hand, maximum values refer to the Kobe earthquake, highlighting as critical incidence angles for seismic pounding θ = 225° (X direction in Fig. 9a, c, e, g) and θ = 135° (Y direction in Fig. 10a, c, e, g), which confirm a strict relation to the directivity effects (see orientation of the first pulse reported in Table 7). As expected, the insertion of rigid links (RL.B) provides the lowest relative mean and maximum displacements, resulting in full compliance with all design thresholds. Maximum values of g_X and g_Y exceed some thresholds for flexible (see FL.B in Fig. 9) and viscous (see VDL.B in Fig. 10) links, respectively.

Finally, magnetic links confirm their effectiveness for both maximum and mean values, highlighting a comparable safety factor at all levels differently from viscous links whose behaviour worsen moving to the highest levels. This leads to a notable reduction in the gap size required to prevent seismic pounding, that can be interpreted observing that MDLs are also benefiting of the restoring force contribution resulting from the helicoidal springs while a pure viscous response is assumed for the VDLs.

Similar plots are shown in Fig. 11 with reference to mean absolute accelerations of the elevator at the floor levels, with regard to the in-plan X (Fig. 11a, c, e, g) and Y (Fig. 11b, d, f, h) principal directions. All cases highlight an almost constant value of acceleration with varying incidence angles of the seismic loads, but the worst response at the upper levels is obtained in the cases without link and with FL.B where are reached values which could compromise the functionality of the elevator. Here too, the RL.B is confirmed as the best choice, because the rigid connection is able to take advantage of the reduction of seismic loads resulting from the base-isolation of the superstructure, with similar behaviour at all levels. Finally, a comparable response is observed for the VDL.B and MDL.B connections that help to halve the acceleration of the elevator at the top level with respect to free vibration.

Fig. 11

Mean acceleration of the elevator along the X and Y directions, for different links at all floors (case B)

With a view to demonstrating that the connection with MDL.B is the best compromise in all respects, all presented solutions to mitigate pounding effects are compared referring to mean values of storey drift of the elevator (Fig. 12) and mutual force transmitted by the connecting elements (Fig. 13).

Fig. 12

Mean storey drift of the building, for different links at all floors (case B)

Fig. 13

Mean mutual force, for different links at all floors (case B)

It should be underlined, that the application of magnetic dampers significantly reduces drift ratio of the lighter and more flexible framed structure of the elevator, with values ever decreasing compared to the case of spring (FL.B) and dashpot (VDL.B) elements applied alone. It can be also seen that the application of the additional rigid links (RL.B) is confirmed as the best solution at the three upper three levels (Fig. 12a, b, c), while this significantly changes with regard to the response of the elevator at the ground level (Fig. 12d), where too high values of drift ratio are attained related to shear deformation of the isolation system. Small and comparable values of mean mutual force, responsible of local critical damage in r.c. and steel frame members around the corner joints of the internal connection, are found for link elements in the form of springs (FL.B), dashpots (VDL.B) and their combination (MDL.B). This also means that the installation process of the devices is facilitated, because of the lower values of design forces for the anchor bolts of steel flanges and plates to which the link elements are fastened. On the other hand, RL.B links are responsible for a substantial increase of mutual forces, also inducing stress concentration in their connection, at the third level (Fig. 13a), while corresponding values at the second (Fig. 13b), first (Fig. 13c) and ground (Fig. 13d) levels are not reported for the sake of clarity, resulting from fifty to one hundred times greater than those obtained with the other additional links. As evident from the mean results presented in Figs. 12 and 13, as well as for maximum values not presented here, the incidence of the orientation of the seismic loads is negligible. Further results omitted for the sake of brevity confirm that the additional link elements does not induce significant changes in the seismic response of the isolation system and superstructure of the Augusta building.

Afterwards, plots of the maximum internal pounding parameter (i.e. the relative displacements g_X and g_Y between Sb and Es) along the building height are reported in Fig. 14, for the adjacent corner joints n.3 (Fig. 14a, b) and n.4 (Fig. 14c, d) and both directions. Results refer to the horizontal components of the Kobe earthquake rotated to the critical incidence angle θ = 135°. Flexible (FL) and rigid (RL) links without dissipation are compared with viscous (VDL) and magnetic (MDL) damped links, assuming connection only at the top floor (case A) or at all floors (case B). As can be observed, a mitigation of torsional effects is obtained for the FL, VDL and MDL solutions, although rigid links allow to the base-isolation of the superstructure to be used for eliminating these adverse effects. As shown, internal pounding is confirmed for the unlinked configuration, exceeding in some cases the EC8.2 and NTC18 thresholds (Fig. 14b, c, d) and in all cases the EC8.1 value. In terms of mitigation of the internal pounding, the best performance is attained when more than one connection is considered (case B), with an almost constant vertical distribution of g_X and g_Y. Moreover, coupling of stiffness and damping (i.e. MDLs) is more effective than a viscous connection on its own (i.e. VDLs) or a flexible spring (i.e. FLs). With reference to rigid links, the observed performance highlights remarkable reduction of internal pounding. Graphs similar to the previous ones are shown in Fig. 15, where maximum values of floor acceleration (Fig. 15a, b) and storey drift (Fig. 15c, d) of the elevator shaft at corner joint n. 2 are plotted, with a view to serviceability and damage conditions, respectively. It is interesting to note that MDLs continue to prove the best coupling solution for both vertical distributions (i.e. cases A and B). On the contrary, FLs and RL.A correspond to accelerations comparable with those of the solution without link, while RL.B is ineffective at reducing storey drift, producing too high values at level 0 where the elevator shaft is forced to undergo the same displacement as the isolation system when connection at all levels is assumed.

Fig. 14

Maximum internal pounding along the building height, for different links only at the top floor (case A) or at all floors (case B)

Fig. 15

Maximum floor acceleration (a, b) and storey drift (c, d) of the ES along the building height, for different links only at the top floor (case A) or at all floors (case B)

The following evaluations focus on the effectiveness of the insertion of magnetic links only at the top level (MDL.A) instead of at all floor levels (MDL.B). To this end, maximum and mean internal relative displacement without (Sb and Es not connected structures) and with (Sb and Es connected structures) magnetic damped links are plotted in Fig. 16, with reference to the four corner joints at the third level. Note that similar behaviour is maintained for the couples of corner joints (Es1-Bs1; Es3-Bs3) and (Es2-Bs2; Es4-Bs4), along the X direction, and (Es1-Bs1; Es2-Bs2) and (Es3-Bs3; Es4-Bs4), along the Y direction. As expected, MDL.B leads to a significant reduction of g_i, representing the solution complying with all design gap sizes, while MDL.A raises problems for maximum values (Fig. 16a, c, e, g), exceeding EC8.1 threshold for some incidence angles of seismic loads.

Fig. 16

Maximum and mean internal pounding for corner joints at the third level, for the MDL.A and MDL.B links

Less marked differences are observed in terms of maximum and mean acceleration of the elevator at the third level (Fig. 17), where both solutions prove effective at reducing elevator vibrations, and maximum and mean mutual force at the third level (Fig. 18), resulting in low values in both cases. As regards effects on the superstructure of the seismically isolated part of the building, maximum and mean drift at the third level (Fig. 19) are practically identical when considering MDL.A and MDL.B are considered, highlighting the fact that the additional magnetic links does not affect its response.

Fig. 17

Maximum and mean acceleration of the elevator at the third level, for the MDL.A and MDL.B links

Fig. 18

Maximum and mean mutual force at the third level, for the MDL.A and MDL.B links

Fig. 19

Maximum and mean drift at the third level of the elevator, for the MDL.A and MDL.B links

Finally, mean values of the effective stroke required for the coupling made with magnetic damped links, placed at the top floor (case A) or at all floors (case B), are reported in Table 8, with the aim of verifying the feasibility of their practical application. At each storey, relative displacements resulting from nonlinear seismic analysis are calculated as an average of the maximum values corresponding to the four corners of Sb and Es and all orientations of the set of seven earthquakes. Then, space available for installation of the MDLs is evaluated by subtracting the effective stroke from the design gap provided by the Italian (NTC18) and European (EC8.1 and EC8.2) seismic codes. As can be observed, the EC8.1 gap has proven always unsuitable for designing magnetic damped links, even with negative value in some cases, the same as with NTC18 gap at the zero and third levels of the MDL.B and MDL.A cases, respectively, where too small positive values are attained. Only the EC8.2 gap is resulted effective to connect magnetic damped links at all levels (case B), while similar problem to that of the Italian gap is evident when only connection at the top floor is considered (case A). It should be underlined that the mean effective stroke corresponding to structural parts linked by elastic springs (i.e. FL.A and FL.B) and viscous dashpots (i.e. VDL.A and VDL.B) is expected to be greater than that reported in Table 8, thereby making also the EC8.2 gap unsatisfactory.

Table 8 Mean effective stroke and available space for designing magnetic damped links (unit in cm)

6 Conclusions

The effectiveness of coupling between independent units of seismically isolated buildings located to mitigate internal pounding is investigated here, through a case study of a four-storey r.c. framed structure in the Italian town of Augusta (Sicily). An elastomeric-friction hybrid isolation system at ground level, crossed by the steel framed structure of a fixed-base elevator shaft, is considered. Rigid and flexible (elastic) links are compared to traditional (viscous) and innovative (magnetic) damped links placed only at top level or at all levels. An extensive numerical investigation is carried out analysing the effects on potential seismic pounding related to incidence angle and frequency content of near-fault earthquakes.

The following conclusions can be drawn with respect to the design and application of the link devices.

• An effective and reliable four-sweep-four-step iterative design procedure of the links is developed to evaluate their vertical distribution of stiffness and/or damping, with the aim of minimizing horizontal displacement of the elevator at all levels.

• An optimized design procedure of magnetic damped links is proposed, which can change thickness and radius of the magnet, and consequently thickness of the pole, until maximum values of magnetic flux and energy dissipation are attained.

• The mean effective stroke required from MDLs highlights that EC8.1 design gap is always unsuitable, the same holds for the NTC18 gap at the zero and third levels of the MDL.B and MDL.A cases, respectively. Only the EC8.2 gap is effective at connecting magnetic damped links at all levels, while a similar problem to that of the Italian gap arises when the connection at the top floor only is considered.

• The mean effective stroke corresponding to structural parts linked by elastic springs (FL.A and FL.B) and viscous dashpots (VDL.A and VDL.B) is greater than that obtained for the viscoelastic link elements (MDL.A and MDL.B), thereby making also the EC8.2 gap unsatisfactory.

The following conclusions can be drawn from the viewpoint of the effectiveness of seismic codes for gap size and different types of link elements.

• Mean values of relative displacements for the original structure fulfill the upper bound design gap imposed by EC8 and largely exceed the corresponding lower bound while result in a few cases they obtain values slightly above the NTC18. A revision of the EC8.1 threshold and the addition of a specific threshold on the CP seismic gap for base-isolated structures currently lacking from the NTC18 are required.

• Maximum values of relative displacement underscore a strict relation between critical incidence angle for seismic pounding and directivity effects of near-fault earthquakes.

• The insertion of rigid links (RL.B) provides the lowest relative mean and maximum displacements, resulting in full compliance with all design thresholds. Some thresholds are exceeded for flexible (FL.B) and viscous (VDL.B) links, while MDL.B confirm their effectiveness, highlighting a comparable safety factor at all levels unlike viscous links whose behaviour worsens as the highest levels are reached.

• MDLs significantly reduce drift ratio of the elevator, with values ever decreasing compared to the case of spring (FL.B) and dashpot (VDL.B) applied alone; rigid links (RL.B) are the best solution at the three upper levels, while they significantly change the response of the elevator at the isolation level.

• All cases highlight an almost constant value of acceleration with varying incidence angles of the seismic loads, but the worst response at the upper levels is obtained in the cases without link and with FL.B where values endangering the elevator’s functionality are attained.

• Small and comparable values of mean mutual force are found for FL.B, VDL.B and MDL.B, while RL.B links are responsible for a substantial increase of mutual forces at all levels.

• MDL.B leads to a significant reduction of internal pounding representing the solution that complies with all design gap sizes, while MDL.A raises problems for maximum values, exceeding the EC8.1 threshold for some incidence angles of seismic loads.

• All additional link elements does not induce significant changes in the seismic response of the isolation system and superstructure of the Augusta building.