Abstract
The selection of ground motion models, and the representation of their epistemic uncertainty in the form of a logic tree, is one of the fundamental components of probabilistic seismic hazard and risk analysis. A new ground motion model (GMM) logic tree has been developed for the 2020 European seismic hazard model, which develops upon recently compiled ground motion data sets in Europe. In contrast to previous European seismic hazard models, the new ground model logic tree is built around the scaled backbone concept. Epistemic uncertainties are represented as calibrations to a reference model and aim to characterise the potential distributions of median ground motions resulting from variability in source scaling and attenuation. These scaled backbone logic trees are developed and presented for shallow crustal seismic sources in Europe. Using the new European strong motion flatfile, and capitalising on recent perspectives in ground motion modelling in the scientific literature, a general and transferable procedure is presented for the construction of a backbone model and the regionalisation of epistemic uncertainty. This innovative approach forms a general framework for revising and updating the GMM logic tree at national and European scale as new strong motion data emerge in the future.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The effective mitigation of seismic risk within a region begins with a quantitative assessment of the shaking hazard posed by earthquakes. Probabilistic seismic hazard assessment (PSHA) is now well-established as the tool through which this is achieved, integrating our understanding of earthquake behaviour and quantification of its related uncertainties into clear and communicable probabilities that can guide decision making in the mitigation process. Probabilistic seismic hazard models and maps can now be found for every country in the world, providing stakeholders such as engineers, insurers and government officials with the necessary information to quantify risk. As PSHA has become established as the primary means of transforming the growing understanding of the earthquake process into effective tools for engineers and other end users, the need arises for regular updating of the models, as new data emerge day-by-day that reveal deeper insights into the earthquake process.
Within Europe there is an established legacy of seismic hazard models both at a national scale and at a pan-European scale. Direct mitigation of earthquake risk via the use of seismic design codes, including Eurocode 8 (CEN 2004), anticipates that seismic hazard information is managed and conveyed by the responsible national design authority within each country, meaning such national scale maps would naturally take precedence over pan-European initiatives. As European economies become more international and inter-connected in scope, however, it becomes unavoidable that the consequences of earthquakes upon trade, infrastructure and society can have an impact beyond the borders of the countries struck by the events themselves. It is into this domain that pan-European seismic hazard and risk models assume greater prominence, conveying to stakeholders the potential risks across a wider region.
Recognising the significance of pan-European analyses of seismic risk, combined with the need to ensure high quality, Eurocode 8 compatible seismic hazard assessments, the 2013 European Seismic Hazard Model (ESHM13) was developed under the Seismic Hazard Harmonisation in Europe (SHARE) project (Woessner et al. 2015). Completed at the end of 2013, the ESHM13 was a generational leap-forward in seismic hazard mapping in the region. It introduced explicit modelling of active faults into PSHA in Europe, a comprehensive logic tree capturing epistemic (or model-to-model) uncertainty, and a hybrid expert- and data-driven procedure for the selection and weighting of ground motion models. The latter is of particular significance here, and is described in detail by Delavaud et al. (2012). Since the completion of the ESHM13, however, more recent national seismic hazard models have built upon some of the central developments of the ESHM13 process, refining and improving the hazard estimates from one country to another. Given the evolution of seismic hazard models in Europe since the completion of the ESHM13, and in light of new data and lessons from subsequent damaging earthquakes, a new pan-European seismic hazard model (ESHM20) is now being developed as part of the Horizon 2020 Seismology and Earthquake Engineering Research Infrastructure Alliance for Europe (SERA) project.
Distribution of data in the ESM flatfile (Lanzano et al. 2019) according to source, path and station
For the characterisation of strong motion, a new and updated selection of ground motion models (GMMs) is required, alongside a corresponding representation of the epistemic uncertainty. This update is motivated by several fundamental factors. Since the completion of the ESHM13, new generations of GMMs from different regions of the globe have been published, including those derived from European and Middle Eastern data (Akkar et al. 2014; Bindi et al. 2014; Derras et al. 2014; Kotha et al. 2016; Kuehn and Scherbaum 2016). In addition, several selected GMMs from other regions that were adopted within the EHSM13 have been superseded by subsequent updates (Cauzzi et al. 2015; Chiou and Youngs 2014; Zhao et al. 2016a, b, c). The second factor is that in the last decade the volume of strong motion data from earthquakes in Europe has grown by an order of magnitude. Systematic efforts to process and harmonise this database of European strong motion records and their associated metadata has culminated in the European Strong Motion (ESM) flatfile (Lanzano et al. 2019) (Fig. 1), a crucial archive of more than 20,000 records represented by peak ground motion values, response spectral accelerations and Fourier spectra. Finally, not only have recent years seen a growth of data and developments in ground motion modelling, so too have ideas on the nature of epistemic uncertainty and its representation in PSHA evolved rapidly. This will be elaborated upon in the next section.
This paper describes the new developments of the ESHM20 ground motion model logic tree for Europe in order to characterise the seismic hazard on Eurocode 8 class A rock, with a measured 30 m average shearwave velocity (\(V_{S30}\)) of 800 m/s. The required outputs of the ESHM20 include seismic hazard curves, maps and uniform hazard spectra (UHS) for peak ground acceleration (PGA) and spectral acceleration, \(S_a \left( T \right)\), for a broadband range of spectral periods (0.01–8 s). Section 2 highlights the changes in philosophy that underpin the directions taken in its construction when compared to its ESHM13 predecessor, before elaborating on the shallow crustal ground motion model around which the logic tree will be built (Sect. 3), its components of variability and how they constrain epistemic uncertainty (Sect. 4), and how insights from strong motion data can help calibrate the logic tree in different regions of Europe (Sect. 5). In addition, three electronic supplements accompany this paper, in which further explorations of the proposed ground motion model, its comparison against observed strong motion data and its scaling in terms of magnitude, distance and spectral period are shown.
The approach adopted for constructing the logic tree represents a radical departure from both its ESHM13 predecessor and from other national seismic hazard models in Europe. As such, it is afforded a detailed treatment in this manuscript. Its application in the ESHM20, however, is limited only to regions of predominantly shallow crustal seismicity. The complete logic tree for Europe also requires characterisation of ground motions from earthquakes originating from subduction zones, deep non-subduction sources such as the Vrancea deep seismic zone, and the stable shield region in the Baltic and surroundings (all shown in Fig. 2). Though the shallow crustal environment hosts the largest proportion of damaging earthquakes in Europe, adaptation to the other environments presents different challenges. Each tectonic environment has required a different approach in order to define the ground motion logic tree for regions of limited or no available strong motion data. The characterisation of ground motion and its epistemic uncertainty for these regions is addressed in separate publications concurrent to the present one. In addition, the SERA project also includes the objective of performing probabilistic seismic risk analysis for all of Europe, for which it will be necessary to characterise the ground motion taking into account local site response. Though tightly connected to the ground motion logic tree of the ESHM20, the European site response model itself requires such a sufficient level of detail that this too will be addressed in a subsequent paper.
Tectonic regions of Europe defined within the ESHM20 including shallow seismicity (adapted from Basili et al. 2019), stable craton, subduction interface (depths in km), subduction in-slab (depths in km) and the Vrancea deep seismic zone (DSZ)
2 Epistemic uncertainty: insights from new data and new perspectives
The approach to characteristic epistemic uncertainty in ground motion models within the ESHM13, and described in detail by Delavaud et al. (2012), invokes what shall be referred to hereafter as the “multi-model” approach. For each of the tectonic domains considered within Europe, the ground motion model logic tree was constructed by selecting multiple models from the literature according to an expert panel, then refining and weighting them using metrics describing the fit of each model to existing strong motion data for each tectonic region where possible. This approach was one of the first of its kind to attempt, at a regional scale, a hybrid expert- and data-driven logic tree construction. An obvious starting point for a more comprehensive update of a ground motion logic tree for Europe would therefore be to repeat this process, integrating new ground motion models published since the ESHM13 and the ground motion records from new ESM database. The results of this approach can be seen in Weatherill et al. (2018), who find that generally newer ground motion models provide an improved fit to ESM data than their predecessors within ESHM13, and that in the range of magnitudes and distances best sampled by the data the median ground motions predicted by different GMMs are converging. The impacts of the a new “multi-model” ground motion logic tree can be seen in PSHA for Europe undertaken by Weatherill and Danciu (2018), who update the ESHM13 GMM logic tree using for the purposes of defining the seismic hazard at a broader range of spectral periods (0.05 \(\le\) T (s)\(\le\) 10.0). They identify a general trend toward lower hazard for the return periods of interest (475–2475 years) throughout much of Europe, albeit with exceptions in some specific regions such as Romania.
Although the application of the Delavaud et al. (2012) approach could form a basis for regular updating of a pan-European ground motion logic tree as new data becomes available, there are more fundamental questions on the nature of epistemic uncertainty in ground motion modelling that continue to be posed. These form the motivation for a change of approach. The first question is that of regionalisation. The ESHM13 mapped the seismic sources in Europe into seven different tectonic regions: active shallow crust, stable shallow crust, shield, subduction interface, subduction in-slab, volcanic and non-subduction deep (i.e. Vrancea). Until recently only the active shallow crustal environment has produced a sufficient number of ground motions from which to explore the question of regionalisation in further depth. Subsequent European ground motion studies investigating differences from country-to-country have shown that even within the regions classified as belonging to the active shallow crustal domain there are potentially significant differences (Kale et al. 2015; Kotha et al. 2016; Kuehn and Scherbaum 2016; Weatherill et al. 2018). This raises new questions as to how best to approach epistemic uncertainty, several of which reflect broader debates in the seismic hazard modelling community on this issue:
-
1.
What are the different tectonic and geological domains in Europe and how do they differ in terms of ground motion characterisation?
-
2.
For each tectonic environment how do we ensure that the models capture the centre, the body and the range of the defensible technical judgements regarding the ground motion models (U. S. Nuclear Regulatory Commission 2012), and how many models are sufficient?
-
3.
Do the selected GMMs fulfil the criterion of being mutually exclusive and collectively exhaustive (MECE), insofar as it is achievable, by adequately representing the range of possible ground motions and minimising the overlap between models?
-
4.
Does the resulting spread of median ground motions with magnitude, distance and period reflect appropriately the degree to which they are constrained by ground motion records?
When addressing these questions to the ground motion models within the ESHM13 selection, we find that they cannot be answered satisfactorily at a European scale by continuing with the approach of Delavaud et al. (2012), even where new data and models are available. Amongst the problems encountered are the sometimes disproportionate influence of the sharp boundaries between one region and another, particularly between active and stable regions, and the contradiction that in places most poorly constrained by the available ground motion data (e.g. shield, volcanic, subduction etc.) fewer models are used than for those regions in which a large volume of data are available. Such an assumption will, at a minimum, provide a poorer constraint on the epistemic uncertainty, and may incorrectly narrow the uncertainty in cases where the selected GMMs represent similar data sets, tectonic regions or modelling choices.
Recognising these shortcomings in the multi-model approach to GMM logic tree construction, a decision has been made to consider instead the scaled backbone approach (e.g. Bommer 2012; Atkinson and Adams 2013; Atkinson et al. 2014; Bommer et al. 2015). This requires the definition or identification of a single ground motion model (the backbone) that is then adjusted, or re-scaled, to describe a range of median ground motions that captures the epistemic uncertainty. The scaling factors are intended to represent the influence of uncertainties in the seismological properties of the ground motion in the target region such as, for example, local characteristics of stress-drop and attenuation. These factors may be applied to the backbone model as a whole or they may depend on the specific scenario and period of interest. Scaled backbone approaches, or some elements of the concept, have been adopted within many seismic hazard projects both for critical facilities (e.g. Bommer et al. 2015; Coppersmith et al. 2014) and in national seismic hazard models (Atkinson and Adams 2013; Edwards et al. 2016; Grünthal et al. 2018; Akkar et al. 2018).
There are several key theoretical advantages to the adoption of a scaled backbone approach. Chief among these is the conformity with the objective of mutual exclusivity and, provided the backbone is scaled sufficiently, collective exhaustiveness. It permits a greater degree of control to ensure that the epistemic uncertainty is greatest where the data are most limited and not necessarily just where models may coincidentally converge or diverge. In terms of practical implementation, the adoption of a scaled backbone GMM logic tree may be more efficient, defining the centre, body and range in a smaller number of mutually exclusive models as opposed to requiring more published models in the hope of capturing the differences. Several applications have demonstrated that through the scaled backbone the epistemic uncertainty in the median ground motions, \(\sigma _{EPI} \left( {M, R, T} \right)\) where M is magnitude, R is distance and T period, can be described in terms of a probability distribution (usually log-normal). In this situation it is possible to approximate the first and second modes of the distribution with a discrete number of weighted branches using, for example, the methodology of Miller and Rice (1983). Alternatively, computationally efficient procedures are available for numerically approximating the distribution using analytical methods such as polynomial chaos (Lacour and Abrahamson 2019) or Monte Carlo sampling (Assatorians and Atkinson 2013), rather than requiring repeated re-calculations of the hazard with different GMMs.
Where the scaled backbone approach in the form presented in some of the aforementioned studies can be problematic, however, is their potential degree of inflexibility in controlling or accounting for differences in the scaling of ground motions with magnitude or the attenuation properties with distance. Atkinson and Adams (2013) and Goulet et al. (2017) do account for this by adopting a magnitude- and distance-dependant scaling factor, but such approaches can result in some variability in \(\sigma _{EPI}\) from scenario to scenario or period to period, and do not necessarily reflect the uncertainties in the underlying physical ground motion scaling properties within the models. This can be remedied in part by adopting a hybrid of the multi-model and scaled backbone approaches, selecting multiple ground models in order to capture the uncertainty in magnitude and distance scaling but applying additional adjustment factors to each in order to account for uncertainty in target region properties such as stress-drop. Examples of this can be seen in the Thyspunt Nuclear Power Plant PSHA (Bommer et al. 2015), the 2015 Swiss National Seismic Hazard Model (Edwards et al. 2016) and the 2018 German National Seismic Hazard Model (Grünthal et al. 2018), amongst others. More elaborate approaches to overcome this have been suggested by Goulet et al. (2017), who regress the medians of multiple ground motion models into a single backbone model in which the uncertainty in the backbone model’s coefficients can be used to generate many thousands of median models. From this large sample of models, dimensionality reduction techniques are applied in order to define a manageable number of representative GMMs that capture the model space. Other approaches for generating the scaling factors, some of which do account for magnitude and distance-dependent scaling, are also possible and a more detailed review can be found in Goulet et al. (2017) and Douglas (2018a).
If one is convinced of the merits of the scaled backbone approach for application to seismic hazard analysis in Europe, the obvious question to address is how to determine the scaling factors for the different branches of the logic tree and the corresponding weights, and to which geographical regions should these be applied? García-Fernandez et al. (2019) propose one such scaled backbone ground motion model for application in Europe, which builds upon a similar approach first proposed by Atkinson and Adams (2013) for use in eastern Canada, in which three alternative branches are described for a reference rock of Eurocode 8 class B (\(360 \le V_{S30} \text { m/s} < 800\)). In their formulation, the three branches are constructed by taking at each magnitude, distance and period the geometric mean of the median ground motion from six candidate GMMs at the centre of the site class range (\(V_{S30} = 580\) m/s), and defining upper and lower branches as the corresponding geometric means at the site class limits (\(V_{S30} = 360 \text { m/s}\) and \(V_{S30} = 800\) m/s). These are reduced on both sides by one standard deviation determined from the six median models. Whilst this approach in itself is innovative, it has limitations insofar as it ties the scaling of the epistemic uncertainty to the site scaling of the candidate GMMs, and would not necessarily be adaptable to the calibration of regional differences in ground motion scaling, nor be applicable to different tectonic region types not represented in the data set.
A more suitable approach to address the questions posed previously is devised by Douglas (2018a), who presents the general structure of a scaled backbone logic tree that explicitly captures the epistemic uncertainties on three critical, and regionally-variable, facets of ground motion: the anelastic attenuation (\(\pm \Delta Q\)), the source stress parameter (\(\pm \Delta \sigma\)) and the statisical uncertainty (\(\sigma _{\mu }\)). In its original presentation, Douglas (2018a) adopts the GMM of Kotha et al. (2016) as the scaled backbone, utilising its three regionalisations (Italy, Turkey and “rest of Europe”) as representative of the epistemic uncertainty on anelastic attenuation. The stress parameter scaling is based on the residuals of observed ground motions from different regional subsets of the strong motion database (e.g. Italy, Greece, Turkey) as well as predicted motions from various local GMMs each normalised with respect to the Kotha et al. (2016) GMM. The data set was limited only to the best constrained subset (\(5.0 \le M_W \le 6.0\) and \(20 \le \text {Joyner-Boore Distance, } R_{JB} \text {[km]} \le 60\)) over distances where regional differences anelastic attenuation are likely to be minor. The average of these normalised residuals was then used to define a scalar factor representing the average region-to-region variability within this data set, which is then mapped into a three-point distribution within the logic tree. Finally, the statistical uncertainty is captured using the 5th, 50th and 95th percentiles of the asymptotic variance of the ground motion model, following the procedure of Al Atik and Youngs (2014). This complete formulation is outlined in Fig. 3 and results in a 27-branch logic tree.
As a general framework for not only defining a comprehensive scaled backbone logic tree but also adapting it to different tectonic environments in Europe, the proposal of Douglas (2018a) forms the basis for the characterisation of epistemic uncertainty that will follow. Not only is it practical, it shifts the problem of characterising epistemic uncertainty away from one of model selection and multi-model inference and toward that of capturing explicitly the quantifiable differences in seismological properties across a region, particularly one as tectonically diverse as Europe. There are, however, limitations that will be addressed in due course. Douglas (2018b) also discuss the calibration of the backbone factors for models developed using stochastic simulations of ground motions, which may be more applicable in regions of low seismicity, though we do not consider this any further here. With the general framework set in place, the core of this paper will demonstrate how this has been adapted for application to shallow seismicity within Europe, illustrating how observed strong motion data can be used to identify further sub-divisions on the basis of regional seismological properties.
Proposed structure of a ground motion logic tree according to the schema of Douglas (2018a)
3 The shallow crustal backbone model
Given the wealth of new ground motion data for Europe, the core backbone model for shallow crustal seismicity is that of Kotha et al. (2020), which is fit to data from the Engineering Strong Motion flatfile of Lanzano et al. (2019). The full details of the GMM itself, including the records used and the resulting coefficients, are found in the their manuscript and need not be repeated here. What is relevant for the construction and calibration of the backbone GMM, however, is the general functional form and the specific definition of the random effects within this process. The functional form of the shallow crustal backbone model is described as:
where Y is the intensity measure of interest (e.g. PGA [in \(\mathrm{{cm}}\ \mathrm{{s}}^{-2}\)], PGV [in \(\mathrm{{cm}}/\mathrm{{s}}\)], \(S_a \left( T \right)\) [in \(\mathrm{{cm}}\ \mathrm{{s}}^{-2}\)]) \(R_{JB}\) is the Joyner–Boore distance in km, \(M_h\) is the period-independent hinge-magnitude of \(M_W\ 6.2\), \(M_{ref}\) and \(R_{ref}\) are the reference magnitude and reference distance, which take the fixed values of \(M_W\ 4.5\) and 30 km respectively. \(\delta B_{el}^0\), and \(\delta S2S_S\) and \(\varepsilon _0\) describe the event-to-event, site-to-site and site-corrected within-event variability, and are Gaussian distributed random variates with zero means and standard deviations of \(\tau _0\), \(\phi _{S2S}\) and \(\phi\) respectively. As explained in further detail by Kotha et al. (2020), the GMM is fit using a robust linear mixed effects regression technique, reducing the influence of outliers when fitting the main coefficient sets. As shall be seen in due course, however, there are cases when these outliers may be manifestations of important local features of seismicity that are relevant for seismic hazard assessment.
Joyner–Boore distance is adopted as the distance metric owing, in part at least, to substantial uncertainty in the finite rupture dimensions and hypocentral depth distribution. Recognising that source depth is still an influental factor on the geometric spreading and on stress-drop, the data are grouped into three bins (\(h \le 10\) km, \(10 < h \text { (km)} \le 20\) and \(h \ge 20\) km, where h is hypocentral depth) and \(h_D\), the corresponding effective depth used to control the geometric spreading, is assigned to 4 km, 8 km and 12 km for each respective bin based on iterative fitting and non-parametric observations. Further details regarding the choice and influence of the functional form can be seen in Kotha et al. (2020).
While the basic model described by Eqs. 1–4 is kept relatively simple with respect to some of the more complex forms found in recent ground motion models, the substantial volume of strong motion data available from ESM permits the introduction of more random effects within the model. Two terms in the model are held as additional random effects in the regression analysis: a region-dependent coefficient of attenuation, \(\delta c_{3,r}\), and another region-dependent source scaling factor \(\delta L2L_l\). The \(\delta c_{3,r}\) and \(\delta L2L_l\) terms are assumed to be normally distributed such that \(\delta c_{3,r} \sim {\mathcal {N}} \left( {0, \tau _{c_3}} \right)\) and \(\delta L2L_l \sim {\mathcal {N}} \left( {0, \tau _{L2L}} \right)\).
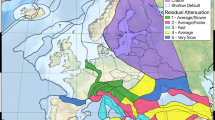
The interpretation of the \(\delta c_{3,r}\) should be treated with some care, for reasons that may become obvious later. Although it affects the part of the GMM commonly recognised as the apparent anelastic attenuation term, regional variation in \(\delta c_{3,r}\) should be thought of not necessarily as a manifestation of regional differences in the intrinsic attenuation properties of the crust per se (though that is a contributing factor). Instead it is a statistical residual term that may be a manifestation of several phenomena affecting the apparent rate of decay of ground motion from the source, but in a manner that is specific to the region in question and not necessarily to any particular source or site. We refer to this term therefore as “residual attenuation”, and it may be influenced by additional factors such as Moho reflections and/or local variability in source depth and scaling distributions resulting in differences in the geometrical spreading within each specific region as well as intrinsic attenuation. Indeed, it must also be recognised that in acting as an offset to the apparent anelastic scaling factor, this term has an impact in strong motions at both shorter and longer distances, albeit less significant for the shorter distances, and the actual range of distances represented in the records in any specific region for which this term is calibrated may vary. To a certain extent therefore, we believe that this term entrains a degree of epistemic uncertainty in the near source factors, even though records from short distances are not so well represented in the data set.
Notable in its absence in Eq. 1 is the discussion of the site amplification term. The development of the 2020 European Seismic Hazard and Seismic Risk model requires not only the characterisation of the ground motion on reference Eurocode 8 class A rock for engineering application, but also the estimation of ground motion at the soil surface for the seismic risk modelling applications. These requirements illustrate the need for a more fully encompassing approach to site amplification modelling at a regional scale; one in which the aleatory variability in the ground motion model is appropriately calibrated to reflect the uncertainty in the input site information and the intended application (e.g. Weatherill et al. 2020). The complete characterisation of the pan-European seismic site response model and its implications for seismic hazard and risk analysis is therefore addressed in a separate publication.
4 Region-specific components of variability
The residual attenuation region coefficient, \(\delta c_{3,r}\), and the source location scaling coefficient, \(\delta L2L_l\), are both spatially variable factors. This has several consequences. The first is that they may represent systematic and/or persistent properties of a given locality, such as faster or slower attenuation and/or higher or slower stress-drop with respect to the centre of the data set as a whole, which should be taken into consideration in their application inside a seismic hazard analysis. In this sense they are not dependent on the specific event or record, as would be the case for \(\delta B_{el}^0\) or \(\varepsilon_0\), but are instead attributes of a region that describe the extent to which the characteristics of the region deviate from the “average” across all of those considered. The second is that their full distribution is representative of the full region-to-region variability implied within the data set. As such, both can be treated as epistemic variables, whose distributions can be refined from one region to another and the resulting uncertainty within a region reduced with the availability of more data. The obvious challenge underpinning this approach is to define the extent of the regions upon which the \(\delta c_{3,r}\) and \(\delta L2L_l\) are calibrated. From the beginning it must be established that there is no stable, fixed solution to the problem of regionalisation, particularly at the scale at which we are approaching it here, and that practicality is as much a driving factor as any other. With this in mind, do not necessarily attempt a new regionalisation of Europe in terms of ground motion, but rather develop upon two prior regionalisation schemes.
4.1 Residual attenuation (\(\delta c_{3,r}\))
For the residual attenuation coefficient a tectonic regionalisation proposed by Basili et al. (2019) for the purposes of the 2019 TSUMAPS-NEAM Tsunami Hazard Model is adopted (shown in Fig. 2). This divides Europe, North Africa and the North Atlantic into 105 regions primarily on the basis of geological and tectonic criteria (e.g. dominant faulting regime, stress orientation, geological domain etc.). Within the robust mixed effects regression the \(\delta c_{3,r}\) term is determined according to the region to which each station is assigned. As the Basili et al. (2019) regionalisation did not take into account the locations of strong motion recording stations, the distribution of stations is uneven and beyond the pan-Mediterranean countries most regions contain no stations, and therefore no \(\delta c_{3,r}\) can be determined. Some minor modifications to this regionalisation have been made to reduce the number of cases where recording stations are all located in the edge of a particular zone. These adjustments include: i) division of Romania to introduce northwest Carpathian zone in order to separate out the area covered by Romanian strong motion data from the rest of Central Europe, ii) the Dinarides zone on the eastern Adriatic has been split by a north/south division, and iii) western Turkey separated from the central Anatolian plateau.
From the mixed effects regression analysis a \(\delta c_{3,r}\) term is determined for 45 out of a total of 110 regions across Europe, and their complete distribution with respect to spectral period is shown in Fig. 4. As one might expect, the variability (\(\tau _{c_3})\) diminishes with increasing period. The colour scale indicated in Fig. 4 describes the weighting of each data point in the robust mixed effects regression (Koller 2016), and demonstrates clearly the diminished influence of the outliers; both those showing a particularly slow attenuation (high \(\delta c_{3,r}\)) and those showing a fast attenuation (low \(\delta c_{3,r}\)). This approach has the advantage of identifying random effects that are outlying to the data set whilst still enabling them to be calibrated.
\(\tau _{c_3}\), represents the total region-to-region variability in the attenuation term implied by this data set and regionalisation. As each region has its own distribution, described by \(\delta c_{3,r} \left( T \right)\) and its standard error, this uncertainty can be minimised where data allow. We therefore remove this uncertainty from the total aleatory uncertainty of the model and adopt it as the first branching level of our logic tree, as envisaged by Douglas (2018a). Adopting the three-point discretisation of a Gaussian distribution of Miller and Rice (1983), we then define our three branches as a slow residual attenuation (\(+\varepsilon \cdot \tau _{c_3}\)), central or average residual attenuation (\(0 \cdot \tau _{c_3}\)) and fast residual attenuation (\(-\varepsilon \cdot \tau _{c_3}\)) with weights of 0.167, 0.666 and 0.167 respectively, where \(\varepsilon = 1.732051\).
4.2 Region-dependent source variability (\(\delta L2L_l\))
For the source location coefficient a different regionalisation is adopted, this time using one of the area source branches of the SERA seismic source model, namely the “TECTO” branch. The construction of the area source model is beyond the scope of this publication; however, the “TECTO” branch is intended to describe large scale seismic sources representing the major tectonic features across Europe believed to influence the distribution of seismicity. The region-dependent source variability is determined during the regression as a random effect describing the area source in which each earthquake in the database is located. Constraint of the random effect is only possible with two or more events occuring in the source, with the standard error diminishing with increasing seismicity. Once again, the full distribution of \(\delta L2L_l\) with period is shown in Fig. 5, with the colours indicating the weighting within the robust mixed effects regression.
As an explanatory variable \(\delta L2L_l\) is not as closely dependent on the stress-drop of an event in comparison to the between-event term, \(\delta B_{el}^0\). Some insight as to its meaning can be gained from exploring the spatial distribution of \(\delta L2L_l\), which is shown for the case of Sa \(\left( {0.1 s}\right)\) in Fig. 6. Here it is obvious that although there is considerable variability there are some regional trends visible, with some of the lower \(\delta L2L_l\) values found in central Italy, Sicily and the southern Hellenic Arc, and the largest around the Sea of Marmara and in Romania. It is tempting to intuit this as perhaps a property of the predominant style-of-faulting in a region. In central Italy and central and southern Greece, where extensional faulting is dominant, we see lower \(\delta L2L_l\), whilst in northern Turkey and the eastern Balkan countries a mixture of strike-slip and transpressional regimes dominate this value is higher. When the dependence upon style-of-faulting was investigated, however, it was not found to be significant. From this we infer that \(\delta L2L_l\) is a regional property of the source-scaling of ground motions but not necessarily a source-specific property. This too is borne out by Fig. 6 in which many counter-examples can be seen, such as the high \(\delta L2L_l\) in the extensional Rhine graben or the low \(\delta L2L_l\) in the eastern Adriatic and Dinarides where compressional faulting is dominant.
As with the case of \(\delta c_{3,r}\), the region-dependent source variability is described by a Gaussian distribution with a zero mean and a standard deviation of \(\tau _{L2L}\). Likewise, it can be interpreted as describing the full epistemic uncertainty the source-region specific amplification factor for regions represented in the sample data set. As a property directly related to the local stress regime at the source, we therefore use this distribution as the second branching level of the logic tree and map it according to the same three-point discrete approximation to the Gaussian distribution as adopted for \(\delta c_{3,r}\), namely a “low stress” branch (\(-\varepsilon \cdot \tau _{L2L}\)) a “central” branch (\(0 \cdot \tau _{L2L}\)) and a “high stress” branch (\(+\varepsilon \cdot \tau _{L2L}\)), weighted in the same manner as for the attenuation uncertainty.
4.3 Within-model statistical uncertainty
The third branching level of the framework proposed by Douglas (2018a) is that of the within-model statistical uncertainty (\(\sigma _{\mu }\)). This is a property of the ground motion model itself and is derived for a range of M, R, and T using the approach of Al Atik and Youngs (2014). The variation of \(\sigma _{\mu }\) with period is shown in Fig. 7 and compared for different magnitudes and distances. In general, this term is relatively stable with respect to period and to distance, and the only clear trend is that is increases significantly at higher magnitudes (\(M_W \ge 6.5 - 7.0\)), where the ESM data set contains very few records. For comparison, the source variability \(\tau _{L2L}\) is also shown, and it can be seen clearly that this exceeds \(\sigma _{\mu }\) by some margin, except at the very largest magnitudes found in the data.
Variation in statistical uncertainty, \(\sigma _{\mu }\), with period for different magnitudes (left) and distance (right), the shaded area indicates the range of short period \(\sigma _{\mu }\) values from various site-specific PSHA studies, as described in Table 6.2 of Douglas (2018a)
4.4 The “default” shallow crustal logic tree
The proposed framework for a regional logic tree outlined by Douglas (2018a) has been mapped into three branching levels (residual attenuation variability, region dependent source variability, and statistical uncertainty) using the distributions of random effects within the regression of the backbone model. In doing so, we have treated each of the different uncertainties as independent from one another, such that, in theory, each of the 27 potential branches is independent. Although it can be argued that in the approach taken here the source region variability and the residual attenuation region variability can be considered independent, this is not necessarily true of the statistical uncertainty, which emerges from properties of the data set and not explicitly of the earthquake process. It cannot be considered truly independent of the other branches, as a proportion of the source region and residual attenuation region variability is already represented by \(\sigma _{\mu }\); hence we are potentially double counting uncertainty. Furthermore, in the range of magnitudes and distances where the model is well-constrained by the data (mostly \(4.5 \le M \le 6\), \(30 \le R_{JB} \text { (km)} \le 100)\), \(\sigma _{\mu }\) is considerably smaller that the source-region to source-region variability, whilst at the extremes of the data ranges (very high magnitudes and/or short distances) \(\sigma _{\mu }\) exceeds it. To minimise the impact of the double counting, and by doing so simplifying the logic tree, the statistical uncertainty branching level is removed and instead the source-region to source-region branches are replaced with the envelope of \(\tau _{L2L}\) and \(\sigma _{\mu }\). The resulting logic tree is thus reduced to nine branches, an illustrative example of which is shown in Fig. 8.
As a means of comparison of the total epistemic uncertainty implied by the combined source-region and statistical uncertainty term, the shaded regions Fig. 7 show the range of short period ground motion epistemic uncertainty factors (\(\sigma _{\mu }\)) for several site-specific PSHA studies originally mentioned in Table 6.2 of Douglas (2018a). These mostly fall within the range of 0.4–0.5 natural log units of g, which is comparable to the short-period \(\tau _{L2L}\) values and thus much of the epistemic uncertainty for the most well constrained range of magnitudes and distances. For PGA and for longer periods the epistemic uncertainty in the new model is lower, which is also in agreement with indications of Douglas et al. (2014) and Douglas (2018a). However, the complete \(\sigma _{\mu }\) from the full ground motion logic tree will also incorporate the influence of attenuation uncertainty, and will therefore likely increase at longer distances. Whilst the specific values will ultimately be dependent on the model in question, this suggests that new epistemic uncertainty in ground motion implied by the current logic tree is more comparable to that found within site-specific studies.
Whilst comprehensive comparison of the epistemic uncertainty range predicted by this logic tree compared to previous models can be found in Electronic Supplement 3, Figs. 9 and 10 show trellis plot comparisons of the new model versus those GMMs used for shallow crustal regions in the ESHM13. These include Akkar and Bommer (2010), Cauzzi and Faccioli (2008), Chiou and Youngs (2008), and Zhao et al. (2006) for “active shallow crustal regions”, plus Toro (2002) and Campbell (2003), which were added for “stable shallow crustal regions (excluding the Shield region)”. For those magnitudes and distances well-constrained by the data (typically \(M_W < 6.0\) and \(10 \le R_{JB} \text { (km)} \le 100\)) the centre and range of this backbone agree relatively well with the range predicted by the ESHM13 selection for active shallow crust for periods greater than approximately 0.2 - 0.3 s. The greatest differences can be seen at very short periods (\(< 0.1\) s) where the new models seem to predict lower motions in general. Greater divergences emerge at longer distances, where the general trend of the newer models is toward faster attenuation and thus the centre and body of the new GMM logic tree predict lower motions in general. Two factors are likely to be influential in accounting for this discrepancy. The first is that in comparison to the previous strong motion databases for Europe, particularly that used by Akkar and Bommer (2010), the proportion of records from the central and northern Appenine region is significantly increased and therefore skews the centre of the data set toward these conditions, which are generally faster attenuating than the rest of Europe on the whole. This is compounded by the second factor, which is that the ESHM13 model selection contains GMMs constrained by data from other regions outside Europe and the Middle East, including those that may be more slowly attenuating or display particular source or site characteristics that are distinct from those of the records found in the ESM.
Trellis plots comparing the response spectra of the nine branch default shallow logic tree against the ESHM13 shallow GMPE selection Delavaud et al. (2012) for a strike-slip earthquake with hypocentral depth between 10 and 20 km, assuming a measured site condition of \(V_{S30}\ 800\) m/s
Trellis plots comparing the scaling with distance of the nine branch default shallow logic tree against the ESHM13 shallow GMPE selection Delavaud et al. (2012) for a strike-slip earthquake with hypocentral depth between 10 and 20 km, assuming a measured site condition of \(V_{S30}\ 800\) m/s
By constraining \(\tau _{L2L}\) and \(\tau _{c_3}\) on the entire source-region to source-region and residual attenuation-region to residual attenuation-region variability implied by the model, what is really represented is a maximum uncertainty, or least informed case. In the strictest sense this is the epistemic uncertainty for regions analogous to those represented by the ESM, where very little or no strong motion observations are available to refine or reduce it. Hence, this is referred to as the default scaled backbone logic tree for shallow crustal regions. By definition then, this logic tree should only be applied in regions where no strong motion data are available. For many of the more seismically active regions of Europe, however, these strong motions are available and therefore the epistemic uncertainty in these regions should be not only lower than the default but with a centre, body and range calibrated to the data available.
5 Regional calibration
The two regionalisations implied by the \(\delta L2L_l\) and \(\delta c_{3, r}\) distributions form the basis for the regional adjustment of the logic trees. Whilst there is some evidence for a regional trend in source-region to source-region uncertainty, given the small number of earthquakes available in each source the standard errors on each individual \(\delta L2L_l \left( T \right)\) are substantial. With more time and more earthquakes this uncertainty will be reduced, but even in spite of the large volume of data in the ESM database we do not feel sufficiently confident at present to attempt to regionalise \(\delta L2L_l\). Therefore it is believed appropriately conservative that the “stress parameter” term (\(\max \left[ {\tau _{L2L}, \sigma _{\mu }} \right]\)) is retained without regionalisation.
For the \(\delta c_{3,r} \left( T \right)\) term the prospects for regional refinement are encouraging. The spatial distribution of \(\delta c_{3,r}\) for PGA is shown in Fig. 11, and provides many crucial insights into the variation of residual attenuation across Europe, mostly re-enforcing trends that have emerged from other studies. The fastest attenuation (lowest \(c_3 + \delta c_{3,r}\)) can be seen in central and western Italy, the Tyrrenhean Sea, the South Aegean and the Corinth region. Attenuation is generally slower in the Eastern Alps, the northern Dinarides mountains and the Caucasus, whilst the slowest attenuation is seen in the Pyrenees and northern Black Sea coast. The remainder of Europe tends to sit somewhere in the middle. Given the large number of records from the Pyrenees and northern Black Sea regions, this particularly slow attenuation is unlikely to be simply a statistical artefact. Neither is the fast attenuation in central Italy and Southern Greece. These patterns reinforce what have, to this point, been largely country-by-country based explorations of attenuation differences, such as those of Scasserra et al. (2009) and Kotha et al. (2016) who also infer fast attenuation in Italy when compared to Turkey and the rest of Europe.
In theory, a full logic tree could be constructed using each region-by-region calibration of residual attenuation. Here the full distribution of \(\tau _{c_3}\) would be replaced by \(\pm \varepsilon \cdot \sigma _{c_{3,i}}\), where \(\sigma _{c_{3,i}}\) is the standard error of \(\delta c_{3,r}\) for each region. In a continental scale PSHA, assuming a nine-branch GMM logic tree per region, the number of end-branches is raised by the total number of regions considered, thus the 42 calibrated zones here, plus the default, would result in \(9^{43}\) end-branches for the entirety of Europe. Not only is this practically impossible for calculation at a continental scale, even if choosing to randomly sample the GMM logic tree rather than enumerating the branches, but it is almost certainly over-modelling the regional differences that may not in fact be so significant from one zone to another. To clarify this perhaps surprising point regarding the scale of the logic tree, this does not mean that each site in Europe is influenced by all \(9^{43}\) branches of the logic tree. The actual number of branches affecting a site will depend on its proximity to the different regions, with some sites sites such as northern UK influenced by only nine branches (the default backbone alone), whilst the maximum number of branches that can be considered for any one site would depend only on the number of regions that occur within the user-defined maximum distance of a site (typically 200–300 km). So the maximum number of branches is tens of orders of magnitude less than the full set of \(9^{43}\) end-branches, but still an intensive calculation nonetheless.
The challenge in translating this to application in the ESHM20 is then how to capture the principal regional trends in residual attenuation, and thus justifiably reduce the epistemic uncertainty in these areas, without necessarily defining a different GMM logic tree for each zone. The obvious answer is to group together zones of similar \(\delta c_{3,r} \left( T \right)\). As \(\delta c_{3,r}\) is a vector, we need to determine which zones display similar characteristic trends in their period-dependent residual properties. This problem is ideally suited for the application of common cluster analysis algorithms. Several different methods of cluster analysis were compared, including those that preserved the spatial contiguity of the resulting partitions, which is a desirable (but not necessarily critical) property of the regionalisation. Ultimately, however, although more complex clustering approaches were applied, simple hierarchical clustering proved to be remarkably robust in finding a suitable partition that separated out the main differences in the zones within a smaller number of suitable clusters.
Distribtion of \(c_3\) for each of the five clusters, with the default backbone mean, 5th and 95th quantiles shown as blue lines (solid and dashed respectively) the individual \(c_3\) values for each zone as grey lines, and the cluster-specific mean and quantiles (solid and dashed respectively) indicating the frequentist-defined (black) and the Bayesian-defined (red) Gaussian distribution
A five-cluster partition, shown in Fig. 12, was found to provide the best balance between identifying clearly separable distributions of \(\delta c_{3,r}\) whilst preserving an acceptable degree of spatial coherence and reduction of the epistemic uncertainty. The distributions of the resulting \(c_3\) (i.e. the fixed effect \(c_3\) plus \(\delta c_{3,r}\)) within each of the five clusters are subsequently shown in Fig. 13. The blue lines shown in Fig. 13, indicated the \(c_3\) range (centre and 5\(^{th}\) to 95\(^{th}\) percentiles) implied by the default backbone model, whilst the red lines describe the corresponding distribution within each specific cluster. Cluster 1 incorporates set of zones with \(c_3\) marginally higher than the default of the GMM, implying slightly slower attenuation than the “average” of the data set, thus it is the “average/slow” cluster. It contains zones mostly to the north and east of the Alps as well as others on the edge of the data set including the Dead Sea transform, the Hyblean plateau (southern Sicily) and the outer rise of the Hellenic arc. Cluster 2 is centred close to the middle of the default \(c_3\) range, albeit marginally lower and thus implying slightly faster attenuation but with reduced variability, otherwise referred to as the “average/fast” cluster. It is mostly centred on regions around the western and southern Adriatic and northern Italy, as well as the eastern Anatolian fault, north Aegean and northern Caucasus. Cluster 3 is of particular interest as it consists of particularly fast attenuating zones (low \(c_3\)) values in western Italy (therefore named the “fast” cluster), the Tyrrhenean Sea and the south Aegean; the latter will be discussed in more detail subsequently. Cluster 4 shares a similar centre and range of values as that of Cluster 2, with the centre matching closely the default \(c_3\) at periods shorter than 1 s (thus slightly slower attenuation than cluster 2), drifting toward slower attenuation still at longer periods. As this cluster is the closest to the centre of the data set it can be though of as the most “average” cluster. The majority of regions within this cluster are in Turkey and the southern Causasus, with the addition of the southern Dinarides and Albanides as well as much of Sicily and the Carpathian belt. The final cluster, cluster 5, contains two zones of anomalously slow attenuation that are outliers with respect to the rest of the zones for which \(\delta c_{3,r}\) is determined. These are the Pyrenees and the northern Black Sea region. Here \(c_3\) tends toward zero, implying virtually no additional residual attenuation besides geometric spreading. This is referred to as the “very slow” cluster in Fig. 12.
Note that in the final partition, the large zone encompassing much of Germany, southwestern Poland, Czechia, Slovakia and Hungary (Fig. 11) is assigned to the default backbone in spite of a calibrated \(\delta c_{3,r}\) being determined. The same applies for the Betics zone of southern Spain. In both cases the \(\delta c_{3,r}\) was constrained on a small number of records from only one or two stations, and their corresponding means and standard errors found to be almost identical to the full \(\tau _{c_3}\) distribution of the backbone. As such there was an insufficient grounds for attempting to regionalise these areas in place of the default model.
5.1 A pseudo-volcanic GMM?
Although each cluster provides some insights into the ground motion attenuations within a given region, Cluster 3 holds some particular interest in terms of its implications for seismic hazard analysis. This cluster contains a set of zones that are relatively well-constrained by data and show fast attenuation compared to the main body of the full data set. In the case of the Italian zones it is important to note that virtually all of the volcanic regions of Italy are contained within this set of zones, including the Aeolian islands to the south, the peri-Neopolitan volcanic regions (Vesuvius, Campi Flegrei and Ischia) and older volcanic complexes in the Lazio and Tuscany provinces. This region set therefore contains a large number of records for which the travel paths have a proportionately greater distance passing through, or close to, active or recent volcanic environments. A similar situation is encountered in the case of Greece, where many travel paths traverse, or at least propagate close to, the Cyclades volcanic belt. The region of the entire data set with the lowest \(c_3\) is in fact the eastern Corinth zone, where high heatflow (Lucazeau 2019), shallow source depths and high strain (Carafa et al. 2015) combine to produce an environment of particularly fast attenuation even within the broader domain of active shallow crustal seismicity in Europe.
Although the calibration of the backbone model in Cluster 3 suggests an influence from volcanism within its dataset, we cannot refer to it as a truly volcanic model in a sense that might be comparable with other such volcanic models in the literature (e.g. Tusa and Langer 2015; Lanzano and Luzi 2019). In our case the records are not exclusively from volcanic earthquakes, meaning that the depth distributions of those events calibrating the attenuation in the cluster are deeper and of typically larger magnitude (\(M_W > 4.0\)) than those often used for deriving volcanic ground motion models. We use the term pseudo-volcanic to emphasise that this model reflects a volcanic influence on ground motion attenuation instead. We do, however, believe this distinction to be relevant and that this model can be applied in other regions of active volcanism and high strain in Europe, namely Iceland. Additionally, as discussed in Sect. 4, \(\delta c_{3,r}\) is a residual attenuation, and not exclusively representative of the impact of anelastic attenuation associated with volcanism, but can also be influenced by regional variation in geometric spreading that in itself may be indicative of regional differences in source depth. As a result, at short distances the ground motions within this cluster may in fact be higher than those predicted by the default backbone. The influence that these calibrations have on seismic hazard therefore is dependent on both the region and the proximity of the active sources to the site.
5.2 Constraining the \(c_3\) distribution per cluster
The cluster analysis has identified five clusters of significance, yet it does not by itself constrain the actual values of \(c_3\) intended to represent the epistemic uncertainty. For this purpose a Gaussian distribution of \(\delta c_{3,r}\) is fit per period and per cluster, i, each with a corresponding mean (\(c_{3_{cl,i}}\)) and standard deviation (\(\tau _{c_3,cl_i}\)). These are shown in the red and black lines in Fig. 13. Two different approaches to the fitting are shown: a frequentist interpretation (taking the mean and standard deviation of the \(\delta _{c_{3_i}}\) values directly from the within-cluster range), and a Bayesian interpretation, which updates a prior distribution to provide estimates of the mean and variance of within cluster \(c_3\) values. The Bayesian fitting of the Gaussian model uses a Markov-Chain Monte Carlo approach with a No U-Turn Sampler (Hoffman and Gelman 2014; Salvatier et al. 2016). A Gaussian prior of \({\mathcal {N}} \left( {c_3 , \tau _{c_3}} \right)\) is assumed for the estimation of each mean \(c_{3_{cl,i}}\), and a uniform prior of \({\mathcal {U}} \left( {0, \tau _{c_3} + 0.05} \right)\) for each within-cluster standard deviation \(\tau _{c_3,cl_i}\). The Bayesian approach is preferred in order to reduce the sensitivity of the localised distribution to the specifics of a small number of observations in the case when the cluster contains very few regions, as can be seen from the frequentist range for cluster 5, which tends to zero at certain periods where the two constituent \(c_3\) data sets converge. As such, clusters containing a larger number of regions are better constrained, with close agreement between the frequentist and Bayesian means and a reduced variance compared to the original \(\tau _{c_3}\). Clusters 3 and 5 contain fewer regions, and though the means of the Bayesian fitted Gaussians broadly reflect the regional trends, the within-cluster variances reduce less compared to the original \(\tau _{c_3}\). We believe this is an appropriate compromise between aiming to reflect regional differences from one cluster to another (and thus reduce the modelled epistemic uncertainty), without being overly steered to exceptionally anomalous values in the small number of outlying regions. A comparison of the site-corrected within-event residuals and the region-corrected residuals against the regionalised GMMs, limited only to the subset of recording within each of the regional clusters, can be seen in Electronic Supplement 1.
5.3 Aleatory uncertainty
Whilst the primary focus of the construction of the GMM logic tree is on the representation of epistemic uncertainty, as a means of understanding the potential implications of the new backbone model for PSHA it is also important to compare the aleatory uncertainty in the new model with others derived previously. The model is intended for application on a Eurocode 8 site class A assuming a measured condition, and thus the total ergodic standard deviation (\(\sigma _T = \sqrt{\tau _0^2 + \phi ^2 + \phi _{S2S} ^ 2}\)) will be applied. Kotha et al. (2020) provide a homoskedastic model for the source-region corrected between-event variability, \(\tau _0\), and the site-corrected within-event variability \(\phi _0\). The site-to-site variability, \(\phi _{S2S}\), is calibrated according to whether the \(V_{S30}\) refers to a measured or inferred site condition, the latter accounting for the addition uncertainty on the site condition contributing to the overall site-to-site variability. For running seismic hazard on Eurocode 8 class A rock we assume a measured \(V_{S30}\) condition, whilst for applications to the 2020 European Seismic Risk model, where ground motion should correspond to that at the soil surface in any location, the site condition is mostly inferred from proxy information and therefore an inferred condition is assumed.
To determine how the components of aleatory variability have changed in the Kotha et al. (2020) model with respect to previous generations, Fig. 14 compares each of the three components with those found in selected preceding models. Bindi et al. (2014) and Kotha et al. (2016) are based on the previous RESORCE European strong motion data set, whilst Rodriguez-Marek et al. (2013) and Tromans et al. (2019) present or adopt models of \(\phi _0\) and \(\phi _{S2S}\) inferred from global databases and consider both heteroskedastic and homoskedastic alternatives.
There is an increase in \(\tau _0\) from Kotha et al. (2020) with respect to Kotha et al. (2016) and Bindi et al. (2014). This is most likely due to the significant increase in the number of events, particularly in the \(4.0 \le M_W \le 4.5\) range where robust estimates of \(M_W\) are not routinely determined for much of the data set and errors in magnitude estimation may propagate into the inter-event term. For the residual variability, \(\phi _0\), the new model is similar to that of the preceding models, and substantially lower than Bindi et al. (2014). At periods longer than 1 - 2 seconds, \(\phi _0\) in the Kotha et al. (2020) model is in fact the lowest of the models compared, which may reflect the influence of adopting a robust mixed effects regression compared to conventional approaches.
Comparison of components of aleatory uncertainty of the current model those found in previous models: \(\tau _0\) (left), \(\phi\) (centre) and \(\phi _{S2S}\) (right). Labelled models: Bi2014 (Bindi et al. 2014), Ko2016 (Kotha et al. 2016), Ko2020 (Kotha et al. 2020), Tr2019 (Tromans et al. 2019) and RM2013 (Rodriguez-Marek et al. 2013)
The two \(\phi _{S2S}\) models (measured and inferred \(V_{S30}\)) are compared and here there are some notable differences. The model for the measured sites provides values that are similar to those of Bindi et al. (2014) and Rodriguez-Marek et al. (2013). That only the measured-\(V_{S30}\)\(\phi _{S2S}\) is only comparable with other models, despite use of a robust regression method and removal of inferred site parameter cases, is actually a reflection of the extent to which the larger number of sites represented in the ESM data set increases the site-to-site variability with respect to preceding studies. As might be expected, when calibrating \(\phi _{S2S}\) using only the inferred \(V_{S30}\) the variability increases substantially, especially at shorter periods.
Although individual components of the homoskedastic aleatory uncertainty model from Kotha et al. (2020) may be comparable to those found in some preceding models, initial calculations of both seismic hazard and risk revealed an unduly large influence from excessive ground motions at moderate-to-large magnitudes in the range of \(+1 \cdot \sigma _T\) to \(+3\cdot \sigma _T\). Despite the addition of several events with \(M_W \le 6\) in the ESM database, the constraint of aleatory uncertainty at large magnitudes remains poor in comparison to other global data sets such as NGA West 2.
Many studies of ground motion variability, as well as preceding ground motion models, have shown evidence of heteroskedastic variability in both the \(\tau _0\) and \(\phi _0\) terms (e.g Youngs et al. 1995; Rodriguez-Marek et al. 2013; Al Atik 2015), resulting in reduces aleatory variability for larger magnitudes at short-periods. To assess whether there is evidence of heteroskedasticity in the random-effects residuals of the Kotha et al. (2020), Fig. 15 shows the trends in the source-region corrected between-event residual (\(\delta B_{el}^0\)) with respect to magnitude, and the site corrected within-event residual (\(\varepsilon _0\)) with respect to magnitude and distance. Each residual is colour scaled according to their weight in the robust linear mixed-effects model. Results are shown here only for \(Sa \left( {0.1 s} \right)\), but a more detailed set of comparisons for multiple periods of ground motion can be seen in Electronic Supplement 2.
Dependence of variability in random-effect residuals with respect to magnitude and distance for \(Sa \left( {0.1 s} \right)\) and compared with the corresponding variances found in the literature. Binned means and variances shown by purple error bars. Top: Source-region corrected between-event residuals plotted with respect to magnitude (binned every 0.5 M units), Middle: site-corrected within event residuals plotted with respect to magnitude (binned every 0.5 M units), Bottom: site-corrected within-event residuals plotted with respect to distance
In the case of \(\delta B_{el}^0\), the homoskedastic \(\tau _0\) of Kotha et al. (2020) is compared against the heteroskedastic models from Abrahamson et al. (2014) and the “global” model Al Atik (2015). The latter are both calibrated using the NGA West 2 database, which contains a substantially greater number of large (\(M_W \ge 6\)) events than ESM. From the available data there is some weak evidence of a reduction in \(\tau _0\) at larger magnitudes, whilst for the magnitude range well constrained by the ESM data \(4.0 \le M_W \le 5.5\) both the homoskedastic and heteroskedastic models are comparable. As the model of Al Atik (2015) is better constrained by larger magnitude events and agrees well with the homoskedastic \(\tau _0\) in the lower magnitude range, their “global” heteroskedastic between-event variability model is used in favour of the original \(\tau _0\) values from Kotha et al. (2020) in the hazard and risk applications.
For \(\varepsilon _0\), Fig. 15 suggests a decrease in \(\phi _0\) with magnitude but no significant trend with respect to distance. As the few large events in the ESM database are generally well recorded, we believe this trend to be robust, suggesting that a heteroskedastic \(\phi _0\) may too be more appropriate. Here, however, whilst the “global” model of Al Atik (2015) seems to agree well with the observed variance at larger magnitudes, the original \(\phi _0\) model of Kotha et al. (2020) agrees better with the observed distribution of the data in the \(4.0 \le M_W \le 5.5\) range. Rather than adopting the \(\phi _0\) model of Al Atik (2015) without adjustment, we instead fit their magnitude-dependent heteroskedastic model to the binned \(\varepsilon _0\) distribution for \(M_W > 6\) and retain the Kotha et al. (2020) \(\phi _0\) values for \(M_W \le 5\). This new heteroskedastic \(\phi _0\) model is shown in the black lines in the middle plot of Fig. 15.
The proposed heteroskedastic aleatory uncertainty models are shown in Fig. 14, labelled as “Current Model”. For smaller magnitudes, both the \(\tau _0\) and \(\phi _0\) values are in good agreement with both the original homoskedastic model and the low-magnitude heteroskedastics model adopted by previous studies such as Tromans et al. (2019) and Rodriguez-Marek et al. (2013). At larger magnitudes, the new model predicts slightly lower standard deviations than other studies. In the case of \(\tau _0\) this may reflect the improved calibration of the “global” \(\tau _0\) by Al Atik (2015), whilst for \(\phi _0\) this may better reflect the influence of removing the region-to-region variability from the total aleatory uncertainty, which is now being treated as epistemic uncertainty via the \(\tau _{c_3}\) term. For most return periods of engineering interest (e.g. 475–2475 years) the adoption of the heteroskedastic aleatory uncertainty model leads to a small reduction in seismic hazard with respect to the homoskedastic model, nevertheless it does reduce the levels of ground motion for lower probabilities of exceedance in the resulting hazard and loss curves.
6 The complete shallow crustal logic tree
For shallow crustal seismicity in regions analogous to those sampled within the ESM database, it has been possible not only to define a scaled backbone ground motion model logic tree to capture uncertainty in regional stress scaling and anelastic attenuation, but also to tune it in order to model large scale regional variations. For the Mediterranean region and much of western and southern Europe, the epistemic uncertainty is represented by the shallow crustal ground motion logic tree shown in Fig. 16. In effect, this tree contains six sets of nine branches, one set for the default backbone (shown above the dashed line in Fig. 16) to be applied where no ESM data are available, and one for each of the five clusters or sub-regions implied from the exploration of the residual attenuation random effects \(\delta c_{3,r}\).
In Electronic Supplement 3, a more exhaustive set of comparisons is made against ground motion model selections made by recent national models for Germany (Grünthal et al. 2018), the United Kingdom (Tromans et al. 2019) and Italy, as well as against the previous ESHM13 selection for each cluster. In the cases of the UK and Germany the centre and range of the models agrees generally well with the full default backbone, suggesting the source-region variability is encompassing well the stress parameter uncertainty implied by alternative model selections. Other factors such as the choice of cluster and/or the hypocentral depth bin used are also influential in terms of determining agreement around the centre of the distribution. The general trend of lower ground motions at very short periods does, however, seem persistent and this may have an impact in lowering seismic hazard estimates throughout much of Europe with respect to ESHM13. As can be inferred from the further comparisons in the electronic supplement, such reductions do seem to be persistent also in national models suggesting that this trend is not necessarily a consequence of the scaled backbone logic tree adopted here but rather a systematic reduction in ground motion estimates apparent in many recent GMMs.
7 Conclusions
The complete ground motion model logic tree proposed for the ESHM20 represents a radical departure from its ESHM13 predecessor. This has been firstly necessitated, and subsequently facilitated, by the volume of ground motion data that has been acquired in Europe and homogeneously processed within the ESM flatfile (Lanzano et al. 2019). Collectively, a total of six branch sets have been considered for application to shallow seismicity, including the default shallow crustal backbone and its five regional “clusters”. In contrast to the previous European ground motion logic tree, and addressing one of the most serious shortcomings of the multi-model approach, the number of alternative models is kept fixed in each branch set but their actual distribution generally widens in regions where little or no data are available. As such, we believe this is a more appropriate depiction of the epistemic uncertainty than that of previous models. It must be re-iterated, however, that this does not represent the complete ground motion logic tree for Europe, nor even for all types of earthquakes found in shallow crust. The key caveat here is that even with the default backbone there is a critical assumption that it represents the broadest epistemic uncertainty in residual attenuation and source location implied by the extent of the ESM data set, and can therefore be considered representative only in regions that are, from a ground motion perspective, similar to those sampled by the ESM data. This would exclude both the non-shallow seismic regions and the stable shield, which will be addressed in subsequent publications.
Whilst the actual calibrations and weights of the scaled backbone itself are clearly relevant for the purposes of the PSHA calculations, what may be of most value to the broader community within this approach is the construction of a general framework through which new strong motion data can inform, refine and reduce the epistemic uncertainty. In the approach adopted here, the ESM data has steered the calibration of the logic tree via the constraint of region-to-region variability in both source and attenuation, and then using this same information permitted the centre, body and range of the GMM logic tree to be tuned according to the regionalisation. Not only does this approach provide scope for future data to continue to refine the models, both spatially and in terms of the calibrations of the backbone, it also introduces some necessary inertia into the process such that one may not necessarily expect large changes in the distribution following a well-recorded event or sequence based on the characteristics of that event(s). Indeed Stafford (2019) proposes a more formal framework for such an approach using Bayesian updating, to which the present logic tree seems ideally suited. This would form an obvious avenue for future research, setting in place an operational process for regular updating of hazard models as new data feed into them.
Although the development of the calibrations and their regional adjustments has been based upon a single extensive database of ground motion observations, adjustments can also be made without necessarily needing to re-run the regression or to have strong motion data feed into this common database, desirable though that might be. Where sufficient data are collected locally and not necessarily integrated directly into the ESM, these can still be used to identify regional differences in the models by virtue of systematic trends in the inter- and intra-event residuals with respect to either the “central” or the regionalised models. If adopted with the necessary rigour, a means to long-term harmonisation in ground motion modelling at a national level can emerge. Future applications will illustrate how this can be achieved in a practical manner that can be implemented by scientists working locally within their own country or region.
The time-frame for development of the ESHM20 obviously sets a constraint on the number of issues in ground motion modelling that can be addressed at the present time. The framework set out by the scaled backbone logic tree leads to a practical result that can better reflect the regional variability in ground motion modelling within Europe. There remain many outstanding issues, however, which should form the basis for future directions. These can be broken down into two categories: (1) continual revisions driven by new local data, (2) new models and/or model components that emerge from scientific developments. In the first category one would place the refinements to the regionalisation of the models and the distributions of \(\tau _{L2L}\) and \(\tau _{c_3}\). In the second category are the developments driven by modelling and/or global data, such as improvements in near-fault ground motion characterisation or large magnitude scaling, in which physics-based simulations of ground motion may be needed to constrain the respective parametric models that would be integrated into the GMMs subsequently. Indeed, hanging wall effects and directivity should form key targets for the next generation ground motion model logic tree.
A complete picture of the impact of the ground motion models on the hazard can only be fully ascertained once all pieces of the seismic hazard input models have been assembled. The ground motion models presented in this paper are available for use in PSHA within the OpenQuake-engine (Pagani et al. 2014), and further exploration and comparisons with respect to local and national ground motion models is strongly encouraged. To this end, concurrent to the development of the ESHM20 has been the creation of the European Ground Shaking Intensity Measure (eGSIM) portal, an open platform for the exploration of OpenQuake’s ground motion model library and quantitative comparison and testing against observed strong motion data. Though only one component of the complete ESHM20, work is now ongoing to assess how this new compilation will influence the assessment of seismic hazard across Europe, and where to focus efforts for future improvements to better constrain the differences in ground motion and its uncertainty from one region to another.
References
Abrahamson N, Silva W, Kamai R (2014) Summary of the ASK14 ground motion relation for active crustal regions. Earthq Spectra 30(3):1025–1055
Akkar S, Bommer J (2010) Empirical equations for the prediction of PGA, PGV, and spectral accelerations in Europe, the Mediterranean region, and the Middle East. Seismol Res Lett 81(2):195–206
Akkar S, Sandıkkaya MA, Bommer JJ (2014) Empirical ground-motion models for point- and extended-source crustal earthquake scenarios in Europe and the Middle East. Bull Earthq Eng 12(1):359–387
Akkar S, Kale O, Yakut A, Çeken U (2018) Ground-motion characterizarion for the probabilistic seismic hazard assessment in Turkey. Bull Earthq Eng 16:3439–3463
Al Atik L (2015) NGA-East: ground-motion standard deviation models for Central and Eastern North America. Tech. Rep. PEER Report No. 2015/07, Pacific Earthquake Engineering Research Center
Al Atik L, Youngs R (2014) Epistemic uncertainty for NGA-West2 models. Earthq Spectra 30(3):1301–1318
Assatorians K, Atkinson GM (2013) EqHaz: an open-source probabilistic seismic-hazard code based on the monte carlo simulation approach. Seismol Res Lett 84(3):516–524
Atkinson GA, Bommer JJ, Abrahamson NA (2014) Alternative approaches to modeling epistemic uncertainty in ground motions in probabilistic seismic-hazard analysis. Seismol Res Lett 85(6):1141–1144
Atkinson GM, Adams J (2013) Ground motion prediction equations for application to the 2015 Canadian national seismic hazard maps. Can J Civ Eng 40(10):988–998
Basili R, Brizuela B, Herrero A, Iqbal S, Lorito S, Maesano F, Murphy S, Perfetti P, Romano F, Scala A, Selva J, Taroni M, Thio H, Tiberti M, Tonini R, Volpe M, Glimsdal S, Harbitz C, Løvholt F, Baptista M, Carrilho F, Matias L, Omira R, Babeyko A, Hoechner A, Gurbuz M, Pekcan O, Yalçıner A, Canals M, Lastras G, Agalos A, Papadopoulos G, Triantafyllou I, Benchekroun S, Agrebi Jaouadi H, Attafi K, Ben Abdallah S, Bouallegue A, Hamdi H, Oueslati F (2019) NEAMTHM18 documentation: the making of the TSUMAPS-NEAM Tsunami Hazard Model 2018. Tech. rep., InIstituto Nazionale di Geofisica e Vulcanologia (INGV). DOI: https://doi.org/10.5281/zenodo.3406625
Bates D, Mächler M, Bolker BM, Walker SC (2015) Fitting linear mixed-effects models using lme4. J Stat Softw. https://doi.org/10.18637/jss.v067.i01
Bindi D, Massa M, Luzi L, Ameri G, Pacor F, Puglia R, Augliera P (2014) Pan-European ground-motion prediction equations for the average horizontal component of PGA, PGV, and 5 %-damped PSA at spectral periods up to 3.0 s using the RESORCE dataset. Bull Earthq Eng 12(1):391–430
Bommer JJ (2012) Challenges of building logic-trees for probabilistic seismic hazard analysis. Earthq Spectra 28(4):1723–1735
Bommer JJ, Coppersmith KJ, Coppersmith RT, Hanson KL, Mangongolo A, Neveling J, Rathje EM, Rodriguez-Marek A, Scherbaum F, Shelembe R, Stafford PJ, Strasser FO (2015) A SSHAC Level 3 probabilistic seismic hazard analysis for a new-build nuclear site in South Africa. Earthq Spectra 31(2):661–698
Brock G, Pihur V, Datta S, Datta S (2008) clValid: an R package for cluster validation. J Stat Softw 25(4):1–20
Campbell KW (2003) Prediction of strong ground motion using the hybrid empirical method and its use in the development of ground-motion (attenuation) relations in Eastern North America. Bull Seismol Soc Am 93(3):1012–1033
Carafa M, Barba S, Bird P (2015) Neotectonics and long-term seismicity in Europe and the Mediterranean region. J Geophys Res Solid Earth 120(7):5311–5324
Cauzzi C, Faccioli E (2008) Broadband (0.05 to 20 s) prediction of displacement response spectra based on worldwide digital records. J Seismol 12:453–475
Cauzzi C, Faccioli E, Vanini M, Bianchini A (2015) Updated predictive equations for broadband (0.01–10 s) horizontal response spectra and peak ground motions, based on a global dataset of digital acceleration records. Bull Earthq Eng 13(6):1587–1612
CEN (2004) Eurocode 8, design of structures for earthquake resistance—part 1: general rules, seismic actions and rules for buildings. Comité Europèan de Normalisation, Brussels
Chiou BJ, Youngs R (2008) An NGA model for the average horizontal component of peak ground motion and response spectra. Earthq Spectra 24(1):173–215
Chiou BJ, Youngs R (2014) Update of the chiou and youngs NGA model for the average horizontal component of peak ground motion and response spectra. Earthq Spectra 30(3):1117–1153
Coppersmith K, Coppersmith R, Hanson K, Unruh J, Wolf L, Bommer J, Al Atik L, Rodriguez-Marek A, Toro G, Youngs R, Montaldo-Falero V (2014) Hanford sitewide probabilistic seismic hazard analysis. Report Prepared for the U. S. Department of Energy under Contract DE-AC05-76RL01830, Pacific Northwest National Laboratory, Richland, Washington, 99352
Delavaud E, Cotton F, Akkar S, Scherbaum F, Danciu L, Beauval C, Drouet S, Douglas J, Basili R, Sandikkaya MA, Segou M, Faccioli E, Theodoulidis N (2012) Toward a ground-motion logic tree for probabilistic seismic hazard assessment in Europe. J Seismol 16(3):451–473
Derras B, Bard PY, Cotton F (2014) Towards fully data driven ground-motion prediction models for Europe. Bull Earthq Eng 12(1):495–516
Douglas J (2018a) Capturing geographically-varying uncertainty in earthquake ground motion models or what we think we know may change. In: Pitilakis K (ed) Recent advances in earthquake engineering in Europe: 16th European conference on earthquake Engineering-Thessaloniki 2018, vol 46, pp. 153–181. Geotechnical, Geological and Earthquake Engineering, vol 46, Cham. https://doi.org/10.1007/978-3-319-75741-4_6
Douglas J (2018b) Calibrating the backbone approach for the development of earthquake ground motion models. In: Best practices in physics-based fault rupture models for seismic hazard assessment of nuclear installations: issues and challenges towards full seismic risk analysis, vol Cadarache-Chateau, France, 14–16 May 2018, pp 1 – 11
Douglas J, Ulrich T, Bertil D, Rey J (2014) Comparison of the ranges of uncertainty captured in different seismic hazard studies. Seismol Res Lett 85(5):977–985
Edwards B, Cauzzi C, Danciu L, Fäh D (2016) Region-specific assessment, adjustment, and weighting of ground-motion prediction models: application to the 2015 Swiss seismic-hazard maps. Bull Seismol Soc Am 106(4):1840–1857
García-Fernandez M, Gehl P, Jiménez MJ, D’Ayala D (2019) Modelling Pan-European ground motions for seismic hazard applications. Bull Earthq Eng 17:2821–2840
Goulet C, Bozorgnia Y, Kuehn N, Al Atik L, Youngs RR, Graves RW, Atkinson GM (2017) NGA-east ground-motion models for the U. S. geological survey national seismic hazard maps. Tech. Rep. PEER Report No. 2017/03, Pacific Earthquake Engineering Research Center
Grünthal G, Stromeyer D, Bosse C, Cotton F, Bindi D (2018) The probabilistic seismic hazard assessment of Germany—version 2016, considering the range of epistemic uncertainties and aleatory variability. Bull Earthq Eng 16(10):4339–4395
Hoffman MD, Gelman A (2014) The No-U-Turn sampler: adaptively setting path lengths in Hamiltonian Monte Carlo. J Mach Learn Res 15:1593–1623
Kale O, Akkar S, Ansari A, Hamzehloo H (2015) A ground-motion predictive model for Iran and Turkey for horizontal PGA, PGV, and 5% damped response spectrum: investigation of possible regional effects. Bull Seismol Soc Am 105(2A):963–980
Koller M (2016) robustlmm: an R package for robust estimation of linear mixed-effects models. J Stat Softw 75:1–24
Kotha S, Bindi D, Cotton F (2016) Partially non-ergodic region specific GMPE for Europe and the Middle-East. Bull Earthq Eng 14(4):1245–1263
Kotha SR, Weatherill GA, Bindi D, Cotton F (2020) A regionally-adaptable ground-motion model for shallow crustal earthquakes in Europe. Bull Earthq Eng. In press
Kuehn NM, Scherbaum F (2016) A partially non-ergodic ground-motion prediction equation for Europe and the middle east. Bull Earthq Eng 14:2629–2642
Lacour M, Abrahamson NA (2019) Efficient propagation of epistemic uncertainty in the median ground-motion model in probabilistic hazard calculations. Bull Seismol Soc Am 109(5):2063–2072
Lanzano G, Luzi L (2019) A ground motion model for volcanic areas in Italy. Bull Earthq Eng 18:57–76
Lanzano G, Sgobba S, Luzi L, Puglia R, Pacor F, Felicetta C, D’Amico M, Cotton F, Bindi D (2019) The pan-European engneering strong motion (ESM) flatfile: compilation criteria and data statistics. Bull Earthq Eng 17:561–582
Lucazeau F (2019) Analysis and mapping of an updated terrestrial heat flow data set. Geochem Geophys Geosyst 20:4001–4024
Miller AC, Rice TR (1983) Discrete approximations of probability distributions. Manag Sci 29(3):352–362
Pagani M, Monelli D, Weatherill G, Danciu L, Crowley H, Silva V, Henshaw P, Butler L, Nastasi M, Panzeri L, Simionato M, Vigano D (2014) Openquake engine: an open hazard (and risk) software for the global earthquake model. Seismol Res Lett 85(3):692–702
Rodriguez-Marek A, Cotton F, Abrahamson NA, Akkar S, Al Atik L, Edwards B, Montalva GA, Dawood HM (2013) A model for single-station standard deviation using data from various tectonic regions. Bull Seismol Soc Am 103(6):3149–3163
Salvatier J, Wiecki TV, Fonnesbeck C (2016) Probabilistic programming in Python using PyMC3. PeerJ Comput Sci. https://doi.org/10.7717/peerj-cs.55
Scasserra G, Stewart J, Bazzurro P, Lanzo G, Mollaioli F (2009) A comparison of NGA ground-motion prediction equations to Italian data. Bull Seismol Soc Am 99(5):2961–2978
Stafford PJ (2019) Continuous integration of data into ground-motion models using Bayesian updating. J Seismol 23(1):39–57
Toro GR (2002) Modification of the Toro et al (1997) attenuation equations for large magnitude and short distances. Tech. rep., Risk Engineering Inc
Tromans IJ, Aldama-Bustos G, Douglas J, Lessi-Cheimariou A, Hunt S, Daví M, Musson RMW, Garrard G, Strasser FO, Robertson C (2019) Probabilistic seismic hazard assessment for a new-build nuclear power plant site in the UK. Bull Earthq Eng 17:1–36
Tusa G, Langer H (2015) Prediction of ground motion parameters for the volcanic area of Mount Etna. J Seismol 20(1):1–42
U S Nuclear Regulatory Commission (2012) Practical implementation guidelines for SSHAC Level 3 and 4 Hazard Studies, NUREG-2117 rev. 1. Tech. rep., U. S. Nuclear Regulatory Commission, Washington D. C
Weatherill GA, Danciu L (2018) Regional variation of spectral parameters for seismic design from broadband probabilistic seismic hazard analysis. Earthq Eng Struct Dyn 47(12):2447–2467
Weatherill G, Bindi D, Cotton F, Danciu L, Luzi L (2018) Building a new ground motion logic tree for Europe: needs, challenges and new opportunities from European seismological data. In: Proceedings of the 16th European conference on earthquake engineering, Thessaloniki, 18–21 June 2018, Paper No. 10729
Weatherill G, Kotha SR, Cotton F (2020) Re-thinking site amplification in regional seismic risk assessment. Earthq Spectra. In press
Woessner J, Laurentiu D, Giardini D, Crowley H, Cotton F, Grünthal G, Valensise G, Arvidsson R, Basili R, Demircioglu M, Hiemer S, Meletti C, Musson R, Rovida A, Sesetyan K, Stucchi M, The SHARE Consortium (2015) The 2013 European seismic hazard model: key components and results. Bull Earthq Eng 13(12):3553–3596
Youngs RR, Abrahamson NA, Makdisi FI, Sadigh K (1995) Magnitude-dependent variance of peak ground acceleration. Bull Seismol Soc Am 85(4):1161–1176
Zhao J, Zhang J, Asano A, Ohno U, Oouchi T, Takahashi T, Ogawa H, Irikura K, Thio H, Sommerville P, Fukushima Y (2006) Attenuation relations of strong ground motion in Japan using site classifications based on predominant period. Bull Seismol Soc Am 96(3):898–913
Zhao J, Zhou S, Zhou J, Zhao C, Zhang H, Zhang Y, Gao P, Lan X, Rhoades D, Fukushima Y, Somervile P, Irikura K (2016a) Ground-motion prediction equations for shallow crustal and upper-mantle earthquakes in Japan using site class and simple geometric attenuatiion functions. Bull Seismol Soc Am 106(4):1552–1569
Zhao J, Liang X, Jiang F, Xing H, Zhu M, Hou R, Zhang Y, Lan X, Rhoades D, Irikura K, Fukushima Y, Somervile P (2016b) Ground-motion prediction equations for subduction interface earthquakes in Japan using site class and simple geometric attenuations functions. Bull Seismol Soc Am 106(4):1518–1534
Zhao J, Jiang F, Shi P, Xing H, Huang H, Hou R, Zhang Y, Yu P, Lan X, Rhoades D, Somerville P, Fukushima Y (2016c) Ground-motion prediction equations for subduction slab earthquakes in Japan using site class and simple geometric attenuation functions. Bull Seimol Soc Am 106(4):1535–1551
Acknowledgements
Open Access funding provided by Projekt DEAL. The development of the ground motion logic tree has been undertaken in as part of the Horizon 2020 Seismology and Earthquake Engineering Research Infrastructure Alliance in Europe (SERA, Grant Agreement No. 730900). It has benefited enormously from inputs and discussions among an active community of ground motion and seismic hazard modellers. The authors would like to thank in particular John Douglas, Laurentiu Danciu, Roberto Basili, Stefan Wiemer, Domenico Giardini, Celine Beauval, Pierre-Yves Bard, Susana Vilanova, Lucia Luzi, Giovanni Lanzano, Dino Bindi, Paola Traversa, Marco Pagani, Helen Crowley, Abdullah Sandikkaya, Ilaria Mosca, Adrian Oth, Kris Vanneste, Nikos Theodoulidis, Benedikt Halldorson, Milad Kowsari, Sinan Akkar, Nicolas Kuehn, Norm Abrahamson, and all participants to the ESHM20 hazard model review meetings. We are also grateful to Julian Bommer and Gail Atkinson for providing thorough and insightful reviews of this manuscript. Ground motion data has been taken primarily from the European Strong Motion flatfile (http://esm.ingv.mi.it) (Lanzano et al. 2019), whilst the exploration and application of the models has been built upon the OpenQuake-engine (Pagani et al. 2014) for which we thank the Global Earthquake Model. The analysis presented herein has been undertaken using several open-source scientific software packages in both the R (https://www.r-project.org/) Python (https://www.python.org/) languages, including Numpy/SciPy (https://www.scipy.org/) Pandas (https://pandas.pydata.org/), GeoPandas (https://geopandas.org/), PyMC3 (https://docs.pymc.io/), clValid (Brock et al. 2008), ggplot2 (https://ggplot2.tidyverse.org/) and lme4 (Bates et al. 2015). Graphics are constructed using QGIS (https://www.qgis.org) and Matplotlib (https://matplotlib.org/).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Weatherill, G., Kotha, S.R. & Cotton, F. A regionally-adaptable “scaled backbone” ground motion logic tree for shallow seismicity in Europe: application to the 2020 European seismic hazard model. Bull Earthquake Eng 18, 5087–5117 (2020). https://doi.org/10.1007/s10518-020-00899-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10518-020-00899-9