Seismic collapse capacity assessment of SDOF systems incorporating duration and instability effects

Abstract

This paper presents a detailed investigation into the seismic response of non-deteriorating and deteriorating single degree-of-freedom systems controlled by $P -\Delta$ effects, with due account for the influence of earthquake duration. In order to isolate the effect of duration from other ground motion characteristics, 77 pairs of records with equivalent spectral shapes are considered in the study. The structural characteristics examined include the structural period, applied gravity loading, post-yield stiffness, viscous damping, material hysteretic behaviour, as well as the level of cyclic deterioration within the pinching systems. Detailed incremental dynamic analyses are carried out, considering an intensity measure corresponding to the spectral acceleration at the structural period of vibration of the system. Based on the incremental dynamic analysis results, predictive relationships are proposed for determining the structural collapse capacity, accounting for the influence of key parameters including instability and duration effects. The median and dispersion of the collapse capacity distribution embedded in the predictive models are also presented. The effect of duration is shown to increase with longer structural periods and to decrease with higher $P -\Delta$ levels. The more rapid instigation of dynamic instability in relatively stiff systems is also shown to reduce their comparative sensitivity to variations in ground motion characteristics. Overall, it is indicated that disregarding the influence of duration could lead to over-estimations of up to 50% in the collapse capacity. The paper concludes with a discussion of other sources of structural damage that instigate collapse when using records with equivalent spectral shape but without especial consideration for duration effects.

1 Introduction

There has been a renewed interest in recent years on the influence of earthquake duration, particularly in the assessment of seismic collapse risk of modern buildings, primarily due to the availability of new long duration strong motion records from subduction regions. The effects of duration on the structural collapse capacity have been addressed in several recent studies (e.g. Raghunandan and Liel 2013; Barbosa et al. 2017, Chandramohan et al. 2016; Bravo-Haro and Elghazouli 2018a). Nonetheless, these studies have not given specific attention to structural systems governed by second-order instabilities due to gravity loads, i.e. $P -\Delta$ effects. The latter, coupled with cyclic degradation effects, are typically responsible for the side-sway collapse of a building (Krawinkler et al. 2009). In addition, existing seismic provisions for design and assessment do not explicitly incorporate the effects of duration, although this can sometimes be implicitly accounted for by performing nonlinear dynamic analysis based on ground motion recordings which are selected to reflect duration effects. New methods have only recently started to emerge for incorporating duration effects in simplified design procedures, such as the pervasive lateral force approach (Chandramohan et al. 2018).

Existing structures, which may have been designed to outdated seismic codes or without considering any seismic provisions, are usually characterised as ‘non-ductile’ or ‘brittle’ systems. Their response is often characterised by a negative-slope post-yield stiffness, such that they exhibit reduction in post-yield lateral resistance with increasing lateral drifts, leading to dynamic instability and subsequent structural collapse (Miranda and Akkar 2003). However, this type of instability-sensitive behaviour is not limited to code-deficient structures. Modern seismic provisions enable inelastic deformations in predefined regions of the structure which, together with $P -\Delta$ effects, can result in a post-yield negative slope particularly in the case of relatively flexible frame-type systems (Adam and Jäger 2012a). Therefore, the quantification of earthquake duration effects can lead to a significant improvement in the assessment of collapse capacity in a wide range of existing as well as modern structures. The assessment of duration effects is particularly important in regions such as the west coast of South America, where long duration earthquakes take place along the subduction zone in the coast. This is also often coupled with the presence of a significant stock of vulnerable non-ductile structures in some areas (Petersen et al. 2018).

Fundamental early assessments on the structural collapse of single-degree-of-freedom systems (SDOF) controlled by $P -\Delta$ effects, were carried out in a number of previous analytical studies (e.g. Bernal 1987, Jennings and Husid 1968) and subsequently in experimental investigations (e.g. Kanvinde 2003; Vian and Bruneau 2003; Yamada et al. 2008). Miranda and Akkar (2003) considered bilinear systems with negative post-yield response, subjected to $72$ earthquake records, and investigated the effect of period and post-yield slope on the collapse capacity. Higher periods and lower post-yield stiffness were shown to be beneficial to the collapse capacity. An analytical relationship was also proposed to estimate the collapse capacity or ‘collapse strength ratio’ ($R_{c}$). Vamvatsikos et al. (2009) extended this study and examined the more general case of tri-linear pinching systems with an intermediate hardening branch (i.e. ductile systems). The collapse capacity was found to increase with increasing period, decreasing post-yield stiffness and increasing ductility, while strain hardening was shown to be of secondary importance. More recently, Adam and Jäger (2012a) explicitly considered $P -\Delta$ effects to define the slope of the post-yield negative stiffness, and assessed the collapse capacity using $44$ ground motion records. The results confirmed the positive influence of period of vibration and the adverse impact of post-yield stiffness, in agreement with the other above-mentioned studies. Pinched and peak-oriented hysteretic models were found to be beneficial compared to bilinear cases, and the collapse capacity was also shown to increase with lower values of viscous damping. Analytical expressions were proposed for representing Collapse Capacity Spectra (CCS), which were later refined by Tsantaki et al. (2015a) where $P -\Delta$ epistemic uncertainties were included. It was shown that the contribution of these uncertainties to the whole variance of the collapse capacity could be as significant as the contribution of record-to-record (RTR) variability. The study of multi-degree-of-freedom systems is beyond the scope of this paper; however, it is important to note that due consideration of the influence of $P -\Delta$ effects in multi-storey structures is still a matter of debate. Recently, and by taking advantage of the period dependency of the pervasive stability coefficient $\theta$, which is defined and discussed further in this paper, the concept of Stability Collapse Response Spectrum (SCRS) has been put forth and shown to be a useful approach to account for stability coefficient limits from the early stages of design (Mousavi and Sensoy 2019).

Regarding the assessment of collapse capacity based on deteriorating SDOF systems, a detailed study was presented by Ibarra and Krawinkler (2011), focused on quantifying the effects of RTR variability and uncertainty in deterioration parameters (i.e. negative tangent stiffness plus cyclic strength and stiffness deterioration) on the variance of median collapse capacity. To this aim, the peak-oriented deterioration model developed by Ibarra et al. (2005) was used, whose cyclic deterioration behaviour is controlled by the model developed by Rahnama and Krawinkler (1993). For the set of 20 SDOF systems considered, within $0.1 - 4.0s$, it was reported that uncertainty in deterioration parameters plays a significant role in the variance of collapse capacity, with the uncertainty in cyclic deterioration being less significant than the negative stiffness slope. In this seminal study, albeit the $P -\Delta$ effects were considered by simply rotating the backbone curve of the hysteretic model according to the elastic stability coefficient $\theta$, it was shown that $P -\Delta$ effects contribute to the reduction of the collapse capacity variance due to uncertainty in negative tangent stiffness parameter.

Although a number of previous studies have proposed and compared various CCS models (e.g. Adam and Jäger 2012a, b; Han et al. 2010; Miranda and Akkar 2003; Vamvatsikos et al. 2009), these have not typically considered the influence of duration in an explicit manner. Therefore, their suitability is typically limited to relatively short duration records, as discussed in detail in this paper. It should also be noted that previous studies have not considered that the inelastic stability coefficient, $\theta$, representing second-order effects, can be much larger than its elastic counterpart (Miranda and Akkar 2003; Vamvatsikos et al. 2009), hence necessitating the inclusion of gravity effects in dynamic analysis, an aspect which is examined in this paper. It is worth noting that other ground motion characteristics have been studied in the light of CCS, such as the effect of velocity pulses commonly observed in near-fault ground motions as a consequence of forward-directivity effects (e.g. Jäger and Adam 2013). Smaller median collapse capacity was reported for short period structures (i.e. $T < 1.5\,{\text{s}}$) due to near-fault ground motion with pulse characteristics with respect to a control set compounded by far-field records; whereas the opposite trend was observed for long period systems.

It should be noted that the characterisation of effective strong motion duration has produced a wide range of metrics (Bommer and Martinez-Pereira 1999). However, these are not necessarily comparable, given the different assumptions adopted (Luco and Cornell 2007). The merits of selected metrics, including the significant duration ($D_{s}$), for the assessment of structural collapse have been recently appraised (Chandramohan et al. 2016), making use of pairs of records (i.e., short and long) with equivalent spectral shapes. This approach, which is also adopted in the study presented herein, can isolate the effect of duration from other ground motion characteristics, such as amplitude and frequency content. It is also important to note that whilst the effects of duration on the collapse assessment of reinforced concrete and steel structures have been examined in previous studies (Barbosa et al. 2017; Bravo-Haro and Elghazouli 2018a; Chandramohan et al. 2016; Raghunandan and Liel 2013), the influence of duration on the structural collapse capacity of structural systems controlled by $P -\Delta$ effects has not been individually assessed and quantified.

Recent studies, without specific consideration for duration effects, have shown bias on the probability of collapse induced by acceleration amplitude scaling using records with matched spectral shapes (i.e., response spectrum) (Dávalos and Miranda 2019a). This was attributed primarily to the changes induced in the amount and distribution of input energy of the records due to amplitude scaling, which are quantified through energy metrics and distribution of damaging pulses. In other words, a pair of records with matched spectral shape and similar duration could lead to different probabilities of collapse. This can be largely explained by the limitations of the response spectrum that only accounts for the maximum response of elastic SDOF systems, whilst neglecting full ground motion characteristics that can contribute to significant degradation and ratcheting linked to $P -\Delta$ effects. The decoupling of these aspects and duration effects is not a simple task and requires detailed future studies, yet key issues related to the influence of energy and pulse distribution at collapse are highlighted herein. Overall, there is increasing recognition of the significant limitations of using the spectral acceleration as an intensity measure to build the response spectrum and as a damage proxy at collapse (Dávalos and Miranda 2019b; Eads et al. 2015; Kohrangi et al. 2017).

This study therefore aims at examining the role of strong motion duration on the collapse capacity of structures controlled by $P -\Delta$ effects. To this end, a parametric investigation into the collapse capacity of deteriorating and non-deteriorating SDOF systems subjected to long and short duration seismic events is conducted through incremental dynamic analysis. The effect of duration is isolated from other ground motion characteristics by considering two sets of short and long duration spectrally-equivalent records. The SDOF systems are defined by an elastic-negative backbone curve, for which the period and slope of the post-yield negative branch (defined by the level of $P -\Delta$) are varied. The gravity loading is explicitly considered during the dynamic analysis in order to account for the nonlinear lateral instability. Moreover, the influence of the hysteretic characteristics is examined by considering idealised bilinear response as well as two distinct types of pinching behaviour with and without due consideration of cyclic degradation.

2 Modelling procedures

2.1 Structural systems

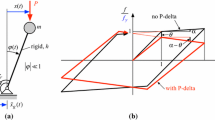
To capture the second order effects due to gravity loading in SDOF systems, an inverted pendulum can be employed (Bernal 1992). The mechanical model employed herein is shown in Fig. 1a, which corresponds to an inverted pendulum with mass ($m$) at its tip, and the rod is a massless element pinned at the base. The properties of the moment-rotation are assigned to a rotational spring at the base. Viscous damping is considered using a rotational dashpot damper acting in parallel with the main rotational spring. Note that this simple yet versatile system can be readily calibrated to idealise the response of a multi-degree-of-freedom system (MDOF) (Bravo-Haro and Elghazouli 2018b). As shown in Fig. 1b, there is a strength reduction from the original yield strength $F_{y}$ to the lowered $F_{y}^{P}$ once gravity loading has been applied. However, the corresponding displacement at yield $\Delta_{y}$ is unaffected, as shown in the figure. This “rotation”, exhibited by the force–displacement relationship due to the gravity loading, primarily affects the post-yield stiffness, with the elastic stiffness less significantly affected and can be quantified through the stability coefficient $\theta$ which is defined as follows:

$$\theta = \frac{Ph}{K}$$

(1)

where $P$ is the gravity force, $h$ is the total height of the SDOF inverted pendulum system, and $K$ is the elastic stiffness of the original system before applying gravity loads. Accordingly, the reduced yield strength can be expressed as:

$$F_{y}^{P} = \left( {1 - \theta } \right)F_{y}$$

(2)

where $F_{y}$ is the yield force of the original system before applying gravity loads. In this framework, in order to enable the onset of dynamic instability when subjected to earthquake excitations, the stability coefficient $\theta$ has to be larger than the strain hardening parameter $\alpha$ (Vamvatsikos and Cornell 2006).

Fig. 1

a SDOF model representation, and b effects of $P -\Delta$ on static pushover capacity curve

Adam and Jäger (2012a) also demonstrated that the main parameters governing the collapse capacity of inelastic SDOF systems controlled by $P -\Delta$ are: the post-yield stiffness slope $\theta - \alpha$, the elastic structural period of vibration $T$, the viscous damping ratio $\xi$, and the hysteretic material law. Accordingly, these four parameters are considered in this investigation in order to quantify their influence in conjunction with earthquake duration effects in such systems, as discussed in this study.

2.2 Hysteretic behaviour

To examine the effect of earthquake duration in a wide range of structural systems which are prone to global dynamic instability, various fundamental hysteretic behaviour models are considered. To serve as the basis for comparison, a model with bilinear kinematic hardening in addition to two variations with moderate pinching are considered with and without cyclic deterioration. It has been noted in previous studies that kinematic hardening models for loading–unloading are less realistic of the general behaviour of actual structures, when compared with models defined by hysteretic pinching loops (Rahnama and Krawinkler 1993; Vamvatsikos and Cornell 2006). It was also indicated that the ratcheting behaviour of models with kinematic rules can trigger unrealistically severe loss of structural capacity (Vamvatsikos et al. 2009). In this respect, Adam and Jäger (2012a) showed that systems with bilinear kinematic behaviour are more vulnerable to $P -\Delta$ than those characterised by pinching or peak-oriented hysteretic rules. This favourable performance of pinching systems, in comparison to bilinear counterparts, is attributed to the dominance of the ‘pinched’ inner loops which, despite having reduced strength, maintain a positive stiffness slope. Based on the above discussion, the following hysteretic models are examined in this investigation: (1) bilinear kinematic, (2) non-deteriorating with moderate pinching, and (3) deteriorating with moderate pinching (Fig. 2 and Fig. 3).

Fig. 2

a Monotonic behaviour, and b hysteretic behaviour of bilinear systems (without gravity loading)

Fig. 3

Hysteretic behaviour of pinching systems (without gravity loading): a moderate pinching, and b degrading pinching

The first pinching system considered does not incorporate cyclic degradation, whereas the second pinching system takes due consideration of cyclic degradation. The degree of pinching is mainly determined by the length of the inner or pinched loops, as shown in Fig. 3a for non-deteriorating moderate hysteretic pinching. The degree of cyclic strength and stiffness deterioration corresponds to a moderate level, as shown in Fig. 3b, which was defined based on moderate levels of cyclic deterioration available in the literature (e.g. Ruiz-García and Miranda 2006). Ibarra and Krawinkler (2005) showed that the level of pinching in this type of models is less significant than the shape of the backbone curve in the structural response.

2.3 Ground motion records

Several approaches have been suggested previously for quantifying ground motion duration. Bommer and Martinez-Pereira (1999) referred to 30 different metrics to define duration. Out of these, the significant duration ($D_{{s_{5 - 75} }}$) proposed by Somerville et al. (1997) upon earlier studies developed by Trifunac and Brady (1975) is used herein to characterise the ground motion records, as several studies indicated its suitability for assessing the performance of structural systems (Barbosa et al. 2017; Chandramohan et al. 2016; Foschaar et al. 2012). Two paired sets of spectrally equivalent short and long records are selected. Large magnitude earthquakes in subduction zones were chosen for the long duration motion (e.g., Maule earthquake, Chile 2010; and Tohoku earthquake, Japan 2011). As these records were collected from different databases, they were filtered and baseline-corrected (Boore and Bommer 2005). Similarly, ground motions due to shallow crustal earthquakes were selected from the PEER NGA-West 2 database (Ancheta et al. 2014). Subsequently, a matching process was performed in order to minimise the mean squared error of the $5\%$-damped linear response spectra between short and long records. To enable this procedure, response spectra of short ground motion records were scaled, where necessary, by a factor limited to 5. This process ruled out records with very low spectral intensity, which would need larger scaling factors to match their long duration response spectrum counterparts. The criteria to establish a ground motion as long or short duration were based on a significant duration, $D_{{s_{5 - 75} }}$, higher than 25 s for long duration and lower than 25 s for short duration. This threshold was initially set by Chandramohan et al. (2016) by inspecting the histograms of $D_{{s_{5 - 75} }}$ in order to observe an effect of duration without resulting in a too small set of records. Overall, 77 pairs of records were selected (i.e., 144 individual ground motions). For brevity, the list of earthquakes and number of ground motions considered for both sets are not given here but can be found elsewhere (Bravo-Haro and Elghazouli 2018a). Figure 4a, b show the 77 individual response spectra for short and long duration records, respectively, and Fig. 4c shows a direct comparison of their median spectra.

Fig. 4

Short duration (a) and long duration (b) ground motion sets log–log median spectra with 16 and 84 percentiles; c median response spectra of the 77 pairs of short and long duration ground motion records

2.4 Main parameters

The intensity measure adopted herein for the assessment of the effects of ground motion duration in structural systems controlled by $P -\Delta$ is based on the relative collapse capacity computed for each individual record, and is expressed as follows:

$$CC = \frac{{S_{a} \left( {T_{1} } \right)_{collapse} }}{g\gamma }$$

(3)

where $S_{a} \left( {T_{1} } \right)_{collapse}$ corresponds to the $5\%$-damped spectral acceleration at the structural period of the structure; $g$ is the gravity constant; and $\gamma$ is the base shear coefficient (i.e. ratio of yield strength to seismic weight). By considering the normalisation by $g\gamma$, the relative intensity measure resembles the conventional strength reduction factor R for systems without over-strength (Miranda and Akkar 2003). To reach the collapse capacity of each individual system under each individual ground motion record, IDAs are performed until dynamic instability is attained. This collapse state does not assume any predefined thresholds for engineering demand parameters (e.g., inter-storey drift, plastic hinge rotation), but is defined as the state at which the lateral displacements increase without limit as a result of a slightly increased earthquake intensity. The issue of numerical non-convergence is carefully treated, as it does not necessarily imply structural collapse (Haselton et al. 2009). The structural response is assessed using the global ductility $\mu$ as the engineering demand parameter, which is defined as the ratio of the maximum displacement $\Delta_{max}$ to the elastic displacement capacity $\Delta_{y}$.

Finally, for the parametric assessments presented herein, in addition to the three hysteretic systems described above, and the sets with spectrally equivalent short and long duration ground motion records, some key structural characteristics are also examined. Firstly, the structural period is considered at six levels ($T\left( s \right) = 0.2, 0.5, 0.7, 1.0, 2.0, 3.0$). Secondly, the effective slope of the negative post-yield branch, is also included for six levels ($\theta - \alpha \left( {rad} \right) = 0.02, 0.04, 0.06, 0.1, 0.2, 0.3$). In addition to the above parameters, viscous damping effects are examined by considering two damping ratios, namely $2\%$ and $5\%$ but for the case of deteriorating pinching systems where only $5\%$ is considered. The maximum considered value of $\theta - \alpha$ (i.e., high $P -\Delta$ effects) is determined based on preliminary sensitivity assessments as discussed later on. However, with respect to seismic provisions, $P -\Delta$ effects can be neglected if $\theta$ is less than 0.1 (e.g. Eurocode 8 (CEN 2004) and ASCE 7-10 (ASCE/SEI 2016)), whereas if $\theta \,\epsilon\, [{0.1,0.3}]$ in Eurocode 8 (CEN 2004) or $\theta \,\epsilon\, [{0.1,0.25}]$ in ASCE 7-10 (ASCE/SEI 2016), the $P -\Delta$ effect can be incorporated approximately by amplifying the static lateral force used in the structural design. Levels of $\alpha$ ranging from 0.03 to 0.18 were obtained for a large set of steel moment resisting frames designed according to EC8 guidelines (e.g. Bravo-Haro and Elghazouli 2018a, b), hence the limits for $\theta - \alpha$ are considered to be representative.

3 Incremental dynamic analysis

This section presents the main results obtained, in the form of IDA curves (Vamvatsikos and Cornell 2002), in order to examine the differences in dynamic response up to structural collapse. Particular attention is given to assessing the influence of ground motion duration for systems with different hysteretic behaviour, structural periods, and $P -\Delta$ levels.

Within the parametric variations, a reference SDOF structural system is considered with the following properties: $T = 0.5\,{\text{s}}$, $\xi = 0.05$, and $\theta - \alpha = 0.06$. Figures 5, 6 and 7 show the IDA response for the reference system with bilinear, moderate pinching and deteriorating pinching, respectively. The figures illustrate the differences in performance due to earthquake duration effects. Longer duration causes a reduction in the ordinates of the IDA curve, including the ultimate collapse capacity, while the state of collapse is attained at an earlier stage, with the system reaching a flat-line response at lower ductility levels. These trends are more pronounced for the $16\%$ IDA curve, as expected. A reduction in collapse capacity can also be noticed moving from the moderate pinching to the deteriorating pinching and bilinear behaviour, which is again more pronounced for the $16\%$ IDA curve. The differences due to cyclic deterioration, upon inspection of pinching systems, are the reduction of collapse capacity and dispersion in the presence of deterioration, which is more apparent for the latter, on the 84th fractile of the IDA curves. In contrast to duration, the hysteresis type has virtually no effect on the ductility threshold for dynamic instability. In the following subsections, the results are presented in terms of the median IDA response (i.e., $50\%$ fractile).

Fig. 5

IDA relevant fractiles for bilinear hysteretic systems for: a long duration and b short duration sets

Fig. 6

IDA relevant fractiles for moderate pinching systems for: a long duration and b short duration sets

Fig. 7

IDA relevant fractiles for deteriorating pinching systems for: a long duration and b short duration sets

3.1 Influence of $P -\Delta$ level

From Figs. 8, 9 and 10 the influence of the level of $P -\Delta$ on the median IDA curves of all three hysteretic systems is depicted; a short period system ($T = 0.5\;{\text{s}}$) is considered and the results due to long and short duration sets of records are shown respectively. The first observation is that, as expected, there is a clear reduction in the structural collapse capacity with the increase in the level of $P -\Delta$. For these particular systems (i.e., $T = 0.5\,{\text{s}}$, $\xi = 0.05$) with variable $P -\Delta$, up to about $200\%$ difference in the collapse capacity is observed for the extreme levels of $\theta - \alpha$ considered herein. This observation applies to both non-pinching and pinching cases. Furthermore, a higher variation in the median IDA curves occurs for the case of short duration records, indicating a greater influence from $P -\Delta$ effects compared to long duration records. It is also worth noting that, with respect to the influence of second-order effects, the difference between non-pinching and pinching systems appears to be insignificant. Overall, the lower the level of $\theta - \alpha$, the higher the reduction rate in the median collapse capacity for the long duration records set compared to short duration cases. On the other hand, for higher levels of $\theta - \alpha$, the collapse capacity tends to saturate as it approaches the yielding capacity of the system (i.e., more rapid collapse), a phenomenon that becomes particularly evident when $\theta - \alpha \ge 0.2$.

Fig. 8

$P -\Delta$ effect in IDA curves for bilinear systems, for: a long duration and b short duration sets

Fig. 9

$P -\Delta$ effect in IDA curves for pinching systems, for: a long duration and b short duration sets

Fig. 10

$P -\Delta$ effect in IDA curves for deteriorating pinching systems, for: a long duration and b short duration sets

3.2 Influence of structural period

In this case, the level of $P -\Delta$ was maintained (i.e., $\theta - \alpha = 0.06, \xi = 0.05$), while varying the structural period. The mean IDA curves are shown in Fig. 11, 12 and 13 for systems with bilinear, pinching, and deteriorating pinching hysteretic behaviour, respectively. The first observation is that longer period systems exhibit a superior collapse capacity performance, which is widely recognised (Cornell 1997). It is worth noting that this is typically the case for SDOF systems, for which the stability coefficient $\theta$ is assumed to be constant in the elastic and inelastic ranges. However, in nonlinear multi-storey systems, the inelastic stability coefficient exceeds the elastic counterpart and increases with period (Medina and Krawinkler 2004), which results in a reduction in collapse capacity that can prevail over the beneficial effect of the period. Therefore, the influence of structural period on the collapse capacity needs to be examined in conjunction with the effect of other parameters such as the stability coefficient (Adam and Jäger 2012a; FEMA 2009b). When compared at the same structural period, the reduction in collapse capacity due to duration effects is evident and becomes more significant for longer periods. As with the influence of $P -\Delta$ effects, there is a higher variation in the median IDA curves for short duration records, indicating a larger effect of the structural period than in long duration cases. For this moderate level of $P -\Delta$ (i.e., $\theta - \alpha = 0.06$), the influence of period is shown to be much more limited when long duration records are considered, especially in the case of bilinear (non-pinching) systems, as depicted in Fig. 11a.

Fig. 11

Period effect in IDA curves for bilinear systems, for: a long duration and b short duration sets

Fig. 12

Period effect in IDA curves for pinching systems, for: a long duration and b short duration sets

Fig. 13

Period effect in IDA curves for deteriorating pinching systems, for: a long duration and b short duration sets

4 Collapse capacity assessment

In this section, the median IDA curves are used to determine the median collapse capacity for all the systems considered. These values are used to gain further insight into the detrimental role of duration on collapse capacity for different levels of structural period, $P -\Delta$, and hysteretic behaviour. For all these cases, the dispersion in median collapse capacity is also reported given its importance for the construction of collapse capacity spectra in the subsequent section.

4.1 Influence of P-delta level

The negative impact of $P -\Delta$ on the median collapse capacity was indicated in a qualitative manner above. The significant rate of variation observed in the collapse capacity for perturbations of low levels of $\theta - \alpha$, in contrast to the saturation in collapse capacity for high levels of $\theta - \alpha$, is quantified in Figs. 14 and 15 for representative systems with long ($T = 3.0\;{\text{s}}$) and short ($T = 0.2\;{\text{s}}$) periods, respectively. For long-period systems, it can be observed that an increase in $\theta - \alpha$ produces a more severe reduction (i.e., larger slope) in collapse capacity when short records are used, in contrast to long duration records. Bilinear non-pinching systems also tend to be more sensitive to the duration effect compared to pinching cases. The largest drop in the median collapse capacity due to the duration effect is attained for the minimum level of $P -\Delta$ (i.e., $\theta - \alpha$), reaching up to $43\%$ and $34\%$ reduction for bilinear and pinching systems, respectively. On the other hand, short period structures are significantly less sensitive to the level of $P -\Delta$, and these systems are largely unaffected by the hysteretic behaviour and ground motion duration, as shown in Fig. 15.

Fig. 14

Effect of $P -\Delta$ on collapse capacity for long period cases, for: a bilinear, b pinching systems, and c degrading pinching

Fig. 15

Effect of $P -\Delta$ on collapse capacity for short period cases, for: a bilinear, b pinching systems, and c degrading pinching

4.2 Influence of structural period

The influence of structural period needs to be examined in conjunction with the level of $P -\Delta$, as discussed before. Accordingly, two distinct levels of $\theta - \alpha$ are considered here to assess the median collapse capacity for all structural period levels. For low levels of $P -\Delta$ (i.e., $\theta - \alpha = 0.02$), as shown in Fig. 16 for bilinear and pinching systems, the significant influence of period is evident. The influence of ground motion duration is also clear and increases with the increase in structural period, with both hysteretic types exhibiting similar trends. In contrast, for systems with large levels of $P -\Delta$ (i.e., $\theta - \alpha = 0.3$), as shown in Fig. 17, the median collapse capacity is largely unaffected by the structural period. This reflects the rapid collapse of such systems once the lateral yield resistance of the system is approached, and hence the duration effect does not play a notable role. The observations made on the behaviour of non-deteriorating pinching systems remain valid for the case of deteriorating systems, hence are not shown here for the sake of brevity.

Fig. 16

Effect of structural period and duration on collapse capacity in the case of $\theta - \alpha = 0.02$, for: a bilinear, b pinching hysteretic systems

Fig. 17

Effect of structural period and duration on collapse capacity in the case of $\theta - \alpha = 0.30$, for: a bilinear and b pinching hysteretic systems

4.3 Influence of degradation

To assess the impact of strength and stiffness deterioration in seismic collapse capacity in the light of earthquake duration, the percentage reduction of collapse capacity due to deterioration is calculated as the difference in CC between non-degrading and degrading pinching divided by the CC of non-degrading pinching. Figure 18 shows the results corresponding to this additional system considering long and short duration record sets, respectively. More significant reductions in collapse capacity are observed for higher structural periods and lower levels of $P -\Delta$, indicating that the effect of degradation is larger in such systems. Moreover, on average, the role of degradation is slightly more important when the structural systems are subjected to long duration records, given that more inelastic cycles are usually imposed by longer duration earthquakes, which is the ultimate behaviour that controls the cyclic degradation rules of these systems. For the lower end of $\theta - \alpha$, the average reduction in collapse capacity due to degradation is approximately 40% in the case of long duration records and 34% in the case of the short duration set, and increases with the structural period. In the higher end of $\theta - \alpha$, this reduction is similar on average and around 30% for both ground motion sets, and decreases also with the structural period. It is worth noting that a more significant role of degradation due to longer duration records has been observed when a higher rate of cyclic degradation is considered on the same pinching systems used in this study (Liapopoulou et al. 2019).

Fig. 18

Collapse capacity reduction due to degradation computed as the difference in CC between non-degrading and degrading pinching divided by the CC of non-degrading pinching under a long duration and b short duration records

4.4 Viscous damping ratio

Although the equivalent level of viscous damping is typically considered as $5\%$ (i.e., $\zeta = 0.05$), a lower level of around $2\%$ may often be more appropriate, such as in some steel structures (Bernal et al. 2015). The influence of this variation is examined in Fig. 19 which shows the ratio of collapse capacity of bilinear systems with $5\%$ damping to those with $2\%$ damping, for long and short duration records, respectively. It should be noted that similar viscous damping effects are also observed in hysteretic systems with pinching rules. In general, the viscous damping ratio has a relatively more pronounced effect in the case of long duration records. The higher the $P -\Delta$ level, the more significant is the role of the viscous damping ratio. A larger scatter is observed in the case of long duration records for all levels of $P -\Delta$. On average, a reduction in the median collapse capacity ranging from $15$ to $25\%$ is observed in the case of long records, corresponding to a change in viscous damping from $5$ to $2\%$. On the other hand, in the case of short records, an average collapse capacity reduction of about $15\%$ is observed, which is consistent with the conclusions of Adam and Jäger (2012a), where an average of about $12\%$ reduction was observed for levels of $\theta - \alpha$ ranging from $0.04$ to $0.2$. Based on these findings, both levels of damping are considered below in the derivation of the proposed predictive relationships for collapse capacity due to the influence of short and long duration records.

Fig. 19

Effect of viscous damping ratio and duration on the collapse capacity of bilinear systems, for: a long duration and b short duration records

4.5 Typical dispersions

Characterisation of median collapse capacity for use in performance-based seismic design (e.g., FEMA 2013) also necessitates an assessment of the dispersion due to RTR variability (Vamvatsikos et al. 2009). Given the assumed log-normal condition of the collapse capacity distribution (Ibarra and Krawinkler 2011; Shome 1999), the dispersion around the median is quantified herein through the ratio of the median collapse capacity (i.e. $50\%$ fractile) to the $16\%$ fractile of the counted distribution. Hence, deviation from unity indicates higher dispersion around the median. Particular attention is given here to the counted dispersion due to duration effects, hence, Figs. 20, 21 and 22 depict these ratios for bilinear, pinching and degrading pinching systems, respectively, for both long and short duration records.

Fig. 20

Ratio of 50% to 16% fractile collapse capacities for bilinear systems, for: a long duration, and b short duration records

Fig. 21

Ratio of 50% to 16% fractile collapse capacities for pinching systems for: a long duration, and b short duration records

Fig. 22

Ratio of 50% to 16% fractile collapse capacities for deteriorating pinching systems for: a long duration, and b short duration records

Upon inspection of the results, the dispersion decreases when the $P -\Delta$ level increases, and the opposite trend occurs with respect to the structural period. This behaviour is in agreement with the more rapid structural collapse observed for systems with short periods and those controlled by $P -\Delta$. It is evident that records with longer duration produce significantly lower dispersion around the median, and less scatter due to variations in the level of $P -\Delta$, as indicated in Fig. 20a. Similar trends are also observed for pinching systems in Figs. 21a and 22a, but slightly less scatter is observed due to variations in the $P -\Delta$ level. Although significantly lower median collapse capacities are observed due to duration effects, the dispersion around the median is lower.

4.6 Collapse fragility curves

While previous sub-sections have examined the influence of various parameters, the overall effect of duration may be collectively captured through the construction of collapse fragility curves. As discussed before, pinching systems typically exhibit higher collapse capacities than their bilinear counterparts. However, for any specific hysteretic type, it was shown that the influence of $P -\Delta$ and structural period on the response is relatively uniform. Therefore, for brevity, the results presented in here are only provided for the case of bilinear systems as a typical illustration. It should be noted however that the predictive relationships subsequently proposed in this paper include these effects.

Figure 23 shows a matrix of cases of collapse fragility curves for all structural configurations with bilinear hysteresis, when subjected to short and long duration record sets. In addition, the percentage reduction in the median probability of collapse (i.e., $P_{c} |CC = 0.5$) due to duration effects is shown for every configuration in the top-right corner of each plot. As discussed before in Sect. 4.1, the influence of $P -\Delta$ is negligible in the case of short-period systems, but becomes more significant for long-period cases. The influence of duration also follows a similar trend to $P -\Delta$ where, for short-period systems, the short-duration (grey lines) and long-duration (black lines) fragility curves are closely aligned but diverge significantly for long-period systems. Consequently, long-period systems are evidently more vulnerable compared to short-period cases. It is also worth noting the range of median collapse capacity reduction produced by duration effects for the same structural period and different levels of $P -\Delta .$ In the case of short-period structures (i.e., $T = 0.2s$), it varies between $8\%$ to $28\%$, whereas in the case of long-period structures (i.e., $T = 3.0\;{\text{s}}$), it ranges from $14\%$ to $46\%$.

Fig. 23

Matrix of cases of collapse fragility curves for all systems with bilinear hysteretic behaviour. Black and grey lines correspond to long and short duration sets, respectively. Vertical axis of each plot represents the cumulative distribution, $P_{c} |CC$, and horizontal axis corresponds to the collapse capacity, $CC$

Close examination of Fig. 23 indicates that when $P -\Delta$ controls the system (i.e., high levels of $\theta - \alpha$), the large negative post-yield stiffness leads to a rapid collapse, hence overshadows the effects of other factors such as structural period, duration or hysteresis type. For example, considering the uppermost row in Fig. 23 (i.e. $\theta - \alpha$ = 0.3), the high collapse vulnerability makes the system insensitive to the structural period and ground motion duration. In contrast, considering the lowermost row in Fig. 23 (i.e. $\theta - \alpha$ = 0.02), a relatively low structural period reduces the vulnerability of the system irrespective of duration. Moreover, as noted in Sect. 4.2, for low levels of $P -\Delta$, the longer the structural period, the larger the influence of ground motion duration.

The above assessments have given an insight into the key influence of ground motion duration on the collapse capacity of a SDOF system. This reduction can approach $50\%$ in the case of long period systems coupled with low $P -\Delta$ levels. An overview of the influence of duration is depicted in Fig. 24 considering systems with bilinear and pinching hysteretic behaviour. The figure shows the reduction in collapse capacity as a ratio of long-to-short duration cases, and shows the influence of both $T$ and $\theta - \alpha$. The reduction fluctuates between $2\%$ and $46\%$ in the case of bilinear systems, and between $0\%$ and $34\%$ for pinching cases.

Fig. 24

Reduction in collapse capacity (%) due to ground motion duration (long-to-short) for: a bilinear systems, b pinching, and c pinching deteriorating systems

5 Collapse capacity spectra

Based on the results and observations from the above assessments, nonlinear regression analyses are carried out in this section in order to develop predictive relationships for collapse capacity spectra (CCS). The characterisation of CCS is offered in terms of the median and dispersion values. Subsequently, the merits and limitations of the CCS expressions proposed herein are also appraised through a comparative evaluation against other relationships available in the literature.

5.1 Predictive relationships

A series of nonlinear regressions are carried out for developing the collapse capacity spectra. The structural period and $P -\Delta$ effect, through the post-yield negative slope $\theta - \alpha$, are the main parameters considered given that they have the most dominant influence on the behaviour, as discussed above. The functional form considered for the collapse capacity spectra is given in Eq. 4 which corresponds to a hyperbolic-like behaviour as $\theta - \alpha$ changes (Miranda and Akkar 2003).

$$CC = 1 + m\left( {\theta - \alpha } \right)^{n}$$

(4)

where $m$ and $n$ are constants that depend on the structural period of the system, ground motion duration, and hysteretic behaviour. These can be obtained by performing a two-step nonlinear regression analysis, and their functional forms are expressed as follows

$$m = m_{1} \left( {m_{2} + e^{{m_{3} T}} } \right)T^{{m_{4} }}$$

(5)

$$n = n_{1} + n_{2} T^{{n_{3} }} + n_{4} { \ln }\left( T \right)$$

(6)

Nonlinear regression analyses are individually performed for the bilinear and pinching hysteretic cases, as well as for short and long duration records, respectively. The least-squares was adopted through the widely-used Levenberg–Marquardt algorithm.

For bilinear kinematic cases, the coefficients obtained to compute the median, $16\%$ and $84\%$ fractiles of the collapse capacity, due to short and long duration records are presented in Tables 1 and 2, for $5\%$ and $2\%$ viscous damping ratio, respectively. Figures 25 and 26 depict the design collapse capacity spectra obtained using the relationships derived in this study. For brevity, only the results for $5\%$ damping are discussed, as the results for 2% damping follow similar trends. As expected, the fitting accuracy in the case of long records is slightly better than in the case of short records, due to the lower dispersion of the collapse capacity around the median as discussed in Sect. 4.5. For infinitely rigid systems (i.e., $T_{{}} = 0$), the collapse capacity is $1.0$ for which the lateral-strength for collapse avoidance is the yielding capacity of the system.

Table 1 Regression coefficients for bilinear systems (short and long duration sets) considering $5\%$ damping

Table 2 Regression coefficients for bilinear systems (short and long duration sets) considering $2\%$ damping

Fig. 25

Collapse capacity spectra for long duration records (bilinear hysteretic behaviour)

Fig. 26

Collapse capacity spectra for short duration records (bilinear hysteretic behaviour)

The period-dependent constants, $m$ and $n$, for systems with non-deteriorating pinching hysteretic behaviour, can be determined using the coefficients given in Tables 3 and 4, for $5\%$ and $2\%$ damping, respectively. Whereas the coefficients based on the results of systems with deteriorating pinching hysteretic behaviour are presented in Table 5 for the 5% damping considered for these systems. As before, short and long duration ground motions are considered separately. By employing these coefficients in Eq. 4 the design collapse capacity spectra can be obtained. Figures 27 and 28 depict the design CCS (for $5\%$ damping), for long and short duration records, respectively. The same trends discussed above with regards to bilinear systems are also similarly observed in this case.

Table 3 Regression coefficients for pinching systems (short and long duration sets) considering $5\%$ damping

Table 4 Regression coefficients for pinching systems (short and long duration sets) considering $2\%$ damping

Table 5 Regression coefficients for degrading pinching systems (short and long duration sets) considering $5\%$ damping

Fig. 27

Collapse capacity spectra for long duration records—non-degrading pinching behaviour (solid lines) and degrading pinching behaviour (dashed lines)

Fig. 28

Collapse capacity spectra for short duration records—non-degrading pinching behaviour (solid lines) and degrading pinching behaviour (dashed lines)

The accuracy of the model can be examined by quantifying the mean square error (MSE) between the actual counted median collapse capacities and those estimated by the nonlinear predictive relationships, as follows:

$$MSE = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {CC_{{c_{i} }} - CC_{{d_{i} }} } \right)^{2}$$

(7)

where $CC_{{c_{i} }}$ is the counted mean collapse capacity computed from incremental dynamic analysis; $CC_{{d_{i} }}$ corresponds to the design collapse capacity obtained from the nonlinear relationships; and $n$ is the total number of SDOF systems considered in the regression, determined by the combinations of structural periods and $P -\Delta$ levels.

Table 6 summarises the MSE of the design collapse capacity spectra for each duration and level of $P -\Delta$, and for the bilinear and pinching cases. The lowermost row gives the corresponding mean values of MSE over all levels $P -\Delta$ levels. Overall, it is shown that the proposed functional forms and the identified constant coefficients reflect accurately the actual behaviour of the SDOF systems in terms of median collapse capacity. The models are relatively more accurate for long duration records for the same hysteretic behaviour, which is in agreement with observations made above regarding the levels of dispersion around the observed median collapse capacity.

Table 6 MSE for bilinear and pinching systems for each level of $P -\Delta$

5.2 Comparative assessments

This section compares the predictions of the relationships developed in this paper, with those of other expressions available in the literature. Although a general review was given in the introduction, more specific relevant information from the selected studies is given below.

Miranda and Akkar (2003) developed a predictive relationship for the mean capacity of collapse, based on non-deteriorating SDOF systems subjected to 72 firm soil earthquake records. The expressions are valid for bilinear systems with structural periods ranging from $0.2$ to $3.0$ s, post-yield negative stiffness slope ranging from $0.03$ to $2.0$, and a unique level of $5\%$ viscous damping. The SDOF systems considered correspond to simple classical oscillators where the post-yield negative stiffness is characterised through the initial backbone curve of the system. Therefore, the destabilising gravity load effects are not explicitly accounted for in the nonlinear time history analysis. Ground motion duration effects are also not considered.

Vamvatsikos and Cornell (2006) proposed predictive relationships for estimating structural collapse capacity, based on non-deteriorating SDOF systems with pinching hysteretic behaviour subjected to 30 firm soil ground motion records. The expressions are valid for oscillators with periods ranging from $0.2$ to $4.0\;{\text{s}}$, and post-yield negative slopes ranging from $0$ (i.e., perfectly plastic system) to infinite (i.e., no post-yield capacity), and $5\%$ viscous damping. A tri-linear backbone representation was used to characterise the oscillators. Again, destabilising gravity load effects are not explicitly accounted for in the nonlinear time history analysis, and ground motion duration effects are also not considered.

The predictive relationships suggested by Adam and Jäger (2012a) were derived for several hysteretic systems, including bilinear and pinching hysteresis, and are valid for non-deteriorating SDOF systems with periods ranging from 0 to $5.0\;{\text{s}}$, post-yield negative stiffness ranging from $0.04$ to $0.8$, and two levels of viscous damping, namely $2\%$ and $5\%$ respectively. The approach used captures the influence of gravity loads during nonlinear dynamic analysis, as in the current investigation. However, the effects of earthquake duration are not explicitly examined. Recently, Tsantaki et al. 2015b refined the predictive CC relationships developed by Adam and Jäger 2012, by means of multiple linear regression analyses applied on the same non-deteriorating SDOF with second-order effects, resulting in significantly improved accuracy. Once again, this study did not include duration effects.

Han et al. (2010) developed expressions to estimate the collapse potential, based on analysis of non-deteriorating SDOF systems that can include higher modes effects from modal pushover analyses on multi-storey systems. The fundamental relationships derived for the case of SDOF systems are valid for periods ranging from $0.2$ to $4.0\;{\text{s}}$, post-yield negative slope from $0.1$ to $0.5$, and several levels of viscous damping, including $5\%$. Gravity loads are not explicitly accounted for in the dynamic analysis of the oscillators, and earthquake duration effects are also not examined.

Selected comparisons between the predictive relationships developed in this study and those described above are depicted in Figs. 29 and 30. The results are presented in terms of collapse capacity versus structural period, resembling the appearance of collapse capacity spectra. Two levels of $P -\Delta$ are considered to illustrate the differences, namely a moderate value of $\theta - \alpha = 0.1$, and a severe value of $\theta - \alpha = 0.3$. To highlight the influence of duration effects, the expressions derived in this study for short and long duration record sets are both shown in the plots.

Fig. 29

Comparison of design collapse capacity spectra from this study and others (for $\theta - \alpha = 0.1)$

Fig. 30

Comparison of design collapse capacity spectra from this study and others (for $\theta - \alpha = 0.3)$

Figure 29 shows the significant differences in the predictions of collapse capacities obtained from different models. The largest differences are obtained for relatively long periods, which is in part attributed to the increasing dispersion in the predicted median collapse capacity with period. Moreover, considerable differences occur between the predictions of existing studies and those based on long duration records from this study. This highlights the significant over-estimation in collapse capacity assessment of systems controlled by $P -\Delta$ effects, when ground motion duration effects are disregarded. This is also emphasised by the close correlation between the predictions of Adam and Jäger (2012a), with the expression developed in this study for short duration records, noting that both approaches explicitly account for gravity load effects in the nonlinear dynamic analysis. However the study by Adam and Jäger (2012a) did not explicitly consider duration effects and was based on the $44$ ATC-63 (FEMA 2009a) far-field set of recorded ground motions. It is worth noting that recent studies on the influence of ground motion duration indicate that the ATC-63 set provides results which are consistent with short-duration records (Bravo-Haro and Elghazouli 2018a). Figure 29 also indicates that previous studies that do not explicitly account for the destabilising effect of gravity loads in nonlinear time-history analysis tend to over-estimate the collapse capacity even when compared to the relationships proposed herein for short duration cases.

Figure 30, on the other hand, depicts a typical comparison for the case of severe levels of $P -\Delta$ (e.g. when $\theta - \alpha$ = $0.3)$. As shown in the figure, as the structural period increases, the collapse capacity tends to become period-independent and less affected by ground motion duration. Therefore, the differences in the predicted collapse capacities obtained from various models become less significant, and primarily arise from the specific assumptions and variabilities considered within the analysis.

6 Duration metrics and damage potential

The assumption of using ground motion records with equivalent spectral shape (i.e., similar response spectra) and different duration metrics (i.e., large and small) in order to study the influence of duration on collapse capacity, requires further discussion. This is particularly the case with respect to the resulting premise that records with an equivalent response spectrum and comparable duration would lead to a similar demand in a given structural system, hence to corresponding levels of collapse capacity. Recently, Dávalos and Miranda (2019a) have shown that amplitude scaling of acceleration in ground motion records with matched spectral shapes leads to distortions in the content and distribution of energy of the recordings, consequently overestimating the probability of collapse when larger scaling factors are used. It was shown that recordings with similar response spectra, reached through amplitude scaling, could have different acceleration pulses and total energy, measured by means of the incremental velocity (IV) of relevant pulses (Bertero et al. 1978) and Fourier amplitude spectra (Arias 1970), respectively. The IV corresponds to the area below a specific acceleration pulse and is firmly correlated with the damage potential of a recording (Bertero et al. 1978; Dávalos and Miranda 2019a). For the current study, although the significant duration of the records is unaffected by the induced amplitude scaling during the IDA process, the level of contained energy and pulse distribution might be distorted at the collapse level.

To examine this, in light of amplitude scaling effects, Fig. 31a shows the IDA resulting scaling factors needed to reach structural collapse, in terms of the mean of the ratio between records of the short and long duration sets, considering all combinations of structural periods and levels of induced $P -\Delta$. As can be seen, larger scaling factors are needed to instigate structural collapse, which in turn increases with the structural period of the system and, for a given period, tends to decrease as $\theta - \alpha$ increases. This expected behaviour is explained by the spectral matching procedure used in the selection of the records, where $S_{a} \left( {T_{1} } \right)$ of any pair of unscaled records tends to be remarkably similar, in addition to the larger collapse capacity obtained in the case of short duration records (i.e., larger CC, hence larger $S_{a} \left( {T_{1} } \right)$ at collapse). Subsequently, Fig. 31b presents the same ratio for the case of $IV_{peak}$ at collapse, which shows a behaviour similar to the scaling factor, increasing with the period of vibration, and for given structural system, tends to decrease as the level of induced $P -\Delta$ increases. In general, $IV_{peak}$ of short duration records is larger than their long duration counterpart scaled at collapse. Lastly, Fig. 31c, shows the same ratio but using the average of the cumulative incremental velocity of the first 10 largest pulses of the signal ($IV_{avg}$), namely of the 10 most damaging pulses. In this case, a trend similar to $IV_{peak}$ is observed, but with lower ratios across the structural periods and within a given period of vibration for the different levels of $\theta - \alpha$. In all, from the perspective of input energy and pulses distribution of scaled ground motion records at collapse, the family of short duration recordings selected in this study, tends to display a higher structural damage potential, which in turn increases with larger scaling factors, as reported by Dávalos and Miranda 2019a. However, on average, significantly lower collapse capacity levels are yet computed in the case of structural systems exposed to the long duration family of records.

Fig. 31

Mean ratios of: a scale factors of short to long duration records scaled at collapse level. b peak incremental velocity, and c average incremental velocity

The discrepancy between the response spectrum, which by definition only accounts for the maximum displacement of a set of elastic SDOF systems (i.e. $S_{a} \left( {T_{1} } \right)$), and a broader proxy of the distribution and energy content (e.g., FAS and IV) of a ground motion record, needs further examination. Also, when duration is considered, a methodology is still necessary to refine the separation of duration as the only source of damage in a structural system. Moreover, correlations of duration with other well-known metrics of ground motion damage potential (e.g., Araya and Saragoni 1985) require further detailed assessment.

7 Concluding remarks

This paper examined the influence of ground motion duration on the collapse assessment of non-deteriorating and deteriorating SDOF systems controlled by $P -\Delta$ effects. In order to isolate the effect of earthquake duration from other ground motion characteristics, two sets of records with equivalent spectral shapes but different durations were used. A series of SDOF systems that explicitly account for the destabilising effect of gravity loads were considered in the nonlinear dynamic analysis. The study included structural periods ranging from $0.2$ to $3.0\;{\text{s}}$, negative slopes of the post-yield branch varying from 0.02 to 0.3, viscous damping ratios of $2\%$ and $5\%$, as well as bilinear, pinching, and deteriorating pinching hysteretic systems. The structural collapse capacity was assessed through extensive incremental dynamic analyses using the short and long duration record sets. In general, the influence of duration was shown to be a primary factor in determining the collapse capacity in the structural systems considered herein. If duration effects are disregarded, the collapse capacity may be significantly overestimated, which can have significant implications on the reliability of the design and assessment procedures for such structures.

The influence of duration, quantified through collapse capacity assessments and fragility curves, was shown to be significant, exhibiting differences in the median collapse capacity ranging from $8$ to $46\%$, depending on the characteristics of the structural system in terms of structural period and level of $P -\Delta$. The effect of duration increases with the structural period and decreases with the $P -\Delta$ level. This is explained by the lower lateral resistance of such systems, and hence the more rapid instigation of dynamic instability, and in turn limiting the influence of ground motion characteristics. The levels of reduction in collapse capacity due to cyclic deterioration were computed, ranging from 30 to 40%, which decreases with the structural period for lower levels of $\theta - \alpha$, and increases with the period for larger levels of $\theta - \alpha$, with similar behaviour.

The uncertainties due to RTR variability were quantified in terms of the dispersion around the median of the collapse capacity distribution. In general, a decreasing trend in the dispersion with increasing level of $P -\Delta$ and decreasing period was observed, which is valid for both hysteretic types considered. Pinching systems had a higher dispersion when compared directly with their bilinear counterparts. Long duration ground motions exhibited lower dispersions in the collapse capacity distribution compared to short records, as they tend to result in consistently lower collapse capacities and hence lower variability in the collapse capacity of individual records. For higher levels of $P -\Delta$, up to about $35\%$ higher dispersion was observed due to duration effects.

A series of predictive relationships for estimating the collapse capacity of SDOF systems was proposed based on the results obtained in this investigation. These suggested expressions can be used to construct a design collapse capacity spectrum that incorporates duration effects, and readily provide a reliable evaluation of the lateral strength required to avoid structural collapse. Overall, the study shows the importance of improving current assessment and design guidelines by accounting for the influence of ground motion duration, and highlights other sources of damage that may be coupled with duration effects.