On the seismic fragility of pipe rack—piping systems considering soil–structure interaction

Abstract

Piping systems constitute the most vulnerable component in down- and mid-stream facilities posing immediate threat to human lives, communities financial robustness and environment. Pipe racks present several mechanical and geometrical idiosyncrasies compared to common buildings and the seismic response is governed by the pipework layout. Important design requirements e.g. dynamic interaction between pipelines and supporting structure are commonly overlooked during pipe racks design process and uncertainties relevant to modelling of soil or seismic input are not quantified. In the present work, after reviewing the technical literature and codes, a 3D RC rack was used as a testbed and analysed as coupled and decoupled with a non-seismic code conforming piping system accounting for soil–structure interaction. Incremental dynamic analysis was adopted as an assessment methodology for deriving fragility curves considering ground motions in near- and far-field conditions. It was deduced that the modelling (boundary conditions of pipes) was the most considerable uncertainty since it increased the probability of collapse limit state of structural members from 0 to 59%. It was also demonstrated that soil deformability as well as source conditions altered considerably the dispersion of intensity measure conditional on engineering demand parameter of structural and nonstructural members. The results may be another indication that code provisions should be more normative regarding industrial pipe racks.

1 Introduction

1.1 Background and motivation

Liquified Natural Gas (LNG) terminals and petrochemical plants constitute strategic lifeline facilities, and thus should remain intact during Natural Technological (NaTech) events towards achieving resilience in modern communities. The connection between process plants and the prosperity of nearby communities is highly reciprocal since a loss of containment event due to a failure to nonstructural components or nonbuilding structures may cause loss of human lives and catastrophic repercussions to the plant and environment. Nowadays, the resilience of industrial facilities may not be adequate or in other words the design process followed by industrial engineers may not be up to par against natural hazards e.g. inundation or seismic events due to several uncertainties involved. To this effect, European Union (EN) and other societies have put at the top of their portfolio the risk assessment of these plants against natural hazards accounting also for the increasing risk due to climate change (see EN regulation Seveso III 2012 for industrial accidents prevention). The seismic hazard is a highly accountable one in European countries e.g. Italy, Greece and Portugal considering that 28 LNG terminals and several oil refineries are located along European coastline some of which are planned or being expanded and the number is going to increase in the future particularly in the Mediterranean Sea due to the rise of LNG imports as well as future exploitation of natural resources in the region (EN 2018). The location of midstream facilities is a strategic choice towards minimizing the cost for transferring the feedstock gas via pipelines, and thus the construction in a seismic-prone area may be inevitable.

Aside from storage tanks and other process units, process plants include nonbuilding structures similar to buildings or Pipe Racks (PRs) that are outfitted by pipelines and other nonbuilding structures in order to process and distribute combustible or toxic materials from one unit to another (the equipment is above grade for maintenance, operational and safety reasons, Fig. 1). There are ample key parameters when modelling, designing and assessing a pipe rack—Piping System (PS) that increase considerably the risk due to uncertainties included in; the analysis methodology (static or dynamic), the dynamic interaction of nonbuilding structure– nonstructural components [Coupled Case (CC) or Decoupled Case (DC)], the type of pipe elements (stick or refined) and the Boundary Conditions (BCs) of pipes, to name just a few. PRs could support a complex system of components as shown in Fig. 1 that attribute mass, stiffness and geometrical irregularities to the system, causing torsional effects, and thus the use of dynamic analysis methodologies could be more appropriate as recommended by code provisions such as EN 1998-1 (2004) and ASCE/SEI 7-16 (2017).

Fig. 1

http://www.pentechglobal.com/en)

Typical configuration of nonstructural components and nonbuilding structures within a process plant (

Earthquake events of the past have shown that PRs may not be the most vulnerable structure themselves, however, the differential movement with the supported equipment may cause material leakage (Krausmann et al. 2010; Paolacci et al. 2012). Furthermore, PSs are placed first in the catalogue of the most vulnerable equipment in process industries with the main contributors being the human/organizational errors, fabrication, installation and layout (FKD 2011; Kidam and Hurme 2013). To minimise the computational cost, many times the seismic risk assessment focuses on components e.g. elbows, T-joints and nonbuilding structures that have been found to be the most critical during earthquake events of the past neglecting the dynamic interaction. In this vein, the seismic response of PRs has not been examined in unison with the supported equipment. Indeed, this is a common practice that is followed even by engineers in the industrial sector who overlook critical design aspects due to the lack of provisions of codes (particularly of EN) and in order to meet the time constraints (Bedair 2015). Therefore, it is essential the design process to account, if necessary, for the dynamic interaction between the multiply supported nonstructural components and supporting structure considering additional parameters apart from the relative weight ratio that is mostly prescribed in the codes.

Suffice it to say that the soil deformability could be the most decisive design parameter for the seismic risk mitigation in mid- and down-stream facilities. The soil composition beneath LNG terminals and oil refineries is rather weak and liquefiable since they are located at the seaside, and thus strengthening measures are undertaken. Even though storage tanks have been examined mostly with respect to soil deformation in virtue of heaviness and large plan area, the seismic response of PRs along with the complex piping when accounting for SSI could be an intriguing research topic since racks may be massive and stiff due to the numerous supported structures and components as well as rigid connections, as shown in Fig. 1 and the following Case Study (CS), and thus it might impact the response on nonstructural components. The 2010 Chile earthquake caused high relevant displacements of pipe rack spread footings in an LPG terminal due to the unimproved soil (marsh) beneath, though, the performance of soil that an adjacent storage tank was rested upon was viewed as a success due to the soil strengthening (Soules et al. 2016a). This is a clear example of liquefaction potential that should also be examined for PRs. The period elongation of PRs could exceed 20% resulting in higher or lower spectrum demand. Nonstructural components e.g. pipelines are mostly designed as flexible systems on PRs, and thus the higher displacement demand could sensationally affect the design requirements. The robustness of SSI investigation comes along with the soil modelling. Seismic code provisions do not prescribe nonlinear soil behaviour, however, it is possible near-field soil to experience nonlinearity causing decrease or increase to seismic demand (Raychowdhury and Ray-Chaudhuri 2015; Sáez et al. 2011).

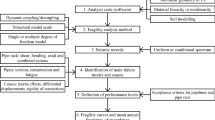
The next type of uncertainty refers to earthquake characterization that appears to be predominant and could supersede other sources e.g. modelling (Kwon and Elnashai 2006). A couple of decades ago, it was very much in vogue to simply separate near- and far-source conditions based upon the Epicentral Distance (ED); nowadays, engineers espouse a more advanced perspective view that considers the impulsive type of records (near-source) especially for structural inelastic response. The interested reader could find more information in Baltzopoulos et al. (2016), Chioccarelli and Iervolino (2010) and Pacor et al. (2018). All the aforementioned design and modelling challenges for pipe racks are summarized and prioritized in Fig. 2.

Fig. 2

Summarisation and prioritization of pipe rack modelling and analysis challenges

1.2 Objectives

To the best of Authors’ knowledge, there is no research effort that addresses the seismic fragility of PRs accounting for SSI effects among other uncertainties. To this effect, an analytical study is conducted herein for deriving Fragility Functions (FFs) for structural members and nonstructural components incorporating nonlinear soil deformation. This paper aims at reviewing the technical and non-technical literature, and then estimating the fragility of the system shedding some light on the seismic response variability of structural and nonstructural components by considering uncertainties in the seismic input (near- and far-field), modelling e.g. nonlinear soil deformation and coupling effects, Engineering Demand Parameter (EDP) e.g. shear force and pipe strain as well as Intensity Measure (IM) selection. By virtue of limitations that are discussed in the following, the FFs that are produced might not reflect the exact response of the system.

2 Modelling and analysis of pipe racks

The hostile environmental conditions at coastal sites makes the use of steel a workable solution for corrosion avoidance, though, concrete is used as well to minimize the cost (lower cost of the material and less time consuming compared to the long installation period of steel frames) and the high uncertainty in the welding process. When it comes to LNG terminals in particular, concrete racks may be selected at critical regions to avoid the low fire resistance of steel and high cost of fire protection systems. The answer to the question whether the response of steel and concrete could be similar given the supported equipment is not straightforward. Usually, pinned connections are typically utilized for beams in the longitudinal direction (struts) and shear tabs for the transverse (bent) beams where pipes are supported on. Also, a bracing system is also installed not only for reducing the lateral displacement but also for carrying equipment that might run out of the pipe rack frame (Di Sarno and Karagiannakis 2019). Therefore, steel racks could be stiff but they are not as much heavy as concrete racks, which may lead in different SSI impact. In this section, code provisions and research endeavors regarding the analysis of PRs are examined. The analysis methods of supported components e.g. floor response spectra, relative displacement accommodation or allowable stress are excluded; however, some references are made to the point that are related to the connection with the supporting structure.

2.1 Code provisions

Industrial PRs are also called building-like nonbuilding structures in the codes since they are designed and constructed in a manner similar to buildings, respond to strong ground motion in a fashion similar to buildings and constitute moment, braced or dual systems. Building-like structures may share design parameters and expected behaviour with regard to common building ones but they might have also considerable differences. The main European contribution for seismic-resistant design of structures EN1998-1 (2004) does not make reference to process plant PRs yet to irregular structures only, and thus could be inapplicable. Even though EN regulations deal with other type of structures included in process plants such as tanks, silos, towers and pipelines (EN1998-4 2006; EN1998-6 2005), the important design aspects of PRs along with the pipelines are not stipulated. On the other hand, the American (AM) code ASCE/SEI 7-16 (2017) or the petrochemical plant structures guideline ASCE (2011) encompass a few regulations for the design and analysis of PRs. In addition to these codes, there are several other national codes and guidelines that make reference particularly to industrial facilities regarding modelling considerations, analysis methods and design parameters e.g. importance factors. More information could be found in (Butenweg and Holtschoppen 2014; Pecker 2014; Soules et al. 2016a, b). Finally, the International Standard ISO/DIS (2013) addresses performance objectives and seismic design analysis specifically for non-structural components.

The analysis methodology determination is not straightforward and relies on the consideration of several parameters, viz the vertical and horizontal irregularities, the configuration of nonbuilding structures e.g. heat exchanger or tower vessels mass, the relative rigidity of beams that should not be confused with the rigid or flexible way of supporting e.g. a PS on a nonbuilding structure, the seismic design category (the last is defined in the AM code as a function of importance class, seismicity and site class) and the fundamental period, T. In contrast with the EN codes, the AM ones specify several analysis methodologies and give high latitude to the engineer in selecting the most suitable. Petrochemical PRs are usually subjected to vertical irregularities since horizontal ones are defined in the code based upon the differential drift between perimeter points when there is diaphragmatic behaviour but PRs most commonly have no diaphragms. The vertical irregularity could be due to the inequality of stiffness, strength, geometry and/or weight of adjacent storeys. It is rather usual PRs to be outfitted by nonbuilding structures with significant mass (W_P1) among one or multiple storeys leading in the denomination of response by the first mode (Fig. 3a); in this case, the equivalent lateral force analysis method may be applied. Also, it is rather common inconsistencies in stiffness and strength to be found due to the distinct vibration of concentrated masses on upper floors, which cause higher mode effects, as well as geometry e.g. side overhang cantilevers that support nonstructural components running out of the main frame (Fig. 3a, b) in order to attribute flexibility into a PS making the use of dynamic analyses e.g. response spectrum or linear time-history an inevitable choice. Severe concentrated mass e.g. W₂ may also cause torsional effects to the entire system or local modes of weak beams compared to strong columns or braces since there is no diaphragmatic behaviour (Fig. 3b). The code implies that the nonlinear time-history shall be used with caution due to higher uncertainties induced in modelling and interpretation of results.

Fig. 3

a Support of a heavy nonbuilding structure on pipe rack, b mass irregularity among storeys and c piping system analysis along with the supporting towers

It is a common industrial practice that engineers analyze supported components and supporting structure separately. This comes from the lack of code provisions that fail to stipulate clearly design requirements for dynamic interaction or the unavailability of analysis software. Concerning the seismic design criteria that the AM code stipulates, if the weight of nonbuilding structures not similar to buildings as well as nonstructural components (the code specifies that the total operating weight of permanent equipment should be considered) W_P (W_P1 + W_P2 + W_P3) compared to the one of nonbuilding structure similar to building W_S (Fig. 3a) is less than 25% of the effective weight W (W_s + W_p), the decoupled case could be addressed. Of course, this is a very rough rule that relies on the low influence the supported components will have on the system response and intents some nonlinearity to be appeared on the nonbuilding structure to avoid resonance phenomena, reduce the Peak Floor Acceleration (PFA) and lessen the interaction. Also, the supporting structure and nonstructural components design parameters e.g. behaviour factor (q-factor) or component force amplification factor a_p are defined separately. Should this not be the case, the dynamic interaction is considered. However, if nonbuilding structure and/or nonstructural components are rigidly attached to the supporting structure (T_p < 0.06 s, the value is estimated by considering the flexibility of beams that the components is attached to e.g. the towers in Fig. 3c), they should be analyzed as rigid elements considering only the q-factor of the rack, otherwise both the supporting and nonbuilding structure should be modelled together in a combined model adopting the lesser q-factor between them. All the above-mentioned aspects of PRs modelling and analysis are recapped in Table 1.

Table 1 Modelling and analysis considerations for pipe racks

2.2 Previous studies

Even though experiences from past earthquakes have shown that pipelines constitute the most vulnerable component being 44% more damage-prone than the runner-up storage tanks and reactors out of 364 industrial accidents (Kidam and Hurme 2013), to-date, it still remains to be examined the dynamic interaction between a supporting structure and a PS towards highlighting the most critical design challenges and preventing accidents in the future. The research is rather limited on this topic since the majority of research has focused on the analysis of critical components individually, whereas research efforts that undertake the dynamic interaction and assess both PR and PS are rather obscure. For instance, Salimi Firoozabad et al. (2015) considered various support excitation analysis techniques for a nuclear plant piping system e.g. single or multiple response spectrum, however, no coupling effects were considered probably in virtue of different nature of nuclear piping. An interesting research upon the effects of dynamic interaction on pipe-way and piping system response by considering different weight ratio, diameters and end-condition of pipes as well as thickness of U-rings (they encircle pipes without restraining the longitudinal direction) was conducted in Azizpour and Hosseini (2009). The governing result of the case-study referred to the significant role the end-conditions and the stiffness of U-bolt rings played in the seismic response. Another study that highlighted the idiosyncrasy of multiply-supported secondary systems could be found in Chaudhuri and Gupta (2002). The research deduced that the dynamic interaction could be ignored only in those secondary modes which are at least 7 times as stiff as the governing mode of the primary system. The conclusions above emphasize that apart from the weight ratio, the rigidity of connection of multiple-supported components and not only of single-supported nonbuilding structures as the ASCE 7 specifies should be taken into consideration. Finally, a fragility analysis was conducted in Salem et al. (2019) on different pipe rack configurations by altering the height, the span length and section dimensions. The fragility affected mostly due to the first two parameters, however, no dynamic interaction was considered in order to demonstrate the performance e.g. of pipes.

3 Soil–structure interaction

The grey areas of knowledge that exists to date not only for the analysis methodologies but also for the soil deformability effects on structural and nonstructural members necessitates the investigation of this topic. Site response analysis towards acquiring a better insight of soil stratigraphy underneath PRs and SSI effects evaluation constitutes logically a sine qua non in the overall design process of oil refinery structures.

3.1 State-of-the-art

Except for the well-known effects of SSI on system response, namely period elongation and damping increase, the SSI has been found to affect mostly heavy and stiff structures. The longer period as well as the additional damping in the system reduce the seismic demand forces (lower response spectrum) and thus SSI could be beneficial from this point of view. On the other hand, the higher displacement demand due to the soil deformation could be strictly necessary within the displacement-based design particularly for pipe racks that are outfitted by sensitive to high-deformation pipelines. According to Elnashai and Di Sarno (2015), the ratio of h/(V_s·T) (h is the effective height, V_s is the shear velocity and T is the natural period) could be a reliable indicator of the degree of period elongation and damping increase.

Depending on the rigorousness of soil constitutive models and analysis method, the evaluation of SSI effects could be a challenging task. The influence of SSI has been examined mostly for storage tanks and nuclear containment structures so far (Peña Ruiz and Guzmán Gutiérrez 2015; Wang et al. 2017), although process plant pipe racks could be stiff due to the vertical and horizontal bracing that intend to keep low the ductility as well as heavy since other nonbuilding structures and components are usually supported on them (Di Sarno and Karagiannakis 2019).

3.2 SSI models

The literature is fraught with models that are used to describe the soil–foundation–structure interaction. A categorization of SSI models could be made into three scales; first, ‘domain type models’ pertain to local scale since the soil is examined by constitutive laws, secondly macroelements (intermediate-scale) where the soil–foundation–structure interface is described by a link element, and finally soil springs that is the simplest and most commonly adopted type of model by practitioners based on impedance functions considering only for the fundamental frequency of the superstructure (global scale).

Spring models represent the soil compliance and are considered mainly for shallow foundations making the assumption that the superstructure is underneath by a homogeneous, elastic and semi-infinite medium (Mylonakis et al. 2006). When the foundation is rigid enough and the seismic excitation is not severe, the assumption of linear behaviour in the vicinity of foundation could be acceptable. The energy dissipation of soil due to radiation and hysteretic damping is represented by dampers. Spring models are less time consuming and can account for soil nonlinearity. They are suggested by code-of-practice provisions as a practically acceptable method (Elnashai and Di Sarno 2015). That being said, the latter model accounting for soil nonlinearity will be described hereafter and used for the fragility analysis in the following CS. A representative spring-foundation-pipe rack layout as considered in the CS is illustrated in Fig. 4.

Fig. 4

Representative layout of spring-foundation configuration

The soil develops nonlinear response under strong ground motion and in the vicinity of foundation interface (near-field) even at low strain levels. The soil hysteretic behaviour (or hysteresis loop) is described by the inclination (that refers to soil stiffness) and the breadth of the loop (the larger the loop, the higher the energy dissipation, Fig. 5a). Usually, the secant stiffness (G_sec = τ_c/γ_c) is used to describe the average stiffness of soil along an entire loop instead of the tangent G_tan (= G_max) and the damping ξ for the dissipation of energy due to the material nonlinearity. The G_sec and ξ constitute the equivalent linear soil properties; the increase of shear strain amplitude decreases the secant modulus and increases the energy dissipation due to the hysteresis phenomenon (Tsinidis 2015).

Fig. 5

a Hysteresis loop of soil element subjected to symmetric cyclic loading (Tsinidis 2015), and b typical G-γ-D curves of a soil deposit

Plentiful nonlinear constitutive models of different rigorousness and complexity exist in the literature. Soil models with hysteretic behaviour can be rather difficult to be calibrated since they require a lot of parameters. In this respect, a simplified model is adopted in the sequel to account for the nonlinear behaviour of soil underneath an LNG RC rack. The model relies on the Ramberg–Osgood (RO) curve (SeismoSoft 2019), which is described by the following equation:

$$\frac{\gamma }{{\gamma_{y} }} = \frac{\tau }{{\tau_{y} }}\left( {1 + a\left| {\frac{\tau }{{\tau_{y} }}} \right|^{r - 1} } \right)$$

(1)

where γ_y and τ_y are the yield strain and stress (G_max = t_y/γ_y) and the parameters α and r are positive constants (r ≥ 1 and a ≥ 0). When the strain is very small (γ → 0 and τ → 0 given that r > 1), the eq. 1 can be rewritten according to Masing’s rule as follows:

$$\frac{\gamma }{{\gamma_{y} }} = \frac{\tau }{{G_{max} \cdot \gamma_{y} }}\left( {1 + a \cdot \left| {\frac{\tau }{{G_{max} \cdot \gamma_{y} }}} \right|^{r - 1} } \right)$$

(2)

also, the hysteretic damping according to RO model is defined as:

$$\frac{G}{{G_{max} }} = 1 - \frac{{D \cdot \pi \cdot \left( {r + 1} \right)}}{{2\left( {r - 1} \right)}}$$

(3)

The parameters a, r and γ_y are to be determined by using a code that tries repetitively to estimate the best fit of the original soil properties with G_max. The selected soil for the CS pertains to an alluvium deposit of sandy clay to clayey sand that can be found at coastal sites with some plasticity I_p that shifts the G-γ-D curve to the upper and right-hand direction and reduces the damping ratio D. According to Ishibashi and Zhang (1993), the modified equations that describe such a kind of soil have the following form:

$$\frac{G}{{G_{max} }} = K\left( {\gamma ,I_{p} } \right) \cdot \bar{\sigma }_{0}^{{m\left( {\gamma ,I_{p} } \right) - m_{0} }}$$

(4)

$$D = D_{sand} \cdot A\left( {I_{p} } \right)$$

(5)

where K(γ, Ι_p) and m(γ, Ι_p) is a decreasing and increasing function of the cyclic shear strain γ, respectively, $\bar{\sigma }_{0}$ is the mean confining (or overburden) pressure, m₀ = m(γ ≤ 10⁻⁶) and A(I_p) is a modification function that modifies D_sand so as to incorporate soil plasticity in the damping ratio. The complete provision of all equations is omitted for brevity, however, the same nomenclature has been used so that the reader could find easily all the information for the construction of the target curves in the pertinent reference.

Finally, a code has been developed on MATLAB (2018) using two fitting methods, namely the Root Mean Square Error (RMSE) and the coefficient of determination (R²), in order to compare the results. Since the former method calibrated better the G-γ curve, the pertinent parameters were selected as an input in SeismoSoft (2019). The original G-γ-D curves, nearly 50 curves by the iterating process of the method as well as the final selected are shown in Fig. 5b.

4 Fragility analysis methods

Numerical analyses of structural models are plagued with uncertainties and this is why the research has lent weight in the probabilistic seismic assessment of structures. There are three main parameters to be considered when selecting a fragility assessment methodology for structures, viz the structural type, the assessment target e.g. evaluation of serviceability or ultimate Limit State (LS) and time constraints related to model scale and computational capacity. As highlighted above, the mass and stiffness irregularities as well as local mode effects of PRs may constitute nonlinear static analysis methodologies inappropriate (Baltzopoulos et al. 2017; Fragiadakis et al. 2014; Di Sarno and Karagiannakis 2019). To this effect, probabilistic dynamic analysis methods are more capable to reveal hidden epistemic e.g. errors in modelling assumptions and aleatory e.g. seismic input or soil properties uncertainties in the models, and thus they are selected for review in the following.

4.1 Methodologies

The most common analytical approach is the so-called Incremental Dynamic Analysis (IDA) (Vamvatsikos and Allin Cornell 2002), where a suite of records is incrementally applied to a structural model at various IMs, resulting in response curves (or IDA curves) that parameterize the intensity level with the EDP. The selection of EDP in the abscissa depends on the structural model; for instance, the interstorey drift ratio in the vicinity where nonbuilding structures not similar to building are supported on, the base shear resistance (V) or the peak floor acceleration for the assessment of nonstructural components could be a reasonable choice for oil/gas nonbuilding structures.

In contrast with the IDA, the Multiple-Stripes Analysis (MSA) method is performed at specific IMs each of which has a unique set of ground motions (Jalayer and Cornell 2009). Both MSA and IDA can be characterized as wide-range assessment methods, since they can be conducted for a large range of IMs. A competitive edge of MSA versus IDA is the accuracy due to the compatibility of records with the conditional spectrum at different IMs. Furthermore, another popular method particularly during the recent years that attempts to substitute the IDA towards minimizing even more the computational time by performing analysis at different IMs for un-scaled records is the so-called cloud analysis. The method is not only used to describe the uncertainty in ground motion representation but also to propagate other types of uncertainties such as modelling or component capacity. More information about this method can be found in Jalayer et al. (2015). In Table 2, the main benefits and limitations that each method encounters are quoted.

Table 2 Comparison of analytical assessment analysis methods

The relationship between the IM and structural response is well described by the Lognormal Distribution (Eads et al. 2013). The random variable X e.g. IM is lognormally distributed if Y = lnX has lognormal distribution. The lognormal cumulative distribution function (or CDF) is used to describe the relation between the IM and probability of collapse of a certain LS and holds:

$$P_{f} \left( {ds \ge ds_{i} |IM = x} \right) = \varPhi \left( {\frac{{{ \ln }\left( {\frac{x}{\theta }} \right)}}{\beta }} \right)$$

(6)

where P_f (·) is the probability of being at or exceeding a particular damage state (ds) given the IM = x, Φ is the CDF function and θ and β are the median and standard deviation (or dispersion of IM), respectively. The central values of the distribution can be calculated by simple and advanced e.g. maximum likelihood estimation formulae, which are adopted for the CS, or fractiles for each LS.

4.2 Fragility assessment in previous studies

The seismic fragility evaluation of RC buildings but also of nonstructural components is reviewed to compare the results in conjunction with the fragility analysis of the RC PR and PS in the following. A fragility assessment of a sample of existing regular RC buildings by considering both flexural and shear failure modes according to EN 1998-3 (2004), which were also adopted for the CS, as well as Peak Ground Acceleration (PGA) as IM was conducted in Tsonis and Fardis (2014). Among others, the research showed that the shear failure mode is the predominant for the collapse LS of columns, as it was also deduced in the sequel for the RC rack, and the modelling e.g. space of stirrups in columns could affect considerably the fragility. The predominance of shear failure mode against flexural one is not acceptable and this is what the capacity design intents to prevent. In the majority of assessment efforts of RC buildings when adopting the IDA method, interstorey drift ratio or chord rotation was used as an EDP (Al Mamun and Saatcioglu 2017; Karapetrou et al. 2015). RC structures should be assessed accounting for both modes due to uncertainties in the design process or when addressing existing structures that do not comply with modern codes (EN 1998-3 2004). This conclusion is more stringent for pipe racks due to the higher importance class and the load exerted by the pipelines and other nonbuilding structures. Also, researchers have been trying during the last decade to evaluate the effects of another modelling parameter, namely soil deformability, in a probabilistic manner. Even though this attempt has been partially completed for common building structures and bridges (Karapetrou et al. 2015; Kwon and Elnashai 2007; Mitropoulou et al. 2016), the literature lacks clearly of a probabilistic methodology that investigates the damage of pipe racks accounting for dynamic coupling and soil–structure interaction.

Except for the estimation of fragility quantitatively, assessment methodologies intend to evaluate as much as possible the number of uncertainties. An intriguing fragility assessment of a typical high-rise building by using the IDA method accounting for linear regression and considering different sources of uncertainty, namely linear and nonlinear soil, coupled and decoupled SSI approach as well as soil depth and stratigraphy was conducted in Karapetrou et al. (2015). The results highlighted that different assumptions on modelling e.g. linear or nonlinear soil, stratigraphy omission, higher soil depths and seismic input may result in inverse SSI effects. A sufficient number of uncertainty sources related to record selection (natural and artificial records were selected accounting for spectral acceleration-to-velocity ratio), statistical processing of results and material modelling were considered within a fragility analysis framework of RC building in Kwon and Elnashai (2006). The most relevant result was the significant higher effect of seismic source conditions compared to modelling parameters.

The assessment of nonstructural components, which mostly present flexible behaviour and high geometrical irregularities e.g. piping, relies on different damage parameters and thus alternative probabilistic estimators should be adopted. For instance, the IDA method was applied to nonstructural components for near- and far-field conditions (rigid blocks) that were included in healthcare facilities by considering different IMs in Di Sarno et al. (2017). The research clearly showed that the PGA was the most efficient IM for short rigid blocks, whereas PGV was the most appropriate for taller ones. Also, the fragility estimation of a nuclear power plant piping system was addressed in Salimi Firoozabad et al. (2015) and it was found that the fragility estimation yielded better results when considering as an EDP the relative displacement between the pipe support and the ground. Thus, the selection of common IMs e.g. Sa or PGA and unique EDP may not be the best choice for nonstructural components because of dynamic incompatibility with the supports that are attached to. A question that arose in the following CS regarded the selection of spectrum-related IM on the principal period of supporting structure or nonstructural component. Finally, a numerical study that addressed the dynamic coupling of an example primary-secondary system accounting for uncertainties in soil Poisson’s ratio and shear wave velocity was conducted in Chaudhuri and Gupta (2002). It was proved that if the fundamental period of the system due to the soil deformability gets increased by more than 20%, then the uncertainties should be addressed.

5 Model description

A RC pipe rack included in an existing LNG terminal is addressed (Fig. 6a). Except for the process pipe rack area, the terminal constitutes several utility zones e.g. knock-out drum, or ethylene storage tank that are interconnected with pipelines (Fig. 6b). This study focuses exclusively on the process pipe rack area that serves to support the pipelines that come from the tank and distribute ethylene to the surrounding units (Fig. 6a). The RC rack consists of two sub-racks; a 6 × 9 × 8.3 m short rack that supports the pipelines that come immediately from the LNG storage tank and a 102 × 6.5 × 7.3 long rack that transfers ethylene to the surrounding process area. Intermediate spans of 3 m exist in the transverse direction for both floors of the long rack and upper floor of short one. The present LNG subplant has also been investigated within INDUSE-2-SAFETY project (Bursi and Reza 2019) focusing mainly on the response of pipework e.g. leakage of flanges on the storage tank and assuming linear PR behaviour for the fixed-base case. Τhe previous research work considered the same geometry, though, different assumptions regarding the modelling of RC pipe rack and boundary conditions of pipes were made given the analysis software capabilities.

Fig. 6

a LNG terminal layout, b the pipe rack under consideration and a process area, c dimensions of short and long racks in two planes

The concrete has mean compressive strength 48 MPa (tensile the 1/10th of the compressive) and is described by the Mander model, which accounts for transverse reinforcement, whereas the Menegotto-Pitto one is used for the ribbed reinforcement with isotropic hardening. In particular, the steel yield strength (f_y) is equal to 575 MPa and the strain hardening parameter (μ) equal to 0.5% (more info for the concrete and rebar modelling can be found in SeismoSoft (2019). Distributed inelasticity was attributed to columns and beams described by inelastic force-based frame elements that rely on the nonlinear fibre section method (uniaxial stress–strain relationship). Structural members with 6 Gauss–Lobatto integration sections were chosen to describe the spread of member inelasticity. The reinforcement layout of a column and beam as well as reinforcement specifications for all structural members are summarised in Fig. 7. It is common for pipe racks, additional uniform load to be considered for the beams where pipes are supported on for safety and future installation. Thus, all the beams on the upper floor were subjected to 4 kN/m, which refer to 2 times the maximum concentrated load that a pipe applies on beam.

Fig. 7

Representative specification of reinforcement for a a beam (BL6) and b a column (CL) as well as c for the rest of structural members

Numerous pipelines are supported on the pipe rack, however, to facilitate the modelling, only the 7 pipelines that run from the short to the long rack have been selected for the fragility assessment. The pipelines are all welded (no flange joints or other pipework is considered) and tranfer ethylene. The steel constitutive law of pipes was examined in Bursi et al. (2018) by conducting tensile testing at very low temperature to take into account the operation conditions of the plant. The A312/TP304L yielding strain and strength was found equal to 1.7‰ and 370 MPa, respectively, whilst the strength was equal to 461 MPa at 5% strain. It should be emphasised that in view of large model under investigation and the availabilities of the analysis software (SeismoSoft 2019), stick pipe models considering distributed inelasticity as the structural members are used both in coupled and decoupled case. In particular, the pipe bents have been calibrated according to the equivalent straight elbow method that derives the principal stiffnesses of the original curved pipe (elbow) by using a refined finite element model on ABAQUS (2017) and subjecting it separately under axial, shear and bending loading. Then, a modified Euler–Bernoulli matrix that accounts for the coupling between bending and shear loading through a weight factor is formed. The factor is maximised by setting equal the modified matrix with the classical one and changing iteratively the thickness of the straight beam, which is the only unknown parameter for the latter matrix. This method was proposed by Bursi et al. (2015) and was found less conservative in comparison with the simplified method of (EN 13480-3 2012) that relies on flexibility factor (k_b). Also, the low operating pipe pressure (P_max = 1.63 MPa) had no significant impact on the pipe response and in order to stay on the safe side it was neglected (Bursi et al. 2015, 2018).

To minimise the computational cost particularly in the decoupled case due to the numerous BCs of the PS, the pipe with the greatest (P1) and lowest diameter (P3) was considered for the analysis (Fig. 8). In more details, the assessment was conducted for two pipelines both in CC and DC, however, the inertia effects of all pipelines were accounted for the analysis in the former case. The modelling of the entire length of pipelines is not practically feasible due to the complexity and high computational cost, thus any part of pipelines that runs out of the main frame of the rack was not considered. Usually, pinned connections are adopted for the pipe ends, which is a conservative assumption, since pipes that present relative flexibility -mostly bend downwards or upwards after the main frame- are considered more rigidly restrained. Regarding the internal supports of the pipes on the rack, it is generally acceptable the longitudinal and all the rotational degrees of freedom to be unrestrained in order to attribute flexibility to the system. During the initial design process of the rack that placed the structure in a low-seismicity region, except for the previous type of BC, fixed supports with special clamps were considered as well, probably, for operational purposes. To examine the performance of the pipes and rack for earthquake events of higher probability of occurrence, that consideration was not modified in our CS (Fig. 8, see also Fig. 6b for global coordinate system). Finally, it is a common industrial practice detailed isometric drawings of piping systems including the location and type of supports to be shared among engineers to facilitate the design or assessment process (Table 3).

Fig. 8

The PS layout and pipe supports IDs

Table 3 Coordinates (midline) and piping system support types

The bearing capacity of the soil, which is categorized as soil type C in EN 1998-1 (2004), as well as the surface foundation that consists of centered footings and strip beams has been checked under axial, bending and shear loading according to Fardis (2009) after placing the structure in a high seismicity area (Priolo Gargalo, Sicily, Italy) in contrast with the initial design. The mechanical and geometrical properties of RC rack, pipelines (reduced thickness of pipe bents in parentheses to account for higher flexibility), foundation and soil modelling are recapped in Table 4 and the final model of RC rack in CS considering SSI is illustrated in Fig. 9.

Table 4 RC rack, pipelines, foundation and soil properties

Fig. 9

The mathematical model of soil–foundation, pipe rack and pipelines

6 Assessment of RC rack

6.1 Methodology

The assessment of RC pipe rack entails six main successive steps that have been followed for this CS and can be used as a guidance for the reader. After the material and frame element modelling that have been presented in the previous sections, the pushover analysis of RC rack follows for the determination of the weakest direction for which the fundamental period will be used for the record selection. The results from the modal analysis with (W/) and without (W/O) SSI both in horizontal and vertical directions are presented in Table 5 and Fig. 10. The SSI caused nearly 20% increase in the first two principal periods of the structure and modal mass decreased considerably. Furthermore, the selection of records considering the fundamental period should comply with the recommendations of EN1998-1 (2004). In this CS, 21 spectrum-compatible records were selected in total for far- and near-field conditions and Safe Life Limit State (SLLS) accounting for soil type C. The number of ground motions was probably insufficient to fully depict the record-to-record variability, however, it constituted the minimum number of records for seismic assessment proposed in ASCE/SEI 7-16 (2017) and made the analysis computationally feasible given the large model scale. The compatibility was achieved in REXEL software (Iervolino et al. 2010) and the records attained compatibility separately in the horizontal and vertical direction for near-field conditions (NEAR-HOR and NEAR-VERT) and only in the horizontal for far-field conditions (FAR-HOR) (Table 6, Fig. 11), although all the components were used in all cases. As mentioned in the introduction, the ED could be used as a parameter for the source characterisation, and thus it was assumed that ED < 15 km referred to near-source effects (Heydari and Mousavi 2015).

Table 5 The fundamental periods of the rack

Fig. 10

The two principal modes of the RC rack in a Y direction, and b X direction

Table 6 Seismic records considered for near- and far-field conditions

Fig. 11

Response spectra for a near- and far-field conditions in the X-direction, b near- and far-field in the Y-direction, and c near-field in the Z direction

A fundamental step in the assessment process is the determination of acceptance criteria of structural members and pipes. Concerning the former type, two failures modes were considered, viz shear and flexure, according to Fardis (2014) (Table 7). The failure modes that were taken into account for the pipes referred to failure in tension and local buckling according to Vathi et al. (2017). The three LSs for each of the failure modes considered are shown in Tables 7 and 8 for the structural and nonstructural components, respectively.

Table 7 Acceptance criteria of concrete members (Fardis 2014)

Table 8 Acceptance criteria of steel pipelines (Vathi et al. 2017)

In particular, the SLS pertained to tensile strain ε_p = 0.5%, whereas the conservative value of ε_Τu = 2% is considered as ultimate tensile strain. Furthermore, the compressive strain resistance ε_Cu in the axial pipe direction primarily depends on the diameter to thickness ratio (D/t) and is given by (Vathi et al. 2017):

$$\varepsilon_{Cu} = 0.5\left( {\frac{t}{D}} \right) - 0.0025 + 3000\left( {\frac{{\sigma_{h} }}{E}} \right)^{2}$$

(6)

where σ_h is the hoop stress due to internal pressure (null for this CS), and E is the elastic modulus.

The sixth step of the assessment framework includes the decision-making for the fragility analysis selection. The limited number of earthquakes found given the constraints on epicentral distance and spectrum compatibility gave rise to the IDA method employment. The number of runs per each record was dependent on the record. The initial run was determined roughly at 0.05 g and step increments of 0.05 g for a_g ≤ 1 g and 0.1 g for a_g > 1 g were employed. The scaling factor was applied both for the horizontal (H) and vertical (V) component in order to keep the ratio V/H constant. The same procedure was considered for the case with SSI. Both PGA and spectral acceleration (S_a) are selected to describe the damage-to-record variability, albeit the latter is commonly preferred since it is more informative and structural-oriented. The PGA as recorded on the free field considering site effects could be employed as a simple and consistent with the initial design IM and compare new with existing FFs.

Before proceeding with the IDA analysis, it was found necessary to explain graphically the main failure modes of the structural members and pipelines. The former presented higher sensitivity to shear, and that might come from the initial design of pipe rack in the nonseismic-prone area. As shown in Fig. 12a, b, the shear demand overpassed the SLS for two records (up to 2.3 times) (farfield, Fig. 12a) and for DC, whilst the chord rotation supply was higher for the four representative cases of Fig. 12c, d. The histories referred to Col61 as highlighted in Fig. 10a for the same PGA (a_g) and the rack presented either the principal (farfield) or the runner-up (nearfield) modal shape, probably, because it was stiffer in the longitudinal direction.

Fig. 12

Time histories referring to a and b shear force and c and d chord rotation at Col61 for far- and near-field conditions

Furthermore, the initial assumption of BCs affected significantly the seismic response. As clearly illustrated in Fig. 13a, the P1 subjected the beam (B20) into considerable loading resulting in the exceedance by 17% of the SLS for PGA = a_g. On the other hand, the chord rotation of the pertinent joint did not exceed by more than 4% the yielding value. This is another indication of pipe rack sensitivity to shear due to the initial design as it was observed for existing buildings in Tsonis and Fardis (2014). It should be emphasized that the conservative assumption of fixed point (P16) as well as the rigid support did not account for energy dissipation due to the relative stiffness between the support and pipelines (Azizpour and Hosseini (2009)) and pipe friction (with snubbers) that may act as a fuse for the seismic response.

Fig. 13

Dynamic coupling: a shear force diagram at a critical point and b time histories of normalised shear and chord rotation

Finally, the main failure mode of pipeline regarded the differential displacement between adjacent supports, particularly between the short and long rack. To demonstrate this effect, the plan view of that region was captured at a representative time point, which is shown in Fig. 14a. It was quite evident that differential movements in virtue of out-of-phase displacement of the two racks and/or earthquake frequency content were appeared resulting in high pipe strains. For instance, moment and peak strain of P1 were recorded in the middle of ELB1 and it was deduced that the peak values where consistent in time with the highest relative displacement between points SR12 and LR13 (Fig. 14b).

Fig. 14

Differential movements: a deformed shape of rack and pipelines and b differential displacement (Y direction) and time histories of normalised moment (M) and peak strain (ε)

The relation between the base shear force (V_E) and maximum chord rotation (θ), which was observed in the middle of the rack, coming from IDA and pushover (PUSH) with uniform distribution were demonstrated in Fig. 15a, b for the X and Y direction, respectively. It is worthy of attention that the dispersion of response was higher in the longitudinal direction (X) and the pushover underestimated the response in the transverse (Y) one. The selected rack is not highly irregular, however, the absence of slab might have caused inconsistencies between the static and dynamic analysis methods.

Fig. 15

Capacity curves for different compatibility of records (IDA) and from pushover analysis in a X and b Y direction without SSI

The IDA curves, which were formed through the spline interpolation, for the RC rack in DC without SSI considering both PGA and S_a as well shear force (V_E), since it was found more predominant as proved above, were presented in Fig. 16a, b. The first remark pertained to the higher dispersion of response in case of S_a that proved PGA a better estimator of IM variability. Another interesting outcome shown in Fig. 16c, and it was also depicted in Fig. 12, concerned the considerable higher fragility of the system when the far-field records were used and this might be due to the closer to the rack fundamental frequency of far-field records predominant period (Table 6 and Fig. 11). In particular, the SLS and SLLS for the worst case was exceeded for PGA equal to 10% and 39% greater than the a_g, respectively. The relationship between the PGA and PFA, which may be useful for the response of pipelines for future assessment, was plotted in Fig. 16d. It can been seen that around 30% of records have passed the PFA limit by ASCE 7 (3S_a(T₃)) at the a_g let alone the limit of 2.5·S_a(T₃) as defined by EN1998-1 (2004). This behaviour was expected since the rack was initially designed for lower PGA.

Fig. 16

IDA curves considering shear force a V_s versus PGA, b V_s versus S_a, and c PFA versus PGA without SSI in decoupled case [S_a(T₀) is the design input acceleration including site effects]

The records belonging to the far-field conditions were also more damaging for pipelines (Fig. 17). This consistency was also expected since the initial BCs of pipes were not modified, and thus the pipes might follow up to a point the response of structural beams. The response of pipes in terms of PGA and strain is shown in Fig. 17a. The peak strain observed for far-field conditions at a_g without SSI based upon the polynomial fitting was nearly 4·ε_y and that means the exceedance of SLLS. Furthermore, the strain exceeds more than 5 times the yielding one at the PFA limit (3·S_a(T₃)) as defined by ASCE-7 (Fig. 17b) that corresponded based upon the previous figure to PGA = 0.37 g, which was mildly greater than a_g. The high strain levels that were observed on the considered pipes even at PGA = a_g highlighted the high vulnerability of the system, which was also illustrated by the fragility curves in the sequel.

Fig. 17

Seismic response of pipelines in terms of a PGA versus strain (ε), b PFA versus strain strain (ε) and c PGA versus PFA in decoupled case without SSI (ε_y is the yield strain of the material)

6.2 Structural components

Initially, the FFs were derived for far-field conditions considering the CC and DC accounting also for linear and nonlinear soil. The FFs of structural beams were illustrated in Fig. 18 only for the shear failure mode and nonlinear soil for brevity. The fragility increased from 0 to 24% when SLLS and a_g seismic level were considered (Fig. 18a). It is rather intriguing that the nonlinearity of soil decreased considerably the dispersion of IM conditional to V_E (FF came towards the vertical direction), and thus the fragility rose significantly for mildly greater IM than a_g. This tendency was observed for columns as well. The soil nonlinear behaviour surely dissipated more energy, and that might constitute the structural modelling independent of seismic input. Detrimental effects of SSI considering different soil modelling for RC buildings have also been observed in Karapetrou et al. (2015) and Anvarsamarin et al. (2018). When it comes to CC (Fig. 18b), the dynamic interaction of pipelines and beams significantly deteriorated the system response rising the fragility up to 59% for the CLS at a_g. Of course, this behaviour was not acceptable and signified the important role the individual pipe supports played for the integrity of the system. It also signified that shear failure mode could be a better option for pipe racks with supported equipment since chord rotation, which refers to global scale, might not capture efficiently the damage of individual members.

Fig. 18

Fragility curves for beams considering a decoupled, b coupled system in far-field conditions without (W/O) and with (W) SSI (nonlinear)

The seismic input seemed to affect considerably the system performance as demonstrated in Sect. 6.1 (Fig. 12). Considering the response for horizontal (Fig. 19a) and vertical compatibility (Fig. 19b), the probability of exceedance of SLLS W/O SSI was found at 7% and 25%, respectively, compared to the 3% value for far-field conditions. The most useful remark that was drawn when comparing the source conditions regarded the lower dispersion that was observed far from the earthquake source compared to the other two cases (Table 9). A straightforward comparison of modelling and seismic input influence on system fragility is not always feasible given that it depends on LS, number of records and seismic level, however, considering the previous results, it was obvious that the modelling assumption of fixed pipe support sensationally affected the response of the system (as illustrated also in Fig. 13), and thus it overpassed the seismic input impact.

Fig. 19

Fragility curves for beams considering near-field conditions with a horizontal and b vertical compatibility with soil nonlinearity

Table 9 Dispersion β of beams in far- and near-field conditions (decoupled case)

To compare the appropriateness of IM to describe the pipe rack damage, the fragility curves of columns and beams in the decoupled case as well as far-field conditions considering for IM = S_a(T₃) with 5% damping were derived (Fig. 20). The SSI had negative impact on the system as previously. The spectral acceleration S_a(T₃) yielded either greater or lower dispersion depending on the IM and source conditions. Also, it is worthy of attention that the standard deviation was higher for the vertical compatibility than the other two cases for the same IM.

Fig. 20

Fragility curves in decoupled case and far-field conditions considering for IM = S_a ($T_{3}^{\prime }$ is the fundamental period considering SSI). a beams and b columns

6.3 Nonstructural components

The consideration of the piping system BCs without modifying the initial modalities resulted in the significant dependence of fragility curves upon the response of most critical components and particularly fixed supports. First, it was considered important to compare the response of structural and nonstructural components in unison and DC (Fig. 21a, b). The pipes failed earlier than the beams for SLLS and a_g seismic level (24% compared to 4%), however, the dynamic interaction rose excessively the fragility of beams at 89%. This is justified by the excessive force that the pipes imposed on beams on fixed points leading in the early failure in shear. With respect to seismic input, it was observed that the pipes fragility did not change as much as that of beams did particularly for the first two LSs. For instance, the fragility of pipes remained almost constant for the SLLS in both conditions, whereas the risk that beams imposed to the system decreased considerably for IM > a_g due to the higher dispersion. As mentioned in Sect. 6.1, the records with compatibility in the vertical direction proved more vulnerable to pipelines than the horizontal one rising the probability of collapse from 22 to 32% for the SLLS (Fig. 22).

Fig. 21

Fragility curves in a. decoupled and b. coupled case considering far- and near-field conditions (B: beam, and P: pipe)

Fig. 22

Fragility curves for pipes in near-field condition with nonlinear soil considering. a PGA and b S_a as IMs

Lastly, the effects of soil deformability with nonlinear properties on pipelines were considered, which is another interesting topic since very few publications deal with this issue as well. The SSI decreased the dispersion of IM but again not as much as the structural members, probably in virtue of the incompatibility and differential movements that acted as safepad to soil-induced higher displacements (Fig. 22). The SSI did not prove to influence the pipelines at a_g, however, the influence was accountable for higher IMs, and may attribute a dependency of SSI effects on IM level. The detrimental impact of pipelines verified the statement of Chaudhuri and Gupta (2002) that considered the SSI effects for nonstructural components when period amplification was equal or higher than 20%. Finally, the dispersion and median of pipelines fragility functions are quoted in Tables 10 and 11. The dispersion was comparable between S_a(T₃) and PGA among the LSs, however, the vertical component did not cause higher dispersion, as it was observed for the structural members. It should be stated that the S_a was also estimated at the principal mode of pipelines, however, the dispersion occurred even higher. The median occurred rather high for structural members W/O SSI, which was not observed for pipelines. The Table 12 quotes the error estimation with respect to fixed-base assumption where it was demonstrated that the fixed-base underestimated the pipelines fragility in the majority of cases with the maximum value coming from the nonlinear soil by 17% for SLLS and far-field conditions.

Table 10 Dispersion β of pipelines in far- and near-field conditions (decoupled case)

Table 11 Median θ in far- and near-field conditions (decoupled case)

Table 12 Error estimation in median θ for the fixed-base assumption

7 Conclusions

The present work inferred that uncertainties in the modelling e.g. assumption of boundary conditions and reinforcement, seismic input, intensity measure selection as well as soil–structure interaction phenomenon may have considerable impact on pipe rack—piping system seismic integrity. Overall, the following conclusions can be drawn:

• the fragility of RC beams surged from 0 to 59% for CLS at a_g seismic level due to the severe loading exerted by the pipelines.

• the maximum rise of beams fragility due to soil-deformability observed for far-field conditions soaring from 0 to 24% for the SLLS at a_g. Also, compatibility in near-field conditions increased the dispersion of conditional IM making the soil effects dependent on seismic level.

• The impact of all sources of uncertainty to pipework was not as much intense as for the structural members. For instance, the fragility increased from 4 and 24% to 89 and 42% at a_g for beams and pipelines in the CC, respectively considering SLLS. The influence of soil and seismic input was even lower.

• The IM sensitivity analysis proved that PGA and S_a yielded comparable dispersion among the LSs and source compatibility. The dispersion for the vertical component compatibility was higher among all the other cases.

Considering the aforementioned results, it is deduced that soil-deformability and dynamic interaction may act as a fuse to pipelines response making it partially independent of supports. Also, it should be considered that soil modelling may alter the dispersion of IM, and thus nonlinear response seems definitely a better choice. Arguably, the high probability of SLLS exceedance of pipelines at a_g when accounting for dynamic interaction and deformable soil may not be acceptable in an LNG terminal, and thus interventions by altering the boundary conditions of pipes and/or foundation type e.g. piles might improve the system performance.