Dimensionless fragility analysis of seismic acceleration demands through low-order building models

Abstract

This paper deals with the estimation of fragility functions for acceleration-sensitive components of buildings subjected to earthquake action. It considers ideally coherent pulses as well as real non-pulselike ground-motion records applied to continuous building models formed by a flexural beam and a shear beam in tandem. The study advances the idea of acceleration-based dimensionless fragility functions and describes the process of their formulation. It demonstrates that the mean period of the Fourier Spectrum, $T_m$, is associated with the least dispersion in the predicted dimensionless mean demand. Likewise, peak ground acceleration, PGA-, and peak ground velocity, PGV-based length scales are found to be almost equally appropriate for obtaining efficient ‘universal’ descriptions of maximum floor accelerations. Finally, this work also shows that fragility functions formulated in terms of dimensionless $\varPi$-terms have a superior performance in comparison with those based on conventional non-dimensionless terms (like peak or spectral acceleration values). This improved efficiency is more evident for buildings dominated by global flexural type lateral deformation over the whole intensity range and for large peak floor acceleration levels in structures with shear-governed behaviour. The suggested dimensionless fragility functions can offer a ‘universal’ description of the fragility of acceleration-sensitive components and constitute an efficient tool for a rapid seismic assessment of building contents in structures behaving at, or close to, yielding which form the biggest share in large (regional) building stock evaluations.

1 Introduction

Recent earthquakes have highlighted the importance of quantifying the dynamic effects on non-structural building components (Braga et al. 2011; Fierro et al. 2011). Besides being associated with the largest portion of economic losses, non-structural component failure may also lead to the closure of facilities which would have otherwise responded nearly elastically or with minor structural damage during a seismic event. Many of these components, including mechanical and electrical installations as well as furniture, equipment and contents, are acceleration-sensitive, and represent the biggest investment in building projects (i.e. 70 to 90% of the total building cost (Miranda and Taghavi 2005)).

Seismic damage to acceleration-sensitive building contents is caused by the large inertia forces generated by floor accelerations. The mangnitudes of these floor accelerations exceed those of ground accelerations and are commonly calculated by means of a direct amplification of the ground response spectra (Biggs and Roesset 1970; Pan et al. 2017). Alternatively, response-history analyses can be carried out to compute the temporal evolution of acceleration demands at a specific building location (Lin and Mahin 1985; Medina et al. 2006). However, when the uncertainty in structural modelling parameters is high or when large building stocks are considered, the advantages of using continuum building models can offset the merits offered by more detailed finite element simulations (Eroglu and Akkar 2011).

Continuum building models have been extensively used in earthquake engineering (Khan and Sbarounis 1964; Iwan 1997; Chopra and Chintanapakdee 2001). Khan and Sbarounis (1964) were among the first to use simple beam formulations to estimate earthquake-induced deformations in buildings while Iwan (1997) and Chopra and Chintanapakdee (2001) employed shear beam models to approximate framed structures. Taghavi and Miranda (2003) and Miranda and Akkar (2006) utilized continuum models to estimate the behaviour of structures including higher mode effects. More recently, continuum beam models have been extended to consider non-linear variations of stiffness along the height of buildings (Alonso-Rodriguez and Miranda 2016) as well as structure-specific stiffness distributions that enable an accurate estimation of inelastic capacity demands (Eroglu and Akkar 2011) or shear plastic constitutive behaviour (Cennamo et al. 2017) based on rigid-plastic approximations (Málaga-Chuquitaype et al. 2009). Importantly, the type of models employed in this study have been validated against the recorded response of six tall instrumented buildings by Reinoso and Miranda (2005). Moreover, although structural damage is usually observed for drifts of 1% or more (Pagni and Lowe 2003; Ramirez et al. 2012), non-structural damage can be extensive for drifts well below that value (Charleson 2007; Magenes et al. 2009). Therefore, the use of simple low-order building models, such as those employed herein, is considered pertinent, particularly for the estimation of acceleration-related damage in cases where minor or no yielding is expected.

Although the solutions to the partial differential equations governing the dynamic motion of continuous systems are usually expressed in dimensionless terms, formal dimensional analysis has not been applied to the seismic response assessment of these models, especially when acceleration response is concerned. This is despite the significant advantages in terms of dispersion reduction and ‘universal’ response formulation that can be brought about by combining continuum models amenable to closed-form solutions with dimensional response analysis. Therefore, this paper seeks to apply dimensional principles to the fragility analysis of acceleration demands in continuum building models.

The use of dimensional analysis for presenting the response of structures subjected to strong ground-motion was first introduced by Makris and Black (2004a, b). By expressing the displacement response of rigid-plastic, elastoplastic and bilinear single-degree-of-freedom (SDOF) systems in dimensionless $\varPi$-terms, they showed that dimensionless deformations become independent of the intensity of the ground-motion and follow a single ’master curve’. Dimensional analysis has also been applied for assessing the displacement response of SDOF structures simulating multi-storey moment resisting steel frames subjected to pulse-like ground-motions (Karavasilis et al. 2010), to the analysis of the earthquake-induced pounding between adjacent structures (Dimitrakopoulos et al. 2009b) and, more recently, to structures representing moment-resisting, partially-restrained, and concentrically-braced frames under real non-pulselike earthquake actions (Málaga-Chuquitaype 2015).

While pulse-type excitations have the advantage of possessing clear time and length metrics (Vassiliou and Makris 2011), the implementation of dimensional analysis for non-coherent earthquake action involves the challenge of selecting an adequate set of ground-motion time and length scales (Dimitrakopoulos et al. 2009a; Málaga-Chuquitaype 2015). Although a comprehensive investigation on the merits of different time and length scale was carried out in Málaga-Chuquitaype (2015), their study, like the vast majority of prior research, focused on dimensionless deformation demands while dimensionless floor acceleration response remains largely unexplored. An investigation on the relevant literature yielded only one article related to the dimensional analysis of peak floor accelerations, in the context of investigating the effect of pounding on the seismic response of adjacent multi-degree-of-freedom (MDOF) buildings (Zhai et al. 2015). Accordingly, there is no precedent for the application of dimensional analysis to fragility studies of acceleration demands in buildings and the only related study examined the issue of overturning of rocking structures subjected to near-fault ground-motions (Dimitrakopoulos and Paraskeva 2015).

This paper revisits the formulation of acceleration-based fragility functions with the help of dimensional analysis and low order building models. A fragility function is a mathematical relationship that represent the cumulative distribution function associated with the attainment of a certain limit state—such as the state of overturning in Dimitrakopoulos and Paraskeva (2015). Due to the high uncertainty involved in the assessment of seismic demands, the expected level of damage is defined in a probabilistic way (Cornell 1996). Hence, the mean annual frequency of exceedance of a decision variable (DV) can be obtained through the total probability theorem as (Cornell and Krawinkler 2000):

$$\begin{aligned} \lambda (DV)={\int \!\!\!\!\int \!\!\!\!\int }P(DV|DM)dP(DM|EDP)dP(EDP|IM)d\lambda (IM) \end{aligned}$$

(1)

The Engineering Demand Parameter, EDP, is computed through the structural analysis and is defined in terms of peak floor acceleration, peak floor displacement, interstorey drift ratio or any other structural performance measure. The intensity measure, IM, is linked to the ground motion characteristics, and $\lambda (IM)$ denotes the annual frequency of exceedance of the IM. The estimation of the conditional probability $P(EDP \ge edp | IM)$, where edp represents a rational demand threshold, is a major challenge for the earthquake engineer (Mai et al. 2017). Is this conditional probability which is usually provided via fragility functions (Miranda and Akkar 2006; Mai et al. 2017).

The objective of this paper is to put forward and assess the benefits of employing seismic floor acceleration fragility functions obtained through formal dimensional analysis and continuum building models. In this respect, it is expected that the formal superiority of dimensionless fragilities in offering an approximate ‘universal description’ of the phenomena (Dimitrakopoulos and Paraskeva 2015) will be translated into lower dispersion values and improved estimates. Therefore, comparisons are established in terms of measures of dispersion like standard deviation and Coefficient of Variation (COV). The paper starts with a brief introduction to the low-order structural representations and principles of dimensional analysis employed. This is followed by a discussion on the efficiency of alternative ground-motion length scales in terms of dispersion measures of acceleration response. To this end, a series of regression analyses are presented and comparisons are established between dimensionless and non-dimensionless formulations. Finally, dimensionless fragility functions at different acceleration levels corresponding to light and extensive component damage are constructed and contrasted with their non-dimensionless counterparts. It is shown that the suggested dimensionless fragility functions can offer a superior, ‘universal’, description of the fragility of acceleration-sensitive components and the ranges over which these advantages are more clearly expressed are identified. The fragility functions here proposed constitute an efficient tool for, among other applications, a rapid seismic assessment of building contents in structures behaving at (or close to) yielding which form the biggest share in large (regional) building stock evaluations.

2 Low-order building models and ground-motion database

2.1 Low-order building models

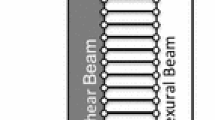
The continuous model of Fig. 1 can be used to approximate the seismic response of multi-storey buildings (Taghavi and Miranda 2003). It consists of flexural and shear beams connected laterally by an infinite number of pin-jointed axially-rigid links which enforce the same lateral deformation in both beams. The mass and stiffness are considered to be uniformly distributed along the height in this study. The vertical evolution of lateral deformations is controlled by the dimensionless stiffness parameter, $\alpha$ (Miranda and Taghavi 2005):

$$\begin{aligned} \alpha =H\sqrt{\frac{GA}{EI} } \end{aligned}$$

(2)

where H is the height of the building, GA is the shear rigidity of the shear beam, and EI is the flexural rigidity of the flexural beam. The continuous model behaves as a Bernoulli beam when $\alpha =0$ and it approximates a pure shear beam when $\alpha \rightarrow \infty$. Typically, $\alpha$ takes values in the range of $0 \le \alpha \le 30$ for conventional structures (Alonso-Rodriguez and Miranda 2015; Miranda and Taghavi 2005), with shear wall systems presenting values of $0<\alpha <2$, dual structural systems of $2<\alpha <5$ , and moment-resisting frames (MRF) having $\alpha$ values largely in the range of $5<\alpha <20$ (Alonso-Rodriguez and Miranda 2015).

Fig. 1

Simplified lower-order model

The amplitude of the building’s mode shape at a given dimensionless height $x=(z/H)$ is defined by (Miranda and Taghavi 2005):

$$\begin{aligned} \phi _{i} (x)=\sin (\gamma _{i} x)-\frac{\gamma _{i} }{\beta _{i} } \sinh (\beta _{i} x)-\eta _{i} \cos (\gamma _{i} x)+\eta _{i} \cosh (\beta _{i} x) \end{aligned}$$

(3)

where the dimensionless parameters $\eta _{i}$ and $\beta _{i}$ are determined from:

$$\begin{aligned} \beta _{i} &= \sqrt{\alpha ^{2} +\gamma _{i}^{2} } \end{aligned}$$

(4)

$$\begin{aligned} \eta _{i} &= \frac{\gamma _{i}^{2} \sin (\gamma _{i} )+\gamma _{i} \beta _{i} \sinh (\beta _{i} )}{\gamma _{i}^{2} \cos (\gamma _{i} )+\gamma_{i}\beta _{i} \cosh (\beta _{i} )} \end{aligned}$$

(5)

and $\gamma _{i}$ is the eigenvalue of the ith mode of vibration which can be estimated from the roots of the following equation:

$$\begin{aligned} 2+\left( 2+\frac{\alpha^{4} }{\gamma _{i}^{2} \beta _{i}^{2} } \right) \cos (\gamma _{i} )\cosh (\beta _{i} )+\frac{\alpha^{2} }{\gamma _{i} \beta _{i} } \sin (\gamma _{i} )\sinh (\beta _{i} )=0 \end{aligned}$$

(6)

The complete definition of the model requires the definition of the fundamental structural period, ${T}_{0}$, and a modal damping ratio, $\xi$. The fundamental period is treated parametrically in this study (but can be computed as a function of the lateral resisting system and geometry of the building by means of available empirical expressions). A constant damping ratio of $\xi =5\%$ is assumed herein.

After computing the eigenvalue $\gamma _{i}$, the ratio between the period of the ith mode and the fundamental structural period can be estimated as:

$$\begin{aligned} \frac{T_{i} }{T_{0} } =\frac{\gamma _{i} }{\gamma _{0} } \sqrt{\frac{\gamma _{0}^{2} +\alpha ^{2} }{\gamma _{i}^{2} +\alpha ^{2} } } \end{aligned}$$

(7)

Therefore, the definition of the dynamic characteristics of the buildings (i.e., periods and mode shapes) rely only on the dimensionless stiffness parameter $\alpha$. This allows the user to perform rapid and relatively accurate parametric studies.

The displacement response of a damped continuous system can be calculated by the superposition of its modal responses. To this end, the total displacement response, u(x, t), at a specific dimensionless height, x, can be expressed as:

$$\begin{aligned} u(x,t)=\sum _{i=1}^{\propto }\varGamma _{i} \, \phi _{i} (x)\, u_{i} (t) \end{aligned}$$

(8)

where $\varGamma _{i}$ is the modal participation factor of the ith mode; $\phi _{i}(x)$ is the amplitude of the ith mode at a dimensionless height $x = z/H$, and $u_{i}(t)$ is the displacement response of a damped SDOF system subjected to an earthquake ground motion which can be obtained by solving the corresponding equation of motion ($\ddot{u}_{i} (t)+2\xi \omega _{i} \dot{u}_{i} (t)+\omega _{i}^{2} u_{i} (t)=-\, \ddot{u}_{g} (t)$). In the case of a beam with uniform mass along its height, the modal participation factor is given by:

$$\begin{aligned} \varGamma _{i} =\frac{\int _{0}^{1}\, \, \phi _{i} (x)\, dx }{\int _{0}^{1}\, \, \phi _{i}^{2} (x)\, dx } \end{aligned}$$

(9)

Importantly, Eq. (8) will yield an exact solution only if an infinite number of vibration modes with exact modal shapes and participation factors are employed. Nevertheless, the response can be reasonably well approximated by considering a lower number of modes, N, and approximate mode shapes of vibration (Miranda and Taghavi 2005):

$$\begin{aligned} u(x,t)\cong \sum _{i=1}^{N}\varGamma _{i} \, \phi _{i} (x)\, u_{i} (t) \end{aligned}$$

(10)

The response history of total accelerations at a specific dimensionless height of the building can be obtained by differentiating Eq. (10) twice with respect to time and taking into account the absolute ground acceleration such that:

$$\begin{aligned} \ddot{u}(x,t)\cong \ddot{u}_{g} (t)+\sum _{i=1}^{N}\varGamma _{i} \, \phi _{i} (x)\, \ddot{u}_{i} (t) \end{aligned}$$

(11)

The number of modes, N, required for the accurate approximation of the response depends on the dynamic characteristics of the building. Miranda and Taghavi (2005) proposed that three modes of vibration are enough to obtain a relatively good approximation of the seismic response of conventional buildings, whereas flexible tall buildings might require a larger number of modes to be considered. Alonso-Rodriguez and Miranda (2015) investigated the influence of number of modes in the structural response due to ideal pulses (Mavroeidis and Papageorgiou 2003). They found that a single mode grossly underestimates the response while 3 modes can approximate peak floor demands with an error of less than 5% compared to a seven-mode solution. Similarly, Miranda and Akkar (2006) found that 5–6 modes of vibration are required to achieve a reasonable estimation of floor acceleration and drift demands for buildings subjected to realistic earthquake records. This variation in recommendations reflect the influence of ground-motion frequency content on the response estimation with the Mavroeidis and Papageorgiou pulses (Mavroeidis and Papageorgiou 2003) employed in (Alonso-Rodriguez and Miranda 2015) involving fewer frequency components than real non-pulselike records and hence requiring a smaller number of modes to be considered. A total number of $N = 7$ is used in the present study in all cases, in light of the relatively minor computational effort demanded by the simplified models.

The assessment of peak floor acceleration demands requires the determination of peak floor response values over a range of periods and for different locations along the building’s height. To this end, Fig. 2a shows the peak floor acceleration (PFA) response in buildings with globally shear-dominated lateral deformation ($\alpha =20$) for a constant damping ratio of $\xi =5\%$. The responses presented in Fig. 2a correspond to Mavroeidis and Papageorgiou (MP) velocity pulses (Mavroeidis and Papageorgiou 2003) with amplitudes, $A_p$, ranging from 0.7 to 1.3 m/s at 0.2 increments. When the peak floor acceleration (PFA) is normalized against the peak ground acceleration, (PGA), the response follows a single curve and becomes independent of the velocity pulse amplitude (Fig. 2b). This response symmetry is unsurprising given the elastic nature of the model. More interesting, however, are the insights that this normalization allows. Figure 3 presents normalized peak floor acceleration PFA / PGA demands for buildings with flexural-dominated response (like shear-walled structures, $\alpha = 0$) and structures dominated by overall shear deformations (like moment resisting frames, $\alpha = 20$). It is obvious from this figure that larger peak accelerations at the roof are expected in flexural-dominated buildings compared to shear-governed buildings at low period ratios, $T_p/T_0$, corresponding to flexible structures or high frequency ground-motions. This is evidently due to the higher-mode contribution (Fig. 3 left) that affects more the peak floor acceleration at the roof of the flexural-dominated structure ($\alpha =0$) compared to the shear-dominated structure ($\alpha =20$). This is a direct expression of Eq. 3 which shows that the mode shapes of flexural structures are affected more by resonance associated with each mode, since they are a function of only one frequency parameter ($\gamma$) that controls the shape and thus the amplification; while the shear structures have more complex mode shapes with both $\beta$ and $\gamma$ affecting their mode shape and thus they are not that sensitive to the resonance areas. The latter observation leads to the general tendency of flexural structures to exhibit larger peak roof accelerations compared to shear structures for the whole period range.

Fig. 2

Peak accelerations along building height for MP pulses ($\alpha =20$ and $\xi =5$%)

Fig. 3

Peak floor acceleration master curves for different pulse frequencies. $\xi =5\%$

2.2 Ground motion database

This paper makes use of coherent pulse idealizations of Mavroeidis and Papageorgiou (2003), referred to above, together with a database of real non-pulselike earthquake acceleration histories. Both sets of ground-motions are described in this section. The analytical expressions developed in Mavroeidis and Papageorgiou (2003) for representing the ground velocity and acceleration histories of ideal near-field pulse-like ground motions are presented in Eqs. 12 and 13, respectively:

$$\begin{aligned} \dot{u}_{g} (t) &= \frac{A_{p} }{2} \left[ 1+\cos \left( \frac{2\pi f_{p} }{g_{p} } \left( t-t_{0} \right) \right) \right] \cos \left[ 2\pi f_{p} \left( t-t_{0} \right) +a\right] \, \, \, \, \, \, \, \, \, \, \, \, \,\nonumber \\&t_{0} -\frac{g_{p} }{2f_{p} } \le t\le t_{0} +\frac{g_{p} }{2f_{p} } \end{aligned}$$

(12)

$$\begin{aligned} \ddot{u}_{g}(t) &= \frac{A_p\pi f_p}{g_p} \left\{ \! \begin{aligned}&{\sin \left( \frac{2\pi f_{p} }{g_{p} } (t-t_{0} )\right) \cos \left( 2\pi f_{p} (t-t_{0} )-\pi g_{p} +a\right) -}\\&g_{p} \sin \left( 2\pi f_{p} (t-t_{0} )-\pi g_{p} +a\right) \left[ 1-\cos \left( \frac{2\pi f_{p} }{g_{p} } \left( t-t_{0} \right) \right) \right] \end{aligned} \right\} \nonumber \\&t_{0} - \frac{g_{p} }{2f_{p} } \le t\le t_{0} +\frac{g_{p} }{2f_{p} } \end{aligned}$$

(13)

In these equations, the parameter $A_{p}$ defines the velocity-pulse amplitude, a is the phase angle of the harmonic excitation, $f_{p} (=1/T_{p})$ is the prevailing frequency of the pulse, $g_{p}$ determines the oscillatory character of the pulse, and $t_{0}$ defines the peak of the of the excitation envelope. A graphical representation of the MP pulse is shown in Fig. 4. An important feature of the model is the determination of the pulse duration according to the input parameters (i.e., pulse duration equals $g_{p}$/$f_{p}$). The relative simplicity of Eqs. 12 and 13 together with the physically realizable nature of the motions, makes MP pulses ideal for exploratory studies on the evolution of peak response demands in buildings under earthquakes.

Fig. 4

Acceleration history response for the MP pulse

In addition to MP pulses, our analyses use two sets, A and B, of 20 strong-ground motions each, as listed in Tables 1 and 2, respectively. Set A corresponds to the catalogue of human-induced earthquakes proposed by Foulger et al. (2017). The acceleration series were collected from the Pacific Earthquake Engineering Research Center (PEER) (2009) database, the European Engineering Strong Motion (ESM) (2009) database, and the Hellenic Accelogram Database (HEAD) (2009). The earthquake events are associated with Moment Magnitudes, $M_{w}$, ranging between 5.2 and 6.8. Besides, their mean period, $T_{m}$, calculated as the weighted average of the amplitudes of the Fourier Spectra, varies from 0.17 s to 0.67 s.

Table 1 Strong ground-motion record set A

Table 2 Strong ground-motion record set B

Set B, comprises of 20 acceleration records from the NGA-West2 Pacific Earthquake Engineering Research Center (PEER) (2009) database with similar seismological characteristics (e.g. magnitude, $M_w$, and distance, $R_{rup}$) to that of Set A. This set is considered herein to highlight, albeit in a limited manner, the indistinct effects of human and naturally-induced earthquakes as well as to emphasize the scale invariance of acceleration demands liberated from the ground-motion frequency content brought about by the self-similar response that will be discussed later. To this end, the differences in statistical distributions of $T_{m}$ and $T_{p}$ between sets A and B is illustrated in Figs. 5 and 6. The distributions of PGA and PGV values in both sets are also presented in Figs. 5 and 6 for completeness. It can be noted from these figures that, the $T_{m}$ distribution of record Set B ranges from 0.1 to 0.8 s and the largest bin population corresponds to the 0.1–0.2 s and 0.5–0.6 s ranges, which contrasts with the corresponding values of record Set A. Also, 30% of the records in Set B have $T_{p}$ varying from 0.4 to 0.5 s whereas $T_{p}$ varies from 0.1 to 0.8 s in Set A.

Fig. 5

Statistical distribution of ground-motion parameters in record set A

Fig. 6

Statistical distribution of ground-motion parameters in record set B

3 Physically-similar acceleration response to MP pulses

3.1 Dimensional response analysis

The maximum acceleration response, $a_{max}$, of a structure of a given stiffness ration ($\alpha =$ constant) subjected earthquake loading can be written as a function of its fundamental structural frequency, $\omega _{o}$, its damping ratio, $\xi$, and the ground motion time, $\omega _{g}=2\pi /{T}_{g}$ and length, $L_{g}$, scales. Here, $\omega _{g}$ is a characteristic measure that describes the frequency content of the ground motion and $L_{g}$ is a measure of the ground shaking persistence (Makris and Black 2004b; Málaga-Chuquitaype 2015). Therefore, the peak floor acceleration at a given building height is a function of five characteristic variables:

$$\begin{aligned} a_{\max } =f\,\left( \omega _{0} ,\xi ,L_{g} ,\omega _{g} \right) \end{aligned}$$

(14)

Equation (14) involves only 2 reference dimensions (i.e., length [L] and time [T]) and 5 parameters. According to Vaschy-Buckingham’s $\varPi$-theorem (Vaschy 1892; Buckingham 1915), only $5-2=3$ independent dimensionless $\varPi$-terms are required to fully describe the response of this system. Therefore, Eq. (14) can be re-written as a function of the independent $\varPi$-terms:

$$\begin{aligned} \varPi _{1} &= \frac{a_{\max } }{L_{g} \omega _g^2} \end{aligned}$$

(15)

$$\begin{aligned} \varPi _{2} &= \frac{\omega _{o} }{\omega _{g} } \end{aligned}$$

(16)

$$\begin{aligned} \varPi _{3} &= \xi \end{aligned}$$

(17)

such that:

$$\begin{aligned} \varPi _{1} =f\left( \varPi _{2} ,\varPi _{3} \right) \end{aligned}$$

(18)

In the case of MP pulses, which have distinctive amplitude and duration parameters, the obvious candidates for time and length scales can be constructed from the prevailing frequency ($f_{p}$) and peak amplitude values of acceleration and velocity (PGA or PGV), such that:

$$\begin{aligned} \omega _{g} = 1/f_p \end{aligned}$$

(19)

and

$$\begin{aligned} L _{g} = \frac{PGA}{\omega _g^2} \vee L _{g} = \frac{PGV}{\omega _g} \end{aligned}$$

(20)

Alternatively, the mean period of the ground motion, $T_m$, which is a weighted average of the Fourier spectrum (Rathje et al. 2004) can also be employed to construct a dimensionless temporal term, $\varPi _2$ when no distinct pulse can be identified in the ground-motion. The mean period was first used to predict inelastic displacements by Dimitrakopoulos et al. (2009b) and has since been employed by other researches (Málaga-Chuquitaype and Elghazouli 2012; Hickey and Broderick 2019) to improve the estimate of seismic demands. This parameter is consistent with the dimensional space under consideration and liberates the study from any reference to an equivalent structure, which will not be the case for any other response spectral quantity.

3.2 Peak floor acceleration response

In order to generate a dataset of acceleration responses, MP pulses with parameters covering expected ranges proposed in the literature (Mavroeidis and Papageorgiou 2003) were employed together with the structural model described above. To this end, the velocity pulse amplitude was varied from 0 to 1.3 m/s at increments of 0.1 while the prevailing pulse frequency ranged from 0.1 to 1.0 Hz at 0.1 intervals. The phase angle of the pulse, a, and the parameter $g_{p}$ that defines the oscillatory character of the pulse were assumed to remain constant throughout the first set of analyses, as they do not have a significant influence over the intensity of the pulse or the peak acceleration response (Alonso-Rodriguez and Miranda 2015). Also, the effect of the duration of the pulse ($duration=g_{p}$/$f_{p}$) was not examined since there is a consensus that duration is not a main factor affecting peak response values (Hancock and Bommer 2006, 2007).

Figure 7a plots the self-similar peak floor acceleration demand for pulses with prevailing frequency $f_{p}=0.5$ Hz, and buildings with dimensionless stiffness parameter $\alpha =12$. The total peak floor accelerations are calculated at a dimensionless height $z/H=1.0$. When expressed in the adequate dimensionless terms, the dimensionless demand parameters are independent of the intensity of the pulse and follow a single curve (master curve—Fig. 7b). Figure 7c, d shows the dimensionless peak floor acceleration demands when the mean period, $T_m$, and the prevailing frequency of the pulses, $T_{p}$, are used, respectively. It is clear that in the case of MP pulses, both $T_{p}$ and $T_m$ are able to unleash a self-similar response. In fact, complete similarity is also observed when any of the individual harmonics of the MP pulse are employed, as shown in Fig. 7e, f. Figure 7c presents acceleration master curves for frequencies ranging from 0.1 to 1.0 Hz at 0.1 intervals when $T_{m}$ is used as the ground-motion time scale. It can be seen that dimensionless peak floor accelerations ($\varPi _1$) are mainly influenced by the first two modes of vibration.

Fig. 7

Acceleration response under MP pulses

The proposed ‘master curves’ are relatively simple and can offer a universal description of the response along the whole range of $\varPi _{1}, \varPi _{2}$ values. To stress this fact, Fig. 8 presents peak floor acceleration spectra normalized by the peak ground acceleration PGA and the spectral acceleration at the fundamental structural period $S_a(T_0)$ as well as in full dimensionless terms. The results of multi-linear regression analyses are included in this figure for illustrative purposes. The benefits of a universal description (master curve) of the response brought about by the application of dimensional analysis are evident in Fig. 8 where the self-similarity of the response identified previously leads to significant improvements in the coefficient of determination, $R^2$, that is increased from 0.18 when non-dimensionless parameters are employed to 0.99 when expressed in terms of the dimensionless $\varPi$-terms. The previously noted observation that shear-wall type structures ($\alpha =0$) appear to exhibit higher peak accelerations with respect to the first mode when $T_p /T_0 = 1$ (resonance) is also confirmed by Fig. 8c.

Fig. 8

Regression analysis for MP Pulses

A crucial aspect that enabled the emergence of the type of symmetry in the response scaling observed in Figs. 7 and 8, is the unequivocal relationship between the phase angle of the different harmonic components of the MP pulse and the other pulse parameters leading to the relative independence of the oscillatory character of the pulse from its intensity (Alonso-Rodriguez and Miranda 2015). In fact, if the phase of the different harmonics was not set up in such a predefined manner, by keeping a constant, an additional phase parameter, $\phi$, would have to be included in our previous analysis (Eq. 14). This is explored here with reference to Fig. 9 that presents the dimensional analysis for the case of a pulse composed of two harmonics of amplitude 1 ${\mathrm{m}}/{\mathrm{s}}^2$, $f_p=1$ Hz where the second harmonic has a varying phase angle $\phi$. The pulse motion has always a $T_m=1$ s and results for structures with flexural type lateral deformation ($\alpha = 0$) as well as shear-governed behaviour ($\alpha = 20$) are analysed. The phase difference of the second harmonic, $\phi$, can be considered as a fourth dimensionless $\varPi -$term equal to $\varPi _4 = \phi /\pi$, since the phase angle, $\phi$, is actually a dimensionless-orientationless parameter. It is clear from the ‘master surfaces’ depicted in Fig. 9, that, beyond the self-similarity observed with respect to amplitude, the surfaces (and contour plots) show a very non-symmetric and complex evolution that complicates their representation. The minimum response, valley, observed at $\varPi _4 = 1$ corresponds to the case where both harmonics act completely out of phase. In reality, the path dependency of the spectral contribution of real acceleration records, will give rise to a rich phase distribution that will prevent the observation of full similarity in the acceleration response in the $\varPi _1 - \varPi _2$ plane projection, even for the simplified structures considered herein. Nevertheless, significant improvements in the reduction of dispersion would still be possible by following a dimensional approach as will be discussed in the following sections.

Fig. 9

Acceleration response under two harmonic pulses with different phases ($\phi$), $\varPi _3 = 0.05$

4 Acceleration response and regression analysis for real records

4.1 Alternative time and length scales for real records

A number of recent studies have investigated the challenging issue of selecting appropriate time and length scales for earthquake response analysis (Dimitrakopoulos and Paraskeva 2015; Málaga-Chuquitaype 2015; Málaga-Chuquitaype and Bougatsas 2017). This selection is relatively straightforward in the case of pulse-like ground-motions due to the clear and distinguishable time and length scales of a pulse. However, these features are not obvious in non-pulselike ground motions and the efficiency of different time and length scales needs to be carefully evaluated.

In this study, seven ground-motion parameters of non-pulselike accelerograms were examined, including: the mean period, $T_{m}$, and the predominant period, $T_p$, as time-scales; and the peak ground acceleration, PGA, the peak ground velocity PGV, root mean square acceleration, $a_{RMS}$, and root mean square velocity $v_{RMS}$, as basis for the construction of length-scales. An extensive parametric study on more than 250 simplified building models representing different stiffness distributions with $\alpha = \{0, 4, 8, 12, 16, 20\}$ was performed to analyse the effects of different parameters on the amplitude and the shape of floor response spectra. A total of 8000 and 7000 peak floor demand analyses were carried out for buildings subjected to real earthquake records and synthetic MP ground motions, respectively.

The previous section offered an insight into the height-wise variation of acceleration demands in different building-types. It was observed that the peak roof acceleration demand (at $z/H=1$) offers a reasonable estimation of maximum demands along the height in a good number of cases. Therefore, the ordinates of the floor response spectra as obtained at the top of the building are discussed in this section. The Newmark-beta method with a constant acceleration scheme ($\gamma =0.5$ and $\eta =0.25$) was employed for the analyses in light of its unconditional stability.

Table 3 presents the calculated coefficient of determination, ${R}^{2}$, and standard deviation, $\beta$, associated with the different ground-motion sets employed. It can be appreciated from Table 3 that a higher $R^{2}$ value is not necessarily associated with a lower dispersions ($\beta$). In general, the length scales constructed on the basis of PGA and PGV appear to perform better than their alternatives. This, in addition to the widespread familiarity of the engineering community with PGA lends support to the use of the pair $T_m$—$PGA/\omega ^2$ as time and length scales for acceleration response analyses. Therefore, PGA is employed in subsequent sections of this paper.

Table 3 Efficiency of alternative ground-motion scales

4.2 Dimensional response analysis

The self-similar acceleration responses due to earthquake records TH4, TH5 and TH9 are shown in Fig. 10. The convention for record nomenclature followed is provided in Table 1. A total of 200 floor response spectra were analysed in this way for each record set (A and B), respectively, and the results will be discussed in later sections of this paper. It can be seen that the peak dimensionless amplitude in Fig. 10 tends to occur when the fundamental period coincides with the mean period of the ground motion. In general, the mean period is able to adequately explain the maximum amplification of peak ground acceleration and to reduce the dispersion of the whole dataset. Some distinct peaks on the dimensionless acceleration amplitude are observed for $\varPi _{2}>1$ in Fig. 10b. These peaks represent the contribution of the higher modes of vibration and depend strongly on the frequency content of the ground motion. A general trend is manifest in Fig. 10b whereby peak dimensionless acceleration values in the order of $\varPi _1 \approx 8$ are obtained for $\varPi _2 \approx 1$, decreasing steadily at larger$\varPi _1$s. Such consistency on the trends is not apparent when the response is presented in terms of acceleration, $a_{max}$, and structural period, T, in Fig. 10a.

Fig. 10

Acceleration response under real records TH4, TH5 and TH9, $T_g = T_m$

It follows from the previous discussion that, besides the building configuration ($\alpha$), a good portion of the high variability in peak floor accelerations is influenced by the frequency content of the ground motion, in terms of both amplitude and phase. Before discussing the formulation of time-scale-normalized fragility functions, this section presents and discusses a series of regression studies performed on dimensionless and non-dimensionless terms by means of the linear least square approach. To this end, the transformation of the responses into the logarithmic space was observed to reduce the dispersion in the response data and, most importantly, to reveal a tendency in peak acceleration values which is hidden in the normal space and which can be well described by simple linear regression models. In order to facilitate the discussion of the proposed functional forms and the effect of various parameters in the response, only the analyses of the most efficient time- and length-scales are presented herein. Also, the discussion is centred around the two stiffness-bounding cases of $\alpha =0$ and $\alpha =20$. Our studies found that these values of dimensionless stiffnesses are also associated with the worse and most efficient functional form performance, respectively, as will be argued later in this paper with reference to Table 8 and Fig. 15. A feature that can be explained by the lesser or greater propensity to higher-mode effects. Figures 11 and 12 show sample results of the linear regressions analyses performed for record sets A and B of real ground-motions, respectively while Tables 4 and 5 summarise the main results. Some results are also expressed in terms of the spectral acceleration at the initial period of the building, $S_a(T_0)$. These results are included for completeness but it should be noted, that the use of spectral acceleration values is discouraged in formal dimensional response analysis due to their dependency on equivalent oscillators in contrast with peak ground-motion characteristics (like PGA or PGV) which are intrinsic to the acceleration series. The models associated with the lowest dispersion are identified with bold fonts in these tables.

The following expressions can be employed for approximating the dimensionless peak floor acceleration demands in buildings subjected to real earthquake records.

$$\begin{aligned} \ln \varPi _1= \left\{ \! \begin{aligned}&\ln c_1+c_2(-\ln \varPi _2+c_3)&\ln \varPi _2 \le c_3 \\&\ln c_1+(c_2+c_4)(\ln \varPi _2- c_3)&\ln \varPi _2 \ge c_3\\ \end{aligned}\right\} \end{aligned}$$

(21)

The proposed expression was found adequate to fully describe the accelerations floor demands. Tables 4 and 5 summarize the regression results, while Table 6 presents the obtained coefficients of the proposed expressions for dimensionless stiffness parameters of $\alpha = 0$ and $\alpha = 20$. Two distinct trends can be identified in Figs. 11 and 12. This means that irrespectively of the ground motion intensity, the demand steadily increases up until resonance (i.e., for $\ln \varPi _{2} =0$ or $T_{m}/T_{0}=1$). After this point a linear decrease is observed. It is worth noting that as the dimensionless period parameter decreases, the gradient of the slope for $\ln \varPi _{2} \le 0$ decreases as well (Fig. 11d). Therefore, for $\ln \varPi _{2} \le 0$ acceleration-sensitive non-structural components attached to buildings with flexural lateral shape of deformation are expected to have the same or slightly different level of damage. This is not necessarily the case for framed structures (Fig. 11d, 12d). This difference from Fig. 3 (response to MP pulse excitations) is directly linked to the non-coherent part of the input ground motions that excite the higher modes of the structures and thus the peak floor accelerations of the more sensitive-to-resonance flexural structures ($\alpha =0$). Furthermore, the increase of dispersion for small values of dimensionless period parameter confirms that higher mode effects are more significant for buildings with flexural lateral shape of deformation.

Fig. 11

Regression analysis for record set A

Fig. 12

Regression analysis for record set B

Table 4 Regression analysis for record set A

Table 5 Regression analysis for record set B

Table 6 Linear regression analyses coefficients for $\varPi _1 - \varPi _2$

It is important to measure the level of dispersion around the predicted mean value. A high value of the coefficient of determination indicates that most of the variation of the data set is accounted by the regression. Similarly, the standard deviation of $ln\varPi _{1}$, provides a good estimate of the level of variability in the estimation. This measure is especially accurate when the set of data is lognormally distributed. In addition, linear regression analysis is based on the assumptions that (i) the residuals are normally distributed and the variance is constant, and (ii) the residuals are independent of each other (Nathabandu and Rosso 1996). In this regard, the aforesaid statistical measures have been used to evaluate the adequacy of the functional models proposed in Tables 4 and 5. Even though the dispersion measures may be reduced further at the cost of using more complicated non-linear regression functions, the proposed equations are judged appropriate for the comparisons established in this study. To this end, it is important to note that the regression analyses presented herein are not intended to provide precise values to be used in practice but rather they are employed as a tool to enable comparisons between calculations made on the basis of dimensional and dimensionless terms. This generality of purpose is reflected in the simple functional forms employed. It is expected that, given that consistency in methods and models is maintained, the general conclusions based on the relative performance of dimensional and dimensionless formulations presented herein should hold for more complex physically-motivated and case-specific scenarios. Likewise, the choice of the only available catalogue of human-induced earthquakes should not be understood as a desire to prove any difference between these records and records coming from non-human induced events, quite the contrary, the limited results here presented should confirm that, given their common tectonic nature, the structural response to two datasets of relatively different mean time-scales ($T_m$), when normalized by means of dimensional analysis, should yield broadly similar and consistent results.

It has also been highlighted above, that the relative efficiency of the dimensionless peak floor acceleration equations is reduced for buildings with flexural-type deformation in comparison with the use of spectral acceleration values ($S_a(T_0)$) for the normalization. This reduction in the efficiency arises from the importance of higher modes in walled structures. Also, in those cases, the response tends to associate with higher variabilities at or near to frequency tuning. Interestingly, the regression analyses on record sets A and B yield reasonably close results when expressed in terms of dimensionless $\varPi$-terms, highlighting the advantages of the application of formal dimensional response analysis.

Figure 13a presents the histograms of residuals from the regression in terms of dimensionless terms for Record Set A. Similar results were observed for Record Set B. It can be seen from Fig. 13a that the residuals are normally distributed. Likewise, Fig. 13b. depicts the plot of the residuals versus the estimated fitted response values. In general, Fig. 13 offers sufficient indication that the residuals are symmetrically distributed with tendency to cluster at the middle of the plot. No clear pattern was identified and the constant and the linear model is considered adequate for representing the set of data.

Fig. 13

Residual analysis for regression in terms of dimensionless terms. Record set B

It follows from the results presented in Tables 4 and 5 and Figs. 11 and 12 that there is a significant benefit in employing dimensionless terms for presenting the structural response parameters. For both record sets dimensionalization of the response results in lower levels of dispersion. However, more definite and discrete comparisons can be established with reference to the CDF at given performance levels. The procurement of such functions will be the subject of the next section.

5 Dimensionless fragility analysis

This section is devoted to the computation of the conditional probability of exceedance peak floor accelerations for acceleration sensitive non-structural components. To this end, a set of damage states for non-structural components are considered in accordance with current guidelines for seismic performance assessment of buildings (FEMA 2000). Both sets of real earthquake records previously described are employed. In order to facilitate the discussion, focus will be placed on the damage states for non-structural elements as presented in Table 7.

Table 7 Damage states of acceleration-sensitive non-structural components

Since the analysis of the individual clusters (divided according to the regression analysis results presented above) involve a limited number of observations and do not allow a direct calculation of the probability of exceedance in an efficient manner, a Maximum Likelihood Estimation (MLE) is applied herein to define fragility functions. To this end, the parameters of the fragility function (i.e., its median $\mu$ and standard deviation $\beta$) required in Eq. (22), can be calculated by maximizing the likelihood function (Dimitrakopoulos and Paraskeva 2015; Málaga-Chuquitaype and Bougatsas 2017). For a N number of ground motions, the likelihood function can be written as:

$$\begin{aligned} L=\prod _{j=1}^{m} \begin{pmatrix} n_j \\ z_j \end{pmatrix} \varPhi \left( \frac{\ln \varPi _{i} -\mu }{\beta } \right) ^{z_{j} } \left( 1-\varPhi \left( \frac{\ln \varPi _{i} -\mu }{\beta } \right) \right) ^{n_j-z_{j} } \end{aligned}$$

(22)

where $n_j$ is the number of independent observations of ‘failure’ or ‘no failure’ and $z_j$ is a Binomial distribution which gives the total number of ‘failures’ for a given analysis. The parameters $\mu$ and $\beta$ are then obtained by maximizing the likelihood function through numerical optimization, such that:

$$\begin{aligned} \left\{ \mu ,\, \, \beta \right\} =\arg max \prod _{j=1}^{m} \begin{pmatrix} n_j \\ z_j \end{pmatrix} \varPhi \left( \frac{\ln \varPi _{i} -\mu }{\beta } \right) ^{z_{j} } \left( 1-\varPhi \left( \frac{\ln \varPi _{i} -\mu }{\beta } \right) \right) ^{n_j-z_{j} } \end{aligned}$$

(23)

It should be noted that fragilities are routinely defined either as the probability of exceedance of threshold for a given IM or the probability of exceedance of a threshold for a given EDP. In our case, $\varPi _{i}$ would correspond to either a dependent or an independent dimensionless $\varPi$-term. To this end, normalized damage states of the following form are employed to represent the damage thresholds:

$$\begin{aligned} DS_{s} =\frac{DS_{i} }{PGA} \end{aligned}$$

(24)

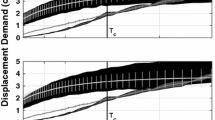
Fragility functions in terms of a dimensionless EDP and a dimensionless IM were derived for the database of MP pulses and earthquake records described above. Figure 14 presents typical fragility functions obtained considering dimensionless univariate IM and EDPs while the full range of estimated fragility parameters is presented in Table 8. Dimensionless fragilities are illustrated for a $DS1_a$ damage state and for both flexion and shear-dominated structures in Fig. 14 . Importantly, the base data is also presented in Fig. 14 in the form of compact binned box-plots. These box-plots depict the median as well as the 25th and 75th percentiles in each data bin without making any assumption of the underlying statistical distribution and thus showing the quality of the fragility fits within the constraints of the data employed. In order to facilitate the comparison, the Coefficient of Variation (COV) is also presented in Table 8 together with the mean and standard deviation values. The largest (italics) and lowest (bold) normalized dispersion (COV) values are identified in this table. Besides, Fig. 15 shows the ratios of dimensionless versus non-dimensionless COVs for the fragility analysis performed. A ratio of less than 1 in Fig. 15 denotes a reduction in the dispersion of the data and a corresponding improvement in the quality of the estimation.

It is generally observed from Figs. 14 and 15 and Table 8 that in comparison with non-dimensionless fragilities, the acceleration dimensionless fragility formulation is associated with less dispersion for real earthquake records and shear-wall type buildings at all damage threshold levels here analysed, with COV reductions in the order of 15% to 35%. On the other hand, when global shear deformations dominate the overall building response, the dimensionless formulation is more efficient only at larger demand levels (i.e. DS2a for Record Set B and DS2b for Record Set A) and the dispersion improvement is now reduced to the range of 10% to 20%. Perhaps more important is the fact that the widely adopted assumption of lognormal distribution (Limpert et al. 2001) in ‘failure’ points (i.e. observations in which exceedance of a DSs is observed) is more accurate when the dimensionless EDP is employed (Fig. 14). On the other hand, the ‘failure’ points are not strictly log-normally distributed when a dimensional IM is used. It should be noted that despite formal tests indicating that drifts are not always log-normally distributed (Buratti et al. 2010), no similar results exist yet for acceleration demands and hence the common practice of assuming lognormality was followed in this paper.

The greater proneness to experience larger floor accelerations at their upper levels of shear-wall type buildings (flexural-dominated structures), discussed before, is also appreciated from the results and fragilities presented in Fig. 14 and Table 8. It is important to note that the dimensionless fragilities presented in Fig. 14 denote the probability of exceedance of a given value of $a_{max}$, which for the case of $DS1_a$ is $a_{max} = 0.55$ g (Table 7). Therefore, a larger mean, $\mu$, implies the need for a lower PGA to attain the same mean probability of exceeding the $DS1_a$ damage level or for a given probability of exceedance $DS1_a$, the flexural-dominated structures ($\alpha =0$) correspond to higher $\varPi _1$ values and therefore lower PGA values compared to the shear-dominated structure ($\alpha =20$). This higher susceptibility to acceleration damage observed for flexural (shear-wall buildings) in comparison with buildings with shear-dominated response (e.g. MRF) is consistent with the findings discussed before with reference to Figs. 3, 8, 11 and 12.

Fig. 14

Dimensionless fragility curves as a function of dimensionless EDP and IM corresponding to damage state $DS1_a$ and buildings with $\alpha = 0$ and $\alpha = 20$

Table 8 Fragility analysis

Fig. 15

Dimensionless fragilities relative COV for different damage states

6 Conclusions

A study has been performed on the estimation of acceleration demands in building structures by means of dimensional analysis principles and low-order continuum models with a view to assessing the fragility of non-structural contents in structures behaving linearly or at the verge of yielding. To this end, ideal pulselike ground-motions and real records are employed. The mean period of the Fourier Spectrum, $T_m$, is adopted as an appropriate time-scale, although its ability to adequately describe the frequency content of the ground-motion is observed to decrease as the prevailing pulse frequency increases. Similarly, Peak Ground Acceleration and Peak Ground Velocity based length scales are found to be equally adequate for normalizing the Peak Floor Acceleration values and create dimensionless $\varPi$-terms. Furthermore, it is observed that flexural-dominated structures (shear-wall type buildings, $\alpha =0$) are more sensitive to resonance with the first and higher-modes leading to larger acceleration amplification effects in comparison with shear-dominated structures (moment resisting frames, $\alpha =20$). These increased peak floor accelerations are closely linked to the non-coherent components of the ground-motion and are more noticeable at the roof of flexural-dominated structures with period ratios in the range of $T_m/T_0=1$ and $T_m/T_0<0.5$.

A large database of peak acceleration responses was created for different levels of ground-motion intensity and various combinations of flexural-shear building stiffness contributions. The transformation of the response dataset into the log–log space unveiled tendencies in the response which were otherwise hidden in the normal space. To this end, a bi-linear regression model was found adequate for describing the evolution of dimensionless acceleration demands caused by real earthquake records. Besides, dimensionless functions for the assessment of acceleration fragilities in buildings were obtained by means of maximum likelihood estimations. These dimensionless fragility functions can offer a universal ‘description’ of the fragility of acceleration sensitive components invariantly from the intensity and mean period of the ground motion.

It is shown that fragility functions formulated in terms of dimensionless $\varPi$-terms have a superior performance in comparison with those based on conventional non-dimensionless terms (like peak or spectral acceleration values) for structures dominated by global flexural-type lateral deformation over the whole intensity range and for large peak floor acceleration levels in structures with shear-governed deformations. The dimensionless fragility curves formulated support the observation that flexural-dominated structures are more susceptible to damage (for all damage states) than shear-controlled structures. Likewise, both the regression and the fragility analyses, yielded comparatively lower dispersion values for shear-dominated buildings ($\alpha =20$). These observations can be used as a macroscopic criterion for the preliminary assessment of such buildings.

Although the ground-motion datasets employed have not been defined with a particular hazard scenario in mind, a consideration that can be included in future studies, the results presented herein confirm that the use of datasets of different mean time-scale distribution, but common tectonic origin, yields remarkably similar response results when expressed in dimensionless terms. Further studies are under way to evaluate the relative contributions of coherent and non-coherent ground-motion components to peak floor accelerations and other response quantities using the tools proposed in this study. The insights and dimensionless fragilities offered can be employed for the future development of a more rational approach for practical initial rapid seismic assessment of building contents in regular structures behaving at, or close to, yielding during large building stock evaluations.