Vertical peak floor accelerations of elastic moment-resisting steel frames

Abstract

The scope of this study is the quantification of vertical peak floor acceleration demands at column lines and along the length of beams of elastic moment-resisting steel frames subjected to recorded ground motions. These demands correlate with the maximum strength demands on rigid nonstructural components attached to a frame structure. Since it is commonly assumed that buildings behave flexibly in the horizontal direction and rigidly in the vertical direction, the assessment of vertical acceleration demands is typically not considered in most cases. The results of this study show that vertical peak floor accelerations can be up to five times larger than the vertical peak ground acceleration, in contrast to horizontal peak floor accelerations that are only up to two times larger than the horizontal peak ground acceleration for the numerical models used in this study. The most significant amplifications estimated in the vertical direction are found at the center of the girders. Further investigations of modified steel frames indicate that the story-wise mass distribution has an influence not only on the vertical acceleration demand, but also on the horizontal component of the response, though to a lesser degree. In contrast, the response in the vertical and horizontal direction is only slightly affected by an increase in the flexural stiffness of the beams. The results of this study strongly indicate that in steel frames it can be considered highly questionable to ignore the amplification of the vertical acceleration component along the height of the structure.

1 Introduction

Several seismic events of the last decades left many buildings not operational although the load-bearing structure remained virtually unimpaired. In those buildings, nonstructural components (NSCs), such as partition walls, suspended ceilings, electrical and mechanical equipment, etc., were heavily damaged. As a result, a myriad of papers, such as Adam and Fotiu (2000), Sankaranarayanan and Medina (2007), Vukobratovic and Fajfar (2017) and Obando and Lopez-Garcia (2018), were devoted to the prediction of the seismic response of NSCs. Nowadays, it is well understood in the engineering community that NSCs contribute significantly to the total seismic risk of a building (Miranda and Taghavi 2009). However, there is still the need to improve seismic design provisions to minimize damage of NSCs and consequently to mitigate earthquake induced losses (NIST GCR 17-917-44 2017).

Arguably, many NSCs are both drift- and acceleration-sensitive; however, they are commonly classified as either drift-sensitive or acceleration-sensitive. Drift-sensitive NSCs such as partition walls are attached to the load-bearing structure at different fixed points, and therefore, are damaged if the drift between these attachment points becomes too large. The damage potential of acceleration-sensitive NSCs associated to the loss of position retention is primarily a result of absolute acceleration (strength) demands imposed at their supports and/or attachment point(s) to the load-bearing structure. Thus, seismic assessment of very stiff NSCs is directly correlated with the acceleration response of the load-bearing structure.

Recognizing the importance of the total acceleration response of structures for seismic loading of NSCs, the estimation of this seismic response quantity has been the subject of a series of studies, most of them concerning the horizontal component only, such as the studies of Taghavi and Miranda (2012), Medina (2013), Pozzi and Der Kiureghian (2015), Flores et al. (2015) and Moschen and Adam (2017). The amplification of the vertical base acceleration component along the building height is usually neglected because it is assumed that structures respond rigidly in the vertical direction. For instance, in ASCE/SEI 7-16 (2016), for components located above ground level, the seismic design vertical force is assumed to be constant and equal to 0.2S_DSW_p, where S_DS is the site specific short-period design spectral acceleration and W_p the weight of the component. However, the vertical modal frequencies of a load-bearing structure may be in tune with the high-frequency content of vertical ground motions, thus, providing a non-uniform distribution of vertical accelerations along the height and in many cases amplifying the vertical acceleration response to levels that are higher than those predicted by current design standards. Hence, neglecting the filtering effect of the building on the vertical base excitation component of ground motion would in some cases underestimate the magnitude of vertical NSC acceleration demands. A recent study by Moschen et al. (2016) of the vertical peak floor acceleration (PFA_v) demand of a generic stick model, representing the column line of steel perimeter moment resisting frames, confirmed these considerations. It was found that the median PFA_v demand at column lines can be up to four times larger than the vertical peak ground acceleration (PGA_v). The PFA_v demands at beams (girders) of moment-resisting steel structures have been studied only recently by Francis et al. (2017), utilizing 20 ground motion records of the Christchurch earthquake. Further research was conducted by Ryan et al. (2016), who studied experimentally the vertical peak accelerations of a full-scale, 5-story steel building. However, these few studies, including a preliminary investigation of the authors (Gremer et al. 2018), do not provide an in-depth understanding of the relationships between frame parameters (such as number of stories, mass and stiffness distribution, etc.), horizontal and vertical base excitation, as well as horizontal and vertical acceleration response demand in seismically excited buildings.

The objective of the present contribution is to evaluate parametrically the vertical peak floor acceleration normalized with respect to the corresponding peak ground acceleration component (PFA_v/PGA_v) of the column lines and also of the beams of elastic steel moment resisting frames. Horizontal acceleration amplifications are also assessed to highlight the difference between vertical and the horizontal acceleration response. Response history analyses are conducted on a set of planar frame models whose design is based on the FEMA P-695 archetypes (FEMA P-695 2009) subjected to the horizontal and vertical acceleration components of different record sets. Since the acceleration records excite directly the supports of the structures without taking into account the interaction between structural response and excitation (i.e., component-structure-foundation-soil interaction), in particular the vertical PFA demand might be overestimated. However, this issue is out of the scope of this investigation and is the subject of ongoing research. More specifically, the impact of the number of stories, different beam stiffness, story-wise mass distribution along the beams and damping ratios on vertical PFA demands is examined. The aim of this evaluation is to quantify the normalized vertical peak floor acceleration demand at each floor level to (1) assess the influence of variations in the aforementioned parameters, as well as (2) how the normalized vertical PFA demand compares to the normalized horizontal PFA demand.

The paper is organized as follows. Firstly, the characteristics of the utilized ground motion record sets are briefly presented. Then, the structural and modal properties of the frame models are discussed. The results of response history analyses are presented in terms of the statistics of the peak floor acceleration demands normalized by the corresponding peak ground acceleration component. A detailed discussion of the effect of the conducted parameter variations on the normalized floor acceleration demands is provided. The differences between the vertical and horizontal responses are also evaluated.

2 Ground motion record sets

In the present study, the assessment of the seismic acceleration response is based on two sets of recorded ground motions to account for record-to-record variability of ground motion sets generated under different assumptions. Both the vertical and the two corresponding horizontal components of these ground motion sets are used as input excitation for response history analyses. Because two-dimensional structural models are used, for each analysis a single horizontal component and the vertical component of ground motion are applied simultaneously.

2.1 Vertical ground motion record set

The first considered ground motion record set is denoted as the vertical ground motion (VGM) record set in this study. It was assembled by Moschen et al. (2016) focusing on the characteristics of vertical ground motion components. The median of the vertical components matches in the frequency range of 3.33–40.0 Hz the normalized vertical response spectrum (NEHRP-spectrum; FEMA P-1050-1 2015), and its dispersion complies with a predefined target dispersion of σ_t = 0.80. In the multi-objective optimization procedure (Moschen et al. 2017) applied for selecting these records, the following constraints were considered:

• Moment magnitude M_W ≥ 5.5

• Site classification D according to NEHRP (stiff soil, shear wave velocity: 180 m/s ≤ v_s30 ≤ 360 m/s)

• Joyner and Boore distance (Joyner and Boore 1981) less than 30 km

• Fault mechanism: strike-slip, reverse, reverse-oblique

• Same scale factor for all ground motions.

This algorithm yielded 91 vertical ground motion records from the PEER-NGA database (PEER 2010) and a scale factor of α = 2.10. Since the time histories of ground motion EQR 189 are no longer available in the database, response history analyses are conducted with the remaining 90 ground motion records. Figure 1 displays the corresponding response spectra of both the horizontal and vertical ground motion components, where thin gray lines represent the response spectrum of a single record, and bold blue lines refer to the statistical measures (median, 16th percentile, 84th percentile).

Fig. 1

Response spectra of the utilized vertical ground motion (VGM) record set

2.2 Horizontal ground motion record set

Mathiasson (2013) selected from the PEER-NGA database (PEER 2010) a record set consisting of both horizontal components of 112 ground motion sites, based on the following constraints:

• Moment magnitude in the range 6.5 ≤ M_W ≤ 8.0

• Site classification D according to NEHRP (shear wave velocity: 180 m/s ≤ v_s30 ≤ 360 m/s)

• Closest distance to the fault rupture area less than 30 km.

For the present study, this set is complemented by the vertical ground motion components. However, since the time histories of records EQR 189, EQR 829 and EQR 1481 are no longer available in the database, and the vertical components of records EQR 719, EQR 720, EQR 722 to EQR 728 and EQR 1048 are missing, the ground motion records for the remaining 99 sites are condensed to the so-called horizontal ground motion (HGM) record set utilized in the present study. Figure 2 displays the corresponding response spectra of both horizontal and vertical component. Again, the response spectra of the single records are shown by thin gray lines, and the bold blue lines represent median (solid line), 16th and 84th percentile (dashed lines) of the individual spectra.

Fig. 2

Response spectra of the utilized horizontal ground motion (HGM) record set

3 Frame models

The analyses are conducted on frame structures that are based on the FEMA P-695 archetypes (FEMA P-695 2009). In particular, the acceleration response of 1-, 2-, 4-, 8-, 12-, and 20-story frames with three bays is studied. The structural properties of the base case structures are adopted from the steel-moment resisting frames proposed as part of NIST GCR 10-917-8 (2010) and designed in accordance with AISC 358-05 (2005), AISC 341-05 (2005) and ASCE/SEI 7-05 (2006). The design of the shorter frame models (1-, 2- and 4-story frames) is based on the equivalent lateral force (ELF) approach, and the taller frames (8-, 12-, and 20-story frames) on response spectrum analysis (RSA). All frame models are designed for the maximum spectral acceleration D_max (NIST GCR 10-917-8 2010).

In this study, some simplifications are made, such as the application of a centerline model, consideration of the structural framing only (i.e., the effect of the slab on the beam is accounted for approximately by varying the beam stiffness), and the assumption of linear-elastic material behavior in the structure. Further, panel zones and reduced beam sections are not considered. The software OpenSees (McKenna et al. 2014) is used to create the frame structures. In all frame models, the height of the first story is h₁ = 4.57 m, whereas all other stories have a height of h = 3.96 m. Each bay has a width of b = 6.10 m. In each story of every frame the dead load is 4.31 kN/m², the cladding load 1.20 kN/m², and the floor live load is 2.40 kN/m², except for the roof in which the roof live load is 0.96 kN/m². The structural mass of the models includes 105% of the design dead loads and 25% of the live loads. The tributary area for direct load transfer to the frame structure is 28.6% of the tributary area for the total story mass (see Fig. 3a). That is, 28.6% of the total story mass is distributed directly to the nodes of the frame structure in terms of lumped masses (blue area), and the remaining 71.4% of the total mass (green area) is lumped to leaning columns on both sides of the frames at a given level to achieve symmetric frame structures. For the base case of the investigated frame models, the seismic active mass is distributed along the beams and the beam-column connections, as depicted in Fig. 3b, since both the vertical and horizontal acceleration response of columns and beams is studied. To each node with a lumped mass, the seismic active mass is assigned to two translational degrees of freedom, i.e., in the horizontal and in the vertical direction. No degree of freedom is slaved. The lumped masses at the exterior beam-column nodes are larger than the ones at nodes along the beams because at exterior beam-column nodes the tributary area is larger and the mass of the cladding is also included. All beam nodes have the same tributary area, and thus, the corresponding lumped masses have story-wise the same value. The beam and column elements are defined as elastic Bernoulli–Euler beam elements. The cross section and the moment of inertia are taken from NIST GCR 10-917-8 (2010) and the Young’s modulus of steel, i.e., E = 2 × 10¹¹ N/m² is used. Linear elastic material behavior is also assigned to the rotational spring elements at the base.

Fig. 3

a Horizontal section of the underlying frame building (modified from NIST GCR 10-917-8 2010). b Half of the 8-story 3-bay base case frame model with leaning columns

For all frame models, viscous damping is considered through Rayleigh damping. In the base case frames, a damping ratio of ζ = 0.05 is assigned to the fundamental mode and to the mode in which a 95% cumulative seismic active vertical mass participation is obtained. The appropriate damping ratio in the vertical direction is an open issue but 5% is deemed to be reasonable as a base case value in the absence of additional information.

Different parameters of the previously defined base case frame models are varied separately to examine their effect on the acceleration response. In a first study, the lateral stiffness of the beams is increased by 125% and 150%, respectively, to approximately account for the contribution of the slab to the overall beam stiffness. In a subsequent study, the distribution of the lumped masses within each story is modified to study the sensitivity of the responses to modeling assumptions associated with the distribution of story masses. In particular, modified models in which the seismic active story mass is distributed equally along the beams and the beam-column connections are used, maintaining the value of the total story mass of the corresponding base case frame. As a result, the lumped masses at the exterior column lines of the modified frames exhibit approximately 30% of the masses of the base case, whereas the mass of the remaining nodes is increased by approximately 160%. Eventually, in a final study, the same Rayleigh damping approach is used but with a first-mode damping ratio and a damping ratio of the mode with a 95% cumulative seismic active vertical mass participation varying in a range from ζ = 0.01 to ζ = 0.08 to account for the variability associated with this parameter.

In Table 1, the fundamental periods both for the horizontal and vertical direction (T_1H and T_1V, respectively) and the period of the mode with a 95% cumulative seismic active vertical mass participation (T_95%V) of the original frame setups listed in NIST GCR 10-917-8 (2010) (referred to as “FEMA”) and of the considered simplified frame models are summarized. The models with 25% (50%) increased beam stiffness compared to the base case frames are referred to as “stiffness 125%” (“stiffness 150%”). “Mass modification” indicates the modified frames with story-wise equally distributed lumped masses. Since in NIST GCR 10-917-8 (2010) only the horizontal periods are provided, there are no entries for the vertical periods of the original frames. It should be noted that the regular layout of the frames implies that horizontal and vertical degrees of freedom are decoupled, and thus, horizontal and vertical structural periods can be specified independently.

Table 1 Fundamental periods (T_1H and T_1V) and the period of the mode with a 95% cumulative seismic active vertical mass participation (T_95%V) of the FEMA P-695 frame models, the corresponding base case models, and their modified counterparts

The relatively stiff single-story base case frame exhibits a fundamental horizontal period of 0.51 s, and the 20-story frame a period of 4.47 s. While for the single- and 2-story structures the adopted modeling strategy (i.e., the base case) underestimates the fundamental horizontal periods with respect to the FEMA values, for the taller structures these periods are overestimated. The fundamental horizontal period of the tallest base case frame model matches exactly the one of the original frame setup. The fundamental horizontal periods of the models with increased beam stiffness are slightly smaller compared to the corresponding base case. The distribution of the horizontal seismic active story mass has no apparent influence on the fundamental horizontal period, thus confirming the common assumption that assigning one horizontal degree of freedom at each floor level of a frame model is in most cases sufficient to estimate this period.

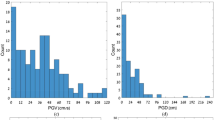
According to Wieser et al. (2012), floor slab systems of steel frame structures exhibit fundamental vertical periods in the range of 0.33 s (3 Hz) to 0.07 s (13.5 Hz). Figure 4 shows the vertical fundamental frequency of mechanical and electrical components that underwent shake-table seismic qualification testing in the U.S. These component frequencies do not take into account the potential contribution of the floor-system flexibility to component frequencies given that components were attached to a rigid shake table. For NSCs that are connected rigidly to the floor (Fig. 4a), their fundamental frequency range is much larger than for NSCs that are mounted to the floor with spring isolators (Fig. 4b). The latter frequencies are also within the frequency range specified in Wieser et al. (2012). Comparing this expected range of vertical periods with the fundamental vertical periods of the considered frame models, it is apparent that only the period of the single-story base case model and its stiffened modifications, which have a lower period, is not within this range. The Wieser et al. (2012) values are provided herein just as reference given that in this study the floor slabs are not explicitly part of the model. In contrast to the effect on the horizontal periods, the fundamental vertical period of the single- and 2-story frame with equally distributed story masses is longer than the period of the base case. The fundamental vertical periods of the taller frame structures remain virtually unaffected by the applied parameter modifications.

Fig. 4

Vertical natural frequency distribution of a unit under test (UUT). a Rigidly mounted to the floor, b with spring isolators mounted to the floor (modified from NIST GCR 17-917-44 2017)

The periods of the modes in which a 95% cumulative seismic active vertical mass participation is obtained are similar for the base case and for the models with increased beam stiffness, except for the single-story frame. For this frame, T_95%V of the model with 50% increased stiffness is 1.7 times larger than that of the corresponding base case frame. In contrast, T_95%V of the models with story-wise equally distributed lumped masses is much smaller than that of the base case.

In Fig. 5 the fundamental mode shape and the first vertical mode shape of the single-story base case and the 8-story base case frame model are shown. The fundamental mode shape, depicted in the first column, is dominated by horizontal displacements and vertical deflections are negligible. For the first vertical mode shape, represented in the second column, vertical/transverse beam displacements control the dynamic response. The first vertical mode shape of the single-story frame has the largest deflections at the center of the beams, while the displacements of the nodes of the column lines are virtually nonexistent. In contrast, the maximum vertical displacement of the first vertical mode shape of the 8-story frame occurs at the exterior column lines.

Fig. 5

Mode shapes of the single-story base case frame model (first row) and the 8-story base case frame model (second row)

4 Results and discussion

Response history analyses are performed to estimate the vertical and horizontal peak floor acceleration demands (referred to as PFA_v and PFA_h, respectively) of the considered frame models. The analyses are conducted in OpenSees (McKenna et al. 2014) by imposing simultaneously the horizontal and vertical ground motion components of the considered HGM and VGM record sets, respectively. For each combination of building model and vertical component of ground motion, two runs are performed using two different ground motion pairs. First, the vertical component of ground motion is combined with the first horizontal component; and then, the vertical component of ground motion is combined with the second horizontal component. Since the statistical response quantities of the two different horizontal components differ slightly only, just the outcomes of the first ground motion pair, i.e., the combination of the first horizontal component and the vertical component of ground motions, is subsequently presented. For each combination, the ratio of PFA_h to the corresponding peak ground acceleration component PGA_h (PFA_v/PGA_v) is calculated separately and subsequently the statistical measures (median, 16th percentile, 84th percentile) of all individual ratios are assessed. The outcome of the response history analyses has been evaluated at all nodes, but only the results of the left half of the symmetric frame structures are shown and discussed. In particular, the normalized PFA demands of the left column line, the central beam nodes of the left bay, the left interior column line, and the central beam nodes of the second bay are displayed in these figures. The horizontal axes show the PFA_h (PFA_v) normalized with respect to the corresponding peak ground acceleration component, PGA_h (PGA_v), while the ordinate represents the height of the examined structure normalized with respect to its total height. The normalized horizontal peak accelerations are presented up to a value of 3.0 or 2.5, while the maximum displayed normalized vertical PFA demand is 10.0.

4.1 Normalized peak floor acceleration demand of the 8-story base case frame model

Initially, the normalized peak floor acceleration demand of the 8-story base case frame model subjected to the ground motions of the VGM record set is discussed in detail, in an effort to reveal some characteristics of the seismic response behavior of the considered frame set. At first, the well-researched horizontal component of the peak acceleration response is presented, which serves as reference for the subsequent discussion on the vertical acceleration response. Figure 6 shows the normalized horizontal peak floor acceleration demand, and Fig. 7 the corresponding normalized vertical response component of selected nodes of the considered frame model. Thin gray lines refer to the response to the individual records, whereas the bold blue lines represent the statistical response measures (median, 16th percentile, 84th percentile). In this and all subsequent figures, the statistical measures are computed from the ratios of the individual responses. When assessing solely the horizontal response of regular frame structures, a single horizontal degree of freedom is commonly assigned in horizontal direction when it is reasonable to assume that the diaphragm is infinitely rigid in plane. The median profiles of the ratio PFA_h/PGA_h (Fig. 6) show that they are floor-wise almost equal for each examined node, thus confirming this assumption. The maximum median response amplification of 1.7 occurs at the roof level. The studies of Miranda and Taghavi (2009) and López-Garcia et al. (2008) obtained similar shapes and values of the normalized median horizontal PFA_h as the ones shown in Fig. 6 for elastic frame structures with similar heights and periods.

Fig. 6

Ratio of horizontal peak floor acceleration demand to horizontal peak ground acceleration of the 8-story base case frame structure. a Left exterior column line, b central beam nodes of the left bay, c left interior column line, and d central beam nodes of the second bay

Fig. 7

Ratio of vertical peak floor acceleration demand to vertical peak ground acceleration of the 8-story base case frame structure. a Left exterior column line, b central beam nodes of the left bay, c left interior column line, and d central beam nodes of the second bay

The vertical PFA component (PFA_v) shows a significantly different behavior than the horizontal PFA component (PFA_h). As observed in Fig. 7, the vertical response ratio PFA_v/PGA_v varies within a floor level, depending on the location of the considered node. At the exterior column line and the central beam node of the second bay the vertical accelerations are larger than in the remaining structure, with its peak median value of 4.4 at roof level. In general, the PFA_v demand of the interior column line is the smallest, with the maximum median amplification response equal to 2.8 at the roof level, which is, however, still significantly larger than the corresponding maximum horizontal amplification value of 1.7 (see Fig. 6). In contrast to the horizontal component, the location of the beam node has a significant influence on the vertical acceleration amplification, thus, more than one degree of freedom per story is needed to assess the vertical accelerations of steel frames.

Since the seismic peak response can be approximated by a log-normal distribution, the record-to-record variability of the normalized horizontal (vertical) peak floor acceleration, PFA_h/PGA_h (PFA_v/PGA_v), is subsequently quantified through the unbiased estimator of dispersion $\beta_{h}$ ($\beta_{v}$) (Shome and Cornell 1999),

$$\beta_{h} = \sqrt {\mathop \sum \limits_{i = 1}^{r} \frac{{\left( {\ln \left( {PFA_{h,i} /PGA_{h,i} } \right) - \mu_{lnPFA/PGA h} } \right)^{2} }}{r - 1}} ,\quad \beta_{v} = \sqrt {\mathop \sum \limits_{i = 1}^{r} \frac{{\left( {\ln \left( {PFA_{v,i} /PGA_{v,i} } \right) - \mu_{lnPFA/PGA v} } \right)^{2} }}{r - 1}}$$

(1)

where r is the number of ground motion records, and ln(PFA_h,i) (ln(PFA_v,i)) denotes the natural logarithm of the horizontal (vertical) peak floor acceleration demand due to the ith record. The variable $\mu_{lnPFA h}$ ($\mu_{lnPFA v}$) represents the mean of ln(PFA_h,i) (ln(PFA_v,i)), i = 1,…,r.

Figure 8a illustrates the dispersion parameter β both for the normalized horizontal (red lines) and vertical (blue line) PFA demands. Additionally, Fig. 8b shows the ratio of $\beta_{h}$ to $\beta_{v}$. In both subfigures, solid lines refer to the dispersion of the nodes at left exterior column line, dashed lines to the central beam nodes of the left bay, dotted lines to nodes at the left interior column line, and dash dotted lines to the central beam nodes of the second bay. As can be seen, the dispersion of normalized horizontal PFA demands is almost the same for all nodes in a particular floor. The maximum of $\beta_{h}$ = 0.50 is attained at a roof node corresponding to the central beam node of the second bay. The estimated dispersion range $0.27 \le \beta_{h} \le 0.50$ is consistent with the fluctuation margin due to record-to-record variability commonly observed in seismic response. It should be noted here that dispersion parameter β of the unscaled PGA_h of the VGM record set is 0.71 for the first horizontal and 0.67 for the second horizontal component. In contrast, $\beta_{v}$ varies up to 40% in all the nodes of a floor. This variation is much more pronounced than in the horizontal direction. As a general tendency, the dispersion parameter $\beta_{h}$ is larger than $\beta_{v}$ at all considered nodes, up to factor of 2.34 as seen in Fig. 8b. In contrast, the dispersion of the vertical PGA (PGA_v) is 0.82, which is larger than the PGA_h dispersion of both horizontal record components.

Fig. 8

a Dispersion of the normalized peak floor acceleration demand, b ratio of the normalized horizontal peak floor acceleration to the normalized vertical peak floors acceleration of the 8-story base case frame structure

4.2 Normalized peak floor acceleration demand of the base case frame models

Subsequently, the studies are expanded to all base case frames, capturing the response of a series of structures from one to 20 stories, also subjected to the VGM record set. The median ratio of the PFA components to PGA of the considered frame structures is shown in Fig. 9. The black lines represent the outcomes of the shorter frame structures designed according to the ELF approach, whereas the blue lines refer to the response of the taller frame structures designed based on the RSA method. Since the median profiles of the horizontal component are floor-wise almost identical for each node, the response of all nodes is illustrated only in subfigure Fig. 9a. The horizontal floor acceleration component of the 2-story frame increases almost linearly with respect to height, indicating that it is dominated by the fundamental mode shape, as shown in the plots by dotted black lines. For this structure, the median PGA_h is amplified 2.1 times at the top floor, which is the maximum value of all considered structures. The median profiles of taller frames exhibit a slight S-shape, indicating the influence of higher modes, which is also reported in a study of Chaudhuri and Hutchinson (2004). The influence of the higher modes increases with the number of stories. In general, the median PFA_h/PGA_h ratio of the taller structures is smaller than those of the 2-story frame.

Fig. 9

a Horizontal and b–e vertical component of the median normalized peak floor acceleration of the base case frame structures. a Horizontal component of all nodes, vertical component of b left exterior column line, c central beam nodes of the left bay, d left interior column line, and e central beam nodes of the second bay

The vertical peak acceleration demand at the roof of the single-story frame is virtually not amplified, i.e., median PFA_v/PGA_v ratio is close to 1, due to the relatively high axial rigidity of the columns and flexural rigidity of the beams of the single-story structure model. This quasi-rigid response behavior can also be observed at the interior column line of the 2-story structure. However, when the mass of the single-story frame is significantly increased, the periods increase and subsequently the median PFA_v/PGA_v ratio of this frame becomes slightly larger than one, as it has been shown in an additional computation to verify this outcome. In this latter case, the vertical period shifts to the frequency region in which the vertical ground motions possess a higher energy content. In contrast, in the taller frame models the largest vertical response amplification occurs at the nodes of the exterior column line and the central node of the second bay, as it has been previously described for the 8-story structure (see Fig. 7). Furthermore, it is apparent that the taller frame structures exhibit the largest median PFA_v to PGA_v ratio with its maximum value of 4.8 at the roof level of the center node of the left bay of the 20-story frame structure. This large amplification is in accordance with results of Moschen et al. (2016) and Francis et al. (2017). Moschen et al. (2016) computed the vertical accelerations of a generic stick model, representing the interior column line of a steel frame, in an effort to assess the vertical accelerations at or very close to column lines. PGA_v amplifications up to four times were observed, as in the present study. Since the location of the node on the beam has a large influence on the vertical acceleration response, the simple stick model of Moschen et al. (2016) is only useful to predict the PFA_v at column lines, but it does not capture the acceleration demand of a steel frame in general, especially in regions between column lines where the majority of NSCs are located. In contrast to the horizontal component, in general, the normalized vertical PFA increases with the total height of the structure.

The ratio of the median horizontal to the median vertical PFA demand, PFA_h/PFA_v, is evaluated next. At the ground, this ratio is analogous to the median horizontal to median vertical PGA ratio, which is about 1.4 for the VGM record set. According to Fig. 10, for the taller structures (four stories and more), the median vertical acceleration demand becomes much larger than the horizontal demand as the relative height increases, indicated by a PFA_h/PFA_v ratio smaller than one. In these structures, the PFA_h/PFA_v ratio decreases with the relative height until a minimum is attained close to the roof. This behavior is due to the sharp increase of the horizontal acceleration demand at the roof due to higher-mode effects, as it is observed in Fig. 6. The smallest ratio of 0.25 (i.e., the vertical PFA demand is four times larger than the corresponding horizontal one) appears in the center node of the left bay in the next-to-last floor. In contrast, for all nodes of the single-story frame and for the nodes at the column lines of the 2-story frame, the PFA_h/PFA_v ratio is larger than 1.0 because at these nodes virtually no vertical acceleration amplification has been observed, as discussed previously.

Fig. 10

Median ratio of horizontal to vertical peak floor acceleration demand of the base case frame structures. a Left exterior column line, b central beam nodes of the left bay, c left interior column line, and d central beam nodes of the second bay

4.3 Effect of modified transverse beam stiffness

In Fig. 11 both the median normalized horizontal and vertical peak floor acceleration demand for selected frames with transverse beam stiffness increased by 25% (dashed lines) and 50% (dotted lines), respectively, are presented in contrast to the results of the corresponding base case models (solid lines). Blue lines refer to the response of the single-story, black lines of the 8-story, and red lines of the 20-story frame structures. Inspection of Fig. 11a reveals that the horizontal components are only slightly affected by the increase in beam stiffness. The largest difference of 10% is observed at the roof nodes of the 20-story structure. The graphs of Fig. 11b–e indicate a more pronounced impact of the modified transverse beam stiffness on the vertical response. However, the median vertical peak floor acceleration ratio of the frames with 25% and 50% increased beam stiffness is virtually the same, as dashed and dotted lines lie almost on top of each other. The largest deviation in the vertical direction from the base case is observed for the 20-story structure, where the median of PFA_v/PGA_v of the center beam node in the second bay is 18.4% larger. These observations show that for the models and ground motions evaluated herein, the stiffening effect provided by the presence of the floor slab on the beam flexural stiffness does not contribute significantly to the estimation of peak floor acceleration demands. This result is relevant given that this contribution is commonly disregarded in models used for numerical seismic response prediction. It should be noted that the frame models used in this study do not account for three-dimensional effects such as in-plane or out-of-plane flexibility of the diaphragm.

Fig. 11

a Horizontal and b–e vertical component of the median normalized peak floor acceleration of the 1-, 8-, and 20- story frame structure with different stiffness of beams. a Horizontal component of all nodes, vertical component of b left exterior column line, c central beam nodes of the left bay, d left interior column line, and e central beam nodes of the second bay

4.4 Effect of modified mass distribution

Modified structures with a different distribution of the seismic active story masses are considered. In the base case frames the lumped masses at nodes of the exterior column lines are larger than at the interior nodes, whereas the corresponding modified structure has equally distributed lumped masses over all nodes, keeping the total story mass the same as in the base case.

Figure 12 sets the median of the normalized horizontal (a) and the vertical (b) peak acceleration demand of the 8-story base case (solid lines) and the corresponding mass-modified frame (dashed lines) in contrast. The results for the nodes at the left exterior column are shown in black, for the central beam nodes of the left bay in blue, for the left interior column line in red, and for the central beam nodes of the second bay in green. An increase of the horizontal response components of about 18.8% is observed, when equally distributing the story mass. This response behavior can be attributed to higher-mode effects due to the longitudinal beam flexibility, although commonly it is assumed that the translational mass distribution within a story does not considerably affect the horizontal seismic response. As shown here, this assumption does not hold true for the horizontal PFA demand of these simplified models that do not have floor slabs as explicit part of the model, which would provide additional constraint between column lines parallel to the longitudinal axis of the beams.

Fig. 12

a Horizontal and b vertical component of the median normalized peak floor acceleration of the 8-story frame structure with different mass distribution

The vertical response amplification components are much more affected by the mass distribution modification. As observed, the median normalized peak floor acceleration demand of nodes with larger mass than the base case (i.e., beam nodes and nodes of the interior column line) increases significantly up to 226% (central roof beam node of the second bay), i.e., the median of PFA_v/ PGA_v is about 10.0 compared to 4.44 of the 8-story base case frame. The observed median amplification of 10.0 represents the maximum for all structures investigated in this study. In contrast, the vertical response of the nodes located at the exterior column line, where the lumped mass is about 70% less than in the base case frame, is reduced. For instance, at the roof node of the exterior column line the median vertical amplification ratio decreases from 4.43 to 3.78, i.e., 14.7%.

An assessment of these results reveal that all structures except the 20-story frame exhibit this response behavior. Thus, subsequently, the response of the 20-story base case frame and its mass modified counterpart, shown in Fig. 13, is discussed in more detail. According to Fig. 13a, the horizontal median peak acceleration ratio of the mass-modified frame is for all nodes significantly larger than one, i.e., PFA_h is amplified with respect to the PGA_h. In contrast, in the base case this response quantity is only significantly amplified at the roof, whereas in the remaining floors, the median ratio PFA_h/PGA_h is close to one or even less than one (which corresponds to a reduction of the horizontal median peak floor acceleration). The general vertical response amplification behavior of the 20-story structure with equal mass distribution is significantly different compared to the shorter frames. That is, the median of the ratio PFA_v/PGA_v is larger for all nodes of the modified structure, even for the nodes of the exterior column, with lower lumped masses than in the base case. The median normalized vertical peak floor acceleration of the roof node at this column is 5.12 compared to 4.42 of the base case. As in the 8-story frame, the largest vertical response increase occurs at the central roof beam node of the second bay, with the median of PFA_v/PGA_v = 9.76, which is 2.12 times larger than the dynamic amplification of the base case.

Fig. 13

a Horizontal and b vertical component of the median normalized peak floor acceleration of the 20-story frame structure with different mass distribution

4.5 Effect of modified damping ratio

In this study, additionally to the 5% Rayleigh damped base case frames, the effect of n = 1, 2, 3, and 8% damping on the median of the horizontal and vertical PFA ratios is quantified. The median horizontal (vertical) peak floor accelerations of the 5% base case frames denoted as PFA ^ζ=0.05 _h (PFA ^ζ=0.05 _v ) serve as reference solution, and thus, in the subsequent figures PFA ^{ζ= n} _h (PFA ^{ζ= n} _v ) of the n%-damped structures is normalized with respect to PFA ^ζ=0.05 _h (PFA ^ζ=0.05 _v ).

Figure 14 shows the median peak floor acceleration ratios of the 8-story frame structures, with solid lines representing the response of nodes at the exterior column line, dashed lines of the central beam nodes at the left bay, dotted lines of the nodes at the interior column line, and dash dotted lines of the central beam node at the second bay. Red lines refer to 1% damping, green lines to 2% damping, black lines to 3% damping, and blue lines to 8% damping. As expected, modification of the damping ratio does not change the general horizontal response behavior but only the response amplitude. That is, the median ratio PFA ^{ζ= n} _h / PFA ^ζ=0.05 _h is nearly constant over the structural height. Increased damping reduces the response, whereas smaller damping yields larger peak floor acceleration. The floor-wise scatter of the horizontal acceleration component is small for all damping ratios, see Fig. 14a. To quantify the damping effect, the horizontal response of the roof nodes is considered: PFA ^ζ=0.08 _h is 14.7% less than PFA ^ζ=0.05 _h , PFA ^ζ=0.03 _h is 15.9% larger, PFA ^ζ=0.02 _h is 29.8% larger, and PFA ^ζ=0.01 _h is 50.7% larger than PFA ^ζ=0.05 _h .

Fig. 14

a Horizontal and b vertical component of the median of the ratio PFA (n% damping) to PFA (5% damping) of the 8-story frame structure with different damping ratio

Interestingly, damping affects the vertical response component of the various nodes quite differently, as indicated by the scatter of the median ratio PFA ^{ζ= n} _v / PFA ^ζ=0.05 _v at each floor of a single structure, see Fig. 14b. The vertical component is influenced more by the damping variation than the horizontal component. Also, the top half of the structures is affected differently than the bottom half. It is observed that the reduction of the normalized vertical PFA due to modified damping at the second-floor nodes is less pronounced than at the nodes of the higher floors. Considering, for instance, the central roof node at the second bay, 8% damping leads to 21.2% reduction of vertical median peak acceleration demand compared to the base case, whereas 1% damping increases this demand by 86.5%, 2% damping by 45.3%, and 3% damping by 25.0%. That is, at this particular node, the normalized vertical PFA due to variations in damping is larger than the normalized horizontal PFA.

The effect of damping on the horizontal and vertical median PFA demand of the 1-, 2-, 4-, 12-, and 20-story structures is similar to that of the 8-story frame, as seen in Fig. 15. For instance, the median of the PFA ^{ζ= n} _h /PFA ^ζ=0.05 _h (PFA ^{ζ= n} _v /PFA ^ζ=0.05 _v ) ratios are shown for the central node at the second bay of the 8-story frame (solid lines), the 1-story (dotted lines) and the 20-story frame (dashed lines). Globally, for the same damping ratio, both the median normalized horizontal and vertical peak floor acceleration demand are of similar magnitude. The difference in the median of PFA ^{ζ= n} _v /PFA ^ζ=0.05 _v of the 8-story and the 20-story frame is a result of higher-mode effects, which are more pronounced in the taller structures.

Fig. 15

a Horizontal and b vertical component of the median of the ratio PFA (n% damping) to PFA (5% damping) of the central node at the second bay of the 1-, 8-, and 20- story frame structure

4.6 Effect of different record sets

The effect of different ground motion sets on the median of the estimated normalized acceleration response is studied, utilizing the previously described VGM and HGM record sets. Figure 16 shows the median PFA_h/PGA_h and PFA_v/PGA_v ratios, respectively, of the 1-(blue lines), 8-(black lines), and 20-story (red lines) base case models. The median normalized horizontal floor response of all nodes is depicted in one diagram (Fig. 16a), considering that the horizontal nodal acceleration is virtually the same for all nodes within a story. Subfigures Fig. 16b–e illustrate the corresponding median normalized vertical acceleration demand of the considered nodes. Solid lines refer to the outcomes of the models subjected to the VGM record set, whereas dashed lines show the results for the HGM record set. Although the underlying selection approach and response spectra of both record sets are different (see Figs. 1 and 2), inspection of Fig. 16 reveals that the shape of the median response is the same for both record sets, and only the response magnitude shows some minor differences. The maximum difference of 16% is observed for the median of PFA_v/PGA_v of the roof node at the exterior column line of the 20-story base case model. It can be, thus, concluded that all previously discussed results based on the VGM record set represent qualitatively (and with some minor limitations also quantitatively) the response behavior of the considered frame models.

Fig. 16

a Horizontal and b–e vertical component of the median normalized peak floor acceleration of the 1-, 8-, and 20- story base case frame structure subjected to different record sets. a Horizontal component of all nodes, vertical component of b left exterior column line, c central beam nodes of the left bay, d left interior column line, and e central beam nodes of the second bay

The dispersion parameter $\beta$ according to Eq. 1 for the normalized horizontal ($\beta_{h}$, red lines) and vertical ($\beta_{v}$, blue lines) PFA demand of the 8-story frame structure subjected to the HGM record set is illustrated in Fig. 17a, the ratio of $\beta_{h}$ to $\beta_{v}$ is shown in in Fig. 17b. Solid lines represent the dispersion parameter of the nodes at the left exterior column line, dashed lines of the central beam node of the left bay, dotted lines of nodes at the left interior column line and the dash dotted lines of the central node of the second bay. The dispersion of the normalized horizontal PFA demand is for all nodes in a particular floor almost identical, as it is observed for the VGM set (Fig. 8a). Between the first and the eighth story, $\beta_{h}$ varies in the range $0.25 \le \beta_{h} \le 0.42$, which is slightly narrower and also smaller than the corresponding range for the VGM set. Note that dispersion parameter $\beta$ of the first component of PGA_h of the HGM record set is 0.66 while it is 0.62 for the second component, i.e., less than the PGA_h$\beta$-values of the VGM record set (0.71 and 0.67, respectively). Dispersion parameter $\beta_{v}$ of the nodal vertical peak acceleration responses varies within each floor within approximately 40%, a value also observed for the VGM record set. For comparison, $\beta$ of PGA_v of the HGM record set is 0.76 compared to 0.82 of the VGM record set. In general, $\beta_{h}$ is larger than $\beta_{v}$ by a factor up to 1.93 except for the node of the exterior column line in the 5th and 6th story, where $\beta_{v}$ exceeds $\beta_{h}$ by about 2%. In summary, also the normalized response dispersion is consistent for both ground motion record sets.

Fig. 17

a Dispersion of the normalized peak floor acceleration demand, b and ratio of the normalized horizontal peak floor acceleration to the normalized vertical peak floors acceleration of the 8-story base case frame structure subjected to the HGM record set

5 Conclusions

Recent studies have indicated that in elastic mid- and high-rise steel moment resisting structures the filtering effect of the building can significantly amplify the vertical peak ground acceleration (PGA_v) along the height. This conclusion is in contrast to the common assumption that the vertical peak floor acceleration (PFA_v) demand is constant along the height of a structure. In many cases, the presence of a substantial PGA_v amplification along the height raises another issue: its value with respect to the horizontal peak ground acceleration (PGA_h) amplification (or reduction) along the height, which has received considerable attention and it has been the subject of many research studies during the past couple of decades. Thus, in this paper the horizontal peak floor acceleration (PFA_h) and PFA_v demands normalized with respect to the corresponding peak ground acceleration (PGA) of elastic, two-dimensional multi-story steel frame structures, and several variations of these models, subjected to two sets of ground motion records have been quantified. The studied multi-story structural models have been designed based on the FEMA P-695 archetypes, and the absolute floor acceleration demands have been assessed statistically at column lines and at various locations along the length of the girders. Results show that the normalized PFA_v demand depends on the height of the structure, as well as, for a given floor level (i.e., height above base), the location of the nonstructural component along the length of a girder, and the distribution of building vertical translational masses along a given floor. Another important consideration is the appropriate choice of the upper mode to which the second modal damping ratio is assigned when Rayleigh damping is used in a numerical model. In this respect, the choice of the fundamental mode and the vertical mode at which the seismic active mass exceeds 95% for the first time seems to be sufficient to reliably quantify the PFA_v demand, as proven in additional calculations conducted by the authors.

In this study, the median horizontal peak acceleration demand is assessed to emphasize its difference with respect to the vertical peak acceleration demand. The PFA_h is up to two times larger than the PGA_h, which is in accordance with results from previous numerical studies. The median vertical peak acceleration demand normalized by the corresponding vertical PGA tends to increase with the height of the structure, with a maximum between two and five, depending on the number of stories and the period of the considered frame. The maximum median PFA_v amplification of 4.8 occurs at the roof of the 20-story frame model, which is the tallest examined structure. The location of the considered node has a significant influence on the vertical acceleration demand. The largest amplification in a floor occurs at the center of the beams, while the smallest amplification is at the interior column lines. If the seismic active story mass is distributed equally to the nodes at a given floor level, the vertical amplification increases up to 9.76 at the center of the girder. In contrast, increasing the transverse stiffness of the beams up to 50% (i.e., to approximately account for the stiffening effect of a floor slab on the flexural beam stiffness) does not significantly affect the horizontal and vertical PFA demand estimates. This result indicates that, for this purpose, the influence of the stiffness of floor slabs on the transverse beam stiffness can be disregarded, as it is commonly done in engineering practice. Response history analyses have been conducted using the vertical and horizontal ground motion components of two different record sets as input excitation, yielding two similar statistical measures of the normalized horizontal and vertical PFA demand (i.e., central values and dispersion). It is, thus, reasonable to assume that the global response behavior of the considered structural systems can be extrapolated to systems exposed to seismic excitations with similar general characteristics. The results of a parametric study varying modal damping ratios from the standard 5% show that the magnitude of both the normalized horizontal and the normalized vertical acceleration demands are affected in a similar manner by damping, i.e., the larger the damping ratio the smaller the normalized response.

Current seismic design criteria applied to typical buildings do not consider the amplification of vertical floor acceleration demands with respect to the vertical peak ground acceleration (and its variation along the height and along the length of girders). Therefore, it is reasonable to conclude that cases exist in which these demands might be underestimated in the design of buildings. Moreover, the results from the evaluation conducted in this paper highlight the importance of modeling assumptions associated with the distribution of seismic active masses at floor levels, and to a lesser extent, the value of inherent structure viscous damping on the estimation of peak vertical floor acceleration demands. It should be noted that various decisions and assumptions have been made to assess the acceleration demands in this study and conclusions should be interpreted within this context. For instance, the peak response has been presented in terms of PFA with respect to the corresponding PGA component without explicitly evaluating absolute demands, which are the ones that would be ultimately and directly related to the magnitude of nonstructural component seismic design forces. Important issues to be further investigated include the appropriate value of inherent structure viscous damping ratio in the vertical direction, component-structure-foundation-soil interaction, nonlinear behavior and three-dimensional effects.