1 Introduction

Seismic fragility is commonly used to measure seismic performance of structures, and estimates the probability of entering specified damage states for given levels of ground shaking (Hazus 2003). Traditionally, seismic fragility is used in performance seismic design as functions of scalar seismic intensity measures. Graphical representations of seismic fragilities expressed as functions of scalar intensity measures are known as fragility curves. They describe the relationship between earthquake hazard and the structural response expressed as engineer design parameters (e.g., maximum inter-story drift, maximum displacement). Peak ground acceleration (PGA) (Shinozuka et al. 2000; Sasani et al. 2002; Choun and Elnashai 2010; Garcia and Soong 2003; Banerjee and Shinozuka 2008) and pseudo-spectral acceleration (PSA) (Gardoni and Rosowski 2009; Liel et al. 2009; Ellingwood et al. 2007; Lin et al. 2013a; Jalayer et al. 2015) are among the most widely used intensity measures in fragility analysis. Two major issues regarding fragility are discussed in this paper and solutions to overcome them are sought. First, the number of ground-motion records available at a site is insufficient to calculate fragility curves. Secondly, the traditional seismic intensity measures are assumed to carry enough information on the ground motion to rate the performance of realistic complex systems for selected damage parameters. A comprehensive review of the existing methods for constructing fragility curves is available in Rossetto (2013).

One popular method to resolve the first issue of insufficient number of ground-motion records available is by scaling existing ground-motion records to common intensity measures. Scaling ground motions is conceptually simple but may yield unsatisfactory fragilities (Kafali and Grigoriu 2010) for certain non-linear systems. Scaling only changes the intensity of the ground motions, and the ground motions used to construct fragilities have the same frequency content irrespective of their intensity (Grigoriu 2011). One approach, known as incremental dynamic analysis, involves repeated scaling of seismic ground motions to increasing intensity measures until the specified damage state is reached (Vamvatsikos and Cornell 2002; Zareian and Krawinkler 2007; Goulet et al. 2007). Another method for calculating fragility curves, known as multiple stripes analysis (Lin et al. 2013b; Baker 2015), uses ground-motion records from a large dataset selected to be consistent with different spectral values of the response (Ozer and Akkar 2012; Baker 2011). The log-normal cumulative distribution function is commonly used as a parametric model for fragility curves (Singhal and Kiremidjian 1996; Baker 2007; Jalayer et al. 2007). This model is also adopted by the Federal Emergency Management Agency (FEMA) through ATC-58 (Porter et al. 2006; FEMA 2012). Various methods have been proposed to estimate the parameters of the log-normal distribution from data (Koutsourelakis 2010; Baker 2015; Jalayer et al. 2015).

The second issue related to the construction of fragility curves is imposed by the commonly used intensity measures, i.e., they are attractively simple, but they have limitations. Recent studies have shown that fragilities viewed as functions of a single scalar seismic intensity measure can be unsatisfactory. It was shown in Grigoriu et al. (2014) that response statistics calculated for non-linear systems subjected to different ground motion processes with similar intensity measures can yield significant differences. A comprehensive study on the efficiency and sufficiency of seismic intensity measure (Grigoriu 2016) examines the dependence of PSA on the demand parameters for non-linear structures with elements of information theory. Also, a critical study (Klügel 2007) on the probabilistic seismic-hazard analysis notices the limitations of PSA by energy-conservation principles, noticing that seismic events with very different energy content may have similar PSA. Concerns regarding the performance of the spectral acceleration in estimating demand parameters of realistic structures have been expressed also in Kohrangi et al. (2016a, b) and Schotanus et al. (2004), which analyse a set of intensity measures used in practice for realistic 3D structures, or in Kostinakis et al. (2017) and Douglas et al. (2015), which express the need of intensity measures to be structure-specific. A similar observation is offered in Vargas et al. (2013), which uses ordinates of the spectral displacement as intensity measure, but seeks an approach that takes into account the non-linear behaviours of structures. Alternative two-dimensional vector-valued seismic intensity measures were proposed in Baker and Cornell (2006), Baker and Cornell (2005), Tothong and Luco (2007) and Kohrangi et al. (2016b). Graphical representations of seismic fragility as functions of vector intensity measures are called fragility surfaces. They provide the same information as fragility curves, that is, probabilities of exceedance of limiting engineering design parameters, but are calculated as functions of two-dimensional vector-valued intensity measures (Gardoni et al. 2002). For example, fragility surfaces have been constructed as functions of the absolute maxima of the ground-motion metrics, such as peak ground-acceleration, velocity or displacement (Seyedi et al. 2009; Gehl et al. 2013); spectral ordinates at distinct structural periods (Gehl et al. 2011); or structure-specific parameters such as imposed drift and aspect ratio (Yazdi et al. 2016). Similar approaches use response surfaces (Rajashekhar and Ellingwood 1993; Buratti et al. 2010) for reliability studies for structures.

This paper proposes a solution for the two issues stated above, through the use of (1) simulated ground-motion records characterized by the moment magnitude m and source-to-site distance r, and (2) a vector measure (m, r) for fragility analysis (Kafali and Grigoriu 2010). We only use synthetic records to have full knowledge of structural performance so that the accuracy of different fragilities can be assessed precisely. Our objectives are (1) to show that fragilities defined as failure/damage probabilities conditional on current IMs are unsatisfactory and (2) to develop a practical framework which defines fragilities as failure/damage probabilities conditional on the defining parameters of the ground-acceleration stochastic process rather than responses of linear oscillators to these processes. Synthetic ground-motion records are simulated for each pair of values (m, r) considered in the fragility analysis. A regional seismological model which uses the specific barrier model (Halldorsson and Papageorgiou 2005) allows the simulation of ground motion samples as a function of (m, r). Calculating fragility surfaces is computationally expensive, since it is based on response analyses of structures subjected to seismic ground motions characterized by various values of (m, r). To overcome this drawback, an efficient method for calculating fragility surfaces based on stochastic reduced order models (Radu and Grigoriu 2014b; Grigoriu 2009) and a parametric model for fragility surfaces are proposed. These models are The stochastic reduced order model (SROM) resembles the Monte-Carlo method. Like Monte-Carlo, the method calculates structural responses to samples of the ground-motion process. Unlike Monte-Carlo, which uses a large number of samples selected at random, the proposed method uses a small number of samples selected in an optimal way. Similarly to the method adopted by the ATC-58 in which a log-normal distribution function is adopted as a model for fragility curves, a parametric bi-variate log-normal cumulative distribution function is used as a parametric model for fragility surfaces. Fragility surfaces are essential tools in performance-based seismic design and are used to estimate the life-cycle damage and cost of structures subjected to seismic loads. A related study (Shome et al. 1998) also did a comprehensive analysis on the nonlinear response of structures in the context of the (m, r) space, but with respect to the PSA. That study proposed several alternative, equivalent approaches to the approach presented in the current study, referred therein to as the direct approach. The approaches proposed in Shome et al. (1998) focus on the reduction of the number of dynamic analyses, achieved by scaling the few ground-motion records available in the four (m, r) bins considered in their study. This paper is an extension of the direct approach, which is now possible for a refined mesh of the (m, r) space, by considering (m, r)-synthetic ground-motion records and the SROM for the reduction of the number of nonlinear dynamic analyses. Numerical results in this paper are presented for simple linear and non-linear systems subjected to synthetic ground motions, with fully defined probabilistic laws. The seismic performance of systems is assessed through fragility surfaces. The advantages of using fragility surfaces with the proposed (m, r) intensity measure are discussed by comparison with traditional fragility curves. It is shown that fragility surfaces in (m, r) coordinates are superior to fragility curves in terms of sufficiency and efficiency of uncertainty quantification.

2 Problem description

The goal of the paper is to estimate accurately the performance of structural systems subjected to seismic loads. The framework used for this purpose comprises of two main parts: the input, which is the seismic ground motion, assumed to be a stochastic process; and the structural system, modelled as simple linear and non-linear structural models. The response of the structural systems to the ground-motion samples will then be used to assess the performance of the structural systems in the form of seismic fragilities.

2.1 Seismic ground motion

We define the seismic ground-motion records at a site, produced by a seismic event with magnitude m and source-to-site distance r, as samples of a stochastic process A(t). The ground motion process A(t) is assumed to be a zero-mean, non-stationary, Gaussian process given by

$$A(t)=h(t)Z(t),\,0\le t \le t_f,$$
(1)

where \(t_f\) is the duration of the record and

$$h(t)=\alpha t^{\beta } \exp \{-\gamma t\}$$
(2)

is a deterministic modulation function with constant parameters \(\alpha\), \(\beta\) and \(\gamma\), which gives the non-stationary character of the ground motion. The process Z(t) is a zero-mean, stationary, Gaussian process with marginal distribution \(\varPhi (z)=\int _{-\infty }^z1/\sqrt{2\pi }\exp (-0.5x^2)dx,\forall 0 \le t \le t_f\), with second-order moment properties given by the one-sided spectral density function \(g(\nu ;m,r),\,\nu \ge 0\). Function \(g(\nu ;m,r)\) is the result of a seismological model based on the specific-barrier model (SBM) (Halldorsson and Papageorgiou 2005) and depends on parameters (m, r), type of soil and tectonic regime. Constants \(\alpha\), \(\beta\), \(\gamma\) and the duration \(t_f\) in Eqs. (1) and (2) are also outputs of the specific barrier model. A statistically updated version of this model, to allow simulation of site-specific ground motion samples, is available in Radu and Grigoriu (2014a). The updated version is able to produce site-specific spectral density functions consistent with the site seismicity.

The simplified seismological model used for the purpose of this paper may be replaced by other simple stochastic (Tsioulou et al. 2018) or more complex physics-based (Goda et al. 2016) models that can produce synthetic processes as functions of (m, r). The general character of the proposed methodology allows for the use of ground-motion records produced by complex seismological models, that account for types of seismic sources, directivity, local-amplification conditions, such as the point-source model SMSIM (Boore 2005), the finite-fault model EXSIM (Motazedian and Atkinson 2005), or hybrid models (Seyhan et al. 2013), that combines physics-based and stochastic models for the low and high frequency contents, respectively.

Figure 1 illustrates two samples of the ground-motion process A(t) in Eq. (1) for two one-sided power-spectral-density functions shown in Fig. 3a, respectively, for \((m,r)=(5.4,30\,\hbox {km})\) and \((m,r)=(7.5,100\,\hbox {km})\) and a soil type with shear velocity in the top \(30\,\hbox {m}\) of soil of \(v_{30}=620\,\hbox {m}/\hbox {s}\). Important differences in the frequency content of the two processes are noticed as parameters (m, r) change.

Fig. 1
figure 1

Samples of the ground motion process A(t) for a \((m,r)=(5.8,50\,\hbox {km})\) and b \((m,r)=(7.6,150\,\hbox {km})\)

Full size image

2.2 Structural systems

Let X(t) be the relative displacement of a single-degree-of-freedom system subjected to the seismic ground acceleration A(t). For the linear and the non-linear Bouc–Wen systems, X(t) satisfies Eqs. (3) and (4), respectively, shown as follows:

$$\begin{aligned}&\ddot{X}(t)+2\zeta _0\nu _0\dot{X}(T)+\nu _0^2X(t)=-A(t) \end{aligned}$$
(3)
$$\begin{aligned}&\ddot{X}(t)+2\zeta _0\nu _0\dot{X}(T)+\nu _0^2(\rho X(t)+(1-\rho )W(t))=-A(t), \end{aligned}$$
(4)

where

$$\begin{aligned} \dot{W}(t)=\gamma \dot{X}(t)-\alpha |\dot{X}(t)||W(t)|^{n-1}W(t)-\beta \dot{X}(t)|W(t)|^n, \end{aligned}$$
(5)

is the hysteretic displacement of the non-linear system and \(\nu _0,\,\zeta _0,\,\rho ,\,\alpha ,\,\beta ,\,\gamma ,\,n\) are system parameters. Numerical results are shown for \(\nu _0=2\pi \,rad/s\), \(\zeta _0=0.02\), \(\rho =0.15\), \(\alpha =0.001\), \(\beta =2\), \(\gamma =4\) and \(n=1\). Note that for \(\rho =1\), the Bouc–Wen system is identical with the linear system.

The behaviors of the two systems in Eqs. (3) and (4) are shown in Fig. 2, represented by the backbone curves, i.e., the maximum restoring force and the hysteretic restoring force, respectively, as functions of the maximum absolute displacement \(\max _{t \ge 0}|X(t)|\).

Fig. 2
figure 2

Backbone curves for the linear and the non-linear Bouc–Wen SDOF systems

Full size image

3 Background on intensity measures

The metric used for the assessment of the seismic performance of the structural systems is the seismic fragility, which is the probability the system enters a damage state for a specified seismic ground-motion intensity measure. Graphic representations of seismic fragility are known as fragility curves for univariate intensity measures, and fragility surfaces for multi-variate intensity measures. Traditionally, PGA and PSA are used as intensity measures for the construction of seismic fragility curves. The current paper proposes a novel alternative bi-variate intensity measure for the representation of seismic fragility, in the form of vector (m, r), where m is the moment magnitude and r is the source-to-site distance r. As seen in Sect. 2.1, the SBM characterizes the frequency content of the ground-motion process. Furthermore, under the assumption stated, the probability law of the process A(t) conditional on (m, r) is completely defined and, thus, the fragility surfaces indexed by (m, r) are uniquely defined. The uniqueness of fragility surfaces is a reasonable assumption even for real ground-motion records, since (m, r) define almost completely their frequency content (Boore 2003; Halldorsson and Papageorgiou 2005). The limitations of the traditional intensity measures and the advantages of using the alternative (m, r) are discussed further in this section.

Following the problem definition in Sect. 2, the PGA is defined as the maximum absolute acceleration A(t), i.e., \(PGA=\max _{0\le t \le t_f}|A(t)|\), and the PSA is defined as the maximum absolute response acceleration for a linear SDOF system characterized by the natural frequency \(\nu _0\) and damping ratio \(\zeta _0\), i.e., \(PSA=\nu _0^2\max _{0\le t \le t_f}|X(t;\nu _0,\zeta _0)|\), where \(X(t;\nu _0,\zeta _0)\) is the response of the linear SDOF system in Eq. (3). It is shown below that ground-motion records with similar PGA or PSA can have very different frequency content, which is their main limitation, because the structural response is sensitive to the frequency content of the input excitation.

3.1 Peak ground acceleration (PGA)

Two versions of the input process A(t) defined in Eq. (1), with parameters \((m,r)=(7.5,100\,\hbox {km})\) and \((m,r)=(5.4,30\,\hbox {km})\), respectively, are characterized by the one-sided power spectral densities \(g(\nu ;m,r)\), shown in Fig. 3a.

Fig. 3
figure 3

a Power spectral densities and b PGA probability density functions, of ground motions with parameters (m, r) equal to \((7.5,100\,\hbox {km})\) and \((5.4,30\,\hbox {km})\), respectively

Full size image

Probability density functions of the PGAs of A(t) can easily be calculated, either by using simulations of ground-motion records using the model in Eq. (1), or by analytically using mean crossing-rates (Radu and Grigoriu 2014a), and they are shown in Fig. 3b. It is seen that the two processes have similar probability densities of the PGA, and identical modes (value of the PGA for which the probability density function reaches its maximum), even though they have significantly different frequency contents.

Fig. 4
figure 4

Probability \({\mathbb {P}}\{\max _{t\ge 0}|X(t)|>x_{cr}\}\) for a the linear and b the Bouc–Wen SDOF systems

Full size image

Since the response of the systems is sensitive to the frequency content of the motion rather than to its maximum absolute amplitude alone, in Fig. 4 the responses of (a) the linear and the (b) non-linear Bouc–Wen systems are compared when subjected to the two motions described in Fig. 3. Large differences between the exceedance probabilities of the maximum absolute displacement of X(t) of critical values \(x_{cr}\), i.e., \({\mathbb {P}}\{\max _{t\ge 0}|X(t)|>x_{cr}\}\), are noticed for each of the systems when subjected to the two motions, despite their being apparently indistinguishable with respect to their PGAs.

Fig. 5
figure 5

Correlation between the PGA for 1000 motions with \((m,r)=(7.0,30\,\hbox {km})\) and the corresponding maximum absolute displacement for a the linear and b the Bouc–Wen SDOF systems

Full size image

Furthermore, scatter plots of the PGAs of the ground motions with parameters \((m,r)=(7.0,30\,\hbox {km})\) versus the maximum absolute displacements of the linear and the Bouc–Wen systems, respectively, are shown in Fig. 5. It is seen that the PGA measure of the ground motion and the response of the systems are uncorrelated, with correlation coefficients below \(3\%\).

3.2 Pseudo spectral acceleration (PSA)

A similar analysis is conducted with respect to the PSA, for which two other processes A(t) defined by the parameters \((m,r)=(8.0,210\,\hbox {km})\) and \((m,r)=(5.4,30\,\hbox {km})\), respectively, are chosen. Their one-sided power-spectral-density functions \(g(\nu ;m,r)\) are shown in Fig. 6.

Fig. 6
figure 6

a Power spectral densities and b PGA probability density functions, of ground motions with parameters (m, r) equal to \((5.4,30\,\hbox {km})\) and \((8.0,210\,\hbox {km})\), respectively

Full size image

Probability density functions of the PSAs of A(t) are calculated as before, and it is seen in Fig. 6 that even though the two processes have very different frequency contents, they have almost identical probability density functions of their respective PSAs. Thus, the two processes, characterized by different (m, r), are indistinguishable with respect to the PSA.

Fig. 7
figure 7

Probability \({\mathbb {P}}\{\max _{t\ge 0}|X(t)|>x_{cr}\}\) for a the linear and b the Bouc–Wen SDOF systems

Full size image

Also the response statistics in the form of the probability of exceedance \({\mathbb {P}}\{\max _{t\ge 0}|X(t)|>x_{cr}\}\) are compared for the two systems individually in Fig. 7. It is noticed that they are identical for the linear system subjected to the two distinct motions, but fairly different for the non-linear system. As expected, the PSA is a suitable measure for linear SDOF systems since its maximum displacement is directly proportional to the PSA.

Fig. 8
figure 8

Correlation between the PSA for 1000 motions with \((m,r)=(7.0,30\,\hbox {km})\) and the corresponding maximum absolute displacement for a the linear and b the Bouc–Wen SDOF systems

Full size image

Similar observations can be made when looking at the scatter plots of the PSAs of the ground motions with parameters \((m,r)=(7.0,30\,\hbox {km})\) versus the maximum absolute displacements of the linear and the Bouc–Wen systems, respectively, in Fig. 8. As expected, the correlation coefficient between the PSA and the absolute maximum displacement of the linear response is \(100\%\), but it decreases to approximately \(25\%\) in the case of the non-linear system.

It has been shown above that the traditional ground-motion intensity measures may be uninformative. The PGA is unsatisfactory even for linear SDOF systems. The PSA, however, which is widely used in the earthquake-engineering community, though a good measure for linear SDOF systems, fails to perform well for simple non-linear systems. Thus, PSA may be used as a proper intensity measure only under the assumption that structures behave as linear SDOF systems, which may be unreasonable for complex, realistic systems. Since the SBM, as well as other seismological models (Boore 2003; Goda et al. 2016), show that the frequency content of the motion is highly dependent on the moment magnitude m and the source-to-site distance r, the bi-variate intensity measure (m, r) would seem to be a more appropriate choice. Additionally, it has also been shown in this section that the response is highly dependent on the frequency content and therefore varies with (m, r) for apparently indistinguishable ground motions in terms of PGA or PSA. This conclusion agrees with previous observations (Grigoriu 2011) that scaling ground-motion records with respect to PGA or PSA, for the purpose of calculating fragility curves, is unsuitable because scaling only changes the amplitude of the motion and fails to capture the variability in the frequency content of seismic events.

4 Fragility surfaces

Fragility surfaces \(P_f(m,r)={\mathbb {P}}\left( \max _{0\le t \le t_f} |X(t)| > x_{cr}\right)\) are graphical representations of probabilities that a structural response X(t) exceeds a critical limit \(x_{cr}\) under a seismic ground motion A(t) corresponding to moment magnitude m and source-to-site distance r.

4.1 Construction of fragility surfaces using Monte Carlo

Monte-Carlo (MC) is the only general method for calculating response statistics. The following algorithm can be used to calculate fragility surfaces for a structural system.

  1. 1.

    Generate N samples \(a_i(t),\,i=1,\ldots ,N\) of the seismic ground motion process A(t) in Eq. (1) for fixed (m, r);

  2. 2.

    Calculate samples of response \(x_i(t),\,i=1,\ldots ,N\) for the structural system in Eq. (3) or (4) subjected to \(a_i(t)\);

  3. 3.

    Calculate the value of the fragility surface at coordinates (m, r) for a specified critical limit for the displacement \(x_{cr}\)

    $$\begin{aligned} P_f(m,r)=\frac{1}{N}\sum _{i=1}^N {\mathbf {1}} \left\{ \max _{0\le t\le t_f} |x_i(t)| > x_{cr} \right\} , \end{aligned}$$
    (6)

    where \({\mathbf {1}}\) is the indicator function, i.e., \({\mathbf {1}} \{x > x_0 \}=1\) if \(x>x_0\), and zero otherwise.

Fig. 9
figure 9

Evolution of fragility surfaces using MC, with increasing demand: a \(x_{cr}=0.5\,cm\), b \(x_{cr}=1\,cm\), c \(x_{cr}=2\,cm\)

Full size image

The algorithm above describes a simple method to construct fragility surfaces for the maximum displacement of simple SDOF systems. The same procedure is applicable to any other system for any desired engineering-design parameter (e.g., inter-story drift, angle of rotation etc.). Figure 9a–c shows fragility surfaces calculated for the Bouc–Wen system in Eq. (4) for increasing demand \(x_{cr}=\{0.5,1,2\}\,cm\).

Monte Carlo simulation usually requires a large number N of samples for the analysis. Since fragility surfaces are calculated by response analyses, their construction could be computationally expensive for complex structural systems. A more efficient, accurate method to calculate fragility surfaces is presented in the next section.

4.2 Construction of fragility surfaces using stochastic reduced-order models (SROM)

A new, highly efficient and non-intrusive method based on stochastic reduced-order models (SROM) (Grigoriu 2009) is proposed for calculating response statistics. The stochastic reduced-order model can be viewed as a smart Monte Carlo method. Like Monte Carlo, the method uses random samples of the seismic ground-motion process to characterize the structural response. Unlike Monte Carlo, which uses a large number N of samples at random, SROM uses only a small number of samples \(\tilde{N}<<N\), selected in an optimal way. The SROM samples can be regarded as representative ground-motion records. Similar to the studies on ground-motion selection in Lin et al. (2013b) and Lin et al. (2013a), the SROM-based method selects just a small number of records from a large database of real or synthetic ground motions. In contrast to the aforementioned studies, the SROM samples are selected to match the probability law of the ground-motion records, rather than just the response spectra of linear SDOF systems.

Our goal is to construct SROMs for the process A(t) for each (m, r) and to use them to calculate fragility surfaces. A stochastic reduced-order model \(\tilde{A}(t)\) for A(t) is a stochastic process with \(\tilde{N}\) samples \(\{a_i(t),\,i=1,\ldots ,\tilde{N}\}\) of A(t). Usually the samples of \(\tilde{A}(t)\) are not equally likely and are weighed by some probabilities \({\mathbf {p}}= \{p_i\ge 0,\,i=1,\ldots ,\tilde{N}\}\) such that \(\sum _{i=1}^{\tilde{N}}p_i=1\). The pairs of samples and their probabilities \((a_i(t),p_i)\) define completely the probability law of \(\tilde{A}(t)\).

To construct \(\tilde{A}(t)\) we select sets of \(\tilde{N}\) samples of A(t) and calculate their corresponding probabilities \(p_i,\,i=1,\ldots ,\tilde{N}\) such that the discrepancy between the probability laws of A(t) and \(\tilde{A}(t)\) is minimized. Consider the metric

$$\begin{aligned} \varphi ({\mathbf {p}})=w_1\varphi _1({\mathbf {p}})+w_2\varphi _2({\mathbf {p}})+w_3\varphi _3({\mathbf {p}}), \end{aligned}$$
(7)

where \(\varphi _1,\, \varphi _2,\) and \(\varphi _3\) are functions which account for the differences between the marginal distributions, the moments and the correlation functions of A(t) and \(\tilde{A}(t)\). The weights \(\{w_i>0,\,i=1,2,3\}\) can be used to focus on certain properties of the two processes. For each set of \(\tilde{N}\) samples we calculate an optimal probability vector \({\mathbf {p^{opt}}}\) of \({\mathbf {p}}\) by minimizing \(\varphi ({\mathbf {p}})\), such that \(p^{opt}_i\ge 0,\,i=1,\ldots ,\tilde{N}\) and \(\sum _{i=1}^{\tilde{N}}p^{opt}_i=1\). Functions \(\varphi _k({\mathbf {p}}),\,k=1,2,3\) have the expressions

$$\begin{aligned} \varphi _1({\mathbf {p}})&=\int _{-\infty }^{\infty }\int _0^{t_f} \left( \tilde{F}(x,t)-F(x,t)\right) ^2dtdx, \end{aligned}$$
(8)
$$\begin{aligned} \varphi _2({\mathbf {p}})&=\sum _{q=1}^{n_q}\int _0^{t_f} \left( \tilde{\mu }(t;q)-\mu (t;q)\right) ^2dt, \end{aligned}$$
(9)
$$\begin{aligned} \varphi _3({\mathbf {p}})&=\int _{0}^{t_f}\int _0^{t_f} \left( \tilde{c}(t,s)-c(t,s)\right) ^2dtds, \end{aligned}$$
(10)

where \(\tilde{F}(x,t),\,F(x,t)\) are marginal distribution functions, \(\tilde{\mu }(x,t),\,\mu (x,t)\) are moments and \(\tilde{c}(t,s),\,c(t,s)\) are correlation functions for \(\tilde{A}(t)\) and A(t), respectively, and \(n_q\) is the order of the highest moment considered. Functions \(F(x,t),\,\mu (x,t)\) and c(t, s) can be calculated directly from the distribution of A(t), or from its samples if the distribution of A(t) was unknown. Properties for the SROM \(\tilde{A}(t)\) are calculated as follows

$$\begin{aligned} \tilde{F}(x,t)&={\mathbb {P}}\{\tilde{A}(t)\le x\}=\sum _{i=1}^{\tilde{N}} p_i{\mathbf {1}}\{a_i(t)\le x\} \end{aligned}$$
(11)
$$\begin{aligned} \tilde{\mu }(t;q)&={\mathbb {E}}\left[ \tilde{A}(t)^q\right] =\sum _{i=1}^{\tilde{N}} p_ia_i(t)^q \end{aligned}$$
(12)
$$\begin{aligned} \tilde{c}(t,s)&={\mathbb {E}}\left[ \tilde{A}(t)\tilde{A}(s)\right] =\sum _{i=1}^{\tilde{N}}p_ia_i(t)a_i(s), \end{aligned}$$
(13)

under the zero-mean assumption of A(t).

Fig. 10
figure 10

Fragility surface obtained by a MC with \(N=1000\), b SROM with \(\tilde{N}=20\), and c parametric bi-variate log-normal model fit

Full size image

The set of \(\tilde{N}\) samples which provides the minimum value for the metric \(\varphi ({\mathbf {p^{opt}}})\) defines the SROM \(\tilde{A}(t)\). The range of \(\tilde{A}(t)\) is sub-optimal because we use a fixed, relatively small number of distinct sets of \(\tilde{N}\) samples of A(t) to select the samples for the SROM.

$$\begin{aligned} P_f(m,r)=\frac{1}{\tilde{N}}\sum _{i=1}^{\tilde{N}} p_i{\mathbf {1}}\left\{ \max _{0\le t\le t_f} |\tilde{x_i}(t)| > x_{cr} \right\} \end{aligned}$$
(14)

Figure 10a, b shows fragility surfaces calculated by Monte Carlo and SROM for the Bouc–Wen system in Eq. (4) subjected to the stochastic process A(t) for \(x_{cr}=2\,cm\), for \(N=1000\) and \(\tilde{N}=20\) samples for each value of (m, r) in the fragility surface, respectively. The approximate surfaces are satisfactory good by comparing them with the MC surfaces, with errors below \(5\%\).

4.3 Parametric model for fragility surfaces

Similar to the common approach of using a log-normal cumulative distribution function as a model for fragility curves, a bi-variate log-normal cumulative distribution function is proposed as a parametric model for fragility surfaces. This model can be easily calibrated to data, which allows for efficient development of fragility surfaces.

The bi-variate log-normal distribution function \(F_{LN}(m,r;\mu _1,\sigma _1,\mu _2,\sigma _2,\rho )\) is completely defined by five parameters \(\{\mu _1,\sigma _1,\mu _2,\sigma _2,\rho \}\) and has the following form

$$\begin{aligned} F_{LN}(m,r;\mu _1,\sigma _1,\mu _2,\sigma _2,\rho )=\int _{0}^{m}\int _{0}^{r}f_{LN}(\xi ,\eta ;\mu _1,\sigma _1,\mu _2,\sigma _2,\rho )d\xi d\eta , \end{aligned}$$
(15)

where

$$\begin{aligned} f_{LN}(m,r)&=\frac{1}{2\pi \sigma _1\sigma _2\sqrt{1-\rho ^2}mr}\exp \left( -\frac{f'}{2(1-\rho ^2)}\right) \nonumber \\ f'&=\left( \frac{\ln m -\mu _1}{\sigma _1}\right) ^2 - 2\rho \left( \frac{\ln m -\mu _1}{\sigma _1}\right) \left( \frac{\ln r -\mu _2}{\sigma _2}\right) + \left( \frac{\ln r -\mu _2}{\sigma _2}\right) ^2, \end{aligned}$$
(16)

is the the probability density function for the bi-variate log-normal distribution.

We use the fragility surface calculated in Eqs. (6) and (14) to estimate the values of the bi-variate log-normal distribution’s parameters. These parameters will define the parametric model in Eq. (15) for the fragility surface for any m and r. Figure 10c shows the parametric models for the fragility surfaces calculated for the Bouc–Wen calculated by MC and SROM methods shown in Fig. 10a, b, respectively. The parameters of the bi-variate parametric model for the fragility surface estimated are \(\mu _1=1.803\), \(\sigma _1=0.054\), \(\mu _2=4.978\), \(\sigma _2=0.107\) and \(\rho =-0.977\), for the data obtained by Monte Carlo; and \(\mu _1=1.809\), \(\sigma _1=0.046\), \(\mu _2=5.003\), \(\sigma _2=0.122\) and \(\rho =-0.962\), for the data obtained by SROM.

5 Discussion

This paper proposes a novel, improved bi-variate intensity measure in the form of the vector (m, r), where m and r are the moment magnitude and the source-to-site distance characterizing the seismic ground motion. It has been shown that m and r (together with other secondary parameters, which, for simplicity’s sake, are disregarded here) control the frequency content of the seismic ground motion. The main advantage of using (m, r) rather than the traditional intensity measures PGA and PSA is the accuracy of the estimates of the response statistics. It has been shown in Sect. 3 that the ground motion is well defined by (m, r) for motions that are otherwise indistinguishable with respect to the traditional scalar measures.

Fig. 11
figure 11

Fragility curves (solid lines) obtained from fragility surface data \(P_f(m,r)\) for all samples of PSA|(M, R) (dots), for increasing demand: a \(x_{cr}=0.5\,cm\), b \(x_{cr}=1\,cm\), c \(x_{cr}=2\,cm\)

Full size image

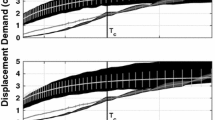
Thus seismic fragility is still used as a measure of the seismic performance of structures, but they are expressed in (m, r) coordinates. The differences between the fragility curves as functions of PSA and fragility surfaces as functions of (m, r) are discussed. It has been shown why the representation of seismic fragility in (m, r) coordinates is more accurate. For a more appropriate comparison between fragility curves and surfaces, two methods for calculating equivalent fragility curves from fragility surfaces are suggested. Since a one-to-one transformation between (M, R) and PSA is not possible, we can use either (1) samples of the conditional random variable PSA|(M, R) or (2) statistics of PSA|(M, R), in this case, its mode. Note that (M, R) denotes the random vector with coordinates moment magnitude M and source-to-site distance R. In the first attempt to represent fragility surfaces as fragility curves by using samples of PSA|(M, R), the value of the probability of failure \(P_f(m,r)\), uniquely defined by (m, r) in Eq. (6), is assigned for various samples of PSA|(M, R). Figure 11 shows in dots the values of \(P_f(m,r)\), for \(N = 1000\) samples of PSA|(M, R), for each value of (m, r) used in the representation of the fragility surfaces in Fig. 9, in each of the three cases with different thresholds of the critical displacement \(x_{cr}\). In other words, Fig. 11 should be regarded as a mapping of the fragility surfaces in Fig. 9 to fragility curves, i.e., each discrete point on the vertical axis represents the probability \(P_f(m,r)\) for a given value of \((M,R)=(m,r)\), while the points on the horizontal axis, for a given \(P_f(m,r)\), represent the \(N=1000\) sampled of \(PSA|(M,R)=(m,r)\). Additionally, log-normal parametric models of fragility curves are fitted to the data from the fragility surfaces and are shown in Fig. 11 as the solid lines. Analysing the ranges of PSA values for fixed values of \(P_f(m,r)\), it can be clearly seen that the fragility surfaces are able to capture the large uncertainties in the ground motions, unlike fragility curves, and therefore they are more desirable for uncertainty quantification in the structural response.

In the second attempt to represent fragility surfaces in Fig. 9 as curves using statistics of PSA|(M, R), the values of \(P_f(M,R)\) for the mode of PSA|(M, R), for each value of (m, r), are represented by the circles in Fig. 12. As before, the fragility curves in Fig. 12 can be regarded as the mapping of the fragility surfaces in Fig. 9 to curves. As in the first attempt, fragility curves are fitted to this data obtained from the fragility surfaces. Visually comparing the curves in Figs. 11 and 12, we notice that using the mode of PSA|(M, R) alone, rather than the entire distribution of PSA|(M, R), overestimates the probability of failure. Fragility curves obtained using the entire distribution of \(PSA|(M,R)=(m,r)\), through its samples, resemble more the fragility curves calculated empirically using the same data and shown in Fig. 13.

Fig. 12
figure 12

Fragility curves (solid lines) obtained from fragility surface data \(P_f(m,r)\) for the modes of PSA|(M, R) (circles), for increasing demand: a \(x_{cr}=0.5\,cm\), b \(x_{cr}=1\,cm\), c \(x_{cr}=2\,cm\)

Full size image

The empirical fragility curves in Fig. 13 have been calculated using the same response data used to calculate the fragility surfaces, i.e., all \(N = 1000\) samples of ground motion A(t) simulated for each (m, r). The motions were grouped in bins with similar values of PSA, for which probabilities \(P_f(PSA)\) were calculated. The slight deviation from the curves estimated from the fragility surfaces at high values of PSA may be explained by the smaller number of events simulated in that range.

Fig. 13
figure 13

Fragility curves for the Bouc–Wen system obtained from a fragility surfaces (see Fig. 11) and b empirically

Full size image

The discussion of fragility analysis using surfaces in (m, r) coordinates rather than fragility curves can be concluded with the observation that fragility surfaces provide important advantages over fragility curves, among which the most important are (1) the uniqueness of the probability of failure for a given (m, r), and (2) the superior quantification of the uncertainty in the ground motion. It is also important to note that the comprehensive characterization of the ground motion by (m, r) allows for an easy transformation of the fragility surfaces to the traditional curves expressed as functions of PSA, the reverse not being possible.

6 Conclusion

This paper analyses critically the currently used intensity measures, i.e., the peak ground acceleration (PGA) and the pseudo-spectral acceleration (PSA), showing that they are inadequate for the representation of seismic fragility for complex non-linear systems. The response of the structures is sensitive to the frequency content of the ground motions, and seismic ground motions with significantly different frequency content may have similar or identical intensity measures. As an alternative to these traditional scalar intensity measures, the current study proposes a bi-variate intensity measure with coordinates moment magnitude m and source-to-site distance r, which define almost completely the frequency content of the seismic ground motion. Seismic fragilities expressed in the (m, r) space are called fragility surfaces and they are calculated using synthetic ground-motion records, using Monte Carlo simulations, which may be computationally challenging when dealing with complex systems. An efficient method for calculating fragility surfaces using stochastic reduced-order models (SROM), as well as a parametric model for fragility surfaces, are proposed to overcome the computational issue. Finally, fragility surfaces expressed in (m, r) coordinates are translated into fragility curves expressed in PSA and compared with empirical fragility curves. It is shown that fragility surfaces capture better the uncertainty in the ground motion and that they are unique with respect to (m, r), which makes them desirable for seismic fragility analysis.