1 Introduction

Data provided by accelerometric networks are of great importance for seismic hazard assessment, especially for the derivation of ground-motion prediction equations (GMPEs), which are the basis of most deterministic or probabilistic seismic hazard analysis. However, the optimal use of accelerometric waveforms is closely linked to the quality of the station ‘site-metadata’, that needs to provide reliable information about local soil conditions, such as for the EC8 soil class (EUROCODE8 1998), VS30, velocity profiles, and all of the relevant information that can help to quantify site effects. Unfortunately, these metadata are often only poorly known (Sandikkaya et al. 2013; Seyhan et al. 2014; Akkar et al. 2014). Soil classes or VS30 parameters are indeed most often indirectly derived, such as through the use of geological maps, where a given lithology is associated to a given shear-wave velocity. However, this approach does not take into account possible weathering of geological material, nor the presence of shallow quaternary deposits that are not always indicated on geological maps. Another indirect approach is to correlate VS30 and the slope of the topography (Allen and Wald 2009), which has been shown to require further calibration through additional local constraints to reach reliable prediction capabilities (Lemoine et al. 2012; Thompson et al. 2014; Yong 2016). Nevertheless, indirect approaches can also often lead to VS30 estimates of high uncertainty. To tackle these issues, important efforts have been made in recent years to perform in situ site characterization of accelerometric stations: e.g., in Italy (Foti et al. 2011; Pileggi et al. 2011), Switzerland (Michel et al. 2014), and the USA (Yong et al. 2013).

In France, the ‘Réseau Accélérométrique Permanent’ (RAP; permanent accelerometric network) consists of approximately 150 stations (Guéguen et al. 2007; Pequegnat et al. 2008). Previous studies have already proposed soil classes or VS30 for some or all of the RAP stations. For example, Régnier et al. (2010) gathered a wide range of pre-existing geophysical and geotechnical information in the vicinity of the RAP sites. Other studies (Drouet et al. 2008, 2010) have been aimed at estimation of VS30 using generalized inversion methods.

The present paper addresses recent efforts that have led to the characterization of 33 of the RAP station sites that are located in the Pyrenees, Alps, Auvergne and Provence–Côte d’Azur regions (Fig. 1), using in situ systematic measurements of VS profiles. One key issue for this measurement campaign is the choice of methods to be used, which obviously impacts on the survey budget. The use of classical geotechnical methods such as cross-hole and down-hole measurements leads to high costs and high logistic constraints. Moreover, these methods can be limited in terms of the investigation depth. Alternatively, methods based on analysis of Rayleigh-wave and/or Love-wave surface-wave dispersion characteristics can allow the derivation of shear-wave velocity profiles. Even if the capabilities of these methods have been debated for a long time, they provide good estimates when implemented with care, as demonstrated within the InterPacific project (Garofalo et al. 2016a, b; Foti et al. 2017). In particular, Garofalo et al. (2016b) outlined that VS30 can be equally well estimated using ‘noninvasive’ approaches (e.g., surface-wave-based methods) and ‘invasive’ approaches (e.g., cross-holes, down-holes). However, Garofalo et al. (2016a) also showed that noninvasive methods are less accurate for locating a given lithological interface, low velocity layers or bedrock depth. They attribute this to surface wave depth resolution issues, non-uniqueness of the inversion procedures and/or the energy content of the signals used. The consequences of the uncertainties related to non-uniqueness of site responses have been a matter of discussion in recent years (Cornou et al. 2006; Foti et al. 2009; Socco et al. 2012; Boaga et al. 2013; Jakka et al. 2014; Comina and Foti 2015; Griffiths et al. 2016; Cox and Teague 2016), with some authors claiming that the great uncertainty in Vs profiles leads to high variability of the site responses, although others do not agree. However, considering that the bedrock velocity is well known (e.g., through large arrays or other indirect information) and the velocity profiles are coherent with other indicators (e.g., the ambient vibration H/V frequency peak), the impact of non-uniqueness on site responses remains acceptable. Therefore, with the main objective of the survey being the estimation of site effects, noninvasive surface-wave-based methods represent good candidates, and were chosen for the present study.

Fig. 1
figure 1

Map of the southern half of France with the locations of the RAP network stations and stations that benefited from the characterization presented here. Right upper frame zoom in on the Annecy area. Right lower frame zoom in on the Grenoble area

Full size image

This study starts with a brief description of the chosen accelerometric stations, the methods used, and the related acquisition layout. Next, the different steps of processing are presented, which include data quality control, derivation of dispersion curves, and shear-wave velocity profile inversions. Finally, the results are shown, and we draw implications from these results, as well as for the overall methodological feedback.

2 Choice of rap sites

The choice of the accelerometric sites to be characterized was a compromise between the wish to characterize sites that produce the largest number of accelerograms, and the wish to characterize sites that were used as ‘reference sites’ in Drouet et al. (2010). Finally, some sites were ruled out due to logistical constraints (e.g., difficulties in site access).

The acquisitions were carried out in different phases, with each new phase taking into account the feedback of the previous phase, in terms of the survey plan, geophysical material, logistic organization in the field, and data processing. This explains the successive changes in the standard acquisition layout, as well as the overall level of successfully recorded data for each site (considering that we usually dedicated one working field day to one site, with a team of 6 to 8 people).

The first site that was characterized was NALS station, in the city of Nice (April, 2012), followed by three sites in Auvergne (OCLD, OCOR, OCOL) in late April 2012, and nine sites in the Pyrenees (EPF, PYAS, PYAT, PYBB, PYLI, PYLL, PYLO, PYLU, PYOR) in September 2012. In July and August 2014, five sites were characterized in the Provence–Côte d’Azur area (IRPV, OGCA, IRVG, CALF, NBOR) and 15 in the French Alps (OGDH, OGPC, OGCH, OGBL, SURF, OGFO, OGMU, OGIM, OGLE, GRN, OGAN, OGAP, OGME, OGMA, OGSI). Some necessary additional measurements were performed from November 2014 to January 2015 to complete the datasets for NBOR, OGBL, OGCA and IRVG stations. Table 1 gives the main geological features of the 33 studied stations, and Fig. 1 shows their locations. The former OCKE station was located very close to the OCLD one. The results obtained for OCLD are also valid for OCKE. The station OGFO corresponds to the Montbonnot borehole site. It involves three stations: a first one at the surface (also known as OGFH), a second one at 40 m depth (also known as OGFM) and a third one at 556 m depth (also known as OGFB).

Table 1 Brief description of the geological formations underlying the accelerometric stations studied here
Full size table

3 Acquisition layout

The acquisition layout basically consisted of both active surface-wave recording through the implementation of the multi-analysis surface-wave (MASW) method, and passive surface-wave recording through the deployment of seismic ambient vibration arrays (AVAs).

For the MASW approach, we used a 24-channel acquisition device (Geometrics) connected to either 24 4.5-Hz vertical geophones, or 24 horizontal geophones. We usually performed the acquisition with both vertical polarization (for Rayleigh-wave analysis) and horizontal polarization (for Love-wave analysis). We tried to systematically record one profile with a geophone spaced every 2 m (i.e., a 46 m profile length), but according to the site specificity, this geophone spacing could be reduced to 1 m (i.e., a 23 m profile length). In some sites, several profiles were deployed, with inter-traces of up to 4 m (i.e., a 92 m profile length). For Rayleigh-wave acquisition, an aluminum plate on the ground was hit vertically with a 4-kg hammer, on both sides of the profile and in the middle of the profile. For Love-wave acquisition, the same hammer was used to hit the ground on both sides of the profile using an oak beam weighed down by a car or a few volunteers.

For the AVA acquisition, 30-s broadband seismometers (Güralp CMG6TD) were used for most of the sites. The survey conducted for nine sites in the Pyrenees used 5-s velocimeters (Lennartz LE-3D) connected to a wireless array analysis system (Ohrnberger et al. 2006). The first experiments were performed in 2012, and consisted of the successive deployment of several single-circle array geometries at each site, using either 10 sensors (one in the center; nine equally spaced in a circle) or eight sensors (one in the center; seven equally spaced in a circle). The number of circles and the circle diameters were chosen site by site, according to the site conditions, the remaining time during the survey, and other factors. For the acquisitions performed in 2014, a more systematic layout was applied to most sites, due to the larger number of seismological instruments available and the successful initial feedback of the InterPacific project (Foti et al. 2017). Indeed, we usually used 15 sensors, which allowed double-circle geometry (one in the center; 2× seven equally spaced around two circles). The azimuth of the sensors for the larger circle was shifted by ~26° (360°/14) with respect to the azimuth of the smaller circle sensors, to optimize the azimuthal coverage of the whole array. A radius ratio of 3.0 was chosen for the increase between two consecutive array radii, starting from a circle with a 5-m radius, up to a circle with a 405-m radius. For consecutive acquisitions, the inner/smaller circle was moved to form the next larger circle. Hence, in addition to a center station, the four different sets of array layouts used the increasing paired radii of: 5 and 15 m (denoted as array #1); 15 and 45 m (array #2); 45 and 135 m (array #3); and 135 and 405 m (array #4). This standard layout was adjusted to take into account local constraints. For (a priori) rock sites, array #1 was usually omitted (due to lack of energy at high frequency in the seismic ambient noise wavefield), and instead two MASW profiles were performed (the standard 46-m profile length, and a 92-m profile length). For sites that had very difficult access, array #4 was also sometimes omitted. Figure 2 shows the example of the acquisition layout of the OGIM station survey.

Fig. 2
figure 2

Acquisition layout used for the OGIM station measurements (presented at two scales). The ‘ideal’ geometry is adapted to the local logistic constrains (e.g., buildings, roads…). All of the array use the center sensor; ‘array #1’ is composed of stations with radii ‘R1’ and ‘R2’; ‘array #2’ is composed of stations with radii ‘R2’ and ‘R3’; ‘array #3’ is composed of stations with radii ‘R3’ and ‘R4’; ‘array #4’ is composed of stations with radii ‘R4’ and ‘R5’

Full size image

Only MASW measurements were performed for four sites (OGLE, OGMU, GRN, OGSI), as their topography was too pronounced to allow AVA acquisition (for both logistic and theoretical considerations). For the OGFO site, we benefited from previously measured AVAs (Bettig et al. 2001; Cornou et al. 2008), and so only the new MASW data were recorded in the framework of the present study. Figure 3 summarizes the different acquisition geometries that were performed at each site.

Fig. 3
figure 3

Summary of MASW and AVA layouts used for each station studied here. For MASW, ‘V’ indicates vertically polarized acquisition (for further Rayleigh-wave processing); ‘H’ indicates horizontally polarized acquisition (for further Love-wave processing); the number following the letter indicates the geophone inter-distance. As all acquisitions used a 24-channel system, ‘V2’ indicates vertically polarized acquisition with 2 m geophone inter-distance, for a 46-m length profile. For AVA, dotted lines indicated single-circle arrays, solid lines indicate double-circle arrays. The number indicates total number of sensors used for further processing (sensors that failed are not counted here). Gray lines indicate AVA that failed to produce dispersion curves (whatever the processing method: FK, HRFK or MSPAC). Other colors indicate AVA that produced a dispersion curve with at least one of the processing methods. The different bright colors are just used for ease of reading

Full size image

4 Processing

4.1 Quality monitoring and H/V

The overall processing procedure from the ‘raw data’ to the velocity profiles and the other outcomes was consistent with the current state-of-the-art practices. A description of this procedure can be found in the recommendations of the InterPacific project guidelines (Foti et al. 2017), which focus on fundamental Rayleigh-wave processing and inversion. In the present study, when possible, we also use multi-mode inversion, and Rayleigh-wave and Love-wave joint inversion. The data processing was performed using the Geopsy software (Wathelet et al. 2004, 2008; Wathelet 2005, 2008). The first step of the analysis consisted of examining the Fourier amplitude spectra to estimate the energy content of the seismic ambient noise wavefield, as well as to identify stations that produced spurious estimates, which were then removed from the analysis (e.g., Fig. 4). The data quality monitoring then included evaluation of the classical ambient vibration H/V ratio (Nakamura 1989; SESAME team 2004; Bard et al. 2010) (Fig. 4). As well as providing the fundamental resonance frequency of the site that could be used later in the dispersion curve inversion, the H/V curves provided estimates of the spatial variation of the sediment-to-bedrock depth interface, and allowed checking whether one-dimensional (1D) wave propagation can be assumed throughout the array.

Fig. 4
figure 4

H/V ambient vibration ratio for all of the sensors of the four arrays of the OGIM station measurements. Array #1 and array #2 show good site homogeneity at array scale. Array #3 still shows relatively good site homogeneity, while homogeneity is degraded for array #4

Full size image

4.2 Dispersion curves

The seismic ambient vibrations recorded by the AVA arrays were systematically processed by using: (1) the frequency-wavenumber (FK) (Neidell and Taner 1971; Douze and Laster 1979; McMechan and Yedlin 1981); (2) the high-resolution frequency-wavenumber (HRFK) (Capon 1969); and (3) the modified spatial autocorrelation (MSPAC) method (Bettig et al. 2001; Köhler et al. 2007). Dispersion curves were then extracted for each array and each processing method. For the FK and HRFK methods, only phase-velocity estimates within the array resolution capabilities were considered. At low frequencies, the minimum resolvable wavenumber was controlled by the array aperture and was easily derived from the array response (Henstridge 1979; Di Giulio et al. 2006; Wathelet et al. 2008). While the array resolution for the FK method was fixed to the width of the main lobe of the array response at its mid-height (k min ), the HRFK technique usually provided improved resolution capabilities. Although numerous authors (e.g., Asten and Henstridge 1984; Tokimatsu 1997; Satoh et al. 2001) have reported resolution improvements of a factor of three to six, we chose to limit the minimum resolvable wavenumber to k min /2 (Cornou et al. 2006; Wathelet et al. 2008), which allowed for the retrieval of larger wavelengths compared to the FK approach. At high frequencies, all of the dispersion curves were picked as high as the aliasing features allowed.

For MSPAC processing, the phase-velocity estimates were derived from the autocorrelation curves (Wathelet 2005). SPAC based methods are usually reported to resolve wavelengths that are typically five to seven times larger than those predicted by k min (e.g., Horike 1985; Asten et al. 2004).

When FK (or HRFK) and MSPAC provided different dispersion curves within the same frequency band, we monitored the azimuth of the dominant seismic-noise waves. Indeed, the MSPAC approach assumes that the seismic ambient-noise sources are randomly distributed in space. When this assumption was not fulfilled (i.e., the seismic noise wavefield was dominated by a single dominant source direction), we disregarded the MSPAC estimates. Conversely, when MSPAC provided lower phase-velocity estimates than FK-based methods in the low frequency range, we favored the MSPAC estimates, on the assumption of a lack of resolution capability of the FK-based methods.

Not all of the arrays produced usable dispersion curves. The passive experiments that failed to provide phase-velocity estimates were mainly those that corresponded to very ‘quiet’ sites, in connection with a too limited duration of the recording, and a reduced number of stations. Figure 3 (gray) shows the arrays that did not produce usable information in terms of dispersion curves from passive experiments. Globally, over the whole dataset, the HRFK method provided most of the dispersion curves. One example is given in Fig. 5, which shows the FK, HRFK, and MPSAC dispersion images, together with the extracted dispersion curves, for the OGIM station. In this example, all of the processing methods succeeded in providing dispersion estimates, except the MSPAC analysis for the largest array, due to the very strong dominating source between 1 and 4 Hz.

Fig. 5
figure 5

Systematic AVA processing of the OGIM station survey. Left FK, centre HRFK, right MSPAC. Dashed and continuous black lines indicate the theoretical array resolution; namely kmin and kmin/2. All frames have the same scale. All processing allowed the picking of a dispersion curve, except for MSPAC for array #4

Full size image

Active MASW measurements were processed for both horizontal and vertical polarization using the FK method. Here, the dispersion curves were also carefully picked, especially at low frequencies, to avoid near-field effects (e.g., cylindric propagation, near-field). For all of the sites, for the shots that were performed with a relatively short distance between the source and the first geophones, the closest geophones from the source were excluded from the processing (typically, 5–10 m far from the source). Next, for the sites where AVA processing led to dispersion curves up to high frequencies (indeed, in most cases), the ‘O’Neil criterion’ (O’Neil 2003) low-frequency limit was used (maximum interpretable wavelength = 0.4 × profile length; e.g., 18.4 m for a line of 24 geophones with a 2-m interstation interval). This criterion was rather constraining, especially for near-source offset; however, using large source offsets helped to relax this rule for larger interpretable wavelengths (O’Neil 2003). For other sites, where only the MASW measurements were performed or where small aperture AVA failed to produce dispersion curves at high frequency, the dispersion curves beyond the O’Neil limit were picked with care, although wavelengths that were larger than the profile length were never picking, for the sake of safety. Figure 6 shows some examples of the processing and dispersion-curve picking for active MASW measurements performed for the OGIM site.

Fig. 6
figure 6

Example of MASW processing of the OGIM station survey. Left vertically polarized acquisition leading to Rayleigh-wave dispersion curve. Right horizontally polarized acquisition leading to Love-wave dispersion curve. Black solid line indicates wavelength corresponding to the O’Neil criterion (0.4× profile length)

Full size image

All of the dispersion curves were then combined to build a broadband dispersion curve for each site. Most of the sites showed several dispersion curves: Rayleigh-wave fundamental mode and higher modes, and Love-wave fundamental mode and higher modes. Note also that in some cases, the dispersion curve corresponding to one given mode was not necessarily continuous from low to high frequencies as frequency gaps can exist. At this step in the whole procedure, the mode attribution of each dispersion curve was indicative and could be further monitored and revised during the inversion tests. Figure 7 shows an example of the individual dispersion curves and combined dispersion curves for the OGIM site. Here, the fundamental mode of Rayleigh waves (denoted as R0) was identified, with no higher modes. The combined R0 dispersion curve for the OGIM station covered a wide frequency range, from 1.3 to 70 Hz. FK and HRFK provided dispersion estimates up to 30 Hz, while MASW allowed the extension of the dispersion curve up to 70 Hz. The dispersion curve derived from MSPAC was rejected here: it was not coherent with the other dispersion curves, and a complementary analysis showed that the wavefield was dominated by a single dominant source of vibration, when MSPAC processing needs a relatively good azimuthal distribution of sources. Figures 8 and 9 show all of the broadband dispersion curves for 30 of the 33 sites, with the phase velocity either expressed as a function of the frequency or as a function of the wavelength. OGBL was the site that was characterized by a dispersion curve that started at the lowest frequency, at 0.4 Hz, inferred from the MSPAC processing on a very wide passive-array aperture (1200 m) leading to the measurement of a 5-km wavelength. At high frequencies, the higher picked frequency (95 Hz) was found for the PYLO site. Several sites (PYOR, IRPV and OGAP) had dispersion curves down to 2 m wavelengths. Statistically, and not surprisingly, sites that were investigated with the most extensive surveys (several 15-sensor double-circle AVA and MASW measurements) had the most continuous dispersion curves over the wider frequency band.

Fig. 7
figure 7

Gathering of all dispersion curves (DCs) derived from AVA and MASW analysis of the OGIM station survey. Dispersion curves are shown as frequency–velocity plot (left) and wavelength–velocity plot (right). Colored lines shows dispersion curves for each type of processing. Black line shows the final ‘broadband composite’ dispersion curve that is used for inversion. Here, the MSPAC dispersion curve and the lower frequency (<40 Hz) segment of the MASW dispersion curve are rejected due to a wavefield dominated by a single source of vibration

Full size image
Fig. 8
figure 8

Frequency–phase velocity plots of all of the broadband composite dispersion curves for the 30 sites that led to a successful processing. The different colors indicate the dispersion-curve mode (e.g., red Rayleigh fundamental mode; orange Rayleigh first higher mode; etc.). The green line indicates the wavelength of 40 m that is a proxy to roughly infer VS30 from the R0 dispersion curve. All frames have the same scale

Full size image
Fig. 9
figure 9

As for legend to Fig. 8, but for the phase velocity-wavelength plots

Full size image

Three sites did not allow derivation of significant dispersion curves. For two of these (EPF, PYLL), AVA did not succeed and the MASW results were very heterogeneous, and only the information at high frequencies (i.e., associated to very shallow layers) was ‘extractable’ from the data. For OGSI, the MASW was indeed performed within a tunnel, which did not allow the generation of a surface wave at a sufficiently large wavelength.

5 Inversion and derivation of velocity profiles

The inversions were performed with the inversion tool of the Geopsy software package, which uses a global search approach with a neighborhood algorithm (Wathelet 2008). The broad-band dispersion curves previously derived were inverted, which in most cases involved joint inversion of both the Rayleigh and Love dispersion curves, with sometimes several various modes. The inversion scheme used here required the identification of surface wave modes. Such identification could be done iteratively starting by the ‘simplest’ solution (fundamental mode for both Rayleigh and Love dispersion curve) and checking whether this assumption provided satisfactory ground profiles in terms of inversion misfit. The Geopsy software package also allows letting free the mode identification and computes different mode attribution possibilities, which helps attributing propagation modes.

Other information than dispersion curves can be used for inversion. For example, for sites where a clear fundamental frequency can be deduced from the H/V analysis, the f0 value was also used in a joint inversion. In general, the usable ‘a-priori’ available geological information was poor, although it could be used in some cases to select between different ground structure parameterization hypotheses. For example, in the case of rock sites that showed visible hard rock outcrops with no evidence of large weathering, the parameterizations that resulted in profiles with shallow layers associated with too low velocity values were rejected in favor of the parameterizations that produced more realistic results. At the OGFO site, the bedrock depth was also set as a priori information, due to the availability of a deep borehole that reached the bedrock at 535 m in depth (Nicoud et al. 2002). For the OGDH and OGFO sites, the availability of nearby geotechnical boreholes also allowed the inclusion of a low-velocity layer in the ground-model parameterization. A low velocity layer was also introduced for the OGBL site. Table 2 summarizes the information that was used for the inversion of each site.

Table 2 Summary of information used in the inversion procedures for each site studied here
Full size table

For sites where horizontally polarized MASW acquisition was available and usable, a standard shear-wave seismic refraction analysis was also performed, to provide an alternative evaluation of the ‘first layer’ shear-wave velocity and related thickness. Even if the concept of the first layer is not the same between surface-wave inversion and shear-wave seismic refraction, the order of magnitude of these values were compared and helped to identify sites that showed inconsistencies. These sites were then revised in the inversion procedure. An important additional ‘control’ was included using the phase velocity of the fundamental Rayleigh-wave dispersion curve (when available) at the wavelengths of 40 and 45 m. Some studies have indeed shown that these values provide a good proxy of the VS30 (Martin and Diehl 2004; Albarello and Gargani 2010). Here also, when the difference between VS30 inferred from the velocity profiles and Vλ40 or Vλ45 were too high, the inversion procedures were revised.

In order to limit the depth of provided profiles to account for the real investigation depth, we followed the usual rule of thumb that relates the maximum resolution depth to half the largest wavelength, while also being aware that the actual maximum resolvable depth could be much smaller, especially for sites that show large impedance contrast in the near surface. As for the thickness of the first (shallower) layer, the usual rule of thumb suggests that the smallest thickness should not be smaller than half to a third of the smallest wavelength. While this is suitable when only the fundamental Rayleigh-wave mode is inverted, this criterion can be relaxed with joint inversion of Love-wave mode(s) and Rayleigh-wave mode(s) (Eslick et al. 2008; Xia et al. 2012; Yin et al. 2014).

In order to provide an optimized evaluation of uncertainties associated to velocity profiles inferred from inversion and to VS30 values, the following procedures was used. Once the mode numbering determined, different inversion parametrizations were tested (e.g., 2 layers, 3 layers, etc. up to 6 layers, using uniform velocity layers or gradient velocity layers). Only parametrization that produced satisfactory results and misfit were retained. For those parametrization, we used the ‘acceptable misfit’ approach (Lomax and Snieder 1995; Souriau et al. 2011), which led to a set of equivalent VS profiles that explain the dispersion estimates within their uncertainty bounds. In such a case, the search algorithm does not try to find the best misfit Vs profile, but rather a large number of Vs profiles (50,000 or more) that explain the data equally well. For each site, at least three different parametrizations were used. This way helps in the identification of the VS profile uncertainties that were associated to the non-uniqueness of the inversion, and the effects of the dispersion-curve uncertainty on the inversion data. Once the inversions done, at least 6000 profiles were randomly extracted from the obtained tens of thousands profiles. These profiles were then used to compute average VS30 value and associated uncertainty, \(\sigma\). In order to deal with a reasonable set of profiles (for example to compute 1D soil response), we then randomly extracted 33 profiles from the former large set, such as this set of profiles reproduce the VS30 average and uncertainty \(\sigma\). We have thus extracted:

  • 7 profiles that led to VS30 values between \(\bar{V}_{S30} - 0.25 \sigma\) and \(\bar{V}_{S30} + 0.25 \sigma ,\)

  • 6 profiles that led to VS30 values between \(\bar{V}_{S30} - 0.75 \sigma\) and \(\bar{V}_{S30} - 0.25 \sigma ,\)

  • 6 profiles that led to VS30 values between \(\bar{V}_{S30} + 0.25 \sigma\) and \(\bar{V}_{S30} + 0.75 \sigma ,\)

  • 4 profiles that led to VS30 values between \(\bar{V}_{S30} - 1.25 \sigma\) and \(\bar{V}_{S30} - 0.75 \sigma ,\)

  • 4 profiles that led to VS30 values between \(\bar{V}_{S30} + 0.75 \sigma\) and \(\bar{V}_{S30} + 1.25 \sigma ,\)

  • 2 profiles that led to VS30 values between \(\bar{V}_{S30} - 1.25 \sigma\) and \(\bar{V}_{S30} - 1.75 \sigma ,\)

  • 2 profiles that led to VS30 values between by \(\bar{V}_{S30} + 1.25 \sigma\) and \(\bar{V}_{S30} + 1.75 \sigma ,\)

  • 1 profile that led to VS30 value between by \(\bar{V}_{S30} - 1.75 \sigma\) and \(\bar{V}_{S30} - 2.25 \sigma ,\)

  • 1 profile that led to VS30 value between by \(\bar{V}_{S30} + 1.75 \sigma\) and \(\bar{V}_{S30} + 2.25 \sigma ,\)

\(\bar{V}_{S30}\) being the average VS30 value and \(\sigma\) being the standard deviation.

Figure 10 shows the inversion results (subset of the ‘acceptable’ VS profiles) for the OGIM site by using a 3-layers-over-half-space parametrization. To visualize the robustness of these results, the forward-modeled dispersion curves were compared to the measured dispersion curves (i.e., Rayleigh and Love, fundamental and first higher modes). For the OGIM site, the most consistent results were obtained by attributing the fundamental mode (R0) to the Rayleigh dispersion curve, while the first higher mode was chosen for the Love dispersion curve (L1). Figure 11 shows the VS profiles derived for all of the 30 stations (here, for each station, only the 33 selected VS profiles are represented, together with the envelope of all ‘acceptable’ Vs profiles).

Fig. 10
figure 10

Inversion results for the OGIM station survey for one given parametrization. Left set of statistically acceptable VS profiles explaining the observed dispersion data within their uncertainty bounds. Center and right theoretical dispersion curves inferred from the full inverted profile set for Rayleigh phase (center) and Love phase (right), compared to the measured dispersion curves and estimated standard deviation

Full size image
Fig. 11
figure 11

‘Acceptable’ Vs profiles (blue lines) obtained by inversion for the 30 sites that led to successful processing. For each site, a set of 33 profiles are shown, randomly chosen to explore the uncertainty within the full set of ‘acceptable’ profiles. Red lines show the envelopes of all computed ‘acceptable’ profiles. All frames have the same scale, but note the unusual log-scale on the depth axis, used here to show all of the stations results in the same way

Full size image

The derived VS profiles have to be considered as profiles that satisfyingly explain the experimental dispersion curves(s). The VS profiles do not necessary reflect the exact lithological layering. For example, the most general ‘staircase shape’ of the ground profiles may reflect the way the inversion accommodated a ‘gradient-like’ real VS profile (i.e., continuous increase in VS with depth).

When the seismic bedrock velocity was well constrained, we could also compute the local 1D site responses, even though the VS profiles themselves were non-unique as a result of the inversion process, or were ‘simplified’ by the inversion ground-model parameterization choices. The determination of the bedrock velocity could appear rather difficult, but nonetheless achievable as shown in this study. This estimation was made possible in this study in most cases through the use of rather large arrays. Until recently, it was considered that passive surface wave-based methods were not suitable for rock sites, especially due to the low level of ambient vibration characterizing such sites. However, as far as careful signal analysis is performed (seismic noise level, instrument setup, recording durations), consistent results can be obtained. Another example of hard rock site characterization could be found in Garofalo et al. (2016a, b).

6 Contribution of Love-wave active measurements

In most common surveys, only Rayleigh waves are recorded and considered for inversion. In the present study, for the MASW acquisition, we recorded both Rayleigh waves (with vertical geophones and excitation) and Love waves (with horizontal geophones and excitation). In several cases, and especially on rock sites, the Love-wave MASW acquisition allowed us to obtain clearer dispersion curves than the Rayleigh-wave MASW acquisition. This observation has also been outlined through numerical and experimental studies (Safani et al. 2005; Dal Moro and Ferigo 2011; Xia et al. 2012; Boaga et al. 2013). Measuring Love waves thus greatly helps in the identification of the modes of propagation, especially at those sites that show weathered rock material at the near surface overlying much stiffer geological units, or at sites with low-velocity zones.

When possible, we jointly inverted Rayleigh and Love wave dispersion curves, thus allowing for better-constrained inversions and a more robust set of VS profiles. Figure 12 shows the example of the OGCA site with only Rayleigh R0 mode inversion, and with both Rayleigh and Love inversion (R0 and L0 modes). For this site, the use of the Love dispersion curve allowed the VS model to be better constrained within the first meters below the surface, and especially for the weathered near-surface layers. This information in the near surface is also important to understand the high frequency content of the accelerograms recorded at these stations.

Fig. 12
figure 12

Example of the contribution of Love-wave dispersion curves (DC) in addition to Rayleigh-wave dispersion curves within the inversion, for the OGCH station survey. On the top result of the inversion when only the Rayleigh dispersion curve is used to constrain the inversion (the empirical Love dispersion curve is shown in blue but is not used for inversion). On the bottom both Rayleigh and Love dispersion curves are used, leading to a more constrained velocity profile (the empirical Love dispersion curve is shown in black, all direct dispersion curves computed with inverted profiles fit now the empirical Love dispersion curve). Left ensemble of statistically acceptable VS profiles. Center and right theoretical dispersion curves inferred from the full inverted profile set for Rayleigh phase (center) and Love phase (right), compared to the measured dispersion curves and estimated standard deviations

Full size image

7 Vs30 and soil class results

Table 3 gathers all the results in terms of VS30 and the associated uncertainties and EC8 soil classes. Most of the VS30 values in Table 3 (i.e., 30 out of 33) were computed from velocity profiles derived from surface-wave dispersion-curve inversion. These sites correspond to the indication of ‘1’ in the ‘VS30 source’ column of Table 3. For three of the 33 sites (EPF, PYLL, OGSI), it was not possible to build up a broadband dispersion curve, and VS profile inversion was thus not possible (or simply for the few meters of the uppermost layers). In this case, VS30 was roughly evaluated on the basis of the velocity within the shallowest layers determined from the VS seismic refraction analysis and the phase velocity at very high frequencies, and by analogy with the other sites with the same velocity within the shallower layers. These sites correspond to the indication ‘2’ in the ‘VS30 source’ column of Table 3. For three other sites (OCOL, OGLE, OGMU), the VS profiles do not reach the depth of 30 m as far as we respect the rule of thumb that limits the maximum resolution depth to half the largest wavelength of the measured dispersion curve. For these sites, we used the deepest velocity value of the calculated velocity profile (which is for all these cases rather high and corresponds to unweathered rock) and used it to complete the profile up to 30 m. From a general point of view, as the velocity profile usually increases with depth, these extrapolated values may underestimate the real VS30 value.

Table 3 Summary of the VS30 and soil class estimations (medians and standard deviation) for each studied site
Full size table

We attempted to estimate the uncertainties in three ways. The first was from the inversion using the ‘acceptable misfit’ concept applied on multi-parametrization results. This option probably underestimates the real uncertainty. The second option consisted of the use of the Rayleigh experimental dispersion-curve standard deviations at the wavelength of 40 m (i.e., when the dispersion curve was ‘available’ at this wavelength, and when the dispersion curve corresponded to the fundamental Rayleigh mode). Indeed, some studies have shown that this value is a good proxy of the VS30 (Martin and Diehl 2004; Albarello and Gargani 2010). For some sites where the dispersion curves were not strictly available at 40 m, we slightly extrapolated (or interpolated) dispersion curves to get the standard deviation at 40 m. The third option was to apply a ‘minimum’ fixed coefficient of variation based on the InterPacific project feedback (Garofalo et al. 2016b) for the variability between the various analysts on the ‘best’ VS estimates. This minimum coefficient of variation was set at 10% when the R0 dispersion curve was available at λ = 40 m, and was set at 20% when it was not available (this was often the case when only the MASW experiments were usable). Obviously, these ‘uncertainty estimates’ were not comparable to one another. However, due to a lack of scientific consensus and any well-established method to quantify the uncertainty of inverted VS profiles (Cornou et al. 2006; Di Giulio et al. 2012; Michel et al. 2014; Cox and Teague 2016), we finally chose the ‘worst’ uncertainty estimation. In Table 3, the ‘σ source’ column gives the chosen uncertainty estimates:

  • 1: based on the acceptable misfit, mutli-parametrization approach;

  • 2: based on a fixed minimum 10% uncertainty;

  • 3: based on a fixed minimum 20% uncertainty;

  • 4: based on the dispersion-curve uncertainty at λ = 40 m;

  • 5: large uncertainty in the case of VS30 roughly estimated for the VS refraction data.

In Table 3, the ‘site VS30’ and ‘station VS30’ were distinguished. The site VS30 corresponds to values computed from the surface to 30 m, inferred directly from the survey. In some cases, the accelerometric station was not installed at the surface, but at a certain depth (e.g., when the station was installed in the basement of a building). In this case, a second value was computed, from h to h + 30 m, where h is the sensor depth. This value corresponds to the ‘station VS30’ value. In our study, the maximum station depth is 5 m. When the ‘station VS30’ values are higher than the ‘site VS30’ values, this means that the shallower (and often softer) layers are not accounted for in the calculation. In Table 3, the uncertainties values are associated to the “station VS30”. When this uncertainty comes from the experimental dispersion-curve standard deviation at the wavelength of 40 m, no distinction is made between site and station VS30 since there are no significant differences between 40 and 45 m on the dispersion curves in terms of in standard deviation.

A comparison between the present study and the previous studies can be carried out. For example, Régnier et al. (2010) gathered a wide range of pre-existing geophysical and geotechnical information in the vicinity of the RAP sites. However, the sources of this information were very heterogeneous and the soil conditions of numerous stations were inferred from very indirect inputs, such as geological maps. The comparison between the present work and the previous one by Régnier et al. (2010) can be carried out for 28 sites. Among these stations:

  • 3 previously assumed ‘A class’ stations now ‘downgraded’ to B class;

  • 1 previously assumed ‘B class’ station now ‘downgraded’ to C class;

  • 2 previously assumed ‘C class’ stations now ‘downgraded’ to D class.

  • 1 previously assumed ‘E class’ station may be now ‘upgraded’ to B class (but an uncertainty remains for the OCLD site).

In terms of VS30 values:

  • 9 stations now have lower VS30;

  • 15 stations remain unchanged (within ±25%).

  • 4 stations now have higher VS30.

Another previous study was done by Drouet et al. (2010) that have been aimed at estimation of VS30 using generalized inversion methods and by comparing site-transfer functions from the inversion to generic amplification curves derived from generic VS profiles (Boore and Joyner 1997; Cotton et al. 2006). This study was focused on 21 presumed rock sites. Here, the comparison can be made for 14 stations. In terms of VS30 values:

  • 5 stations have now lower VS30;

  • 7 stations remain unchanged (within ±25%);

  • 2 stations now have higher VS30.

Of course, these previous studies did not use extensive in situ measurements, and the station soil classes and VS30 were often estimated indirectly. However, this overall observation shows that VS30 of the network stations is usually and statistically overestimated when classification is not based on in situ measurements (this has already been observed for other networks, such as in Italy, see e.g., Pileggi et al. 2011).

8 Reference stations

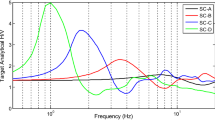
Beyond the discussion of the VS30 values, one important issue is the concept of the reference stations. These reference stations can be defined as stations that were not affected by local amplification due to site effects. To comment on this concept, we chose the stations from our set that were clearly within the A soil class, and for which it was possible to derive a shear-wave velocity profile (OCOL, OCOR, PYAT, PYLI, PYLO, CALF, IRVG, OGCA, GRN, OGAN, OGCH, OGMU). For each of these, the theoretical 1D transfer function (1DTF) for vertically incident S-waves was then computed, using the Haskell-Thomson computation. All 33 representative profiles were used; mean and standard deviation were computed for each site. These curves are divided by 2 to correct for the free surface effects (i.e., the ‘1’ value means no amplification). The simulations were carried out with damping defined as QS = VS/20. As an example, the amplification of three of these sites (OGAN, OGCH, PYLI), are given in Fig. 13 (these stations also have an ambient vibration H/V ratios characterize by a peak frequency that was coherent with the 1DTF). Most of the stations showed important amplification at high frequency. This amplification can have an impact on the evaluation of the ‘high-frequency parameters’, such as κ (Ktenidou et al. 2014). It would then be interesting to define a parameter that can determine for a given station the frequency up to which the station site response function can be assumed to remain ‘flat’. For example, we identify for each station the frequency above which the amplification is >1.5. This frequency is relatively low for some of the stations (e.g., OGAN: 6.6 Hz), whereas it is high for others (e.g., OGCH: 14.6 Hz).

Fig. 13
figure 13

Example of 1D transfer functions (1DTF) computed using the shear-wave velocity profiles inferred from surface-wave inversion. We chose stations that are clearly within the EC8-A soil class and for which the ambient vibration H/V ratio frequency peaks are coherent with 1DTFs. For each station, 33 1DTF were computed using 33 different ‘acceptable’ profiles (grey lines), as well as the means and standard deviation of these (red line). All stations show high-frequency amplification due to shallow ‘softer’ layers. The frequency identified by the green vertical line is the one above which amplification >1.5

Full size image

9 Topographic amplification

Although this study is not intended to provide a systematic assessment of the topographic site effect, the magnitude of this effect could be assessed in relation to the lithologic effect. In order to perform this evaluation, the ‘frequency-scaled curvature’ (FSC) proxy proposed by Maufroy et al. (2015) was computed using available digital terrain models. This approach was applied on four selected stations (IRVG, OGCA, GRN and IRPV). IRVG and GRN are interesting for this study since they are likely the stations that are located on the steepest relief among our station set. IRVG is also the station that has the highest VS30 value (2090 m/s) and the only one that shows almost no amplification (even at high frequency) according to the previous lithological amplification analysis. In contrast, OGCA is a station that has a high VS30 (1383 m/s), while being located on a gentle slope. IRPV has a lower VS30 (605 m/s) and is located on a sand and molassic Miocene deposit basin. IRVG, OGCA and IRPV FSC proxies were computed using digital terrain models (DTM) with a high resolution of 1 m, whereas GRN was computed with a 25 m DTM. FSC proxy is expressed as a function of shear wave wavelength. In order to convert as function of frequency, the velocity of 3000 m/s was used for all of the four considered stations. This value corresponds to the order of magnitude of velocity at depth for all stations, the one to be considered for the large wavelengths impacted by topographic effect. FSC proxies were computed down to the minimum wavelength of 100 m for IRVG, OGCA and IRPV, and down to 300 m for GRN. Results are shown on Fig. 14 where topographic amplification (computed with Maufroy et al. 2015, FSC proxy) and lithological 1D amplification (computed following the procedure described above) are compared.

Fig. 14
figure 14

Estimation of lithological amplification and topographic amplification on four sites (IRVG, OGCA, GRN and IRPV). Lithological amplification is computed with 1D numerical simulation using the 33 shear wave velocity profiles for each site obtained in the present paper. Topographic amplification is predicted using the frequency-scaled curvature proxy proposed by Maufroy et al. (2015) using digital terrain models (with a resolution of 1 m for IRVG, OGCA and IRPV; and 25 m for GRN—causing the evaluation limitation at high frequency)

Full size image

Among the tested sites, two of them show no topographic amplification, i.e., OGCA and IRPV. While IRPV is located close to a small ridge, its closeness to that topographic feature is not enough for that station to be affected. The station itself is located over a very weak and regular slope that doesn’t produce amplification according to the FSC proxy. Similarly, OGCA is located over a gentle slope and no topographic amplification is awaited. Only a weak deamplification occurs at OGCA below 3 Hz, but that effect is too weak to be observable. Given such results, any amplification effect observed at OGCA or IRPV should be attributed to lithological origins. On the contrary, IRVG and GRN are both located over sharp topographies, and thus the FSC proxy predicts a noticeable topographic amplification at both sites. IRVG appears affected over a large frequency bandwidth, with the level of amplification being remarkably stable among frequencies, decreasing only towards 1 Hz. GRN is even more affected, but the low-resolution DTM used for the proxy calculation doesn’t allow observing if the effect remains in the higher frequencies.

This figure shows that the topographic amplification is a broadband smooth function, compared to the lithological effect that produces strong peaks of amplification in narrow bandwidths. The topographic site effect may affect rock sites typically used as reference sites, which underlines the importance to carefully analyse the amplitude of the ground motion at those sites even if no clear peak of amplification appears, keeping in mind that the topography may smoothly amplify the ground motion over a large bandwidth.

One remaining issue is the combination of both lithological and topographic site effects at the same site. Predictions are available for separated effects, but there is currently no method to conjointly predict both effects, or on how to combine both predictions. As illustrated by our results at IRVG and GRN, both effects can overlap in the same frequency band, and thus this issue should be tackled in order to better understand the origins of the amplification measured at topographic sites.

Note also the strong deamplification around 25 Hz for the GRN station. In fact, the station is not located at surface, but in a small cave, at a depth of around 5 m. This deamplification is due to the destructive interference of the downgoing wave. This situation should also be taken into account for high frequency analysis of accelerometer records since it can also widely affect signal spectrum.

10 Conclusions

We carried out site characterization surveys on 33 sites of the French RAP network. This campaign was performed using surface-wave-based methods that allowed the derivation of the shear-wave velocity profiles from the dispersion characteristics of the surface waves. Even if the logistic context was sometimes difficult, the use of surface-wave-based methods is suitable for accelerometric station characterization, and also on rock sites (where the applicability of these methods has sometimes been disputed). It was possible to retrieve broadband dispersion curves for 30 sites to derive shear-wave velocity profiles, and then to propose VS30 values and EC8 soil classes, with their associated uncertainties. For three sites, the EC8 soil classes could be deduced from S-wave refraction seismic processing, although the surface-wave-based processing failed to produce significant results, probably due to a too-low level of ambient vibration and/or a too-short duration of recording and/or a too-low number of sensors. To maximize the chances of obtaining usable data, we recommend the use of a relatively high number of sensors for AVA (15 sensors in this study) with the proposed double-circle geometry and with successive increasing apertures. We also strongly recommend the joint use of active (MASW) and passive (AVA) methods, to obtain ‘broadband’ dispersion curves. The use of Love waves (for MASW in this case) is also very valuable in the inversion process, to reduce the probability of misidentification of surface-wave modes and to increase the inverted VS profile resolution within the shallower layers.

In comparison with previous studies, which have mainly estimated VS30 indirectly, these new values are globally lower, and a few of the stations were ‘downgraded’ in terms of the EC8 soil classes, although there remain many EC8-A class sites. Interestingly here, the seismic bedrock velocity could be measured at some rock sites due to the large-aperture arrays. Some high frequency amplification is suggested at most of the rock sites due to the near-surface weathering. This feature should definitely be accounted for in terms of the good use of accelerometric data in the case of high-frequency studies.

As mentioned by Michel et al. (2014), future comparisons of predicted 1D seismic responses with those obtained on earthquake recordings, as well as inclusion of other dispersion features (e.g., polarization, ellipticity, use of Love-wave dispersion curves from passive recordings, use of various ground model parameterization) will definitely help in the constraining of VS profiles and the related uncertainties, to reach robust and very reliable site characterization, and hereafter, better estimates of local site effects.

11 Data and resources

The data from field measurement can be obtained by simple request to the authors. The results presented in this paper will be available on the RESIF webportal (http://www.resif.fr/).