Practical Modal Pushover Design of one-way asymmetric-plan reinforced concrete wall buildings for unidirectional ground motion

Abstract

This paper presents a new displacement based seismic design method called Practical Modal Pushover Design (PMPD). The method is applied to multistory one-way asymmetric-plan RC wall structures. PMPD combines concepts from Direct Displacement-Based Design with an inverse version (formulated herein) of Practical Modal Pushover Analysis (PMPA). PMPD generates designs which achieve peak deformations exactly equal to the governing deformation limits when analyzed with PMPA. An alternative method, Modal Pushover Design (MPD), which is, to some extent, an inverse version of Modal Pushover Analysis, is also discussed. MPD is computationally more demanding than PMPD, but has improved performance in cases where yielding may occur due to ‘higher mode’ response. Advantages of PMPD include explicit consideration of nonlinear, torsional and ‘higher mode’ effects. Iteration is limited to the response spectrum level, so multiple analyses of Multi-Degree of Freedom systems are not required. Capacity design principles are implemented directly from the start of the design process. A significant advantage of PMPD is that the engineer can have the same confidence in the structure’s seismic performance as he has in PMPA’s ability to predict the structure’s peak seismic responses. Therefore PMPD can be used for the seismic design of any structure for which PMPA is expected to provide acceptably accurate predictions of peak seismic responses. The effort required to carry out PMPD is similar to that required for PMPA. The only additional work consists of specifying a relative flexural strength distribution and executing a small number of iterations at the Single Degree of Freedom level.

Appendix: PMPD procedure outline

Obtain the structure’s geometry (see Fig. 1) and material properties: $f_{y}$ and $\epsilon _{sy}$

• 1. Specify a rational distribution of relative flexural strength.

  • (a) Define a horizontal distribution of relative flexural strength $M_{hi}^{'}$, as a row vector, where $i=1{:}\,N_{w}$ and $N_{w}$ is the number of walls. The tag (apostrophe) denotes values characterizing the FE model used in the pushover analysis. Use the approximately known axial load contributions to base moment capacities and target 1st story reinforcing steel ratios in Eq. 3. See Fig. 4.

    $$\begin{aligned} M_{hi}^{'} = 0.5 \left( f_{y} b_{i} \rho _{1,i}^{'} L_{i}^{2} + L_{i} N_{1,i} \right) \end{aligned}$$

    (3)

    where $b_{i}$ is the $i$th wall’s thickness, $\rho _{1,i}^{'}$ corresponds to a target 1st story longitudinal reinforcing steel ratio, and $N_{j,i}$ is the design axial force for the $j$th story of the $i$th wall for the selected load case. Note that Eq. 3 is not intended for use in section design and is only used to define the horizontal distribution of relative flexural strength.

  • (b) Define a vertical distribution of relative flexural strength $M_{vj}^{'}$, as a column vector, where $j=1{:}\,N_{s}$ and $N_{s}$ is the number of stories. See Fig. 3.

  • (c) Compute relative flexural strength matrix:

    $$\begin{aligned} M_{yji}^{'} = M_{vj}^{'} M_{hi}^{'} \end{aligned}$$

    (4)

• 2. Compute relative elastic wall flexural stiffnesses and modal characteristics:

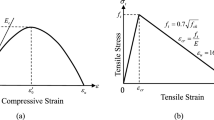
  • (a) Estimate wall yield curvatures using, for example, Eq. 5 from Priestley et al. (2007):

    $$\begin{aligned} \varphi _{yi} = 2\epsilon _{sy}/L_{i} \end{aligned}$$

    (5)

    (for RC walls with rectangular cross sections) where $\epsilon _{sy}$ is the longitudinal reinforcing steel yield strain and $L_{i}$ is the length of the $i$th wall.

  • (b) Compute relative flexural section stiffness: $EI_{ji}^{'} = M_{yji}^{'}/\varphi _{yi}$.

  • (c) Solve the eigenvalue problem of the known floor masses $m$ and rotational inertias $I$ and the stiffnesses $EI_{ji}^{'}$ to find the elastic mode shapes of free vibration $\mathbf{\phi _{n}}$ (normalize each mode by its roof $c_{M}$ translational term), the periods $T_{n}^{'}$ and the ratios between periods $\gamma _{Tn} = T_{n}^{'}/T_{1}^{'}$, the modal participation factors $\varGamma _{n}$, and the modal effective masses $m_{n}$ and heights $h_{n}$ (Chopra 2007):

    The first $N$ global degrees of freedom can be taken as the center of mass translations of the floors (numbered like the floor numbers). The last $N$ global degrees of freedom can be taken as the floor rotations about a vertical axis through the mass centers numbered consecutively from $N+1$ to $2N$. $\bar{M }$ is associated with the floor translational degrees of freedom and $\bar{I }$ with the rotational ones. The mass matrix can be formulated as $M = \left[ {\begin{array}{*{20}c} {\bar{M}} & {\bar{0}} \\ {\bar{0}} & {\bar{I}} \\ \end{array} } \right]$ where $\bar{M }$ and $\bar{I }$ are diagonal matrices of order $N_{s}$, having respectively $m$ and $I$ on the diagonals and $\bar{0 }$ is a null matrix of order $N_{s}$.

  • (d) Truncate the number of modes considered by including only the first $N_{m}$ modes having modal effective masses summing to at least 90 % of the total seismic mass of the building.

• 3. Conduct pushover analysis for 1st ’mode’ response and define bilinear SDOF system.

  • (a) Estimate plastic hinge lengths $L_{pi}$ using, for example, Eq. 6 from Priestley et al. (2007):

    $$\begin{aligned} L_{pi} = kh_{ei} + 0.1L_{i}+L_{SP} \end{aligned}$$

    (6)

    where $k = 0.2(f_{u} / f_{y} -1) \le 0.08$ where $h_{ei}$ is the effective height of the $i$th wall estimated, at this stage, as 0.75 of the wall’s total height. $L_{SP}$ is the strain penetration length computed as $L_{SP} = 0.022f_{y} d_{bl}$ where $d_{bl}$ is a reasonable estimate of the diameter of the longitudinal reinforcing steel bars.

  • (b) Develop the base shear reference displacement ($V_{b}^{'} - u_{r}$) curve by conducting a pushover analysis on the 3D MDOF structural model characterized by the modal parameters above and the strengths $M_{yji}^{'}$. Neglect geometric nonlinearity. Apply an invariant load vector distribution ${\mathbf{p}} = {\mathbf{M}} \phi _{1}$ equal to the 1st mode effective earthquake force distribution. At each load increment, record center of mass translations and rotations (about the vertical axis) and the response parameters to be limited (e.g. wall curvatures and story shears).

  • (c) Approximate the pushover curve bilinearly without changing the initial elastic stiffness, $k_{el}^{'}$ by defining the yield displacement $u_{ry}$ and a ’post yield’/elastic stiffness ratio $\alpha$.

  • (d) Define an equivalent bilinear SDOF system having the yield shear $F_{y} = k_{1} D_{y}$ and ’post yield’/elastic stiffness ratio $\alpha$ and the spectral yield displacement defined as

    $$\begin{aligned} D_{y} = \frac{ u_{ry}}{\Gamma_{1} \phi_{r1}} \end{aligned}$$

    where $\phi_{r1}$ is the value of the 1st mode shape at the location of the pushover reference node.

• 4. Determine the value of $T_{1}$ corresponding to the critical story or plastic hinge achieving its limit deformation:

  For each applicable limit state:

  • (a) Define the design response spectrum (see for example Fig. 7).

  • (b) Calculate initial values $T_{1}^{it_{o} = 1}$ and $D_{1}^{it_{i} = 1}$:

    (i) For each wall compute:

    $$\begin{aligned} D_{1i} = \frac{u_{rdi}}{\sqrt{\sum _{n=1}^{N_{m}}({\mathbf{a}} _{i} \varGamma _{n} \mathbf{\phi _{n}} \gamma _{Tn})^{2}}} \end{aligned}$$

    (7)

    where $u_{rdi}$ is the $i$th wall’s traditional DDBD limit roof displacement, ${\mathbf {a_{i}}}$ is the $i$th wall’s roof displacement global to local coordinate transformation vector.

    (ii) Take $D_{1}^{it_{i} = 1}$ as the smallest $D_{1i}$.

    (iii) Using $\mu = max(D_{1}^{it_{i} = 1}/D_{y} ,1)$ enter the design response spectrum (for a constant ductility of $\mu$ and bilinear factor of $\alpha$) at $D = D_{1}^{it_{i} = 1}$ to estimate $T_{1}^{it_{o} = 1}$ (initial elastic period) and calculate the corresponding higher mode periods $T_{n}^{it_{o} = 1} = \gamma _{Tn} T_{1}^{it_{o} = 1}$.

  • (c) Outer iteration loop: for $it_{o} = 1, 2 \ldots$

    (i) Modify SDOF system to account for $P\varDelta$ effects:

    Compute 1st mode stiffness $k_{1} = \frac{4\pi ^{2} m_{1}}{\left( T_{1}^{it_{o}}\right) ^{2}}$.

    Compute stability index $\theta ^{P\varDelta } = W_{t}/(k_{1} h_{1})$ where $W_t$ is the structure’s total seismic weight.

    Modify period to account for $P\varDelta$ effects: $T_{1}^{it_{o}} = 2\pi \sqrt{\frac{m_1}{(1-\theta ^{P\varDelta })k_1}}$

    Modify $\alpha$ to account for $P\varDelta$ effects: $\alpha ^{P\varDelta } = \frac{\alpha -\theta ^{P\varDelta }}{1-\theta ^{P\varDelta }}$

    (ii) Inner iteration loop: for $it_{i} = 1, 2 . . .$ Compute $\mu ^{it_{i}} = D_{1}^{it_{i}}/D_{y}$, then retrieve $D_{1}^{it_{i}+1}$ from design response spectra using $T_{1}^{it_{o}}, \mu ^{it_{i}}$ and $\alpha ^{P\varDelta }$. Repeat this computation until $\left| 1-\frac{D_{1}^{it_{i}+1}}{D_{1}^{it_{i}}}\right|$ is acceptably close to zero.

    (iii) Extract $D_{n=2:N_{m}}^{it_{i}+1}$ from the elastic response spectrum using $T_{n}^{it_{o}} = \gamma _{Tn} T_{1}^{it_{o}}$ where $n = 2:N_{m}$.

    (iv) Extract the peak 1st mode contribution to wall interstory drifts from the pushover analysis results occurring between $u_{r} = 0$ and $u_{r} = \varGamma _{1} \phi _{r1} D_{1}^{it_{i}+1}$.

    (v) Compute the higher mode contributions to interstory drifts using $D_{n=2:N_{m}}^{it_{i}+1}$.

    (vi) Estimate total wall interstory drifts $\theta _{j,i}^{it_{o}}$ using an appropriate modal combination rule.

    (vii) Compute drift performance indices for each story $j$ at each wall $i$:

    Typical drift limits for serviceabilty and damage control limit states are 1 and 2 % respectively.

    $$\begin{aligned} dPI_{j,i}^{it_{o}} = \frac{\theta _{j,i}^{it_{o}}}{\theta _{lim}} \end{aligned}$$

    (8)

    Compute the maximum drift PI for the current iteration.

    $$\begin{aligned} DPI^{it_{o}} = max_{ji}(dPI_{j,i}^{it_{o}}) \end{aligned}$$

    (9)

    (viii) Extract the peak 1st mode contributions to intended plastic hinge region (wall base) curvatures $\varphi _{i,n=1}^{it_{o}}$ from the pushover analysis results occurring between $u_{r} = 0$ and $u_{r} = \varGamma _{1} \phi _{r1} D_{1}^{it_{i}+1}$.

    (ix) Compute the higher mode contributions to wall curvatures using $D_{n = 2:N_{m}}^{it_{i}+1}$.

    (x) Estimate total base curvatures $\varphi _{i = 1:N_{w}}^{it_{o}}$ using an appropriate modal combination rule.

    (xi) Define the strain based curvature limits using, for example, Eq. 10 from Priestley et al. (2007):

    For the serviceability limit state, limits were recommended in Priestley et al. (2007) for concrete and steel material strains of $\epsilon _{c,ls} = 0.004$ and $\epsilon _{s,ls} = 0.015$ respectively. For a damage control limit state the recommended limits on concrete and steel material strains were $\epsilon _{c,ls} = 0.018$ and $\epsilon _{s,ls} = 0.6\epsilon _{su}$ (where $\epsilon _{su}$ is the steel strain at peak steel stress) respectively. These allowable strains are based on stringent requirements regarding the transverse reinforcement provided.

    $$\begin{aligned} \varphi _{lsi} = \frac{1.2\epsilon _{s,ls}}{L_{i}} \end{aligned}$$

    (10)

    (for RC walls having rectangular cross sections) for all intended plastic hinge regions.

    (xii) Compute curvature performance indices for the intended plastic hinge regions at the wall bases:

    $$\begin{aligned} cPI_{i}^{it_{o}} = \frac{\varphi _{i}^{it_{o}}}{\varphi _{lsi}} \end{aligned}$$

    (11)

    Compute the maximum curvature PI for the current iteration:

    $$\begin{aligned} CPI^{it_{o}} = max_{i}(cPI_{i}^{it_{o}}) \end{aligned}$$

    (12)

    (xiii) Compute the key PI for the current iteration as

    $$\begin{aligned} kpi^{it_{o}} = max(DPI^{it_{o}},CPI^{it_{o}}) \end{aligned}$$

    (13)

    (xiv) If $kpi^{it_{o}}$ is not acceptably close to one:

    Adjust estimate of $T_{1}$ according to Eq. 14:

    $$\begin{aligned} T_{1}^{it_{o}+1} = T_{1}^{it_{o}} \left( \frac{1}{kpi^{it_{o}}}\right) ^{P} \end{aligned}$$

    (14)

    where $0<P\le 1$ is a parameter controlling convergence.

    Increase $it_{o}$ by one and repeat step 4c.

    If $kpi^{it_{o}}$ is acceptably close to one, compute final values for the considered limit state as $T_{1} = T_{1}^{it_{o}+1}$, $D_{1} = D_{1}^{it_{i}+1}$ and $\mu = \mu ^{it_{i}}$:

• 5. Compute design moment actions:

  • (a) Compute the flexural strength scale factor:

    $$\begin{aligned} F_{M} = \left( \frac{T_{1}^{'}}{T_{1}}\right) ^2 \end{aligned}$$

    (15)

  • (b) Scale the relative flexural strengths to provide the required stiffness corresponding to $T_{1}$ of the governing limit state:

    $$\begin{aligned} M_{yji} = F_{M} M_{yji}^{'} \end{aligned}$$

    (16)

  • (c) Compute stability index factor $F_{P\varDelta } = max\left( 1, \frac{\mu \theta ^{P\varDelta }}{0.3} \right)$. Multiply flexural strengths by $F_{P\varDelta }$.

  • (d) Design and detail flexural steel reinforcement using the applicable standard section/member analysis method considering the design moments and other actions:

• 6. Compute design shear actions:

  • (a) Extract peak 1st mode contributions to wall story shears $V_{j,i,1}^{'}$ from the push over results in the range $0 \le u_{r} \le \varGamma _{1} \phi _{r1} D_{1}$.

  • (b) Compute higher mode contributions to story shears $V_{j,i,n = 2:N_{m}}^{'}$.

  • (c) Combine modal contributions using an appropriate modal combination rule to determine $V_{j,i}^{'}$.

  • (d) Scale $V_{j,i}^{'}$ by $F_{M} F_{P\varDelta }$ to determine $V_{j,i}$ and adjust if necessary, to ensure that wall shear capacities do not increase with height. This determines the unfactored shear action distribution $V_{j,i}^{unfac}$ up the height of each wall.

  • (e) Factor $V_{j,i}^{unfac}$ up by the flexural reinforcing steel overstrength factor to determine the design shear actions.

  • (f) Design and detail shear steel reinforcement using the applicable standard section/member analysis method considering the design shears and other actions.

  If desired, the design base shear considering higher mode effects and ductility may be estimated as $V_{b} = \sum _{i=1}^{N_{wd}} V_{1,i}^{unfac} = C_{d} W_{t}$ where $N_{wd}$ is the number of walls in the directions considered.