Abstract
In this paper, representational structures of arithmetical thinking, encoded in human minds, are described. On the basis of empirical research, it is possible to distinguish four types of mental number lines: the shortest mental number line, summation mental number lines, point-place mental number lines and mental lines of exact numbers. These structures may be treated as generative mechanisms of forming arithmetical representations underlying our numerical acts of reference towards cardinalities, ordinals and magnitudes. In the paper, the theoretical framework for a formal model of mental arithmetical representations is constructed. Many competitive conceptions of the mental system responsible for our arithmetical thinking may be unified within the presented framework. The paradigm underlying our research may be interpreted philosophically as a neo-Kantian approach to modeling the mind’s representational structures.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The task of constructing formal models of any phenomenon requires its description in terms of its principal constituents. That is why formal models of representational structures encoded in the mind underlying its arithmetical thinking should reproduce its essential characteristics that appear empirically in various experimental data, technically called the SNARC effect, distance effect and size effect. These phenomena which accompany our arithmetical thinking are explained by processes taking place within an arithmetic representational structure of the mind.Footnote 1 Hence, it is justified to assume that basic constituents of the representational structure of our arithmetical thinking appear as properties of the above-mentioned effects. In other words, properties of these empirical effects are empirical, phenomenal manifestations of the architecture of mental arithmetical representational structures encoded in the mind. The main aim of the paper is to describe these properties.
Our research purpose may be interpreted philosophically as the first stage of an attempt to formalize the basic cognitive forms encoded in the mind which are entangled in processes of arithmetical thinking. In accordance with neo-Kantian epistemology, we assume that the mind is equipped with a system of cognitive forms responsible for the generation of so-called core knowledge. This system allows the mind, understood as a functional structure, to perform various basic cognitive acts of reference towards objects given to it in its ordinary experience.Footnote 2
Many researchers interpret the basic form of arithmetical thinking as a mental number line encoded in the mind (Siegler and Ramani 2008a, b; de Hevia and Spelke 2009; for opposing views, see Cipora and Nuerk 2013; Fischer 2006; van Dijck and Fias 2011). SNARC effects detected in psychological experiments are believed to confirm its existence. This line, as a cognitive mechanism, is treated as the basic cognitive arithmetical representation grounding premature arithmetical competence—that is, not comprising expert mathematical knowledge consisted of theorems, strategies and definitions which are required for the solution of various mathematical tasks with different degrees of difficulty—involving abilities of numerical reference. This competence, as the mind’s ability to execute various operations upon the mental number line, is sometimes called number sense (Giaquinto 2001; Dehaene 2001; Berch 2005). Other researchers refer to it as cognitive arithmetic (Ashcraft 1992). It manifests as numerical referential acts on the phenomenological level of intentional consciousness. One may distinguish three different types of acts of numerical reference: towards cardinalities, ordinals and magnitudes. Hence, the following question arises: What are the ways of processing the mental number line or lines by virtue of which representations underlying different acts of numerical reference are formatted and activated? The description of empirical properties of the mental number line or lines, revealed in experiments, should help to distinguish the essential constituents of the formal architecture of these lines and, subsequently, to build their formal model, which will be the theoretical device on the basis of which the answer to the above-formulated question will be given.
2 The Concept of the Mental Number Line
The concept of the mental number line (MNL) is understood as designating some special mental mechanism explaining the so-called SNARC effects (Spatial–Numerical Associations of Response Codes) (Dehaene et al. 1993), which are defined as associations of relative number magnitudes with sides in space. The most frequently used indicator of these effects is a difference in left- and right-hand response times to numeral stimuli presented to people examined in various experiments. In one experiment (Dehaene et al. 1993), participants were to evaluate the parity of a digit presented on the centre of the computer screen. They had two buttons at their disposal: one on the left side and the second on the right side. Responses to smaller digits were faster with the left-side button, whereas responses to relatively greater digits were faster with the right-side button.
SNARC effects appear as so-called slopes, that is, as linear functions of numerical values (magnitudes). The standard SNARC function for n ∈ 〈min, max〉 may be formalized in the following way, where n is the value of a numeral, n ∈ 〈min, max〉, min is the smallest value of a numeral and max is the greatest value of a numeral, 〈min, max〉 is a finite interval of natural number values, RTR is the right-hand response time function, RTL is the left-hand response time function, and, finally, RTR(n) − RTL(n) is the difference between the two response time functions:
The chart of standard SNARC(n), for each n from 〈min, max〉, takes the shape of a line such that RTR(n) − RTL(n) > 0 for relatively small n (equal to min or little greater than min), and RTR(n) − RTL(n) < 0 for relatively large n (equal to max or little smaller than max).
The occurrence of SNARC effects in appropriate experimental situations may be explained by the model of the mental number line, that is, by the mechanism of directly mapping a place in mental space taken by a given representation of a number onto a corresponding place in external space. This model, stemming from Galton’s psychology (Galton 1880) and subsequently found in (Restle 1970), is the most frequently cited in the literature for explaining SNARC effects.
Let us exemplify this rough and rather naive explanation in the following way. Let a digit with a small value be displayed on the screen. Because the representation of the number designated by this digit takes place on the left side of the mental number line, the subject directs its attention to the left side. As a result, he/she assigns the numeral stimulus (the presented digit) and the designated number to the left side of the external space where one of two buttons for the experimental response is located. If the experimental procedure requires the subject to react to a numeral stimulus with the left button, reactions will be faster due to the compatibility between the position of the number representation in the mental space and the position of its projection in the external space. If the experimental procedure, in turn, requires the reaction to a numeral stimulus with the right button, then the subject must change the direction of its attention in the external space. Hence, the reaction time will be prolonged.
If one accepts the MNL-hypothesis, then SNARC-functions observed in experiments as slopes on charts may be interpreted as revealing the spatial orientation of intentional acts of numerical reference. In SNARC-situations, acts of numerical reference towards cardinalities, ordinals or magnitudes would manifest the property of numerical referents consisting in their spatial, linear arrangement. This could mean that acts of numerical reference generate the mental space, understood as the intensional ‘receptacle’ with metrics (in Frèchet or Hausdorff’s meaning) for its different subspaces, filled with various, formally-structured mental contents, called mental representations (on mental spaces, see Fauconnier 1994, 36–37, Harder 2003, 91–99).
The MNL-hypothesis might be used in phenomenology as a theoretical tool explaining various properties of the so called horizons of consciousness (on phenomenological horizons of consciousness, see Krysztofiak 1995). The mental number line, activated in the mind during the execution of intentional acts of numerical reference, might be interpreted as the generator of the horizon of a given reference act. Such a horizon would be a reference-space of a given act with metrics determined by an activated mental number line. In accordance with standard SNARC-functions, reference-spaces of intentional reference acts would be geometrically arranged in a direction from left to right. Relatively small numbers are located on the left side of the reference-space and relatively large numbers are located on the right, which might mean that in a given reference-space the counting direction of referents (objects of reference acts) runs from left to right. From this phenomenological point of view, mental number lines might be reduced to geometrical counting schemata encoded in the mind which enable and facilitate subjects’ counting practices. Properties of SNARC effects might be treated as markers indicating the formal architecture of reference-spaces (horizons of consciousness) correlated with acts of numerical reference.
Some researchers argue that the mental number line is at most a culturally learned construct. Furthermore, they maintain that the mind uses this construct in various cognitive tasks as a metaphorical tool determined by chosen cognitive strategies. That is why these researchers assert that the mental number line, understood as the number-to-space mapping, is not an innate system of numerical representations encoded in the mind (Núñez 2011). Lakoff and Núñez (2000) defends the view that our mathematical skills stem from an innate skill of subitizing and a large number of metaphorical constructions and cognitive schemata acquired during the cognitive development of humankind. One of them is the metaphor of moving along a path. Defenders of the so-called embodied account of mathematical thinking try to justify the hypothesis by saying that the number-to-space mapping observed in experiments is not evoked by a so-called mental number line encoded in the mind (Fischer 2006). The flexibility of SNARC effects and individual differences in the way numbers are associated with space are the main data supporting this hypothesis. Núñez’ arguments show that it is extremely difficult to decide on the philosophical hypothesis of arithmetical nativism. However, they do not falsify the moderate standpoint according to which the mental number line is a representational structure encoded in contemporary human minds, regardless of whether it is acquired through education or it is innate. The system of core knowledge may be understood as historically and/or even evolutionarily changeable. In this way, the mental number line may be interpreted as a representational mental structure which is historically and culturally inherited, serving minds in acts of reference towards cardinals, ordinals and magnitudes.
Some authors (Fischer 2006, 2008) assert that in some task situations, an observed SNARC effect indicates that the subject has applied some cognitive strategy consisting in the use of a schema of mapping number values into spatial directions. Because the use of such schemata improves the processing of numerical information, subjects select those schemata which are best for improving information processing in the short term. For some tasks, a schema with small numbers at the bottom and big numbers at the top is better than one with small numbers on the left side and big numbers on the right. In (Fischer 2006, p. 1067), it is even suggested that ‘presence or absence of an association between numbers and space is the result of an individual’s strategic decision /…/ and not a reflection of their mental representation of numbers.’ On the other hand, individual strategic decisions, consisting in the use of cognitive schemata which help in the processing of numerical information, are also enforced by appropriate mental representations. The choice of cognitive axial schemata by a subject during arithmetic task solving, or the failure to make this choice, may be explained by processes of activation or deactivation of the MNL encoded in the mind.
The MNL, as a cognitive form or pattern encoded in the mind, calls to mind Kant’s pure form of time arranging perceptual presentations. For him, arithmetic is the theory of this form. The pure form of time was understood by Kant as the arrow of time, that is, as the mental number line with direction and turn. From this point of view, the MNL may be analogously interpreted as the mental pattern which enables the contemporary mind to produce various presentations with numerical content comprising cardinals, ordinals or magnitudes. Since our numerical presentations usually reflect the content of standard semantic models of arithmetic, each MNL must also reflect the algebraic structure of the standard model of Peano’s arithmetic. If one even assumes that the MNL is a historically and culturally acquired pattern, then one has to explain the fact that this pattern is an effective tool which enables us to understand expert arithmetical knowledge on the level of calculations appearing in various acts of numerical reference towards fragments of the experienced world. Hence, one may put the subsequent question: Is the acquisition of the MNL by the human kind during historical and cultural learning practices determined by some deeper or innate neural structures encoded in the brain?
Walsh’s ATOM theory (A Theory Of Magnitude) may be treated as a positive response to the above-mentioned question (Walsh 2003; Bueti and Walsh 2009). Neural mechanisms described in ATOM may be interpreted as Kantian a priori conditions enabling the mind to acquire or generate the MNL in historical and cultural learning processes of humankind. This theory postulates the existence of one cognitive system functioning in the mind from the beginning of life, which is responsible for processing magnitudes which may appear in three forms: numeral (values of numerals), spatial (for instance, distances) and temporal (times of duration). It is partially supported by empirical data which show that representations of these magnitudes in the brain neighbor each other within the parietal lobe and that numerous interactions occur between them in various configurations of these representations during the solving of behavioral tasks. Undoubtedly, the theory stems from Kantian philosophy of pure cognitive forms as mental tools arranging our experience. The one difference between these conceptions is that in Kant’s epistemology, cognitive forms of space and time are separable, whereas according to ATOM, they are aspects or transformations of one, uniform cognitive system which generates them.
3 The Theoretical Framework: Brain Models, Mind Models and Semantic Models
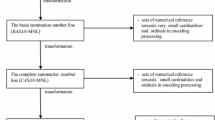
The theoretical framework within which our model of the mental number line is constructed may be illustrated with the help of the Fig. 1.
We assume that exactly one integrated representational system responsible for generating mental number lines is encoded in the mind. Every mental number line has its grammatical and algebraic structure. Hence, the processing of mental number lines in the mind may be modeled as sequences of appropriate algebraic and grammatical transformations. Their counterparts in the brain are activation and deactivation processes determined by cells in a neural net. That is why two types of models of mental number lines should be distinguished: mind models and brain models. Mind models are only tools for explaining the main experimental data concerned with the mind’s ability to perform numerical acts of reference. Brain models of processing mental number lines within neural networks are presented in Verguts and Fias (2004), Verguts et al. (2005), Verguts and Fias (2008) and Chen and Verguts (2010).
What is the theoretical relationship between mind models and brain models of mental number lines? Brain models of mental number lines should generate output arithmetic decisions observed in experiments. The neural model constructed in (Verguts et al. 2005) predicts, for instance, experimental responses on the following output fields: number naming, parity judgments and number comparison. Mental representations encoded in the mind may, in turn, be understood as semantic structures of brain representations, understood as processes of activation and deactivation of cells in a neural network. In this way, brain representations may be interpreted as physical vehicles of information on various fragments of different worlds, understood as semantic models in the meaning of Tarski’s model theory. To speak metaphorically, brain models are implementations of mind models in physical matter. And since mind models reflect semantic models by virtue of semantic relations of correspondence, brain models also indirectly reflect semantic models by virtue of the superposition of semantic correspondence with the converse of the implementation function. Mind models of MNL are theoretical tools explaining that brain models of MNL satisfy semantic functions of representing arithmetic semantic models, which may, in turn, be interpreted as mathematical structures of various worlds (Platonist worlds, physical worlds, life-worlds, worlds of human experience, etc.). Without mind models, brain models of MNL behave as men in The Chinese Room.
Both brain and mind models of the MNL stand in some relation to the field of output numerical decisions appearing as numerical referential attitudes correlated with physical states of the human body. These numerical referential attitudes and states of the body enforce the intentional activity of subjects in various numerical situations. The architecture of these relations may be illustrated with the help of Fig. 2.
One may say that mental numerical representations motivate or evoke numerical decisions, whereas the implementations of mental numerical representations in the brain cause physical states of our bodies correlated to these decisions. The field of output numerical decisions enforces, in turn, appropriate acts of numerical reference towards entities existing in some semantic model of arithmetic understood as mathematical structures of worlds. These acts also comprise the movements of the human body such as movements of a head, eyes, hands, fingers or even legs, etc. which appear as constituents of responses in numerical experimental and communicational situations.
From an epistemological point of view, the following question should be put: In what way may the mental number line be transformed into a standard semantic model of Peano’s arithmetic (PA)? If one assumes that PA is a theory explaining the validity or invalidity of results in calculations executed by the mind in various, ordinary-life situations, and since these calculations are governed by mechanisms of the formation and the activation of appropriate number representations as fragments of the mental number line, then PA should also ‘indirectly’ explain the validity and invalidity (or to generalize, the effectiveness) of processes of the formation and activation of mental representations of numbers. For example, when a person calculates that 3 + 2 = 5, in his/her mind an appropriate complex arithmetical representation is formatted and activated by its derivation from the appropriate mental number line. Because the calculation in this example is valid, its representation in the mind must correspond to the appropriate arithmetical proposition which is true in semantic models of PA. Hence, such a correspondence should be a relation between the representation of the calculation, 3 + 2 = 5, and any standard semantic model of PA. Such a relation should, in turn, assign constituents of the representation of the calculation under analysis to arithmetical objects belonging to a given semantic model composed of numbers, functions, set-theoretic relations holding between numbers and functions, etc. Since all cognitively efficient, arithmetical representations of calculations which are formatted by the mind in various task-situations are derived from the mental number line, the mechanism of such a derivation together with the mental number line functions as a generator, in the algebraic sense, of the system of arithmetical representations encoded in the mind. This mechanism of generating arithmetical representations may be called the mature number competence. Hence, the above-put question may be rephrased as two epistemological questions: (1) in the spirit of epistemological realism: How does the mechanism of the mature number competence picture semantic models of PA?; (2) in a constructivist way: How are semantic models of PA constructed or prefabricated by virtue of the mechanism of the mature number competence encoded in the mind?
The two diagrams above are not compatible with the dual route processing model formulated in (Fias 2001). According to this theoretical proposal, written verbal numerals may be processed in a non-semantic way. This means that in some situations verbal numerals are processed by the mind without mediation of the mental number line. This statement is inferred from the more general hypothesis according to which SNARC effects possess various degrees of intensity. This hypothesis requires at least two experiments for its verification. In the first experiment, participants are forced to process some semantic property of a numeral stimulus; in the second one, this property is replaced with some non-semantic property of a numeral stimulus. The font color of a digit may serve as the non-semantic property. In the experiment reported in (Fias 2001), participants were exposed to spoken verbal numerals and asked to indicate whether the vowel ‘e’ occurs in a given Dutch verbal numeral. In this case, the SNARC effect was not observed. Fias explains this asymmetry by distinguishing two ways of transcoding numerals. It seems that Fias’ model results in the over-interpretation of empirical data. First of all, one must notice that in some situations, our words cease to function as words designating various fragments of worlds. For example, when the mind recites words in an unknown language, it does not use them as words with meanings but rather as language sounds without meaning. In Fias’ experiment, the task requires participants to treat written verbal numerals not as words designating cardinals, ordinals or magnitudes, but as written expressions which should only be translated into spoken words. Fias’ empirical data show that subjects may comprehend verbal numerals within two referential attitudes towards the world. The first of them, which may be called the arithmetic attitude, evokes acts of numerical reference. The second of them, which may be called the non-arithmetic attitude, evokes acts of non-numerical reference. When one has to learn some telephone number, for example, she/he usually does not comprehend the sequence of digits as an arithmetic expression designating some numerical entity. In such situations, the subject does not treat rows of digits as numerals, that is, as expressions designating various numerical entities. This is why the framework presented in the paper passes over the non-semantic route of processing word numerals, which may be interpreted as the mental mechanism underlying the non-arithmetic referential attitude taken by the mind in special situations. Failure to activate the MNL indicates that numerals are processed in the mind in a non-semantic way and, thereby, numerical referential attitudes enforcing acts of numerical reference are not evoked. To speak metaphorically, in such a situation, the brain and the mind do not process numerals for the sake of representing arithmetic semantic models as mathematical structures immersed in various worlds.
Some researchers maintain that mental number lines are not the only ways of coding numerical representations. On the basis of empirical research, they defend the view that the mind is able to synthesize numerical representations in the form of mental abacuses (Frank and Barner 2012). They argue that mental abacuses are systems of visual working memory for representing exact (precise) numerosities. It seems, however, that this hypothesis may be compatible with the theoretical framework sketched above, according to which all numerical representations stem from mental number lines. Mental abacuses are peculiar systems of coding digit numerals. It may be easily proved that their logical grammar is the specification of a general logical grammar of numerals which assumes a multi-axial way of representing numerosities. Let O i be an operator of a mental axis where an index i indicates an established axis for representing: units, fives, tens, hundreds, thousands, etc. Let 1 be the numeral one, 0 be the numeral zero and P be the operator of the synthesis of complex digit numerals. Let ITk be the k-tuple function of iteration whose arguments are expressions with the shape O 1(1) and values are sequences of O 1(1). Mental numerical representations generated by a Japanese Soroban abacus may, for instance, be symbolized as expressions of the shape: P[O i (O 5(n), ITk O 1(1)), …, O j (O 5(m), ITk O 1(1))], where k ≤ 4, i and j range over indexes from the set of axes of decimal digit system, while n and m range over the set of elements {0, 1}. For instance, the digit numeral 126 possesses the following grammatical shape: P[O 100(O 5(0), IT1 O 1(1)), O 10(O 5(0), IT2 O 1(1)), O 1(O 5(1), IT1 O 1(1))]. From the point of view of the logical grammar of numerals, mental abacuses are devices which generate multi-axial syntactic structures in visual working memory. Hence, they may be treated as secondary mental representational structures derived from a structure composed of many mental number lines (on the logical grammar of numerals, see Krysztofiak 2012).
4 Types of Numerals and Numerical Acts of Reference
Acts of numerical reference are understood as intentional acts of using numerals to refer to various objects given to the mind in its experiences, images and conceptual presentations. The category of numerals comprises both symbolic numerals and non-symbolic numerals.
Non-symbolic numerals are manifolds, arrays and other diversities. For instance, black dots scattered on a computer screen, ducks in a children’s ABC-book and an array of students sitting in a classroom during a lecture are non-symbolic numerals. They always appear in some empirical situations as manifolds of objects through which humans, unambiguously or approximately, refer to some cardinalities. Acts of numerical reference with non-symbolic numerals may be expressed in a language. For instance, when one comprehends five black dots on the screen of a computer, it may react with the utterance: There are five dots. This utterance may be understood unambiguously or approximately. In the latter case, the utterance under discussion is synonymous with There are about five dots. Acts of numerical reference towards cardinalities which are not articulated in language appear in infants and some animals (e.g., pigeons, rats and chimpanzees) (Brannon and Merritt 2011; Xu and Spelke 2000). In some cases, subjects may refer with non-symbolic numerals to cardinalities in an unambiguous way (Feigenson et al. 2002; Hauser and Carey 2003). Subitizing is such a case of unambiguous numerical referencing. Hence, ambiguity and exactness, as features of acts of numerical reference, are not always determined by their linguistic articulation.
Symbolic numerals are expressions of a given language constructed in accordance with grammatical rules. They may also be used unambiguously or approximately. The category of symbolic numerals divides itself into two sub-sets: verbal numerals, belonging to various ordinary languages; and digit numerals, being concatenations of digits. The grammatical rules governing the processes of production of verbal numerals are usually special instantiations of more general grammatical rules of a given language. In the case of digit numerals, their grammar falls under the category of so-called Jumblese grammar (Sellars 1962; Krysztofiak 2012), comprising hidden functors which are not expressible in any natural language. Translatability relations hold between digit numerals and verbal numerals. It is possible to construct the logical grammar of numerals as the calculus of numerals. This logical system describes the formal structure underlying both systems of digit numerals and systems of verbal numerals (Krysztofiak 2012). It is therefore justifiable to assume that the logical grammar of numerals constitutes the deep Chomskian structure of both types of systems. On the basis of this assumption, one may model the non-semantic route of processing of numerals (Fias 2001) as the mental mechanism by virtue of which the processing of representations of numerals takes place without the mediation of logical representations of numerals.
The following diagram presents the types of numerals with respect to the ways they are used in acts of numerical reference (Fig. 3).
In cognitive science, one assumes that acts of numerical reference with symbolic and non-symbolic numerals are accompanied by formation processes of numerical representations in the mind and their implementation in the brain, as well as their activation and deactivation both in the mind and in the brain. Hence, one should distinguish between numerical processing in brain models and in mind models.
5 Types of Semantic Numerical Processing in Mind Models
The distinction between symbolic and non-symbolic numerals is parallel to that between two types of processes occurring in the mind when subjects perform acts of numerical reference. The former comprises processes of encoding number representations and the latter comprises processes of decoding number representations. Both classes of processes form the class of coding processes. The starting-point in processes of encoding number representations is the effect on the mind created by any non-symbolic numeral, understood as a sensory stimulus. When a non-symbolic numeral is comprehended by a subject, appropriate number representations are activated in his/her mind. The starting-point in processes of decoding number representations is, in turn, the effect on the mind of any symbolic numeral, understood as a language stimulus. When a verbal numeral or digit numeral is comprehended by a subject, appropriate representations of numerals are activated in his/her mind. Inputs of encoding processes are representations of numbers, whereas inputs of decoding processes are representations of numerals. Sometimes representations of numbers are called numerons (Gallistel and Gelman 1992). They should be distinguished from representations of numerals. Numerons are semantic representations of categories or concepts, whereas representations of numerals are linguistic representations as digit or verbal representations in graphemic or phonological forms.
Both types of processes are modeled as being composed of the same processing phases. They only differ in the order of their occurrence. In encoding processes, the first phase comprises formation processes of number representations (numerons), whereas the first phase in decoding processes consists of formation processes of representations of numerals. In encoding processes, states at input are activations of representations of numbers, whereas states at output are activations of appropriate representations of numerals. In decoding processes, states at input are activations of representations of numerals, whereas states at output are activations of representations of numbers. Encoding processes are inversely related to decoding processes. Encoding processes consist in the assignment of number representations to corresponding representations of numerals, whereas decoding processes consist in the inverse assignment. In other words, encoding processes are responsible for subjects’ arithmetic understanding of non-symbolic numerals, whereas decoding processes are responsible for subjects’ arithmetic understanding of symbolic numerals.
Another difference between the types of processes under discussion is that representations of numbers should be encoded in the mind prior to decoding processes, whereas encoding processes require the prior encoding of representations of numerals. This means that, in the development of arithmetical abilities, children’s minds must first learn to encode numbers: that is, children must learn to format, store and process some primitive representations of numbers before they acquire the abilities to decode numerals in the subsequent developmental stage.
5.1 Processes of Encoding
The processes of encoding may be modeled schematically in Fig. 4.
At the input of an encoding process, some non-symbolic numeral as a sensory stimulus is comprehended by the subject. The result of this action is the formation or activation of an appropriate number representation via MNL, encoded in the mind. In the next phase, this representation may be sent to (or written in) memory. After coding the number representation in memory, it is associated in the mind with appropriate representations of numerals. The completion of such a process comprises: (1) associations of number representations (numerons) with representations of verbal numerals of a given language and representations of digit numerals, and (2) translatability associations between representations of verbal numerals (both graphemic and phonological) and representations of digit numerals. Among the representations of numerals, logical representations of numerals play a crucial role in mental processes of translating digit numerals into verbal numerals, and vice versa (Krysztofiak 2012). They enable the mind to group all co-denotational representations of numerals together
If some of the phases of encoding specified above cannot be accomplished in a subject’s mind, then he/she is not able to perform any language acts of numeral reference. The mind’s inability to store number representations in memory results in the inability to refer to cardinalities in remembrance and imagination. The failure to associate number representations with representations of numerals in turn causes the subject to be unable to express its numerical reference acts in a language. It is possible that the subject is able to distinguish between cardinalities; however, simultaneously, he/she is not capable of articulating intentional acts of reference in a language. The failure of translatability associations between representations of numerals results in the subject’s inability to use digit numerals or verbal numerals in linguistic acts of numerical reference.
5.2 Processes of Decoding
The processes of encoding may be modeled schematically in Fig. 5.
At the input of a decoding process, some symbolic numeral, understood as a language stimulus, is comprehended by the subject. The formation and activation of an appropriate representation of the numeral is a result of this impact. For different languages or systems of digit numerals, representations of verbal or digit numerals differ. All representations of numerals encoded in the mind are grouped by virtue of translatability relations in co-denotative representations. Activations of representations of symbolic numerals cause, by virtue of their associations with representations of numbers (numerons), activations of appropriate representations of numbers. This evokes, in turn, acts of numerical reference towards various fragments of a given world
For instance, if a subject comprehends the numeral twelve, he/she associates the graphemic representation of this numeral with its logical representation. A similar process proceeds when the subject comprehends the numeral dozen. He/she associates its graphemic representation with the same logical representation which is associated with the graphemic representation of twelve. Such processes are determined by mechanisms of lexical processing (McCloskey et al. 1985). In the next stage, the subject associates these numeral representations with the representation of the number twelve. This motivates him/her to perform an intentional linguistic act of numerical reference toward some fragment of the given world, for example, toward the twelfth person on a list of convicts. If the subject is not able to accomplish all of the specified phases of the decoding process, then he/she is not able to perform any linguistic act of numeral reference. For instance, if the exposition of any symbolic numeral does not evoke any state of its comprehension in the mind, then representations of numerals are not encoded in the mind. This occurs in the case of illiterates. If the exposition of digit numerals evokes, in turn, mental states of their comprehension in the mind, but a graphemic exposition of verbal numerals does not evoke such mental states, then only representations of digit numerals are encoded in the mind. In the literature, one may find many descriptions of cases presenting various deficits resulting from damage to mechanisms involving both the formation and the activation of representations of symbolic numerals (Benson and Dencla 1969). In accordance with the model, associations of representations of numerals with logical representations of numerals enable the subject to understand them in such a way that he/she is able, inter alia, to translate digit numerals into verbal numerals (and vice versa) and to estimate them with respect to their values. Failures of these associative mechanisms may be understood as causing various disorders, such as dyscalculia.
6 Experimental SNARC Effects
SNARC effects manifest flexibility as well as some regular properties. The flexibility is caused by cultural or experimental factors. Properties of SNARC effects concern: the interval of presented numerals, the format and modality of numerals, the way a numeral stimulus is spatially arranged, the way of responding to presented stimuli, the estimated property and the age of participants. Moreover, in some experiments, it is possible to observe effects similar to SNARC effects, which may be called quasi-SNARC effects.
6.1 Flexibility of SNARC Effects
6.1.1 The Cultural Factors of the Flexibility of SNARC Effects
Empirical data show that the direction and turn of a SNARC effect may take various shapes, depending on the culture to which subjects belong. In Europe, mental number axes discovered in SNARC experiments are directed horizontally from left to right. This direction and turn are determined by the European reading and writing style. In countries where people read and write from right to left, SNARC effects reflect mental number lines directed horizontally from right to left. This means that responses to relatively smaller numerals are carried out faster on the right side, whereas responses to relatively bigger numerals are carried faster on the left side (Shaki et al. 2009; Zebian 2005). Some authors have investigated the relationship between the writing direction of digits and SNARC effects. In Hung et al. (2008), two kinds of SNARC effect are described. For Chinese verbal numerals, SNARC effects manifest the direction from top to bottom, whereas for digits they manifest the direction from left to right.
The acquisition of a second language with the opposite writing direction—for instance, English by an Arab—may weaken the intensity of the SNARC effect or even reverse the turn of the SNARC effect formed for the first language. This, of course, depends on the degree of proficiency in the second language (Dehaene et al. 1993). Moreover, in research on bilingual people whose two languages have opposite writing direction (for instance, Hebrew and Russian), an oscillating change of the SNARC effect is observed when participants are asked to change the reading direction of texts expressed in languages with opposite writing directions (Shaki and Fischer 2008; Fischer et al. 2009).
6.1.2 Experimental Factors on the Flexibility of SNARC Effects
SNARC effects may also be modified in various ways—for instance, by manipulating reply buttons, by the mechanism of priming or by introducing additional instructions into the standard experimental design.
The standard schema for the arrangement of buttons, with the first on the left and the second on the right, may be changed into a vertical arrangement with one on top and the other on the bottom. It appears that in both Western culture (Schwarz and Keus 2004; Gevers and Lammertyn 2005) and Japanese culture, SNARC effects are observed with the direction from the bottom to top. Responses to smaller numerals are executed faster with the button at the bottom, whereas responses to greater numerals are executed faster with the button at the top. Furthermore, it is possible to induce SNARC effects with a diagonal direction. Responses to smaller numerals are executed faster with buttons localized in the lower left corner, whereas responses to greater numerals are executed faster in the upper right corner (Gevers et al. 2006).
In research reported in Bächtold et al. (1998), before being given the main task (to evaluate values of presented numbers), some participants of the experiment were asked to imagine a clock face and others, a ruler. In the first case, recalling the image of the clock face during the execution of the main task reversed the turn of the SNARC effect. Responses to smaller numbers were faster when subjects had to react with the right hand, whereas responses to greater numbers were faster when they had to react with the left hand. Those subjects who imagined a ruler did not demonstrate a change in turn from left to right. This asymmetry of a turn in SNARC effects is caused by the mechanism of priming. In the case of the clock face, greater digits occur on the left side, whereas smaller digits occur on the right side.
Another way of modifying the turn of SNARC effects consists in reading a text in which smaller digits appear at the beginning and greater digits at the end (Fischer et al. 2010), or in the memorization of a decreasing sequence of digits (Lindemann et al. 2008). Van Dijck and Fias (2011) asked subjects to memorize a displayed sequence of digits (for instance, 8, 1, 5, 7, 2) which were selected at random. Subsequently, the subjects had to estimate their parity. The result of the experiment show that, for the sequence 8, 1, 5, 7, 2, responses to 8 and 1 were faster on the left side, whereas responses to 7 and 2 were faster on the right. The researchers received a similar result for the names of fruits.
Some authors have paid attention to how the direction of counting on fingers can influence SNARC effects (Lindemann et al. 2011; Fischer and Brugger 2011). For instance, in Fischer (2008) it is noticed that beginning counting from the left hand strengthens a SNARC effect from left to right.
In the case of Hebrew users, SNARC effects for digits disappear during reading practice (Shaki et al. 2009). This experimental fact is explained by the conflict between the reading direction in Hebrew and the writing direction of Arabic digits.
6.1.3 Conclusions
On the basis of such observations indicating the flexibility and instability of SNARC effects, one might formulate some hypotheses:
H1
The turn of the mental number lines is culturally and situationally variable.
H2
In encoding and decoding processes, the formation or activation of number representations on the mental number line may be blocked in some cognitive situations.
H3
Geometrical properties of reference-spaces, determined by an activated mental number line in virtue of which acts of numerical reference are executed, are flexible.
H4
The direction and turn of a mental number line are not computationally relevant properties.
In accordance with hypotheses (H1) to (H4), directions and turns of the mental number line may be described as ways or styles of representing or implementing number representations in the mind. They are always mediated by various attention control schemata in reference-spaces. It seems that people learn many of these schemata in virtue of their participation in cultural practices, such as writing, arranging objects in space or crossing the street. These schemata may be activated in the short term in the mind for the sake of executing various tasks, because the use of such schemata facilitates the processing of numerical information: Subjects select schemata which are best for improving information processing in the short term. For some tasks, a schema with small numbers at the bottom and big numbers at the top is better than one with small numbers on the left side and big numbers on the right.
It is worth noting that spatial schemata are also activated in the mind during the processing of non-numerical information on the linguistic level (Proctor and Cho 2006; van Dijck et al. 2009; van Dijck and Fias 2011; Imbo et al. 2012). Such schemata may take the following shapes: right—good and left—bad, or right—big and left—small. They may be applied in many diverse types of evaluation. Similarly, mental number lines with various directions and turns may be interpreted as schemata arranging the geometrical architecture of reference-spaces. This could mean that the metrics of mental number lines, understood as determining the geometrical arrangement of reference-spaces, are not rigid properties. This also means that acts of numerical reference may be executed within various numerical attitudes (see Fig. 2) differing in terms of their properties determined by these metrics.Footnote 3
The flexibility and instability of SNARC effects only means that the mental number line may take various geometrical shapes and also be easily deactivated in some cognitive situations. It does not undermine, however, the existence of processes of its encoding or decoding in the mind.
6.2 Properties of SNARC Effects
6.2.1 The Interval of Presented Numerals
In SNARC experiments, the most commonly applied range of numerals comprises digits from 0 (zero) or 1 (one) to 9 (nine). However, in appropriate conditions, the effect under discussion may be evoked for all numerical sub-intervals contained in the ranges [0, 9] or [1, 9]. It turns out that relative number values, and not absolute number values, from a given interval influence the speed of reactions performed on the left or right side. In one version of Dehaene’s procedure (Dehaene et al. 1993, Experiment 3), participants evaluated the parity of digits selected randomly from one of the two following ranges: [0, 5] and [4, 9]. The SNARC effect was obtained for both intervals. In the case of stimuli selected from the interval [0, 5], the effect of the predominance of the left hand was registered for digits 0 and 1, whereas the effect of the predominance of the right hand manifested itself for digits 4 and 5. However, in the case of stimuli from the interval [4, 9], the predominance of the left hand was registered for digits 4 and 5, whereas the predominance of the right hand was observed for digits 8 and 9 (Fias et al. 1996).
Up to now, the SNARC effect has been observed in experiments with two-digit (Dehaene et al. 1990, 1993; Zhou et al. 2008; Brysbaert 1995) and three-digit numerals (Tlauka 2002). However, these experimental results are problematic. They show that digit numerals may be processed compositionally or holistically. According to the first way, SNARC effects may be induced by processing decade digits in two-digit numerals (Zhou et al. 2008). The hypothesis that two-digit numerals are processed compositionally is also supported by the so-called congruence effect, where congruent (compatible) pairs of numerals are processed faster than incongruent (incompatible) pairs in comparison tasks (Nuerk et al. 2001). A pair of digit numerals is defined as congruent if and only if both the decade and unit digits of one numeral are greater than those of the second numeral. In the case of two-digit and three-digit numerals, it is possible that the comprehension of the decade digit in acts of numerical reference is responsible for the SNARC effects. Spatial associations of multi-digit numerals may be evoked by peculiar focus on constituent digits (Nuerk et al. 2011, pp. 4–5).
The observation of SNARC-effects for negative numerals also appears to be problematic. One may conjecture that negative numbers are not represented on the mental number axis, but that they form a mirror contrast for representations of positive numbers. On this view, the SNARC effect for negative numerals is a mirror image of the SNARC effect for positive numerals. In the task of evaluating the parity of negative digits from the range [−9, −1], the largest numerals, −1 and −2, induce faster reactions for the left hand than for the right. This means that they are treated by participants as numerals 1 and 2 from the interval [1, 9] (Fischer and Rottmann 2005; Shaki and Petrusic 2005). In other experimental conditions, however, it seems that the real values of negative numerals, and not their absolute values, produce the effect. If a participant is to compare two numerals with respect to their values, such that the former is positive and the latter is negative, then one observes faster responses to negative numerals with the left hand and faster responses to positive numerals with the right (Shaki and Petrusic 2005).
6.2.2 The Format and Modality of Numerals
The SNARC effects hold not only in the case of visually processed Arabic numerals, but also for numeral stimuli presented and retrieved in different perceptual modalities. In one experiment (Castronovo and Seron 2007), numerals were reproduced from speakers to blind people. Blind participants were asked to judge the parity of heard numerals or, in the second version of the experiment, they had to decide whether a numeral being heard was greater than five. Responses with the left-hand button to the smaller numerals were faster than responses with the right-hand button to the same numerals. Responses with the right-hand button to the greater numerals were faster than responses with the left-hand button. SNARC effects have also been experimentally confirmed in the case of deaf people who were presented with digits on a computer screen (Bull et al. 2005; Iversen et al. 2004) and finger layouts designating numbers in sign language (Iversen et al. 2006; Bull et al. 2006).
The experiments involving people without disabilities show that changing the reception channel of numeral stimuli (sight, hearing) or the format in which numeral stimuli are presented (digits, verbal numerals, sets of objects) does not influence the SNARC effects. Up to now, SNARC effects have been observed in the presentation of Arabic digits, Indo-Arabic numerals (Shaki et al. 2009), Chinese numerals (Hung et al. 2008), written verbal numerals (Fias et al. 1996; Nuerk et al. 2005), spoken verbal numerals (Nuerk et al. 2005; Castronovo and Seron 2007) and non-symbolic numerals in the form of the arrangement of dots on a die (Nuerk et al. 2005) and various, randomly scattered elements on a computer screen (Patro and Haman 2012). Furthermore, analyses of experimental results also show that the strength of the effect under discussion is not dependent upon whether numerals are read or heard (Nuerk et al. 2005; Wood et al. 2008; Dehaene et al. 1993). To summarize, SNARC effects are revealed in both encoding and decoding processes.
6.2.3 The Way Numeral Stimuli are Spatially Arranged
The research pattern with a centrally presented digit and two response-buttons on the sides of the screen may be replaced with a schema in which two digits are presented on the screen simultaneously: The one is exhibited on the left side and the other on the right. In such a schema, two arrangements of digits are checked. One is compatible with the direction of the mental number line —that is, the smaller digit is on the left and the larger digit is on the right—while the other is in the opposite direction. The participants were asked to indicate the larger or smaller numeral (Fischer 2003; Shaki and Petrusic 2005) or to evaluate whether the values of exhibited numerals were equal or different (Zebian 2005). Indicators of SNARC effects in such a research framework are: shorter reaction times to a double numeral stimulus arranged in accordance with the direction of the number line; and longer reaction times to a double numeral stimulus arranged in a way opposite to the direction of the axis.
6.2.4 The Way of Responding to Presented Stimuli
In accordance with the standard schema, participants respond to numeral stimuli with their hands by pressing buttons on their left or right side. In many other experiments, responses were given by pressing buttons with the left and right feet (Schwarz and Müller 2006), by indicating a numeral stimulus with the index finger or middle finger of the right hand (Priftis et al. 2006), by indicating the left or right side with one hand (Fischer 2003), or, finally, by directing their gaze to the left or to the right (Fischer et al. 2003; Schwarz and Keus 2004). In each case, SNARC effects were also observed. To generalize, this effect obtains when a person is required, under the presence of a numeral stimulus, to give spatially-oriented behavioral reactions.
6.2.5 The Estimated Property
The evaluation of parity is the most frequent task used to observe the experimental effect under analysis. Another task in experiments consists in the estimation of digits with respect to their values (van Galen and Reitsma 2008; Herrera et al. 2008; van Dijck et al. 2009). In these tasks, called comparison tasks, a participant has to choose one of two opposing buttons. One represents the answer larger and the other represents the answer smaller. On the middle of the screen, digits are presented from the range [1, 9], with the exception of the digit 5. The participant is asked to indicate whether a given digit is larger or smaller than the digit 5. In some experiments, the task requires the comparison of two numerals with respect to their values, which are presented simultaneously (larger vs smaller or the same vs different) (Zebian 2005). Another task used in SNARC experiments concerns the detection of a stimulus preceded by the presentation of a digit (Fischer et al. 2003; van Galen and Reitsma 2008). Participants respond to the appearance of a point on the left or on the right side of the screen as soon as possible. The appearance of a point is preceded by the presentation of a digit from the range [1, 9]. It turns out that if a digit with a small number-value (for instance, 1 or 2) is presented on the left side of the screen, then the point is detected faster. The same concerns the situation in which digits are presented on the right side of the screen with relatively large number-values (for instance, 8 and 9). It is worth emphasizing that SNARC effects obtain in this case, although the number-values of the presented numerals are not directly processed in the task.
It should be noted that in some tasks which do not require the processing of semantic properties of numerals, SNARC effects are either not observed or are very weak. Experiments show that if processing a numeral stimulus requires the comprehension of other properties (such as the color of a written digit, being a vowel or a consonant by a letter or, finally, being composed of a given phoneme by a spoken numeral), then the SNARC effects disappear or are weakened (Fias 2001). Experiments also demonstrate that if the task-solving process is strongly entangled in the semantic processing of a numeral stimuli, then the force of the expected SNARC effect increases (Wood et al. 2008).
6.2.6 The Age of Participants
The question of the existence of the mental number line in children’s minds is still discussed. Some effects which might be accepted as SNARC effects have been observed in the case of 3 year olds—that is, in a relatively early phase of ontogenesis (Patro and Haman 2012). Many experiments support the thesis that the size of the SNARC effect increases with age. The key issue concerns the age of children in which the SNARC effect is found easily. In (Wood et al. 2008, pp. 495 and 504), it is asserted that SNARC effects are not easily induced in children much younger than 10 years old. This might mean that the age of subjects affects the stability of SNARC effects. The higher the age, to some limit, the effects are more easily induced.
6.2.7 Conclusions
On the basis of observations indicating various properties of SNARC effects, one might formulate additional hypotheses:
H5
The spatial encoding and decoding of numerals occur when the mind is required to produce behavioral reactions in physical space due to the processing of numeral stimuli.Footnote 4
H6
The spatial encoding and decoding of numerals involves numerals from various finite ranges of numbers designated by single-digit and perhaps two- or three-digit numerals. The results of these processes are line segments with directions and turns (in this paper, called mental number axes) encoded in the mind. They are relatively short line segments.
H7
The syntactic format (symbolic vs non-symbolic format, or digital vs verbal format) of numerals does not influence the occurrence of the spatial encoding and decoding of numerals.
H8
The sensual modality of the reception channel for numeral stimuli does not influence the occurrence of the spatial encoding and decoding of numerals.
H9
The way numeral stimuli are spatially arranged may influence the occurrence of the spatial encoding and decoding of numerals.
H10
The processes of spatially encoding and decoding numerals manifest various degrees of intensity. If more semantic properties of numeral stimuli are processed in encoding and decoding, then the degree of intensity of these processes increases. If fewer semantic properties of numeral stimuli are processed, then the degree of intensity decreases.Footnote 5
H11
The spatial encoding and decoding of numeral stimuli is not absolute. This means that the same numeral stimulus may be represented at different positions on various mental number axes depending on changing conditions.
H12
The age of subjects influences the stability of the occurrence of the spatial encoding and decoding of numerals in various cognitive situations.
6.3 Quasi-SNARC Effects
Similar effects to SNARC effects are observed, not only in experiments with numeral stimuli, but also in experiments with the exposition of names designating objects belonging to various linear, non-numeral, ordinal structures, such as: names of weeks, names of months and letters of the alphabet (Gevers et al. 2003, 2004). A quasi-SNARC effect appears when participants have to indicate, with the left or the right hand, whether a given month from the range (January, April) or from the range (September, December) occurs in the calendar before or after July. The same effect, and with similar strength, is observed when participants have to indicate whether the name of a given month from the same ranges ends with the letter ‘R’. In another experiment, subjects were asked whether a letter from the set {E, G, I, L, R, U, W, Y} occurs in the alphabet before or after the letter ‘O’. In this case, the force of the quasi-SNARC effect is even stronger than in the experiment with the names of months (Gevers et al. 2003). A slightly weaker effect appears in an experiment with the exposition of names of days of the week: Participants were asked whether a given day occurs in the week before or after Wednesday (Gevers et al. 2004). In experimental tasks in which participants evaluated the pitch (Rusconi et al. 2006) or the duration of a given event (Vallesi et al. 2008), quasi-SNARC effects were also detected. In this case, the magnitudes under evaluation are continuous, not discrete.
Qusai-SNARC effects may be treated as a derivative of SNARC effects. All linear, non-numeral ordinal, finite structures are isomorphic to linear, ordinal, finite structures composed of consecutive numbers or numerals. It seems that these ordinal conceptual structures function in the minds of experimental subjects as items indexed with the help of successive numbers. Hence, SNARC effects appear when a participant is forced to respond to these indexed items with spatially arranged tools (hands, legs, buttons, response keys, etc.). This means that finite ordinal structures are represented in the mind as complex representations founded upon the mental number line. Activations of these representations might be treated as being associated with the activation of the mental number line encoded in the mind.
The SNARC effect is in a sense similar to the Simon effect (Simon 1969). The latter consists in the correspondence between the dimension of a stimulus and the dimension of the response. When the location of a stimulus in the external space, irrelevant to the task, is compatible with the location of the response, time reactions are faster and responses are more accurate than in the case of incompatibility between both dimensions. For instance, when a stimulus is located on the left side of a fixation point, responses to it with a left key or a left button are faster than responses with a right key or button. This is why researchers might interpret SNARC effects as variants of the Simon effect, because of a dimensional overlap between the response dimension and the stimulus dimension (Gevers and Lammertyn 2005).
Some experimental results show, however, that both effects may be interpreted as differing with respect to some mathematical property. In the case of the SNARC effect, Wood et al. (2008) concludes that the longer the time needed to respond to the numeral stimulus, the stronger the size of the effect. This might mean that the size of the SNARC effect increases with the average response time to the numeral stimuli. In the case of the Simon effect, the longer the time needed to response to the stimuli, the weaker the size of the effect. Furthermore, in some experimental conditions (specifically, for low stimulus discriminability), the size of the Simon effect decreases. Low stimulus discriminability requires a relatively longer reaction time to stimuli. On the basis of experimental results, some researchers conclude that this effect decays with increasing time as an automatic process over time (Hommel 1994; Eimer et al. 1995).
It is justifiable, however, to interpret the Simon effect as the simplest variant of the SNARC effect. In accordance with the MNL-hypothesis, experimental SNARC effects are induced by the activation of the mental number line, consisting of relatively many number representations. Standard mental number lines are, in fact, finite number axes consisting of, at most, little more than a dozen elements. Simon effects might be induced by the activation of a very short mental number line (SMNL) consisting of exactly two, linearly-ordered elements: the starting point and the endpoint, interpreted as representations of ordinal numbers, the first (the former) and the second (the latter). The short mental number line (SMNL) could be activated by the so-called motor code, that is, by the dimension of response. A response with the left hand to a stimulus on the left side would be governed by the mechanism of directly mapping the starting point on the short mental number line onto a corresponding place in the external space occupied by the stimulus. A response with the right hand to a stimulus on the right side would be governed by the mechanism of directly mapping the endpoint on the short mental number line onto a corresponding place in the external space occupied by the stimulus. A longer response time with the left hand to the stimulus on the right side, in comparison to the response time with the right hand to the same stimulus, might be explained by the mechanism of changing direction of attention. The same concerns the situation in which a stimulus appears on the right side and a subject is forced to respond with the left hand. The decay of the Simon effect over time might be explained by the deactivation of the SMNL: If a subject does not take a numerical attitude towards the outside environment of stimuli, then the SMNL, activated in encoding processes, is not prolonged and is thereby deactivated (see Figs. 1, 2, 4). This would mean that the SMNL, consisting of two elements, is activated during each act of sensory perception. If a subject is counting stimuli in the outside space, then the SMNL is prolonged. In this situation, the Simon effect must also decay because of the transformation of the SMNL into a longer MNL.
Acts of subitizing might also be interpreted in terms of the Simon effect. According to Carey (2004) and Le Corre and Carey (2007), the mind of a child encodes numeral representations in virtue of the parallel individuation mechanism. In accordance with the basic assumption of this conception, children are able to generate representations of small manifolds consisting of one, two, three and sometimes four items. Their minds use the mechanism of ascribing the so-called attention-markers to different items given in their perceptual fields. In this way, the mind may track all marked items simultaneously. As a result, the mind may individuate a few objects at the same time. The upper limit of the cardinality of manifolds under parallel tracking is four. The encoded representations of such structures are then associated with representations of the first four verbal numerals. This process of encoding representations of numbers is phasic. The mind first learns the meaning of the numeral one, then two, until the numeral four. This means that unambiguous representations of all natural numbers from one to four are encoded in the mind, and, subsequently, are associated with corresponding linguistic representations of numerals. For instance, the perception of two items (dogs, cats or other objects) causes the mind to encode a representation of the two-element set in its memory. Subsequently, it associates this representation with the representation of the list of verbal numerals: one, two. In this way, the mind ascribes meanings to the first two numerals. In virtue of this mechanism, the mind learns a one-to-one association between two-element sets and the two-element list of numerals. If this representational structure is stable in the mind, then it is able to calculate two-element manifolds given in its perceptual experience and give accurate solutions to tasks consisting in the calculation of any two items. The conception of parallel individuation assumes that the mind has the ability to read up to three or four elements in its perceptual field.
The ability to subitize any two elements may be treated as the result of activation in the mind of the SMNL by the dimension of response. According to (H5), subjects in SNARC experiments are instructed to produce behavioral reactions in physical space. In this way, the dimension of response is activated in their minds, inducing activation of the SMNL. This mental representation may function as an attention-marker ascribed to two different items given in the perceptual field of the mind. This hypothesis seems to be empirically verified by observations that even infants (Feigenson and Carey 2003; Feigenson et al. 2002) and newborns (Antell and Keating 1983) are able to differentiate cardinalities consisting of no more than three items. Greater cardinalities are only recognized approximately by infants (Xu and Spelke 2000; Lipton and Spelke 2003). This might mean that the SMNL is innate.
To summarize, one may draw out the following hypotheses:
H13
Mental number lines are conceptual tools (or generators) upon (or of) which various ordinal conceptual structures (mental axes) encoded in the mind are founded (or derived).
H14
Mental number axes vary in terms of length. The shortest mental number axis (SMNL) is composed of two number representations: the former (the first, one) and the latter (the second, two).
H15
The SMNL is activated during each act of sensory perception and subsequently processed by virtue of its prolongation, depending on the activation of the numerical attitude of the acting subject. Otherwise, the SMNL decays.
Formal, algebraic models of mental number axes should explain the facts registered in various SNARC experiments.
7 Types of Mental Number Axes
Mental number axes are here defined as complex representational structures forming relatively short, finite lines (H6) with specific directions and turns (horizontally, from left to right or right to left, or vertically, from top to bottom) which arrange mental representations of successive natural numbers spatially by attributing them to appropriate, linearly-ordered fragments (H13). According to (H3) and (H5), spatiality is a constitutive, ‘inherent’ feature of representations of numbers. This means that numbers are represented in mental space as geometric objects. Each mental number axis is thus comprehended as homeomorphic to any physical line located in our experiential space. Mental number axes are finite fragments of infinite mental number lines, understood as vehicles of the former.
This last hypothesis about number representations as mental geometric objects, however, has only been partially and indirectly confirmed by neurophysiologic data. On the basis of results presented in (Knops et al. 2009; Hubbard et al. 2005, 2009), we may only assert that some neural networks in the parietal lobe, which are activated in the planning of eye movements, are also engaged in the processing of numeral values or in the execution of arithmetical operations (addition and subtraction). Hence, it is conjectured that the same processes underlying acts of attention control in external space are responsible for controlling attention along the mental number line. On this view, mental number axes are representations formed on the basis of sensorimotor experience. This claim, however, is entangled in the following philosophical question: Do external stimuli located in sensorimotor space activate the mental number line? Conversely, does the activation of the mental number line activate the mind’s intentional direction towards a stimulus?Footnote 6
For the sake of modeling mental number axes, the question of their formal, structural properties is discussed in detail (Verguts and Fias 2008): (1) In what way are particular natural numbers coded on the mental number line? (2) In what way is the function of the distance between number representations scaled on the mental number line?
The literature distinguishes two ways of representing numbers on mental number axes. The first way may be called summation representation of numbers, or summation coding of numbers (sometimes called accumulator representation of numbers); and the second one is place coding, or the point-place representation of numbers (Gallistel and Gelman 1992, 2000). Some researchers accept the view according to which both ways of representing numbers exist in the mind.
In the present paper, we adopt the standpoint according to which the summation representation of numbers concerns merely non-symbolic numerals, whereas point-place representation concerns both symbolic numerals and non-symbolic numerals. This means that the first type of representation only takes place in encoding processes, whereas the second one takes place both in encoding and decoding processes. In encoding processes, corresponding linguistic representations are attributed to semantic representations of numbers located on an appropriate mental number axis. In decoding processes, semantic number representations located on an appropriate number axis are attributed to linguistic representations. In encoding processes, mental number axes are encoded, whereas in decoding processes they are activated as ready-made patterns. This assumption is partly confirmed by experiments described in (Roggeman et al. 2007). Digits exhibit the weaker strength of the distance and size effect in relation to non-symbolic numerals (H10). Hence, representations underlying encoding processes should be different from representations underlying decoding processes.
7.1 Summation Representations of Numbers on the Mental Number Axes
According to the summation model of number representation, a coding unit is a sub-segment of a given axis. This means that for coding the cardinality one or the ordinal first, some initial sub-segment on the number axis is established at input. To subsequently code the cardinality two or the ordinal second, the initial sub-segment representing the number one or the ordinal first must be extended with some sub-segment directly in contact with the initial sub-segment. Similarly, coding the number three or the ordinal third requires that the subsequent sub-segment is summed with the sub-segment representing the number two or the ordinal second. On this view, any mental number axis is treated as a mereological whole which comprises parts determined by a mechanism of coding numbers. The first part is some initial sub-segment and succeeding parts are prolongations of it. This way of representing numbers is sometimes metaphorically compared to the process of fluid replenishment in an accumulator (Meck and Church 1983). From an ontological point of view, any mental number axis would behave ontologically in relation to representations of numbers in a manner analogous to that of a physical medium (fluid, gas or plasma) in relation to its parts (understood as portions of the medium). The physical medium consists of its pieces or portions, and not of set-theoretic elements (Krysztofiak 1991). In the same meaning, representations of numbers are pieces of number axes. Furthermore, each representation of any number is a mereological environment for all representations of numbers smaller than a given number. Representations of smaller numbers are parts of representations of greater numbers.
It should be noted that the summation model has been verified by experimental results. In the cerebral cortexes of primates, including humans, groups of neurons have been discovered which gradually react to cardinalities of sets; that is, their intensity of activity changes monotonically with the cardinality of the set (Roitman et al. 2007; Santens et al. 2010). On the behavioral level, summation coding may be detected by an experimental technique called “priming.” In one experiment (Roggeman et al. 2007), the task consists of naming cardinalities from the range [1, 5] presented in two different formats comprising digits and non-symbolic numerals as sets of dots on a screen. The key operation in the experiment is the technique of preceding the main numeral stimulus by a priming stimulus in the very short time of 83 ms. Because of the short time, participants are not able to respond to the priming stimuli, which are digits or non-symbolic numerals selected from the range [1, 5]. This technique enables researchers to check the influence of the previous encoding of a priming stimulus upon the identification of the main numeral stimulus. In the case of priming by non-symbolic numerals (sets of dots), it was observed that a priming stimulus had facilitated the naming of main numeral stimuli which was smaller or equal to the priming stimulus. The mechanism underlying the priming effect indicates the process of summation coding. The activated value of a priming stimulus on the mental number line activates some part of the segment of the number axis with the initial point at 0 (or 1) and the end point corresponding to the value of a priming stimulus. This segment comprises all sub-segments which represent values of numbers smaller or equal to the value of the priming stimulus. Hence, the activation of a representation of a priming stimulus entails an activation of some piece of a representation of a number smaller than or equal to the number corresponding to the priming stimulus.
It is obvious that, in accordance with the mechanism of summation coding, encoding any cardinality n requires the prior encoding of all cardinalities smaller than n (compare Zorzi and Butterworth 1999).Footnote 7 In the case of relatively large numbers, summation coding could need an extraordinarily long operational time.
The summation model under discussion should be modified in some way. It is assumed that the summation encoding of numerals is preceded by the encoding of some selected number. For example, in order to encode the number 16, the previously encoded representation of the number 10 should be encoded in the mind. Such a representation, the activation of which underlies the process of encoding some other number, may be called a referential number code. In priming experiments, representations of priming stimuli are just referential number codes. However, it should be emphasized that referential number codes do not function as representations of priming numeral stimuli in most referential situations. The priming mechanism uses sensual stimuli. In the case of non-symbolic numerals, only collections of objects with small cardinalities may function as priming stimuli because of the limits of perceptual resolution. If a representation of the number 16 is to be encoded by summation encoding, then the encoded representation of another number must first be activated and then the representation of the number 16 can be formatted. The mechanism of encoding the number 16 consists in the prolongation of a segment of the mental number axis—the referential number code 10—with six units which have contact with each other. It is obvious that in this case the referential number code cannot be the representation of any priming stimulus. However, this process resembles the process of priming. That is why it may be called priming by representations previously encoded in the mind.
A very important question arises: What is the mechanism for encoding referential number codes which function as priming representations? The simplest answer might assume that numerical functioning of the mind is grounded in the general mechanism for generating priming representations of numbers on summation mental number axes. When the mind is synthesizing some number representation on the summation number axis, it must first select and activate another segment of the axis, namely a referential number code. This process is stochastically determined by the net of associations between representations of numbers and numerals. In this way, the fact that the mind’s identification of numerals is primed by appropriate numeral stimuli in some experimental situations might be explained by the mechanism of priming some number representations by other number representations. In other words, the fact that there is a mechanism responsible for priming number representations by other representations in the mind enables experimenters to prime participant’s responses to numeral stimuli.
7.2 The Point-Place Representations of Numbers on the Mental Number Axes
Mechanisms of processing number representations in accordance with the summation mechanism are not economical, because any activation of the representation of a given number enforces the activation of all representations of numbers which are smaller than it. In particular, activations of representations of large numbers evoke a high system processing load. Hence, the mind transforms summation mental number axes into other, more economical structures, here called point-place mental number axes.
The main difference between summation representations of numbers and point-place representations is that, in the latter, representations of numbers as segments of a number axis do not need to include other representations as their parts, whereas in the former case, each representation of a given number includes all the representations of smaller numbers. In this way, point-place scaffolding lessens the high processing load which accompanies summation number axes. The peculiarity of point-place axes is that number representations located on them may take the shape of points and sub-segments beginning at points different than zero. These sub-segments are just places on axes. The point-place number axes, which exclusively consist of points, are idealized mental number axes, called the mental axes of exact numbers.
It turns out that a purely point-structural nature of number axes is not consistent with the results of experiments. First of all, properties of priming effects show that mental number axes cannot merely consist of points. If representations of numbers were points, then they should be activated independently of activations of other representations. This means, for instance, that an activation of the representation of the number five should not be affected by the representation of the number four. Experiments reveal, however, that priming shortens the time needed for identifying non-symbolic numeral stimuli. Furthermore, in the case of symbolic numerals, priming effects obtain in both directions; that is, when the priming symbolic numeral is both greater and less than the symbolic numeral stimulus. This means that activations of representations of numbers which neighbor a given representation on number axes affect the activation process of the latter. There is additional empirical evidence against the existence of purely point-structural mental number axes: the disappearance of priming effects with increased distances between priming numerals and primed numerals on both sides of an axis (Naccache and Dehaene 2001; Roggeman et al. 2007).
To explain this data, it is justifiable to assume that number representations located on mental axes take the shape, not only of points, but also of places, understood as symmetrical neighborhoods of a given point. Some of them may be longer and others may be shorter. For example, the representation of the number six may be a place on the mental number axis occupied by points: 5, 6, 7. It is, however, possible that on another mental number axis, the representation of the number six is formatted as a segment consisting of the points: 4, 5, 6, 7, 8. To use the language of phenomenology, it may be said that representations of numbers on the point-place axes are formatted within the retention-protention structure.Footnote 8 This means that representations of numbers on point-place mental axes possess “common pieces” with number representations immediately preceding as well as immediately following a given representation. Hence, for instance, if a priming stimulus is the numeral 6, then its exhibition evokes the activation of the representation 〈5, 6, 7〉. The reaction time to the numeral stimulus 5 is shorter than the reaction time to the same numeral without priming because some part of the representation of the number five is activated during priming.
For the sake of a more precise characterization of the process under discussion, let us pay attention to some empirical data. According to data presented in (Nieder and Miller 2003, 2004; Nieder and Merten 2007), the brains of macaque monkeys have neurons within the intra-parietal sulcus and the prefrontal cortex which code some established number values. These ‘number neurons’, regarded by many researchers as the nest of the number sense in the brain, react selectively to established cardinalities of non-symbolic numeral stimuli. Each selective neuron is set to encode only one established cardinality. This appears as extreme activity affected by the established cardinality N. In this way, it may be said that a given neuron is set to encode N. Moreover, a given neuron reacts less and less to each cardinality greater or smaller than N until it becomes completely inactive. This means that the same neuron may react to many, but not all, of the different cardinalities of non-symbolic numerals. One of these cardinalities is the one which a given neuron is set to encode. If a neuron n reacts to the cardinality N with moderate (not extreme) activity, then some other neuron m must react to N with extreme activity. To speak metaphorically, m belongs to a group of neurons which encode N centrally, whereas n belongs to the group of neurons which encode N peripherally. Hence, the cardinalities to which these peripheral neurons are set to encode may function as priming tools in the processing of number representations. A similar phenomenon is observed in the adaptation (habituation) of the neuronal net within the intra-parietal sulcus to the established cardinality or number value of a digit. With the progress of habituation, the net reacts to the cardinality N less and less until all reactions to the habituated numeral stimulus disappear. This means that the activity of a neuronal net within the intra-parietal sulcus disappears through habituation. The stimulation of activity of this region of the brain, after its habituation to an established cardinality, may be affected by changing the numeral stimulus acting on the brain. The empirical results indicate that with the increasing distance between a habituated numeral stimulus and an exhibited numeral stimulus, the intensity of activation also increases (Piazza et al. 2004, 2007; Cantlon et al. 2006).
The results of this research also display a peculiarity: The activity of neurons attuned to certain number values changes in accordance with some pattern. For each neuron which encodes a succeeding number on the axis, its activity comprises an increasing interval of neurons representing number values that neighbor a given number. As a result, neurons which encode increasing number values become less selective. A similar effect arises in the adaptation of the neuronal net. If the loss of activity is the result of habituation to a numeral stimulus with a large value, then reactivation of the net is more difficult. The reactivation of a habituated net with a numeral stimulus whose value is high requires stimuli with sizes which differ significantly from the habituating stimulus. This means that numbers are encoded in a neuronal net with different levels of selectivity. These differences correspond to differences between the values of encoded numeral stimuli. If differences between the values of encoded numeral stimuli increase, then the differences between the levels of selectivity of the net habituated to these stimuli also increase. Behavioral data concerned with human acts of numerical reference display similar effects. If the difference between values of numeral stimuli decreases, then our ability to distinguish them also decreases. These effects, called the distance effect and the size effect, are observed in experiments during the processing of digit numerals (Moyer and Landauer 1967) and in experiments with non-symbolic numerals processed both by people and animals (Whalen et al. 1999; Platt and Johnson 1971). These data confirm that neurons which implement representations of numbers located on number axes may be more or less selective.
The degree or level of selectivity discovered in various experiments may be interpreted as the degree of exactness of number representations. If a numeral stimulus induces synthesis or activation of an exact (unambiguous) representation of a given number (see Fig. 3), then the mind refers to the given cardinality unambiguously. This act of numerical reference may be articulated or unarticulated in a language. In such a referential situation, it is impossible for the mind to make a mistake in its reference to a given cardinality. For instance, if a variety of objects experienced by a chimpanzee induces synthesis and activation of the exact representation of the cardinality two, then the mind of the chimpanzee refers to two objects in an unarticulated yet exact way. If, in turn, a numeral stimulus induces synthesis and activation of an approximate representation of a given number, then the mind refers to the given cardinality approximately. In such a referential situation, it is possible for the mind to make a mistake. For instance, if a teacher casts an eye on a variety of students during a lecture, then this variety (as a non-symbolic numeral) induces in her/his mind the synthesis and activation of an approximate representation of some cardinality. Let it be the representation of the number nine. In virtue of this process, the teacher refers to nine students, although there are eleven students in the classroom. If she/he articulates her/his act of numerical reference in a sentence of the shape, There are nine students in the classroom, she/he understands this as saying that there are about nine students in the classroom. If representations of numbers located on an axis are exact (unambiguous), then they take the shape of points on a given axis. If representations of numbers are approximate, then they take the shape of places on a given axis. The size of a place on an axis occupied by a given representation maps the degree of the approximation of a given representation.
7.3 The Purely Point Representations of Numbers on the Mental Number Axes
On the basis of the preceding analysis, we may draw the conclusion that point-place representations of numerals are founded upon the summation encoding of non-symbolic numerals. Therefore, the mind must first encode, for instance, the number nine in the summation way and then has to transform its summation representation into a point-place representation. Experiments show that during the mental processing of cardinalities of various sets, the brain activates two groups of neurons, called summation-neurons and numerically selective neurons. The former are involved in the summation encoding of numerical stimuli, whereas the latter take part in processes of decoding numerals (Santens et al. 2010; Roggeman et al. 2011). What is important is that summation (accumulator) neurons are activated in the initial phase of processing a numerical stimulus (Roitman et al. 2007). This process is likely to stimulate the activation of numerically selective neurons. A similar order of brain neuronal activation processes is predicted by two models of mental processing numbers and numerals (Dehaene and Changeux 1993; Verguts and Fias 2004). The following problem thus emerges: Why does the mind not end the process of encoding representations of numerals in the summation encoding phase? Why does the mind transform summation representations of numbers into point-place representations?
Using the metaphor of work on the Internet, one may regard summation encoding as encoding on-line, whereas point-place encoding may be described as encoding off-line. The mind uses the mechanism of summation encoding in the ostensive estimation of cardinalities of objects which appear in perceptual situations; that is, in computational tasks in which a non-symbolic numeral stimulus acts on the mind. The mechanism of point-place encoding is activated when the mind is focused upon the transfer of information obtained as a result of the impact of non-symbolic numerals to memory. Using phenomenological language, we may say that if the retentional intention to maintain numerical information in consciousness is sufficiently strong, then it enforces the transformation of a summation number representation into a point-place representation. This process is empirically confirmed only when the mind is influenced by non-symbolic numeral stimuli. In the case of processing digits, point-place encoding passes without neuronal accumulation. The brain uses point-place coding neurons instead of summation coding neurons to record representations of numerals (Santens et al. 2010). Moreover, the priming effect for digits occurs in accordance with the rules of point-place encoding, in contrast to the summation encoding of representations of non-symbolic numerals (Roggeman et al. 2007).
Hence, it may be conjectured that the main cause of the difference between processes of decoding digits and encoding cardinalities of sets is the mechanism which participates in processes of transferring information to memory. In the case of encoding non-symbolic numeral stimuli, the mind uses the summation mechanism as well as the point-place mechanism, whereas in the case of decoding symbolic numerals, the mind uses only the point-place mechanism. When the mind responds to an exhibited digital stimulus, it activates a linguistic representation which is associated with a corresponding number representation. This means, for instance, that the arithmetical use of digits requires previous encoding representations of numbers towards which the mind refers during the arithmetical processing of digits. Because these representations form an axis-shaped structure, so the processing of digits is the decoding of digits. That is why the process of decoding digits is founded upon processes of synthesis and activation of number representations previously encoded in the mind, whereas processes of encoding cardinalities participating in perceptual situations lead to processes of synthesis, the activation of number representations and, subsequently, to their associations with representations of digit and verbal numerals. In other word, summation processing appears as the starting point in processes of number acquisition, whereas point-place processing appears as the point of arrival in processes of storing number representations in memory or in processes of decoding linguistic representations of numerals.
Point-place number axes may take purely point shapes. It seems that transformations of summation number axes into point-place axes and the latter into purely point number axes are accompanied by transformations of their logarithmic scaling into linear scaling. Summation number axes are logarithmically scaled, whereas purely point axes are linearly scaled.
In some tasks in which the values of numerals are compared, the reaction time and the number of errors increase with the value of numerals, but decrease as the difference between values of compared numerals increases (Moyer and Landauer 1967). The first effect is called the size effect, whereas the second is called the distance effect. Between these effects there holds the following relationship: When numerical values increase, then for the sake of preserving the same reaction time, the distance between them must also increase. Consequently, one may assert that efficiency in comparing the sizes of numerals depends on the ratio between them. Experiments show that the numerals 2 and 4 are compared faster than the numerals 6 and 8 because the ratio between 2 and 4 is greater than the ratio between 6 and 8. This reaction time-dependence is described by the psychophysical Weber-Fechner law, according to which the perceived size of a stimulus increases logarithmically with respect to its objective value. If the mental number axis was scaled in a linear fashion, that is, in such a way that every number was equally far from its predecessor, then the Weber-Fechner law would not be valid. For instance, in the linear scale, the distance between 2 and 4 is the same as the distance between 6 and 8; hence the reaction times needed for the choosing the greater value should be the same. Experiments show that this is not always the case. In the logarithmic scale, distances between consecutive numbers decrease as their values increase. Hence, the distance between 6 and 8 is smaller than the distance between 2 and 4; and that is why it causes the loss of response time in the first case.
Other experiments show that in some situations, the mind uses a representation of the linearly scaled mental axis. Let us consider the task of estimating a number’s position on the axis (Number Line Estimation; Number-to-Position, Siegler and Opfer 2003). Test takers are presented with a screen showing a section with ends appropriately marked with the digit 0 on the left and the digit numeral 100 on the right. This section is a part of the number axis without any graphic scale. Above the section, some digit numeral from the interval (0, 100) is displayed. The subjects must indicate the position of the displayed number on the section shown on the screen. Methods of solving this task vary depending on the age of the test subjects. Children seem to use the axis with a logarithmic scale because in their solutions the distance between 50 and 25 is not described by a linear function. A logarithmic function provides a more detailed description of the marked positions of numbers on the axis. Adults, however, seem to apply a linearly scaled axis. In their solutions, distances between numbers in pairs (25, 50) and (0, 25) are rather similar. The experimental results show that minds undergo a process of exchanging a logarithmic scaling of the mental number axis into a linear scaling. In other words, the development of mental competence causes a transition from logarithmic scaling of number representations to their linear scaling on the mental number axis (Siegler and Opfer 2003; Siegler and Booth 2004; Booth and Siegler 2006; Berteletti et al. 2010). Some researchers (e.g., Siegler and Opfer 2003) postulate that this transition is gradual; that is, a child in some developmental period may use logarithmically scaled number representations as well as linearly scaled number representations, depending on the context of the task and the child’s arithmetic competence. Eight-year-old children may estimate positions of numbers logarithmically when they look at a section with ends (0, 1000) and in a linear way when they look at a section with ends (0, 100) (Siegler and Booth 2004). In the minds of 5-year-old children, the linearly scaled number axis is activated when they must position numbers on the axis (0, 10). But if a task concerns positioning numbers on the axis (0, 20), they activate a logarithmically scaled mental number axis (Berteletti et al. 2010). In accordance with the hypothesis of many-axes number representations, the child’s mind activates the axis which is the most effective for the solution of a given arithmetic task. If a given range of numbers is known to the child, then she/he will activate that mental number axis to which representations of numbers from the given range belong.
Recent research (Barth and Paladino 2011; Cohen and Blanc-Goldhammer 2011) challenges the existence of the mechanism responsible for the logarithmic scale of the mental number axis. These authors assert that experimental tasks concerned with positioning numbers on a representation of the number axis consist in estimating the ratio of the length of some part of the given segment and the length of the whole segment. For the sake of positioning the number three on a section from zero to ten, the mind must first divide the segment into two parts: 〈the beginning, the center〉 and 〈the center, the end〉. Then the mind is ready to find the location of the number three on the axis (0, 10). The assumption is that the mind scales the mental number axis with the help of exponential models constructed by Stevens’ function: F(n) = Kn β, where F(n) is the value of the subjective location of the number n on the mental number axis, K is a constant correlated to the given experimental task and β is a parameter which is unique to the given mind. If β is equal to 1, then Stevens’ function becomes a linear function. If β is greater than 1, then the values of Stevens’ function manifest the subjective overestimation of the objective value of the stimulus. If β is smaller than 1, then the values of Stevens’ function manifest the subjective underestimation of the objective value of the stimulus. The models, constructed with the help of Stevens’ function, were elaborated by Spence (1990) for the perception of the size of fields or surfaces in tasks consisting in the partition of whole surfaces into parts. Three types of model can be distinguished: one-cycle, two-cycle and many-cycle models. In the first type, two Stevens’ functions describe the mechanism of scaling the mental number axis. The mind scales an axis in two phases. In the first, the mind distinguishes three points in a precise manner: the beginning, the center and the end. The first Stevens’ function overestimates all number values belonging to the range 〈the beginning, the center〉, whereas the second underestimates all number values from the range 〈the center, the end〉. Spence’s one-cyclic model has been verified in only some cases. The two-cycle model, in turn, is described by four Stevens’ functions and it sets five critical points on any number axis: the beginning, the center, the end, the center of the range 〈the beginning, the center〉 and the center of the range 〈the center, the end〉. The two-cycle model is the result of the fractalization of the one-cycle model because, after fixation of the middle point on the axis, the mind fixes middle points on sections obtained by the first operation. By successive fractalizations, one may thus generate many-cycle models. All of these models impose non-linear scales on number axes; and for some values of the constant β, the course of the Stevens’ function for some ranges of estimated values of a number stimulus becomes similar to the course of the logarithmic function. In Cohen and Blanc-Goldhammer’s model (2011), the non-linearity effect is explained by two factors: the variance of estimation of the number-location on the axis and the perceived distance between “middles” of numbers. According to the researchers, any representation of a number on the mental number axis is a construction consisting of its relative point-location on the axis and the average variance of its localization on the axis settled by the mind during the experiment. Any representation of a number on an axis is a pair consisting of a point and its neighborhood, that is, a pair 〈n, δ n 〉, where n is a point-location of a given number and δ n is the average variance of its location given in experimental estimations. With an increase of n, the variance δ n also increases as the constant ratio for all numbers greater than 5 (δ n /n = const). According to the authors, the perceived distance between consecutive numbers, understood as the distance between the middles of representations of two consecutive numbers on the axis, also increases. The increase of this distance is described by an exponential function with an exponent greater than one. This conclusion stands in contradiction to empirical data and to theories which maintain that the effect is reversed: With the increase of number values, the perceived distances between numbers decrease. The authors introduce some additional parameter, namely, the difference between representations of numbers. According to the described model, although the distance between consecutive numbers increases with the increase of their values, their difference decreases. The parameter of difference between numbers n and m is inversely correlated to the arithmetic average of their variances δ n + δ m /2. This means that if δ n + δ m increases, then representations of n and m (understood as sections on the axis) overlap to a greater extent. Hence, they become harder to distinguish.
What determines, in any given moment, whether the mind activates non-linear (logarithmic) representations of numbers or linear representations of numbers? It seems that a logarithmic, non-linear mental number axis, which probably constitutes a primitive, immature system of number representations, is activated in situations in which a person must execute fast, automatic calculations or estimations where precision is not the most important element. This occurs when a person must compare the values of digits under time pressure. On the other hand, the linear mental number axis is indispensable when the mind is forced to operate with precise number values. Some experimental data show that the activation of a linear axis requires greater involvement of attention (Anobile et al. 2012).
8 Concluding Notes
The present paper presents, on the basis of empirical data, an architectonic of the system of number representations as a multiplicity of mental number axes with a hierarchical structure. The first level of hierarchy consists of the shortest mental number line (the SMNL), which is responsible for our early abilities of parallel individuation. The subsequent level of hierarchy involves summation (or accumulator) mental number axes. In the successive phase of cognitive development, the mind transforms the generative mechanism for generating summation mental number axes into a generative mechanism for synthesizing point-place mental number axes. The development of abilities to control attention supports processes of synthesizing point-place mental axes with increasingly precise values. This phase is ended when the mind acquires the ability to synthesize exact mental number axes. In this phase, the logarithmic scale of mental number axes is transformed into a linear scale. Its success may be crowned only when the mind acquires verbal numerals. If the mind creates associations of number representations with representations of verbal numerals, then it may synthesize representations of arbitrarily large numbers on the mental exact-number axes.
The system of number representations is thus correlated in the mature mind with a system of linguistic representations of symbolic numerals which is also divided into at least two subsystems: One comprises representations of verbal numerals, whereas the other consists of representations of digit numerals. Both subsystems are associated in every mind which functions efficiently. However, it seems that the translatability of both subsystems is settled by a third system: namely, the system of representations of logical symbolic numerals, which enables the mind to translate verbal numerals into Arabic digit numerals and vice versa.
This system of number representations may be formally modeled as a system of hierarchical algebraic structures which are transformable one into another. A formal model of this system should also explain the mechanisms of these transformations and generate empirical predictions. A subsequent paper, entitled Algebraic models of mental number axes. Part II, will be devoted to the task of constructing such a formal model.
Notes
In the paper, the term “mind” is understood as designating a cognitive system of various functions whose arguments are states of the brain and values are cognitive representations.
Some cognitive researchers emphasize that the system of core knowledge consists of five modules responsible for (1) representing inanimate objects and their mutual interactions (for instance, continuity, spatial connections in a movement, etc.); (2) representing agents and their goal-oriented acts; (3) representing cardinalities, orders and magnitudes; (4) representing geometrical places in a special layout; and, finally, (5) representing social partners, groups and their members in mutual social entanglement (Kinzler and Spelke 2007; Spelke and Kinzler 2007). These modules may be interpreted as cognitive mechanisms underlying the mind’s ability to refer to (1) individual objects and their constellations; (2) subjects and their acts; (3) cardinals, ordinals and magnitudes; (4) places, regions and fields in the experienced physical space; and, finally, (5) human communities and relationships between and within them. To generalize, these modules are responsible for the mind’s ability to perform acts of reference towards objects belonging to basic ontological categories of the human life-world (lebenswelt). This Kantian research program is proposed in Dehaene and Brannon (2010).
Styles of representing number representations in the mind might be also explained by biological mechanisms. Although this type of explanation is not widely accepted at the moment, some experiments with birds show that they tend to ‘count’ holes arranged horizontally from the left. Some authors (Rugani et al 2010) attribute this fact to left-hemisphere dominance in attention control processes in the external space. Furthermore, some effects which might be identified as SNARC effects have been observed in the case of three year olds—that is, in a relatively early phase of ontogenesis (Patro and Haman 2012). Although empirical data are not sufficient, the hypothesis that there is some primitive direction and turn of the mental number line which is modified as a result of cultural and situational factors has not been falsified. According to this hypothesis, the variability of directions and turns of number mental lines is caused by cultural and situational pressures. If so, the variability and flexibility of the direction and turn of the mental number line should satisfy some adaptive functions.
One may put the following question: Is the spatial orientation revealed in experiments a property of a numeral stimulus or a property of the response to it? In accordance with epistemological realism, the spatial orientation revealed in SNARC experiments is a property of the numeral stimuli. According to this standpoint, the spatial orientation of numeral representations encoded in the mind is a result of the influence on the mind of numeral stimuli located in physical space. On a neo-Kantian view—that is, in accordance with epistemological idealism (or epistemological anti-realism)—the mind, being required to respond to numeral stimuli, imposes on them the property of spatial orientation. One may adopt a third solution according to which the spatial orientation is a property of the system composed of a numeral stimuli and the response to it.
The hypothesis according to which SNARC effects possess various degrees of intensity requires at least two experiments for its verification. In the first experiment, the mind is forced to process some semantic property of a numeral stimulus, whereas in the second one, this property is replaced with some non-semantic property of a numeral stimulus. The font color of a digit may serve as the non-semantic property in such an experiment. Our hypothesis is derived from experimental results reported in (Fias 2001).
In accordance with Kant’s epistemology, one should answer these questions by asserting that the activation of the mental number line evokes the mind’s intentional (referential) directing to a stimulus. In this way, such a mental mechanism explains that the mind imposes forms of space and time on stimuli located in sensorimotor space. .
In the case of ‘small’ cardinalities, such a phenomenon is often observed among pre-school children. For example, when children are asked how many sweets they want, they often respond by reciting all the numerals from one to the numeral designating their response.
According to the phenomenological conception of intentionality, moments understood as ‘windows of presence’ in the stream of consciousness possess the retention-protention structure. On phenomenology in cognitive science and the mathematical modeling of phenomenological conceptions, see (anonymous, Yoshimi 2007). In accordance with Kantian epistemology, arithmetic describes the form of time encoded in the mind. This form may be modeled in the phenomenological manner as the retention-protention structure of a number axis.
References
Anobile G, Cicchini GM, Burr DC (2012) Linear mapping of numbers onto space requires attention. Cognition 133(1):454–459
Antell SE, Keating D (1983) Perception of Numerical Invariance in Neonates. Child Dev 54:695–701
Ashcraft MH (1992) Cognitive arithmetic: a review of data and theory. Cognition 44:75–106
Bächtold D, Baumüller M, Brugger P (1998) Stimulus-response compatibility in representational space. Neuropsychologia 36:731–735
Barth HC, Paladino AM (2011) The development of numerical estimation: evidence against representational shift. Dev Sci 14(1):125–135
Benson DF, Dencla MB (1969) Verbal paraphasia as a source of calculation disturbance. Arch Neurol 21:96–102
Berch DB (2005) Making sense of number sense: implications for children with mathematical disabilities. J Learn Disabil 38(4):333–339
Berteletti I, Lucangeli D, Piazza M, Dehaene S, Zorzi M (2010) Numerical estimation in preschoolers. Dev Psychol 46:545–551
Booth JL, Siegler RS (2006) Developmental and individual differences in pure numerical estimation. Dev Psychol 41:189–201
Brannon EM, Merritt D (2011) Evolutionary foundations of the approximate number system. In: Dehaene S, Brannon EM (eds) Space, time, and number in the brain: searching for the foundations of mathematical thought. Elsevier, Amsterdam
Brysbaert M (1995) Arabic number reading: on the nature of the numerical scale and the origin of phonological recoding. J Exp Psychol Gen 124(434):452
Bueti D, Walsh V (2009) The parietal cortex and the representation of time, space, number and other magnitudes. Philos Trans R Soc B 364:1831–1840
Bull R, Marschark M, Blatto-Valle G (2005) SNARC hunting: examining number representation in deaf students. Learn Individ Differ 15:223–236
Bull R, Blatto-Valle G, Fabich M (2006) Subitizing, magnitude representation and magnitude retrieval in deaf and hearing adults. J Deaf Stud Deaf Educ 11:289–302
Cantlon JF, Brannon EM, Carter EJ, Pelphrey KA (2006) Functional imaging of numerical processing in adults and 4-y-old children. PLoS Biol 4:844–854
Carey S (2004) Bootstrapping and the origins of concepts. Daedalus 133(1):59–68
Castronovo J, Seron X (2007) Semantic numerical representation in blind subjects: the role of vision in the spatial format of the mental number line. Q J Exp Psychol 60:101–119
Chen Q, Verguts T (2010) Beyond the mental number line: a neural network model of number–space interactions. Cogn Psychol 60:218–240
Cipora K, Nuerk HC (2013) Is the SNARC effect related to the level of mathematics? No systematic relationship observed despite more power, more repetition, and more direct assessment of arithmetic skill. Q J Exp Psychol 66(10):1974–1991
Cohen DJ, Blanc-Goldhammer D (2011) Numerical bias in bounded and unbounded number line tasks. Psychon Bull Rev 18(2):331–338
De Hevia MD, Spelke ES (2009) Spontaneous mapping of number and space in adults and young children. Cognition 110(2):198–207
Dehaene S (2001) Precis of the number sense. Mind Lang 16(1):16–36
Dehaene S, Brannon EM (2010) Space, time, and number: a Kantian research program. Trends Cogn Sci 14(12):517–519
Dehaene S, Changeux JP (1993) Development of elementary numerical abilities: a neuronal model. J Cogn Neurosci 5:390–407
Dehaene S, Dupoux E, Mehler J (1990) Is numerical comparison digital: analogical and symbolic effects in two-digit number comparison. J Exp Psychol Hum Percept Perform 16:626–641
Dehaene S, Bossini S, Giraux P (1993) The mental representation of parity and number magnitude. J Exp Psychol Gen 122(3):371–396
Eimer M, Hommel B, Prinz W (1995) S–R compatibility and response selection. Acta Psychol 90:301–313
Fauconnier G (1994) Mental spaces: aspects of meaning construction in natural language. Cambridge University Press, Cambridge
Feigenson L, Carey S (2003) Tracking individuals via object-files: evidence from infants’ manual search. Dev Sci 6:568–584
Feigenson L, Carey S, Hauser M (2002) The representations underlying infants’ choice of more: object-files versus analog magnitudes. Psychol Sci 13:150–156
Fias W (2001) Two routes for the processing of verbal numbers: evidence from the SNARC effect. Psychol Res 65:250–259
Fias W, Brysbaert M, Geypens F, d’Ydewalle G (1996) The importance of magnitude information in numerical processing: evidence from the SNARC effect. Math Cogn 2(1):95–110
Fischer MH (2003) Spatial representations in number processing—evidence from a pointing task. Vis Cogn 10:493–508
Fischer MH (2006) The future for SNARC could be stark…. Cortex 42:1066–1068
Fischer MH (2008) Finger counting habits modulate spatial–numerical associations. Cortex 44:386–392
Fischer MH, Brugger P (2011) When digits help digits: spatial–numerical associations point to finger counting as prime example of embodied cognition. Front Psychol 2:260–266
Fischer M, Rottmann J (2005) Do negative numbers have a place on the mental number line? Psychol Sci 47:22–32
Fischer MH, Castel AD, Dodd MD, Pratt J (2003) Perceiving numbers causes spatial shifts of attention. Nat Neurosci 6:555–556
Fischer MH, Shaki S, Cruise A (2009) It takes only one word to quash the SNARC. Exp Psychol 56:361–366
Fischer M, Mills RA, Shaki S (2010) How to cook a SNARC: number placement in text rapidly changes spatial–numerical associations. Brain Cogn 72:333–336
Frank MC, Barner D (2012) Representing exact number visually using mental abacus. J Exp Psychol Gen 141(1):134–149
Gallistel CR, Gelman R (1992) Preverbal and verbal counting and computation. Cognition 44:43–74
Gallistel CR, Gelman R (2000) Non-verbal numerical cognition: from reals to integers. Trends Cogn Sci 4:59–65
Galton F (1880) Visualised numerals. Nature 21:252–256
Gevers W, Lammertyn J (2005) The hunt for SNARC. Psychol Sci 47:10–21
Gevers W, Reynvoet B, Fias W (2003) The mental representation of ordinal sequences is spatially organised. Cognition 87:B87–B95
Gevers W, Reynvoet B, Fias W (2004) The mental representation of ordinal sequences is spatially organised: evidence from days of the week. Cortex 40:171–172
Gevers W, Lammertyn J, Notebaert W, Verguts T, Fias W (2006) Automatic response activation of implicit spatial information: evidence from the SNARC effect. Acta Psychol 122(3):221–233
Giaquinto M (2001) Knowing numbers. J Philos 98(1):5–18
Harder P (2003) Mental spaces: exactly when do we Need them. Cognitive Linguistics 14(1):91–99
Hauser M, Carey S (2003) Spontaneous representations of small numbers of objects by rhesus macaques: examinations of content and format. Cogn Psychol 47:367–401
Herrera A, Macizo P, Semenza C (2008) The role of working memory in the association between number magnitude and space. Acta Psychol 128:225–237
Hommel B (1994) Spontaneous decay of response-code activation. Psychol Res 56:261–268
Hubbard EM, Piazza M, Pinel P, Dehaene S (2005) Interactions between number and space in parietal cortex. Nat Rev Neurosci 6:435–448
Hubbard EM, Piazza M, Pinel P, Dehaene S (2009) Numerical and spatial intuitions: A role for posterior parietal cortex? In: Tommasi L, Nadel L, Peterson MA (eds) Cognitive biology: evolutionary and developmental perspectives on mind, brain and behavior. MIT Press, Cambridge, pp 221–246
Hung Y, Hung DL, Tzeng OJ, Wu DH (2008) Flexible spatial mapping of different notations of numbers in Chinese readers. Cognition 106:1441–1450
Imbo I, De Brauwer J, Fias W, Gevers W (2012) The development of the SNARC-effect: evidence for early verbal coding. J Exp Child Psychol 111:671–680
Iversen W, Nuerk HC, Willmes K (2004) Do signers think differently? The processing of number parity in deaf participants. Cortex 40:176–178
Iversen W, Nuerk HC, Jäger L, Willmes K (2006) The influence of an external symbol system on number parity representation or what’s odd about 6? Psychon Bull Rev 13:730–736
Kinzler KD, Spelke ES (2007) Core systems in human cognition. In: von Hofsten C, Rosander K (eds) Progress in brain research, vol 164. Elsevier Science, Amsterdam, pp 257–264
Knops A, Thirion B, Hubbard EM, Michel V, Dehaene S (2009) Recruitment of an area involved in eye movements during mental arithmetic. Science 324:1583–1585
Krysztofiak W (1991) Struktury ontologiczne w modelu hydrodynamiki In: Hadryś H, Krysztofiak W, Okulski S (eds) Rozwój paradygmatu mechaniki klasycznej. Uniwersytet Szczeciński, Szczecin, pp 27–53
Krysztofiak W (1995) Noemata and their formalization. Synthese 105:53–86
Krysztofiak W (2012) Logiczna składnia liczebnika. Studium kognitywistyczne. Część I. Filozofia Nauki 20(1):59–91
Lakoff G, Núñez RE (2000) Where mathematics comes from. Basic Books, New York
Le Corre M, Carey S (2007) One, two, three, four, nothing more: an investigation of the conceptual sources of the verbal counting principles. Cognition 105:395–438
Lindemann O, Abolafia JM, Pratt J, Bekkering H (2008) Coding strategies in number space: memory requirements influence spatial–numerical associations. Q J Exp Psychol 61:515–524
Lindemann O, Alipour A, Fischer MH (2011) Finger counting habits in Middle-Eastern and Western individuals: an online survey. J Cross Cult Psychol 42:566–578
Lipton JS, Spelke ES (2003) Origins of number sense: large-number discrimination in human infants. Psychol Sci 14:396–401
McCloskey M, Caramazza A, Basili A (1985) Cognitive mechanisms in number processing and calculation: evidence from dyscalculia. Brain Cogn 4:171–196
Meck WH, Church RM (1983) A mode control model of counting and timing processes. J Exp Psychol Anim Behav Process 9:320–334
Moyer RS, Landauer TK (1967) Time required for judgments of numerical inequality. Nature 215:1519–1520
Naccache L, Dehaene S (2001) The priming method: imaging unconscious repetition priming reveals an abstract representation of number in the parietal lobes. Cereb Cortex 11:966–974
Nieder A, Merten K (2007) A labeled-line code for small and large numerosities in the monkey prefrontal cortex. J Neurosci 27:5986–5993
Nieder A, Miller EK (2003) Coding of cognitive magnitude: compressed scaling of numerical information in the primate prefrontal cortex. Neuron 37:149–157
Nieder A, Miller EK (2004) A parieto-frontal network for visual numerical information in the monkey. Proc Natl Acad Sci USA 101:7457–7462
Nuerk HC, Weger U, Willmes K (2001) Decade breaks in the mental number line? Putting the tens and units back in different bins. Cognition 82:B25–B33
Nuerk HC, Wood G, Willmes K (2005) The universal SNARC effect. The association between number magnitude and space is amodal. Exp Psychol 52:187–194
Nuerk HC, Moeller K, Klein E, Willmes K, Fischer MH (2011) Extending the mental number line. A review of multi-digit number processing. J Psychol 219(1):3–22
Núñez RE (2011) No innate number line in the human brain. J Cross Cult Psychol 42:651–668
Patro K, Haman M (2012) The spatial–numerical congruity effect in preschoolers. J Exp Child Psychol 111:534–542
Piazza M, Izard V, Pinel P, Le Bihan D, Dehaene S (2004) Tuning curves for approximate numerosity in the human intraparietal sulcus. Neuron 44:547–555
Piazza M, Pinel P, Le Bihan D, Dehaene S (2007) A magnitude code common to numerosities and number symbols in human intraparietal cortex. Neuron 53:293–305
Platt JR, Johnson DM (1971) Localization of position within a homogenous behavior chain: effects of error contingencies. Learn Motiv 2:386–414
Priftis K, Zorzi M, Meneguello F, Marenzi R, Umilta C (2006) Explicit versus implicit processing of representational space in neglect: dissociations in accessing the mental number line. J Cogn Neurosci 18:680–688
Proctor RW, Cho YS (2006) Polarity correspondence: a general principle for performance of speeded binary classification tasks. Psychol Bull 132:416–442
Restle F (1970) Speed of adding and comparing numbers. J Exp Psychol 95:437–444
Roggeman C, Verguts T, Fias W (2007) Priming reveals differential coding of symbolic and nonsymbolic quantities. Cognition 105:380–394
Roggeman C, Santens S, Fias W, Verguts T (2011) Stages of nonsymbolic number processing in occipitoparietal cortex disentangled by fMRI adaptation. J Neurosci 31:7168–7173
Roitman JD, Brannon EM, Platt ML (2007) Monotonic coding of numerosity in macaque lateral intraparietal area. PLoS Biol 5:e208
Rugani R, Kelly DM, Szelest I, Regolin L, Vallortigara G (2010) Is it only humans that count from left to right? Biol Lett 6:290–292
Rusconi E, Kwan B, Giordano B, Umiltà C, Butterworth B. (2006) Spatial representation of pitch height: the SMARC effect. Cognition 99:113–129
Santens S, Roggeman C, Fias W, Verguts T (2010) Number processing pathways in human parietal cortex. Cereb Cortex 20:77–88
Schwarz W, Keus I (2004) Moving the eyes along the mental number line: comparing SNARC effects with manual and saccadic responses. Percept Psychophys 66:651–664
Schwarz W, Müller D (2006) Spatial association in number-related task: a comparison of manual and pedal responses. Exp Psychol 53(1):4–15
Sellars W (1962) Naming and saying. Philos Sci 29:7–26
Shaki S, Fischer MH (2008) Reading space into numbers—a cross-linguistic comparison of the SNARC effect. Cognition 108:590–599
Shaki S, Petrusic WM (2005) On the mental representation of negative numbers: context-dependent SNARC effects with comparative judgments. Psychon Bull Rev 12(5):931–937
Shaki S, Fischer MH, Petrusic WM (2009) Reading habits for both words and numbers contribute to the SNARC effect. Psychon Bull Rev 16:328–331
Siegler RS, Booth JL (2004) Development of numerical estimation in young children. Child Dev 75:428–444
Siegler RS, Opfer JE (2003) The development of numerical estimation: evidence for multiple representations of numerical quantity. Psychol Sci 14:237–243
Siegler RS, Ramani GB (2008a) Playing linear numerical board games promotes low-income children’s numerical development. Dev Sci 11(5):655–661
Siegler RS, Ramani GB (2008b) Promoting broad and stable improvements in low-income children’s numerical knowledge through playing number board games. Child Dev 79(2):375–394
Simon JR (1969) Reaction toward the source of stimulation. J Exp Psychol 81:1974–1976
Spelke ES, Kinzler KD (2007) Core knowledge. Dev Sci 10(1):89–96
Spence I (1990) Visual psychophysics of simple graphical elements. J Exp Psychol Hum Percept Perform 16:683–692
Tlauka M (2002) The processing of numbers in choice–reaction tasks. Aust J Psychol 54:94–98
Vallesi A, Binns MA, Shallice T (2008) An effect of spatial-temporal association of response codes: understanding the cognitive representations of time. Cognition 107:501–527
van Dijck JP, Fias W (2011) A working memory account for spatial–numerical associations. Cognition 119:114–119
van Dijck JP, Gevers W, Fias W (2009) Numbers are associated with different types of spatial information depending on the task. Cognition 113:248–253
van Galen MS, Reitsma P (2008) Developing access to number magnitude: a study of the SNARC effect in 7- to 9-year-olds. J Exp Child Psychol 101:99–113
Verguts T, Fias W (2004) Representation of number in animals and humans: a neural model. J Cogn Neurosci 16:1493–1504
Verguts T, Fias W (2008) Symbolic and nonsymbolic pathways of number processing. Philos Psychol 21:539–554
Verguts T, Fias W, Stevens M (2005) A model of exact small-number representation. Psychon Bull Rev 12(1):66–80
Walsh V (2003) A theory of magnitude: common cortical metrics of time, space and quantity. Trends Cogn Sci 7:483–488
Whalen J, Gallistel CR, Gelman R (1999) Nonverbal counting in humans: the psychophysics of number representation. Psychol Sci 10:130–137
Wood G, Willmes K, Nuerk HC, Fischer M (2008) On the cognitive link between space and number: a meta-analysis of the SNARC effect. Psychol Sci Q 50:489–525
Xu F, Spelke ES (2000) Large number discrimination in 6-month old infants. Cognition 74:B1–B11
Yoshimi J (2007) Mathematizing phenomenology. Phenomenol Cogn Sci 6:271–291
Zebian S (2005) Linkages between number concepts, spatial thinking, and directionality of writing: the SNARC effect and the REVERSE SNARC effect in English and Arabic Monoliterates, Biliterates, and Illiterate Arabic Speakers. J Cogn Cult 5:165–190
Zhou X, Chen C, Chen L, Dong Q (2008) Holistic or compositional representation of two-digit numbers? Evidence from the distance, magnitude, and SNARC effects in a number-matching task. Cognition 106:1525–1536
Zorzi M, Butterworth B (1999) A computational model of number comparison. In: Hahn M, Stoness SC (eds) Proceedings of the twenty first annual conference of the cognitive science society. Erlbaum, Mahwah, pp 778–783
Acknowledgments
The paper is part of the Project No. [DEC-2011/01/B/HS1/04029], supported by The National Centre of Science in Poland. The author thanks to Katarzyna Patro from The University of Warsaw for her creative assistance in developing empirical evidence of formal models constructed in the paper. My discussions with K. Patro contributed to a number of theoretical ideas proposed in the article.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Krysztofiak, W. Representational Structures of Arithmetical Thinking: Part I. Axiomathes 26, 1–40 (2016). https://doi.org/10.1007/s10516-015-9271-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10516-015-9271-1