Multi-directional Interaction Force Control with an Aerial Manipulator Under External Disturbances

Abstract

To improve accuracy and robustness of interactive aerial robots, the knowledge of the forces acting on the platform is of uttermost importance. The robot should distinguish interaction forces from external disturbances in order to be compliant with the firsts and reject the seconds. This represents a challenge since disturbances might be of different nature (physical contact, aerodynamic, modeling errors) and be applied to different points of the robot. This work presents a new $\hbox {extended Kalman filter (EKF)}$ based estimator for both external disturbance and interaction forces. The estimator fuses information coming from the system’s dynamic model and it’s state with wrench measurements coming from a Force-Torque sensor. This allows for robust interaction control at the tool’s tip even in presence of external disturbance wrenches acting on the platform. We employ the filter estimates in a novel hybrid force/motion controller to perform force tracking not only along the tool direction, but from any platform’s orientation, without losing the stability of the pose controller. The proposed framework is extensively tested on an omnidirectional aerial manipulator (AM) performing push and slide operations and transitioning between different interaction surfaces, while subject to external disturbances. The experiments are done equipping the AM with two different tools: a rigid interaction stick and an actuated delta manipulator, showing the generality of the approach. Moreover, the estimation results are compared to a state-of-the-art momentum-based estimator, clearly showing the superiority of the EKF approach.

1 Introduction

The field of aerial robotics has boomed in the last decades with an increasing number of aerial systems and applications (Ollero et al., 2022; Ruggiero et al., 2018). This was especially pushed by the raising amount of public infrastructure in need of inspection and maintenance, which can no longer be covered by traditional manual techniques (ASCE, 2021). Initially, $\hbox {micro aerial vehicle (MAVs)}$ were mostly used for infrastructure visual inspection and damage assessment (Outay et al., 2020; Gopalakrishnan et al., 2018). However, in the last decade, aerial platform have slowly migrated from visual inspection to physical inspection, maintenance, and construction tasks, requiring interaction and manipulation capabilities (Darivianakis et al., 2014; Chan et al., 2015; Sanchez-Cuevas et al., 2020; Cacace et al., 2021; Ivanovic et al., 2021; Brunner et al., 2022). To this end, standard aerial vehicles have been augmented with active or passive manipulators to improve precision and stability at the point of contact, becoming $\hbox {aerial manipulators (AMs)}$ (Lee et al., 2021; Chermprayong et al., 2019; Naldi et al., 2018; Tognon et al., 2017). Among the possible choices, fully actuated $\hbox {MAVs}$ and tiltrotor $\hbox {omnidirectional micro aerial vehicle (OMAVs)}$ have proven particularly suited for $\hbox {Aerial Physical Interaction (APhI)}$ because of their capability of generating a six $\hbox {degrees of freedoms (DOFs)}$ control wrench in any orientation (Hamandi et al., 2021; Bodie et al., 2020; Pfändler et al., 2019). Considering infrastructure’s inspection, typical $\hbox {nondestructive testing (NDT)}$ tasks usually require the $\hbox {AM}$ to possess onboard force-sensing as well as push-and-slide capabilities. Interactive push-and-slide tasks have been extensively studied first for robotic manipulators (Ortenzi et al., 2017) and lately for aerial robots (Tognon et al., 2019; Nguyen & Lee, 2013; Park et al., 2018) as well, through the use of hybrid force-motion controllers (Nava et al., 2020), and learning-based adaptive strategies  (Zhang et al., 2022). When $\hbox {AM}$ interacts with the environment, it needs to control at the same time the position at the contact, and the interaction force, preserving the stability of the entire system (Meng et al., 2018a). Interaction control techniques with a hybrid control approach have been actively explored since the 1970s for fixed-base manipulators but have not been possible for aerial robots until the past decade. For flying platforms, the system is controlled by two complementary feedback loops. One for the motion and the other for the interaction force, along the unconstrained and constrained axes, respectively. Such a control strategy has been implemented for uni-directional thrust (Nguyen & Lee, 2013) and fully actuated (Park et al., 2018; Nava et al., 2020) vehicles.

Fig. 1

Picture of the OMAV aerial robot equipped with a manipulator

However, most interaction tasks so far have been conducted in controlled laboratory environments with little to no outside disturbances. In order to perform high-accuracy interaction tasks in outdoor conditions, it is of utmost importance to investigate methods to reliably distinguish wrenches that arise from interaction at the contact point, and the ones arising from external disturbances (such as aerodynamic effects from wind).This becomes an important aspect while performing physical interaction tasks since the platform should be compliant to contact forces, while compensating external disturbances.

Thanks to new developments in sensor technology, innovative $\hbox {Force-Torque (FT)}$ sensors lightweight and small enough to be carried onboard are now available to the robotics community. Still, the ability to reliably separate between interaction and external forces remains challenging. Nowadays, the $\hbox {FT}$ sensors have been used to estimate and control interaction forces (Pankert & Hutter, 2020; Wang, 2021; Bodie et al., 2019; Buzzato et al., 2018; Sanchez-Cuevas et al., 2020), but those do not measure external disturbances.

On the other hand, sensor-less solutions has been applied to estimate external forces, either interaction during contact (Meng et al., 2018b) or disturbance during flight. For disturbance wrench estimation different works have already employed momentum-based approaches as in Ruggiero et al. (2014), Ruggiero et al. (2015) and Rajappa et al. (2017), depending on linear and angular velocity measurements. The momentum-based method was also applied for physical interaction with the environment in Ryll et al. (2019), and with humans in Tognon et al. (2021). But when interaction and disturbance happen at the same time, momentum-based observers measure only the sum of the external forces. Thus, it is impossible to do precise force control rejecting at the same time external disturbances.

Other estimation approaches based on the system’s acceleration Tomić (2014) or hybrid linear acceleration and angular velocity measurements Tomić et al. (2017) were also proposed. The residual-based contact detector  Tomić et al. (2020) was developed for estimation of contact and aerodynamic wrenches, without the need for dedicated sensors, however, without interaction control for $\hbox {AMs}$. $\hbox {Kalman filter (KF)}$-based estimators overcome the limitations of the previous approaches by taking into account sensor noise and more complex models. Moreover, the momentum-based methods can’t efficiently enable the estimation of the external forces coming from different sources. Among them, an $\hbox {extended Kalman filter (EKF)}$ external wrench observer for an $\hbox {AM}$ was developed in Wilmsen et al. (2019), a steady-state Kalman filter in Augugliaro and D’Andrea (2013), and $\hbox {unscented Kalman filter (UKFs)}$ in McKinnon et al. (2016) and McKinnon and Schoellig (2020). However, all of these approaches treat measured and disturbance wrenches as two separate entities, coming from two different estimation processes (the former usually being just a low-pass filtered version of the $\hbox {FT}$ sensor measure). Since contact forces represent a valuable source of information while in interaction, designing a unified mathematical framework for external force estimation is among the main contributions of this work.

1.1 Contributions

In this work, we design a hybrid motion-force controller to perform push-and-slide tasks with an aerial manipulator along any direction, while rejecting external wind disturbances. In particular, we propose a new method to allocate and adapt the desired force and motion directions during the task execution. While the current state of the art is mostly limited in interactions along the robot’s tool direction, here we successfully perform force tracking control sideways as well, by opportunely optimising the interaction direction. This becomes possible by independently combining the robot’s position and orientation, exploiting the platform’s omnidirectionality. The controller relies on the external wrench estimate of a novel $\hbox {EKF}$ formulation. While state-of-the-art approaches treat measured and disturbance wrenches as two separate entities, we propose to simultaneously and reliably estimates both of them in a unified fashion. Thus, the estimation framework enables rejecting occurring disturbances while performing high-accuracy physical interaction tasks. This is made possible by combining the aerial platform’s twist information and $\hbox {FT}$ sensor measurements, together with an analytical model of the platform dynamics. Furthermore, increasing the measurement model by employing the full state will improve the framework performance. In the end, as the method is designed for generic $\hbox {AMs}$, we specifically apply it to an aerial system with two different arms: an active delta manipulator and a rigid stick. In particular, we compare the disturbance estimation quality with a state-of-the-art momentum-based estimator, clearly showing the superiority of the proposed $\hbox {EKF}$. For this purpose, the $\hbox {AM}$ tracks interaction forces and motion trajectories along different orientation surfaces under the presence of wind disturbance.

1.2 Outline

Section 2 presents the modeling of the $\hbox {AM}$ dynamics, as well as a few assumptions on the $\hbox {FT}$ sensor model. Section 3 details the proposed hybrid force-motion controller, together with the force reference adaptation law and the $\hbox {EKF}$ formulation. Then, Sect. 5 shows an extensive testing of the proposed interaction framework considering different scenarios and $\hbox {AM}$ configurations. Finally, Sect. 6 offers concluding remarks and some hints on future works.

2 Modeling

This chapter describes a system model of an omnidirectional flying platform with a generic manipulator attached to the flying base for aerial interaction.

2.1 Definitions and Notation

Table 1 Symbols and definitions

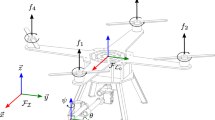
In this section, we provide a schematic description of the $\hbox {AM}$ in Fig. 1. Let us define an inertial (world) frame $\mathcal {F}_{W}$ $= \{O{}_W, {\varvec{x}}{}_W, {\varvec{y}}{}_W, {\varvec{z}}{}_W\}$ and a body frame $\mathcal {F}_{B}$ $=\{O{}_B, {\varvec{x}}{}_B, {\varvec{y}}{}_B, {\varvec{z}}{}_B\}$ rigidly attached to the platform. $\mathcal {F}_{B}$ is placed such that its center $O{}_B$ corresponds to the $\hbox {center of mass (CoM)}$ of the $\hbox {OMAV}$. The vector ${}_W{\varvec{r}}{}_B\in \mathbb {R}^{3}$ describes the position of $O{}_B$ with respect to $\mathcal {F}_{W}$ and ${\varvec{R}}_{WB} \in$ ${\text {SO}}\left( 3\right)$ describes the orientation of $\mathcal {F}_{B}$ with respect to $\mathcal {F}_{W}$.

We assume a general articulated arm consisting of $n \in \mathbb {N}^{}_{\ge 0}$ joints. The configuration of such as a robot can be described by the generalized coordinate vector:

$$\begin{aligned} {\varvec{s}} = \begin{bmatrix} s_1, \ldots , s_n \end{bmatrix}^\top \in \mathbb {R}^{n}. \end{aligned}$$

(1)

Therefore, the vector of the generalized coordinates which defines the configuration of the flying platform and attached arm reads:

$$\begin{aligned} {{\varvec{q}}} = \begin{Bmatrix} {{}_W{\varvec{q}}{}_B}, {\varvec{s}} \end{Bmatrix} = \begin{Bmatrix} {}_W{\varvec{r}}{}_B, {\varvec{R}}_{WB}, {\varvec{s}} \end{Bmatrix}. \end{aligned}$$

(2)

Furthermore, let ${}_W{\varvec{v}}{}_B\in \mathbb {R}^{3}$ be the linear velocity of the aerial vehicle expressed in the world frame $\mathcal {F}_{W}$ and ${}_B{\varvec{\omega }}{}_B\in \mathbb {R}^{3}$ the angular velocity of the body expressed in $\mathcal {F}_{B}$. Thus, the generalized velocity reads

$$\begin{aligned} \dot{{\varvec{q}}} = \begin{bmatrix} {}_W{\varvec{v}}{}_B^\top , {}_B{\varvec{\omega }}{}_B^\top , \dot{{\varvec{s}}}^\top \end{bmatrix}^\top , \end{aligned}$$

(3)

and the generalized acceleration is

$$\begin{aligned} \ddot{{\varvec{q}}} = \begin{bmatrix} {}_W\dot{{\varvec{v}}}{}_B^\top , {}_B\dot{{\varvec{\omega }}}{}_B^\top , \ddot{{\varvec{s}}}^\top \end{bmatrix}^\top . \end{aligned}$$

(4)

For later convenience, we define the end-effector pose of the $\hbox {AM}$ with respect to $\mathcal {F}_{B}$ as ${\varvec{q}}{}_E$, which is a function of the arm generalized coordinates ${\varvec{s}}$:

$$\begin{aligned} {{\varvec{q}}{}_E} = \begin{Bmatrix} {}_B{\varvec{r}}{}_E({\varvec{s}}), {\varvec{R}}_{BE}({\varvec{s}}) \end{Bmatrix}. \end{aligned}$$

(5)

Lastly, as the $\hbox {AM}$ interacts with workpiece surface (see Fig. 1), we define the following workpiece frame $\mathcal {F}_{P}$ $= \{O_P, {\varvec{x}}_P, {\varvec{y}}_P, {\varvec{z}}_P\}$. The above-defined frames and common symbols used throughout this article are summarized in Table 1.

2.2 System Dynamics

The system dynamics are derived in Lagrangian form similarly to Bodie et al. (2020), Brunner et al. (2020) as

$$\begin{aligned} {\varvec{M}}({\varvec{q}})\ddot{{\varvec{q}}} + {\varvec{C}}(\dot{{\varvec{q}}},{\varvec{q}}) + {\varvec{w}}_{g}({\varvec{q}}) = {\varvec{S}}^\top {\varvec{w}}_{act} + {\varvec{J}}_{ext}^\top ({\varvec{q}}){\varvec{w}}_{e}, \end{aligned}$$

(6)

consisting of the following components: mass matrix ${\varvec{M}}$, coriolis and centrifugal terms ${\varvec{C}}$, gravitational terms ${\varvec{w}}_{g}$, selection matrix of the $\hbox {AM}$ actuated joints ${\varvec{S}}$ and geometric Jacobian ${\varvec{J}}_{ext}$ corresponding to the external forces acting on the flying vehicle, e.g. contact forces. Thus, this matrix maps the interaction forces acting at at the end-effector (or any other point) into a wrench and torques applied to the flying platform and the arm joints, respectively. We consider a general rigid-body model of the flying vehicle with mass $m$ and inertia matrix ${\varvec{I}}\in \mathbb {R}^{3\times 3}$, such that the body axes correspond with the principal axes of inertia. We assume to be able to generate a full and instantaneous actuation wrench ${\varvec{w}}_{act} \in \mathbb {R}^{6}$ which is applied in the aerial vehicle center of mass. In the specific case of our $\hbox {OMAV}$, we assume that the system achieves commanded wrench instantly without transients. Our model neglects detailed modeling of aerodynamic effects, which are estimated by the proposed filter as further disturbances. Furthermore, those effects are negligible during interaction tasks where velocities are generally very small.

We consider slow motion of the arm attached to the flying base while performing physical interaction tasks. Thanks to that, we ensure that the end-effector tracking tasks are performed precisely and with high accuracy. Furthermore, for modelling the robotic arm, we assume low manipulator inertia comparing to the aerial vehicle. Therefore, we treat the dynamics of the arm as an additional gravity wrench ${\varvec{w}}_{a}$ exerted by the arm on the flying base. Therefore, the simplified system dynamics model reads

$$\begin{aligned} {}_B{\varvec{M}}\ddot{{\varvec{q}}}{}_B+ {}_B{\varvec{C}}{\dot{\varvec{q}}{}_B} + {}_B{\varvec{w}}_{g} = {\varvec{w}}_{act} + {\varvec{w}}_{ext}, \end{aligned}$$

(7)

where ${\varvec{M}} \in \mathbb {R}^{6\times 6}$ is the symmetric positive definite inertia matrix, ${\varvec{C}} \in \mathbb {R}^{6\times 6}$ contains the centrifugal and Coriolis terms. When expressed in the body-fixed frame $\mathcal {F}_{B}$,

$$\begin{aligned} {}_B{\varvec{M}}&= \text {blkdiag}\left( m\mathbb {I}_{3\times 3}, \hspace{3mm} {\varvec{I}} \right) , \end{aligned}$$

(8)

$$\begin{aligned} {}_B{\varvec{C}}&= \text {blkdiag}\left( m[_B{\varvec{\omega }}_B]_\times , \hspace{3mm} -{\varvec{I}}[_B{\varvec{\omega }}_B]_\times \right) , \end{aligned}$$

(9)

$$\begin{aligned} {}_B{\varvec{w}}_{g}&= \text {blkdiag}\left( m{\varvec{R}}_{BW}{}{\varvec{g}}, \hspace{3mm} {\varvec{0}}_{3\times 3} \right) + {\varvec{w}}_{a}, \end{aligned}$$

(10)

where $[*]_\times$ is the skew-symmetric matrix associated with vector $*$ and ${\varvec{g}}=\begin{bmatrix} 0,0,-9.81 \end{bmatrix}^\top$ is the gravity vector. The terms ${\varvec{w}}_{act}$ and ${\varvec{w}}_{ext}\in \mathbb {R}^{6}$ are both stacked force and torque vectors exerted on the system by base actuation and external sources, respectively. In particular, the actuator wrench reads:

$$\begin{aligned} {\varvec{w}}_{act} = [{\varvec{f}}_{act}^\top , {\varvec{\tau }}_{act}^\top ]^\top , \end{aligned}$$

(11)

where ${\varvec{f}}_{act}\in \mathbb {R}^{3}$, ${\varvec{\tau }}_{act}\in \mathbb {R}^{3}$ are the actuation force and torque vectors, respectively. In this work, the external wrench is defined as

$$\begin{aligned} {\varvec{w}}_{ext} = {\varvec{w}}_i + {\varvec{w}}_{d} = {\varvec{J}}_i ^\top {\varvec{f}}_i + {\varvec{w}}_{d}, \end{aligned}$$

(12)

where ${\varvec{w}}_i$ is the wrench exerted by the interaction force ${\varvec{f}}_i$ on the vehicle’s $\hbox {CoM}$, and ${\varvec{w}}_{d}$ is the wrench exerted on the vehicle by disturbances (e.g., wind gusts and turbulence), all expressed in the body-fixed frame $\mathcal {F}_{{}_W}$. The mapping between the interaction wrench acting on the system’s body and the corresponding interaction force at the contact point is described by the interaction Jacobian ${\varvec{J}}_i \in \mathbb {R}^{6\times 3}$. Since we consider only a pure three-dimensional contact force at the tip of the arm, the interaction wrench ${\varvec{w}}_i$ reads

$$\begin{aligned} {\varvec{w}}_i = {\varvec{J}}_i ^\top {\varvec{f}}_i = \begin{bmatrix} {\varvec{f}}_i \\ {}_W{\varvec{r}}{}_E\times {\varvec{f}}_i \end{bmatrix}, \end{aligned}$$

(13)

where ${}_W{\varvec{r}}{}_E$ is the position of the end-effector with respect to the vehicle’s $\hbox {CoM}$ in the world-fixed frame.

Lastly, as the end-effector moves with respect to the flying base, it is necessary to compensate for the changes of the attached arm $\hbox {centre of gravity (COG)}$ in the system dynamics. Based on the current manipulator configuration ${\varvec{s}}$, known $\hbox {COG}$ positions of each link and total arm mass $m_a$, we obtain the current position of the robotic arm $\hbox {COG}$, ${{\varvec{r}}_{{COG}_a}}$. Thus, the wrench ${\varvec{w}}_a$ from (10) induced by the arm gravity on the system is equal to:

$$\begin{aligned} {\varvec{w}}_a = \begin{bmatrix} m_a {\varvec{R}}_{WB}^\top \hspace{1mm} {_W{\varvec{g}}}\\ m_a{_B{\varvec{r}}_{{COG}_a}} \times ({\varvec{R}}_{WB}^\top \hspace{1mm}{_W{\varvec{g}}}) \end{bmatrix}, \end{aligned}$$

(14)

where $_B{\varvec{r}}_{{COG}_a}$ is the position of the manipulator COG expressed in $\mathcal {F}_{B}$. Simultaneously, we are able to update the COG of the entire flying platform ${\varvec{r}}_{{COG}}$. The updated position ${\varvec{r}}_{{COG}}$ is employed while designing the controller for the vehicle.

Fig. 2

Block diagram of the interaction control framework, combining hybrid force-motion control with $\hbox {EKF}$ estimator. The red box indicates the physical platform prototype, while in green we mark the sensors used in the experimental setup and in blue, software segments of the interaction controller framework (Color figure online)

2.3 Force-Torque Sensor

The interaction force controller and the ability to distinguish between external wrenches acting on the platform, require either additional sensors or other actuation of the robotic arm, namely joint torque controlled. But available torque controlled motors are significantly too big for $\hbox {AM}$. Therefore we decided to equip the system with a $\hbox {FT}$ sensor. The device is placed in between the manipulator base and the flying vehicle. Compared with the previous work (Bodie et al., 2020), shifting the sensor position from the tip to the base of the manipulator provides, in addition to a three-dimensional force, also a torque measurement of the interaction force (Bätz et al., 2013). Thus, while knowing the distance between the interaction point and the sensor, we obtain the contact force directly as well as through the torque measurement. The six-dimensional wrench measurement ${\varvec{w}}_{{FT}}$ of the FT sensor defined in the body frame $\mathcal {F}_{B}$ is

$$\begin{aligned} {\varvec{w}}_{{FT}}&= \begin{bmatrix} {\varvec{f}}_m^\top , {\varvec{\tau }}_m^\top \end{bmatrix}^\top \nonumber \\&= \begin{bmatrix} f_x, f_y, f_z, \tau _x, \tau _y, \tau _z \end{bmatrix}^\top . \end{aligned}$$

(15)

Due to aging of the electronic components and changes in the operating temperature, the sensor experiences drift over time, resulting in biased measurements. We assume that it does not change significantly across the same interaction task. Furthermore, considering the location of the $\hbox {FT}$ sensor, the manipulator mass induces a force due to its gravity. This quantity contributes to the wrench measurement and varies depending on the flying platform orientation in the global reference frame and the actual aerial manipulator configuration. Thus, following Yu et al. (2021), Vougioukas (2001), the $\hbox {FT}$ sensor measurement is defined accordingly:

$$\begin{aligned} {\varvec{w}}_{{FT}} = {\varvec{w}}_b + {\varvec{w}}_a + {\varvec{w}}_{i, {FT}} + {\varvec{w}}_w, \end{aligned}$$

(16)

where ${\varvec{w}}_b$ represents the wrench bias and ${\varvec{w}}_a$ is the arm gravity wrench already introduced in (14) and ${\varvec{w}}_{i, {FT}}$ is the interaction wrench measured by the $\hbox {FT}$ sensor

$$\begin{aligned} {\varvec{w}}_{i, {FT}} = \begin{bmatrix} {\varvec{f}}_i \\ {_W{\varvec{r}}_{{FT}}} \times {\varvec{f}}_i \end{bmatrix}, \end{aligned}$$

(17)

where ${_W{\varvec{r}}_{{FT}}}$ is the position of the end-effector with respect to the $\hbox {FT}$ sensor in the world-fixed frame. The vector ${\varvec{w}}_w$ describes the measurement noise due to vibration and inertial forces. Additionally, we assume constant sensor measurement bias ${\varvec{w}}_b$ over the duration of an interaction task.

2.4 Problem Formulation

With a given system model, the flying platform should be capable of:

• Interacting with the environment through the end-effector while exerting the desired reference interaction force ${\varvec{f}}_{i,ref} \in \mathbb {R}^{3}$ in any direction of the world frame.

• Keeping a stable body pose in the remaining non-interacting directions.

• Distinguishing between external disturbance wrench ${\varvec{w}}_d$ and interaction wrench ${\varvec{w}}_i$, which can simultaneously act on the flying vehicle. Their reliable estimate becomes crucial to ensure high accuracy and precise interaction.

3 Control

This chapter describes the $\hbox {AM}$ control strategy to perform high-accuracy physical interaction tasks even in presence of external disturbances. The controller structure of the system is depicted in Fig. 2. We introduce the hybrid force-motion controller which allows the $\hbox {AM}$ to control and perform various physical interaction tasks.

3.1 Hybrid Force-Motion Control

We employ a hybrid force-motion control framework composed of a PD motion controller combined with a contact force tracking PI controller. We then design an EKF to provide external disturbance and interaction force estimates that will be used by the motion and force tracking controllers, respectively. There exist many situations where the robot should apply a specific force in some direction while it needs to control the motion in others. An example is polishing a surface, whereby the robot applies a specific pressure force in the normal direction and controls the motion in all other directions. To achieve this capability on the flying vehicle, we make use of the so-called operational space control (Khatib, 1987). Thus, in order to exert and maintain a contact force on the environment, the $\hbox {AM}$ is able to adjust appropriately either its position or attitude to fulfil desired physical interaction task. In upcoming subsections, we introduce the motion and force controllers which implement this routine.

3.1.1 Motion Tracking Control

For the motion control, we use the PD position and attitude controller. This control approach enables achieving pose-omnidirectionality with highly dynamic capabilities. The controller generates an appropriate motion control action ${\varvec{w}}_M$ based on the control errors. Those are expressed in the inertial frame relative to reference values with subscript ref, with angular error terms defined by the following equations according to Lee et al. (2010):

$$\begin{aligned} {\varvec{e}}_{{\varvec{r}}}&= {\varvec{r}}- {\varvec{r}}_{ref} \end{aligned}$$

(18)

$$\begin{aligned} {\varvec{e}}_{{\varvec{v}}}&= {\varvec{v}}- {\varvec{v}}_{ref} \end{aligned}$$

(19)

$$\begin{aligned} {\varvec{e}}_{{\varvec{R}}}&= \frac{1}{2} ({\varvec{R}}_{ref}^\top {\varvec{R}}_{WB} - {\varvec{R}}_{WB}^\top {\varvec{R}}_{ref})^{\vee } \end{aligned}$$

(20)

$$\begin{aligned} {\varvec{e}}_{{\varvec{\omega }}}&= {_B{\varvec{\omega }}_{B}} - {\varvec{R}}_{WB}^\top {\varvec{R}}_{ref} {\varvec{\omega }}_{ref}. \end{aligned}$$

(21)

We use the vee-operator $*^\vee$ to extract a vector from a skew symmetric matrix. Then, the motion controller provides 6 DOF wrench ${\varvec{w}}_M = [{\varvec{f}}_M, {\varvec{\tau }}_M]^\top$ as

$$\begin{aligned} {\varvec{f}}_M&= m\left( {\varvec{R}}_{WB}^\top (-k_{{\varvec{r}}}{\varvec{e}}_{{\varvec{r}}} - k_{{\varvec{v}}} {\varvec{e}}_{{\varvec{v}}} + \dot{{\varvec{v}}}_{ref} \right. \nonumber \\&\left. \quad + {{}_W{\varvec{g}}}) + ({}_B{\varvec{\omega }}{}_B\times {\varvec{R}}_{WB}^\top \dot{{\varvec{v}}})\right) \end{aligned}$$

(22)

$$\begin{aligned} {\varvec{\tau }}_M&= {\varvec{I}}(-k_{{\varvec{R}}}{\varvec{e}}_{{\varvec{R}}} - k_{{\varvec{\omega }}}{\varvec{e}}_{{\varvec{\omega }}}) \nonumber \\&\quad + ({_B{\varvec{\omega }}_{B}} \times {\varvec{I}}{_B{\varvec{\omega }}_{B}}) + ({\varvec{r}}_{COG} \times {\varvec{f}}_M) \end{aligned}$$

(23)

where $k_*$ are positive constant gains. To compensate for a center of mass offset ${\varvec{r}}_{COG}$, a counter-torque is added to the desired torque equation. Then, this motion action is fused to the hybrid controller. The detailed description of the 6 DOF geometric PD controller together with the relative motor allocation algorithm can be found in Bodie et al. (2018).

3.1.2 Force Tracking Control

Here we design a control law to track a reference interaction force at the manipulator’s tip ${{}_B{\varvec{f}}}_{i,ref} \in \mathbb {R}^{3}$ using the platform’s full six-dimensional control wrench ${}_B{\varvec{w}}_F$. The mapping between the two is given by

$$\begin{aligned} {\varvec{w}}_F = {\varvec{J}}_i^\top {{}_B{\varvec{f}}}_{i,ref} = \begin{bmatrix} \mathbb {I}_{3\times 3} \\ [{_B{\varvec{r}}_E}]_\times \end{bmatrix} {{}_B{\varvec{f}}}_{i,ref}, \end{aligned}$$

(24)

where ${\varvec{J}}_i \in \mathbb {R}^{6 \times 3}$ represents the interaction Jacobian matrix. Starting from this relation, we design a PI tracking control law as

$$\begin{aligned} {\varvec{w}}_F = {\varvec{J}}_i ^\top \left( {{}_B{\varvec{f}}}_{i,ref} + k_p {\varvec{e}}_i + k_i \int {\varvec{e}}_i\text {dt}\right) , \end{aligned}$$

(25)

where $k_p$, $k_i \in \mathbb {R}^{}$ are positive, constant gains and

$$\begin{aligned} {\varvec{e}}_i = {{}_B{\varvec{f}}}_{i,ref} - {{}_B\hat{{\varvec{f}}}}_i \end{aligned}$$

(26)

is the contact force error, with ${{}_B\hat{{\varvec{f}}}}_i$ the interaction force estimate in the body frame. This is provided by the dedicated estimator introduced in Sect. 4.1.

3.1.3 Hybrid Control

Following the work of Khatib (1987), we define specification matrices in the end-effector frame $\mathcal {F}_{{}_E}$ for position and orientation:

$$\begin{aligned} {\varvec{\Sigma }}_{p} = \begin{bmatrix} 0 &{}0 &{}0 \\ 0 &{}0 &{}0 \\ 0 &{}0 &{}\sigma _{p{\varvec{\chi }}}\end{bmatrix}, \hspace{2mm} {\varvec{\Sigma }}_{r} = \begin{bmatrix} \sigma _{r{\varvec{\chi }}} &{}0 &{}0 \\ 0 &{}\sigma _{r{\varvec{\chi }}} &{}0 \\ 0 &{}0 &{}0\end{bmatrix}, \end{aligned}$$

(27)

where $\sigma _{*} \in (0,1)$ are binary numbers assigned the value 1 when free motion is specified along (linear with subscript p) or around (rotation with subscript r) specific axis, and zero otherwise. Simultaneously, we introduce the leading axis of the manipulator ${\varvec{\chi }}$, depicted in Fig. 3 with light blue colour. This vector defines the direction in the body frame that connects the platform COG of the AM and the end-effector position.

In general, the system applies only force when the interaction force is aligned with the tool axis, such by purely pushing along that while still keeping the pose controller enabled on the two remaining directions. However, this might be impossible due to external constraints, like nearby obstacles that might limit the platform’s range of motion. Additionally, we assume that the end-effector of the manipulator is the most protruding part of the flying platform. Thus, by drawing the circle around the platform COG with radius defined by the manipulator end-effector, we obtain a safety region around the COG of the AM while the platform is close to the interaction surface, as presented in Fig. 3. In reference to Fig. 3, to avoid possible collisions between the AM and the interaction surface in the safety region, we impose additional constraints while defining the entries of the specification matrices in (27). Thus, we induce the platform to rotate in order to exert the specific contact force in the safety region. These constraints on the interaction directions ensure that the vehicle will first establish contact with a surface by its end-effector while simultaneously, any other part of the platform will not touch the surface beforehand. An example of a possible situation is shown in Fig. 3 where the flying vehicle is above the interaction surface. Then, if the AM would move downwards to exert the normal force against this surface instead of changing its attitude, it might lead to the collision of the rotors or landing legs before establishing contact with the end-effector. Therefore, to exert a force which does not coincide with the leading axis of the manipulator ${\varvec{\chi }}$, we employ pure torque control by changing the platform’s attitude. When the interaction surface does not lie inside the safety region, we employ the standard approach where the vehicle aligns its manipulator leading axis with the normal direction $_P\hat{{\varvec{n}}}$ to push against the surface (Bodie et al., 2021). Thus, with the above implementation of the specification matrices in (27), we prefer to purely rotate, exploiting the angular part, to approach interaction when the desired contact force is not aligned with the ${\varvec{\chi }}$-axis. The underlying motivation for such a choice is given in Sect. 3.2. Finally, following Khatib (1987), to formulate the control law, we introduce two selection matrices ${\varvec{S}}_M~\in ~\mathbb {R}^{6\times 6}$ and ${\varvec{S}}_F~\in ~\mathbb {R}^{6\times 6}$ in the body frame $\mathcal {F}_{{}_B}$ for the motion and force directions, respectively:

$$\begin{aligned} {\varvec{S}}_F&= {\varvec{R}}{}_B{}_E\begin{bmatrix} {\varvec{\Sigma }}_p &{} {\varvec{0}} \\ {\varvec{0}} &{} {\varvec{\Sigma }}_r \end{bmatrix}, \nonumber \\ {\varvec{S}}_M&= {\varvec{R}}{}_B{}_E\begin{bmatrix} (\mathbb {I}_{3\times 3} - {\varvec{\Sigma }}_p) &{} {\varvec{0}} \\ {\varvec{0}} &{} (\mathbb {I}_{3\times 3} - {\varvec{\Sigma }}_r) \end{bmatrix}. \end{aligned}$$

(28)

This yields the following combined control law:

$$\begin{aligned} {\varvec{w}}_{act} = {\varvec{S}}_M {\varvec{w}}_M + {\varvec{S}}_F {\varvec{w}}_F, \end{aligned}$$

(29)

where ${\varvec{w}}_M$ is the motion control action Eqs. (22) and (23), ${\varvec{w}}_F$ is the interaction force control action (25), and ${\varvec{w}}_{act}$ is the final wrench output of the hybrid force-motion controller, all expressed in the body frame $\mathcal {F}_{B}$.

Fig. 3

Safety region around the AM while the platform is brought closely to the interaction surface, is depicted in dotted red line. We present this region for different robotic arms attached to the flying base while in black possible interaction surfaces which lie inside this region. For reference, we depict the leading axis of the manipulator marked in in light blue for both AM configurations (Color figure online)

3.2 Interaction Space Control

For each interaction task, we define the reference force in the workpiece frame $\mathcal {F}_{P}$, namely $_P{\varvec{f}}_{i,ref} = {_P\hat{{\varvec{n}}}} f_{i,ref}$, where $_P\hat{{\varvec{n}}}$ represents the interaction surface normal direction which can be arbitrary with respect to $\mathcal {F}_{{}_B}$. In order to apply the control law from (25), we transform the desired force into the vehicle’s body frame with

$$\begin{aligned} {{}_B{\varvec{f}}}_{i,ref} = {\varvec{R}}_{PB}^\top \hspace{1.5mm} {_P{\varvec{f}}_{i,ref}}, \end{aligned}$$

(30)

where ${\varvec{R}}_{PB}$ represents the rotation from the body frame to the workpiece frame. Notice that, even if the desired interaction force is aligned with the surface normal, this might result in an arbitrarily rotated vector in the vehicle’s body frame.

Fig. 4

An example of offset-free reference force tracking. The black arrow is desired interaction force ${_P{\varvec{f}}_{i,ref}}$. In orange we depict the components of the original reference force in body frame. In this scenario the controlled direction is ${\varvec{\zeta }} = {\varvec{z}}{}_B$ while uncontrolled is ${\varvec{x}}{}_B$. The vehicle adjusts its pitch angle to exert the normal force to the surface. The force estimate in the uncontrolled direction ${_B\hat{{\varvec{f}}}_{i}^{\bar{\zeta }}}$ is marked in purple (most right image). That force can be larger or smaller than the desired reference in uncontrolled direction. Thus, we correct for the forces along ${\varvec{\bar{\zeta }}}$ and for misalignment between frames, $\mathcal {F}_{B}$ and $\mathcal {F}_{P}$. Therefore, obtaining the offset-free reference in controlled direction ${{}_B{\varvec{f}}}^{\zeta }_{i,ref}$ depicted in light blue (Color figure online)

To set appropriately the entries in (27), we formulate a discrete optimization problem which aims to find the optimal interaction direction ${\varvec{\zeta }}$ in $\mathcal {F}_{B}$. We want to keep the distance of the vehicle COG from the interaction surface while the AM should change its position as less as needed to establish the contact. Thus, the problem objective is defined as a search among the three body axes a body frame direction ${\varvec{\zeta }}$, which contributes the most to the desired interaction force ${{}_B{\varvec{f}}}_{i,ref}$

$$\begin{aligned} {\varvec{\zeta }} = \underset{{\varvec{\lambda }}\in \begin{Bmatrix} {\varvec{x}}_B,{\varvec{y}}_B,{\varvec{z}}_B \end{Bmatrix}}{\arg \max }\Vert \langle {{}_B{\varvec{f}}}_{i,ref} , {\varvec{\lambda }}\rangle \Vert , \end{aligned}$$

(31)

where $\langle \cdot , \cdot \rangle$ denotes the scalar product between two vectors. This formulation ensures that we minimize the necessary vehicle’s motion to establish the interaction since we choose one body direction along or around which the platform will move. Hence, we enable only the position change of the flying base if the interaction direction in the body frame ${\varvec{\zeta }}$ predominantly coincides with the leading axis of the manipulator ${\varvec{\chi }}$, which reads

$$ \begin{aligned} {\varvec{\zeta }} = {\varvec{\chi }} \rightarrow \sigma _{p{\varvec{\chi }}} = 1 \ \& \ \sigma _{r{\varvec{\chi }}} = 0. \end{aligned}$$

(32)

Otherwise, the system exerts lateral, sideways forces only by the attitude change, namely

$$ \begin{aligned} {\varvec{\zeta }} \ne {\varvec{\chi }} \rightarrow \sigma _{p{\varvec{\chi }}} = 0 \ { \& } \ \sigma _{r{\varvec{\chi }}} = 1, \end{aligned}$$

(33)

Thus, according to (24), the system controls the specific contact force through force along the leading manipulator direction ${\varvec{\chi }}$ and through torque otherwise.

3.3 Adaptation Law For Reference Force Tracking

The problem in (31) provides only one body direction ${\varvec{\zeta }}$ along which we control the contact force, while the original force reference might be in any arbitrary orientation. To still achieve offset-free force tracking we present an adaptation method for the force reference ${{}_B{\varvec{f}}}_{i,ref}$ to account for misalignment between the workpiece and body frames. Then, when the flying platform is in contact with a surface, we estimate the interaction force in the uncontrolled direction $\bar{{\varvec{\zeta }}}\in \mathbb {R}^{3}$

$$\begin{aligned} _B\hat{{\varvec{f}}}_{i}^{\bar{\zeta }} = \underbrace{ \begin{bmatrix} \begin{bmatrix} 1\\ 1\\ 1 \end{bmatrix} - {\varvec{\zeta }} \end{bmatrix}}_{\bar{{\varvec{\zeta }}}} \circ {_B\hat{{\varvec{f}}}_{i}}, \end{aligned}$$

(34)

where $\circ$ denotes the Hadamard product between two vectors. As mentioned above, the system is not able to control $_B{{\varvec{f}}}_{i,ref}^{\bar{\zeta }}$, thus we need to compensate for force along ${\varvec{\bar{\zeta }}}$. We use the estimate ${_B\hat{{\varvec{f}}}_{i}^{\bar{\zeta }}}$ to compensate for the excess forces applied in the uncontrolled direction. This yields a new force reference ${_P{\varvec{f}}}^{new}_{i,ref}$ in the workpiece frame:

$$\begin{aligned} {_P{\varvec{f}}}^{new}_{i,ref} = {_P{\varvec{f}}_{i,ref}} - {\varvec{R}}_{PB} \hspace{1.5mm} _B\hat{{\varvec{f}}}_{i}^{\bar{\zeta }}, \end{aligned}$$

(35)

Next, taking into account the new reference, we find the appropriate force ${{}_B{\varvec{f}}}^{\zeta }_{i,ref}$ in the controlled direction of the body frame ${\varvec{\zeta }}$, such that the original reference force is tracked offset-free. The approach employs projecting ${{}_B{\varvec{f}}}^{\zeta }_{i,ref}$ in the controlled direction ${\varvec{\zeta }}$ on the newly found reference vector ${_P{\varvec{f}}}^{new}_{i,ref}$. It is achieved by solving the following equation:

$$\begin{aligned} {{}_B{\varvec{f}}}^{\zeta }_{i,ref} = \frac{1}{\cos (\theta )}{_P{\varvec{f}}}^{new}_{i,ref}, \end{aligned}$$

(36)

where $\theta \in \begin{Bmatrix} 0, \frac{\pi }{4} \end{Bmatrix}$ is the angle between the axis of the controlled force ${\varvec{\zeta }}$ and the direction of the desired interaction force $_P{\varvec{f}}_{i,ref}$. For reference, the method is illustrated in Fig. 4.

3.4 Disturbance Rejection

In order to compensate for external disturbances, the disturbance wrench estimate is fed to the hybrid force-motion controller by updating the wrench command ${\varvec{w}}_{act}$ from (29) as

$$\begin{aligned} {\varvec{w}}_{act} = {\varvec{S}}_M {\varvec{w}}_M + {\varvec{S}}_F {\varvec{w}}_F - \hat{{\varvec{w}}}_d. \end{aligned}$$

(37)

Thus, the platform reactively counteracts the estimated disturbances.

4 Estimation

4.1 EKF External Wrench Estimation

In our estimation framework, we assume that the interaction point of the platform with the environment is at the manipulator end-effector as tip of the arm is meant to interact with the environment. Furthermore, as the point is zero-dimensional per definition, then only a pure three-dimensional contact force can be induced during the interaction task.

4.1.1 Prediction Model—Translational Dynamics

Under the assumptions stated above, the continuous-time translational dynamics read:

$$\begin{aligned} _W\dot{{\varvec{r}}}&= {_W{\varvec{v}}}, \end{aligned}$$

(38)

$$\begin{aligned} _W\dot{{\varvec{v}}}&= \frac{1}{m} [{\varvec{R}}_{WB}({\varvec{f}}_{act}+ {\varvec{\eta }}_{{\varvec{f}}_{act}} + {\varvec{f}}_i)+{\varvec{f}}_d] + \\&\quad - {_W{\varvec{g}}} \nonumber , \end{aligned}$$

(39)

where ${\varvec{f}}_{act}\in \mathbb {R}^{3}$ is the input thrust and ${\varvec{\eta }}_{{\varvec{f}}_{act}}\in \mathbb {R}^{3}$ represents the input thrust process noise. The process noise in (39) is to account for uncertainty in the model of the thrust produced by each propeller. The thrust mapping is derived close to hover and is not accurate when the platform airspeed and attitude are non-zero. Moreover, the measurements of the motor turn rates are quantized which adds quantization noise to the system. To account for these effects, we add zero-mean Gaussian noise,

$$\begin{aligned} {\varvec{\eta }}_{{\varvec{f}}_{act}} \sim \mathcal {N}({\varvec{0}},\,{\varvec{Q}}_{{\varvec{f}}_{act}}), \end{aligned}$$

(40)

to the nominal thrust with ${\varvec{Q}}_{{\varvec{f}}_{act}}\in \mathbb {R}^{3\times 3}$ being the corresponding covariance matrix. The contact forces ${\varvec{f}}_i$ are expressed in the body frame and the disturbance forces ${\varvec{f}}_d$ in the global world frame. We do not assume any specific underlying dynamics for the external forces and model their dynamics as a random walk, namely:

$$\begin{aligned}&\dot{{\varvec{f}}}_i = {\varvec{\eta }}_{{\varvec{f}}_i}, \end{aligned}$$

(41)

$$\begin{aligned}&\dot{{\varvec{f}}}_d = {\varvec{\eta }}_{{\varvec{f}}_d}, \end{aligned}$$

(42)

where ${\varvec{\eta }}_{{\varvec{f}}_i}\in \mathbb {R}^{3}$ and ${\varvec{\eta }}_{{\varvec{f}}_d}\in \mathbb {R}^{3}$ are both zero-mean Gaussian noise vectors,

$$\begin{aligned}&{\varvec{\eta }}_{{\varvec{f}}_i} \sim \mathcal {N}({\varvec{0}},\,{\varvec{Q}}_{{\varvec{f}}_i}), \end{aligned}$$

(43)

$$\begin{aligned}&{\varvec{\eta }}_{{\varvec{f}}_d} \sim \mathcal {N}({\varvec{0}},\,{\varvec{Q}}_{{\varvec{f}}_d}), \end{aligned}$$

(44)

and ${\varvec{Q}}_{{\varvec{f}}_i}\in \mathbb {R}^{3\times 3}$, ${\varvec{Q}}_{{\varvec{f}}_d}\in \mathbb {R}^{3\times 3}$ define their diagonal covariance matrix, respectively. This choice for the external forces’ dynamics allows the EKF to cope with discrepancies between prediction and measurements, introduced by any additional external force acting on the system.

The covariances ${\varvec{Q}}_{{\varvec{f}}_i}$ and ${\varvec{Q}}_{{\varvec{f}}_d}$ represent tuning parameters in the presented framework. A smaller covariance indicates that we expect the force to change slowly, while a greater covariance means that we expect it to change quickly. A diagonal noise covariance implies that force components vary independently. Modelling force dynamics as a random walk has proven sufficient to estimate unknown, changing forces.

4.1.2 Prediction Model—Rotational Dynamics

The orientation of the body frame with respect to the global frame is represented by the $(4\times 1)$ unit quaternion $_W{\tilde{{\varvec{q}}}}$:

$$\begin{aligned} _W{\tilde{{\varvec{q}}}} = \begin{bmatrix} q_0,\tilde{{\varvec{q}}}_v^\top \end{bmatrix}^\top , \hspace{3mm} \tilde{{\varvec{q}}}_v \in \mathbb {R}^{3}. \end{aligned}$$

(45)

Following the work in Sola (2012), we then derive the continuous-time rotational dynamics as

$$\begin{aligned} _W\dot{\tilde{{\varvec{q}}}}&= \frac{1}{2}{\varvec{\Omega }}({{}_B{\varvec{\omega }}{}_B}) \hspace{1mm} {_W\tilde{{\varvec{q}}}}, \end{aligned}$$

(46)

$$\begin{aligned} {}_B\dot{{\varvec{\omega }}}{}_B&= {\varvec{I}}{}^{-1}({\varvec{\tau }}_{act}+ {\varvec{\eta }}_{{\varvec{\tau }}_{act}} + {\varvec{r}}_i \times {\varvec{f}}_i + {\varvec{\tau }}_d +\nonumber \\&\quad - {{}_B{\varvec{\omega }}{}_B}\times {\varvec{I}}{{}_B{\varvec{\omega }}{}_B} - m{\varvec{r}}_{{COG}} \times {_B{\varvec{g}}}) , \end{aligned}$$

(47)

where

$$\begin{aligned} {\varvec{\Omega }}({{}_B{\varvec{\omega }}{}_B}) = \begin{bmatrix} {{}_B{\varvec{\omega }}{}_B} \end{bmatrix}_{\times }. \end{aligned}$$

(48)

Subsequently, the model includes torques induced by interaction forces ${\varvec{f}}_i$. The vector ${\varvec{r}}_i$ describes the position of the interaction force in the body frame. In this work, the interaction point is assumed to be at the tip of the manipulator, ${\varvec{r}}_i$ represents the end-effector position

$$\begin{aligned} {\varvec{r}}_i = {_B{\varvec{r}}_E}. \end{aligned}$$

(49)

Additionally, the model accounts for the torque caused by COG body offset ${\varvec{r}}_{{COG}}$ with respect to the geometrical centre of the vehicle. As the command motor torque, ${\varvec{\tau }}_{act}$, is uncertain for the same reasons as a command thrust, we model this uncertainty as an additive zero-mean Gaussian noise,

$$\begin{aligned} {\varvec{\eta }}_{{\varvec{\tau }}_{act}} \sim \mathcal {N}({\varvec{0}},\,{\varvec{Q}}_{{\varvec{\tau }}_{act}}), \end{aligned}$$

(50)

with diagonal covariance matrix ${\varvec{Q}}_{{\varvec{\tau }}_{act}} \in \mathbb {R}^{3\times 3}$. The external torque ${\varvec{\tau }}_d$, which comes from unmodeled external disturbance sources, is expressed in the body frame. Similar to the external disturbance force ${\varvec{f}}_d$, we introduce the external disturbance torque and model it as a random walk,

$$\begin{aligned}&\dot{{\varvec{\tau }}}_d = {\varvec{\eta }}_{{\varvec{\tau }}_d} \hspace{2mm} \text {with} \hspace{2mm} {\varvec{\eta }}_{{\varvec{\tau }}_d} \sim \mathcal {N}({\varvec{0}},\,{\varvec{Q}}_{{\varvec{\tau }}_d}), \end{aligned}$$

(51)

where ${\varvec{Q}}_{{\varvec{\tau }}_d}\in \mathbb {R}^{3\times 3}$ being the diagonal covariance matrix.

Finally, the state vector of the proposed EKF approach reads:

$$\begin{aligned}&{\varvec{x}}_{{EKF}} = \begin{bmatrix} {_W{\varvec{r}}}^\top , {_W\tilde{{\varvec{q}}}}^\top , {_W{\varvec{v}}}^\top , {_B{\varvec{\omega }}}^\top , {\varvec{f}}_i^\top , {\varvec{f}}_d^\top , {\varvec{\tau }}_d^\top \end{bmatrix}^\top , \end{aligned}$$

(52)

4.1.3 Observation Model

A high-precision, external, camera-based motion capture system, provides us with measurements of the full 6 DOF vehicle’s pose. Additionally, this is fused with the onboard $\hbox {inertial measurement unit (IMU)}$ to provide angular rate and linear acceleration measurements of the platform. Note that the pose measurement is not required since only the twist information would be sufficient for proper estimation. As the motion capture system provides the pose measurement, we include these readings to improve the EKF performance by increasing the measurement model. Therefore, we use the measurement of the body position, orientation and twist in the EKF observation model. Finally, we add the FT sensor wrench measurement, which consists of three-dimensional force ${\varvec{f}}_m$ and three-dimensional torque ${\varvec{\tau }}_m$ measurements. This yields the following definition of the EKF measurement vector:

$$\begin{aligned}&{\varvec{z}}_{{EKF}} = [{_W{\varvec{r}}_m^\top }, {_W\tilde{{\varvec{q}}}_m^\top }, {_W{\varvec{v}}_m^\top }, {_B{\varvec{\omega }}_m^\top }, {\varvec{f}}_m^\top , {\varvec{\tau }}_m^\top ]^\top , \end{aligned}$$

(53)

where all the quantities with a subscript m are measurements of the corresponding state components. Additionally, we include additive, zero-mean Gaussian noise for the odometry measurements:

$$\begin{aligned} {\varvec{\nu }}_{_W{\varvec{r}}_m} \sim \mathcal {N}({\varvec{0}},\,{\varvec{G}}_{_W{\varvec{r}}_m}), \end{aligned}$$

(54)

$$\begin{aligned} {\varvec{\nu }}_{_W\tilde{{\varvec{q}}}_m} \sim \mathcal {N}({\varvec{0}},\,{\varvec{G}}_{_W\tilde{{\varvec{q}}}_m}), \end{aligned}$$

(55)

$$\begin{aligned} {\varvec{\nu }}_{_W{\varvec{v}}_m} \sim \mathcal {N}({\varvec{0}},\,{\varvec{G}}_{_W{\varvec{v}}_m}), \end{aligned}$$

(56)

$$\begin{aligned} {\varvec{\nu }}_{_B{\varvec{\omega }}_m} \sim \mathcal {N}({\varvec{0}},\,{\varvec{G}}_{_B{\varvec{\omega }}_m}). \end{aligned}$$

(57)

Similar, we define additive, zero-mean Gaussian noise for the interaction wrench measurements:

$$\begin{aligned} {\varvec{\nu }}_{{\varvec{f}}_m} \sim \mathcal {N}({\varvec{0}},\,{\varvec{G}}_{{\varvec{f}}_m}), \end{aligned}$$

(58)

$$\begin{aligned} {\varvec{\nu }}_{{\varvec{\tau }}_m} \sim \mathcal {N}({\varvec{0}},\,{\varvec{G}}_{{\varvec{\tau }}_m}). \end{aligned}$$

(59)

The diagonal covariance matrices ${\varvec{G}}_{*} \in \mathbb {R}^{3\times 3}$ depend on the properties of the sensors and devices being used to obtain those measurements. The EKF is easily extendable to incorporate additional measurements such as those from other sensors, e.g., $\hbox {Global Positioning System (GPS)}$. Thus, the final observation model reads:

$$\begin{aligned} {\varvec{z}}_{{EKF}}&= \begin{bmatrix} \mathbb {I}_{13\times 13} &{} 0_{13\times 3} &{} 0_{13\times 6} \\ 0_{3\times 13} &{} \mathbb {I}_{3\times 3} &{} 0_{3\times 6} \\ 0_{3\times 13} &{} [{_B{\varvec{r}}_{{FT}}}]_\times &{} 0_{3\times 6} \end{bmatrix} {\varvec{x}}_{{EKF}} + {\varvec{\nu }}, \end{aligned}$$

(60)

where $[*]_{\times }$ describes the skew-symmetric matrix and measurement noise vector ${\varvec{\nu }}$ reads

$$\begin{aligned} {\varvec{\nu }}&= \begin{bmatrix} {\varvec{\nu }}_{_W{\varvec{r}}_m}^\top , {\varvec{\nu }}_{_W\tilde{{\varvec{q}}}_m}^\top , {\varvec{\nu }}_{_W{\varvec{v}}_m}^\top , {\varvec{\nu }}_{_B{\varvec{\omega }}_m}^\top , {\varvec{\nu }}_{{\varvec{f}}_m}^\top , {\varvec{\nu }}_{{\varvec{\tau }}_m}^\top \end{bmatrix}^\top \end{aligned}$$

(61)

4.2 Discrete-Time EKF

We discretize the above-depicted continuous-time dynamics model Eqs. (38), (39), (46), (47), (41), (42) and (51) to get the discrete-time prediction model f:

$$\begin{aligned}&{\varvec{x}}_{{EKF}}(k) = f({\varvec{x}}_{{EKF}}(k-1), {\varvec{\eta }}(k-1)). \end{aligned}$$

(62)

As the measurement model has already its discrete nature (60), we obtain directly the following observation discrete-time EKF model h:

$$\begin{aligned}&{\varvec{z}}_{{EKF}}(k) = h({\varvec{x}}_{{EKF}}(k), {\varvec{\nu }}(k)), \end{aligned}$$

(63)

where k defines the discretized time. The initialization procedure sets the state estimate $\hat{{\varvec{x}}}_{m}(0)$ and the covariance estimate matrix ${\varvec{P}}_m(0)$ under the assumption that no interaction and disturbance wrenches are acting on the platform.

The prediction step of the Extended Kalman Filter reads:

$$\begin{aligned} \hat{{\varvec{x}}}_{p}(k)&= f(\hat{{\varvec{x}}}_{m}(k-1), {\varvec{0}}), \end{aligned}$$

(64)

$$\begin{aligned} {\varvec{P}}_p(k)&= {\varvec{A}}(k-1){\varvec{P}}_m(k-1){{\varvec{A}}^\top (k-1)} + \nonumber \\&\quad + {{\varvec{L}}(k-1)}{{\varvec{Q}}(k-1)}{{\varvec{L}}^\top (k-1)} \end{aligned}$$

(65)

where

$$\begin{aligned} {\varvec{A}}(k-1)&= \frac{\partial f(\hat{{\varvec{x}}}_{m}(k-1), {\varvec{0}}) }{\partial \hat{{\varvec{x}}}_{m}}, \end{aligned}$$

(66)

$$\begin{aligned} {\varvec{L}}(k-1)&= \frac{\partial f(\hat{{\varvec{x}}}_{m}(k-1), {\varvec{0}}) }{\partial {\varvec{\eta }}}, \end{aligned}$$

(67)

$$\begin{aligned} {\varvec{Q}}(k-1)&= \text {blkdiag}\left( \text {Var}[{\varvec{\eta }}(k-1)] \right) . \end{aligned}$$

(68)

The measurement update step reads:

$$\begin{aligned} {\varvec{K}}(k)&= {\varvec{P}}_p(k){\varvec{H}}^\top (k) \nonumber \\&\left( {\varvec{H}}(k){\varvec{P}}_p(k){\varvec{H}}^\top (k) + {\varvec{M}}(k){\varvec{R}}(k){\varvec{M}}^\top (k) \right) \end{aligned}$$

(69)

$$\begin{aligned} \hat{{\varvec{x}}}_{m}(k)&= \hat{{\varvec{x}}}_{p}(k) \nonumber \\&\quad +{\varvec{K}}(k) \left( \bar{{\varvec{z}}}(k) - h(\hat{{\varvec{x}}}_{p}(k), {\varvec{0}}) \right) \end{aligned}$$

(70)

$$\begin{aligned} {\varvec{P}}_m(k)&= (\mathbb {I}- {\varvec{K}}(k){\varvec{H}}(k)){\varvec{P}}_p(k) \end{aligned}$$

(71)

where

$$\begin{aligned} {\varvec{H}}(k)&= \frac{\partial h(\hat{{\varvec{x}}}_{p}(k), {\varvec{0}}) }{\partial \hat{{\varvec{x}}}_{p}}, \end{aligned}$$

(72)

$$\begin{aligned} {\varvec{M}}(k)&= \frac{\partial h(\hat{{\varvec{x}}}_{p}(k), {\varvec{0}}) }{\partial {\varvec{\nu }}}, \end{aligned}$$

(73)

$$\begin{aligned} {\varvec{R}}(k)&= \text {blkdiag}\left( \text {Var}[{\varvec{\nu }}(k)] \right) . \end{aligned}$$

(74)

and $\bar{{\varvec{z}}}(k)$ represents the recently obtained measurements from the sensors.

Fig. 5

The vehicle slides along L-shaped trajectory with fix manipulator end-effector position w.r.t. the flying base (Color figure online)

5 Experiments

The vehicle used in this work takes the form of a traditional hexarotor with equally spaced arms about the body z-axis. Each propeller group can independently rotate around the arm’s axis by a dedicated servo motor, allowing various rotor’s thrust combinations. The platform structure consists of custom carbon fibre, aluminium, and 3D printed plastic parts. The system is categorized as fully actuated and omnidirectional. The platform uses lithium-polymer batteries for onboard power. Finally, processing occurs on an onboard Intel NUC computer and Pixhawk flight controller (Bodie et al., 2020).

In our system configuration, we employ a six-axis Rokubi¹ Force-Torque sensor for interaction tasks. The small size and mass (230 g) of the sensor allow simple integration between the flying platform and the manipulator base. This reduces the effect of inertial disturbances and the vibration on the sensor measurements. With integrated EtherCAT electronics, no additional processing hardware is required.

Through a series of experiments, we demonstrate the new capabilities and applications of the system. The manipulator is tightly mounted to the Rokubi sensor. A safety tether is loosely connected to the robot and minimally affects results. The hybrid controller and EKF estimator are implemented in C++ in the $\hbox {Robot Operating System (ROS)}$ framework, running at 200 Hz.

We validate our approach with two kinds of robotic arms attached to the flying base. First, with a parallel 3-DOF delta manipulator (Bodie et al., 2021), which is mounted at the bottom of the vehicle. Secondly, we employ simple homogeneous carbon fibre stick as a manipulator arm. The Rokubi FT sensor is located between the OMAV body and the arm (dynamic or static) base.

The complete delta manipulator assembly weighs 0.72 kg, of which only 0.28 kg is moving relative to the delta arm mounting base. The delta manipulator is mounted on a 4.6 kg flying robot, such that the proportion of moving to total vehicle mass is less than 5 %. Dynamixel M430-W210 motors are selected for the arm’s joints because of their sufficient torque capability and integrated position and velocity feedback. The second manipulator setup consists of the homogeneous carbon fibre stick. In this AM configuration, the arm length from the sensor to the end-effector is 0.395 m, and the distance from the body origin to the manipulator’s tip is measured to be 0.555 m. The carbon fibre stick attached to the FT sensor weighs 72.5 g. A video showcasing the experiments is available as supplementary material.

5.1 Force/State Trajectory Generation

Each physical interaction task is described as a collection of specific constrained subsequent waypoints. Each waypoint consists of information about desired vehicle position and attitude. Additionally, it holds the pose of the workpiece surface in the world frame defined by the transformation matrix ${\varvec{T}}_{WP}$. Lastly, for each waypoint we define the desired reference contact force $_P{\varvec{f}}_{i,ref}$ which the AM should exert on the surface. We use polynomial trajectory interpolation (Richter et al., 2016) and nonlinear optimization as described in Burri et al. (2015) to obtain smooth paths for the platform between next waypoints. Then the polynomial trajectory is sampled at 200Hz and passed to the controller as an array of timestamped reference points.

5.2 Sliding Along Surface with Fixed End-Effector Position

In this experiment with a delta arm, we evaluate the ability of the system to maintain the normal orientation to a table, rejecting forces from virtual disturbances when tracking a desired normal interaction force. For reference, we present a series of freeze-frames showing the described test scenario in Fig. 5. The platform performs described L-shaped trajectory twice. In the first attempt, the system interacts with a table without any external disturbance occurring, while in the second run we apply three-dimensional virtual force disturbance ${\varvec{f}}_v$. The virtual disturbance signal ${\varvec{d}}_v \in \mathbb {R}^{3}$ is given by

$$\begin{aligned} {\varvec{d}}_v = {\varvec{f}}_v, \end{aligned}$$

(75)

and perturbs the control action (37) accordingly

$$\begin{aligned} {\varvec{w}}_{act} = {\varvec{S}}_M {\varvec{w}}_M + {\varvec{S}}_F {\varvec{w}}_F + - \hat{{\varvec{w}}}_d - \begin{bmatrix} {\varvec{R}}_{WB}^\top {\varvec{d}}_v \\ {\varvec{0}} \end{bmatrix} , \end{aligned}$$

(76)

where ${\varvec{R}}_{WB}$ is the rotation matrix from world to body frame. We apply a virtual disturbance force of 5 N in each direction of the world frame $\mathcal {F}_{W}$ and zero virtual torque disturbance ${\varvec{\tau }}_v$. The disturbance ${\varvec{d}}$ is involved while the platform already established a contact with the interaction surface. In Fig. 6, we show the framework’s ability to precisely estimate current disturbance and to distinguish between external wrenches acting on the system. Without introducing any change in the controller, the system can handle transitions in and out of contact with good stability and without significant difference in tracking on the surface plane, as presented in Fig. 7. At the initiation of the interaction phase, around ninth second on the chart, we command the force of 5 N. However, while sliding along L-shaped trajectory, the reference is reduced to 3 N. Even if not necessary to initiate the contact, we found that commanding a higher initial force leads to more stable contact initiations. This might be especially true for articulated manipulators, since oscillations in the structure during the transients might lead to a temporary contact loss. Still, small forces can be directly commanded as we show in the next experiments.

Fig. 6

Estimated force disturbance while sliding along L-shaped trajectory with fixed arm. Without (left column) and with (right column) virtual disturbance. From top to bottom, the rows show virtual force disturbance (solid orange) and EKF estimates (dotted blue) along $x_W$, $y_W$ and $z_W$, respectively. Yellow background indicates exact time period when the disturbance was applied (Color figure online)

Fig. 7

Normal force tracking while sliding along L-Shaped Trajectory with fixed end-effector. On the left without and on the right with virtual force disturbance. The solid orange line shows normal force reference while in blue dotted the EKF interaction force is depicted. The yellow background indicates the period when the three dimensional virtual force disturbance is applied (Color figure online)

While sliding, the noticeable loss of the force tracking with a maximal tracking error of 1.8 N happens at roughly 25 s of the experiment. From this time, we start to apply a 5 N virtual force disturbance along the perpendicular direction to the surface, which the controller promptly recovers. In this case, this direction corresponds to the manipulator leading axis ${\varvec{\chi }}$-axis which is the body ${\varvec{z}}{}_B$-axis. The $\hbox {root mean square error (RMSE)}$ of the interaction force tracking without any virtual disturbance is 0.54 N while for the scenario with a virtual force disturbance the reported RMSE is 0.79 N.

5.3 Sliding Along Surface with Fixed Body Position

This experiment makes active use of the delta arm to perform more advanced interaction tasks. The objective of this task is still to exert the desired normal force against the surface. But now, the flying base should remain at the same position, and only the arm will move relative to the robot body to make the end-effector follow a pre-defined desired trajectory as presented in Fig. 8. This means that the leading interaction axis of the manipulator ${\varvec{\chi }}$ changes its direction while executing the end-effector trajectory. Here, the planner traces a triangular trajectory for the end-effector along the table while the vehicle base position and orientation are fixed in $\mathcal {F}_{W}$. The system is autonomously positioned to a start point and the ${\varvec{z}}{}_B$ axis aligns with the normal interaction surface axis. Then, the aerial manipulator autonomously approaches the workpiece surface to exert a specific interaction force. As contact is made, the end-effector starts to slide along the table surface.

Fig. 8

The end-effector is sliding along the table surface while the flying base is hovering at a fixed pose. The desired end-effector trajectory is presented by a green dashed line (Color figure online)

Fig. 9

In the upper plot we show the normal force tracking performance while the end-effector is moving w.r.t. the platform and slides along the table surface. In orange the normal force reference is presented while in blue the EKF interaction force estimate. Below we plot the delta end-effector position tracking. In blue, green and red we depict the reference (solid) and measured (dotted) position of the end-effector along ${\varvec{x}}{}_W$, ${\varvec{y}}{}_W$ and ${\varvec{z}}{}_W$, respectively (Color figure online)

In Fig. 9, we depict the normal force tracking performance. The desired normal force is set to the constant value of 3N and is tracked offset-free by the hybrid force-motion controller, as presented in Fig. 9. Comparing to the previous case, the normal force estimate varies significantly more. It is caused by the fact that the end-effector does move with respect to the flying base. This influences the tracking performance as in the control strategy we modelled the manipulator to be quasi-static.

Fig. 10

Experimental setup for the OMAV with a rigid manipulator. In green we depict the desired trajectory of the end-effector while sliding along the consecutive workpiece surfaces (Color figure online)

Fig. 11

Disturbance wrench estimate while interacting in presence of wind disturbance. The yellow background indicates the time when the wind fan is active. Blue, red, yellow plots correspond to x, y and z directions, respectively. The disturbance force is plotted in the world frame $\mathcal {F}_{W}$ while the disturbance torque in the body frame $\mathcal {F}_{B}$ (Color figure online)

5.4 Interaction Along Consecutive Workpieces

The next experiment will focus on showcasing the framework capabilities while transitioning from one to the other interaction surface. Here we equipped our flying platform with a passive carbon stick arm which is rigidly attached to the Rokubi sensor. Now, we demonstrate that the platform can interact with the environment while not being fully aligned to its contact surface and perform advanced tasks with subsequent workpieces. For this purpose, we introduce the following experimental setup presented in Fig. 10. We place two tables perpendicular to each other such that the platform will slide over these two surfaces by autonomously executing the following waypoint sequence, depicted in Fig. 10 by red numbers:

$$\begin{aligned} \text {Free Flight} \rightarrow 1 \rightarrow 2 \rightarrow 3 \rightarrow 2 \rightarrow 1 \rightarrow \text {Free Flight.} \end{aligned}$$

According to the Sect. 3.1.3, the platform will pitch on the way between points 1 and 2 and yaw between 2 and 3 as for this trajectory the normal direction of those surfaces is not along the leading axis of the manipulator. Thus, the vehicle controls the desired contact force on the environment by adjusting the torque. Furthermore, we aim at reproducing outdoor conditions during the interaction: instead of applying virtual disturbances, a wind fan generates a wind gust disturbing the robot, as shown in Fig. 10. Two tests are performed in a row: first while the fan is active and the second while the device is switched off. The objective for the flying robot is to track the normal force reference along the consecutive workpieces, while distinguishing between external wrenches, and rejecting the disturbance. In Fig. 11, we present the disturbance wrench estimate obtained with our framework. Based on plotted experiment outcome, it turns out that the air disturbance mainly induced an external torque on the platform, with magnitude change of 0.4N m. Furthermore, we observed that the disturbance force along the ${\varvec{z}}_W$ direction (yellow) varies the most, as one could expect since the fan is located on the floor. After switching off the wind fan, the force and torque disturbance estimates converge to their steady-state values This justifies the EKF performance since only an interaction force acts on the system as an external wrench. Finally, we present the normal force tracking performance in Fig. 12. It is remarkable that the control approach is robust and does not experience much difference in the tracking performance, although in the first period the air disturbance acted on the flying system indicated by the yellow background. Furthermore, during this physical interaction the AM changes its contact surface what showcase the ability of the framework to interact with a multiple subsequent workpieces. The transition phase between the contact surfaces is indicated by peaks of the normal force in Fig. 12 as the vehicle needs some time to adjust its pose to the new interaction surface. But without introducing additional changes in the controller framework, the platform can handle transition between subsequent workpieces without loosing the contact with them. This experiment demonstrates also that the platform gained a novel ability to exert the force in any direction of the body frame. Thus, the system is able to interact with the surfaces which are not aligned with the arm’s main axis while keeping a stable body pose in the remaining non-interacting directions.

Fig. 12

Normal force tracking during interaction in presence of wind disturbance (yellow background). The reference force ${\varvec{f}}_{i,ref}$ is set to 3N for each test. The normal force estimate (blue) follows as expected its reference (Color figure online)

Fig. 13

Orientation (left) and position (right) of the aerial vehicle in the world frame while sliding along two interaction surfaces. The blue line indicates the test scenario when the wind fan is active while in orange we show the vehicle’s pose without any air disturbances (Color figure online)

Additionally, we depict the orientation and position (Fig. 13) of the vehicle’s $\hbox {CoM}$ for this experiment. In the figure, we plot the platform pose during both scenarios simultaneously on the same graph. This test demonstrates that the proposed hybrid motion-force controller with $\hbox {EKF}$ Wrench Estimator can compensate right for external disturbance, maintaining attitude error within 4.5$^\circ$. It is worth to emphasize that we do not observe significant change in the position tracking as well.

Fig. 14

Estimated interaction and disturbance wrench while sliding along consecutive workpieces (Fig. 10). In green, the $\hbox {EKF}$ contact force estimates are plotted to mark the contact phase of the $\hbox {AM}$ with the surface. Here, we do not apply any virtual disturbance, thus the solid orange line is zero all the time. From top to bottom, the rows show disturbance force estimates obtained with $\hbox {EKF}$ (blue), momentum-based with high cutoff frequency (purple) and with lower cutoff frequency (magenta) along $x{}_W$, $y{}_W$ and $z{}_W$, respectively. The three last rows present the disturbance torque estimates obtained with all described methods. Later, the three-dimensional virtual force disturbance is applied while the $\hbox {AM}$ is performing an interaction task. For comparison, the $\hbox {EKF}$ and momentum-based estimator with higher and lower cutoff frequency are depicted. Re-tuning the estimator gain reduces the noise in the estimated disturbance force but simultaneously increases the response time of the disturbance force estimate of the momentum-based observer (Color figure online)

5.5 Momentum-Based Estimation

As a last experiment, we validate and compare the proposed estimation framework with a state-of-the-art momentum-based estimator (Bodie et al., 2020). The implementation of this estimator follows the method described in Ruggiero et al. (2014), while now we can incorporate the interaction wrench measurement ${\varvec{w}}_i$ provided by the $\hbox {FT}$ sensor, according to (16). Thus, the momentum-based observer is expressed as

$$\begin{aligned} \hat{{\varvec{w}}}_{ext}&= {\varvec{K}}_I \left( {\varvec{M}}\begin{bmatrix} {\varvec{v}}\\ {\varvec{\omega }} \end{bmatrix} \right. \nonumber \\&\quad \left. - \int \left( {\varvec{w}}_{act} - {\varvec{C}}\begin{bmatrix} {\varvec{v}}\\ {\varvec{\omega }} \end{bmatrix} - {\varvec{w}}_{g} - {\varvec{w}}_{i} + \hat{{\varvec{w}}}_{ext}\right) \text {dt}\right) , \end{aligned}$$

(77)

where a positive definite diagonal observer matrix ${\varvec{K}}_I \in \mathbb {R}^{6\times 6}$ acts as an estimator gain. Note that this method allows the estimation of external forces and torques without the use of acceleration measurements, only requiring linear and angular velocity estimates.

For this test, we use the experimental setup from the previous scenario (see Fig. 10). Now, instead of using an air fan to generate an external disturbance, we apply a three-dimensional virtual force disturbance, as in Sect. 5.2. Here, we make use of the virtual disturbance as it allows us to precisely know occurring disturbance and quantitatively compare momentum-based observer with $\hbox {EKF}$ estimation approach. The $\hbox {AM}$ equipped with a rigid stick performs the path depicted in Fig. 10 twice. In the first half there is no virtual disturbance. The latter is introduced in the second half of the experiment.

In Fig. 14, we depict the disturbance wrench estimates obtained with $\hbox {EKF}$ and with momentum-based observer. We also present the $\hbox {EKF}$ interaction force estimate to indicate the time period when the end-effector was touching the surface. In this experiment, the interaction and disturbance (virtual) wrench act on the flying platform at the same time. We run the EKF and the momentum-based estimator in parallel with the same data while executing the desired interaction task. The momentum-based observer is able to get the same response time (purple in Fig. 14) to estimate the virtual force disturbance when it starts to occur in each direction. But simultaneously, it performs poorly in handling the noisy $\hbox {FT}$ sensor measurements, even after fine-tuning the filter. Moreover, the momentum-based approach classifies some portion of the forces which appear during the contact phase between the $\hbox {AM}$ and workpiece surface as an external torque acting on the platform even when there are no external disturbances acting on the platform.

If the previous comparison was in terms of response time, we now tune the estimator gain ${\varvec{K}}_I$, to obtain approximately the same noise level of the $\hbox {EKF}$ estimate. In Fig. 14 it is clearly visible that the response time of the momentum-based estimator (magenta in Fig. 14) is significantly longer while the $\hbox {EKF}$ estimates converge instantaneously without noticeable delay. The analysis and comparison of both methods shows the performance increase of our framework and showcases its robustness in estimating disturbance and interaction wrenches which can act simultaneously on the platform.

6 Conclusion

This work presented an $\hbox {EKF}$ framework to estimate and reliably distinguish between disturbance wrenches and interaction forces acting on the flying vehicle. We showed that the proposed algorithm adequately handles noisy measurements, requires only a few intuitive covariance values to be tuned. Furthermore, it can serve as a basis for reacting to aerodynamic perturbations without relying on specialized knowledge of the underlying dynamics of the disturbance or of the aerodynamic properties of the platform, or on specialized sensors for measuring wind speed. We have extensively tested in a set of experiments how the external wrench estimate may be used in conjunction with a hybrid motion-force controller to perform physical interaction even in presence of a wind source. The capabilities of the $\hbox {AM}$ has been extended to track precisely and offset-free the desired interaction force along any desired direction. The presented framework enabled the flying vehicle to gain a novel ability to track reference forces in any direction of the body frame for the first time. Finally, the presented framework can be applied with any type of robotic arm. We demonstrated the framework capabilities with the delta parallel arm in addition to the simple rigid stick as end-effectors of the $\hbox {AM}$. Additionally, the proposed framework outperforms state-of-the-art momentum-based estimation while the vehicle is subjected simultaneously to interaction and disturbance wrenches.

However, the method presents some limitations here summarized. First of all, the system has been examined in a fully controlled laboratory environment. Thus, we plan to reproduce the results in outdoor conditions where the platform would be not able to get precise pose measurements from the camera motion capture system, and we will investigate the use of onboard Visual-Inertial Odometry in combination with $\hbox {GPS}$ to estimate the vehicle relative pose to its environment such that our $\hbox {EKF}$ observation model will not have to be reduced. Additionally, during the experiments, we find out the limits for the interaction force that the platform can track [2,10]N. The next important step is to investigate new methods to increase and go beyond those interaction force boundaries. Especially, to enable the tracking of even lower interaction forces which could be required for assembling fragile structures. Finally, the demonstrated framework could be extended to estimate the actual interaction point of the $\hbox {AM}$ with the environment. This can enable to perform even more complex interaction tasks with a robotic arm attached to the flying base.