A dynamical system approach for detection and reaction to human guidance in physical human–robot interaction

Abstract

A seamless interaction requires two robotic behaviors: the leader role where the robot rejects the external perturbations and focuses on the autonomous execution of the task, and the follower role where the robot ignores the task and complies with human intentional forces. The goal of this work is to provide (1) a unified robotic architecture to produce these two roles, and (2) a human-guidance detection algorithm to switch across the two roles. In the absence of human-guidance, the robot performs its task autonomously and upon detection of such guidances the robot passively follows the human motions. We employ dynamical systems to generate task-specific motion and admittance control to generate reactive motions toward the human-guidance. This structure enables the robot to reject undesirable perturbations, track the motions precisely, react to human-guidance by providing proper compliant behavior, and re-plan the motion reactively. We provide analytical investigation of our method in terms of tracking and compliant behavior. Finally, we evaluate our method experimentally using a 6-DoF manipulator.

1 Introduction

Robots are leaving their traditional and industrial setting to join and help us with our everyday life. They are expected to perform a variety of tasks in environments with considerable amount of uncertainty. In an interaction with such environment, many sources of perturbation to the task-at-hand can be imagined. Some of those are accidental that need to be rejected (in order to fulfill the task autonomously) while some are intentional and must be incorporated into the robotic behavior; e.g., complying with the human intention to switch from one task to another. For example, when carrying heavy-load, the robot should reject the disturbance forces that undermine the stability of the task while providing reactive behavior toward intentional forces of the human to determine his/her intention for path planning. Therefore, it is crucial to provide robots with algorithms that can detect such human guidances, reactive yet stable motion planners, and compliant controllers. To this end, we use dynamical systems (DS) for motion planning where a specific robotic task can be encoded as mapping from robot’s states to robot’s desired velocities (Khansari-Zadeh and Billard 2011). Stability and generalization of such models allow the robot to tolerate perturbations in its states and to generate a reactive motion for successful execution of the task (Kronander and Billard 2016).

Fig. 1

An illustration of human robot collaboration where the robot reacts intelligently to external perturbation. In the first scenario, the robot rejects the undesirable disturbances for a better tracking performance; i.e., to maintain the drilling point and to avoid damaging the object and the tool. In the second scenario, the robot detects and complies with the human guidance; i.e., the robot becomes compliant and passive where the human can easily move the tool and demonstrate his/her intention. Moreover, the robot recognizes the intention and moves to the next drilling point to perform the task autonomously (color figure online)

Compliant control (in the form of impedance or admittance) was initially proposed to provide safe and passive interactions with the environment (Hogan 1988). The robot can track a certain trajectory (e.g. those generated by the DS to fulfill a task) while exhibiting compliant behavior toward external perturbation. In the absence of human-interaction, the robot executes the task autonomously. However, having the human in the interaction, the robot acts as a compliant leader; i.e., damping human-inputs in order to execute the task. Moreover, having no reference trajectory, the robot can only react to human forces and appears as a passive-follower. This is useful when the robot supports a heavy load and renders a lower inertia for the user (Kang et al. 2010). Furthermore, adding prediction capabilities, the robot (while following the human) can estimate the human-desired trajectory, and act upon it (Calinon et al. 2014). This leads to a proactive-follower behavior. In the follower form, the compliance of the robot can be tuned (or varied, using variable-compliance controllers) to provide intuitive and effortless interaction for the human (Duchaine and Gosselin 2007). However, in the compliant-leader form, the compliance parameters (e.g., the impedance gain) are facing a trade-off; i.e., high gains lead to higher precision in execution of the task, while low gains lead to higher compliant behavior toward the human user. To have versatile interaction, robots ought to not only play all these roles, but also know when and how to switch across them with a proper compliance profile; see Evrard and Kheddar (2009) as pioneer of this idea. Consider the example illustrated in Fig. 1 where the robot is initially executing a reaching task autonomously and maintaining the target position. In doing so, the robot is a non-compliant/stiff-leader so as to reach a desirable tracking performance and rejecting the undesirable disturbances. Detecting human guidance, the robot becomes compliant in selective directions, allowing the human to modify only locally its motion. As such, the robot appears as a compliant leader, as it still carries on with the initial task. If the human guidance persists, the robot increases its compliance until it becomes a passive-follower. This allows the human to take over the leadership of the task, which subsequently allows the human to demonstrate a desired behavior to the robot. Next, the robot starts to follow a prediction of the human intention, which renders the robot as a proactive-follower. The human, accepting the robot’s prediction and proactivity, retreats from the interaction allowing the robot to become autonomous (stiff-leader) and to focus on tracking behavior.

Human-guidance can be recognized through several modalities and contextual information such as vision, natural-language processing, etc. However, in this work, we focus on the haptic channel, namely relying on the external forces sensed by the robot. The literature of dyadic task proves that haptic communication plays a crucial role. van der Wel et al. (2011) indicate that the haptic channel is rich enough to recognize the intentions and predict partner actions. Reed et al. (2006), Groten et al (2010) and Oguz et al. (2010) show that dyads can quickly negotiate a more efficient motion strategy using haptic communication and improve their performances. For example, Madan et al. (2015) reports on “persistent conflicts” where one partner insists on applying force in opposite direction of the motion. They argue that such conflicts are recognized and resolved easily. Moreover, haptic information contributes to role distribution (Pham et al. 2010). For instance, Stefanov et al. (2009) infer the dyadic roles based on the sign of interaction forces, velocities, and accelerations. They categorize the roles into “executor” (who performs the task) and “conductor” (who decides on the task). They also report on a persistent phase where the same partner is both executor and conductor (and the other partner is potentially a passive follower). Following the same line, we rely on such persistency of interaction forces to detect human-guidance. This brings us to an analogy to the literature of collision avoidance where a sudden change in the force (or momentum) perceived by the robot are indicative of a collision (Haddadin et al. 2017). The benefits of haptic information in robotic applications are twofold: (1) high-frequency components in the haptic channel (e.g., sudden changes in forces) can contribute to a safe interaction with the environment, and (2) low-frequency components (e.g., persistent forces) can be utilized for human-guidance detection, role distribution, and human-intention detection. In this work, we detect human-guidance based on the persistency of the haptic information and we adapt the robotic behavior accordingly.

Fig. 2

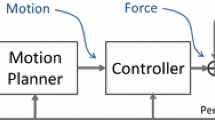
The unified control structure to provide motion-tracking and compliant behavior based on human intention. In this diagram, $F_e$ and ${\tilde{F}}_h$ represent the external and the estimated human-intended forces respectively. h, the human-interaction ratio, is computed based on the external force. ${\dot{x}}_a$ is the admittance-generated velocity based on the estimated human forces (${\tilde{F}}_h$). ${\dot{x}}_t$ represents the task-specific velocity generated by the dynamical system based on the robot’s position ($x_r$). The final desired velocity sent to the robot is represented by ${\dot{x}}_d$. In this architecture, the inner loop provides the tracking behavior and the outer loop provides following behavior toward the human input. Based on the external forces, we detect if the human demands following behavior. Detected human-guidance (h) attenuates the effect of motion planner (color figure online)

In this work, we propose a novel control architecture to provide proper compliance and motion-control based on human-guidance. This architecture is depicted in Fig. 2. We assume that the robot is controlled in velocity (either using pure high-gain velocity controller or via velocity-based impedance controller), and position and force feedback are available. In order to obtain reactive motion planning, we employ state-dependent dynamical systems to encode our desired robotic tasks. Furthermore, in order to achieve intelligent compliant behavior, we propose a human-guidance detection algorithm that only passes intentional forces to an admittance controller. This controller structure can be seen as an interplay of two separated control loops: the inner loop which aims to provide precise tracking behavior, and the outer loop which aims to provide proper compliance behavior (i.e., to reject the disturbances or to allow for human-interaction). Figure 3 shows how this structure enables the robot to take different roles in the interaction. In the following, we review the related works. Later, we put our approach under rigorous mathematical analysis in terms of stability, passivity, and tracking performance. Finally, we conduct several robotic experiments in order to show the efficacy of our method in real-world interaction with human.

Fig. 3

A conceptual illustration of our method. ($Stiff \,leader$) The robots starts by performing a task encoded by a dynamical system ($f_1$). During this period, the robot rejects the external disturbances and focuses on the tracking behavior. ($Compliant \,leader$) The robot detects intentional interaction with human and as a result provides complaint behavior while performing the task. ($Passive \,follower$) The robots neglects the task and stays compliant using the admittance loop. In this phase, the robot observes the motions that human demonstrates which is detected as another task ($f_2$). ($Proactive \,follower$) Knowing the intended task, the robot starts to actively follow the human guidance, which results in human retrieval. ($Proactive \,follower$) The robot starts to autonomously perform the intended task (color figure online)

2 Related works

Safety is the first concern for robotic interactions with the environment. A conservative approach is to ensure a passive interaction; e.g., the kinetic energy of the robot dissipates over time. The control strategies proposed by Hogan (1988) provide straightforward formulations (impedance and admittance) for such passive and compliant interactions. In its simple form, the robot renders a mass-spring-damper behavior around a fixed-point. Having proper parameters (i.e., inertia, damping and stiffness matrix), one can achieve passive interaction. Considering only the damping part allows the robot to passively follow the external forces; i.e., passive-follower. This is useful for transportation tasks (especially for mobile platforms as in Kang et al. 2010) or manipulation tasks where a different and more suitable inertia and damping is rendered for the human user as in Duchaine and Gosselin (2007). In the same line, varying the compliant behavior can improve the interaction from the user point-of view (Duchaine and Gosselin 2007). Moreover, instead of a set-point, the robot can exhibit the compliance behavior around a reference trajectory; i.e., a compliant-leader in the interaction. This trajectory can be pre-computed (Ferraguti et al. 2013), or can be generated reactive the state of the robot (Kronander and Billard 2016). The reference trajectory can also be predicted from the human guidance (Medina et al. 2012; Li et al. 2016; Calinon et al. 2014; Modares et al. 2016), which leads to a proactive following behavior. However, tracking a trajectory potentially undermines the passivity of the system. Energy tank-based controllers were employed to relax the conservative condition on the passivity (Ferraguti et al. 2015; Schindlbeck and Haddadin 2015; Kronander and Billard 2016); i.e., the robot can be temporally active and injects energy into the environment while, on average-over-time, stays passive. Generating motion using dynamical systems with their corresponding storage functions (as proposed in Kronander and Billard 2016) allows us to investigate and control the passivity of the whole system easier. Same approach is used by Shahriari et al. (2017) to include the energy due to the motion planning using Dynamic Movement primitives. The literature of robotic compliant control clearly shows the efficacy of the proposed methods to generate a “single” desired behavior (e.g., compliant leader, passive or proactive follower). However, it falls short from providing robots with intelligence mechanism for detecting the proper behavior and switching mechanisms that are proved to be safe and stable. An initial and interesting approach to switch between leader and follower behaviors was offered in Evrard and Kheddar (2009). In that work, a homotopy variable is used to linearly combine the two behaviors. However, they pose it as a future work to adjust this variable based on the contextual information and guarantee the stability. In a follow-up work, Bussy et al. (2012) utilizes a manual switch from pro-active follower to leadership. We take a similar approach in combining the leader and follower behavior; i.e., generated velocities by dynamical systems and admittance loop respectively. However, we provide an adaptation/estimation for such homotopy variable while guaranteeing the stability of the system.

To endow robots with leader behavior, we employ state-dependent dynamical systems (DS) as motion generators. Such DS can be learned through human demonstrations and provide stable and convergent trajectories (Khansari-Zadeh and Billard 2011). The state-dependency of DS provides a reactive behavior; i.e., the external perturbation to the state results in a different desired velocity. Moreover, considering the storage-function related to the DS leads to simpler design of passive interaction with the environment while performing a task (Kronander and Billard 2016). Furthermore, DS provides a strong framework for adaptive motion generation. To do so, the dynamics can be modulated based on external signals; e.g., Gribovskaya et al. (2011) use external forces to perform a collaborative task, Sommer et al. (2017) use contact information to avoid obstacle, Medina et al. (2016) use the load-share to obtain a fluid hand-over, and Khoramshahi et al. (2018) use tracking error to refine a DS based on human guidance. DS provide a computationally light motion planning which allows for smooth transient behaviors. In our previous works, we proposed adaptive mechanisms to switch smoothly from one task to another (Khoramshahi and Billard 2018). The robot was then acting as an adaptive compliant-leader where the lower/higher compliance favors the tracking-error/human-effort. However, it seems more natural if the robot changes its role and becomes a passive-follower so the human can demonstrate his/her intention with a lower effort. Li et al. (2015) offer a method to vary the robot’s impedance based on the interaction forces as to continuously switch the role between leader and follower. However, such methods are prone to undesirable disturbances, as they do not distinguish between intentional and accidental forces. In this work, we provide a framework where the robot detects the human-guidance and reacts by providing a proper compliant behavior.

To endow robots with compliant behavior, we use an admittance controller; i.e., the robot senses the interaction forces and responds with proper velocities. This controller is widely used in the literature of pHRI: collaborative assembly (Cherubini et al. 2016), insertion tasks (Mol et al. 2016). By responding to human forces, the robot can provide a simple following behavior as in Duchaine and Gosselin (2007). Moreover, human trajectory estimation can provide pro-active following behavior (Jlassi et al. 2014). Duchaine and Gosselin (2009); Ranatunga et al. (2017) proposed a method to adapt to human stiffness as to generate cooperative movements. Admittance control is also suitable for whole body control of robot such as arm-based platform (Dietrich et al. 2012). Hashtrudi-Zaad and Salcudean (2001) argues that performances of this controller depend on the stiffness of the environment and propose a method to switch an impedance controller to have the accuracy of admittance control in free motion with the robustness of the impedance controller. Campeau-Lecours et al. (2016) also argues that admittance control is suitable to perceive the environment and human intentions and to respond accordingly. They mention that the behavior is acceptable if the reference trajectories are highly dynamic. Admittance control provides a simple solution toward active leader behavior: the resulted velocities from the external force can be simply added to task-specific velocities. This idea is used in Corteville et al. (2007) and Shahriari et al. (2017). In this work, we use the same approach to combine task-specific motion planning with proper compliant behavior.

Admittance control is suitable to detect human interaction while performing a task. This controller can provide the proper behavior by filtering/modifying measured forces. This is not the case in impedance control where the input is a displacement. The literature of collision detection exploits this fact. The robot rejects small external forces and delivers a satisfactory tracking behavior. It only reacts to forces detected as collision. Detection algorithms rely on the assumption that collisions result in a fast rate of change in different quantities such as input power (De Luca et al. 2006), generalized momentum (He et al. 2015), external forces (Haddadin et al. 2008; Cho et al. 2012). The collision is detected if the magnitude of such signals surpasses a certain threshold. This threshold can be adapted over time based on the evolution of the force signal as proposed in Makarov et al. (2014). More elaborated method uses the difference between real and nominal dynamics (Landi et al. 2017; Kouris et al. 2018) suggest to use frequency domain approaches to distinguish unexpected collisions from voluntary contact during human–robot collaborations. Interestingly, they conclude that admittance control provide the fastest reaction behavior. Reaction strategies are also of interest to our work where the robot switches from active to passive mode; as in Li et al. (2018) where the robot switches from position control to a passive torque-control upon collision with a human user. In contrast, we use a unified control architecture (i.e., DS-based admittance controller with human-guidance detection) which allows us to smoothly switch back and forth between active and passive modes.

Even though, detection of human-leadership is structurally similar to collision detection, there are a few important differences. First, a human joining the interaction does not necessarily results in high rate of changes in force or energy. Second, it is required to detect not only the human joining the interaction, but also leaving it. Interactions with the environment are usually considered passive while the human is an active agent who intends to inject energy into the system. The literature on variable compliance control offers different approaches where the controller adapts to detected human intentions (Lecours et al. 2012; Kim et al. 2017; Ranatunga et al. 2015; Corteville et al. 2007). However, such works are limited to a single role for the robot, and human-interaction detection is not used to switch from leader to follower. We assume human-guidance forces are consistent (as opposed to noises, oscillations and short-lived disturbances like shocks). In this work, we rely on such properties to detect human-guidance forces (instead of fast rate of changes in the lit. of collision detection). To measure consistency, we compute autocorrelation on the force pattern as a metric to distinguish between intentional (human) guidance and disturbances. Moreover, for reaction/adaptation strategy, we propose a smooth transition between motion tracking and compliant behavior (instead of just varying/adapting the compliance). Our human-guidance detection method is independent from the control structure and our reaction strategy is proved to be stable.

3 Motion-compliance control

We model the robot’s end-effector as a rigid-body described in the task space with the state variable $x \in \mathbb {R}^n$ where the measurement of external forces ($F_e \in \mathbb {R}^6$) is available. As illustrated in Fig. 2, we assume that the robot is velocity-controlled. We combine the task-specific velocity (${\dot{x}}_{t}$) generated by the robot’s nominal DS with the velocity generated by the admittance controller (${\dot{x}}_a$), this yields

$$\begin{aligned} {\dot{x}}_d = (1-h) {\dot{x}}_{t} + {\dot{x}}_a \end{aligned}$$

(1)

where $h \in [0, 1]$ is a modulation factor that is generated by the human-detection algorithm. Moreover, ${\dot{x}}_{t}$ and ${\dot{x}}_a$ are the velocity generated by the DS and admittance respectively. The desired velocity (${\dot{x}}_d$) is sent to the velocity controller to be tracked by the robot. We use a nominal dynamical system for motion planning, given by:

$$\begin{aligned} {\dot{x}}_{t} = f(x) \end{aligned}$$

(2)

where $f:\mathbb {R}^n\mapsto \mathbb {R}^n$ generates task-specific velocities (${\dot{x}}_{t}$) for given robot’s positions (x).

Finally, the compliance behavior is delivered through admittance control with the following formulation:

$$\begin{aligned} M_a \ddot{x}_a = -D_a {\dot{x}}_a + {\tilde{F}}_h \end{aligned}$$

(3)

where $M_a$ and $D_a \in {\mathbb {R}}^{n \times n}$ are admittance mass and damping matrices. The human-guidance forces (${\tilde{F}}_h$) is estimated using our algorithm based on the external forces ($F_e$).

4 Human-interaction detection

Our human detection algorithm can be seen as a soft switch as follows.

$$\begin{aligned} {\tilde{F}}_h = h F_{e} \quad \text {where} \quad 0 \le h \le 1 ~~ \forall t \end{aligned}$$

(4)

where ${\tilde{F}}_h$ is the estimated human-force, and h is the human-interaction ratio: $h=0$ results in stiff behavior whereas $h=1$ brings out the compliant behavior given by the admittance dynamics. In the following, we show how we compute this ratio. First, in order to understand whether there is a consistent intention behind external forces, we simulate the following virtual admittance.

$$\begin{aligned} M_a \ddot{\tilde{x}} = -D_a \dot{\tilde{x}} + F_{e} \end{aligned}$$

(5)

$\dot{\tilde{x}} \in {\mathbb {R}}^d$ is the virtual state. Using this virtual admittance, we estimate the motion resulting from reacting to $F_{e}$. Given $\dot{\tilde{x}}$, we can estimate the persistency of the input using the following powers:

$$\begin{aligned} {\tilde{P}}_{i} = \dot{\tilde{x}}^T F_{e} \quad {\tilde{P}}_{o} = \dot{\tilde{x}}^T {\tilde{F}}_h \end{aligned}$$

(6)

where ${\tilde{P}}_{i}$ and ${\tilde{P}}_{o}$ are the input and output power respectively. Now, we consider an energy tank (with the state E and size $E_{m}$) with the following dynamics.

$$\begin{aligned} \dot{E} = {\tilde{P}}_{i} - {\tilde{P}}_{o} - (1-h) {\tilde{P}}_{d} \end{aligned}$$

(7)

where ${\tilde{P}}_{d} > 0$ is a dissipation rate that is modulated by human-interaction ratio h. This energy is limited between 0 and $E_{m}$. Human-guidance ratio h is decided based on stored energy in the tank as follows.

$$\begin{aligned} h = {\left\{ \begin{array}{ll} 0 &{}\quad E \le E_{t}\\ (E - E_{t})/(E_{m} - E_{t}) &{}\quad E > E_{t} \end{array}\right. } \end{aligned}$$

(8)

where $E_t$ is threshold that triggers the detection of the human-guidance. This linear mapping allows for a straightforward analysis of our method. Nevertheless, other monotonically increasing functions can be considered; e.g., to have smoothness at $h=0$ and 1.

Fig. 4

The block diagram representation of the human-guidance detection method. $F_e$ and ${\tilde{F}}_h$ represent the external and the estimated human-intended forces respectively. $\dot{\tilde{x}}_a$ is generated velocities using the virtual admittance (Eq. 5). ${\tilde{P}}_i$ and ${\tilde{P}}_o$ denote the input and output power respectively, and ${\tilde{P}}_d$ the dissipation rate. E is the accumulated energy in the tank, and h is the human-interaction ratio. $\varDelta$ represents a unit delay in computation of ${\tilde{F}}_h$ due to integration operator

Fig. 5

Comparison between our algorithm for human-guidance detection and low-pass filters. The responses are evaluated for Gaussian noise, step function, and a train of impulses. In simulation, we use $E_m=2$, $E_t=1$, ${\tilde{P}}_d=2$, $M_a=1$, $D_a = 8$, $dt=1$ ms. The Gaussian noise is generated by ${\mathcal {N}}(0,36)$, and impulses last for 10 ms every 50 ms. The lower graph shows the changes of the accumulated energy (E plotted in black with respect to the left-hand side y-axis) and the human-interaction ratio (h plotted in blue with respect to the right-hand side y-axis). The green shade corresponds to the intentional forces; i.e., the step function. The dashed line represents the size of the energy tank (i.e., $E_m=2$) which is mapped to $h=1$ (color figure online)

The block diagram of our method is illustrated in Fig. 4. It can be seen that the velocity of the virtual admittance block (i.e., a mass-damper system) is used to detect a continuous power coming from the external force. More specifically, positive values of ${\tilde{P}}_{i}$ increase the stored energy and consequently increases h. This means the human must contribute to a positive value of the power over a certain period to generate a response from the robot. Positive power is relevant to the consistency in motion and the indication whether there is an intention behind external forces. ${\tilde{P}}_{d}$ acts as a forgetting factor and suppresses the small forces that need to be rejected.

The dynamics of h are investigated further in “Appendix A.1”. It can be seen that in the virtual admittance $\dot{\tilde{x}}$ is the filtered and scaled version of $F_e$. Therefore, ${\tilde{P}}_i$ measure the correlation between $F_e$ and its history; i.e., autocorrelation. This fact is shown with further mathematical details in “Appendix A.2”.

Fig. 6

A simulated interaction in a one-dimensional case. The robot rejects the external disturbances such as noises and shocks to deliver a satisfactory tracking behavior. Moreover, the robot detects the human guidance and complies with human intention as to reduce the required effort. Green and red shades indicate the human guidance and disturbances respectively. The parameters are specified in “Appendix A.5” (color figure online)

Figure 5 shows the result of our detection algorithm for three different types of external forces: Gaussian noise, a persistent force, and a series of impulses. The resulting ${\tilde{F}}_h$ shows that only the persistent human-input will pass the filter and the other undesirable disturbances are rejected. Our method exhibits a delay at $t=3$ s for the detection of the step function. This delay is necessary to ensure that the signal is persistent. Furthermore, we compare our method to low-pass filters with different bandwidths. Even though, low-pass filters can show faster response to the step function, they still suffer in passing the undesirable disturbances. It is also interesting to note that h is smooth over time, except at $h=0$ (with $\dot{h}>0$) and $h=1$ (with $\dot{h}<0$). These exceptions are mainly due to (1) the delay introduced by the forward integration (i.e., $\varDelta$ as illustrated in Fig. 4), and (2) the abrupt and persistent changes in $F_e$ at $t=3$ and $t=6$. However, this is not an issue as our method does not introduce frequencies (in ${\tilde{F}}_h$) higher than those that are already present in $F_e$.

Finally, considering the actual admittance block (Eq. 3), the variation of h renders a variable-admittance control equivalent to the following.

$$\begin{aligned} \bar{M}_a \ddot{x}_a = -\bar{D}_a {\dot{x}}_a + F_{e} \end{aligned}$$

(9)

where $\bar{M}_a = h^{-1} M_a$ and $\bar{D}_a = h^{-1} D_a$. Here, we have variable admittance control without any loss of stability, which is usually the case in impedance controller. This is an advantage of admittance over impedance since we can arbitrarily change the admittance ratio. Finally, the passivity of the close-loop system is investigated in “Appendix A.3”.

5 Illustrative example

For our first example, we consider a one-dimensional problem using the following nominal dynamical system for motion generation:

$$\begin{aligned} {\dot{x}}_{t} = -kx \end{aligned}$$

(10)

The results are shown in Fig. 6. In this simulation, the DS-impedance loop tries to bring x to zero from any arbitrary initial condition. We tested our algorithm against three types of external forces. In $t \in [0, 2]$, we apply zero-mean Gaussian noise (${\mathcal {N}}(0,1)$). As it can be seen, no energy is accumulated in the tank and h remains at 0. This disturbance is hence rejected and the system performs a perfect tracking of the dynamics generated by Eq. 10. In $t \in [3,6]$, a simulated human applies a state-dependent force for 3 s with the intent to bring the system to position $x=1$, using the following applied force:

$$\begin{aligned} F_{e}(x,{\dot{x}}) = -20 (x - 1) - 10 {\dot{x}} \quad 3<t<6 \end{aligned}$$

(11)

Fig. 7

A simulated interaction in a 2-dimensional case. The robot initially tracks the desired velocity generated by the DS. Upon detecting human-interaction, the robot becomes compliant and passively follows the human motion. After human-interaction, the robot returns to tracking mode using the DS. The parameters are specified in “Appendix A.5” (color figure online)

Fig. 8

The results for adaptive DS in simulation where the proposed algorithm is used to adapt the motion only to the detected human-guidance. a The red and blue vector fields denote the DS generating clockwise ($f_2$) and counter-clockwise ($f_1$) motions respectively. The blue and red portions of the trajectory are generated using $f_1$ and $f_2$ respectively. The gray portion denotes the transition phase from $f_2$ to $f_1$. b The upper row shows the result of human-guidance detection along with the task-adaptation. The external forces at time 0.3 s (which are restrictive as the power is negative) is detected as intentional. Complying to this intentional interaction allows the robot to detect the intended task ($f_1$) and switch accordingly. The lower row shows the comparison with impedance control (without human-guidance detection) where low impedance gains lead to poor tracking performance and high gains lead to rigid behaviors where task-adaptation is no longer possible. The simulation parameters are specified in “Appendix A.5” (color figure online)

Fig. 9

Illustration of clearpath ridgeback mobile-robot with Universal UR5 robotic-arm. The motions are generated by the learned DS from the current position of the end-effector toward the corresponding attractor to perform a specific task (color figure online)

The generated forces are saturated to $[-10,10]N$. Due to the consistency of this external force, the energy increases and h smoothly approaches 1. It can be seen that the estimated human-force $F_h$, after a short delay, smoothly converges to $F_{e}$. As the result, the control loop transit to the admittance mode (${\dot{x}}_d = {\dot{x}}_a$) This allows the simulated-human to approach its goal ($x=1$) around $t=6$ s through the expected compliant behavior. Upon human retrieval, the energy of the tank dissipate (due to ${\tilde{P}}_{d}$) and control mode switches to motion tracking ${\dot{x}}_d = {\dot{x}}_{t}$. This enables the robot to follow the motion perfectly and reach $x=0$. At $t=9$ s, we apply a sudden transient force to the robot ($F_e = 10$ for 5 ms every 50 ms). Due to the lack of consistency, this external force is rejected and the motion-tracking is preserved. The last subgraph shows the results of a fixed admittance controller using different damping gains. This graph clearly shows that the proper gain for tracking and human-interaction are drastically different; i.e., 100 and 1 respectively. The intermediate values are also ineffective in delivering a satisfactory behavior. Usually, one behavior needs to be sacrificed for the other. One can think of traditional variable admittance control for this case (i.e., varying $D_a$ over time). However, as discussed before, obtaining a satisfactory tracking behavior and ensuring the stability is not trivial.

It is interesting to note the steady-state error of the simulated-human at $t=6$ s where the target ($x=1$) is not precisely reached. This error is partially due to the choice of the simulated-human; the PD-control in Eq. 11. Furthermore, even after reaching the target precisely, a simulated agent is required to keep exerting forces in order to obtain $h=1$ and remove the effect of ${\dot{x}}_t$ in Eq. 1. This suggests that beside adapting the compliance toward intentional forces, it is essential for effective interactions to adapt the task-specific motions (i.e., ${\dot{x}}_t$) as well. In the next two examples, we show that the reactivity and adaptability of dynamical systems along with the proposed detection algorithm allows for such interactions.

In our second example, we use a 2-dimensional system to better illustrate the reactivity of DS. Figure 7 shows the simulation results. The robot starts in the tracking mode precisely following the DS vector field. In $t \in [3,6]$, human guidance is detected where the simulated human intends to go to $x = [0.5,0.5]^T$. Upon detecting human guidance, the robot becomes compliant and the human can drive the robot with small forces (as shown immediately after the detection $t \in [3.5,6]$). At $t=6$ s, the simulated-human stops exerting forces, which results in dissipating of the energy in the tank and vanishing h. This enables the robot to go back to motion-tracking mode and approaches the equilibrium point following the vector field. This interaction shows the reactivity of the DS where the generated desired trajectories are different before and after human guidance. This can be advantageous over simple methods where the human guidance are simply damped and the robot smoothly goes back to pre-interaction trajectories.

Figure 8 shows the result for case where we apply motion adaptation using our previous method (Khoramshahi and Billard 2018). In this simulated example, two DS are considered: $f_1$ and $f_2$ generating clockwise and anti-clockwise motions respectively. In this scenario, the robot starts performing $f_2$ and a simulated human joins the interaction at $t=0.3$ and intends to perform $f_1$. To do so, the simulated human applies forces as $F_e = - 20 ({\dot{x}}-f_1(x))$. The first row of plots shows the results for our variable admittance control. The first plot shows how the human guidance is detected where h approaches 1 between $t=0.4$ and 0.6. The second plot shows the human effort starting at $t=0.3$ and trying to decelerate the robot. After $t=0.4$ (where the guidance is detected $h\simeq 1$), the human injects energy to demonstrate his/her intention ($f_1$). The last plot shows the tracking behavior which in this simulation assumed to be a perfect tracking case. The second row of plots shows our comparison with a fixed impedance controller. We tested three different conditions.

A low impedance ($D_i=4$) results in switching across task, however, the tracking performance of the robot is unsatisfactory. A High impedance ($D_i=40$) results in satisfactory tracking behavior, however, the switching is not possible anymore due to limits of human forces (2N in this case). This is verified in the third case where increasing this limit (from 2 to 20N with $D_i=40$) leads to a successful switching. It can be seen that in all these three cases, the duration that human tries to decelerate the robot is longer than the variable admittance control. This also results in slower adaptation across tasks. This simulation clearly shows how both compliant and tracking behavior can be achieved through our variable admittance control with human guidance detection.

Fig. 10

Generated desired trajectory using the trained DS systems for different reaching tasks. The square and star marker show the initial and target position respectively (color figure online)

6 Experimental evaluations

For our experiments, we employ a Clearpath ridgeback mobile-robot with Universal UR5 robotic-arm mounted on the top of the base; see Fig. 9. Using the force-torques sensor (Robotiq FT300) mounted on the end-effector, we control the arm in admittance mode. For our motion planning, we trained several DS as illustrated in Fig. 10. The details of the admittance control are provided in “Appendix .A.6”. To train these models, we collected 25 demonstration per task where the human-user moved the end-effector of the robot. We tested our proposed method in the following three different scenarios.

6.1 Null DS

In the first case, we use ${\dot{x}}_{t}=0$ (i.e., ${\dot{x}}_d = {\dot{x}}_a$). In this manner, the robot maintains a fixed position and only reacts to the human guidance. This case is useful when it is required from the robot to maintain the position of an object or a tool in the workspace. The results are shown in Fig. 11. The first plot shows the external forces where in $t \in [5,10]$ and $t \in [25,30]$ robot was perturbed. It can be seen that these disturbances are not detected as human guidance and therefore rejected; i.e., the robot maintains its positions. During $t \in [15,20]$ and $t \in [30,35]$, human interacts with the robot as to move to a desired position. These human interactions are shortly (i.e., after around .5 s) detected and the compliant behavior is provided through admittance as to move in accordance with external forces. Moreover, the comparison between desired and real shows that the robot provides a satisfactory behavior (RMS error of 0.02).

Fig. 11

The result of human–robot interaction in the case of null DS (${\dot{x}}_{t}=0$). A human guidance is presented to the robot and detected during $t\in [15,20]$ and $t\in [30,35]$. The disturbances ($t\in [5,10]$ and $t\in [25,30]$) are successfully rejected and the robot maintain its position (color figure online)

6.2 Nominal DS

In the second case, we use one of the trained DS to perform a reaching task (i.e., Reach right). The results are shown in Fig. 12. The robot starts from an initial condition and follows the DS velocities to reach its target; i.e., $x=0$. After reaching the target, the robot rejects the disturbances around $t=10$ and maintains its position rigidly. Upon human-guidance at $t=15$, the robot becomes compliant so as to follow the human guidance passively. When human retreats from the interaction at $t=32$, the robot smoothly switches to motion-planning mode and follows the DS velocities and consequently reach its target. The velocity profiles (plotted separately for each dimension) show how the desired velocity smoothly transits between admittance-velocities and DS-velocities.

Fig. 12

The result of human–robot interaction in the case of a nominal DS (i.e., reaching a target position). The human-guidance is detected during $t\in [18,35]$ where the human moves the robot compliantly in the workspace regardless of the DS-generated velocities (color figure online)

Fig. 13

The results for adaptive DS for the robotic arm where the proposed algorithm is used to adapt the motion only to the detected human-guidance (color figure online)

6.3 Adaptive DS

Finally, we present an adaptive case where the robot switches between several reaching tasks plotted in Fig. 10. To have the proactive following behavior (i.e., while following, the robot recognize the human intention and starts injecting velocities), we changed our formulation to:

$$\begin{aligned} {\dot{x}}_d = {\dot{x}}_a + {\dot{x}}_{t} \end{aligned}$$

(12)

In this manner regardless of h (which only affects the admittance control), the robot tries to follow the DS-generated velocities. However, in this case, we use our adaptive mechanism previously presented in Khoramshahi and Billard (2018) to generate ${\dot{x}}_{t}$. Given a set of DS for different reaching motion, the adaptive mechanism uses the most similar DS to the human-guidance. The results are illustrated in Fig. 13 The robot starts in the retreat task where it makes the workspace available to the human-user. Upon human-guidance, the robot becomes compliant and follows the human motion. While doing so, the robot adapts to the most similar DS (Reach left in this case). Human observing that his/her intended task is being performed, leaves the interaction while the robot leads and perform the task autonomously. This transition repeated several times where the robot switched to different tasks. In one case (around $t=31$), due to partial human-demonstration, the robot initially switch to a task that it is not intended by the user. Therefore, the human stays in the interaction and provides more demonstrations in order to make sure that the robot recognizes his /her intention. Moreover, the results show that disturbances are rejected successfully and the robot only complies with the human guidance. Furthermore, we can see that the robot adapts its role based on the human-interaction from stiff-leader to compliant-follower, passive-follower and proactive-follower.

7 Discussion

In this section, we discuss our theoretical and experimental results. Furthermore, we provide discussion on practical limitations and possible improvements for our control architecture.

7.1 Detection speed and accuracy

In our detection algorithm for human-guidance, the speed and accuracy are controlled by $E_{m}$, $E_{t}$, and ${\tilde{P}}_{d}$. The theoretical aspect of the detection time is reported in “Appendix A.1”. Lower values (for $E_{m}$, $E_{t}$, and ${\tilde{P}}_{d}$) result in faster but less accurate detections where the built-up energy due to the disturbances passes the trigger level and is detected as human-guidance. Higher values, on the other hand, lead to more accurate but slower detection where the human is required to exert higher force for a longer time to pass the trigger level. This leaves the designer with a trade-off between speed and accuracy. A practical approach is to investigate the expected disturbances in the environment and set these parameters marginally higher as to filter such disturbances. Conversely, one can investigate the expected forces from the human-guidance and set the parameters marginally lower as to detect such guidances. Furthermore, this can be treated as a two-class classification problem which is on our list of future works.

7.2 Low stiffness for fast motions

The stiffness of the robot during the detection delay might appear inconvenient to the human user. While this is tolerable when the robot maintains a fixed position, the stiffness of the robot during a fast motion might undermine the comfort and safety of the user. The tracking performance of fast motion can be sacrificed by lowering the stiffness in order to avoid such issues. To do this, we propose the following formulation for the admittance controller:

$$\begin{aligned} M_a \ddot{x}_a = -D_a {\dot{x}}_a + \tilde{h} F_{e} \end{aligned}$$

(13)

where

$$\begin{aligned} \tilde{h} = max \{ \underline{h}({\dot{x}}) , h \} \end{aligned}$$

(14)

where $\underline{h}$ is a function based on the robot’s velocity providing a minimum required compliance. This function can be of the following piecewise linear form:

$$\begin{aligned} \underline{h}({\dot{x}})={\left\{ \begin{array}{ll} 0 &{}\quad \text {for}\quad {\dot{x}}< \underline{v}\\ ({{\dot{x}} - \underline{v}})/({\bar{v} - \underline{v}}) &{}\quad \text {for}\quad \underline{v}< {\dot{x}}< \bar{v}\\ 1 &{}\quad \text {for} \quad \bar{v} < {\dot{x}} \\ \end{array}\right. } \end{aligned}$$

(15)

where below $\underline{v}$ no additional compliance is required and the robot focuses on tracking performance (unless human guidance is detected which increases h). For velocities higher than $\bar{v}$, the robot tracking performance in sacrificed (only if there are external forces) for safety issues. The linear interpolation part allows for a smooth transition and avoiding the human to experience sudden feeling of blockage or release.

7.3 Damping matrix and variable admittance

As the initial step in this work, we only used diagonal damping matrices of form $D_a=d ~\mathbb {I}_n$ for simplicity. Similar to our previous work (Kronander and Billard 2016), we can provide a different damping behavior in the direction of ${\dot{x}}_t$ vs. other directions. The formulation of this case is presented in “Appendix A.4”. However, to have different damping behavior in a specific direction of the space, we can use the following admittance formulation:

$$\begin{aligned} M_a \ddot{x}_a = -D_a {\dot{x}}_a + h G F_{e} \end{aligned}$$

(16)

where $G \in \mathbb {R}^{n \times n}$ is a diagonal matrix with different diagonal elements. Having these different input gains allows the admittance to exhibit different stiffness in different direction.

Fig. 14

State-dependent compliant through admittance control and state-dependent motion planning through DS. The robot reacts passively to the external force proportionally to h. The external forces are generated using a Gaussian noise. The simulation is repeated five time (color figure online)

Similarly, our DS-based admittance controller is also suitable to deliver task-specific compliant behavior. Consider the following controller:

$$\begin{aligned} M_a \ddot{x}_a = -D_a {\dot{x}}_a + H(x,{\dot{x}}) F_e \end{aligned}$$

(17)

where $H: \mathbb {R}^{n} \mapsto \mathbb {R}^{n}$ modulates the robot’s admittance based on the robot’s state. This formulation allows the robot to vary its compliance in different region of the workspace. A simple example is illustrated in Fig. 14 where the robot provides a compliant behavior only in the designated region and focuses on the tracking of the DS velocities elsewhere. This mapping can be learned from demonstration and be used in this formulation without any loss of stability and tracking performance.

7.4 Guidance detection for an arbitrary link

In this work, we only focused on the external forces exerted on the end-effector where the force-torque sensor is mounted. Therefore, the robot remains stiff toward forces applied to an arbitrary link; due to high-gain position/velocity control or non-back-drivable joints. To overcome this, one can implement the admittance controller at joint level (e.g., as in Kaigom and Roßmann 2013) and filter the external forces (applied to each joint) using our proposed method. The designer would have the choice to treat the joints either in a decoupled (i.e., one h-variable for each joint) or coupled manner (i.e., a global h-variable). In the decoupled form, intentional interaction with an arbitrary link results in compliant behavior only in the same link, whereas in the coupled form, the full-body becomes compliant.

8 Conclusion

In this work, we presented a simple detection algorithm for human-guidance during pHRI. We investigated our algorithm theoretically where we showed how external forces consistency (i.e., autocorrelation) is used for detection. The simulation and experimental results show that this method is effective in distinguishing between disturbances and human-guidance input. For our detection algorithm, no model of the robot and environment is required, and it is easy to implement (i.e., few algebraic equations). The transparency of its parameters (i.e., their physical meaning) allows for simple tuning in order to filter the disturbances and pass the human-guidance. Furthermore, we presented DS-based variable admittance controller as a tool to deliver both tracking and compliant behaviors. We varied the admittance simply through the admittance ratio (i.e., the input gain for the external forces). In this manner, we avoided raising typical instability issues to the time-variability. Even though the variability of the admittance is limited (i.e., a fixed ratio between inertia and damping part), the resulting behavior is effective in rejecting disturbances and complying with human-guidance forces. Finally, we used the output of our human-detection algorithm (h) to vary the admittance controller yielding a robot that adapts its role based on the human-interaction. In the absence of human-guidance, the robot is an autonomous (i.e., a stiff-leader) focusing on the motion tracking and executing the task, while in the presence of human guidance, the robot is a passive follower focusing on tracking human inputs. Moreover, we showed through experimental result that the proactive following behavior can be achieved using adaptive DS. We analyzed our method rigorously and provided sufficient conditions for stability and passivity.

Appendix A Mathematical details

1.1 A.1 Human-guidance detection speed

In order to relate our algorithm to methods used in the lit. of collision detection, we can investigate the time-derivate of h as follows:

$$\begin{aligned} \dot{h} = {\left\{ \begin{array}{ll} 0 &{}\quad E \le E_{t}\\ \dot{E}/(E_{m} - E_{t}) &{}\quad E > E_{t} \end{array}\right. } \end{aligned}$$

(18)

By replacing $\dot{E}$ from Eq. 7 and the approximation that ${\tilde{P}}_{o} = h {\tilde{P}}_{i}$ (since, in the discrete system, ${\tilde{P}}_{o}(k) = h(k-1) {\tilde{P}}_{i}(k-1)$), we have

$$\begin{aligned} \dot{h} = -\gamma (h - 1) \end{aligned}$$

(19)

where $\gamma = ({\tilde{P}}_{i}-{\tilde{P}}_{d})/(E_{m}-E_{t})$. It shows that ${\tilde{P}}_{i} > {\tilde{P}}_{d}$, $h \rightarrow 1$ and otherwise $h \rightarrow 0$. The solution to this equation for an arbitrary initial condition (h(0)) is:

$$\begin{aligned} h(t) = (h(0) - 1) e^{-\gamma t} + 1 \end{aligned}$$

(20)

The rise time (i.e., to reach 0.9 from 0) for a fixed $\gamma$ is $T_r = 2.32 \gamma ^{-1}$. Moreover, the energy first needs to pass $E_{t}$ which requires $T_t = E_{t}/{\tilde{P}}_{i}$. In total the time to reach $h=0.9$ when the tank is empty $E(0)=0$ for constant ${\tilde{P}}_{i} > 0$ is

$$\begin{aligned} T_{u} = 2.32 (E_{m}-E_{t})/({\tilde{P}}_{i}-{\tilde{P}}_{d}) + {E_{t}}/{{\tilde{P}}_{i}} \end{aligned}$$

(21)

Same can be derived for the case where human retreats from the interaction ${\tilde{P}}_{i}=0$. In this case, we reach $h=0$ from $h(0)=0.9$ given the following time constant.

$$\begin{aligned} T_{d} = 2.32 (E_{m}-E_{t})/{\tilde{P}}_{d} \end{aligned}$$

(22)

Note that non-consistent interaction ${\tilde{P}}_{i} < 0$ decrease h faster by reducing the energy in the tank.

Fig. 15

Simulated result for accumulated energy in the storage tank based on the magnitude and duration of external force (color figure online)

Figure 15 shows the accumulated energy based on the magnitude and duration of an external force. By choosing a level set (i.e., $E_{m}$), we can consider the tank as a classifier that passes forces with certain consistency (i,e., magnitude, duration).

1.2 A.2 Autocorrelation of external force

Our human detection algorithm can be investigated from a statistical point of view. First, let us assume diagonal inertia and damping matrices in Eq. 5. Let $m_j$ and $d_j$ be the inertia and damping for the jth dimension ($j\in \{1,...,n\}$). The admittance dynamics in Eq. 5 can be written as a low-pass filter in the following discrete form for each dimension.

$$\begin{aligned} \dot{\tilde{x}}_j(k) = \beta _j \dot{\tilde{x}}_j(k-1) + (1 - \beta _j) d_j^{-1} F_{e,j} \end{aligned}$$

(23)

where $\dot{\tilde{x}}_j(k)$ is the virtual admittance velocity for the time-step k and jth dimension. $F_{e,j}$ is the external force in jth dimension, and $\beta _j = 1 - m_a^{-1} d_j \varDelta t$ where $\varDelta t$ is sampling rate. Therefore, the input power at time-step k can be expanded as:

$$\begin{aligned} \begin{aligned} {\tilde{P}}_{in,j}(k)&= \dot{\tilde{x}}_j(k) F_{e,j}(k)\\&= d_j^{-1} (1-\beta _j) \sum \limits _{l=1}^{\infty } \beta _j^{l-1} F_{e,j}(k-l) F_{e,j}(k) \end{aligned} \end{aligned}$$

(24)

The accumulated energy due to ${\tilde{P}}_{i}$ can be computed as:

$$\begin{aligned} \begin{aligned} E_{j}(n)&= \sum \limits _{k=-\infty }^{n} {\tilde{P}}_{i}(k)\\&= \sum \limits _{k=-\infty }^{n} d_j^{-1} (1-\beta _j) \sum \limits _{l=1}^{\infty } \beta _j^{l-1} F_{e,j}(k-l) F_{e,j}(k)\\&= d_j^{-1} (1-\beta _j) \sum \limits _{l=1}^{\infty } \beta _j^{l-1} \sum \limits _{k=-\infty }^{n} F_{e,j}(k-l) F_{e,j}(k)\\ \end{aligned} \end{aligned}$$

(25)

by defining the autocorrelation function with lag l over the external force at time step n as follows

$$\begin{aligned} \rho _j(l) = \sum \limits _{k=-\infty }^{n} F_{e,j}(k) F_{e,j}(k-l) \end{aligned}$$

(26)

we can rewrite the energy of the tank as:

$$\begin{aligned} \begin{aligned} E_{j}(n)&= d_j^{-1} \frac{ \sum \limits _{l=1}^{\infty } \beta _j^{l-1} \rho _j(l)}{\sum \limits _{l=1}^{\infty } \beta _j^{l-1} } \end{aligned} \end{aligned}$$

(27)

Note that, we used the expansion of $(1-\beta _j)^{-1}$. Therefore, the input energy is the weighted averaged of autocorrelation with different lags.

1.3 A.3 Energy analysis

In this section, we investigate the passivity of our control architecture. First, we assume the following decomposition for the dynamical system.

$$\begin{aligned} f(x) = - \nabla _x V(x) + \tilde{f}(x) \end{aligned}$$

(28)

Where $V(x) \in \mathbb {R}^{+}$ is a potential function and $\tilde{f}: \mathbb {R}^n \mapsto \mathbb {R}^n$ is a residual that accounts for the non-conservative part of the DS. The stability of motion-generation can be investigated with the assumptions of perfect tracking (${\dot{x}} = {\dot{x}}_{t}$) as follows:

$$\begin{aligned} \dot{V}(x) = \nabla _x V(x) {\dot{x}}_{t} = -|| \nabla _x V(x) ||^2 + \nabla _x V(x)^T \tilde{f}(x) \end{aligned}$$

(29)

The Lyapunov stability of the DS can be guaranteed if

$$\begin{aligned} \nabla _x V(x)^T \tilde{f}(x) < || \nabla _x V(x) ||^2 \end{aligned}$$

(30)

which indicates that the conservative part dominates the non-conservative part and vanishes over time.

In the case of perfect tracking (${\dot{x}} = {\dot{x}}_d$), we can write

$$\begin{aligned} {\dot{x}} = \bar{h} {\dot{x}}_{t} + {\dot{x}}_a \end{aligned}$$

(31)

where $\bar{h} = 1-h$. initially, we limit our analysis to $D_a = d_a \mathbb {I}_n$ where $d_a \in {\mathbb {R}}^{+}$. Let’s consider the following storage function:

$$\begin{aligned} W = \frac{1}{2} {\dot{x}}^T M_a {\dot{x}} + d_a V(x) \end{aligned}$$

(32)

Using the admittance dynamics (Eq. 3), the time derivative of this storage function is

$$\begin{aligned} \begin{aligned} \dot{W} =&~{\dot{x}}^T (\bar{h} M_a \ddot{x}_{t} - \dot{h} M_a {\dot{x}}_{t} - d_a {\dot{x}}_a + h F_e)\\&+ d_a \nabla _x V(x) {\dot{x}} \\ \end{aligned} \end{aligned}$$

(33)

$\ddot{x}_{t}$ can be computed based on the Jacobian of f(x) as $\ddot{x}_{t}= f^{\prime }(x) {\dot{x}}$.

$$\begin{aligned} \begin{aligned} \dot{W} =&~ h F_e^T {\dot{x}} - {\dot{x}}^T (d_a \mathbb {I}_n - \bar{h} M_a f^{\prime }(x)) {\dot{x}} \\&+ {\dot{x}}^T (\bar{h} d_a \mathbb {I}_n - \dot{h} M_a ) {\dot{x}}_{t} + d_a \nabla _x V(x)^T {\dot{x}}_r \end{aligned} \end{aligned}$$

(34)

Using Eqs. 2 and 28, and defining the human-induced error as $\dot{e}_h = {\dot{x}}_r - \bar{h} {\dot{x}}_{t}$ we can write

$$\begin{aligned} \begin{aligned} \dot{W} =&h F_e^T {\dot{x}} -{\dot{x}}^T (d_a \mathbb {I}_n - \bar{h} M_a f^{\prime }(x)) {\dot{x}} + \bar{h} h d_a \nabla _x V(x)^T {\dot{x}}_{t} \\&\bar{h} d_a {\dot{x}}^T \tilde{f}(x) + h d_a \nabla _x V(x)^T \dot{e}_h -\dot{h} {\dot{x}}_{t}^T M_a {\dot{x}}\\ \end{aligned} \end{aligned}$$

(35)

Let’s first investigate the two boundary conditions ($h=1$ and $h=0$ with $\dot{h}=0$). For $h=0$ (the absence of human guidance), we have

$$\begin{aligned} \dot{W}|_{h=0} = - {\dot{x}}^T (d_a \mathbb {I}_n - M_a f^{\prime }(x)) {\dot{x}} + d_a {\dot{x}}^T \tilde{f}(x) \end{aligned}$$

(36)

The system is stable if $d_a > \lambda _{max}(M_a f^{\prime }(x))$. This means that forces generated by the damping part of the admittance ($d_a {\dot{x}}$) should dominate the centrifugal forces generated by DS ($M_a f^{\prime }(x) {\dot{x}}$). Moreover, the non-conservative part of DS (${\dot{x}}^T \tilde{f}(x)$) might violate the stability of the system. Nevertheless, having a damped admittance behavior in $h=0$ results in ${\dot{x}}_a \rightarrow 0$, therefore ${\dot{x}}={\dot{x}}_{t}$. Given this, we can rewrite

$$\begin{aligned} {\dot{x}}_{t}^T \tilde{f}(x)= & {} (- \nabla _x V(x) + \tilde{f}(x))^T \tilde{f}(x)\nonumber \\= & {} - \nabla _x V(x)^T \tilde{f}(x) + \tilde{f}(x)^2 \end{aligned}$$

(37)

Therefore, the system is stable if $||\tilde{f}(x)||^2 \le \nabla _x V(x)^T \tilde{f}(x)$ which includes $\tilde{f}(x)=0$. Finally, note that $\dot{W}<0$ only proves the stability of the system. The passivity of the mapping $F_e \mapsto {\dot{x}}$ is ill-defined since the term $F_e^T {\dot{x}}$ does not appear in $\dot{W}$ for $h=0$.

For $h=1$ (the presence of human guidance), we have

$$\begin{aligned} \dot{W}|_{h=1} = F_e^T {\dot{x}} - d_a ||{\dot{x}}||^2 + d_a \nabla _x V(x)^T {\dot{x}} \end{aligned}$$

(38)

The system exchanges energy through the input port $F_e^T {\dot{x}}$. The passivity of the admittance is guaranteed since $d_a > 0$. The last term ($P_{h}$) shows how the human can inject energy into DS potential function by changing the state of the system.

During transitions ($\dot{h}=0$), DS dissipates energy since $\nabla _x V(x)^T {\dot{x}}_{t} <0$ (from Eq. 29) and $\bar{h}h>0$. Since we modulate ${\dot{x}}_{t}$ by $(1-h)$, sudden changes of h result in an acceleration of $-\dot{h} M_a {\dot{x}}_{t}$. This temporary energy generation (which is bounded) can either be neglected or handled by setting a limit on the increase of h based on the state of the system. The other solution is to avoid modulating ${\dot{x}}_{t}$ (as in Eq. 1) and to use the following:

$$\begin{aligned} {\dot{x}}_d = {\dot{x}}_{t} + {\dot{x}}_a \end{aligned}$$

(39)

This leads to a simpler energy analysis as follows:

$$\begin{aligned} \dot{W} = h F_e^T {\dot{x}} - {\dot{x}}^T (d_a \mathbb {I}_n - M_a f^{\prime }(x)) {\dot{x}} + d_a {\dot{x}}^T \tilde{f}(x) \end{aligned}$$

(40)

In this formulation, the desired velocity generated by the DS are always present. This might be a drawback for cases where this velocity perturbs the human during $h=1$ or deteriorate the compliant behavior. However, in cases where human guidance has the purpose of small corrections, the presence of this velocity is beneficial. Moreover, in proactive scenarios, even during $h=1$, it is necessary for the robot to not only rely on ${\dot{x}}_a$ but also generate and follow ${\dot{x}}_{t}$. It is intuitive to see that ${\dot{x}}_a$ accounts for passive-following behavior and ${\dot{x}}_{t}$ can account for pro-active following behavior during $h \ne 0$. For better illustration, the power exchanges for the 1D simulation case are presented in Fig. 16.

Fig. 16

Detection of human guidance for motion adaptation using DS. The graph with no axis is h over time (color figure online)

1.4 A.4 Asymmetric damping matrix

Without any loss of passivity, we can have the following admittance behavior:

$$\begin{aligned} M_a \ddot{x}_a = - d_a^{\parallel } {\dot{x}}_a^{\parallel } - d_a^{\perp } {\dot{x}}_a^{\perp } + h F_e \end{aligned}$$

(41)

where ${\dot{x}}_a$ is decomposed into two parts: ${\dot{x}}_a^{\parallel }$ parallel and ${\dot{x}}_a^{\perp }$ orthogonal to ${\dot{x}}_{t}$ with their respective damping gains ($d_a^{\parallel }$ and $d_a^{\perp }$). The resulting damping matrix is:

$$\begin{aligned} D_a = Q \varLambda Q^T \end{aligned}$$

(42)

where the columns of $Q \in \mathbb {R}^{n \times n}$ are unit vectors that span $R^{n}$ and the first column is parallel to ${\dot{x}}_ds$. $\varLambda$ is diagonal matrix with elements equal to $d_a^{\perp }$ except the first one being $d_a^{\parallel }$. The stability and passivity analysis follows the same procedure only $d_a^{\parallel }$ appears instead of $d_a$ in Eq. 35.

1.5 A.5 The simulation parameters

The parameters used for the 1D simulations are as follows: $M_a=1$, $D_a=10$, $E_{m}=2$, $E_{t}=1$, ${\tilde{P}}_{d}=2$, $h(0)=0$, $E(0)=0$, ${\dot{x}}(0)=0$, $x(0)=1$, ${\dot{x}}_a(0)=0$, $dt=1$ ms. The dynamics system: ${\dot{x}}_{t} = -3x$ but saturated in $[-2,~ 2]$. The external forces:

$$\begin{aligned} F_e = {\left\{ \begin{array}{ll} {\mathcal {N}}(0,36) &{}\quad 0<t<2 \\ -20 (x - 1) - 10 {\dot{x}}_r &{}\quad 3<t<6 \\ 10 &{}\quad 9<t<9.005 \\ 0 &{}\quad \text {elsewhere} \end{array}\right. } \end{aligned}$$

(43)

However, the forces for the simulated human (second row) is saturated between 5 and $-5$, and the pulse (third row) repeats 10 times every 50 ms.

For the 2D simulation example, we use $M_a=\text {diag}\{2,2\}$, $D_a=\text {diag}\{4,4\}$, $E_{m}=2$, $E_{t}=1$, ${\tilde{P}}_{d}=2$, $h(0)=0$, $E(0)=0$, ${\dot{x}}(0)=[0,0]$, $x(0)=[-.9,-.6]$, ${\dot{x}}_a(0)=[0,0]$, $dt=1$ ms. The dynamical system is:

$$\begin{aligned} f(x) = \begin{bmatrix} -1.5 &{}\quad 1.5 \\ -2.4 &{}\quad -6 \end{bmatrix} x \end{aligned}$$

(44)

saturated at 2m/s.

For the adaptive case (Fig. 8), we use $M=\text {diag}\{1,1\}$, $C=\text {diag}\{0,0\}$, $\ddot{x}(0)=[0,0]$, ${\dot{x}}(0)=[0,0]$, $x(0)=[.022,0]$, $D_a=\text {diag}\{2,2\}$, $M_a=\text {diag}\{0.05,0.05\}$, ${\dot{x}}_a(0)=[0,0]$, $h(0)=0$,${\tilde{P}}_{d}=.2$, $E(0)=0$, $E_{t}=.1$, $E_{m}=.2$, $dt=1$ ms. The dynamical system specified in the polar coordinate is:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{\theta } = \pm 10 \\ \dot{r} = -15 (r - 0.022) \end{array}\right. } \end{aligned}$$

(45)

where $x_1 = r \cos (\theta )$ and $x_2= r \sin (\theta )$. $f_1$ represent the counterclockwise and $f_2$ the clockwise rotation. The external forces are simulate as

$$\begin{aligned} F_e = -20 ({\dot{x}}- f_1(x)) \end{aligned}$$

(46)

where the norm of the output is limited to 2N. In one of the comparisons with impedance control (i.e., higher human effort), we increase this limit to 20N.

1.6 A.6 The robot parameters

For the arm admittance, we use the following parameters.

$$\begin{aligned} \begin{aligned} M_a&= \text {diag}\{6,6,6,1,1,.5\}\\ D_a&= \text {diag}\{60,60,60,15,15,15\}\\ dt~&= 8\,\text {ms} \end{aligned} \end{aligned}$$

(47)

However, for the virtual admittance use the following values.

$$\begin{aligned} \begin{aligned} M_a&= \text {diag}\{2,2,2,1,1,1\}\\ D_a&= \text {diag}\{2,2,2,2,2,2\}\\ \end{aligned} \end{aligned}$$

(48)

For the energy tank, we use $E_m= 4$, $E_t=2$ , ${\tilde{P}}_d = 2.5$.

1.7 A.7 Media

A demonstration of our method can be viewed at https://youtu.be/HrR85-IP-Qo.

1.8 A.8 Source codes

A C++ implementation of our method can be found at https://github.com/epfl-lasa/ds_admittance_control/tree/ridgeback.