Abstract
Disturbance observer (DOB) based controller performs well in estimating and compensating for perturbation when the external or internal unknown disturbance is slowly time varying. However, to some extent, robot manipulators usually work in complex environment with high-frequency disturbance. Thereby, to enhance tracking performance in a teleoperation system, only traditional DOB technique is insufficient. In this paper, for the purpose of constructing a feasible teleoperation scheme, we develop a novel controller that contains a variable gain scheme to deal with fast-time varying perturbation, whose gain is adjusted linearly according to human surface electromyographic signals collected from Myo wearable armband. In addition, for tracking the motion of operator’s arm, we derive five-joint-angle data of a moving human arm through two groups of quaternions generated from the armbands. Besides, the radial basis function neural networks and the disturbance observer-based control (DOBC) approaches are fused together into the proposed controller to compensate the unknown dynamics uncertainties of the slave robot as well as environmental perturbation. Experiments and simulations are conducted to demonstrated the effectiveness of the proposed strategy.
Similar content being viewed by others
1 Introduction
Robot teleoperation is a kind of advanced technology in which human operator/operators remotely control the far-end robot manipulator through computer intermediary (Sheridan 1995), and it plays an important role in healthcare, industrial production, rescue and aerospace. One of the most popular teleoperation methods is the master-salve scheme where the operator controls the master device directly to command the slave mobile robots and robotic manipulators (Luo et al. 2019; Yang et al. 2016; Veras et al. 2012).
The technology of robot control has developed rapidly in the past decades (Liu et al. 2008; Yuan and Chen 2013), and plenty of sensors are employed in teleoperation system for capturing human motions, such as inertial measurement units (IMUs), vision sensors (e.g. Kinect) (Schwarz et al. 2012; Xu et al. 2018), haptic devices (Phantom Omni). In Yuan and Chen (2013), multiple wearable IMU sensors were used to determine the limb joint motions and spatial location of the human operator without external additional devices to define the global frame. In Veras et al. (2012), to help the people with disability to perform daily tasks, a control system was proposed to teleoperate a robot manipulator in real-time by Phantom Omni. However, since the device is cumbersome and cannot be carried along by the operator, it is applicable to few teleoperation scenarios. In Schwarz et al. (2012), with the depth data collected by a Kinect sensor, a method of tracking human operator’s full-body pose was developed. However, we cannot track the movements of the human operator when the operator is out of the sight of the Kinect sensor or when there is an obstacle between the operator and the Kinect sensor. In Xu et al. (2016), a robot manipulator was able to track the operator’s arm motion validly and effectively by position control when there is no external force applied on the robot. However, in practical applications, the robotic manipulator is often subjected to uncertain external disturbance. When perturbation is applied on the robot, large errors will appear in the tracking task.
To deduce the effect of disturbance, researchers put forward many methods for different kinds of disturbance in various systems, e.g. a hybrid scheme consisting of an iterative learning composite anti-disturbance structure to handle model uncertainties and link vibration of manipulators in Qiao et al. (2019), a distributed adaptive fuzzy algorithm to cope with system nonlinear uncertainties in Sun et al. (2019), a cerebellar model articulation controller to tackle the effect from parameter uncertainties and external disturbance in free-floating space manipulators (FFSMs) (Li et al. 2019), considering time delay or its effect as system uncertainties or disturbance to be addressed in Wang et al. (2002), designing linear filter to settle the admissible parameter uncertainties in Wang and Qiao (2002). Among these techniques in the scholar society, disturbance observer (DOB) is an efficient and widely-used technology in improving the tracking performance. The DOB technology is proposed by Ohnishi et al. (1996), and, due to the robustness, it is able to be intuitively adjusted in a desired bandwidth, which plays an important role in robust control (Sariyildiz and Ohnishi 2015). What is more, since its efficiency in compensating the influence of disturbance and model uncertainties, it has been widely used in robotics, industrial automation and automotive (Yang et al. 2012; Chow and Cheung 2013). In Iida and Ohnishi (2004), DOB was first applied in teleoperation system by attenuating the influence of disturbance. Disturbance observer is able to compensate for the model uncertainties by estimating external disturbance (Eom et al. 2001; Chen and Chen 2010). A novel nonlinear disturbance observer (NDOB) for robotic manipulator was proposed in Chen et al. (2000), and the effectiveness of the NDOB was demonstrated by controlling a two link robotic arm. A three-link robotic manipulator was controlled by NDOB in Nikoobin and Haghighi (2009), which was the extension of Chen et al. (2000), and the stability of the NDOB was verified by Lyapunov’s direct method. In Chen et al. (2014), a scheme with adaptive fuzzy tracking ability was designed to multi-input and multi-output (MIMO) non-linear systems under the circumstances with unknown non-symmetric input saturation, system uncertainties and external disturbance. DOBC owns the advantage of simplicity and the ability of compensation for model uncertainties. However, when the dynamic model is coupled with fast-time-varying perturbation, it is not adequate to make up for all uncertainties or disturbance.
To tackle the problems concerning robot dynamics uncertainties, the human limb’s stiffness transfer schemes and adaptive control techniques have been utilized in Yang et al. (2006), Ajoudani et al. (2012), whereas human limb’s stiffness transfer and adaptive control might not do well in transient performance or cannot address the influence resulting from unparameterizable external disturbances through parameter adaptation algorithm. To overcome the high-frequency perturbation, in Li et al. (2016b), the authors proposed the control strategy that integrated robot automatic control and human operated impedance control using stiffness by DOB based adaptive control technique. However, this method does not take advantage of the motion skills of the human, and the movement of telerobot is not able to be controlled. In Zhang et al. (2016), to control the variable stiffness joints robot, the DOB based adaptive neural network control is proposed.
In this paper, the main contributions lie in:
-
(i)
A novel variable gain control scheme in teleoperation is proposed, in which the Myo wearable armband is employed to collect human arm’s surface electromyographic (sEMG) signals to generate suitable control gain as well as to collect human arm’s motion to produce the desired trajectory for tele-robot to follow (Xu et al. 2016). In this way, the stiffness and the dexterity of human arm can be transferred to the tele-robot. Through this approach, human operator can easily tune the control gain by adjusting his forearm muscle strength, according to his judgment on whether a high or low gain is needed under current teleoperation task.
-
(ii)
An integration of radial basis function neural networks (RBFNN) algorithm and DOB theory is formulated, by which the one of the main part of the controller is constructed, whose function is to minimize the influence of the potential adverse effect brought by the system dynamics uncertainties or the perturbation from external environment or internal friction, sensor measurement noise, etc.. Through the introduction of integral Lyapunov–Krasovskii function, the system stability is guaranteed.
In the following sections, we show the proposed teleoperation system configuration in Sect. 2, in which the usage of Myo armbands and the mapping from operator’s arm motion to the slave robot’s 5 joint angles are illustrated. We then introduce the proposed controller in Sect. 3, where we develop the variable gain control scheme according to human arm sEMG signals and derive a novel combination of the RBFNN algorithm and the DOB theory. We show the experiments, simulations and the corresponding results in Sect. 4. Finally, we summarize our contributions and outline the future work in Sect. 5.
2 Teleoperation system configuration
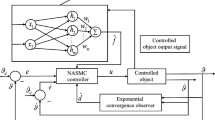
A brief structure of the proposed control system is shown in Fig. 1. The two Myo armbands worn on operator’s arm (one on upper arm and the other on forearm as shown in Fig. 5) work independently and generate their own rotating data (a group of quaternions) as operator moves his arm, which can be then transferred to master computer via bluetooth communication technique. By combining two groups of quaternions collected from the built-in IMU of Myo armbands, we derive 5 joint angles data in real time, which is considered to be the raw reference trajectory for a tele-robot (namely the slave robot) to follow. At the meanwhile, the sEMG signals are collected from 8 sensors of every armband to adjust the control gain according to certain rule (discussed in the Sect. 3).
2.1 Introduction of the structure of a human upper limb
There are seven degrees of freedoms (DOFs) in a human upper limb, containing three DOFs in the shoulder joint, two in the elbow joint and two in the wrist joint. The kinematic model of an upper limb can be depicted in Fig. 2 in accordance with the standard Denavit-Hartenberg (DH) model (Craig 2009). Though it is said to be able to capture 7 joint angles via two Myo armbands (Xu et al. 2016), in this paper, we only employ 5 joints (3 in shoulder and 2 in elbow) to demonstrate the proposed scheme, and the 5 joints DH parameters are shown in Table 1 (Ding and Fang 2013), where \(L_1\) and \(L_2\) represent the lengths of the operator’s upper arm and forearm, respectively.
2.2 Motion capture
First of all, to capture motion of human arm for teleoperation, we need a rotation matrix derived from a unit quaternion (Hamilton 1848) produced by each armband in every sampling time, presenting in the form of (1), then, combine two armbands data together to compute the joint angles for robot manipulator.
According to Rodrigues’ rotation formula, we derive a rotation matrix relevant to every quaternion.
Secondary, since armbands work independently to each other, after they randomly starting up at a random place, one armband does not know the pose of the other armband. Therefore, the primary task, is to establish the relation between two armbands. Seen from Fig. 3a, we can formulate (3), unifying a whole coordinate system for the two rotation matrix indicating two armband poses.
(a) Knowing their randomly start-up coordinate \({\mathrm{O}}_{\mathrm{U0}}\) and \({\mathrm{O}}_{\mathrm{F0}}\), representing the initial coordinate of the armband worn on upper arm and forearm, respectively; (b) Recording one of their real-time poses \(R_{\mathrm{U0}}\) and \(R_{\mathrm{F0}}\) with a certain arm motion at a certain sampling time; (c) Knowing their poses \(R_{\mathrm{U1}}\) and \(R_{\mathrm{F1}}\) regarding to their start-up coordinates; (d) Then, we obtain the two important rotation matrices \(R_{\mathrm{U2}}\) and \(R_{\mathrm{F2}}\), which take certain poses \(R_{\mathrm{U0}}\) and \(R_{\mathrm{F0}}\) as their initial coordinate frames
By now, the two rotation matrices are still disconnected but can be unified to one coordinate frame basing on (4). Then, the armband poses on forearm (\(R_{\mathrm{F2}}^{*}\)) takes \(O_{\mathrm{U2}}\) as the reference coordinate frame.
Then, according to Craig (2009), the Euler angles are derived as
where r represents an element of a rotation matrix, its subscript “U” and “F” denoting \(R_{\mathrm{U2}}\) and \(R_{\mathrm{F2}}^{*}\) respectively and subscript numbers “\(\mathrm{ij}\)” (i, j = 1, 2, 3) means the element position in the matrix; besides, meanings of those Greek alphabets are shown in Fig. 3b. By exploiting differential theory, the corresponding velocities and accelerations of the 5 joints are derived.
2.3 sEMG signals and control gains
There are eight built-in electrodes in every Myo armband and every channel of the eight produces a sEMG signal value in every sampling time. We integrate the N channels values into one by summing them up, and adopt their average, as (10) describes.
where \(N\le 8\), k represents sampling time and \(u_i\) is the real-time sEMG value. Due to measurement noise, we employ a sliding window filter, as described in (11), to gain a smoother curve.
where \(u_f\mathrm{{(}}k\mathrm{{)}}\) is the filtered sEMG value, w is the width of the sliding window filter.
According to Potvin et al. (1996) and Han et al. (2015), supposing that sEMG equals to electromyographic (EMG), we obtain the muscle activity a(k)
where A is a coefficient chosen from interval (-3, 0). To Ensure the stability of the system, the range of the control gain can be constrained to be (\(G_{min}\), \(G_{max}\)). Then, the linear relation between sEMG signals and the control gain can be established as (13) shown.
3 Variable gain control scheme based on DOB and RBFNN
As it is known, to obtain a precise non-linear dynamics model of a robot manipulator is nearly impossible. Even if an accurate model is obtained at the first time, daily usage of the robot will damage its accuracy due to abrasion in joints, ageing of parts, etc., which are hardly measurable. In addition, when robot manipulator carries out tasks, for instance, loading heavy objects, grabbing an alive animal with dynamic movement, or working in a temperature-fluctuating environment, etc., the trajectory tracking performance of the manipulator can be affected. Therefore, we proposed an effective scheme to resist and compensate for these uncertainties and disturbances.
Generally, the dynamics model of a series robot manipulator can be expressed in Lagrange Dynamics Equation (14),
where \(\theta \), \(\dot{\theta }\) and \(\ddot{\theta } \in R^{n\times 1}\) represents joint angles, velocities and accelerations of a series robot manipulator, \(M \in R^{n \times n}\) is the inertia matrix, \(C(\theta ,\dot{\theta }) \dot{\theta } \in R^{n \times 1}\) is Coriolis and centrifugal torque, \(G(\theta ) \in R^{n \times 1}\) denotes gravitational force, \(f_{int}\) and \(f_{ext}\) are internal and external disturbance respectively and \(\tau \in R^{n \times 1}\) is the motor torque vector.
Then it can be transformed into a state-space equation
where \(x_1 = [\theta _1, \theta _2,\ldots , \theta _n]^T\), \(x_2 = [\dot{\theta _1}, \dot{\theta _2}, \ldots , \dot{\theta _n}]^T\),\(F(x)= - C(\theta ,\dot{\theta }) \dot{\theta } -G(\theta )\), \(d(t)=-f_{int}-f_{ext}\).
From the above equations, we can conclude that to execute a mission with high quality, obtaining an accurate dynamics model, precisely measuring the disturbance are inevitable. However, due to difficulties mentioned before, to be feasibly, we need to try another way. That is the purpose of the paper: designing a controller combining the adaptive neural network scheme and the DOB technology to approximate the influence caused by dynamics uncertainties and disturbance, which is discussed in the following subsections.
Before that, we do some preliminary formulation.
We define \(M_d\in R^{n\times n}\) as a diagonal matrix with diagonal elements \(m_{dii}(x)>0\), which represents parts of the dynamics-model and can be easily obtained but has no need for high precision. Then, there must exits an unknown matrix \(\varDelta _M\) making equation \(M_d+\varDelta _M=M\). Considering (15), we have
where \(g(\tau )=-\varDelta _M M^{-1}\tau \), \(r(d)=(I-\varDelta _M M^{-1})d(t)\) and \(\mathbb {F}(x)=(I-\varDelta _M M^{-1})F(x)\).
Remark 1
Generally, according to the saturation of system input, the motor torque of a normal robotic or mechanical system are assumed to be bounded, therefore, \(g(\tau )=-\varDelta _M M^{-1}\tau \) is considered bounded.
Assumption 1
The unknown internal and external disturbance d(t) is assumed to be bounded, namely there exists an unknown positive constant \( d_\mathrm{{m}} \) making \( d(t) \le d_\mathrm{{m}} \).
Then, we define another item, filtered tracking error \(s_i\) Slotine et al. (1991):
In (17), \(\text {C}_a^b\) denotes mathematical combination, lambda = \(\mathrm{diag}[\lambda _1, \lambda _2,\ldots , \lambda _n]\) with \(\lambda _i\) (\(i=1,2,\ldots ,n\)) being positive constant to be designed, and \(e=[e_1, e_2, \ldots , e_n]\) with \(e_i= x_i-x_{di}\). It is easy to confirm \(e_i\) converges to 0 with \(s_i\) converging to 0. Moreover, the “n” represents the state-space dimension, and to be specifically, \(n=2\) in this paper as we have only two state \(x_1\) and \(x_2\). Therefore, we have
and
with \({\nu }=-{\ddot{y}_{di}}+{\lambda }{\dot{e}}\).
3.1 Introduction of integral Lyapunov–Krasovskii function
Before introducing the designed controller, referring to Li et al. (2016a), we firstly present an integral Lyapunov–Krasovskii (20), to facilitate the design of the controller later, which is capable in avoiding singularity problem of a controller.
where \(M_\vartheta =\int _{0}^{1} \vartheta M_\alpha \, d\vartheta =\mathrm{diag} \left[ \int _{0}^{1} \vartheta M_{\alpha ii}(\varvec{\overline{x}_i})\, d\vartheta \right] \), with \(M_\alpha =M_d\alpha =\mathrm{diag}[M_{dii}\alpha _{ii}]_{n\times n}\). And the matrix \(\alpha =\mathrm{diag}[\alpha _{11},\alpha _{22},\ldots ,\alpha _{nn}]\). To be simple for analyzing, we define \(\alpha _{11}=\alpha _{22}=\cdots =\alpha _{nn}\). And the \(\varvec{\overline{x}_i}\) is defined as \(\varvec{ \overline{x}_i}=[x_1^T,x_2^T,\ldots ,x_{n-1}^T,x_{n1},x_{n2},\ldots ,\vartheta s_i+\zeta _i,\ldots ,x_{nm}]^T \in R^{nm}\), with \(\zeta =y_{di}^{(n-1)}-\xi _i\) and \(\xi _i = \lambda _{i1}e_i^{n-2}+\cdots +\lambda _{i,n-1}e_i\). \(\vartheta \) is an independent scalar to \(\varvec{\overline{x}_i}\), including \(\textit{\textbf{s}}\) and \(\varvec{\zeta }\). It is important to choose suitable \(M_d\) and \(\alpha \) such that \(M_{dii}\alpha _{ii}>0\). Then we can write
Applying the symmetric nature of \(M_\alpha \) and \(M_\vartheta \), the partial derivation of (20) with respect to time can be derived
with
For
we derive
For
and \(\dot{\zeta _i}=-\nu _i\), we have
Then,
Substituting \(\varvec{\dot{s}}\) with (19), we obtain
Utilizing the symmetric property of \(\alpha \), \(M_d\) and \(M_d\alpha \), the following equation makes sense.
Applying (30), we have
where
with
3.2 Controller design
The controller design can be divided into two parts. Referring to Zhang et al. (2016), for one, the DOB technology is employed to estimate the internal or external unmeasurable uncertainties and disturbance; for the other, the RBFNN is applied to approximate the residual uncertainties of the robot manipulator. Firstly, we define \(\hat{D}\) as the estimation of unknown disturbance D, with
where \(\tilde{D}\) is the estimation error.
Secondly, Applying RBFNN to approximate the rest unknown dynamics uncertainties, we define
where W is the NN weight and S(X) is the radial basis function output, which is supposed to be bounded \(||S(X)||\le S_{\mathrm{max}}\) with input \(X=[x_1^T, x_2^T]^T\). For the radial basis function, we choose Gaussian function
with \(c_i = [c_{i1},c_{i2},\ldots ,c_{i,m}]\) is the center and \(b_i\) is the width of the Gaussian function. In general, theoretically, RBFNN has the ability to smoothly approximate all continuous function. However, here in practice, errors always occur during updating weight and we define it to be
with \(\hat{W}\) is the updating weight in real time.
Then, we can write
To complete the formulation of DOB, an auxiliary equation is designed as
with \(K=K^T>0\) is diagonal matrix and all its elements are positive constants.
Considering (38), we calculate the derivative of z regarding to time
Combining Remark 1 and Assumption 1, we assume that the system disturbance is slowly time varying. Thus, there must exists an constant \(d_m\) so as to
Therefore, (40) can be updated to be
Consequently, the \(\hat{z}\) can be updated as in every sampling time, and the estimation value of D can be obtained as well
Finally, let us design the DOB and RBFNN based control law:
where \(\mathbb {G}\) is the variable control gain partially computed from (13).
The RBFNN weight updating law is
where \(\varGamma _i\in R^n\) is one of a series of symmetric positive definite constant matrices and \(\delta _i\) is one of a series positive constants.
Employing the above-mentioned Integral Lyapunov–Krasovskii Function, we take the following Lyapunov function as candidate:
With the help of (31), (35) and (46), substituting D, \(W^TS\) and \(\tau \), the derivative of \(V_2\) can be written as
Thanks to the following facts
we derive
For further proving, we need to choose positive definite variable gain matrix \(\mathbb {G}\), K and \(\delta \) in order to make the following inequalities.
Then, by enlarging the right side of inequality (57), to be exactly, the first three terms, we can establish
with
By a similar way to solve a differential equation, inequality (61) can be mathematically “solved” to be
where t denotes time. It is apparent that the right side of inequality (64) exponentially converge to \(\dfrac{C}{k}\), proving \(V_2\) to be bounded, therefore, \(\textit{\textbf{s}}\), \(\tilde{D}\) and \(\hat{W}\) are bounded.
4 Experimental study
The flow chart of the whole experimental setup is shown in Fig. 4. In such framework, we design the following experiments and simulations to verified the performance of the proposed teleoperation scheme and the proposed controller. Section 4.1 shows the strategy that human operator wear two Myo armbands, using them to generate trajectories and sEMG for the controller to control a tele-robot. Section 4.2 demonstrates the feasibility of the proposed controller, including the tacking performance of the proposed controller as well as the functionality of RBFNN in Sect. 4.2.1 and the effectiveness of the variable gain approach in Sect. 4.2.2.
4.1 Human motion capturing and sEMG signals collecting
In this section, we demonstrate the feasibility of human motion capturing and human sEMG collecting.
Above all, the wireless hardware, two Myo armbands, are worn on human operator’s arm (refer to Figs. 3b, 5) to collect movements (quaternion) and sEMG signal (eight channels) data of operator, which are then transferred to the master computer via Bluetooth technique. These data is processed in real-time and transformed into the joint position for the tele-robot manipulator (Baxter) and the gain increment for the proposed controller.
Firstly, with operator wearing two armbands on upper limb [one on upper arm and the other on forearm (Fig. 5)], employing the theory developed in Sect. 2.2, the joint angles are obtained at the meanwhile when the operator moves his arm. They are converted to slave computer connecting to Baxter robot. By employing the left arm of Baxter and commanding it to move its first five joints (from shoulder to elbow) to match the received angles data by executing joint position control mode, we can intuitively see that the left arm of Baxter follows the human well, referring to Fig. 5, which depicts that Baxter’s left arm copies motions of operator’s left arm.
Secondly, the sEMG signals can be extracted from both Myos in any channel of the 16. In this experimental study, for the purpose of simplicity, we recorded sEMG data in one channel on the Myo on the forearm (the MYO 2 in Fig. 6a), and the raw and the filtered time-series of sEMG amplitude are shown in Fig. 6a. This data is then used to estimate human arm’s muscle activity and transformed into the increment for the control gain. In Fig. 6a, the human operator tensed (a little) his arm muscle at around 33 s and tensed (tightly) and persist for a while from 43 to 48 s, while in the other time, he remain his arm relax. Apparently, the sEMG signal are available and controllable: its amplitude climbs up as the operator tense his muscle and stay to a minor value as the operator relax his arm. Then, through the formulation in Sect. 2.3, we obtain the filtered sEMG signal, and then the variable control gain.
From the above figures and explanation, we see the feasibility for the proposed teleoperation scheme, including a wireless way for human motion capturing and muscle activity estimating.
4.2 Tracking performance verification
The tracking performance is verified through the following experiments and simulations.
In this verification, without loss of generality, we utilized the first two joints of the Baxter robot (“left_s0” and “left_s1”), while other joints are not considered a part of the control object but viewed as a payload attached to the joint “left_s1” as well as disturbance, illustrated in Fig. 7.
4.2.1 Performance of different controllers
In this part, we collected trajectories using the proposed scheme developed in Sect. 2.2. These trajectories were collected when human operator stretched out his arm and drew non-regular circles with his hand, depicted in Fig. 6b. The generated trajectories are shown in Fig. 8a with note “\(\theta _{1d}\)” and “\(\theta _{2d}\)”. Then, we utilized them for the two above-mentioned joints of the Baxter to track, while other five joints were forced to keep to 0 position with a widely-used Proportional Derivative (PD) controller. Here, it is important to point out that the coupling dynamics of the last five links can be viewed as time varying stochastic disturbance, affecting the tracking performance of the first two joints. It can be explained by figures from Fig. 8e–i that the last five joints and links moved and collided sometimes as the first two links drawing circles, which certainly contributed to couple dynamical influence “attached” to the first two links. Trajectories were obtained offline and the tracking test were conducted via the Baxter in the Robot Operating System (ROS) Gazebo platform.
For the purpose of a proper comparison between our proposed controller and the others, we referred to a traditional PD controller, which is popularly employed in robot control, and a PD controller integrated with a NDOB proposed by Chen et al. (2000).
The selected PD controller is: \(\tau =-K_{1d} \dot{e} - K_{1p} e\), with \(K_{1d}=\text {diag}[30, 29]\) and \(K_{1p}=\text {diag}[225,220]\).
The chosen PD controller with NDOB is:
where \(c=0.01\), \(K_{2d}=\text {diag}[22, 20]\), \(K_{2p}=\text {diag}[215,215]\) and \(M_{\text {NDOB}}\), \(C_{\text {NDOB}}\) and \(G_{\text {NDOB}}\) are the first two links dynamics model of Baxter robot, which can be nominally obtained through Smith et al. (2016).
As far as to the proposed controller, \(M_d\) was chosen as \(\mathrm{diag}[0.05, 0.05]\), denoting that we did not know much information about the controlled object model. And other variables are listed in Table 2. In this part, the sEMG signal was not yet involved and the control gain stayed constant.
Besides the three controllers mentioned above, to demonstrate the functionality of the RBFNN in the proposed controller, we simply remove the RBF item in the proposed controller (the third item in Eq. (45)) and form another controller to be compared. Hence, four controllers were involved in this comparison.
The experimental results are shown in Fig. 8. Figure 8a, b show the desired and the real-time recorded trajectories and the tracking errors of the four controllers. Figure 8c, d depict the control outputs and the norm of RBFNN weights. Figure 8e–i are the positions and torques in joint 3–joint 7, which certainly raise constant (the weight of the five links and joints), time-varying and stochastic (coupling dynamics, even some collision in joint 4, see Fig. 8f) disturbance to the controlled object, the first two joints.
Based on these results, especially on Fig. 8a, b, we see two facts: (i) comparing to the proposed controller, the tracking trajectory and errors fluctuate more sever when the RBFNN item is cut off, and (ii) tracking errors keep to minimum in most time when the proposed controller was employed. Therefore, we can conclude that: (i) without RBFNN, the system become less stable, and in another words, the RBFNN integrated to the proposed controller has the ability to attenuate the affect caused by model uncertainties, and (ii) the proposed controller can perform well even under such a sever circumstance with hardly measurable disturbance, surpassing the PD controller and the PD controller with a NDOB. This simulation confirms the feasibility of the propose scheme of integrating the RBFNN algorithm and DOB technology in the controller to attenuate the adverse influence caused by model uncertainties and disturbance.
4.2.2 Effectiveness of variable gain control
Let us imagine a scenario where we need to teleoperate a robot to rescue a pet and the tele-robot needs to hold it and put it into a safe box, but the animal is scared and struggling to escape from the robot end effector. In such cases, we need a strategy to keep the end effector closed to the desired position under such condition with unknown and fast time-varying disturbance. Hence, we proposed this variable gain control scheme. Through this method, we can do it easily: the control gain can be conveniently modified by the operator through tensing or relaxing his arm muscles, which is practical in robot teleoperation. The following study demonstrates its effectiveness.
To verify the anti-disturbance performance of the proposed variable control gain scheme, firstly, we collected sEMG time series. The collected sEMG was employed offline, simply supposing that the operator began to tense or relax his arm muscles when he realized the teleoperation situation required him to modify the control gain. Secondly, we created different disturbances with different frequencies and amplitudes through the method depicted in Fig. 9 where the sixth joint of Baxter is driven to follow a sine wave: \(\theta _{6d}=nsin(2m\pi t)\); Thirdly, we employed the developed variable gain method to try to keep the first two joint of Baxter (in Gazebo) to 0 position under circumstances with different disturbances.
In this part, the parameters we utilized are the same as those listed in Table 2 except for those in Table 3
For the part of creating disturbance, we forced the sixth joint to track a sine wave with different frequencies in a fixed direction, the 45\(^\circ \) in Fig. 9. Such direction ensures that this kind of dynamical disturbance generated by the sixth joint influences the first two joints.
Then we conducted the simulations under different kinds of circumstances. One result of them is shown in Fig. 10, while the others are in Table 4.
In every minipage of Fig. 10, we divide the results into 5 stages, which are marked out alternately by two kinds of gray background colour.
Stage 1 is from 0s to 5s and the first two joints are free from fast-time-varying disturbance. They normally stay to the 0 position, see Fig. 10a. We can see the controller functions well in such peaceful environment, though the “attached” static disturbance (payload of the last five joints) never disappears.
Stage 2 is from 5 to 15 s and the fast-time-varying disturbance starts, see Fig. 10h, but the sEMG is not yet employed. We can see the influence of the movement of joint 6 on joint 1 and joint 2: the tracking errors of joint 1 and joint 2 increase up to around \(\pm \,0.6\) rad and \(\pm \,0.5\) rad respectively, see Fig. 10a, b. Though the RBFNN starts working, see Fig. 10f, the DOB is of no use to this kind of fast-time-varying and asymmetrical disturbance. The asymmetry property of disturbance can be reflected by the unsymmetrical errors, which mainly results from the particular movement limit of joint 4.
Stage 3 is from 15 to 30 s, where the sEMG begins to work and the control gain \(\mathbb {G}_{11}\) and \(\mathbb {G}_{22}\) are lightly modified because (suppose) the operator still does not notice the disturbance, see Fig. 10e, and no changing of the tracking errors of joint 1 and joint 2 can be noticed.
Stage 4 is from 30 to 45 s, and (suppose) the operator realizes the disturbance and keeps his muscle tensed at the first time. In this stage, the tracking errors of joint 1 and joint 2 apparently decrease (Fig. 10b) as control gain increases (Fig. 10e).
Stage 5 is from 45 to 60 s, where the movement of joint 6 keeps going but the control gain moves to another higher state, which results in the minimum errors in joint 1 and joint 2 among all stages, see Fig. 10a, b.
The other minipages in Fig. 10 without being mentioned above also describe some information of the procedure, especially in Fig. 10c, we can see the increase of the controller outputs (control torques) as sEMG climbs up.
The root mean square errors (RMSE) are also computed: \(RMSE_{1,1}\) (joint 1, 17.5–27.5 s) = 0.00127, \(RMSE_{1,2}\) (joint 1, 32.5–42.5 s) = 0.00104, \(RMSE_{1,3}\) (joint 1, 47.5–57.5 s) = 0.00079, and likewise, \(RMSE_{2,1}\) = 0.00120, \(RMSE_{2,2}\) = 0.00103, \(RMSE_{2,3}\) = 0.00080. They, in another aspect, contribute to the verification of the effectiveness of the variable gain control scheme.
In Table 4, another 12 simulation results are given, in which all conditions in every single No. are the same to the aforementioned simulation except for those marked out in the second column. Similarly, all RMSE results reveal the fact that as the operator tenses his forearm muscles, the tracking errors of joint 1 and joint 2 tend to decrease, no matter changing the disturbances, modifying the control gain intervals or adjusting different amplitudes of the operator’s arm muscle sEMG (note: these sEMG series were obtained when operator regularly relax-tense his arm muscles alike Fig. 10e).
Therefore, we yield a brief summary that the proposed variable gain control scheme is practical and able to resist such fast-time-varying disturbance.
5 Conclusion
This paper mainly introduces a novel, simple and possible scheme for robot teleoperation. By utilizing Myo armbands in capturing human motion and collecting arm sEMG signals, human motion can be transferred to a tele-robot manipulator, making it work more flexibly as a human being. This wireless way has advantages such as being available to captured human motion anywhere (comparing to those machine-vision methods that might be blocked by obstacles) and being simpler and more comfortable for operators (comparing to those EMG-extracted technique that requires operator to wear complex sensors). In addition, by utilizing the proposed controller, integrating the DOB technology, the RBFNN algorithm and the variable gain strategy, the trajectory tracking performance of robot manipulator is fine, compared to those mentioned controllers. Model dynamics uncertainty problems are out of account, since the proposed combination of DOB and RBFNN reduces the reliability of constructing a precise dynamics non-linear model. And the variable gain control scheme is practical and verified to be effective in resisting the fast-time-varying disturbances to some extent. Experimental and simulation results demonstrate the merits of the proposed approach which enables the tele-robot manipulator to copy human arm motions, and to resist low and high-frequency disturbances.
Though good results in the paper demonstrate the feasibility of the proposed method, we still have a long way to go to improve the system in the future. For instance, we are going to find out more suitable ways to generate position, velocity and acceleration trajectories without using sliding window filter, for which actually brought about many side effects, such as lagging of the trajectories, and causing the missing of actual peak values, etc..
References
Ajoudani, A., Gabiccini, M., Tsagarakis, N., Albu-Schäffer, A., & Bicchi, A. (2012). Teleimpedance: Exploring the role of common-mode and configuration-dependant stiffness. In 2012 12th IEEE-RAS international conference on humanoid robots (Humanoids 2012) (pp. 363–369). IEEE.
Chen, M., & Chen, W. H. (2010). Sliding mode control for a class of uncertain nonlinear system based on disturbance observer. International Journal of Adaptive Control and Signal Processing, 24(1), 51–64.
Chen, M., Chen, W., & Wu, Q. (2014). Adaptive fuzzy tracking control for a class of uncertain mimo nonlinear systems using disturbance observer. Science China Information Sciences, 57(1), 1–13.
Chen, W. H., Ballance, D. J., Gawthrop, P. J., & O’Reilly, J. (2000). A nonlinear disturbance observer for robotic manipulators. IEEE Transactions on Industrial Electronics, 47(4), 932–938.
Chow, H. W., & Cheung, N. C. (2013). Disturbance and response time improvement of submicrometer precision linear motion system by using modified disturbance compensator and internal model reference control. IEEE Transactions on Industrial Electronics, 60(1), 139–150.
Craig, J. J. (2009). Introduction to robotics: mechanics and control, 3/E. New Delhi: Pearson Education India.
Ding, X., & Fang, C. (2013). A novel method of motion planning for an anthropomorphic arm based on movement primitives. IEEE/ASME Transactions on Mechatronics, 18(2), 624–636.
Eom, K. S., Suh, I. H., & Chung, W. K. (2001). Disturbance observer based path tracking control of robot manipulator considering torque saturation. Mechatronics, 11(3), 325–343.
Hamilton, W. R. (1848). Xi. on quaternions; or on a new system of imaginaries in algebra. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 33(219), 58–60.
Han, J., Ding, Q., Xiong, A., & Zhao, X. (2015). A state-space EMG model for the estimation of continuous joint movements. IEEE Transactions on Industrial Electronics, 62(7), 4267–4275.
Iida, W., & Ohnishi, K. (2004) Reproducibility and operationality in bilateral teleoperation. In The IEEE international workshop on advanced motion control (pp. 217–222).
Li, L., Chen, Z., Wang, Y., Zhang, X., & Wang, N. (2019). Robust task-space tracking for free-floating space manipulators by cerebellar model articulation controller. Assembly Automation, 39, 26–33.
Li, Z., Chen, Z., Fu, J., & Sun, C. (2016a). Direct adaptive controller for uncertain mimo dynamic systems with time-varying delay and dead-zone inputs. Automatica, 63, 287–291.
Li, Z., Kang, Y., Xiao, Z., & Song, W. (2016b). Human–robot coordination control of robotic exoskeletons by skill transfers. IEEE Transactions on Industrial Electronics, 64(6), 5171–5181.
Liu, H., Brown, D. J., & Coghill, G. M. (2008). Fuzzy qualitative robot kinematics. IEEE Transactions on Fuzzy Systems, 16(3), 808–822.
Luo, J., Lin, Z., Li, Y., & Yang, C. (2019). A teleoperation framework for mobile robots based on shared control. IEEE Robotics and Automation Letters, 5(2), 377–384.
Nikoobin, A., & Haghighi, R. (2009). Lyapunov-based nonlinear disturbance observer for serial n-link robot manipulators. Journal of Intelligent and Robotic Systems, 55(2–3), 135–153.
Ohnishi, K., Shibata, M., & Murakami, T. (1996). Motion control for advanced mechatronics. IEEE/ASME Transactions on Mechatronics, 1(1), 56–67.
Potvin, J., Norman, R., & McGill, S. (1996). Mechanically corrected EMG for the continuous estimation of erector spinae muscle loading during repetitive lifting. European Journal of Applied Physiology and Occupational Physiology, 74(1–2), 119–132.
Qiao, J. Z., Wu, H., Zhu, Y., Xu, J., & Li, W. (2019). Anti-disturbance iterative learning tracking control for space manipulators with repetitive reference trajectory. Assembly Automation, 39, 401–409.
Sariyildiz, E., & Ohnishi, K. (2015). Stability and robustness of disturbance-observer-based motion control systems. IEEE Transactions on Industrial Electronics, 62(1), 414–422.
Schwarz, L. A., Mkhitaryan, A., Mateus, D., & Navab, N. (2012). Human skeleton tracking from depth data using geodesic distances and optical flow. Image and Vision Computing, 30(3), 217–226.
Sheridan, T. B. (1995). Teleoperation, telerobotics and telepresence: A progress report. Control Engineering Practice, 3(2), 205–214.
Slotine, J. J. E., Li, W., et al. (1991). Applied nonlinear control (Vol. 199). Englewood Cliffs, NJ: Prentice Hall.
Smith, A., Yang, C., Li, C., Ma, H., & Zhao, L. (2016). Development of a dynamics model for the Baxter robot. In 2016 IEEE international conference on mechatronics and automation (pp .1244–1249). IEEE.
Sun, Y., Chen, L., & Qin, H. (2019). Distributed adaptive fuzzy tracking algorithms for multiple uncertain mechanical systems. Assembly Automation, 39, 200–210.
Veras, E., Khokar, K., Alqasemi, R., & Dubey, R. (2012). Scaled telerobotic control of a manipulator in real time with laser assistance for adl tasks. Journal of the Franklin Institute, 349(7), 2268–2280.
Wang, Z., & Qiao, H. (2002). Robust filtering for bilinear uncertain stochastic discrete-time systems. IEEE Transactions on Signal Processing, 50(3), 560–567.
Wang, Z., Qiao, H., & Burnham, K. J. (2002). On stabilization of bilinear uncertain time-delay stochastic systems with Markovian jumping parameters. IEEE Transactions on Automatic control, 47(4), 640–646.
Xu, Y., Yang, C., Liang, P., Zhao, L., & Li, Z. (2016). Development of a hybrid motion capture method using Myo armband with application to teleoperation. In 2016 IEEE international conference on mechatronics and automation (ICMA) (pp. 1179–1184). IEEE.
Xu, Y., Yang, C., Zhong, J., Wang, N., & Zhao, L. (2018). Robot teaching by teleoperation based on visual interaction and extreme learning machine. Neurocomputing, 275, 2093–2103.
Yang, C., Ma, H., & Fu, M. (2016). Advanced technologies in modern robotic application. Berlin: Springer.
Yang, Z. J., Fukushima, Y., & Qin, P. (2012). Decentralized adaptive robust control of robot manipulators using disturbance observers. IEEE Transactions on Control Systems Technology, 20(5), 1357–1365.
Yang, Z. J., Tsubakihara, H., Kanae, S., & Wada, K. (2006). A novel robust nonlinear motion controller with disturbance observer. IEEE Transactions on Control Systems Technology, 16(1), 137–147.
Yuan, Q., & Chen, I. M. (2013). 3-d localization of human based on an inertial capture system. IEEE Transactions on Robotics, 29(3), 806–812.
Zhang, L., Li, Z., & Yang, C. (2016). Adaptive neural network based variable stiffness control of uncertain robotic systems using disturbance observer. IEEE Transactions on Industrial Electronics, 64(3), 2236–2245.
Acknowledgements
This work was partially supported by Engineering and Physical Sciences Research Council (EPSRC) under Grant EP/S001913, and partially by the National Natural Science Foundation of China under Grant 51575412.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Huang, D., Yang, C., Ju, Z. et al. Disturbance observer enhanced variable gain controller for robot teleoperation with motion capture using wearable armbands. Auton Robot 44, 1217–1231 (2020). https://doi.org/10.1007/s10514-020-09928-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10514-020-09928-7