Abstract
We incorporate communication into the multi-UAV path planning problem for search and rescue missions to enable dynamic task allocation via information dissemination. Communication is not treated as a constraint but a mission goal. While achieving this goal, our aim is to avoid compromising the area coverage goal and the overall mission time. We define the mission tasks as: search, inform, and monitor at the best possible link quality. Building on our centralized simultaneous inform and connect (SIC) path planning strategy, we propose two adaptive strategies: (1) SIC with QoS (SICQ): optimizes search, inform, and monitor tasks simultaneously and (2) SIC following QoS (SIC+): first optimizes search and inform tasks together and then finds the optimum positions for monitoring. Both strategies utilize information as soon as it becomes available to determine UAV tasks. The strategies can be tuned to prioritize certain tasks in relation to others. We illustrate that more tasks can be performed in the given mission time by efficient incorporation of communication in the path design. We also observe that the quality of the resultant paths improves in terms of connectivity.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Unmanned aerial vehicles (UAVs), commonly called drones, are employed in search and rescue (SAR), monitoring and surveillance, network provisioning, and other applications. In many cases, a combination of aerial sensor coverage and wireless connectivity is desirable. For instance, in SAR and surveillance—where coverage enables target or event detection—connectivity ensures information dissemination to concerned authorities for quick response and situation awareness. Correspondingly, the drone flight paths should allow the desired connectivity along with complete and successful coverage. Such path planning and optimization solutions are called connectivity-constrained coverage (Scherer and Rinner 2016) and connectivity-aware coverage (Flushing et al. 2013).
Our work is motivated by the fact that different drone applications require different connectivity priorities (e.g., always, periodic, delay-tolerant). Path planning algorithms tunable to connectivity requirements have not been explored in the literature. In our previous work, we studied the coverage and connectivity requirements of drone applications (Hayat et al. 2016) and used the knowledge to design a tunable multi-objective path planning (MOPP) algorithm (Hayat et al. 2017). A single parameter \(\lambda \in [0, 1]\) is used to tune between coverage and connectivity; it offers the full range between coverage-optimized paths (\(\lambda = 1\)) and connectivity-optimized paths (\(\lambda = 0\)). Figure 1 shows the demands of different applications using \(\lambda \). Our analysis (Hayat et al. 2016) then focused on the special case \(\lambda = 0.5\), in which coverage and connectivity are equally important.
Another issue disregarded in common path planning is that different multi-drone applications have different data traffic demands (e.g., in terms of throughput, delay, jitter). The corresponding optimized paths vary vastly.
Taking into account the importance of both connectivity and communication, MOPP is a multi-phase path planning algorithm with special focus on SAR missions. The goals of the SAR mission are the area coverage for target localization, followed by delivery of target location, followed by real-time status information to the first responders. The purpose of phase 1 (coverage) is to search for a single stationary target on a discretized area using discrete time steps. This is performed using the search task, where the multiple travelling salesmen problem (mTSP) (Bektas 2006) is used to design coverage paths. These paths allow the drones to cover the given area and locate the target in the shortest possible time. Phase 2 ensues after a target has been located during phase 1. The purpose of phase 2 (connectivity) is to disseminate information in the network. It consists of two tasks: The inform task carries the target location information to the ground base station (BS). The monitor task establishes a best quality-of-service (QoS) link between the target location and the BS. Such link establishment is required for continuous target state monitoring until help arrives at the target location. A genetic algorithm (GA) is used to evaluate a population of the “shortest time” mTSP-based coverage paths, with the optimal paths resulting in the quickest completion of phase 2 tasks. Thus, GA optimizes mission completion time, which includes time to perform search, inform, and monitor tasks. The resultant GA-optimal paths are the mission flight paths. The initial mission paths are pre-designed but adaptable to new information. Once a target has been located, the drones replan their individual paths by responding to the information about the target and other drones in the network. Replanning helps to quickly spread the victim information and allocate tasks efficiently. In particular, as soon as better-suited drones are encountered (leading to shorter mission time), the drones handover their tasks and head back to the BS.
MOPP optimizes both coverage and connectivity, using \(\lambda \) to favor one over the other, based on the application’s demands. Setting \(\lambda = 1\) optimizes only phase 1 and \(\lambda = 0\) optimizes phase 2. In this sense, our treatment of the problem considers connectivity as a goal rather than a constraint for path planning. To design MOPP paths that enable connectivity with QoS considerations, results from our real-world experiments (see Hayat et al. 2015; Yanmaz et al. 2014a) are used to establish a connectivity map.
This work extends our previously proposed strategy using MOPP called simultaneous inform and connect (SIC) (Hayat et al. 2017). SIC does not take into account the QoS demands: the mission consists of the search and inform tasks only. In this paper, we design and evaluate two SIC-based advanced path planning strategies: (i) SICQ jointly optimizes the search, inform, and monitor tasks and (ii) SIC+ optimizes the search and inform tasks jointly, followed by monitor task optimization. Both strategies aim to minimize mission time. The purpose of comparing the two path planning strategies is to evaluate if jointly optimizing the monitor task with search and inform tasks degrades the overall mission quality by increasing the time to locate the target and inform the BS about the target position. We illustrate that, for sufficiently many drones, such joint optimization allows monitor task to be performed in addition to search and inform tasks in a given mission time. For fewer drones, we witness a considerably shorter mission time.
The main contributions of this work are to:
-
define an SAR mission in terms of causal tasks that need to be performed for successful mission completion;
-
emphasize the role of communication as an enabler for multi-UAV applications;
-
define communication as a goal by incorporating QoS demands in UAV path planning;
-
use real-world link measurements to incorporate connectivity and QoS in path planning in a realistic manner;
-
introduce two adaptive path planning/replanning strategies to illustrate impact of including communication in path planning for SAR missions; and
-
analyze the impact of the tuning parameter on mission times and UAV path quality.
The rest of the paper is organized as follows. Section 2 discusses pre-existing work for path planning for applications requiring coverage and connectivity optimization, such as SAR. Section 3 formulates the problem under consideration, and describes the optimization problem and modeling assumptions. Section 4 describes the proposed path planning algorithms. Sections 5 and 6 focus on the results and conclusions of the work, respectively.
2 Related work
This work proposes a path planning/replanning algorithm for missions where coverage and connectivity-related tasks are dynamically and causally allocated in a drone network. Due to this causal relation, classical task allocation strategies (as Choi et al. 2009; Hoeing et al. 2007; Lemaire et al. 2004; Ponda et al. 2010) do not apply. The causality of tasks is considered in Parker (1998), with the goal to study fault tolerance in a multi-robot system. As timely task completion is not of significance in the proposed architecture, it can not be applied to time-critical applications such as SAR.
2.1 Basic path planning
Several planning strategies are proposed for ground and aerial robots with different objectives and constraints (see Choset 2001; Cole et al. 2009; Elfes 1990; Jin et al. 2006; Kovacina et al. 2002; Poduri and Sukhatme 2004; Potvin 2009; Tisdale et al. 2009; Vincent and Rubin 2004; Zlot et al. 2002). Basic path planning approaches are based on cell decomposition, roadmaps, and potential fields (Frazzoli et al. 2002; Latombe 1991). These can be used for different phases (or combination thereof) in an SAR mission. Cell decomposition methods partition the configuration space into regions inside a grid, marking the obstacles on the grid. Roadmaps (such as visibility graphs and Voronoi diagrams) pre-compute a graph such that obstacles can be avoided by staying on the “roads”. Approaches based on potential fields utilize attractive forces toward the goal and repulsive forces from the obstacles. They rely on the set of all possible configurations of the robot. Complete solutions exist at a high computation cost and are not feasible for high dimensions. Instead, sampling-based planners (such as probabilistic roadmaps) find “good” samples of the configuration space by randomly adding points to a tree and creating possible paths. In all these solutions, path planning discretizes the configuration space and then uses graph-based searches such as A*, D* (for dynamic replanning) and their variations (de Filippis et al. 2012), each with different complexity, optimality, and suitability for dynamic replanning. A further sampling-based planning approach is Rapidly Exploring Random Trees (RRT) that explores the space rapidly in all directions taking into account vehicle dynamics. RRT does not require extensive pre-processing. With all these path planning methods, there is a trade-off between completeness, speed, and practicality in higher dimensions.
2.2 Search path planning
The use of drones has been proposed for target detection in Flint et al. (2002), Gan and Sukkarieh (2011), Lin and Goodrich (2009), Waharte and Trigoni (2010), York and Pack (2012), where search algorithms have been used for path planning. These works focus on target detection (phase 1), using algorithms that provide either fast area coverage (Waharte and Trigoni 2010), or maximize the accumulated probability for target detection (Lin and Goodrich 2009). However, the successful completion of search missions not only relies on locating the target but also on informing the BS about the location. Informing the BS requires some form of connectivity in the network.
Connectivity as a constraint Most research work on multi-drone area coverage assumes basic disk-shaped connectivity amongst the drones (see Beard and McLain 2003; Flint et al. 2002; Gan and Sukkarieh 2011; Lin and Goodrich 2009; York and Pack 2012). Path planning for search usually utilizes communication for information merging to improve the target detection probability through cooperation (Beard and McLain 2003; Khan et al. 2015). Connectivity is treated as a constraint in algorithm design in scenarios where BS needs notification of a target or event (Acevedo et al. 2013; Bezzo and Fierro 2011; Cesare et al. 2015; Hollinger and Singh 2012; Scherer and Rinner 2016; Schleich et al. 2013). Such restrictive approach (constrained connectivity to BS)—whether it be continuous (Scherer and Rinner 2016) or periodic connectivity (Cesare et al. 2015)—leads to coverage performance degradation.
Connectivity as a goal Most auction/consensus-based algorithms for distributed task allocation rely on perfect communication. These algorithms are proven to degrade with the quality of the communication links (Otte et al. 2019). As designing connected search paths is a necessity in such cases, another approach for cooperative search is to treat connectivity as a goal rather than a constraint (see Danoy et al. 2015; Flushing et al. 2013; Goddemeier et al. 2012; Messous et al. 2016; Yanmaz 2012). For instance, Yanmaz (2012) extends Yanmaz and Guclu (2010) to include the demand for maintaining connectivity to the BS (sink node). The paper Goddemeier et al. (2012) ensures efficient exploration using multi-hop connectivity to the BS. This connectivity is not a constraint as the air-to-ground links are expected to be temporarily releasable. Different to these works, our approach allows flexible path planning in terms of coverage and connectivity parameters. Based on the mission demands, the algorithm allows a tradeoff between the two parameters. The paper Flushing et al. (2013) offers the closest solution to ours in this regard. The authors propose a mixed-integer linear programming (MILP) approach, where connectivity directives are introduced in the planning process. Authors state that the inclusion of the proposed directives reduces the quality of the solutions. Drones are employed only for establishing communication between the ground agents, either as relays or data mules. Assigning dedicated tasks to a number of agents in the network may lead to inefficient resource utilization, as the number of agents in the network is limited, and SAR missions are time-critical in nature. We tackle this problem by utilizing all drones for coverage. Communication tasks (relaying/data ferrying) are assigned to the drones when information dissemination is required. Unlike previous work employing data ferrying (Henkel and Brown 2006) or relaying (Grøtli and Johansen 2012), we use a combination of both, with the aim to reduce the overall mission completion time. To the best of our knowledge, no other algorithm exists that ensures a best possible QoS path at the end of the mission.
Optimization criteria Different parameters have been used for the design of connectivity-aware coverage paths. The papers Messous et al. (2016) and Yan and Mostofi (2014) use energy as the design parameter for path planning, where Yan and Mostofi (2014) includes motion, sensing, and communication energy costs in the total energy costs. The papers Flushing et al. (2013) and Kantaros and Zavlanos (2016) use area coverage as the design parameter, keeping in mind the connectivity considerations. In Cesare et al. (2015), area coverage and communication to the BS is optimized. Keeping the time-critical nature of SAR in mind, we choose mission completion time as the parameter to optimize.
Optimization tool Joint coverage and connectivity optimization has been addressed using different solution methods: potential fields (Yanmaz et al. 2013), MILP (Flushing et al. 2013; Scherer and Rinner 2016), space-filling curves (Yan and Mostofi 2014), and GA (Goddemeier et al. 2012). We use GA for evaluating our algorithm. However, it should be emphasized that GA is only a tool for evaluation. The comparison of different metaheuristics is out of the scope of this work.
Preliminary work We proposed a MOPP strategy for SAR missions using GA (Hayat et al. 2017). The strategy, named SIC, aims to optimize mission time, which includes time to locate the target in phase 1 (search task) and the time to inform the BS about the target position in phase 2 (inform task). During phase 1, pre-planned search paths are assigned to the drones. Phase 1 completes when a UAV detects the target. This UAV hovers above the target as a sensing UAV. Phase 2 starts when a second UAV comes in communication range of the sensing UAV. The second UAV then acts as a data mule and flies on a direct path to inform the BS about the target location. SIC is designed such that a relay chain is formed between the BS and the target position for continuous target monitoring during the time it takes the data mule drone to reach the BS. The strategy design does not take into account the application QoS demands.
3 System description
3.1 Mission overview
We consider a SAR mission with multiple UAVs and a single stationary target at an unknown location in a bounded area. Before the mission commences, the path planner is informed about the search area, communication technology (e.g., available data rates), QoS demands (e.g., throughput or delay), and the energy constraints. This information is used to plan collision-free paths specific to the QoS demands with coverage time minimized. Each drone is able to fulfill its tasks and return to the BS before its battery depletes.
A mission starts with the coverage phase (phase 1), where UAVs fly their pre-planned paths to search for the target (search task). The detection of the target triggers the connectivity phase (phase 2). The UAVs now replan their paths in a distributed manner to inform the BS (inform task) and establishing a QoS path between the target location and the BS (monitor task) until help arrives at the target. A UAV follows its coverage path until it is informed about the target detection. It then abandons its coverage path and updates its plan to spread target information through the network. As UAVs come into contact with each other and learn new information, they further replan. The replanning continues until the connectivity phase is completed.
During the mission, for flight safety, the drones periodically broadcast beacons with their current mission status. The status includes the drone id, current time stamp, the task carried out, and the current coordinates. For simplicity, mission failures caused by reasons other than battery outage and drone collisions are not considered.
Table 1 lists the parameters used throughout the paper, and the symbols used to represent them in the algorithm description.
3.2 Mission time
We are interested in the total time \(\tau \) it takes to complete a mission. The search task takes \(\tau _S\) to find the target. The inform task lasts for \(\tau _I\) to inform the BS about the target location after detection. The monitor task is performed in time \(\tau _M\) needed to reorganize the UAVs for best possible QoS link to BS for continuous monitoring. From the algorithm design perspective, the mission is completed when a QoS path has been established. The total mission time is \(\tau = \tau _S + \tau _I + \tau _M\).
3.3 Mission phase tuning
The paths can be designed such that coverage (\(\tau _S\)) is prioritized over connectivity (\(\tau _I, \tau _M\)) and vice versa, depending on requirements. This tuning is done with \(\lambda \in [0,1]\), which has the extreme cases \(\lambda \!=\!0\) for generating connectivity-only paths and \(\lambda \!=\!1\) for coverage-only paths. If an application prefers coverage over connectivity, we choose a value \(\lambda > 0.5\), and if connectivity must be prioritized over coverage, we use \(\lambda < 0.5\).
3.4 Area and QoS demands
As mentioned in Sect. 3.1, the algorithm takes information about the search area, communication technology, and QoS demands as input to pre-plan search paths. The communication technology is an input requisite as different technologies offer various throughput, delay, and coverage range; i.e., supported QoS demands over a certain area also differ for each technology. Thus, assigning generic values for QoS demands in the algorithm design is not realistic. In the following, we explain our assumptions about the input parameters. We use our experimental measurements using sensors and communication interfaces to extract appropriate values for these parameters. While these values may differ for different technologies, the proposed algorithm is not limited to a specific communication technology.
The input search area is divided into n square cells with side length \(n_l\), where each cell corresponds to the sensing range of a UAV at a specific (constant) height h. Using square cells is consistent with the sensing range of the onboard cameras used during our experimental research (Yahyanejad et al. 2011), where \(n_l = 50~\text {m}\) at a height of \(50~\text {m}\). A BS is located at cell ‘0’ which may lie inside or outside the search area. A target is located at a random, uniformly sampled but unknown cell l in the area. The detection sensors are 100 % accurate, i.e., the target is detected once cell l is visited by a UAV. The effects of terrain, ground clutter, and elevation are assumed to be insignificant in terms of coverage, movement, and communication.
During the monitor task, we consider three QoS levels: high, medium, and low quality. These vary in their throughput and delay requirements. The network interfaces communicate using high, medium and low data rates in disk-shaped ranges. We extract the values for these input parameters using our experimental work (Yanmaz et al. 2014b). With 802.11a as the communication technology of choice, we performed experiments in a setup imitating a real-world SAR scenario (Scherer et al. 2015). The high-quality video, low-quality video and image transfers in our experiments serve to extract the demands of the three QoS levels mentioned above. High QoS (high-quality video) requires throughput greater than 13 Mb/s and delays below 50 ms . Medium QoS (low-quality video) requires at least 3 Mb/s and maximum delay of 200 ms. Low QoS (image transfer) requires 700 kb/s with delays no more than 350 ms. The high, medium, and low data rates using 802.11a correspond to 54 Mb/s, 36 Mb/s, and 12 Mb/s, respectively. The edge of the communication range (lowest data rate disk) lies at a radius where the received signal strength from the communicating device drops below \(-80\) dBm. Consequently, the number of packet re-transmissions is too high to sustain a link (Yanmaz et al. 2014b). We consider an obstacle-free (i.e., line-of-sight) scenario as presented in Scherer et al. (2015), where it is safe to assume disk-shaped connectivity.
Figure 2 illustrates the relation between traffic type, distance, and the number of hops (drones) needed to support the traffic type, using our chosen parameter values. As the throughput and delay requirements are considered while extracting this relationship, we assume that the information transfer is real-time if a certain QoS link exists. The blue line shows that a direct link supports high data rates in a radius of two cells (100 m) from the BS. Beyond this range, the error rate causes the data rate to drop. Medium data rate is maintained in a radius of three cells. Low data rate extends by up to six cells. Beyond this range, a single drone can not support any traffic transfer due to the quality of the received signal strength. The figure illustrates that a one-hop link supports high QoS links in a radius of three cells. A two-hop links extends this range to four cells (red line). Beyond this, high QoS can not be supported. Using both one and two-hop links, medium QoS can be supported by up to six cells. Using a two-hop link offers no benefit in range extension compared to a single hop due to the accumulated error rate on the two hops. A three-hop link extends medium QoS range up to nine cells. Beyond this range, only low quality can be supported. This information is used to extract the resource-optimal curve (black dashed line), which provides the optimal number of UAVs (hops) needed to achieve the best possible QoS considering a certain distance from the BS. The area over which a certain QoS is supported is limited by the choice of the communication technology as an input to the algorithm. With the considered radio and QoS requirements, the maximum distance from the BS at which the lowest quality link can still be sustained is 24 cells (1.2 km) using four drones.
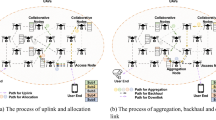
Final paths for a given target position for a SIC+ and b SICQ. QoS waypoints between target location and BS are indicated as \(\star \). The green UAV labelled ‘s’ locates the target in the green shaded cell at \(k_1\), while following its pre-planned coverage path (solid line). a In SIC+, the blue UAV comes in range of s at \(k_2\) and replans to fly to \(w_0\) on a new path (dotted line) as a data mule UAV \(r_d\). At \(k_3\), the red UAV comes in range of blue, where red is closer to \(w_0\). The UAVs then replan their paths. Red is the new data mule UAV \(r_d\), and flies on a newly designed inform path, arriving at \(w_0\) at \(k_4\), while blue replans to fly to the closest QoS waypoint (\(w_1\)) on a monitor path (dashed line). The grey UAV follows its coverage path, until it comes in range of s, after which it replans its monitor path to the unoccupied \(w_2\). b For SICQ, the pre-planned coverage paths are such that at \(k_3\), enough UAVs join the relay set \(\mathcal {R}\) to form a QoS chain between s and BS while BS is being informed. Thus, both red and grey UAVs acquire the system knowledge at \(k_3\) and all the UAVs arrive at their destination waypoints at \(k_4\) (Color figure online)
4 Path planning algorithm
The path planning algorithm chooses pre-planned coverage paths and re-planned connectivity paths based on the shortest time to perform the search, inform, and monitor tasks. A time step needed by a UAV m to complete step k in its coverage path \(p_k^m\) is \(T_k^m = t_k^m + t_s\), where \(t_k^m = \frac{d_{k}}{v}\) is the time to fly the distance \(d_{k}\) with velocity v, and \(t_s\) is a constant time to sense a cell. Once the target is discovered, the UAVs that become aware of it no longer sense the cells. For the purpose of synchronization, the UAVs in flight move to the next cell in their coverage path only after each UAV has completed its previous step. Thus the time \(\Delta _{k}\) needed by all UAVs in flight to finish their step k is:
The reported variance (from the simulation results) in the step duration of all UAVs at any time step k is at most \(2\times t_s\) in the designed paths. To compensate for the variance, the UAV speed may be reduced in real-world implementation to ensure synchronization while guaranteeing collision avoidance. In our experimental work (Scherer et al. 2015), we ensured collision avoidance by varying neighboring drones’ flight altitudes. We also assume that all drones synchronize their clocks at the start of the mission, and that the clock drift during the mission is not significant. After completing the coverage path, each UAV returns to the BS. The number of time steps needed from the start of the mission until all UAVs have returned to the BS is K.
4.1 Coverage phase
At \(k = 0\), M search UAVs forming set \(\mathcal {U}\) take off from the BS and, upon arriving at the first step in their path \(p_1^m\), they sense the cell for time \(t_s\). When the target is detected by UAV m at step \(k_1\) in its coverage path (Fig. 3), m is labeled sensing UAV ‘s’ and is excluded from the set \(\mathcal {U}\). After \(k_1\), s loiters above target location l for continuous monitoring.
The algorithm aims to use time-efficient pre-planned coverage paths for fast discovery of a target located anywhere in the search area. We define search time \(\tau _S\) as:
4.2 Connectivity phase
The ensuing connectivity phase uses UAVs in \(\mathcal {U}\) to perform the inform and monitor tasks. The calculation for this phase depends on the discovery time step, \(k_1\) and discovery drone s. Algorithm 1 presents how to compute the inform time \(\tau _I\). If at \(k_1\), s is in communication range of BS, \(\tau _I = 0\), and Algorithm 1 is not performed. The following takes place only if BS is not informed about the target location at \(k_1\).
The remaining UAVs in \(\mathcal {U}\) are in general unaware that the target has been located and thus continue searching. At some time \(k_2\), the first of these UAVs comes in range of s. At this stage, we assume the UAVs to communicate at the search communication range \(R_{comm}\). There are four ways in which a UAV m may come in range of s:
-
1.
The two UAVs have a direct or multi-hop communication link between them when s is labeled.
-
2.
The two UAVs have a direct or multi-hop communication link between them in the subsequent steps while s hovers over l and m is tracing its specified path.
-
3.
The two UAVs are expected to be in range of each other in the future. If m cannot establish connectivity with s at this future time step, it assumes that s detected the target and starts tracing back the path of s until it comes in contact with s.
-
4.
If no UAV in \(\mathcal {U}\) comes in range of s throughout its path, after returning to the BS, the \(M-1\) UAVs start following the path of s until they come in range of s.
Thus at \(k_2\), m is labeled relay, removed from the set \(\mathcal {U}\), and added to a set of relays \(\mathcal {R}\) (Fig. 3).

After \(k_2\), we use an SIC-based enhanced strategy. We modified SIC (Hayat et al. 2017) to inform BS in the fastest way through a combination of data ferrying and task handover. In SIC, a single data mule UAV performs the inform task, i.e., physically carries the target information to the BS (see Sect. 2.2). Contrary to that, in the enhanced SIC strategy, the inform task may be handed over to a different UAV at each time step, based on the proximity to the BS (Algorithm 1). Figure 3a illustrates the modification: the blue UAV \(r_1\) is the first that comes in range of s and hence is assigned the inform task. It then hands over this task to the red UAV that is closer to BS. This shortens the inform time compared to the original SIC. For clarity, the differences between the strategies are highlighted in Table 2.
We define a set of final QoS waypoints \(\mathcal {W}\) based on the information in Fig. 2, which represents a monitor path ensuring best possible QoS between the BS and target position. In this set, \(w_0\) represents the waypoint closest to the BS, as shown in Fig. 3. At \(k_2\), the state of occupancy of \(w \in \mathcal {W}\) leads to three path replan cases:
-
Case 1: \(w_0\) unoccupied. A UAV \(r_d\) (data mule) closest to \(w_0\) is selected from \(\mathcal {R}\). It replans its path for the following time steps towards \(w_0\) (Algorithm 1, line 7 represented by a dotted line in Fig. 3). The remaining UAVs in \(\mathcal {R}\) fly to the nearest unoccupied waypoints from \(\mathcal {W}\) that have not been claimed by any other (closer) UAVs (Algorithm 1, line 9, dashed lines in Fig. 3). Thus \(r \in \mathcal {R}\) follow a new set of paths \(p_{k}^r\).
-
Case 2: \(w_0\) occupied and \(w \in \mathcal {W} \backslash w_0\) unoccupied. BS has been informed about the target position. The \(r \in \mathcal {R} \backslash r_d\) replan their paths to place themselves at the nearest unoccupied waypoints from \(\mathcal {W}\) in terms of distance (dashed lines in Fig. 3).
-
Case 3: \(w \in \mathcal {W}\) occupied. BS has been informed and QoS path has been established. All remaining UAVs fly back to BS.
In the following time step (\(k = k_2 + 1\)), any UAV that comes in range of s (Algorithm 1, line 13) or any UAV in \(\mathcal {R}\) (Algorithm 1, line 15) join \(\mathcal {R}\). As new UAVs may join \(\mathcal {R}\) at each time step, replanning occurs after each time step if a new r is closer to any of the unoccupied \(w \in \mathcal {W}\). Thus a new \(r_d\) may be chosen at each time step. As it is necessary for drones in \(\mathcal {R}\) to be in communication range of each other to form a relay link to the BS, it is safe to assume that they share a global knowledge of the candidates in \(\mathcal {R}\) and the occupancy of \(\mathcal {W}\). Any new r joining \(\mathcal {R}\) is updated about this knowledge by its neighbor drone(s).
For the inform task, the process continues until case 2 is reached, i.e., BS is informed about l (\(k_4\) in Fig. 3), which happens when \(r_d\) or any newly joined r comes in range of BS in the current time step (Algorithm 1, line 16). As shown in Fig. 3, the inform time is:
For the monitor task, the replanning continues at each time step until case 3 is reached. In Fig. 3, the monitor time corresponds to:
SIC+ connectivity phase SIC+ optimizes the connectivity phase tasks sequentially: The inform task is optimized first, then the monitor task. The inform task requires \(\tau _I\) for completion, using Algorithm 1. The monitor task follows, where the best possible route is taken by a UAV to arrive at its corresponding \(w \in \mathcal {W}\) only after it acquires the system knowledge. In Fig. 3a, the grey UAV u comes across s while on its pre-planned coverage path, and receives knowledge about \(\mathcal {R}\) and \(w \in \mathcal {W}\) occupancy. After that, it replans its shortest path flight to \(w_2\).
SICQ connectivity phase In SICQ, the connectivity phase tasks are optimized jointly. This is illustrated in Fig. 4, which shows the path replanning and the corresponding \(\tau _I\) and \(\tau _M\) calculation during the connectivity phase. In Fig. 3b, the coverage paths for SICQ are planned such that both \(\tau _I\) and \(\tau _M\) are minimized. As illustrated, \(r_1\) and \(r_2\) arrive at \(w_1\) and \(w_2\), respectively in the same time it takes \(r_d\) to arrive at \(w_0\) (inform task). This leads to \(\tau _M = 0\).
4.3 Multi-objective path planning with GA
As discussed in Sect. 2, various optimization tools that evaluate multi-objective algorithms exist. Being a popular candidate amongst evolutionary algorithms for such evaluation, we choose GA. Although GA does not explore the entire search space, it is based on the premise of correlation between the quality of neighboring solutions, resulting in high-quality solutions in the search space in polynomial time. Search is extended to non-neighboring solutions by cross-over between two high-quality parent solutions, which has been shown to result in high-quality offspring in most cases (Mitchell 1998). Comparison of various optimization tools for evaluation of our MOPP algorithm will be the focus of future work.
In the coverage phase the path planning is done centrally, but in the connectivity phase, the replanning is done in a distributed manner. Using GA, the algorithm combines the phases to generate the pre-planned paths with the goal to minimize the overall mission time.
The objective function is designed to prioritize coverage versus connectivity using \(\lambda \). In case of SIC+, only the search and inform times are tunable with \(\lambda \). The separately optimized monitor time \(\tau _M\) is added to compute the total mission time \(\tau _{\text {SIC+}}\). The objective function for SIC+ is:
where the expectation is over possible locations of the target and \(\mathcal {P}\) is the set of all possible paths. Contrary to this, in SICQ, \(\tau _M\) is included in the tunable connectivity part of the optimization function, which is given by:
Since \(\mathcal {P}\) is a large and discontinuous search space, we use GA for path evolution and selection. We let \(\mathcal {P}\) be a population of a subset of all possible paths and then apply GA operators to improve the population. We define \(\mathcal {P}=\{P_1, P_2, \dots P_N\}\) as the population of size N of GA generated strings of paths, such that \(P_n = \{p_n^1, p_n^2, \dots p_n^M\}\) represents the nth possible combination of paths the M UAVs fly for coverage. From the objective function, it can be seen that GA prioritizes coverage paths and considers connectivity based on \(\lambda \) and communication demands. Coverage time is compromised only if a lower \(\tau _S\) leads to higher overall mission time.
Before mission start, the MOPP algorithm is run for a certain number of iterations on a central BS to pre-plan GA-optimal search paths (Fig. 5a). The strings consisting of paths of all the UAVs \(P_n \in \mathcal {P}\) are generated as chromosomes. The resultant set of path strings is evaluated for average \(\tau _{S}, \tau _{I}\), and/or \(\tau _M\) values for all possible target positions (depending on the chosen strategy). This means that the paths are evaluated for (1) the time it takes the drones to fly the waypoint paths assigned to them, and (2) the time it takes a drone to establish a (possibly multi-hop) link to the BS from each waypoint in its path. Minimizing (1) results in each drone flying a path consisting of consecutive waypoints. Minimizing (2) results in the drone paths being chosen such that an instant link from any drone to the BS can be ensured. The path string with the minimum resultant objective function value [Eqs. (3), (4)] is chosen and used in the subsequent iteration. Mutation (flip, swap, and slide) and cross-over are employed to create a new generation of N path strings. Thus, at each iteration, only an N-sized population containing the best chromosomes and their mutations are preserved to be evaluated in the next iteration. Partial-mapped crossover (PMX) is performed between the best chromosome strings and randomly selected chromosomes to expand the search space. After a chosen number of iterations, the path string (\(P_{\tau _{\text {min}}}\)) with the minimum objective function value (\(\tau _{\text {min}}\), which is the mission time \(\tau _{\text {SIC+}}\) for SIC+ and \(\tau _{\text {SICQ}}\) for SICQ) becomes the final MOPP string to be used as pre-planned coverage paths by UAVs during mission (Fig. 5b). UAVs follow these paths to perform the search task, and upon target detection, replan their paths in a distributed manner as described in the previous subsection. The replanned paths ensure that the inform and monitor tasks are performed in minimum time for the specific target position.
5 Results and discussion
We perform simulations for the algorithm analysis. Deriving a closed form solution to Eqs. (3), (4) is a complex task due to the large number of parameters and constraints. The algorithm is simulated for 10 to 15 runs, each over 1000 iterations, with a GA-generated path population size \(N = 80\). We determine the parameter values for N and number of iterations with the help of a preliminary algorithm analysis. The results show that no signification improvement is reported for number of iterations larger than 1000. Moreover, \(N = 80\) provides a rich set of initial solutions. A larger population size does not improve results, as has been proven in literature (Chen et al. 2012). The simulations are performed over a \(10\times 20\) cells area. The maximum number of hops to provide the worst-case QoS in this area is four, so we run the simulation using \(M \ge 4\) UAVs.Footnote 1 The algorithm is evaluated for \(\lambda = \{0, 0.01, 0.25, 0.5, 0.75, 0.99, 1\}\), where 0 and 1 are the extreme values, and 0.01 and 0.99 illustrate how a small weight assigned to coverage or connectivity shortens the corresponding phase. We analyze the duration of the mission \(\tau \) including its decomposition into the three tasks and the path quality, both as a function of \(\lambda \) and M.
5.1 Duration of tasks and overall mission (average values)
Figure 6 shows the impact of \(\lambda \) on the task times \(\tau _S\), \(\tau _I\), \(\tau _M\), and their sum \(\tau \) for three different values of M. In all cases, \(\tau _S\) decreases and \(\tau _I\) increases with increasing \(\lambda \); in some cases, \(\tau _M\) increases slightly with \(\lambda \). The connectivity phase of SICQ tends to be shorter than that of SIC+; especially the monitor task is concluded faster.
For low UAV density, none of the three tasks dominates the system behavior. The inclusion of the monitor task in the optimization does not affect \(\tau _S\), even with small \(\lambda \), but accelerates the overall mission.
Increasing the UAV density makes the search task dominate the system in both strategies. By increasing \(\lambda \) from 0 to 0.01, i.e., by slightly increasing the weight of coverage, the search can be significantly accelerated without prolonging the inform and monitor tasks, which in turn results in a significantly shorter mission time. By further increasing \(\lambda \), the search task is further shortened, but with only small gains for \(\lambda \) beyond 0.5. The search cannot be accelerated by increasing the UAV density beyond a certain threshold. In our setup, this threshold is eight UAVs. We choose \(\lambda =0.5\) and \(M=8\) as benchmark parameters in terms of search time for our setup.
5.2 Comparison of average mission duration with related work
To illustrate the benefits of incorporating communication as a mission goal rather than as a constraint, we compare MOPP to related work, namely to the communication-constrained short horizon algorithm (SH, with deadlocks) and the short horizon cooperative algorithm (SHC, avoiding deadlocks) (Scherer and Rinner 2017). All algorithms are simulated with four UAVs in the same setup as in the paper at hand. For a fair comparison, MOPP is operated with full weight on connectivity (\(\lambda = 0\)), its monitor task is not taken into account, and the energy limitations considered in Scherer and Rinner (2017) are ignored. We analyze the average time that passes from the start of the mission to informing the BS about the target position. We find that SIC+ is about 33 % faster than SH and about 64 % faster than SHC; SICQ is about 23 % faster than SH and 59 % faster than SHC.
5.3 Duration of tasks and overall mission (distributions)
Figures 7, 8 and 9 show the effect of the UAV density on the duration of each task for all target positions. Figures 7 and 8 show inform and monitor times with \(\lambda =0.5\) averaged over 10 runs. The BS is located in the upper left corner. These heatmaps illustrate that there is a certain dependency between the task times and the distance from the BS. However, certain targets close to the BS may suffer more from longer task durations than distant targets, since the algorithm aims to optimize the task times and the overall mission time over all possible target positions. This can be witnessed in the distribution of the inform time using SIC+ in Fig. 7a for \(M=4\) and Fig. 8a for \(M=8\). The resulting pre-planned paths aim to minimize the mission time over all target positions, with a certain guarantee in terms of the worst case task completion time in a specific area, given a UAV density.
Both strategies improve their average inform time when increasing the number of UAVs from \(M = 4\) (Fig. 7) to \(M = 8\) (Fig. 8). Furthermore, SIC+ outperforms SICQ in terms of inform time, i.e., the inform task suffers from the joint optimization of the monitor task. However, the gain in the monitor time is more significant than the loss in the inform time. This is very prominent in case of \(M=4\), where the worst case monitor time for SIC+ is about 10 times that of SICQ; the SICQ monitor time is shortened by 90% at the expense of a 33% longer inform time (Fig. 9b, c).
An increase in UAV density also improves the average monitor time, the worst case monitor time of SIC+ is about 10 times lower with \(M = 8\) than with \(M = 4\). SICQ offers an improvement of up to 21% and 90% for \(M = 8\) and \(M = 4\), respectively. The search time for both SIC+ and SICQ have the same distribution for a certain UAV density (Fig. 9a). This is supported by the plots of Fig. 6a, b.
Figure 9 can be used to compare the performance of the two strategies in a scenario with a fixed number of UAVs or a bound on the task times. Figure 9a shows that independent of the strategy, more UAVs result in faster search task completion. The effect of the choice of strategy is more significant for connectivity tasks. As shown in Fig. 9b, for \(M=4\), the BS is informed about the target location with 80% probability in four time steps (SIC+) or six time steps (SICQ). The inform time shortens significantly with \(M=8\) for both strategies, and SIC+ still outperforms SICQ (with 80% probabilty, BS is informed about the target position in one time step for SIC+ and two time steps for SICQ). Thus, if the time to inform the BS is of critical importance, SIC+ should be the strategy of choice. However, if it is also desirable to continuously monitor the target, SICQ can ensure establishing a QoS path with 100% probability in five time steps, for both \(M=4\) and \(M=8\) (Fig. 9c). Even though SIC+ performs much better with \(M=8\) than with \(M=4\) UAVs, it still performs worse than SICQ for \(M=4\).
In conclusion, although we witness a minor improvement in search time beyond \(M = 8\) and \(\lambda = 0.5\), as mentioned in Sect. 5.3, the connectivity phase tasks mainly benefit from a higher UAV density, which leads to better network connectivity.
5.4 Path analysis
Let us finally analyze the connection quality of the paths obtained at the time of target detection. The quality of the coverage path in terms of the following connectivity tasks depends highly on the network connectivity, which is affected by the UAV density and \(\lambda \).
Figure 10a shows the likelihood that a communication path exists between l and BS as soon as the target is discovered with varying \(\lambda \). On average, this likelihood improves with the UAV density. With high enough UAV density and a more densely connected network (with \(\lambda < 0.5\)), BS is informed about the target position immediately upon discovery. With more weight on coverage, the likelihood of a link to BS upon target discovery diminishes. This likelihood is higher for SICQ than for SIC+. Even with large UAV density, SIC+ may result in UAVs spreading over the area, and the sensing UAV may not immediately encounter a relay UAV. In comparison, SICQ keeps UAVs more connected; for \(M = 12\), the BS is informed immediately upon target discovery, independent of target position in our setup.
Figure 10b shows the likelihood of a QoS communication path between target and BS upon target detection. For high UAV densities (\(M > |\mathcal {W}|\)), the likelihood that an SIC+ path to BS at target detection is a monitor path reduces. Hence, even though on average SIC+ informs the BS faster (see Fig. 6), the probability of a monitor path existing at the time of the target detection is higher for SICQ for all \(\lambda \) values.
6 Conclusions
This article proposed and analyzed two UAV path (re)-planning strategies to optimize coverage and connectivity in search and rescue missions. Both strategies can be tuned to prioritize coverage over connectivity and vice versa. For missions consisting of three tasks—search, inform, and monitor—the SICQ strategy jointly optimizes all tasks, whereas SIC+ first optimizes search and inform, followed by the monitor task.
We illustrated that joint optimization leads to better results than sequential optimization, without significantly compromising any of the tasks. For a small number of UAVs, we observed an improvement in mission completion time when more weight is assigned to the connectivity-related tasks. For a large number of UAVs, it is more beneficial to give more weight to the coverage-related search task. As more tasks are performed using SICQ during the same mission time as compared to SIC+, especially for low UAV density, we can conclude that SICQ leads to better resource utilization. However, if informing the ground personnel is of highest priority, SIC+ should be used. SICQ offers much better performance if target tracking and monitoring is necessary. SICQ outperforms SIC+ in terms of the quality of the search paths in terms of connectivity-related tasks.
Notes
In case M is smaller than the minimum number of UAVs needed for communication path establishment in the area, i.e., there are regions in the area with no direct connection (single or multi-hop) to the BS, we can deploy an existing delay tolerant strategy for the connectivity phase. However, for the existing QoS analysis, such cases are not considered.
References
Acevedo, J. J., Arrue, B. C., Daz-Bez, J. M., Ventura, I., Maza, I., & Ollero, A. (2013). Decentralized strategy to ensure information propagation in area monitoring missions with a team of UAVs under limited communications. In Proceedings of international conference on unmanned aircraft systems (ICUAS), pp. 565–574.
Beard, R. W., & McLain, T. W. (2003). Multiple UAV cooperative search under collision avoidance and limited range communication constraints. In 42nd IEEE international conference on decision and control (IEEE Cat. No.03CH37475), Vol. 1, pp. 25–30. https://doi.org/10.1109/CDC.2003.1272530.
Bektas, T. (2006). The multiple traveling salesman problem: an overview of formulations and solution procedures. Omega, 34(3), 209–219.
Bezzo, N., & Fierro, R. (2011). Decentralized connectivity and user localization via wireless robotic networks. In Proceedings of IEEE GLOBECOM Workshops, pp. 1285–1290.
Cesare, K., Skeele, R., Yoo, S.H., Zhang, Y., & Hollinger, G. (2015). Multi-UAV exploration with limited communication and battery. In Proceedings of IEEE international conference on robotics and automation (ICRA), pp. 2230–2235.
Chen, T., Tang, K., & Chen, G. (2012). A large population size can be unhelpful in evolutionary algorithms. Theoretical Computer Science, 436, 54–70. https://doi.org/10.1016/j.tcs.2011.02.016.
Choi, H., Brunet, L., & How, J. P. (2009). Consensus-based decentralized auctions for robust task allocation. IEEE Transactions on Robotics, 25(4), 912–926. https://doi.org/10.1109/TRO.2009.2022423.
Choset, H. (2001). Coverage for robotics—A survey of recent results. Annals of Mathematics and Artificial Intelligence, 31(1–4), 113–126.
Cole, D., Goktogan, A., Thompson, P., & Sukkarieh, S. (2009). Mapping and tracking. IEEE Robotics & Automation Magazine, 16(2), 22–34.
Danoy, G., Brust, M. R., & Bouvry, P. (2015). Connectivity stability in autonomous multi-level UAV swarms for wide area monitoring. In Proceedings of ACM symposium on development and analysis of intelligent vehicular networks and applications, pp. 1–8.
de Filippis, L., Guglieri, G., & Quagliotti, F. (2012). Path planning strategies for UAVs in 3D environments. Journal of Intelligent and Robotic Systems, 65(1–4), 247–264.
Elfes, A. (1990). Using occupancy grids for mobile robot perception and navigation. Computer, 22(6), 46–57.
Flint, M., Polycarpou, M., & Fernandez-Gaucherand, E. (2002). Cooperative control for multiple autonomous UAV’s searching for targets. In Proceedings of IEEE Conference on Decision and Control (CDC), pp. 2823–2828.
Flushing, E. F., Kudelski, M., Gambardella, L. M., & Caro, G. A. D. (2013). Connectivity-aware planning of search and rescue missions. In Proceedings of IEEE international symposium on safety, security, and rescue robotics (SSRR), pp. 1–8.
Frazzoli, E., Dahleh, M., & Feron, E. (2002). Real-time motion planning for agile autonomous vehicles. Journal of Guidance, Control, and Dynamics, 25(1), 116–129.
Gan, S. K., & Sukkarieh, S. (2011). Multi-UAV target search using explicit decentralized gradient-based negotiation. In Proceedings of IEEE international conference on robotics and automation (ICRA), pp. 751–756.
Goddemeier, N., Daniel, K., & Wietfeld, C. (2012). Role-based connectivity management with realistic air-to-ground channels for cooperative UAVs. IEEE Journal on Selected Areas in Communications, 30(5), 951–963.
Grøtli, E. I., & Johansen, T. A. (2012). Task assignment for cooperating UAVs under radio propagation path loss constraints. In Proceedings of American control conference (ACC), pp. 3278–3283.
Hayat, S., Yanmaz, E., & Bettstetter, C. (2015). Experimental analysis of multipoint-to-point UAV communications with IEEE 802.11n and 802.11ac. In Proceedings of IEEE international symposium personal, indoor and mobile radio communication.
Hayat, S., Yanmaz, E., Brown, T., & Bettstetter, C. (2017). Multi-objective UAV path planning for search and rescue. In Proceedings of IEEE international conference on robotics and automation (ICRA), pp. 5569–5574.
Hayat, S., Yanmaz, E., & Muzaffar, R. (2016). Survey on unmanned aerial vehicle networks for civil applications: A communications viewpoint. IEEE Communications Surveys & Tutorials, 18(4), 2624–2661.
Henkel, D., & Brown, T. (2006). On controlled node mobility in delay-tolerant networks of unmanned aerial vehicles. In Proceedings of international symposium on advanced radio technologies, pp. 1–10.
Hoeing, M., Dasgupta, P., Petrov, P., & OHara, S. (2007). Auction-based multi-robot task allocation in comstar. In Proceedings of the 6th international joint conference on autonomous agents and multiagent systems. Association for Computing Machinery, New York, NY, USA, AAMAS 07. https://doi.org/10.1145/1329125.1329462.
Hollinger, G. A., & Singh, S. (2012). Multirobot coordination with periodic connectivity: Theory and experiments. IEEE Transactions on Robotics, 28(4), 967–973.
Jin, Y., Liao, Y., Polycarpou, M. M., & Minai, A. A. (2006). Balancing search and target response in cooperative unmanned vehicle teams. IEEE Transactions on Systems, Man and Cybernetics, 36(3), 571–587.
Kantaros, Y., & Zavlanos, M. M. (2016). Distributed communication-aware coverage control by mobile sensor networks. Automatica, 63(C), 209–220.
Khan, A., Yanmaz, E., & Rinner, B. (2015). Information exchange and decision making in micro aerial vehicle networks for cooperative search. IEEE Transactions on Control of Network Systems, 2(4), 335–347.
Kovacina, M., Palmer, D., Yang, G., & Vaidyanathan, R. (2002). Multi-agent control algorithms for chemical cloud detection and mapping using unmanned air vehicles. In Proceedings of IEEE/RSJ international conference on intelligent robots and systems (IROS), pp. 2782–2788.
Latombe, J. C. (1991). Robot motion planning. The Springer international series in engineering and computer science. Boston, MA: Springer.
Lemaire, T., Alami, R., & Lacroix, S. (2004). A distributed tasks allocation scheme in multi-UAV context. In Proceedings of IEEE international conference on robotics and automation (ICRA), pp. 3622–3627.
Lin, L., & Goodrich, M. A. (2009). UAV intelligent path planning for wilderness search and rescue. In Proceedings of IEEE/RSJ international conference on intelligent robots and systems (IROS), pp. 709–714.
Messous, M. A., Senouci, S. M., & Sedjelmaci, H. (2016). Network connectivity and area coverage for UAV fleet mobility model with energy constraint. In Proceedings of IEEE wireless communications and networking conference (WCNC).
Mitchell, M. (1998). An introduction to genetic algorithms. Cambridge: MIT Press.
Otte, M., Kuhlman, M. J., & Sofge, D. (2019). Auctions for multi-robot task allocation in communication limited environments. Autonomous Robots, 44, 547–584.
Parker, L. E. (1998). Alliance: an architecture for fault tolerant multirobot cooperation. IEEE Transactions on Robotics and Automation, 14(2), 220–240. https://doi.org/10.1109/70.681242.
Poduri, S., & Sukhatme, G. S. (2004). Constrained coverage for mobile sensor networks. In Proceedings of IEEE international conference on robotics and automation (ICRA), pp. 165–172.
Ponda, S., Redding, J., Choi, H. L., How, J. P., Vavrina, M., & Vian, J. (2010). Decentralized planning for complex missions with dynamic communication constraints. In Proceedings of American control conference (ACC), pp. 3998–4003.
Potvin, J. Y. (2009). A review of bio-inspired algorithms for vehicle routing. Bio-inspired Algorithms for the Vehicle Routing Problem, 161, 1–34.
Scherer, J., & Rinner, B. (2016). Persistent multi-UAV surveillance with energy and communication constraints. In Proceedings of IEEE international conference on automation science and engineering (CASE), pp. 1225–1230.
Scherer, J., & Rinner, B. (2017). Short and full horizon motion planning for persistent multi-UAV surveillance with energy and communication constraints. In Proceedings of IEEE/RSJ international conference on intelligent robots and systems (IROS), pp. 230–235.
Scherer, J., Yahyanejad, S., Hayat, S., Yanmaz, E., Andre, T., Khan, A., et al. (2015). An autonomous multi-UAV system for search and rescue. In Proceedings of workshop on micro aerial vehicle networks, systems, and applications for civilian use, DroNet ’15, pp. 33–38.
Schleich, J., Panchapakesan, A., Danoy, G., & Bouvry, P. (2013). UAV fleet area coverage with network connectivity constraint. In Proceedings of ACM international symposium on mobility management and wireless access. MobiWac, ACM, New York, NY, USA, pp. 131–138, https://doi.org/10.1145/2508222.2508225.
Tisdale, J., Kim, Z., & Hedrick, J. (2009). Autonomous UAV path planning and estimation. IEEE Robotics & Automation Magazine, 16(2), 35–42.
Vincent, P., & Rubin, I. (2004). A framework and analysis for cooperative search using UAV swarms. In Proceedings of ACM symposium on applied computing, pp. 79–86.
Waharte, S., & Trigoni, N. (2010). Supporting search and rescue operations with UAVs. In Proceedings of international conference on emerging security technologies (EST), pp. 142–147.
Yahyanejad, S., Misiorny, J., & Rinner, B. (2011). Lens distortion correction for thermal cameras to improve aerial imaging with small-scale UAVs. In 2011 IEEE international symposium on robotic and sensors environments (ROSE), pp. 231–236, https://doi.org/10.1109/ROSE.2011.6058528.
Yan, Y., & Mostofi, Y. (2014). Efficient communication-aware dynamic coverage using space-filling curves. In Proceedings of American control conference (ACC), pp. 964–971.
Yanmaz, E. (2012). Connectivity versus area coverage in unmanned aerial vehicle networks. In Proceedings of IEEE international conference on communication (ICC), pp. 719–723.
Yanmaz, E., & Guclu, H. (2010). Stationary and mobile target detection using mobile wireless sensor networks. In Proceedings of IEEE conference on computer communications (INFOCOM).
Yanmaz, E., Hayat, S., Scherer, J., & Bettstetter, C. (2014a). Experimental performance analysis of two-hop aerial 802.11 networks. In Proceedings of IEEE wireless communications and networking conference.
Yanmaz, E., Hayat, S., Scherer, J., & Bettstetter, C. (2014b). Experimental performance analysis of two-hop aerial 802.11 networks. In Proceedings of IEEE wireless communications and networking conference (WCNC), pp. 3118–3123.
Yanmaz, E., Kuschnig, R., & Bettstetter, C. (2013). Achieving air-ground communications in 802.11 networks with three-dimensional Aerial Mobility. In Proceeding of IEEE international conference on computer communications (INFOCOM), Mini conference, pp. 120–124.
York, G., & Pack, D. J. (2012). Ground target detection using cooperative unmanned aerial systems. Journal of Intelligent and Robotic Systems, 65(1), 473–478.
Zlot, R., Stentz, A., Dias, M. B., & Thayer, S. (2002). Multi-robot exploration controlled by a market economy. In Proceedings 2002 IEEE international conference on robotics and automation (Cat. No.02CH37292), Vol. 3, pp. 3016–3023, https://doi.org/10.1109/ROBOT.2002.1013690.
Acknowledgements
Open access funding provided by University of Klagenfurt.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The work was supported by the ERDF, KWF, and BABEG (Grant KWF-20214/24272/36084 (SINUS)). Part of this work is linked to the Karl Popper Kolleg on Networked Autonomous Aerial Vehicles at the University of Klagenfurt. Samira Hayat performed a research stay at Carnegie Mellon University sponsored by a research leave grant from the University of Klagenfurt.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hayat, S., Yanmaz, E., Bettstetter, C. et al. Multi-objective drone path planning for search and rescue with quality-of-service requirements. Auton Robot 44, 1183–1198 (2020). https://doi.org/10.1007/s10514-020-09926-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10514-020-09926-9