Merging of appearance-based place knowledge among multiple robots

Abstract

If robots can merge the appearance-based place knowledge of other robots with their own, they can relate to these places even if they have not previously visited them. We have investigated this problem using robots with compatible visual sensing capabilities and with each robot having its individual long-term place memory. Here, each place refers to a spatial region as defined by a collection of appearances and in the place memory, the knowledge is organized in a tree hierarchy. In the proposed merging approach, the hierarchical organization plays a key role—as it corresponds to a nested sequence of hyperspheres in the appearance space. The merging proceeds by considering the extent of overlap of the respective nested hyperspheres—starting with the largest covering hypersphere. Thus, differing from related work, knowledge is merged in as large chunks as possible while the hierarchical structure is preserved accordingly. As such, the merging scales better as the extent of knowledge to be merged increases. This is demonstrated in an extensive set of multirobot experiments where robots share their knowledge and then use their merged knowledge when visiting these places.

1 Introduction

Many robotic tasks such as exploration, rescue and monitoring will benefit from the cooperation of several robots in sharing their knowledge of places. The goal is to have each robot expand its place knowledge via incorporating other robots’ knowledge. As such, its spatial knowledge can become more comprehensive and the robot can relate to places even though it has not actually visited them previously. Appearances are integral to defining places since metric data may not be always available or reliable (Kostavelis and Gasteratos 2015; Lowry et al. 2016). However, how to manage the gathered visual place knowledge has been a major challenge. Related work in this area have been primarily based on merging the two maps (of two different robots) by finding the matching node pairs where each node encodes an appearance from a particular location. However, as the number of nodes increases, both scalability and reliability become problematic (Park and Roh 2016; Garcia-Fidalgo and Ortiz 2017). Furthermore, since such maps can become exorbitantly large, the resulting spatial knowledge is harder to utilize in future revisits.

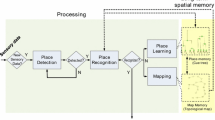
In this paper, we present a novel approach that considers only the merging of place knowledge. Each robot is assumed to have compatible visual sensing and to retain its appearance-based place knowledge in its long-term place memory. This is a memory in which each place refers to a spatial region as defined by a collection of appearances and the knowledge of all learned places is organized in a tree hierarchy (Erkent et al. 2017). In the proposed approach, place knowledge is merged based on long-term place memories. Any two robots can communicate, receive other’s long-term place memory and then incorporate the received knowledge into their respective place memories as shown in Fig. 1. The hierarchical organization of the place memory enables the merging process to be done in a completely different manner. This is because it defines a nested sequence of partitions of the learned places. In turn, these nested partitions correspond to a nested sequence of hyperspheres in the appearance space. Based on this observation, we propose a method in which merging proceeds by considering the extent of overlap of the respective nested hyperspheres—starting with the largest covering hyperspheres and proceeding down the smaller nested ones. This is achieved using a modified version of the RACHET algorithm (Samatova et al. 2002). The advantages of the proposed approach are three-fold: first, differing from most related work each robot incorporates other robot’s knowledge in as large chunks as possible. Thus, the method scales better as the extent of knowledge to be merged increases. Second, as merging is based only on the appearances, unlike the merging of metric maps, spatial relations among different places or robots’ poses are not needed. Hence, the proposed method can be used prior to map merging. Finally, as the number of places is considerably less than the number of associated appearances, the required comparison in the merging of the chunks is much more efficient.

Fig. 1

Each robot merges other robots’ long-term place memories with its own

The outline of the paper is as follows: first, we review related literature in Sect. 2. Next, the form of the place memories is explained in detail in Sect. 3. The merging process is explained in Sect. 4. Experimental results with a team of three robots operating in both indoor and outdoor environment are presented in Sect. 5. The paper concludes with a brief summary and future direction.

2 Related literature

One of the major paradigms in distributed intelligence is a knowledge-based paradigm where the focus is on knowledge sharing among robots (Parker 2008). As discussed, place knowledge is primarily based on appearances (Lowry et al. 2016; Kostavelis and Gasteratos 2015). Even if the connection between places and appearances is subject to indiscriminate boundaries, appearance variability and perceptual aliasing, appearances are the primary environmental feedback since metric data may be unavailable as is the case in gps-denied areas such as indoors or kidnapped robots or unreliable as is the case with odometry. The use of appearances is also motivated by human vision (Matlin 2005).

Related work has primarily focused on how to merge the individual maps of the robots (Lee and Lee 2011). In this work, the goal is to have each robot expand its map as it gets knowledge from another robot. Let it be noted that this problem is different from large-scale mapping (Estrada et al. 2005; Thrun and Montemerlo 2006; Grisetti et al. 2010) or cooperative mapping (Huang and Beevers 2005; Zhou and Roumeliotis 2006; Nieto-Granda et al. 2014) where multiple robots concurrently and continuously contribute their data to a single map. In the former, a single robot tries to integrate multiple maps into one large-scale map while in the latter, multiple robots concurrently and continuously maintain and contribute to a single shared map. The proposed methods in map merging vary depending on whether the appearance data is augmented with metric data (metric) or not (purely appearance-based) and how much is known about robots’ positions.

Metric approaches are categorized depending on whether they require metric data to be directly available or not. In direct metric approaches, robots are assumed to know the initial poses of the other robots (Leung et al. 2011; Aragues et al. 2012) or that they can identify, rendezvous and communicate with each other when in line of sight (Thrun et al. 2000; Williams et al. 2002; Konolige et al. 2003; Ko et al. 2003; Howard 2004; Ozcukur et al. 2009; Gil et al. 2010; Nieto-Granda et al. 2014). If pose information is not reliable or unavailable, it is estimated using localization methods. However, both accuracy and reliability are known to be problematic in large-scale localization (Park and Roh 2016). Alternatively, with indirect metric methods, individual maps are merged via aligning them using a variety of approaches such as random walks, laser scan integration methods or genetic algorithms (Carpin et al. 2005; Birk and Carpin 2006; Amigoni et al. 2006; Adluru et al. 2008; Ma et al. 2008; Tungadi et al. 2010; Marjovi et al. 2012; Tomono 2013). However, the merging process has proven to be costly. In order improve the merging efficiency, different methods such as pose-graph matching are proposed (Tomono 2013; Carpin 2008; Lee and Lee 2011; Saeedi et al. 2014). However, in these methods, usually it is required that the initial positions of the robots are close to each other in order to merge the maps reliably.

Purely appearance-based approaches on the other hand assume that the robots have no explicit position/odometry information. The lack of position data may be due to unreliable (dead reckoning) or unavailable (i.e. being kidnapped, GPS-less environments) position data as well as problematic localization. Here, maps are merged by finding correspondences among different nodes in the two maps. Nodes are considered one-by-one and matched against those of the other—possibly using their connectedness relations. The proposed approaches vary in how appearances are represented and matched with representation schemes varying from local features (Ho and Newman 2005; Huang and Beevers 2005; Ferreira et al. 2008; Marjovi et al. 2012) to global features (Erinc and Carpin 2014). In all, as the number of appearances increases, scalability becomes problematic. Furthermore, a more conceptual definition of a ‘place’  as a visually or physically coherent spatial unit is preferable—as this would facilitate the matching process (Park and Roh 2016).

In this paper, we introduce a novel approach to the merging of place knowledge. The merging efficiency of the proposed approach is comparably much better than the previous approaches due to three reasons. First, since merging is based on the determining the overlap of the hyperspheres in the appearance space starting with the top of the hierarchy, the knowledge is merged in as large chunks as possible. Thus, it is very different from most merging approaches where pairs of places need to be processed one-by-one. Second, with our definition of a ‘place’, as the number of places is considerably less than the number of associated appearances, the required comparison in the merging of the chunks is much more efficient. Finally, as merging is based only on the appearances associated with places, unlike the merging of maps, spatial relations among different places or robots’ poses need not to be considered. Hence, the proposed method can be used prior to map merging. The core of this approach has been previously presented in Karaoguz and Bozma (2016b). Here we extend this work in two aspects: first, we present the details of the algorithms for merging place memories and topological maps. Second, we also present a more comprehensive evaluation of the approach using benchmark indoors and outdoor visual data and also include a study of performance as compared to that of direct experience.

Fig. 2

Place memory $T^X$ of a robot jX

3 Long-term place memory

Each robot is assumed to retain its appearance-based place knowledge in its long-term place memory. Let ${\mathcal {P}}$ denote the known places. This knowledge may have been accumulated either through direct experience¹ or through previous rounds of learning from other robots. The accumulation of knowledge in the long-term place memory has been presented previously in Erkent et al. (2017). Two of its features are integral to the merging of appearance-based place knowledge. As such, long-term visual place memory can be viewed as complementing map memory (commonly referred to as metric or topological map) that encodes the spatial relations among different places.

3.1 Places and hierarchical organization

The first feature is related to what is meant by a place. In this memory, each place $p \in {\mathcal {P}}$ refers to a specific area or region. As such it differs from most related work that considers each place to be a specific location. It is defined by a collection of appearances from a multitude of base points $x_j(p)$ (varying in position and heading) as indexed by $j \in {\mathcal {X}}(p)$. If the odometric information is not available or is unreliable, the coordinates of the base point $x_j(p)$ are not known explicitly—as is assumed here. Sample appearances from sample places are shown in Fig. 2a. The robot internally encodes each appearance by a d-dimensional descriptor $\left\{ I(x_j) \right\} _{j \in {\mathcal {X}}(p)}$. Let ${\mathcal {C}}$ denote the resulting set of descriptors.

$$\begin{aligned} {\mathcal {C}}= \bigcup _{{\mathop {}\limits ^{p \in {\mathcal {P}}}}} \left\{ I (x_{j}(p)) \mid j \in {\mathcal {X}}(p) \right\} \end{aligned}$$

The descriptors can be based on a suitable representation scheme. The only restriction is that similar appearances generate similar descriptors.² Here, we use the previously proposed bubble space representation (Erkent and Bozma 2013). Bubble descriptors³ are rotationally invariant descriptors that simultaneously encode a set of visual features and their relative $S^2$ geometry from an egocentric perspective. We prefer to use this representation due to its demonstrated advantages such as incorporating any number of observations while allowing incremental computation. However, it should be emphasized that the developed system is in no way dependent on this particular choice and thus can be used with any suitable descriptors—as preferred. As the robot navigates through a sequence of base points $x_{k}$, $k \in {\mathcal {K}}$ with ${\mathcal {K}}$ being the index set, place detection—namely determining where a place starts and ends—can be done either by external guidance or autonomously. We consider the latter case and use a method⁴ as presented in Karaoguz and Bozma (2014) based on the iterative clustering of the index set ${\mathcal {K}}$—considering the informativeness, coherency and plenitude of the incoming sequence of appearances as determined by processing the associated descriptors. Consequently, the index set ${\mathcal {K}}$ is partitioned so that appearances belonging to each distinct place are grouped together as $D\subset {\mathcal {K}}$—referred to as a detected place. The detected place is then associated with the descriptor ${\bar{I}}_D = \frac{1}{\left| D\right| } \sum _{k \in D} I(x_k)$ based on the collected appearances from $\left| D\right|$ locations.

The second feature pertains to how knowledge is organized. In particular, the place memory has a tree organization T as shown in Fig. 2b. The hierarchy is defined by a nested sequence of partitions of the learned places ${\mathcal {P}}$. The outer partition corresponds to the root node and represents all the learned places ${\mathcal {P}}$. Inner partitions define a set of inner nodes where each node N corresponds to a cluster ${\mathcal {P}}(N) \subset {\mathcal {P}}$ of places while a terminal node corresponds to a distinct place—namely ${\mathcal {P}}(N) =\left\{ p\right\}$ where $p \in {\mathcal {P}}$. The partitions are defined based on the similarity of collected appearances ${\mathcal {C}}$. The root node is associated with the whole set while each other node N is associated with the set ${\mathcal {C}}(N) \subset {\mathcal {C}}$ of descriptors:

$$\begin{aligned} {\mathcal {C}}(N) = \bigcup _{{\mathop {}\limits ^{p \in {\mathcal {P}}(N)}}} \left\{ I (x_{j}(p)) \mid j \in {\mathcal {X}}(p) \right\} \end{aligned}$$

The hierarchy is built considering the similarity of appearances associated with the nodes—starting with the terminal nodes. The similarity of a node N to another $N^\prime$ is measured by the proximity ${\tilde{\gamma }}$ of their centroids:

$$\begin{aligned} {\tilde{\gamma }}(N, N^{\prime }) = \left\| c(N)-c(N^\prime )\right\| ^2 \end{aligned}$$

(1)

where c(N) is the centroid descriptor defined as:

$$\begin{aligned} c(N) = \frac{1}{ \left\| {\mathcal {P}}(N) \right\| }\displaystyle \sum _{p \in {\mathcal {P}}(N)} {\bar{I}}_{p} \end{aligned}$$

The interested readers are kindly referred to Erkent et al. (2017) for further details.

Whenever a place D is detected, the robot then attempts to recognize it as one of the learned places $p \in {\mathcal {P}}$ via relating the collected appearances to its place memory. Memory association is done via traversing down the hierarchy starting at the root node and comparing the appearances associated with a newly detected place D with the knowledge in the respective nodes. The decision-making at each node N is based on finding the child node having the minimum cost function $g_N(D)$. The cost function is a heuristically defined discriminant function that measures how likely the detected place D is to be associated with the $N^1(D) \in N^\downarrow$ of children nodes N that is most similar to D in the hierarchy:

$$\begin{aligned}&g_N(D) = {\tilde{\gamma }}(D,N^1(D)) + (1 - \xi (D, N^1(D))) \nonumber \\&\quad + \frac{{\tilde{\gamma }}(D,N^1 (D))}{{\tilde{\gamma }}(D,N^{2}(D))} \end{aligned}$$

(2)

The first term measures the similarity of a place D to the offspring node of $N^1(D)$ where

$$\begin{aligned} N^1(D)&\in {{{\,\mathrm{\hbox {arg min}}\,}}_{N^\prime \in N ^\downarrow } {\tilde{\gamma }}(D,N^\prime )} \end{aligned}$$

(3)

A higher value ${\tilde{\gamma }}(D,N)$ indicates the detected place D to be less similar to the places associated with node N. The second term also measures the similarity of detected place D to the offspring node $N^1(D)$, but now considering the overlap of the corresponding hyperspheres. This is based on the function $\xi$ that measures the overlap amount as defined in “Appendix B”. The third term indicates the reliability of comparing with $N^1(D)$ by considering $N^{2}(D)$—namely the offspring node of N that is second most similar to D as:

$$\begin{aligned} N^2(D)&\in {{{\,\mathrm{\hbox {arg min}}\,}}_{N^\prime \in N^\downarrow - N^1(D)} {\tilde{\gamma }}(D,N^\prime )} \end{aligned}$$

(4)

If the detected place D is found to be appearance-wise similar to both of the places $N^1(D)$ and $N^2(D)$, then this term increases. The minimum cost value is checked against an association threshold $\tau _r$ that is manually set:

$$\begin{aligned} g_N(D) \le \tau _r \end{aligned}$$

(5)

In the case this condition is satisfied and $N^1(D)$ is a terminal node, then the detected place D is merged with $N^1(D)$, otherwise the traversal goes to the next level. This is repeated until a terminal node is reached. If the case is not satisfied, the robot invokes place learning in order to add the detected place D into its place memory.

3.2 Place memory versus map-based approaches

The concept of ‘place memory’  may be better conceived after a qualitative comparison with an map-based approach such as FAB-MAP (Cummins and Newman 2011). While both models use only appearance-data and thus appear to be related, in fact they are of quite different nature as summarized in Table 1. The starting point for this discrepancy is the difference in the respective definitions of ‘place’. In our definition of place memory, each place is defined by a collection of appearances having common perceptual signatures. This is in contrast to map-based approaches where each different location is treated as a different place. For example, in one of the experiments as discussed in Sect. 5, while the first robot has collected appearances from 997 locations, it has learned them as 8 places. In parallel, while the second robot has collected visual data from 3200 locations, it has retained this knowledge as 13 places. Places are determined using a place detection algorithm⁵ (Chella et al. 2007; Karaoguz and Bozma 2014). Furthermore, the knowledge of learned places is organized in a tree hierarchy. Such an organization should not be confused with that used for obtaining the visual vocabulary in map-based methods. Note that while there have been hierarchical map-based approaches, as the hierarchy is in metric space, it is used to proceed from coarse to fine localization (Galindo et al. 2005; Beeson et al. 2010; Park and Roh 2016; Garcia-Fidalgo and Ortiz 2017). In contrast, in place memory, since the hierarchical organization is defined in the appearance space, it enables the robot to efficiently retrieve and store its place knowledge. Thus, place memory can enable semantic association—which is not the case in map-based approaches. With place association or recognition, the robot determines its whereabouts coarsely. In contrast, with map-based approaches, the aim is loop-closure with fine localization. Such a reasoning is possible even if the robot does not have any metric information or knowledge of their spatial relations—as may be the case when it is starting a mission, has unreliable odometry or is kidnapped.

Table 1 Comparison of place knowledge: place memory versus map-based

Fig. 3

Place memories of robots m and n, respectively. Robot m knows 6 places while robot n knows 3 places. Note that an identical index across both memories will not necessarily refer to the same place

4 Merging place memories

Consider a robot m that has learned ${\mathcal {P}}^m$ places as retained in its place memory $T^m$. A sample place memory $T^m$ is as shown in Fig. 3a. It is observed that robot’s knowledge of 6 places is organized in a 4-level hierarchy. Suppose it has communicated with robot n with a place memory $T^n$. Suppose $T^n$ is as shown in Fig. 3b. This memory contains 3 places as organized in a 3-level hierarchy. Note that an identical index across both memories does not necessarily refer to the same place. The goal of merging is to incorporate $T^n$ into $T^m$ as:

$$\begin{aligned} T^m(k^m+1) \leftarrow T^m(k^m) \oplus T^n(k^m) \end{aligned}$$

where $k^m$ denotes the update index of robot m and $\oplus$ denotes the merging operator. In the sequel, we will omit update index $k^m$ for notational simplification. There are three requirements for the merging of robot m’s own place memory $T^m$ with place memory $T^n$ of another robot n.

• First, it should incorporate all the places known by the other robot, but not known by itself ${\mathcal {P}}^n - {\mathcal {P}}^m$. As such, the robot learns new places without duplication.

• If possible, it should incorporate the knowledge of places that are also known by the other robot ${\mathcal {P}}^m \bigcap {\mathcal {P}}^n$. As such, the robot augments its knowledge of such places.

• Finally, the resulting place memory $T^m(k^m+1)$ should be comparably similar to the place memory that is generated by visiting all the places individually ${\mathcal {P}}^m \cup {\mathcal {P}}^n$ since the revisited places should be merged into one in both cases. The advantage of the merged memory $T^m(k^m+1)$ is that the whole area is covered faster in a distributed fashion and the resulting place hierarchy will be almost the same.

Our proposed approach is based on the observation that the nested sequence of partitions that define the tree structure corresponds to a nested sequence of hyperspheres in the d-dimensional appearance space. Thus, each node N in the hierarchy $T^m$ is associated with a d-dimensional hypersphere $S(c_m(N),\rho _m(N)) \subset R^{d}$ with centroid $c_m(N)$ and radius $\rho _m(N)$:

$$\begin{aligned} c_m(N)= & {} \frac{1}{ \left| {\mathcal {P}}^m(N) \right| }\displaystyle \sum _{p \in {\mathcal {P}}^m(N)} {\bar{I}}_{p}\\ \rho _m^2(N)= & {} \frac{1}{ \left| {\mathcal {P}}^m(N)\right| ^2} \displaystyle \sum _{p \in {\mathcal {P}}^m(N)} \left\| {\bar{I}}_{p} - c_m(N) \right\| ^2 \end{aligned}$$

Here, recall that ${\mathcal {P}}^m(N) \subseteq {\mathcal {P}}^m$ is the set of places associated with the subtree of $T^m$ having node N as its root. The radius $\rho _m(N)$ is defined as the average squared Euclidean distance of the associated children nodes from the centroid of N, it serves to measure the size of the respective hypersphere. If N is the root node, then the hypersphere $S(c_m(N),\rho _m(N))$ is a covering in the d-dimensional appearance space for the whole place memory $T^m$. Let this hypersphere be denoted by $S(c_m,\rho _m)$ for simplicity of notation. Otherwise, it is a covering for the subtree of $T^m$ having node N as its root. Any nested hypersphere is related to $S(c_m,\rho _m)$ as:

$$\begin{aligned} S(c_m(N),\rho _m(N)) \subseteq S(c_m,\rho _m) \end{aligned}$$

The merging of place memories is then based on the extent and nature of overlap of the respective nested sequence of hyperspheres in the appearance space. This is because any overlap indicates overlap of respective knowledge. For this, we use a modified version of ‘RACHET’  algorithm (Samatova et al. 2002). This is a distributed hierarchical clustering algorithm that is known to satisfy all the three requirements. The original algorithm is summarized in “Appendix C”. It starts from the root nodes in the two hierarchies $T_m$ and $T_n$ and proceeds to the children nodes $N \in T_m$ and $N^\prime \in T_n$ as necessary. The subtrees corresponding to the non-overlapping hyperspheres are simply added together while subtrees corresponding to overlapping hyperspheres are combined depending on the extent of their overlap. As such, while new knowledge is learned, duplication of knowledge is minimized. In the latter case, the robot needs to determine the overlap among the two place memories. There may be a multitude of overlap regions depending on the overlap of the robots’ knowledge. We have modified this algorithm as given in Algorithm 1. First, instead of comparing all inner nodes, we start by comparing the hyperterminals in order to couple them for merging. A hyperterminal is either an inner node that has terminal nodes as children or the union of all children nodes of an inner node that are terminal nodes themselves. For example, there are three hyperterminals in the place memory in $T^m$ of robot m while $T^n$ has two hyperterminals. While merging $T^m$ into $T^n$, each hyperterminal $N^\prime \in T^n$, is paired with a hyperterminal node $N^*\in T^m$ where their hyperspheres overlap maximally—namely

$$\begin{aligned} N^{*} \in \arg \displaystyle {\max _{N \in T^m}} \left| S(c_m(N), \rho _m(N)) \cap S(c_n(N^\prime ), \rho _n(N^\prime )) \right| \nonumber \\ \end{aligned}$$

(6)

The amount of overlap is computed as explained in “Appendix B”. As this is not done for each terminal node separately, there is an increased computational efficiency. Second, in contrast to making the merge decision of two nodes based only on the percentage of the hypersphere overlap, the robots also consider associating the terminal nodes of the maximally overlapping hyperterminals as explained in Sect. 3. Each computation is actually very simple—it involves associating the terminal nodes $N^{*T}$ with the terminal nodes $N^{'T}$ by evaluating the cost function $g_{N^{*}}(N^{'T})$ as given in Eq. 2 with $N={N^{*T}}$ and $D=N'^{T}$. In case of association, the place knowledge is updated. Otherwise, it is learned as a new place via adding it as a terminal node of $N^*$. As such, while redundancy is minimized, the hierarchy of the place memory is preserved as much as possible. Note that as such, each robot is able to handle multiple mergings over time. Namely, if a robot merges another robot’s place memory with its own, and then later does the same thing after covering more territory, the organization of the place memory will change only depending on the new place knowledge—as places learned previously will be recognized—pending on the similarity of their appearances to past experiences.

Fig. 4

Merging of place memories

4.1 Non-overlapping hyperspheres

First, we consider the case in which there is no knowledge common to both of the robots. This occurs when the places ${\mathcal {P}}^m$ known by the robot m are appearance-wise completely different from those ${\mathcal {P}}^n$ of the other robot. Of course, the robots do not know this when they exchange their place memories. This manifests itself with the two corresponding hyperspheres not intersecting at all as shown in Fig. 4a:

$$\begin{aligned} S(c_m, \rho _m) \cap S(c_n, \rho _n) = \emptyset \end{aligned}$$

This can be checked as follows:

$$\begin{aligned} \left\| c_m - c_n \right\| ^2 > (\rho _m+\rho _n)^2 \end{aligned}$$

(7)

The merged place memory is simply the union of two respective memories as shown in Fig. 4c. From the perspective of the individual robots, the resulting place memories are identical—namely

$$\begin{aligned} T^m(k^m+1)= & {} T^n(k^n+1) \end{aligned}$$

Thus, in case of no overlap, the memory hierarchies are preserved.

4.2 Intersecting hyperspheres

Alternatively, we also consider the case in which some of the place knowledge is common to both of the robots. For example, some parts of the knowledge may be overlapping while some are completely different. In this case, the two hyperspheres partially or fully overlap with each other as shown in Fig. 4b:

$$\begin{aligned} S(c_m, \rho _m) - S(c_n, \rho _n)\ne & {} \emptyset \\ S(c_n, \rho _n) - S(c_m, \rho _m)\ne & {} \emptyset \end{aligned}$$

This can be checked as:

$$\begin{aligned} \left\| c_m - c_n \right\| ^2 \le (\rho _m + \rho _n)^2 \end{aligned}$$

The amount of commonality can vary from the perspective of each robot as well. A special case is when one of the robots already knows all the places known by the other robot. This results in one hypersphere being completely contained within the other. It has a simpler check as:

$$\begin{aligned} \left\| c_m - c_n \right\| ^2 \le (\rho _m-\rho _n)^2 \end{aligned}$$

(8)

The restructuring of the individual hierarchies depends on the overlap of the respective knowledge. However, the RACHET algorithm enables a restructuring that is minimal whenever possible.

Note that the learning order does not change the descriptive statistics of the resulting hyperspheres (Samatova et al. 2002). However, this does not necessarily hold for the resulting hierarchies—namely $T^m \ne T^n$ in general. To see this, consider $T^m \leftarrow T^m \oplus T^n$ and $T^n \leftarrow T^n \oplus T^m$. Note that $T^m = T^n$ iff

• (i) $S(c_m,\rho _m) = S(c_n,\rho _n)$

• (ii) $\forall N \in T^m, \exists N^\prime \in T^n \text{ s.t. } S(c_m(N),\rho _m(N)) = S(c_n(N^\prime ),\rho _n(N^\prime ))$

• (iii) $\forall N^\prime \in T^n, \exists N \in T^m \text{ s.t. } S(c_n(N^\prime ),\rho _n(N^\prime )) = S(c_m(N),\rho _m(N))$

Even if condition (i) holds, in general, this will not be the case for conditions (ii) and (iii). Thus, the resulting place memory of robot m after the knowledge transfer from robot n to robot m will not be the same as the place memory of robot n after the knowledge transfer from robot m to robot n. Surprisingly, this implies the organization of prior knowledge is integral to the shaping of incoming new knowledge.

4.3 Merging efficiency

The computational efficiency of the proposed merging process is due to two factors. First, as the merging is done considering the overlap of the nested hyperspheres in the appearance space, its merging complexity depends on the overlap and the structure of the respective place memories. Both are designated by the statistics of the associated hyperspheres, the number of hyperterminals h and the number of terminal nodes belonging to the hyperterminals as denoted by $\left| N^*\right|$ and $\left| N^\prime \right|$, respectively. If there is no knowledge overlap, the merging complexity is constant O(1). In case of overlap, the merging complexity of a pair of hyperterminals will be $O( h^2 + h \left| N^*\right| \left| N^\prime \right| )$. This is comparably much smaller than comparing appearances with complexity $O( \sum _{p=1}^{\left| {\mathcal {P}}^m\right| } M_p \sum _{q=1}^{\left| {\mathcal {P}}^n\right| } M_q)$ or comparing places simply with complexity $O (\left| {\mathcal {P}}^m\right| \left| {\mathcal {P}}^n\right| )$—since both h and $\left| N^*\right|$,$\left| N^\prime \right|$ will be in general much smaller that $\left| {\mathcal {P}}^m\right|$ and $\left| {\mathcal {P}}^n\right|$ respectively. Second, the definition of a place enables efficiency—since the number of places known by each of the robot is considerably smaller than the number of appearances. For example, in one set of experiments, while the first robot has collected appearances from altogether 997 locations, it has learned them as 8 places. In parallel, while the second robot has collected visual data from 3200 locations, it has retained this knowledge as 13 places. Note that with typical map-based approaches, merging would require matching appearances from 997 locations with those from 3200 base points—if each location is viewed as a distinct place. On the other hand, with our definition of place, merging requires the matching of 8 places of the first robot with the 13 places of the second robot.

Moreover, our approach is not communication intensive, as such, the information exchange will only occur on-demand or periodic intervals. As a result, the communication bandwidth will not be allocated for long periods.

4.4 Merging (topological) maps

The merging of place memories also enables the robots to merge their respective topological maps more efficiently. Let topological maps of robots m and n be denoted respectively by the graphs $G^m = ({\mathcal {P}}^m, E ^m)$ and $G^n = ({\mathcal {P}}^n, E ^n)$ where $E ^m$ and $E ^n$ denote the edges existing among the nodes ${\mathcal {P}}^m$ and ${\mathcal {P}}^n$. Note that these correspond to simple adjacency relations.⁶ The merged topological map $G^m(k^m+1)$ is required to satisfy the following:

• First, it should incorporate places known by either while not duplicating common places.

• Second, it should incorporate the spatial relations known to either.

The merging of topological maps is simplified by the merging of the place memories. If the robot can associate a place $P^\prime \in {\mathcal {P}}^n$ known by the other robot to its place memory $T^m(k_m)$, no node addition is done. Memory association is done as described in Sect. 3. Otherwise, a new node is added to $G^m(k^m+1)$. The associated edges are checked to determined if they exist in $E ^m(k_m)$ and are added if necessary. The merging process is summarized in Algorithm 2.

Fig. 5

Learned places non-overlapping

Fig. 6

Learned places mostly overlapping

Fig. 7

Learned places are partially overlapping

5 Experiments

We have conducted extensive experiments using a team of three robots—referred to as jX, jY and jZ respectively. At the beginning of experiments, each robot has its individual long-term place memory. The robots have learned places from direct experience either by using the images collected while navigating in the campus in a tele-operated manner or from the COLD data set (Pronobis and Caputo 2009). All the appearance data have been obtained using perspective cameras, but with possibly different intrinsic and extrinsic parameters. Furthermore, as their fields of view are limited, the appearances at any location may be completely different depending on the robot’s heading. Each robot encodes each incoming appearance with a $d=600$-dimensional bubble descriptor. Learning through direct experience is based on the previously introduced topological spatial cognition (TSC) model (Karaoguz and Bozma 2016a). For ease of visualization, places learned by each robot are identified uniquely as jX:i, jX:k and jZ:l where i, k, l are their indices. We consider the results of merging with varying cases of place knowledge overlap and also evaluate recognition performance with the resulting merged place memories as well as a comparative study with direct learning of places from experience.

5.1 Learned places non-overlapping

This is when two robots navigate in areas with almost no overlap. Here, the expected result is to have both place memories merged from the top node since none of the hyperspheres should be overlapping with each other. In the experiment, robots jX and jZ visit two different sites with no overlaps. Of course, the robots do not know this.

Robot jX knows 13 places based on data collected from 3200 base points along a 175 m path as shown in Fig. 2a. Note that since it returns to where it is started at the end of the tour, the last detected place is recognized as 5th place which is correct. The hypersphere associated with $T^X$ has radius $\rho _{X}=0.478$. Robot jZ has visited the Saarbrucken (Sa) site from the COLD data set and knows 8 places based on appearances collected at 997 base points in a 50 m tour. The associated hypersphere has radius $\rho _{Z}=0.607$. The squared Euclidean distance between the two respective hyperspheres $\left\| c_{X} - c_{Z} \right\| ^2= 1.6118$ is larger than the squared sum of radii $(\rho _{X}\oplus \rho _{Z})^2 = 1.1772$ which satisfies the condition for non-overlapping hyperspheres. The memories $T^X \leftarrow T^X \oplus T^Z$ and $T^Z \leftarrow T^Z \oplus T^X$ resulting from their merging are identical and are as given in Fig. 5b. It is observed that the places of both sites are separated from the top root node. The left subtree corresponds to the place memory of the robot jX prior to merging while the right subtree corresponds to that of the second robot again prior to merging.

Table 2 Descriptive statistics of hyperspheres $S^X$, $S^Y$ and $S^Z$

Fig. 8

Merged place memories–learned places partially overlapping

5.2 Learned places mostly overlapping

Next, we consider when the learned places are overlapping, but one of the robots covers a larger area. Again, the first robot jX has the same place knowledge from the previous case with 13 places based on appearances from 3200 locations along a 175 m path as shown in Fig. 2a. The second robot jY navigates along a longer path similar to robot jX. Its place memory $T^Y$ contains 15 places with radius $\rho _{Y}=0.8445$ based on appearances from 2550 locations. Note that due to variation of appearances based on heading, robot jX and jY detect different number of places. From the perspective of robot jY, the resulting place memory is as shown in Fig. 6. Here, blue nodes represent the places learned by jX while green nodes represent that of jY. Orange nodes indicate the merged place knowledge. For analysis, the actual correspondences between the learned places of robot jX and jY are given in Fig. 6c. The squared Euclidean distance $\left| c_{X} - c_{Y} \right\| ^2= 0.2150$ between the respective hyperspheres is smaller than $\rho _{Y}$. This shows that the place memory of the jY fully covers that of jX. Note that while most of the appearance-wise corresponding places are actually at the same geometric locations, there are also few exceptions. For example, while places jX:3 and jX:4 appear similar to jY:3 and jY:4, they are actually from different physical locations. On the other hand, places jY:10, jY:11, jY:12, jY:13 and jY:14 that are visited only by robot jY do not have any appearance-wise correspondence in ${\mathcal {P}}^X$. As such, we expect the merged memories to contain about 15 places. With association threshold $\tau _r=2$, the merged place memory $T^Y \leftarrow T^Y \oplus T^X$ of robot jY is as shown in Fig. 6d. It contains 18 places. Note that this is the same for robot jX since its place memory is updated as $T^X \leftarrow T^Y \oplus T^X$. It is observed that six of these places are correctly merged. Some of them are merged with nearby places whose appearances are very similar. As such, these mergings are also acceptable. Examples include jX:7 and jX:9. The robot wrongly adds places jX:1, jX:2 and jX:3 as new places. This is attributed to the fact that with limited field of views, appearances change drastically as the traversal heading changes. Perceptual aliasing is also an issue. For example, the robot finds places jX:12 and jX:13 to be the same as jY:4 and jY:2. This is expected since all of these places are views of the garden area with similar vegetation and trees.

5.3 Learned places partially overlapping

We also consider the case when robots visit places that are partially overlapping. This experiment is conducted with a team of three robots—jX, jY and jZ in outdoors settings. Robots start at different parts of the campus and converge to a final destination at the end of their respective tours as shown in Fig. 7a. Robot jX knows of 5 places based on appearances from 1050 locations on a path of 150 m. The resulting place memory $T^{X}$ is as shown in Fig. 7b. It is seen that jX has a memory structure composed of 2 levels. The places 2 and 3 are in one level while places 1,4 and 5 are on the other. Robot jY knows of 7 places based on appearances collected from 370 locations along a path of 80 m. Its place memory has structure $T^{Y}$ as shown in Fig. 7c consists of two levels, where place 5 is at the first level and the remaining places are the second level. Here place 5 serves as a transition region between the street and the campus entrance. Thus, it is placed further away from the other places. The remaining places are on the same level probably due to similarity of their appearances. Finally, robot jZ knows of 8 places based on appearances from 710 locations along a path of 130 m. Its place memory has structure $T^{Z}$ as shown in Fig. 7d. $T^Z$ has a more complex structure with 3 levels. This can attributed to the fact that environmental changes along the robot jZ’s path are more than those of robots jX and jY. Note that while the number of places known to all sum up to 20, there are actually 13 distinct places—since some of these places are the same. These overlaps are shown in Fig. 7e–g based on manual inspection. It is observed that appearances associated with places jX:4, jY:7 and jZ:7 are very similar. They also geometrically correspond to the same area. This is also the case for jX:5 and jZ:8. On the other hand, while some places are geometrically nearby, their appearances are different as the respective robots move through them in opposite directions. For example, places jY:6 and jZ:7 are in this category. Similarly, this holds for jX:5 and jZ:6 as well as jZ:4, jX:2 and jY:4. As such, we expect them to be learned as different places. Finally, there are also places whose appearances are similar while they are geometrically distant such as jX:1and jY:6. Pairwise distances between the centroids of the respective hyperspheres and their radii are given in Table 2(a) and (b).

Table 3 Place memories after merging

Fig. 9

Merged topological maps

s

The merged place memories vary depending on the order of merging as seen in Fig. 8. Places that are only learned by one robot are indicated by corresponding color (blue—robot jX, green—robot jY and red—robot jZ) while places shown by orange nodes indicate merged places. For robot jX, with the merged place memory $T^X\oplus T^Y\oplus T^Z$, the robot increases its place knowledge from 5 to 15 places. When the order of learning is changed, the robot expands its place knowledge from 5 to 14 places. As we expect this number to be 13, this discrepancy is attributed to two factors. First, there are missed mergings. For example while we expect jZ:5 to be merged with jX:2 or jX:3, this is not the case. Similarly, we expect jY:7 to be merged with jX:4, they are learned as different places. Second, there are also wrong mergings. For example, while places jX:1 and jZ:6 are appearance-wise not similar, they are wrongly merged. Closer inspection reveals that wrong mergings tend to occur across places that while appearance-wise different nevertheless contain similar dominant entities such as sky, building and walkway. In case of robot jY, its merged memory $T^Y\oplus T^X\oplus T^Z$ contains 13 places that are arranged in three levels. This is as expected. Manual inspection indicates that some places are wrongly found to be same. When the learning order is reversed to $T^Y\oplus T^Z\oplus T^X$, again the robot increases its knowledge of places from 7 to 13 with the knowledge organized in three levels. As the robot correctly merges five of the seven places, merging performance is considerably much better. This case shows the effect of the merging order. The knowledge that is acquired first considerably affects the hypersphere configurations and as a result affects the further mergings. Finally for the robot jZ, its merged place memory $T^Z\oplus T^X\oplus T^Y$ contains 13 places—again arranged in 3 levels. As such, its knowledge of places expands from 8 to 13. It finds the knowledge associated with 7 places as overlapping with its own. Two of these are correct while the remaining are incorrectly merged. For example, while places jZ:4 and jX:2 are correctly found to be overlapping, this is not the case for places jZ:6 and jX:1 or jX:5. With the reversed merging order $T^Z\oplus T^Y\oplus T^X$, the robots expands its knowledge of places from 8 to 11. Since we expect this number to be 13, some of the places are wrongly merged. The obtained results show that there are 3 places that are correctly merged while 6 places are incorrectly merged. Closer analysis indicates that wrong mergings are due to perceptual aliasing (Table 3).

The robots use their place memories to merge the topological maps. For example, for robot jX, the resulting maps are given in Fig. 9. The number of nodes in each merged map is equal to the number of places in the place memory. Again, places that are known by only one robot are indicated by corresponding color (blue—robot jX, green—robot jY and red—robot jZ) while places shown by orange nodes indicate places that were known by at least two of the robots. As some mergings are correct while some are not, some edges are geometrically correct while others are not. For example, with robot jX, 20 of the 35 spatial relations are geometrically correct in the merged map memory ${{G}}^X\oplus {{G}}^Y\oplus {{G}}^Z$. It is observed that the robot can successfully navigate from place jX : 4 directly to place jZ : 8. On the other hand, as places jX : 1 and jZ : 6 are incorrectly viewed as overlapping, the robot trying to navigate directly from jX : 1 to jZ : 5 will end unsuccessfully. With ${{G}}^X\oplus {{G}}^Z\oplus {{G}}^Y$, there are 14 places with the knowledge associated with three places being revised based on merged knowledge. As such, 39 spatial relations are inferred. 20 of these are geometrically correct while 19 are not—due to incorrectly merged places. In summary, the resulting merged maps are correct with around 50–60% reliability. This is quite good considering only appearances are used in the merging process.

Another aspect of our merging process is that, if the resulting memory is merged with another robot in the future, mismerged places that belong to same physical location might be merged during that process assuming that the third robot also visits the same location. Thus, error recovery to some extent is possible in further mergings although this case did not occur during our experiments. However, when two places are erroneously merged, it is not recoverable in the future mergings since we continue the merging process with available terminal nodes.

5.4 Using the merged knowledge

We have also tested the use of merged knowledge. These experiments aim to assess how the robots leverage each other’s experiences to recognize these places as it actually visits them for the first time. Each of the robots is made to follow two alternative paths as shown in Fig. 10. The places along these paths have been learned by either the robot itself or through merging of knowledge. Let it be noted as these experiments are done about 2 months after knowledge has been merged, appearances have changed to some extent due to seasonal changes. As such, we are able to test the recognition performance of the merged place memories—even under changing environmental conditions.

Fig. 10

Navigating in places that have been learned through merging of place memories after 2 months

The first path shown in blue is about 100 m and goes through two places that have been learned by robot jX in the previous visit. Robots jY and jZ have learned these places via knowledge sharing. As the scenes associated with each of the places are mostly composed of buildings, appearances are not much affected by seasonal changes. The precision-recall results with $\tau _r = 1.5$ for each robot and merged memory are given in Table 4. It is observed that all the robots can perfectly recognize these places except robot jY with the merged memory $T^Y\oplus T^Z\oplus T^X$. In this case, it recognizes one of the places as a new place. As robot jY has learned this place through merging, apparently its knowledge is not sufficient in information content.

The second path shown in red goes through seven places (containing car park, garden and a concrete trail) that have been learned by robot jZ. Robots jX and jY have learned these places through knowledge merging. It is observed that this path is rather challenging compared to the first path because of the significant seasonal changes in the appearance of the garden area. Robot jZ has the highest recognition performance with the merged place memory $T^Z\oplus T^Y\oplus T^X$ memory. It has $80\%$ recall at $25\%$ precision. Interestingly, with merging order changed to $T^Z\oplus T^X\oplus T^Y$, performance changes to $66\%$ recognition at $33\%$ precision. Interestingly, for robot jX which as learned these places based on the knowledge of robot jZ, performance is at the same level with again $66\%$ recognition at $33\%$ precision. The merged memories of Robot jY enable $40\%$ recall at $50\%$ precision. Despite the fact that there are seasonal changes in the appearances of these places, the robots can still recognize them using their merged place memory with acceptable accuracy—even if they have been learned through merging of their knowledge with those of other robots.

Table 4 Recognition performance of merged place memories with $\tau =1.5$

Table 5 Obtained place updates with learning from direct experience

Table 6 Comparative performance: learning from other robots’ versus learning based on direct experience

5.5 Merging versus direct experience

Finally, the recognition performance of knowledge acquired by merging is compared with that of learning from direct experience. The place recognition updates of direct experience are given in Table 5. The comparison is done with respect to processing time and recognition performance (using association threshold $\tau _r=1.5$) as given in Table 6. Interestingly, learning through knowledge merging takes considerably shorter time as compared to learning from direct experience. It takes about 85 ms in contrast to 450–1145 ms for learning from direct experience—ignoring time taken to navigate in the associated places. This is attributed to the processing of knowledge as a whole or in portions. The recognition performance of robot jX does not seem to be affected by how knowledge is learned. On the other hand, this does not seem to be the case for robot jZ. Its performance learning from direct experience is considerably poorer. This is probably due to it not recognizing a lot of the places. With learning from direct experience, the place memory $T^X$ of robot jX contains 8 distinct places while that of robot jZ contains 11 places. For example, robot jX wrongly recognizes places jY:1 and jY:2 as place jX:3. Furthermore the places that are confused are different from those that are confused after knowledge merging. As an example, places jX:3, jY:1 and jY:2 are confused after learning from direct experience—while this is not the case with merging. For $T{^Z}\oplus T^Y\oplus T{^X}$, places jZ:8, jZ:4 jZ:6 and jZ:7 were updated while for jZ after direct experience learning jZ:2, jY:6 were updated. This is attributed to the handling the knowledge as a whole or in portions which implies that knowledge structure is preserved to some extent—in contrast to learning from direct experience where this does not hold.

5.6 Summary

Our evaluations show that appearance based knowledge merging is an efficient way of combining data that is obtained from multiple robots. Each robot maintains its own knowledge hierarchy and this can be exploited further to discover semantics of the tree branches in the future developments. We also observed that the order of merging affects the merged tree structure and place recognition performance considerably for both the current and future mergings. The compactness of appearance data and our non-geometric approach makes the system very flexible for it to be used both in smaller scale indoor environments as well as larger scale outdoor environments. Recognition performance with the merged memories is quite good considering that no metric information is used. The merged place memories also enable efficient merging of the topological maps.

6 Conclusion

This paper has presented a novel approach to the merging of appearance-based place knowledge. Robots are assumed to have compatible visual sensing and to retain their knowledge in their respective long-term place memories. In each place memory, the respective knowledge is organized in a tree hierarchy with terminal nodes corresponding to distinct places and with each place defined by a collection of appearances. The merging is based on the observation that the tree hierarchy corresponds to a nested sequence of hyperspheres in the appearance space. It proceeds by considering the extent of overlap of the respective nested hyperspheres—starting with the largest covering sphere. Thus, differing from the current related work, as knowledge is merged in as large chunks as possible, the merging process scales better as the extent of knowledge to be merged increases. Thus, the approach can be used in large-scale and long-term operations. Furthermore, the hierarchical structure is preserved as much as possible. The resulting merged place memories are compact in the sense that they represent data from thousands of locations with fewer number of places. Interestingly, we observe that merging knowledge from other robots can enable more efficient learning with shorter learning times. This is attributed to the fact that other robot’s knowledge is processed as a whole or in large portions. In parallel, association performance based on merged learned knowledge enables the robot to be relatively less lost in comparison to using only its own gathered knowledge.

For future work, we plan to study related three aspects. The first pertains to how to improve the memory association as to minimize missing mergings and wrongly merged places—as this will improve the reliability of the merged knowledge. The second aspect will be to use the merged topological maps in navigation and multirobot tasks. Finally, since merged place memories differ depending on the order of merging, we plan to integrate some combinatorial exploration of the best order to merge them.

Appendices

Appendix A: Symbols

The summary of the most commonly used symbols in the paper, their definitions and the sections where they are defined are presented in Table 7 for convenience.

Table 7 List of symbols

Appendix B: Measuring overlap

Consider nodes N in the place memory $T^m$ and $N^\prime$ in the place memory $T^n$. Recall that each node encodes a cluster of places. The overlap amount of these places is measured based on the intersecting volume of the two corresponding hyperspheres $S(c_m(N), \rho _m(N))$ and $S(c_n(N^\prime ), \rho _n(N^\prime ))$. These hyperspheres are as defined in Sect. 4 with centroids $c_m(N)$ and $c_n(N^\prime )$ and radii $\rho _m(N)$ and $\rho _n(N^\prime )$ respectively. The intersecting volume is equal to:

$$\begin{aligned}&\left| S(c_m(N), \rho _m(N)) \cap S(c_n(N^\prime ), \rho _n(N^\prime )) \right| = \\&\quad 3\pi \frac{(\rho _l{+}\rho _s-d)^2(d^2{+}2d\rho _s-3\rho _s^2{+}2d\rho _l{+}6\rho _s\rho _l-3\rho _l^2)}{12d}\nonumber \\ \end{aligned}$$

where

$$\begin{aligned} \rho _l= & {} \max \left\{ \rho _m(N), \rho _n(N^\prime ) \right\} \\ \rho _s= & {} \min \left\{ \rho _m(N), \rho _n(N^\prime ) \right\} \\ d= & {} {\tilde{\gamma }}(N, N^\prime ) \end{aligned}$$

The value d measures the distance between two hyperspheres as defined by Eq. 1. The overlap percentage is then computed simply by taking the ratio of intersecting volume to the volume of the smaller hypersphere as:

$$\begin{aligned} \xi (N,N^\prime ) = \frac{3 \left| S(c_m(N), \rho _m(N)) \cap S(c_n(N^\prime ), \rho _n(N^\prime )) \right| }{4\rho _n^3} \end{aligned}$$

Note that as $\xi (N,N^\prime ) \in \left[ 0,1\right]$, a higher percentage indicates a larger overlap. The overlap between a detected place D and a set of places as represented by node N in the place memory $T^m$ can also be computed in the same manner. In this case, the hypersphere $S(c_D,\rho _D)$ associated with a detected place has centroid $c_D= {\bar{I}}_D$ and radius $\rho _D$ defined as:

$$\begin{aligned} \rho _D = \frac{1}{ M_D} \displaystyle \sum _{j \in {\mathcal {X}}(D)} \left\| I(x_j(D)) - c_D \right\| ^2 \end{aligned}$$

(9)

where ${\mathcal {X}}(D)$ is the index set of the appearances associated with the detected place.

Appendix C: RACHET algorithm

RACHET algorithm (Samatova et al. 2002) aims to merge local dendrograms into one global dendrogram. The dendrograms are assumed to be formed by data points that are represented by N-dimensional feature vector $x \in R^N$ The algorithm aims that the dendrogram formed after the merging process is as similar as the dendrogram that can be formed from scratch using the data of both dendrograms. The algorithm is as follows:

• Given a set of local dendrograms $d_i \in \mathcal {D}$, each of those are represented by a mean feature vector $c_i \in R^N$ and the average distance of data points in $d_i$ to the mean vector $r_i$. These two parameters define the covering hypersphere of the local dendrogram.

• In the second step, the closest local dendrogram pairs are formed using the Euclidean distance between their centroids.

• In the third step, for each local dendrogram pair, global dendrogram is formed by checking the amount of overlap between them and merging accordingly. The details of this merging process can be found in Samatova et al. (2002).