Abstract
Stochastic modeling of motion primitives is a well-developed approach to representing demonstrated motions. Such models have been used in kinematic motion recognizers and synthesizers due to their compact representation of types of high-dimensional motions. They allow robots to synthesize their own motions that is kinematically similar to the demonstrated motions. However, when the robots execute a task during physically interacting with the environment, the robots are required to control the dynamical properties such as contact forces in the similar fashion to demonstrated executions. To achieve this goal, the stochastic model needs to be extended to represent both the kinematics and the dynamics of the demonstrations, and subsequently synthesize motions with physical consistency according to this representation. In this paper, we propose a novel approach to encoding sequences of joint angles and joint torques into a hidden Markov model (HMM). Subsequently, joint torques that satisfy the physical constraints of the equations of motion are generated from the HMM by using a sampling method. These joint torques enable a robot to perform motions kinematically similar to training demonstrations and to control its contact with the environment. Experiments on a robot arm with seven degrees of freedom demonstrate the validity of the proposed approach.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Robots are required to perform complex motions and to adapt to their environments. Programming robots with large degrees of freedom to execute motions is time consuming, and transferring the programmed motions to new environments is difficult. A compact representation of motion primitives and their adaptation to new environments are important problems that need to be solved in order to integrate robots into our daily lives.
The motion primitives are useful representations, in which robots record motions and which they can reuse for motion recognition and motion generation. In imitation learning, a teacher demonstrates to the robots in a simple way, and the demonstrations are encoded into motion primitives based on stochastic models or dynamical systems. The robots can recognize a demonstration in terms of selecting the motion primitive most similar to the demonstration, and generate their own motions from queries of motion primitives. Stochastic frameworks are provided with efficient algorithms to optimize model parameters from demonstrations and to calculate the distances between motion primitives and the demonstration; they are, therefore, widely used to represent motion patterns. In particular, they have been successfully used in motion recognition (Inamura et al. 2004), and have been combined with natural language processing such that robots can relate demonstrations to descriptions in the form of sentences (Takano and Nakamura 2015a, b). In addition, the stochastic frameworks allow robots to execute motions almost the same as those they were trained on Calinon et al. (2006). In these frameworks, demonstrations are expressed kinematically but their dynamics, such as joint torques and contact forces, are not handled. Key challenges in imitation learning using stochastic models are including the dynamics in the representation of the demonstration and synthesizing motions that interact dynamically with the environment. In reinforcement learning, the robots incrementally find the policy of the action given the current state by the manner of trial and error. The dynamical systems, typified by dynamic movement primitives (Ijspeert et al. 2003), create the kinematic control policy, and trial and error learning allows for identifying the dynamics in the motion and improving the control policies (Schaal et al. 2003). The motion primitives are expressed by the stochastic graphical model endowed by the cost function, and the optimal feedback controller is designed according to the inference on the graphical model and identified dynamics model (Ruckert et al. 2013). During the execution of the motions, these models are improved by sampled data, but this improvement requires much time especially for systems with a large degree of freedom. Additionally, the profile of the motion depends on the manually given goal and cost function, and it is not necessarily similar to human demonstrations.
In this paper, we propose a novel approach to representing the kinematics and dynamics in demonstrations in stochastic models, and to controlling a robot’s motion to adapt to the environment. Demonstrations are expressed as joint angles and joint torques, and these demonstrations are encoded into hidden Markov models (HMMs). Physically consistent joint angles and joint torques based on the equation of the motion of the robot that are the most likely to be generated from the HMM are computed. These joint angles and joint torques are found by using a Bayesian sampling method. More specifically, when encoding the joint angles and joint torques in the demonstrations, the importance of each joint angle or joint torque is extracted in the form of its distribution in the HMM. During the robot performing the motion where the joint angles are dominant, the joint angles more similar to the training demonstration and the joint torques less similar are generated such that the robot can perform the motion kinematically similar to the demonstration. When the robot performs the motion where the contact forces are important, the joint torques more similar to the demonstration are generated such that the robot can control the reaction forces to become as close as possible to those during the demonstration. We demonstrate the validity of our approach using a robotic arm with seven joints that draws lines or curves on a wall by contact between its end-effector and the wall.
2 Related work
There have been many studies of imitation learning, including learning by observation, learning from demonstration, and programming by demonstration (Breazeal and Scassellati 2002; Schaal 1999; Mataric 2000).
A classic framework for imitation learning is Behavioral Cloning (BC), where the behaviors of skilled human operators are recorded, and a control policy that maps states to actions is exploited (Bain and Sammut 1996). This policy executes complex tasks by tracing behaviors. BC stores direct mappings between the states and actions without taking into account the physics of the robot. Because it is difficult to apply this mapping to a new environment, BC suffers in environments that are different from those in which the policy was trained.
One popular approach to imitation learning is the use of Dynamic Movement Primitives (DMPs) (Ijspeert et al. 2001, 2003). DMPs represent movements as nonlinear differential equations, and modify the shapes of generated movements so that they reach their goals or have desirable durations. Matsubara et al. (2011) extended DMPs to represent multiple movements in order to improve their scalability, and demonstrated their validity on a dual-arm robot. Prada et al. (2013) proposed DMPs specialized for a robot handing over an object to a human partner. Okada et al. designed the vector field, where the demonstration is a closed curve in polynomial form, and any point is attracted to this closed curve. This attractor field stabilizes the robot motion even if it is disturbed (Okada et al. 2002). These approaches define the motion by differential equations or the polynomial forms of kinematic configurations, and do not deal with the dynamics of the robot. Therefore, the synthesized motion is not guaranteed to follow profiles of joint torques or contact forces that are similar to those of the demonstration.
Neural networks are forms of imitation learning that represent movements as network parameters. Tani and Ito (2003) have developed Recurrent Neural Networks with Parametric Bias (RNNPB) which encode demonstrations into parameters on the bias layer and a set of parameters represents a motion primitive. This framework predicts the movement from the current perception, and this leads to motion generation. This framework has been extended to motions and language. One RNNPB learns motion primitives, and another RNNPB learns sequences of words. These two RNNPB are linked with the bias parameters. This framework enables robots to interpret movements in the forms of language, and to generate movements from language commands (Sugita and Tani 2005; Ogata et al. 2007). However, these models represent the kinematics of the movements, but do not handle the dynamics. Kadone and Nakamura (2005) proposed associative neural networks with non-monotonic activation functions. These functions control the abstraction levels of motion primitives, but motion synthesis using the associative neural networks was not discussed. Neural networks using deep learning have been applied to representing high dimensional sensory-motor data (Noda et al. 2014; Finn et al. 2017; Nair et al. 2017). Robots using these networks can generate motions in response to visual perception, but the neural networks do not represent dynamics, such as contact between the motions and manipulated objects.
A human moves the master robot such that the slave robot draws a line or a curve on a whiteboard. We measure the angles and torques of all the joints in the slave robot during drawing. The measurements are used to represent a training motion, which is encoded into an HMM. In this study, we considered the motions of “drawing a horizontal line,” “drawing a vertical line,” “drawing a diagonal line,” and “drawing a circle.”
Many stochastic approaches to representing motion are well-established. Inamura et al. (2004) used HMMs for representing demonstrations. In their framework, whole body motions are generated according to the distribution of the demonstrations by Monte Carlo sampling. The generated motion is likely to become an average of the demonstrations, and does not dynamically adapt to the environment. Calinon et al. (2006) have extended HMMs to joint angles and joint angular velocities. Their approach can compute the joint angular velocities given the current joint angles. This computation results in kinematically adaptive motions. Takano and Nakamura (2017) have proposed a method to encode human motions into HMMs and to kinematically synthesize human-like motion from the HMMs. In this framework. the HMMs handle only joint angles, and plan a sequence of the joint angles, which are modified to dynamically adapt to the environment by the optimal controller (Takano and Nakamura 2017). Herzog et al. used Parametric Hidden Markov Models (PHMMs) (Wilson and Bobick 1999) that represent motions and relevant objects (Herzog et al. 2008). Several motions are encoded into an HMM as a representative motion primitive, and each motion variant is encoded into an individual HMM. The parameters of the individual HMM are expressed as a linear function of the parameters of the representative HMM and the position of the object. The motion acting on the object can be generated from an individual HMM that is created from the representative HMM and the current position of the object. Another method which represents motions and manipulated objects in a task-parameterized mixture model has been proposed (Calinon et al. 2013). Paraschos et al. (2013) proposes Probabilistic Movement Primitives (ProMP) for representing demonstrations. ProMP can derive the feedback controller to synthesize motions according to distributions over the demonstrations. This approach has been extenteded to segmenting demonstrations and subsequently encoding the segments into ProMP (Lioutikov et al. 2015). All of these stochastic approaches represent only the kinematics of the demonstrations, and do not take into account the dynamics of the demonstrations. So the contact forces are not controlled by the motions synthesized by these approaches.
The contributions of this paper are the extension of HMMs to joint angles and joint torques to capsulate both the kinematics and the dynamics of demonstrations, and a method for generating joint angles and joint torques that satisfy the equation of the motion of the robot and are most likely to be generated from the HMM. The resultant joint angles and joint torques realize robot motion that is both kinematically and dynamically valid, and is similar to the demonstrated motion.
3 Motion control through Bayesian sampling
3.1 Motion primitives
A demonstration is expressed as a sequence of vectors \({\varvec{x_t}}\) whose elements are joint angles \({\varvec{\theta _t}}\) at time t. The sequences are encoded into the parameters of an HMM \(\lambda \). An HMM is a stochastic model used to classify input data into specified categories. An HMM is defined by the compact notation \(\lambda = \left\{ {\varvec{A}}, {\varvec{B}}, {\varvec{\varPi }} \right\} \), where \({\varvec{A}}=\left\{ a_{ij} \right\} \) is the matrix whose elements \(a_{ij}\) are the probability of transitioning from the ith node to the jth node, \({\varvec{B}} = \left\{ b_{i}({\varvec{x}}) \right\} \) is the set of output distributions of the vector \({\varvec{x}}\) at the ith node, and \({\varvec{\varPi }} =\left\{ \pi _i \right\} \) is the vector whose elements \(\pi _i\) are the initial probabilities at the respective nodes. The parameters of the HMM are optimized by the Baum–Welch algorithm such that the probabilities of the sequences being generated from this HMM are maximized (Rabiner and Juang 1993). The Baum–Welch algorithm is an expectation-maximization algorithm. In this study, we used left-to-right HMMs.
An HMM is a generative stochastic model, and various approaches have been developed to generate trajectories of joint angles from an HMM. Most of them are based on the Monte Carlo method. More specifically, an initial node \(q_1\) at time \(t=1\) is selected according to the initial node probabilities \({\varvec{\varPi }}\). A vector of joint angles \({\varvec{\theta _1}}\) that is equivalent to \({\varvec{x_1}}\) is sampled according to the output probabilities \(b_{q_1}({\varvec{x}})\). The node \(q_2\) is subsequently selected according to the transition probabilities \(a_{q_1 \, i}\), and a vector of joint angles \({\varvec{\theta _2}}\) is sampled in the same manner as \({\varvec{\theta _1}}\). These processes are iterated to form a sequence of vectors of joint angles. This sequence of joint angles may not form a smooth trajectory, and several sequences of the joint angles to be created are averaged out to produce one smooth sequence of joint angles.
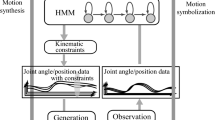
This Monte Carlo style of approach is successful at generating motion that is kinematically close to training motions. However, it does not account for the dynamics of the robot’s motion, such as joint torques and contact forces with the environment. The resultant motion is, therefore, difficult to use for controlling the motion of a robot in a real environment. In this paper, we extend the encoding of motions to both kinematics and dynamics as shown in Fig. 1. The state vector \({\varvec{x_t}}\) is defined as \({\varvec{x}}_t = \left[ {\varvec{\theta }}_t^T \ {\varvec{\tau }}_t^T \right] \), where \({\varvec{\tau _t}} \) is a vector of joint torques at time t. The contact forces can be theoretically added to the state vector \({\varvec{x_t}}\), but this paper assumes that the contact forces are not included in the state vector since an anthropomorphic arm without the force sensor at the end effector is used in the experiment. A sequence of state vectors \({\varvec{x_t}}\) is encoded into the parameters of HMM \(\lambda \). We aim at developing an algorithm that generates joint angles and joint torques that are as close as possible to the training motion and are physically feasible. More specifically, the search for such joint angles and joint torques can be formulated as the following constrained optimization problem.
Here \(P({\varvec{x}}_1, {\varvec{x}}_2, \dots , {\varvec{x}}_T \vert \lambda )\) is the probability of \({\varvec{x}}_1, {\varvec{x}}_2, \dots \), \({\varvec{x}}_T\) being generated by \(\lambda \). The equation of motion of the robot is given as the constraint, where \({\varvec{M}}({\varvec{\theta }})\), \({\varvec{C}}({\varvec{\theta }}, \dot{{\varvec{\theta }}})\) and \({\varvec{G}} ({\varvec{\theta }})\) are the inertia matrix, centrifugal and Coriolis term, and gravitational term, respectively. \({\varvec{J}}\) is the Jacobian matrix that relates the joint angular velocity to the velocity of the end effector, and \({\varvec{F}}\) is the reaction force on the end effector. We assume that only the end effector is in contact with the environment. It is theoretically difficult to find an optimal sequence of \({\varvec{x}}_t\) for this optimization problem. Instead, we search for a solution by sequentially sampling \({\varvec{x}}_t\).
3.2 Bayesian sampling for generating physically consistent motions
This subsection describes a method of computing joint angles and joint torques that are physically consistent and are as likely as possible to be generated from the HMM.
Our approach to generating physically consistent motions from the HMM iterates over three phases: predicting many state vectors according to the current distribution in the state space, evaluating each of those state vectors, and modifying the distribution by resampling the particles. Each state vector is defined as the joint angles \({\varvec{\theta }}_t^{(k)} \), the joint torques \({\varvec{\tau }}_t^{(k)} \) as mentioned above, and the nodes in the HMM at time t is expressed by \(q_{t}^{(k)}\). An individual particle \(s_t^{(k)}, k=1,2,3,\dots , N \) at time t has elements of the joint angles \({\varvec{\theta }}_t^{(k)} \), the joint torques \({\varvec{\tau }}_t^{(k)} \), and the nodes \(q_{t-1}^{(k)}\) and \(q_{t}^{(k)}\). More specifically, the particle can be expressed in the compact notation \(s_t=\left\{ q_{t-1}, q_t, {\varvec{\theta }}_t, {\varvec{\tau }}_t \right\} \).
The node \(q_{t}^{(k)}\) at time t, given the node \(q_{t-1}^{(k)}\) at time \(t-1\), is sampled according to the probabilities \({\varvec{A}}\) of transitioning from the node \(q_{t-1}^{(k)}\). The joint angles \({\varvec{\theta _t}}^{(k)}\) are subsequently sampled according to the output distribution \({\varvec{B}}\) at the node \(q_{t}^{(k)}\). From the measured joint angles \({\varvec{\theta }}_{t-1} \) and \({\varvec{\theta }}_{t-2} \) at times \(t-1\) and \(t-2\), the joint angular velocities \(\dot{{\varvec{\theta _t}}}^{(k)}\) and joint angular accelerations \(\ddot{{\varvec{\theta }}}_t^{(k)}\) are computed. The joint angular accelerations \(\ddot{{\varvec{\theta }}}_t^{(k)}\) are modified, as shown in Eq. 3, in a similar manner to the computed torques.
Here \( \dot{{\varvec{\theta }}}_{t-1} \) is the vector of joint angular velocities at time \(t-1\), and \({\varvec{K_p}}\) and \({\varvec{K_d}}\) are coefficient matrices.
Each figure shows a training trajectory, a generated trajectory, and the distribution of generated trajectories of a joint angle for “drawing a horizontal line.” The profile of the generated trajectory is similar to that of the training trajectory, and the trajectory distribution includes the training trajectory
Each figure shows a training trajectory, a generated trajectory, and the distribution of generated trajectories of a joint angle for “drawing a diagonal line.” The profile of the generated trajectory is similar to that of the training trajectory, and the trajectory distribution includes the training trajectory
Each figure shows a training trajectory, a generated trajectory, and the distribution of the generated trajectories of a joint torque for “drawing a horizontal line.” The profile of the generated trajectory is similar to that of the training trajectory, and the trajectory distribution includes the training trajectory
Each figure shows a training trajectory, a generated trajectory, and the distribution of the generated trajectories of a joint torque for “drawing a diagonal line.” The profile of the generated trajectory is similar to that of the training trajectory, and the trajectory distribution includes the training trajectory
Motions of “drawing a horizontal line,” “drawing a vertical line,” “drawing a diagonal line,” and “drawing a circle” are encoded to their corresponding HMMs. The set of trajectories of joint angles and joint torques that is likely to be generated by the HMM and that satisfies the equations of motion is used as the reference for the motion. The experiments show that the robot can perform a motion similar to the training motion
The joint torques, that are equivalents to the desired reaction force, are applied to the robot. When the board to be contacted is distant from the end effector and the reaction force from the board does not exist, the joint torques move the end effector toward the board. Thus, the proposed controller allows the robot to contact the board even if the board is put at a different location from the training
By substituting the joint angles \({\varvec{\theta _t}}^{(k)}\), the joint angular velocities \(\dot{{\varvec{\theta _t}}}^{(k)}\), the joint angular accelerations \(\ddot{{\varvec{\theta _t}}}^{(k)}\), and the desired reaction force \( {\varvec{F}}_t^{des}\) (which is manually given) into Eq. 2, physically consistent joint torques \({\varvec{\tau _t}}^{(k)}\) can be derived. This can be implemented by an inverse dynamics computation:
Each particle is assigned a score indicating the probability \(P( {\varvec{\theta _t}}^{(k)}, {\varvec{\tau _t}}^{(k)} \vert q_t^{(k)}, \lambda )\) that the HMM generates the joint angles \({\varvec{\theta _t}}^{(k)}\) and joint torques \({\varvec{\tau _t}}^{(k)}\) from the node \(q_t^{(k)}\) at time t.
where \(b_{i}( {\varvec{x}} )\) is expressed by a Gaussian distribution function. The probability \(P( {\varvec{\theta }}_t^{(k)}, {\varvec{\tau }}_t^{(k)} \vert q_t^{(k)}, \lambda )\) for each particle \(s_t^{(k)}\) is then normalized to \(p_k\):
The expected values of the joint angles and joint torques, \({\varvec{\theta }}_t^{ref}\) and \({\varvec{\tau }}_t^{ref}\), are calculated from the following equations by using a set of particles and their associated probabilities.
The vectors \({\varvec{\theta }}_t^{ref}\) and \({\varvec{\tau }}_t^{ref}\) are used as reference joint angles and joint torques at time t. The particles for the next time \(t+1\) are resampled according to \(p_k\) such that the distribution of the resampled particles becomes close to that described by Eq. 7. The node \(q_{t}^{(k)}\) in the resampled particle is used to predict the node \(q_{t+1}^{(k)}\), the joint angles \({\varvec{\theta }}_{t+1}^{(k)}\), and the joint torques \({\varvec{\tau }}_{t+1}^{(k)}\). Figure 2 shows an overview of the process for motion generation.
4 Experiments
The validity of our approach to generating motions from HMMs was verified by using anthropomorphic arms. An individual arm has seven joints. A trunk and an end effector are connected to the arm. The shoulder, elbow, and wrist consist of three, one, and three joints, respectively. Each joint is equipped with an incremental encoder and a torque sensor. Note that the end effector is not equipped with a force sensor, and so the external force acting on the end effector from the contacting environment cannot be measured. The angles of pitch, roll, and yaw in the shoulder are denoted by \(\theta _1\), \(\theta _2\), and \(\theta _3\), respectively; the pitch in the elbow is denoted by \(\theta _4\); and the yaw, pitch, and roll in the wrist are denoted by \(\theta _5, \theta _6\), and \(\theta _7\), respectively. The corresponding joint torques are denoted by \(\tau _1, \tau _2, \tau _3, \tau _4, \tau _5, \tau _6\), and \(\tau _7\), with the same meaning for the subscripts.
Two robotics arms are connected in a bilateral teleoperation system, as shown in Fig. 3. One robotic arm is referred to as the master robot, and the other is referred to as the slave robot. The master and slave robots mutually communicate their joint angles and joint torques with one another. The slave robot attempts to follow the joint angles of the master robot and to act with the same force as the master robot.
Here \({\varvec{\tau }}_c^{(s)}\) is a vector of torques input to the slave robot; \({\varvec{\tau }}^{(m)}\) and \({\varvec{\tau }}^{(s)}\) are joint torques to be measured in the master and slave robots, respectively; and \({\varvec{\theta }}^{(m)}\) and \({\varvec{\theta }}^{(s)}\) are angles of all the joints in the master and slave robots, respectively. \({\varvec{K_p}}\), \({\varvec{K_d}}\), and \({\varvec{K_{\tau }}}\) are coefficient matrices. The master robot is controlled in the same manner as the slave robot.
A human directly moves the master robot such that the slave robot draws a line or a curve on a whiteboard, as shown in Fig. 4. We measured the angles and torques of all the joints in the slave robot during the drawing of a horizontal line, a vertical line, a diagonal line, and a circle. The measurement is conducted at a sampling interval of 1 ms, but measurements at a sampling interval of 100 ms are used as training data for the motion primitive. More specifically, five sequences of the joint angles, \({\varvec{\theta }} = \left( \theta _1, \theta _2, \dots , \theta _7 \right) ^T\), and the joint torques, \({\varvec{\tau }} = \left( \tau _1, \tau _2, \dots , \tau _7 \right) ^T\), for each motion are encoded to its specific HMM. From this, four HMMs are obtained as motion primitives, representing the actions “drawing a horizontal line,” “drawing a vertical line,” “drawing a diagonal line,” and “drawing a circle.” Note that the numbers of nodes and Gaussian distributions on each node in the HMM are set to 30 and 1, respectively,
We tested the HMMs for “drawing a horizontal line” and “drawing a diagonal line” on motion generation without taking into account the dynamics of robot’s motion, as described in Sect. 3.1. Figures 5 and 6 show training and typically generated trajectories of joint angles, along with generated trajectory distributions. Figures 7 and 8 show training and typically generated trajectories of joint torques, along with generated trajectory distributions. The generated trajectories are close to the training trajectories, and the generated trajectory distributions cover the training trajectories well. This implies that the HMMs well represent the trajectories of both joint angles and joint torques.
We tested our approach to generating physically consistent motions from the HMMs. The desired reaction force on the end effector was set to 10 N in magnitude, with force vector \({\varvec{F}}=\left[ -10 \ 0 \ 0 \ 0 \ 0 \ 0 \right] ^T\). As described in the previous section, our approach generates reference angles \({\varvec{\theta }}^{ref}_t\) and torques \({\varvec{\tau }}^{ref}_t\) for all seven joints. The generation of joint angles and joint torques is based on a sampling method using particles, which is time-consuming. Since the computations for each individual particle are independent, the computations are run as parallel processes. In this experiment, computations of 200 particles were implemented across eight parallel processes. In this setting, all processes were completed within 100 ms. We did not use the references of the joint angles but used only the references of the joint torques as the input torques for the robot. However, the motion of the robot was sometimes unstable and the robot failed to perform the drawing motion. We therefore combined the reference joint angles \({\varvec{\theta }}^{ref}_t\) and joint torques \({\varvec{\tau }}^{ref}_t\) to compute the input torques:
where \({\varvec{\theta }}_t\) and \(\dot{{\varvec{\theta }}}_t\) are joint angles and joint angular velocities at time t. The reference angular velocities \(\dot{{\varvec{\theta }}}^{ref}_t\) are calculated as \(( {\varvec{\theta }}^{ref}_t - {\varvec{\theta }}_t) / \varDelta t\), where \(\varDelta t\) is the sampling time, which is set to 100 ms. The coefficient matrices \({\varvec{K}}_{p}\) and \({\varvec{K}}_{d}\) take the same values as in Eq. 10, and the diagonal weight matrices \({\varvec{W}}_{\theta }\) and \({\varvec{W}}_{\tau }\) are manually chosen such that \({\varvec{W}}_{\theta }+{\varvec{W}}_{\tau } = {\varvec{I}}\). The joint torques are controlled at a sampling interval of 125 µm.
Figure 9 shows qualitative experimental results where a robot performs the motions “drawing a horizontal line,” “drawing a vertical line,” “drawing a diagonal line,” and “drawing a circle” as generated by the corresponding HMMs. Note that the location of the board was different from that during training. Even in these cases, the end effector moved on the board. The computed joint torques for command are equivalent to the reaction force that shuld come from the board. When the board is distant from the end effector and the reaction force does not exist, the computed joint torques moves the end effector toward the board until it balances with the reaction force as shown on the left panel in Fig. 10. Therefore, the end effector can contact the board.
Figure 11 shows trajectories of the end effector for six trials of motion generation for the robot performing the motion “drawing a horizontal line.” Five trials are generated by using the proposed approach, and one trial is generated without using the equation of motion. More specifically, HMM generates a sequence of joint angles and joint torques based on the Monte Carlo method, and input joint torques are modified according to Eq.11. The position of the end effector is estimated by a forward kinematics computation using the measured joint angles. The proposed approach results in the motions of moving to the whiteboard in straight lines, drawing the line on the board, and moving the initial position, and attains the high repeatability. The motion generation without using the equation of motion leads to wobbling. Figures 12 and 13 show the corresponding profiles of measurements of the joint angles and joint torques. The whiteboard target for drawing lines or a circle was located at a different position from that of during learning, and the desired reaction force” should be ”a different position from that of during learning, and the desired reaction force profile was also different. Comparing Fig. 12 with Fig. 5 and Fig. 13 with Fig. 7 demonstrate that the profiles of the five generated motions are similar to the profiles of the training motions and that the trajectories of the joint angles and joint torques are modulated such that the end effector can move to follow a horizontal line on the board and maintain the desired reaction force. Figures 14 and 15 show the profiles of measurements of the joint angles and joint torques during the robot drawing a diagonal line on the whiteboard. Comparisons of Fig. 14 with Fig. 6 and Fig. 15 with Fig. 8 also show that joint angles and joint torques are varied to be adaptive to the current environment, but it demonstrates that the five motions are controlled with maintenance of the profiles of training motions.These experiments confirm that our proposed approach of generating physically consistent motions from a stochastic model can generate reference joint angles and joint torques similar to the training values and that the generated motion can adapt to slight variations from the training environment.
5 Conclusions
-
1.
We have developed an approach to generating physically consistent robot motion from a stochastic model. The stochastic model was an HMM that was extended to represent trajectories of both joint angles and joint torques. We proposed a novel method to find joint angles and joint torques that are likely to be generated from the HMM and that satisfy the equations of motion: only joint angles are generated from the HMM, and the joint torques corresponding to the joint angles are estimated by using the equations of motion. The likelihoods of the joint angles and joint torques being generated from the HMM are calculated. The pairs of joint angles and joint torques with the largest likelihood are used as the references of the motion.
-
2.
Our proposed method is based on sampling of joint angles and joint torques. A large number of sampling points leads to better representation of the robot motion, but this computation may be time-consuming. Sampling was implemented on parallel processors: 200 particles of joint angles and joint torques were distributed to eight processors. Experiments show that reference joint angles and joint torques could be computed within 100 ms in real time.
-
3.
We used a bilateral teleoperation system consisting of two robotic arms, each of which has seven joints. A human operator moves a master robotic arm and a slave robotic arm follows the motion of the master robot. Joint angles and joint torques in the slave robot were measured, and were used as training data that were encoded into sets of parameters of the HMMs. In this study, we measured four kinds of motion pattern (“drawing a horizontal line,” “drawing a vertical line,” “drawing a diagonal line,” and “drawing a circle”) and four corresponding HMMs were constructed. An experiment was conducted on generating motions from the HMMs. All the HMMs allowed the robot to perform motions similar to training motions.
References
Bain, M., & Sammut, C. (1996). A framework for behavioural cloning. In Machine intelligence (Vol. 15, pp. 103–129). Oxford: Oxford University Press.
Breazeal, C., & Scassellati, B. (2002). Robots that imitate humans. Trends in Cognitive Sciences, 6(11), 481–487.
Calinon, S., Alisadeh, T., & Caldwell, D. G. (2013). On improving the extrapolation capability of task-parameterized movement models. In Proceedings of the IEEE/RSJ international conference on intelligent robots and systems (pp. 610–617).
Calinon, S., Guenter, F., & Billard, A. (2006). On learning the statistical representation of a task and generalizing it to various contexts. In Proceedings of the IEEE international conference on robotics and automation (pp. 2978–2983).
Finn, C., Yu, T., Zhang, T., Abbeel, P., & Levine, S. (2017). One-shot visual imitation learning via meta-learning. In Proceedings of the conference on robot learning.
Herzog, D., Krueger, V., & Grest, D. (2008). Parametric hidden markov models for recognition and synthesis of movements. In Proceedings of the British machine vision conference (pp. 163–172).
Ijspeert, A. J., Nakanishi, J., & Shaal, S. (2003). Learning control policies for movement imitation and movement recognition. Neural Information Processing System, 15, 1547–1554.
Ijspeert, A. J., Nakanishi, J., Shibata, T, & Schaal S. (2001). Nonlinear dynamical systems for imitation with humanoid robots. In Proceedings of the IEEE-RAS international conference on humanoid robots.
Inamura, T., Toshima, I., Tanie, H., & Nakamura, Y. (2004). Embodied symbol emergence based on mimesis theory. International Journal of Robotics Research, 23(4), 363–377.
Kadone, H., & Nakamura, Y. (2005). Symbolic memory for humanoid robots using hierarchical bifurcations of attractors in nonmonotonic neural networks. In Proceedings of the 2005 IEEE/RSJ international conference on intelligent robots and systems (pp. 2900–2905).
Lioutikov, R., Neumann, G., Maeda, G., & Peters, J. (2015). Learning movement primitive libraries through probabilistic segmentation. International Journal of Robotics Research, 36(8), 879–894.
Mataric, M. J. (2000). Getting humaniods to move and imitate. IEEE Intelligent Systems, 15(4), 18–24.
Matsubara, T., Hyon, S. H., & Morimoto, J. (2011). Learning parametric dynamic movement primitives from multiple demonstrations. Neural Networks, 24(5), 493–500.
Nair, A., Chen, D., Agrawal, P., Isola, P., Abbeel, P., Malik, J., et al. (2017). Combining self-supervised learning and imitation for vision-based rope manipulation. In Proceedings of the IEEE international conference on robotics and automation (pp. 2146–2153).
Noda, K., Arie, H., Suga, Y., & Ogata, T. (2014). Multimodal integration learning of robot behavior using deep neural networks. Robotics and Autonomous Systems, 62, 721–736.
Ogata, T., Murase, M., Tani, J., Komatani, K., & Okuno, H. G. (2007). Two-way translation of compound sentences and arm motions by recurrent neural networks. In Proceedings of the IEEE/RSJ international conference on intelligent robots and systems (pp. 1858–1863).
Okada, M., Tatani, K., & Nakamura, Y. (2002). Polynomial design of the nonlinear dynamics for the brain-like information processing of whole body motion. In Proceedings of the IEEE international conference on robotics and automation (pp. 1410–1415).
Paraschos, A., Daniel, C., Peters, J., & Neumann, G. (2013). Probabilistic movement primitives. In Advances in neural information processing systems (pp. 2616–2624).
Prada, M., Remazeilles, A., Koene, A., & Endo, S. (2013). Dynamic movement primitives for human–robot interaction: Comparison with human behavioral observation. In Proceedings of the IEEE/RSJ international conference on intelligent robots and systems 2013 (pp. 1168–1175).
Rabiner, L., & Juang, B. H. (1993). Fundamentals of speech recognition. In Prentice Hall signal processing series. Englewood Cliffs, NJ: Prentice Hall.
Ruckert, E. A., Neumann, G., Toussaint, M., & Maass, W. (2013). Learned graphical models for probabilistic planning provide a new class of movement primitives. Frontiers in Computational Neuroscience, 6, 1–20.
Schaal, S. (1999). Is imitation learning the route to humanoid robot? Trends in Cognitive Sciences, 3(6), 233–2422.
Schaal, S., Peters, J., Nakanishi, J., & Ijspeert, A. J. (2003). Learning movement primitives. In International symposium on robotics research (pp. 561–572).
Sugita, Y., & Tani, J. (2005). Learning semantic combinatoriality from the interaction between linguistic and behavioral processes. Adaptive Behavior, 13(1), 33–52.
Takano, W., & Nakamura, Y. (2015a). Statistical mutual conversion between whole body motion primitives and linguistic sentences for human motions. International Journal of Robotics Research, 34(10), 1314–1328.
Takano, W., & Nakamura, Y. (2015b). Symbolically structured database for human whole body motions based on association between motion symbols and motion words. Robotics and Autonomous Systems, 66, 75–85.
Takano, W., & Nakamura, Y. (2017). Planning of goal-oriented motion from stochastic motion primitives and optimal controlling of joint torques in whole-body. Robotics and Autonomous Systems, 91, 226–233.
Tani, J., & Ito, M. (2003). Self-organization of behavioral primitives as multiple attractor dynamics: A robot experiment. IEEE Transactions on Systems, Man and Cybernetics Part A: Systems and Humans, 33(4), 481–488.
Wilson, A. D., & Bobick, A. F. (1999). Parametric hidden markov models for gesture recognition. IEEE Transactions on Pattern Analysis & Machine Intelligence, 21(9), 884–900.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This research was partially supported by a Grant-in-Aid for Scientific Research (A) (No. 17H00766) and a Grant-in-Aid for Scientific Research (B) (No. 18H03295) from the Japan Society for the Promotion of Science.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Takano, W., Takahashi, T. & Nakamura, Y. Sequential Monte Carlo controller that integrates physical consistency and motion knowledge. Auton Robot 43, 1523–1536 (2019). https://doi.org/10.1007/s10514-018-9815-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10514-018-9815-5