Abstract
The global localization of multiple mobile robots can be achieved cost efficiently by localizing one robot globally and the others in relation to it using local sensor data. However, the drawback of this cooperative localization is the requirement of continuous sensor information. Due to a limited sensor perception space, the tracking task to continuously maintain this sensor information is challenging. To address this problem, this contribution is presenting a model predictive control (MPC) approach for such cooperative localization scenarios. In particular, the present work shows a novel workflow to describe sensor limitations with the help of potential functions. In addition, a compact motion model for multi-rotor drones is introduced to achieve MPC real-time capability. The effectiveness of the presented approach is demonstrated in a numerical simulation, an experimental indoor scenario with two quadrotors as well as multiple indoor scenarios of a quadrotor obstacle evasion maneuver.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
During the last years, there has been a dramatic increase in the use of Unmanned Aerial Vehicles (UAVs) for all kind of applications such as surveillance, aerial photography, transport, etc. However, the fast dynamics of these systems and the extended operational space makes their autonomous piloting a challenging task. The recent development (Wingfield 2016) of applications for such systems targets not only autonomous flying of single UAVs, but also the coordinated interaction of multiple UAVs or of UAVs and ground robots. One essential task herein is the precise localization of these UAVs and robots in their environment.
Cooperative localization scenario
The precise global navigation of UAVs though typically requires expensive specialized equipment such as differential GPS in outdoor applications or laser-/RF-based global positioning systems in indoor applications. For cooperative mobile robot scenarios, one idea is therefore to deploy a reduced number of mobile robots which are equipped with the costly global localization system. The broadcasting of their global position allows all other UAVs to determine their own global position based on the relative position to these UAVs. The determination of the relative position can be achieved by less expensive onboard sensors such as optical sensors as shown in Fig. 1 in a UAV scenario. The major problem of this approach is the necessity to continuously detect and track the globally localized robots with sufficient accuracy. This is further exacerbated by very dynamical UAV scenarios and the onboard sensor limitations. Accordingly, the UAV motion has to be controlled in order to keep the globally localized UAVs within the perception space of the onboard sensors. The major focus of this work is therefore to provide a central control strategy for such cooperative localization scenarios. To limit the scope of this paper, the estimation and localization itself are not addressed and a stable communication channel is assumed. Yet, it should be mentioned that all robot systems considered here do have internal controllers. A communication failure would thus only lead to missing localization data, but not to a complete system failure.
One method to handle such complex control scenarios is model predictive control. MPC allows defining the control objective by means of an optimization problem. This so-called optimal control problem (OCP) is minimizing a given objective function subject to constraints. In general, the computational burden to solve an OCP is high. Hence, the efficiency of the applied solver is limiting the complexity of the controlled real-time scenarios. Nevertheless, a central MPC is well suited to control a small amount of robots. Such a central control simplifies the implementation of safety features and allows the computation of a global OCP solution without considering additional consensus techniques. However, the presented methods here are also applicable for distributed controllers which will be addressed in future work.
One essential factor for fast MPC is a compact description of the system’s behavior. To tackle this problem, the first contribution of this work is a novel compact motion model for multi-rotor systems which is described in Sect. 4. This simplistic motion model is based on a semi-nonlinear model for multi-rotor UAVs from previous work (Dentler et al. 2016a). Due to its angle discontinuity problem, as shown experimentally in Sect. 4.1, this previous model is not suitable for sensor tracking as considered within this work. To address this issue, Sect. 4.2 is presenting a model, where the typical orientation description with a single yaw \(\psi \) angle is replaced by a direction vector description. For validation, Sect. 4.3 is showing the MPC of a real \(AR.Drone\,2.0\) quadrotor based on the derived direction vector model. The same modeling approach can also be adapted to other velocity controlled mobile robot systems.
Another difficulty of MPC is the translation of the considered control scenario into an OCP. For this purpose, the second major contribution of this paper is a workflow that allows to represent sensor limitations in the form of potential functions, as presented in Sect. 5. The considered use case is a sensor tracking scenario which is introduced in Sect. 5.1. In this scenario, a quadrotor is controlled to keep an object within the cone-shaped perception space of the attached sensor. In this context, the sensor limitations are described as inequality constraints. These are subsequently transformed into weakened constraints that just appear in the OCP cost function, as shown in Sect. 5.2. This transformation is executed with unit steps and is recommended to maintain a low complexity which facilitates the mathematical and graphical validation of the resulting potential function. To improve the properties of the potential function for gradient and Newton based OCP-solvers, Sect. 5.3 is dedicated to the introduction of artificial gradients in undesired regions of the potential function. As last step, Sect. 5.4 is showing how the potential function is finally transformed into an analytical function by approximating all unit step functions by sigmoids.
For the experimental validation in the laboratory, additional safety constraints are introduced in Sect. 6, based on the described workflow. This includes further potential functions to avoid collision in Sect. 6.1 and to limit the operational space in Sect. 6.2. Section 7 is finally presenting the validation of the deduced potential functions in the use case scenario and the chosen control parameters. The numerical validation is described in Sect. 7.1, using the simulation environment \(V\text {-}{\textit{REP}}\). Section 7.2 is subsequently showing the results of the proposed control approach on real \(AR.Drone\,2.0\) quadrotors. In the following Sect. 7.3, the influence of obstacles, utilized constraints and different initial conditions is discussed on the basis of a set of collision avoidance scenarios in which a UAV is evading an obstacle while tracking a target.
Finally, conclusion and future perspective are given in Sect. 8.
2 Related work
In order to solve a cooperative sensor based robot localization, the problem can be divided into a self-localization and a position tracking problem. The present work is focusing on providing a control strategy for the position tracking problem.
To be able to localize a robot by another robot while executing tasks, both robots have to be controlled in a cooperative manner. There is extensive literature regarding such cooperative control scenarios. A comprehensive overview of the subject is given by Gazi and Passino (2011) and (Zhang and Mehrjerdi 2013). Gazi and Passino (2011) is discussing the theory of swarm mechanics and interaction constraints while Zhang and Mehrjerdi (2013) is providing a survey on formation control and coordination of multiple robots. According to Zhang and Mehrjerdi (2013) the coordination and control algorithms can be classified in leader-follower, behavioral based, virtual structure, graph based and potential field based approaches. The leader-follower principle is a well-established approach for non-holonomic mobile robots (Consolini et al. 2008; Cui et al. 2009), particularly regarding decentralized controllers in order to maintain the flexibility of a distributed system. These decentralized controllers are typically based on feedback linearization (Ge and Cui 2002; Desai et al. 1998) or backstepping and can be adapted to different tasks by switching the control law (Das et al. 2002). The same control approaches can also be found in behavioral (Lawton et al. 2003), virtual structure (Beard et al. 2001; Mehrjerdi et al. 2011), graph theory based (Fax and Murray 2004; Cai and Queiroz 2015; Dong and Farrell 2008) and artificial potential (Nascimento et al. 2014, 2013) based control approaches.
A more generic tool for multi-robot control is MPC which is based on formulating the control scenario as optimization problem. One typical example of MPC for UAVs is trajectory tracking in formation flight while considering collision avoidance constraints. Examples of a centralized MPC of cooperative control scenarios is given in Shin and Kim (2009) and Alrifaee et al. (2014). In Shin and Kim (2009) a leader-follower mode is used to perform airplane formation flight with collision avoidance using nonlinear MPC. For this purpose Shin and Kim (2009) compares centralized, sequential decentralized and fully decentralized methods of nonlinear MPC. Alrifaee et al. (2014) is presenting a non-convex MPC for cooperative control. Here, the first objective is to tackle collision avoidance while the secondary performance objective is to deal with the quality of the collision-free trajectory. Examples of the use of decentralized MPC is given by Shin and Kim (2009), Fukushima et al. (2013), Turpin et al. (2012) and Bemporad and Rocchi (2011). The considered scenario in Fukushima et al. (2013) is formation control of a multi-vehicle system with collision avoidance and input constraints. For this purpose a feedback linearization controller is integrated with MPC. The application of Turpin et al. (2012) is trajectory tracking of aerial robots under formation constraints using decentralized MPC. In Bemporad and Rocchi (2011) a decentralized linear time-varying MPC is used for formation control of multiple UAVs using a leader-follower approach.
The generality and the high control performance of MPC come with a high computational burden. Hence, the real-time capability is a crucial aspect of MPC which has led to a variety of fast optimization algorithms to minimize the related computational effort. A theoretically well-established and widely used fast MPC algorithm is sequential quadratic programming (SQP) in combination with Newton-type solvers with e.g. Gauß-Newton or Broyden-Fletcher-Goldfarb-Shannon (BFGS) Hessian approximation. A comprehensive framework with a wide variety of related algorithms is ACADO (Diehl et al. 2009). The computational efficiency and real-time feasibility for fast mobile robot systems have been validated experimentally, as for example in collision avoidance scenarios with an aerial manipulator (Geisert and Mansard 2016) under use of BFGS. A computationally efficient non-SQP variation of a Newton-type method is the continuation generalized minimal residual (CGMRES) method as presented in Ohtsuka (2004). Its underlying concept is introduced in Sect. 3. A compact version in \(C{++}\) code is freely available under (Ohtsuka 2015). The low computational burden of CGMRES makes it particularly suitable to control fast systems, such as e.g. gasoline engines (Kang et al. 2014), hover crafts (Seguchi and Ohtsuka 2003) and Eco cruise control scenarios (Sajadi-Alamdari et al. 2016). To increase the numerical stability, the condensed multiple shooting derivative CMSCGMRES has been developed in Shimizu et al. (2009, 2006). In the previous publication (Dentler et al. 2016a), CMSCGMRES has been successfully implemented to control a commercial quadrotor. The low computation time and real-time capability of CMSCGMRES has been confirmed experimentally for the given scenario. For this reason, this contribution is also based on CMSCGMRES. To reduce the implementational effort of additional inter-robot communication and consensus mechanisms and to compute a globally optimal solution, this contribution is computing the MPC centrally. Yet, in order to maintain the modularity of the distributed system in the central MPC scheme, the modularization scheme from previous work (Dentler et al. 2016b) is utilized in the form of the DENMPC framework, as published in Dentler et al. (2017) (more details are given in Sect. 3).
Within this work the cooperative control for a localization scenario with limited sensor perception is discussed. In the context of formation control the problem of a limited sensor perception space is critical along with collision avoidance and trajectory tracking. One approach for vision sensors is visual servoing based on optical flow or features, as shown in de Ruiter and Benhabib (2008), Kendoul et al. (2009) and Erkent and Işıl Bozma (2012). For traditional backstepping controllers, sensor perception limits are addressed by switching the robot’s formation control according to the compliance with the sensor constraints (Wang et al. 2015). Another approach is to compute the optimal boundary trajectories to satisfy the sensor constraint and track these, as shown for non-holonomic robots in Bhattacharya and Hutchinson (2006) or for visual servoing in Bhattacharya et al. (2007) and López-Nicolás et al. (2010). Nevertheless, the task dependency of the control laws makes it challenging to formulate control laws for complex scenarios with constraints. One way to avoid this loss of generality is to use MPC which allows defining tasks and constraints as optimization problem in a generic way. An example for a cooperative MPC using barrier function constraint handling with sensor and collision avoidance constraint is given in Ding et al. (2016). In Seo et al. (2017) an aerial manipulator is presented with a camera attached to the end-effector. The camera is controlled using a stochastic MPC method for visual servoing in order to keep the target in the field of view. Avanzini et al. (2015) is presenting the direct implementation of sensor constraints in MPC for holonomic mobile manipulators. The handling of constraints in MPC itself is a wide field of research. The major difficulty in MPC is how constraints are handled within the MPC solver. An overview and benchmark of computationally efficient inequality constraint handling techniques with CGMRES is given in Huang et al. (2015). The disadvantage of these simplistic constraint handling techniques, as for example auxiliary variable and logarithmic barrier method, is that a violation leads to an infeasible OCP and accordingly to a crash of the MPC solver. This is particularly problematic for fast MPC solvers, as they do not consider invalid values (inf, nan) within the prediction horizon and do therefore not automatically recover from an infeasible state. If a small constraint violation can be accepted, one way to avoid this problem is the use of weakened constraints. A weakened constraint is approximating the inequality constraint switching behavior by an analytical function [e.g. sigmoid (Lau and Lim 2017), tanh] which leads to a potential function. A comprehensive study on such weakened constraints in combination with MPC for multi UAV control strategies is given in Bertrand et al. (2014). The provided examples are collision avoidance, area exploration and formation flying. The same approach has been successfully implemented for collision avoidance of a MPC controlled quadrotor system in previous work (Dentler et al. 2016a).
To conclude, in order to solve the position tracking problem of cooperative localization scenarios, this work is presenting a workflow to formulate sensor constraints as potential functions. To be more flexible than feedback linearization and backstepping control approaches in task and constraint description, a MPC approach is applied. In order to achieve real-time capability the MPC problem is solved by a central CMSCGMRES approach. To maintain the modularity of the MPC with respect to the distributed problem, this approach is combined with the MPC modularization technique, presented in Dentler et al. (2016b). The prediction model for the MPC is based on the quadrotor model from the previous contribution (Dentler et al. 2016a). An introduction of the utilized MPC approach is given in the following section.
MPC operation cycle
3 Model predictive control principle and modularization
The idea of MPC is to compute optimal controls for a given system objective within a receding horizon as shown in Fig. 2. For this purpose, the current system state is measured at each control update time instance (\(t_k,t_{k+1},\ldots \)). From each of these measured states, the future systems behavior can be predicted by means of a system model within a given horizon (\(0\le \tau \le T\)). The controls for this horizon are then determined to minimize the error of the future system behavior to a given target behavior. After determining the optimal controls, \(\mathbf {u}\left( t_k\right) =\mathbf {u}\left( \tau _0\right) \) is applied to the system and the horizon is shifted by \({\varDelta }t\). The control loop is closed by a new measurement and prediction at time instance \(t_{k+1}\) (\({\varDelta }t\) later). The computation of the optimal controls within the prediction horizon can be formulated as optimization problem, a so called optimal control problem. In this work, OCPs of the form
are considered. The desired behavior is defined by the cost function J which is consisting of an integral cost term. It is subjected to the prediction model dynamics \(\mathbf {f}\left( \mathbf {x},\mathbf {u},\tau \right) \). The initial state condition \(\mathbf {x}_0\) is representative for the measurement at each control update interval. A common way to solve OCPs in real-time applications is to derive the Hamiltonian for (1)
with the Lagrange multipliers \(\varvec{\lambda }\). \(\varvec{\lambda }\) can then be computed via backward integration from \(\mathbf {0}\) over the horizon using
The controls are then typically determined by solving the first order optimality condition
There is a wide variety of methods to solve (4), whereas for real-time MPC common approaches are gradient [e.g. GRAMPC (Graichen and Käpernick 2012)] or Newton-type [e.g. Gauß-Newton in ACADO (Diehl et al. 2009)] line search methods.
Within this work, a continuation generalized minimal residual method CGMRES derivative is used which has been already successfully applied in previous work (Dentler et al. 2016a, b). The continuation idea is to look at the continuous closed loop dynamics of the stabilized system
which can then be used to approximate \(\dot{\mathbf {u}}\)
\(\dot{\mathbf {u}}\) can be computed efficiently with a GMRES method under use of a forward difference approximation of \(H_u^{-1}\). The controls \(\mathbf {u}\) are finally gained by integrating \(\mathbf {u}\) from the previous time step with \(\dot{\mathbf {u}}\)
More detailed information about the CGMRES algorithm can be found in Ohtsuka (2004). By making the continuation assumption (5) also for the states \(\mathbf {x}\), a multiple shooting method can be derived to increase numerical stability. This increases the problem dimension, as the corresponding equation to (5) for the inputs \(\mathbf {u}\) has also to be solved for the predicted system states within the horizon. An additional condensing addresses this issue by reducing the problem dimension again. A detailed overview of the CMSCGMRES method is given in Shimizu et al. (2006). The major advantage of using the continuation approach is the low computation time of the CGMRES method which makes it particularly interesting for real-time MPC, as already discussed in previous work (Dentler et al. 2016a).
Within this work, a modularization of MPC for cooperative control scenarios is applied, as presented in Dentler et al. (2016b). For cooperative scenarios with two entities (\(agent 0:{x_0,u_0}\) and \(agent 1:{x_1,u_1}\)) a cost function can have the form
where \(l_0\) and \(l_1\) represent tracking cost functions, while \(l_c\) is defining some interaction costs. Under this assumption the optimality condition 6 yields to
With the optimality condition (9) \(l_c\) will influence \(u_0\) through \(\frac{\partial l_c\left( \mathbf {x}_0,\mathbf {u}_0,\mathbf {x}_1,\mathbf {u}_1\right) }{\partial \mathbf {u}_0}\) and \(u_1\) through \(\frac{\partial l_c\left( \mathbf {x}_0,\mathbf {u}_0,\mathbf {x}_1,\mathbf {u}_1\right) }{\partial \mathbf {u}_1}\). The modularization allows to switch off the influence of \(l_c\) on e.g. \(u_1\) by neglecting \(\frac{\partial l_c\left( \mathbf {x}_0,\mathbf {u}_0,\mathbf {x}_1,\mathbf {u}_1\right) }{\partial \mathbf {u}_1}\) in the optimality condition (9). This is useful, if one central MPC is used to control the complete cooperation scenario, but some interaction tasks shall just influence one drone (e.g. the use case scenario of this work). The further advantage of this centralized approach is its high performance, as not just the measured, but also the predicted future system states are taken into consideration. In the OCP the exclusion of cost derivatives (e.g. with respect to \(u_0\)) will be marked by an index \( \backslash \{u_0\}\), e.g.
To finally apply a MPC in a mobile robot scenario, a prediction model is required. For real-time applications the complexity of this prediction model is crucial for the performance of the MPC solver. Hence, a very compact model is preferable which is developed in the next section.
4 Direction vector prediction model and validation
Most mobile robots are designed to move in a planar space. Their position is defined in a xy-plane and the height of this plane (z). Accordingly, their attitude is defined by the rotation angle \({\varPsi }\) around the plane normal vector. This description does not only fit for most wheeled ground robots, but can also be applied to multi-rotor unmanned aerial vehicles. Multi-rotor UAVs are typically operated around their static equilibrium. By assuming that rotations around x (roll) and y (pitch) are so small to be be neglected, the quadrotor attitude can be linearized. This yields to a hover controller (Corke 2013), as implemented in most commercial multi-rotor UAVs. As a result, the pose can be described by a single yaw angle \({\varPsi }\), representing the rotation around the z axis. To address the modeling of such systems, this section is introducing a modeling method for hover controlled multi-rotor systems. This model has furthermore the advantage to contain all elements from which omnidirectional and unidirectional ground robot motion models can also be derived.
AR.Drone 2.0\(^1\) coordinate frame definition
To derive the generalized multi-rotor model, the coordinate frames, given in Fig. 3 are considered. A standard approach is to model the system’s behavior in the state-space and to give the system function as an Ordinary Differential Equation (ODE). The state vector \(\mathbf {x}\) of such a system
is composing \(x_{\mathcal {G}}\), \(y_{\mathcal {G}}\), \(z_{\mathcal {G}}\) position in the global frame \(\mathcal {G}\), the \({\varPsi }_{\mathcal {G}}\) rotation around \(z_{\mathcal {G}}\) and the forward \(\dot{x}_{\mathcal {V}}\) and sideward \(\dot{y}_{\mathcal {V}}\) velocity in the vehicle frame \({\mathcal {V}}\). Under use of the forward, sideward, upward and heading velocity as input
the system dynamics \(\mathbf {f}\left( \mathbf {x}\left( t\right) ,\mathbf {u}\left( t\right) \right) \) can be approximated by a semi-nonlinear state-space model (Dentler et al. 2016a)
For low-cost quadrotors the velocity inputs are typically just related to an attitude displacement, e.g. increase pitch angle to increase forward velocity. Accordingly the inputs are not expressing the exact velocity in \(\hbox {m s}^{-1}\). The identification of the linear model parameters helps to describe this attitude control behavior and to accommodate such unnormed system inputs. Representatively for such low-cost mobile robotic systems, the quadrotor \(AR.Drone\,2.0\) is applied as example within this work.
4.1 Angle discontinuity effect on UAV control
The attitude of mobile robots which are moving in a planar plane is typically defined by a single angle \({\varPsi }\) on the interval
For a full rotation of the mobile robot, \({\varPsi }\) is changing the sign between \(\pm \pi \). By artificially limiting the angle on the interval (15) a discontinuity is introduced into the model of the angle. This is problematic, if the attitude is controlled by means of velocity or acceleration. To show the problematic behavior, a model predictive controller is applied to an AR.Drone 2.0 quadrotor under use of the prediction model (11) with
The resulting trajectory is given in Fig. 4. To control the quadrotor attitude, traditionally the error \(e_{{\varPsi }}={\varPsi }_{des}-{\varPsi }\) to the desired yaw angle \({\varPsi }_{des}\) is minimized. The yaw angle plot in Fig. 4 shows a step in the desired angle from \({\varPsi }_{des}\left( 0\,\hbox {s}\right) =\frac{\pi }{2}\) to \({\varPsi }_{des}\left( 2.8\,\hbox {s}\right) =\pi \). To minimize \(e_{{\varPsi }}\), the controller is applying a positive angular velocity to converge asymptotically towards \({\varPsi }_{des}=\pi \). As real mobile robotic systems are exposed to disturbance, the robot is likely to overshoot \({\varPsi }_{des}=\pi \) which leads to a change of sign to \({\varPsi }=-\pi \). This can be seen in Fig. 4 at \(t\approx 5.4\,\hbox {s}\). Hence, the quadrotor will again try to reach the desired value from the new angle \({\varPsi }_{des}=-\pi \). As a result, positions close to \({\varPsi }_{des}=\pm \pi \) cannot be stabilized which leads to a repetitive rotational movement.
Angle discontinuity problem regarding the control trajectories of a real \(AR.Drone\,2.0\) quadrotor
The main use of angle \({\varPsi }\) is the mathematical description for the mapping of the vehicle coordinate frame \(\mathcal {V}\) to the global coordinate frame \(\mathcal {G}\). This is typically done by means of a rotation matrix, as shown in (). For the planar case the rotation matrix yields
To overcome the described angle discontinuity in the transformation, a continuous way to describe the robot attitude has to be used. One way to do so is to use a direction vector. For 3D-space this is well established in the form of quaternions \(\mathbf {q}\in \mathcal {R}^4\) which consist of a real part \(q_0\) and three imaginary parts \(q_1\), \(q_2\), \(q_3\) to describe rotations \(\mathbf {q}=<q_0,q_1,q_2,q_3>\). In state space models these four elements are treated as separate states. For real-time MPC the related increase in the OCP dimension is significant. For the considered robots, the pose control is only based on a rotation in the 2Dxy-plane. Accordingly, a direction vector approach is sufficient to describe the attitude, as discussed in the next Sect. 4.2.
Unit circle
4.2 Direction vector approach
As previously discussed, the direction of a vector can be used to describe a robot attitude. Each position vector of the points on the unit circle can accordingly be used which is directly related to complex number theory. These vectors are uniquely defined by their projections onto the coordinate axis x and y as shown in Fig. 5. In comparison to a single angle description with yaw \({\varPsi }\), this transformation is bijective. In the context of this work, the combination of these two projections (\(d_x\) and \(d_x\)) is called direction vector \(\mathbf {d}\). The direction vector \(\mathbf {d}\) can be written in vector form
As the direction vector is expressing the projection from the unit circle, \(d_x\) and \(d_y\) are fulfilling the circle constraint
To receive the state space description, \(\dot{\mathbf {d}}\) yields under use of (18) to
This is intuitive, as the derivative \(\dot{\mathbf {d}}\) has to be orthogonal to \(\mathbf {d}\) to force \(\mathbf {d}\) to stay on the unit circle.
The system input \(u_{{\varPsi }}\) is expressing the angular velocity \(\dot{{\varPsi }}\) in (20) with the constant factor \(b_{\psi }\). Hence, the derivative yields to
Transformation matrix (17) is transformed with (18) to
To transform the system dynamics () into a direction vector model, \({\varPsi }\) is substituted by the direction vector in the state vector
Using the direction vector (18), the derivative (21) with \(u_{{\varPsi }}\) and the coordinate transformation (22), the system dynamics () finally leads to
To track attitude \(\mathbf {d}\), a simple quadratic penalty can be used
under the assumption, that numerical errors of the MPC solver avoid the singular problem of opposing attitudes, e.g. \(\mathbf {d}_{des}=[1,0]^{\top }\) with \(\mathbf {d}=[-1,0]^{\top }\), or \(\mathbf {d}_{des}=[0,1]^{\top }\) with \(\mathbf {d}=[0,-1]^{\top }\).
Experimental Validation of direction vector quadrotor model
4.3 Experimental validation of direction vector approach
To validate the direction vector quadrotor model (24), the desired drone attitude is rotated anti-clock-wise in steps of \({\varPsi }=\frac{\pi }{2}\). The \({\varPsi }\) plot in Fig. 6 shows the desired and actual attitude of the system. In contrast to the previous instability at \({\varPsi }=\pm \pi \) (Fig. 4), Fig. 6 is showing the desired asymptotic approaching of the desired trajectory. The oscillations in x, y, z around the desired point are caused by disturbance. This includes airflow disturbance, modeling errors, numerical errors and the trade-off between energy optimality and position tracking. Hence, the direction vector approach is resolving the angle discontinuity problem stated in Sect. 4.1. The proposed approach is a trade-off between the continuous attitude description, the computational effort, regarding the quaternion approach (4 states) and the standard angle description (1 state). Regarding the generality of the direction vector model, the same approach can be easily applied also to other planar robots with single angle attitude description. For example ground robots can be modeled by neglecting the z component of (24) with \(u_{z}=0\). For unidirectional robots, the sideward movement can be neglected by setting \(u_{s}=0\). Based on the resulting direction vector based system dynamics, the next sections describe the application of the model in a sensor constrained model predictive control scenario.
5 Sensor based control with potential functions
One major difficulty to control complex tasks autonomously is the mathematical formulation of such tasks. A generic way to do so are inequality constraints. MPC can take such constraints into consideration. In this work, they are considered in the MPC as weakened constraints. This refers to the substitution of hard inequality constraints by a cost function, that imposes a repulsive behavior from a violation of the constraint. This implementation in the cost function equals to a potential function. In this section, a generic procedure to create such potential functions is presented. The formulation of a sensor constraint serves as example. In the example scenario an object is tracked with a sensor attached to a quadrotor. The sensor perception space is thereby shaped like a cone (e.g. ultrasonic distance sensor). How to describe this sensor limitation is shown in the following section.
5.1 Sensor constraints
The considered use case is an \(AR.Drone\,2.0\) quadrotor with the presented dynamics (24). With the example of a cone-formed sensor perception space, the robot/sensor system can be illustrated as shown in Fig. 7. The first step to implement the sensor based control is, to formulate the perception space limitation in terms of constraints. For this purpose, a target object is defined in the sensor frame with the position vector \(\mathbf {\mathbf {p}}_{\mathcal {S}}\in \mathcal {S}\)
Regarding the position of the trackable object in the sensor frame \(\mathbf {p}_{\mathcal {S}}\), the field of view of the sensor can be expressed by the constraints
where (27) is representing a double cone. To receive a single cone perception space, constraint (28) is limiting the cone to the positive half plane of \( x_{p\mathcal {S}}\). In contrast to just pointing the quadrotor into the target’s direction, the formulation of the perception area offers more flexibility to the MPC to optimize the energy consumption and to adapt the scenario to other constraints e.g. obstacles. The question of how to consider the sensor constraint (27) and (28) in an optimal control problem is described in the next section.
Use case scenario: tracking with cone shaped sensor perception of a quadrotor
5.2 Potential function constraint handling
Considering the constraints (27) and (28) as hard constraints is problematic, because their violation would lead to an infeasible optimization problem. In the sensor based tracking scenario this would be the case, if the object is outside the sensor perception space. Such a violation is possible due to disturbance or an infeasible initial pose. For this reason, the sensor constraints are designed as weakened constraints by imposing a repulsive behavior from constraint violation. One way to accomplished this is to add an additional penalty term to the OCP’s integral costs l. Due to the fact that OCPs are typically defined as minimization problems with the optimum \(l=0\), a constraint violation has to be penalized with a higher cost. An intuitive approach to translate the constraint \(c\le 0\) to the weakened constraint \(l_c\) is therefore to penalize the compliant area with \(l=0\) and the constraint violation area with \(l=1\). This can be described by using a unit step \(\epsilon \), such that
For the cone constraint (27) and (28) this leads to
\(c_2\) is used to distinguish between the negative and positive half-space of \(x_{p\mathcal {S}}\):
To initially use the unit step approximation (29) for the constraint transformation has proven to be particularly helpful regarding potential functions developed from nested constraints. More complex approximation functions lead to larger mathematical expression and reduce the readbility of the behavior of the potential function. Furthermore, the behavior of the developed potential function can be easily validated visually by plotting the areas with potential value \(l_c=0\) and \(l_c=1\). For the example of the weakened cone constraint (30), this results in the characterizing cone area with potential value \(l_c=0\) and the corresponding incompliant area outside with \(l_c=1\) as shown in Fig. 8.
Unit step penalty function values of cone constraint)
5.3 Addressing vanishing gradient
The resulting cost function for the xy-plane is shown in the left plot of Fig. 9. As expected, the figure shows that the gradient satisfies
Unit step penalty function of cone constraint in the xy-plane)
As most approaches for searching the minimum of the defined cost function \(l_c\) are based on a gradient descent, this property becomes problematic, as the convergence of the search algorithm cannot be guaranteed. To address this issue a cost slope can be added around the cone as shown in the right illustration of Fig. 9. To impose a gradient, a simple quadratic penalty can be added in the undesired regions. Hence, (30) can be extended to
whereby parameter \(\kappa _G\) is controlling the steepness of the gradient derivative. As a remark, gradient-based solvers typically require convex OCP problems to ensure convergence. Naturally, most sensor perception spaces are convex. However this should be kept in mind for development of more complex constraints or the combination of multiple constraints.
5.4 Addressing differentiability of the potential function
The second problematic property of the proposed unit step constraint translation (29) is that the derivative of the unit step is not an analytical function. Yet, most fast optimal control problem solvers require the differentiability of the cost function. To address this problem, the switching behavior of the unit step, with respect to the constraints, can be approximated by means of a sigmoid function. This has been already validated in previous work for a collision avoidance constraint (Dentler et al. 2016a) and is similar to the \(\tanh \) approximation, as introduced in Bertrand et al. (2014). Accordingly, the unit step can be approximated with
where \(\kappa _A\) is a design parameter. The derivative of \(sig\left( c,\kappa _A\right) \) can be determined analogously
Figure 10 is showing the behavior of the sigmoid function and it’s derivative for a variation of \(\kappa _A\).
Sigmoid approximation of unit step with corresponding derivatives
For increasing \(\kappa _A\), \(sig\left( c,\kappa _A\right) \) is converging towards a step function \(\epsilon (c)\). Its derivative is accordingly converging towards a \(\delta \) impulse
Factor \(\kappa _A\) is therefore determining the trade-off between quality of the approximation and condition number of the function. A bad-conditioned problem for high \(\kappa _A\) is numerically more difficult to solve. The transformation of the extended weakened cone constraint (34) by means of a sigmoid function (35), finally yields to
which is shown in Fig. 11 for \(\kappa _A=10\).
Extended weakened cone constraint transformed with sigmoid
To be able to track an object with known position in the global coordinate system, \(\mathbf {p}_{\mathcal {S}}\) in (30) has to be determined by its counterpart \(\mathbf {p}_{\mathcal {G}}\) in the global coordinate system. The required coordinate transformation is explained in the following section.
5.5 Coordinate transformation
The coordinate transformation from the global coordinate frame to the sensor frame can be described as a sequential transformation with homogeneous transformation matrices. For a matrix that transforms a point \(\mathbf {p}\) from the global coordinates \({\mathcal {G}}\) into the sensor frame coordinates \({\mathcal {S}}\) we use the following nomenclature
This transformation matrix can consist of the position displacement of coordinate systems
the rotational displacement expressed by an angle \(\beta \) e.g. around y
and a direction vector e.g. around z
With the
the transformation matrix from the global frame \({\mathcal {G}}\) into the vehicle frame \({\mathcal {V}}\)
and then to the sensor frame \({\mathcal {S}}\)
leads to the transformation matrix
and the inverse transformation
The global coordinates in the sensor frame is accordingly given by (40) and leads to
Finally the target position in the sensor coordinate frame can be expressed in global coordinates by (48) and applied in \({l_c\left( \mathbf {p}_{\mathcal {S}},\alpha ,\kappa _G,\kappa _A\right) }\) (39). Due to its complexity, the resulting equation is not given here. Figure 12 is showing the resulting costs in the xy-plane for a quadrotor at position \(\mathbf {p}_{r{\mathcal {G}}}=(-1,-1,0)^{\top }\) and orientation \(\mathbf {d}_{r{\mathcal {G}}}=(0.71,0.71)^{\top } \equiv {\varPsi }=45 {^{\circ }}\). The triangular base form of the cone is oriented as expected from the UAV origin in \(\mathbf {p}_{r{\mathcal {G}}}=(-1,-1,0)^{\top }\).
Tracking of global position with weakened cone constraint
6 Safety constraints
To validate the derived potential function experimentally, additional safety measures are necessary. The most important safety constraint is treating collision avoidance and ensures that a safety distance \(d_{min}\) between object and drone is not violated. Second, the maximum distance \(d_{max}\) of the sensor has to be considered. This can be accomplished by implementing a cohesion constraint which introduces a repulsive behavior from large distances between object and robot. Both constraints are derived according to the workflow presented for the sensor constraint in Sect. 5.
6.1 Collision avoidance constraint
Considering that \(\mathbf {p}_{{\mathcal {G}}}\) could also represent an obstacle to avoid, a potential function for obstacle avoidance can be formulated as penalty of a distance below a limit \(d_{min}\):
The norm can be reformulated by means of quadrature
which then is transformed into a potential function with unit steps
To improve the convergence properties, (51) is extended by a quadratic penalty term
Here, \(\kappa _H\) is defining the maximum height and \(\kappa _G\) the decent of the gradient of the potential function. Finally, (52) can be transformed to an analytical function with the help of the sigmoid function (36)
\(\kappa _A\) is describing the quality of the unit step approximation as before. The final result of the potential function is shown in Fig. 13 which shows a high penalty for the area with distance \(d_{min}\) around the origin. The form of the convex top can be adjusted with \(\kappa _G\). Figure 14 is showing penalty values \(l_{minD}>0.5\) for an obstacle in position \(\mathbf {p}_{{\mathcal {G}}}=(x,y,z)^{\top }\) with robot placed at \(\mathbf {p}_{r{\mathcal {G}}}=(-1,-1,0)^{\top }\). As desired any violation of \(d_{min}\) (49) is addressed with a high penalty. This yields a repulsive behavior between robot and object.
Collision avoidance constraint potential function over xy-plane
Collision avoidance constraint potential function in global perspective
6.2 Cohesion constraint
Cohesion can be seen as inversion of the collision avoidance problem (49), where distances bigger than \(d_{max}\) to an object should be avoided. The constraint can therefore be formulated as
As before, the norm can be expressed with a the help of a quadrature
and transformed into a cost function with a unit step function
To manipulate the curvature of the given penalty function, \(\kappa _H\) is introduced to define the maximum height. \(\kappa _G\) is describing the ascent of the gradient of the potential function
The final analytical cost function is gained from an approximation of the unit step \(\epsilon \) with the sigmoid function (36). Which yields
Figure 15 is showing the desired inverse behavior as for the collision avoidance behavior in Fig. 13. The cohesion constraint leads to a high penalty for distances greater than \(d_{max}\) around the origin. Figure 16 is showing penalty values \(l_{maxD}>0.5\) for an obstacle in position \(\mathbf {p}_{{\mathcal {G}}}=(x,y,z)^{\top }\) with the robot placed at \(\mathbf {p}_{r{\mathcal {G}}}=(-1,-1,0)^{\top }\). The figure validates that the whole area of \(\left\| \mathbf {p}_{{\mathcal {G}}}-\mathbf {p}_{r{\mathcal {G}}} \right\| \ge d_{max}\) is highly penalized which leads to an attracting behavior between object and robot.
Cohesion constraint function over xy-plane
Cohesion constraint potential function in global perspective
With the developed safety constraints (53) and (59), the cone constraint has been validated as discussed in the following section.
7 Validation of the sensor based control with potential functions
The validation scenario is a visual quadrotor tracking scenario, where one quadrotor is equipped with a camera and tracking a target quadrotor. The task is to keep the target quadrotor in the camera frame as shown in Fig. 17.
Visual tracking of quadrotor from camera-equipped quadrotor
The control of both quadrotors is accomplished with a central MPC controller (Dentler 2016) and extended by the potential functions that are defining the tracking task. The combination of cone (39), collision avoidance (53) and cohesion (59) constraint with the coordinate transformation (48) and quadrotor dynamics () with parameters (16) in an OCP results in
The index \({ \backslash \{u_1\}}\) of the cost functions \(l_c\), \(l_{maxD}\) and \(l_{minD}\) reflects, that the influence of the cost functions on \({\textit{UAV}}_1\) is neglected, as explained in (10). This means that the cone, collision avoidance and cohesion constraint is only affecting \({\textit{UAV}}_0\). The advantage of this modular approach of a central control for such a scenario is, that future states of both systems are considered for the computation of the optimal controls, while the effect of the tracking costs can be limited to one quadrotor.
The parameters of (60) for the experimental validation are given as
The parameters \(p_{cgmres}\) are referring to the CMSCGMRES solver and are given in a coherent notation to the previous work (Dentler et al. 2016a). To examine the dynamic behavior of the proposed control solution, the target position of \({\textit{UAV}}_1\) is moving in a circular trajectory. For \({\textit{UAV}}_0\), the choice of \(\mathbf {Q}_0\) leads to a tracking of zero forward velocity \(\dot{x}_{uav0\mathcal {V}}\left( t\right) =0\) and sideward velocity \(\dot{y}_{uav0\mathcal {V}}\left( t\right) =0\) which yields to the desired states
Based on the given parameters and target trajectories, the scenario is validated in the following sections.
7.1 Numerical validation
For the numerical validation, two \(AR.Drone\, 2.0\) models have been implemented in the simulation environment \(V\text {-}\)REP (Fig. 18). The position information of quadrotors and target trajectories is shared via a Robot Operating System (ROS) interface.
Numerical validation of the use case scenario with \(V\text {-}{\textit{REP}}\)
Numerical simulation: Trajectories of use case scenario
Figure 19 is showing the trajectories of both UAVs. \({\textit{UAV}}_1\) is following the circular moving target which is reflected by sinusoidal position trajectories. \({\textit{UAV}}_0\) is tracking \({\textit{UAV}}_1\) with the developed sensor constraints which is indicated by likewise sinusoidal position trajectories of \({\textit{UAV}}_0\). The form and position of the resulting trajectory is depending on the initial UAV positions. As the position of \({\textit{UAV}}_0\) is just dependent on the applied constraints, \({\textit{UAV}}_0\) can rotate freely around \({\textit{UAV}}_1\). This explains the drift of the sinusoidal position trajectory of \({\textit{UAV}}_0\). The control trajectories of \({\textit{UAV}}_1\) and \({\textit{UAV}}_0\) are showing that the input limits are respected. The distance d stays in the defined limits \(d_{min}\le d \le d_{max}\) with one exception at the initial phase of the simulation. Here the repulsive behavior of the collision avoidance constraint can be seen, where the controller increases the distance to fulfill \(d\ge d_{min}\). On one hand, the disadvantage of the weakened constraint is, that d can violate the given constraint depending on the parametrization of the potential function and the smoothness of the unit step approximation by the sigmoid (35). On the other hand, the advantage is, that a constraint violation does not lead to an infeasible OCP. To conclude, the distance trajectory is validating the active collision avoidance and cohesion constraint.
To validate that the tracked \({\textit{UAV}}_1\) stays within the sensor beam width angle \(\alpha \), Fig. 19 is therefore also showing the absolute tracking angle \(\alpha _t\)
which is describing the angle between the \({\textit{UAV}}_0\) sensor orientation vector and the distance vector to \({\textit{UAV}}_1\) in the sensor frame. The resulting \(\alpha _t\) plot in Fig. 19 is validating, that the cone constraint keeps the tracking angle \(\alpha _t\) smaller than the sensor beam width angle \(\alpha _t\le \alpha =0.5 \,\hbox {rad}\). It can be seen that the tracking angle \(\alpha _t\) is in fact much smaller. This is caused by the smooth approximation of the unit steps by sigmoids (35) which leads to a convergence towards the center of the cone. Especially for undisturbed systems, this yields to a smaller tracking angle \(\alpha _t\) than the beam width angle \(\alpha \). To reduce this effect \(\kappa _A\) can be increased.
A more intuitive access to the UAV behavior is gained by plotting the UAV positions and the orientation of \({\textit{UAV}}_0\) by means of a vector as shown in Fig. 20. To be able to associate both UAV positions, time-related UAV positions are connected with a line. It is visible that \({\textit{UAV}}_1\) is following the desired circular trajectory, while \({\textit{UAV}}_0\) is tracking \({\textit{UAV}}_1\) in an ellipsoidal movement. The orientation vectors are displayed at each \({\varDelta }t\approx 1.68\,\hbox {s}\) for means of visualization.
xy-plot with \({\textit{UAV}}_0\) orientation of the numerical simulation of the use case scenario (direction samples each \({\varDelta }t\approx 1.67\,\hbox {s}\))
To resume, Figs. 19 and 20 validate the desired behavior of the proposed sensor constrained MPC controller in simulation. The next section is discussing the extension of this numerical validation to the real scenario.
7.2 Experimental validation
The use case scenario with real \(AR.Drone\, 2.0\) quadrotors, as shown in Fig. 21, is subject to a variety of disturbance which is not considered in the numerical validation. Light-weight UAVs like an \(AR.Drone\, 2.0\) quadrotor are particularly responsive to airflow disturbance. In addition, their flight dynamics are very volatile, as their body consist of deformable Styrofoam. These and more influences (communication latency, prediction model errors, measurement uncertainty) are not considered in the MPC model and simulation environment. For this reason an experimental validation is necessary to assess the robustness of the proposed control approach. The position data of the real \(AR.Drone\, 2.0\) quadrotors is hereby measured by a motion capture system.
Experimental validation of the use case scenario with real quadrotors
Trajectories of real use case scenario
The resulting system trajectories are given in Fig. 22. In contrast to the numerical simulation, the real \(AR.Drone\, 2.0\) trajectories are subject to significant disturbance. Especially the mutual airflow disturbance is causing low-frequency oscillations \(\approx 0.5 \hbox {Hz}\) which are visible in the y-position of \({\textit{UAV}}_0\) and \({\textit{UAV}}_1\). As the airflow disturbance error is propagating from the \({\textit{UAV}}_1\) position to the \({\textit{UAV}}_0\) response, the resulting oscillations are particularly visible in the controls of \({\textit{UAV}}_0\).
To evaluate the control performance, the distance d and absolute tracking angle \(\alpha _t\) are given in Fig. 22. The distance plot is stating that \({\textit{UAV}}_1\) is tracked within the given distance limitations. At \(t\approx 55\,\hbox {s}\) the behavior of the weakened constraint is visible which is allowing a minor violation of \(d_{min}\) in return for avoiding infeasible solutions and ease of implementation. The absolute tracking angle (71) in Fig. 22 is measured between the \({\textit{UAV}}_0\) orientation vector and the distance vector to \({\textit{UAV}}_1\). Due to the initial conditions, \(\alpha _t\) is violating the applied cone constraint at the beginning, but is tracked within the given beam width angle \(\alpha _t\le \alpha =0.5 \,\hbox {rad}\) for \(t\ge 6\,\hbox {s}\). Hence, the trajectories in Fig. 22 confirm the desired tracking behavior.
Figure 23 is showing the resulting xy-trajectory with samples of the \({\textit{UAV}}_0\) orientation vector. For means of visualization, the orientation sample time is reduced to \({\varDelta }t\approx 1.68\,\hbox {s}\). Due to different initial conditions (positions, velocities, etc.), the xy-trajectory is not directly comparable with the numerical simulation. However, it visualizes the closed-loop UAV position response to mutual airflow disturbance in the form of small oscillation. In comparison to the simulation trajectory, the rejection of these oscillations (input costs) dominate the minor gradient within the compliant area of the sensor constraint. As a result the absolute tracking angle \(\alpha _t\) and distance d plots in Fig. 22 go closer to their constraint limits and the xy-plot does not follow the ellipsoidal pattern of \({\textit{UAV}}_0\) in Fig. 20. In order to evaluate the tracking without the mutual airflow disturbance and under different initial conditions, a further analysis of the robustness is shown in the experimental discussion (Sect. 7.3).
For the evaluation of the computational efficiency of the proposed approach, Fig. 24 is giving the MPC computation time on a standard computer (\(Dell\text { }Latitude\text { }E5440\)). The peaks in the computation time of \(t_{comp}\approx 20 \hbox {ms}\) are not directly related to the solver, but are caused by CPU interrupts by other processes. The resulting average computation time \(t_{av,comp}=2.5 \hbox {ms}\) is very low in comparison to the control update interval of \({\varDelta }t=10 \hbox {ms}\) and states the real-time feasibility of the MPC.
To conclude, the experimental results are validating the computational efficiency and effectiveness of the MPC control based on potential functions.
xy-plot with \({\textit{UAV}}_0\) orientation of real use case scenario (Direction samples each \({\varDelta }t\approx 1.68\,\hbox {s}\))
Computation time of real use case scenario
7.3 Experimental discussion
In order to discuss the robustness to disturbance and initial conditions, the previous experiment of Sect. 7.2 is altered by substituting \({\textit{UAV}}_1\) by a target with constant position \(\mathbf {p}_{uav0\mathcal {G}}\rightarrow \mathbf {p}_{t\mathcal {G}}=\left[ 0.04, -0.05, 0.96\right] ^{\top }\hbox {m}\) . The disturbance is introduced manually by means of an obstacle with the position \(\mathbf {p}_{O\mathcal {G}}\) and a related collision avoidance constraint (52) \(l_{minD}\left( \mathbf {p}_{O{\mathcal {G}}},\mathbf {p}_{uav0{\mathcal {G}}},d_{O,min},\kappa _H3,\kappa _G3,\kappa _A3\right) \). In order to make the evasive behavior visible in the xy-plane, the z-axis action of \({\textit{UAV}}_0\) is reduced by increasing the input penalty for \(u_z\). The resulting OCP (72)–(78) does consider the obstacle and target position within the prediction horizon as constant
The experimental outline is shown in Fig. 25. As in Sect. 7.2, the pose of \({\textit{UAV}}_0\) is measured with a motion capture system. The constant target position is indicated as green diamond in the center of the pictures. In its initial pose, \({\textit{UAV}}_0\) is not necessarily fulfilling the underlying inequality constraints of the sensor cone constraint (39). The activation of the controller therefore initially leads to a convergence towards a compliant pose. As a next step, an obstacle (red star) is introduced manually by means of the motion capture system. \({\textit{UAV}}_0\) (blue circle) is evading the approaching obstacle by moving in the opposite direction. This evasion maneuver shows the form of an arc due to the active target tracking constraints. Following \({\textit{UAV}}_0\) with the obstacle consequently leads to a circular trajectory around the tracked target point \(\mathbf {p}_{t\mathcal {G}}\). The corresponding \({\textit{UAV}}_0\) orientation is indicated by a blue arrow.
\({\textit{UAV}}_0\) trajectory—tracking target with constant position while obstacle is avoided
\({\textit{UAV}}_0\)xy-trajectory with pose markers every \({\varDelta }t=4.2\,\hbox {s}\) showing circular evasion maneuver pattern
\({\textit{UAV}}_0\) pose trajectory with steps in the \({\varPsi }\)-trajectory due to the limited yaw angle intervall
Manually introduced obstacle position showing circular pattern in order to follow \({\textit{UAV}}_0\) on its evasion trajectory. Any steps are caused by entering the obstacle into the field of detection of the motion caption system
\({\textit{UAV}}_0\) distance to obstacle \(d_{O}\) stays above the defined minimum distance of \(d_{O,min}=1.0\hbox {m}\)
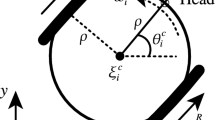
To cope different initial conditions and obstacle patterns, a set of 10 experiments is conducted. Figure 26 is showing the resulting xy-trajectory of \({\textit{UAV}}_0\) (blue line), obstacle (dashed red line) and the fixed target position (green diamond). To visualize the system at different time instances, the position of the obstacle (red star) and pose of \({\textit{UAV}}_0\) (blue circle with arrow) is marked every \({\varDelta }t=4.2\,\hbox {s}\). The distances between \({\textit{UAV}}_0\) and target is signalized as light grey line at each of these time instances. Accordingly, the distance between \({\textit{UAV}}_0\) and the obstacle is indicated as light red line. The resulting circular patters validates the target tracking during the evasion maneuver. Furthermore, the direction of the drone is pointing to the center which is indicating the tracking of the target. In this context, in plot 7 center left and plot 9 center up the drone orientations which are not pointing towards the target are representing initial conditions. These initial poses of \({\textit{UAV}}_0\) have been chosen arbitrarily within the spacial limitations of the laboratory and its exact values can be exerted from the \({\textit{UAV}}_0\) pose plots in Fig. 27. In this initial phase a typical increase in the altitude (z) can be observed which is caused by the inclination angle \(\beta \) of the sensor cone constraint. The steps in the \({\varPsi }\) values in Fig. 27 are based on the limited \({\varPsi }\)-angle interval. The sinusoidal trajectories in x and y evidence the circular evasion maneuver of \({\textit{UAV}}_0\). Figure 28 is showing measurements of the corresponding obstacle position. Also here the sinusoidal trajectory, in order to follow the \({\textit{UAV}}_0\) and provoke an evasion, is visible. The steps in the obstacle position at the beginning are caused by entering the detection zone of the motion capture system.
To analyze the influence of the obstacle collision avoidance constraint \(l_{minD}\) (53), Fig. 29 is showing the distance between \({\textit{UAV}}_0\) and obstacle. The plots show how the obstacle is moved close to \(d_{Omin}\) to provoke an evasion maneuver of \({\textit{UAV}}_0\). The measured minimal distances are given in Table 1. As the collision avoidance design is based on weakened constraints, violations are feasible. For all 10 experiments the highest violation of the obstacle distance \(d_{O}\) appears in run 5 with \(\min (d_{O})=0.601\hbox {m}\). The violation generally depends on \({\textit{UAV}}_0\) and obstacle speed as well as cost gradient design of the collision avoidance constraint. For the here considered UAV and obstacle speeds, the cost gradient is chosen less steep (77) in order to show a smooth repulsive behavior while showing the desired evasion. In reverse conclusion higher violations are accepted. For higher system velocities this cost gradient has to be chosen steeper. Its repulsive behavior can be observed as oscillation around the constraint border in Fig. 29 run 6, 7 and 9.
The influence of the target collision avoidance and cohesion constraints can be evaluated using the Euclidean distance of \({\textit{UAV}}_0\) to the target, as shown in Fig. 30. Both constraints restrict the distance to \(d_{min}=0.7\hbox {m}\le d \le 2.0\hbox {m}=d_{max}\). The measured distance d lies in the interval \(0.941\hbox {m}\le d \le 1.966\) and therefore complies to the target distance constraints for all 10 experiments. The peak distance values are given in Table 1. The minimum tracking distance \(\min (d)=0.941\hbox {m}\) appears in run 2 and its maximum value \(\max (d)=1.966\hbox {m}\) in run 10.
\({\textit{UAV}}_0\) distance to target d stays within the defined minimum distance of \(d_{min}=0.7\hbox {m}\) and maximum distance of \(d_{max}=2.0\hbox {m}\)
Finally, the behavior of the developed sensor cone constraint (39) is validated. For this purpose the absolute tracking angle \(\alpha _t\) (71) is shown in Fig. 31. The sensor constraint (39) is restricting the absolute tracking angle to \(\alpha _t \le \alpha _{t,max}=0.5\). For the set of experiments, the initial conditions do typically not satisfy this constraint due to a low initial \({\textit{UAV}}_0\) altitude z and incompliant orientation \(\psi \). This is directly shown by the controller counteraction as shown in Fig. 32. In the initial phase experiment 1–5 show a direct reaction in the altitude by \(|u_z|>>0\), while a significant adjustment in the \(\psi \)-axis by \(|u_{\psi }|>>0\) is dominating in experiment 5–10. The resulting convergence towards the constraint compliance \(\alpha _{t}\rightarrow \alpha _{t,max}\) can be seen in all plots of Fig. 30 and is followed by a period of low action, as all constraints are satisfied and the obstacle is not considered yet. With the approaching obstacle \(d_O \rightarrow d_{O,min}\) in Fig. 29, the control action in Fig. 32 is increased due to the evasion maneuver. As a result, also the tracking angle \(\alpha _{t}\) in Fig. 31 is disturbed. To measure the constraint violation the maximal absolute tracking angle in the nominal state \(\max (\alpha _{t,ns})\) is given in Table 1. For this purpose, \(\max (\alpha _{t,ns})\) takes into consideration the absolute tracking angle peak values after the initial convergence phase. \(\alpha _{t} \le \alpha _{t,max}=0.5 \,\hbox {rad}\) holds after the initial phase for all the experiments. The measured maximum appears in run 2 with \(\max (\alpha _{t,ns})=0.438 \,\hbox {rad}\).
The experimental results validate the desired behavior of sensor based tracking also under the influence of disturbance introduced as obstacle. The senor field of view limitations are respected and collisions are avoided. Furthermore, the set of experiments shows the robust convergence towards a compliant state under differing initial conditions and constraint violations.
\({\textit{UAV}}_0\) absolute tracking angle \(\alpha _{t}\) stays within the defined maximum of \(\alpha _{t,max}=0.5 \,\hbox {rad}\) of the sensor cone constraint
\({\textit{UAV}}_0\) actuation
8 Conclusion and perspective
The present paper focuses on the presentation of a workflow for the generation of potential functions for sensor constrained MPC. The workflow is tested in simulation and a real-world implementation of a sensor constraint tracking scenario with quadrotors.
For this purpose a compact motion model for multi-rotor UAVs has been developed. To be able to control the robot’s yaw angle orientation in \(360{^{\circ }}\), the problem of the discontinuously defined yaw angle \(-\pi <{\varPsi }\le \pi \) has been addressed. The MPC of the resulting direction vector model has been validated experimentally with an \(AR.Drone\,2\) quadrotor.
Based on the developed system dynamic description, the workflow for a sensor constrained MPC control has been presented. The \(AR.Drone\,2\) quadrotor with attached sensor has served as platform for the sensor based tracking scenario. The first step in the workflow is to formulate the sensor perception space within a sensor coordinate frame by means of inequality constraints. For the use case, the cone shape of the sensor perception space has been described by a combination of two inequality constraints. As second step, these constraints have been transformed into a potential function with the help of unit steps. The idea is to introduce a repulsive behavior for a violation of the constraints which leads to a weakening of the constraints. This allows a small violation to maintaining feasibility of the OCP. The transformation into a weakened constraint with the help of unit steps helps to verify the cost functions without having to deal with the increased complexity of sigmoids. In addition, it allows a simple graphical verification of the potential function with visualization tools. To improve the solvability of the problem for gradient based solvers, the next step has been the introduction of a gradient in the undesired ares of the potential function which is pointing away from the target region. Subsequently, the previously introduced unit steps in the potential function are approximated with sigmoids which leads to a continuous gradient around the constraint borders. As a result the potential function becomes analytical and therefore solvable by standard real-time MPC solvers.
In order to validate the derived potential function for the cone constraint, additional safety measures have been necessary. Therefore, a collision avoidance and a cohesion constraint have been developed, using the previously described workflow. In the validation scenario an \(AR.Drone\,2.0\) is used to track another \(AR.Drone\,2.0\) quadrotor which is following a circular trajectory. The tracking by means of the sensor constraint has been tested experimentally in simulation and a real-world implementation. To further discuss the influence of obstacles, utilized constraints and different initial conditions, a series of real-world collision avoidance scenarios has been presented. In the presented scenarios an \(AR.Drone\,2.0\) is tracking a fixed target using the developed constraints for the cooperative control scenario while disturbance is introduced in form of an obstacle. The results show the desired collision evasion maneuver while maintaining sensor tracking for different initial conditions. The results have validated the developed multi-rotor prediction model as well as the sensor constraint potential function.
Future work will focus on the solution of the localization problem with cameras. A further development will be the analysis of the energy efficiency of the proposed sensor constraint, in contrast to a simple orientation tracking. Particularly interesting would be a statistical analysis of large numbers of real-world experiments. Another direction of future studies is to distribute the presented central MPC and to explore the applicability of cloud computing. In addition, the application of the tracking scenario in heterogeneous systems e.g. ground robots and UAVs, will also be addressed in future work.
References
Alrifaee, B., Mamaghani, M. G., & Abel, D. (2014). Centralized non-convex model predictive control for cooperative collision avoidance of networked vehicles. In 2014 IEEE international symposium on intelligent control (ISIC), October 2014 (pp. 1583–1588).
Avanzini, G. B., Zanchettin, A. M., & Rocco, P. (2015). Constraint-based model predictive control for holonomic mobile manipulators. IEEE International Conference on Intelligent Robots and Systems, 2015–December(i), 1473–1479.
Beard, R. W., Lawton, J., & Hadaegh, F. Y. (2001). A coordination architecture for spacecraft formation control. IEEE Transactions on Control Systems Technology, 9(6), 777–790.
Bemporad, A., & Rocchi, C. (2011). Decentralized linear time-varying model predictive control of a formation of unmanned aerial vehicles. In 2011 50th IEEE conference on decision and control and European control conference, December 2011 (pp. 7488–7493).
Bertrand, S., Marzat, J., Piet-Lahanier, H., Kahn, A., & Rochefort, Y. (2014). MPC strategies for cooperative guidance of autonomous vehicles. AerospaceLab, 8, 1–18. https://hal.archives-ouvertes.fr/hal-01103195.
Bhattacharya, S., & Hutchinson, S. (2006). Controllability and properties of optimal paths for a differential drive robot with field-of-view constraints. Proceedings of IEEE International Conference on Robotics and Automation, 2006(May), 1624–1629.
Bhattacharya, S., Murrieta-Cid, R., & Hutchinson, S. (2007). Optimal paths for landmark-based navigation by differential-drive vehicles with field-of-view constraints. IEEE Transactions on Robotics, 23(1), 47–59.
Cai, X., & Queiroz, Md. (2015). Adaptive rigidity-based formation control for multirobotic vehicles with dynamics. IEEE Transactions on Control Systems Technology, 23(1), 389–396.
Consolini, L., Morbidi, F., Prattichizzo, D., & Tosques, M. (2008). Leader–follower formation control of nonholonomic mobile robots with input constraints. Automatica, 44(5), 1343–1349.
Corke, P. (2013). Robotics, vision and control: Fundamental algorithms in MATLAB (1st ed.). Springer Publishing Company, Incorporated.
Cui, R., Ge, S. S., How, B. V. E., & Choo, Y. S. (2009). Leader–follower formation control of underactuated auvs with leader position measurement. In 2009 IEEE international conference on robotics and automation, May 2009 (pp. 979–984).
Das, A. K., Fierro, R., Kumar, V., Ostrowski, J. P., Spletzer, J., & Taylor, C. J. (2002). A vision-based formation control framework. IEEE Transactions on Robotics and Automation, 18(5), 813–825.
de Ruiter, H., & Benhabib, B. (2008). Visual-model-based, real-time 3d pose tracking for autonomous navigation: Methodology and experiments. Autonomous Robots, 25(3), 267–286. https://doi.org/10.1007/s10514-008-9094-7.
Dentler, J. (2016). An event-based real-time nonlinear model predictive control framework. http://wiki.ros.org/denmpc. Accessed September 01, 2016.
Dentler, J., Kannan, S., Olivares-Mendez, M. A., & Voos, H. (2016a). A real-time model predictive position control with collision avoidance for commercial low-cost quadrotors. In 2016 IEEE multi-conference on systems and control (MSC), Buenos Aires, September 2016.
Dentler, J., Kannan, S., Olivares-Mendez, M. A., & Voos, H. (2016b). A modularization approach for nonlinear model predictive control of distributed fast systems. In 2016 24th mediterranean conference on control and automation (MED), June 2016 (pp. 292–297).
Dentler, J., Kannan, S., Olivares-Mendez, M. A., & Voos, H. (2017). Implementation and validation of an event-based real-time nonlinear model predictive control framework with ros interface for single and multi-robot systems. In 2017 IEEE conference on control technology and applications (CCTA), August 2017 (pp. 1000–1006).
Desai, J. P., Ostrowski, J., & Kumar, V. (1998). Controlling formations of multiple mobile robots. In Proceedings of 1998 IEEE international conference on robotics and automation (Cat. no. 98CH36146), May 1998 (Vol. 4, pp. 2864–2869).
Diehl, M., Ferreau, H., & Haverbeke, N. (2009). Efficient numerical methods for nonlinear MPC and moving horizon estimation. In L. Magni, D. Raimondo, & F. Allgöwer (Eds.), Nonlinear model predictive control. Lecture notes in control and information sciences (Vol. 384, pp. 391–417). Berlin: Springer.
Ding, W., Ganesh, M. R., Severinghaus, R. N., Corso, J. J., & Panagou, D. (2016). Real-time model predictive control for keeping a quadrotor visible on the camera field-of-view of a ground robot. In 2016 American control conference (ACC), July 2016 (pp. 2259–2264).
Dong, W., & Farrell, J. A. (2008). Formation control of multiple underactuated surface vessels. IET Control Theory Applications, 2(12), 1077–1085.
Erkent, Ö., & Işıl Bozma, H. (2012). Artificial potential functions based camera movements and visual behaviors in attentive robots. Autonomous Robots, 32(1), 15–34. https://doi.org/10.1007/s10514-011-9240-5.
Fax, J. A., & Murray, R. M. (2004). Information flow and cooperative control of vehicle formations. IEEE Transactions on Automatic Control, 49(9), 1465–1476.
Fukushima, H., Kon, K., & Matsuno, F. (2013). Model predictive formation control using branch-and-bound compatible with collision avoidance problems. IEEE Transactions on Robotics, 29(5), 1308–1317.
Gazi, V., & Passino, K. M. (2011). Swarm coordination and control problems (pp. 15–25). Berlin: Springer. https://doi.org/10.1007/978-3-642-18041-5_2.
Ge, S., & Cui, Y. (2002). Dynamic motion planning for mobile robots using potential field method. Autonomous Robots, 13(3), 207–222. https://doi.org/10.1023/A:1020564024509.
Geisert, M., & Mansard, N. (2016). Trajectory generation for quadrotor based systems using numerical optimal control. In 2016 IEEE international conference on robotics and automation (ICRA), May 2016 (pp. 2958–2964).
Graichen, K., & Käpernick, B. (2012). A real-time gradient method for nonlinear model predictive control. In Frontiers of model predictive control. InTech
Huang, M., Nakada, H., Butts, K. R., & Kolmanovsky, I. V. (2015). Nonlinear model predictive control of a diesel engine air path: A comparison of constraint handling and computational strategies. Proceedings of 5th IFAC conference on nonlinear model predictive control, Seville, Spain.
Kang, M., Shen, T., & Jiao, X. (2014). Continuation/GMRES method based nonlinear model predictive control for IC engines. IFAC Proceedings Volumes, 47(3), 5697–5702. (19th IFAC World Congress).
Kendoul, F., Nonami, K., Fantoni, I., & Lozano, R. (2009). An adaptive vision-based autopilot for mini flying machines guidance, navigation and control. Autonomous Robots, 27(3), 165. https://doi.org/10.1007/s10514-009-9135-x.
Lau, M. M., & Lim, K. H. (2017). Investigation of activation functions in deep belief network. In 2017 2nd international conference on control and robotics engineering (ICCRE), April 2017 (pp. 201–206).
Lawton, J. R. T., Beard, R. W., & Young, B. J. (2003). A decentralized approach to formation maneuvers. IEEE Transactions on Robotics and Automation, 19(6), 933–941.
López-Nicolás, G., Gans, N. R., Bhattacharya, S., Sagüés, C., Guerrero, J. J., & Hutchinson, S. (2010). Homography-based control scheme for mobile robots with nonholonomic and field-of-view constraints. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 40(4), 1115–1127.
Mehrjerdi, H., Ghommam, J., & Saad, M. (2011). Nonlinear coordination control for a group of mobile robots using a virtual structure. Mechatronics, 21(7), 1147–1155.
Nascimento, T. P., Conceio, A. G. S., & Moreira, A. P. (2014). Iterative weighted tuning for a nonlinear model predictive formation control. In 2014 IEEE international conference on autonomous robot systems and competitions (ICARSC), May 2014 (pp. 2–7).
Nascimento, T. P., Moreira, A. P., & Conceio, A. G. S. (2013). Multi-robot nonlinear model predictive formation control: Moving target and target absence. Robotics and Autonomous Systems, 61(12), 1502–1515.
Ohtsuka, T. (2004). A continuation/GMRES method for fast computation of nonlinear receding horizon control. Automatica, 40(4), 563–574.
Ohtsuka, T. (2015). symlab: CGMRES. http://www.ids.sys.i.kyoto-u.ac.jp/~ohtsuka/code/index.htm. Accessed 26 Feb 2017.
Sajadi-Alamdari, S. A., Voos, H., & Darouach, M. (2016). Nonlinear model predictive extended eco-cruise control for battery electric vehicles. In 2016 24th mediterranean conference on control and automation (MED), June 2016 (pp. 467–472).
Seguchi, H., & Ohtsuka, T. (2003). Nonlinear receding horizon control of an underactuated hovercraft (3-4 ed., Vol. 13, pp. 381–398). Hoboken: Wiley.
Seo, H., Kim, S., & Kim, H. J. (2017). Aerial grasping of cylindrical object using visual servoing based on stochastic model predictive control. In 2017 IEEE international conference on robotics and automation (ICRA), May 2017 (pp. 6362–6368).
Shimizu, Y., Ohtsuka, T., & Diehl, M. (2006) Nonlinear receding horizon control of an underactuated hovercraft with a multiple-shooting-based algorithm. In Computer aided control system design, 2006 IEEE international conference on control applications, 2006 IEEE international symposium on intelligent control, October 2006 (pp. 603–607).
Shimizu, Y., Ohtsuka, T., & Diehl, M. (2009). A real-time algorithm for nonlinear receding horizon control using multiple shooting and continuation/Krylov method. International Journal of Robust and Nonlinear Control, 19(8), 919–936.
Shin, J., & Kim, H. J. (2009). Nonlinear model predictive formation flight. IEEE Transactions on Systems, Man, and Cybernetics: Part A: Systems and Humans, 39(5), 1116–1125.
Turpin, M., Michael, N., & Kumar, V. (2012). Decentralized formation control with variable shapes for aerial robots. In 2012 IEEE international conference on robotics and automation, May 2012 (pp. 23–30).
Wang, J., Liu, J.-y., & Yi, H. (2015). Formation control of unmanned surface vehicles with vision sensor constraints. OCEANS 2015-MTS/IEEE Washington (pp. 1–8).
Wingfield, N. (2016). A field guide to civilian drones. https://www.nytimes.com/interactive/2015/technology/guide-to-civilian-drones.html. Accessed April 18, 2017.
Zhang, Y., & Mehrjerdi, H. (2013). A survey on multiple unmanned vehicles formation control and coordination: Normal and fault situations. In 2013 International conference on unmanned aircraft systems (ICUAS), May 2013 (pp. 1087–1096).
Author information
Authors and Affiliations
Corresponding author
Additional information
This work was supported by FNR “Fonds national de la Recherche” (Luxembourg) through AFR “Aides à la Formation-Recherche” Ph.D. Grant Scheme No. 9312118.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Supplementary material 1 (mp4 9995 KB)
Supplementary material 2 (mp4 5599 KB)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Dentler, J., Kannan, S., Bezzaoucha, S. et al. Model predictive cooperative localization control of multiple UAVs using potential function sensor constraints. Auton Robot 43, 153–178 (2019). https://doi.org/10.1007/s10514-018-9711-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10514-018-9711-z