Efficient collective shape shifting and locomotion of massively-modular robotic structures

Abstract

We propose a methodology of planning effective shape shifting and locomotion of large-ensemble modular robots based on a cubic lattice. The modules are divided into two groups: fixed ones, that build a rigid porous frame, and mobile ones, that flow through the frame. Mobile modules which flow out of the structure attach to the frame, advancing its boundary. Conversely, a deficiency of mobile modules in other parts of the boundary is corrected by decomposition of the frame. Inside the structure, appropriate module flow is arranged to transport the modules in a desired direction, which is planned by a special distributed version of a maximum flow search algorithm. The method engages a volume of modules during reconfiguration, which is more efficient than common surface-flow approaches. Also, the proposed interpretation as a flow in porous media with moving boundaries seems particularly suitable for further development of more advanced global reconfiguration scenarios. The theoretical efficiency of the method is assessed, and then partially verified by a series of simulations. The method can be possibly also applied to a wider class of modular robots, not necessarily cubic-lattice-based.

1 Introduction

The capability of a large-ensemble self-reconfigurable robot to change its shape, move and perform useful physical tasks in an efficient manner is viewed as a milestone of modular robotics—still to be reached. It is also considered to be a promising approach to realizing the Programmable Matter concept. The problem is difficult and manifold, encompassing several strongly interrelated sub-problems, i.e., the design of a “smart” module that can physically interact and communicate with its neighbors, its miniaturization and powering, special distributed algorithms for collective decision making and reconfiguration planning and control, and many more. Especially difficult are densely-packed three-dimensional modular structures. This is because of their intrinsic geometrical and physical constraints which introduce additional complications to the problem of self-reconfiguration and may require special module designs to be addressed efficiently.

The problem of reconfiguration/motion planning and control is strongly interrelated with the assumed design of modules. If the modules can move independently, propelling themselves autonomously through space, then swarm algorithms can be used to drive an ensemble of modules to form a desired shape (Rubenstein et al. 2014). The motion of swarm-type systems can be vastly parallel, with all modules moving simultaneously towards their goal. This makes reconfiguration faster. In typical modular robots, however, modules can only move when they are attached to other modules, using inter-modular actuation to propel themselves. This introduces complications of two kinds. The first one is of mechanical nature. Inter-modular actuation is usually relatively weak and individual modules inside a massive robot may be unable to move or even hold to their neighbors under the action of gravity. Special approaches, such as volumetric actuation (Hołobut et al. 2015; Lengiewicz et al. 2017), which parallelize the work of modules inside the robot, seem necessary to obtain large-ensemble systems of useful overall strength. The second complication is of purely geometric nature. Because every module must always be connected to other modules, time-efficient reconfiguration of a densely-packed system is difficult to plan.

Several methods of reconfiguration planning and control for densely-packed, lattice-based modular robots have been proposed. Locomotion through reconfiguration on a cubic lattice, over a simulated terrain and avoiding obstacles, has been considered in Butler et al. (2004) and Fitch and Butler (2008). The methods are advantageous in many respects, but only produce a surface movement of modules—with appointed modules “flowing” over the robot from its back to its front. This may result in slow reconfiguration of massive robots, for which the number of surface modules is small compared with the number of interior ones. A universal, distributed reconfiguration planning for square and hexagonal-lattice-based robots, using local rules and a reconfiguration tree, has been presented in Hurtado et al. (2015). The shape change, however, proceeds through a canonical, line-shaped intermediate configuration, which slows down the process. Other reconfiguration strategies, for the more difficult case of square-lattice-based modules with only sliding capabilities, have been proposed in Piranda et al. (2013) and further in Piranda and Bourgeois (2016). The introduced reconfiguration rules are quite efficient, but the movement here is restricted to surface modules too. Several reconfiguration algorithms have also been proposed in which modules travel through the volume of the robot. In theory, such methods can achieve the greatest parallelism of motion and consequently the fastest reconfiguration, provided the entire volume of the robot is simultaneously engaged. Notable works in this direction include: Støy (2004, 2006), with parallel reconfiguration of a cubic-lattice-based system, using local rules, attraction gradients, and a skeletal structure to avoid blocking of the moving modules; (Butler and Rus 2003; Aloupis et al. 2009), in which strategies for planning non-intersecting tunnels between “source” and “target” boundaries of square/cubic-lattice-based robots with unit-compressible modules were proposed and developed; and De Rosa et al. (2006), where a hexagonal-lattice-based system reconfigured through the propagation of empty spaces (holes) from the target boundary to the source boundary of the robot.

In the present work, we show a new interpretation of the problem of parallelizing the process of reconfiguration. It is based on an analogy with the physical process of flow in porous media with advancing and retreating boundaries. A special meta-structure and reconfiguration rules are proposed to make global reconfiguration planning more straightforward, as it only requires specifying two sets of meta-modules at the boundary and disjoint pathways between them. The presented approach seems particularly suitable for the development and analysis of, otherwise extremely complicated, global optimal reconfiguration scenarios. We focus on robots on a square/cubic-lattice, and only consider the purely geometric aspects of the problem. The work is influenced by Støy (2004, 2006), Butler and Rus (2003).

In Sect. 2, we introduce the concept of a porous modular meta-structure, and rules of the flow of modules through that structure. The inflow of modules is sustained by decomposition of boundary meta-modules, and the outflow produces new meta-modules. In Sect. 3, we review the existing hardware designs which may be considered for building structures of the discussed kind. In Sect. 4, we provide a multi-step methodology for planning and performing the reconfiguration, and propose an example global reconfiguration planning scheme, based on finding the maximum flow in a corresponding network (the respective distributed max-flow algorithm is introduced in Sect. 5). Possible extensions of the proposed scheme are discussed in Sect. 6. The visualization and basic analyses are provided in Sect. 7. Concluding remarks are given in Sect. 8, and implementation details of the distributed max-flow procedure in “Appendix A”.

2 The paradigm of discrete flow in a porous structure

We consider modular robots based on a cubic lattice, i.e. every module’s position is given by three integral cartesian coordinates. We do not specify the shape of the modules, although we shall present them as spheres. We assume that the modules can perform two elementary moves, much like in Butler et al. (2004) and Hurtado et al. (2015), shown in Fig. 1 (the modules can be arbitrarily oriented with respect to the lattice).

Fig. 1

Two elementary moves which can be performed by the modules: a translation along two stationary modules, and b rotation by $90^{\circ }$ about a stationary module

Fig. 2

Porous structure made of meta-modules. One meta-module is singled out with more intensive colors

Fig. 3

Movement along a zig-zag path in a system built of meta-modules with no empty spaces (four steps). The propagation of the hole, located above the pink module, is slowed down by each turn of the path. a Step 1, b step 2, c step 3, d step 4 (Color figure online)

Move 1 is a transition to the next empty lattice cell along two stationary modules: the red module in Fig. 1a moves from cell 3 to the empty cell 4, along the two stationary modules in cells 1 and 2. As a result, one coordinate of the red module changes by $\pm \,1$. Move 2 is a $90^{\circ }$ rotation about a stationary module through an empty cell: the red module in Fig. 1b rotates, about the stationary module in cell 1, from cell 3 to the empty cell 2, passing through the empty cell 4. Two coordinates of the red module change by $\pm \,1$. The two moves suffice to reconfigure any collection of modules from any connected configuration into any other while preserving connectivity at every step.

We shall only consider robots built of $2\times 2\times 2$ meta-modules, shown in Fig. 2. A single meta-module consists of seven modules and one empty space. The four gray modules form a fixed triad, which can bind with corresponding triads of adjacent meta-modules into a larger skeletal structure, similar to the one used in Støy (2004, 2006). The skeletal modules are fixed in the sense that they only move when the entire meta-module to which they belong is supposed to move. By contrast, the three red modules are active—they can freely move between meta-modules, replacing one another, as shown in Fig. 4b. The empty space in the meta-module is left to allow simultaneous motion of consecutive active modules around corners. Namely, it can be seen in Fig. 4b that if there was an intermediate red active module between B and C, for example, then the three modules could not move simultaneously along the streamline. Such a dense placement of active modules would slow down their motion along zig-zag paths, as is shown in Fig. 3. There, the empty space moves down the path in steps: from 1 to 2 to 3 to 4. For a path with n turns this takes $n+1$ steps. By contrast, all modules in Fig. 4b can move simultaneously, which allows a hole to pass from one end of a path to another in one step, regardless of the number of turns along the way. A thorough discussion of the general problem of module over-crowding and its influence on reconfiguration, an example of which was considered above, can be found in Nguyen et al. (2000).

Fig. 4

Reconfiguration of a robot built of meta-modules. a The concept of flow and streamlines between a source boundary and a target boundary, with each filled cell of the lattice representing a meta-module, b module-level view of the darkened region in a. Each $2\times 2$ cell is a meta-module viewed from the top, with the pink modules lying one level lower than the red and gray ones. Modules move in parallel: A replaces B, B replaces C, C replaces D, and D replaces E, c a graph corresponding to the robot (Color figure online)

Fig. 5

Consecutive steps of the formation of a new meta-module on a boundary. a Step 1, b step 2, c step 3, d step 4, e step 5, f step 6, g step 7, h step 8

Remark

The division of modules into fixed and active is not permanent. When a meta-module is supposed to leave its current location then it “melts”—all its modules become active and move away. Similarly, when a meta-module is supposed to appear at an empty location then active modules move into the target location and “solidify” into a meta-module with fixed/active members. The presented division of modules into active and fixed complies with our earlier use of these terms (Hołobut et al. 2015; Lengiewicz et al. 2017), where we considered modules capable of forming two types of connections with their neighbors: strong but slow-forming and weak but fast-forming.

The use of meta-modules of the presented kind has little impact on the functionality of large-ensemble systems. If the modules are suitably small then a twice greater granularity of the system, introduced by the use of meta-modules, should be acceptable. The meta-modules and the conceptual division of modules into fixed and active are, however, crucial to make reconfiguration planning easier [the use of meta-modules in general is well discussed in Dewey et al. (2008)]. There are two reasons, both resulting from the presence of the fixed skeleton. The first one is the automatic provision for the mechanical rigidity of the robot during volumetric reconfiguration, which is an important advantage. The second one is the existence of predefined pathways for the parallel motion of active modules through the volume of the robot.

The movement of active modules through the skeleton can be, to some extent, likened to the flow of a liquid through a porous material. Reconfiguration can therefore be viewed as a special flow of modules through a porous structure with moving boundaries. At each step of reconfiguration, some part of the boundary recedes—its meta-modules melt and flow into the porous structure, and another part of the boundary advances—modules flow out of the porous structure and form new boundary meta-modules. New boundaries may also be created and old ones may disappear, changing the overall topology of the robot. An example sequence of module movements during the formation of a new boundary meta-module is shown in Fig. 5. The meta-module is constructed by first building the gray skeleton, and then filling the places of red active modules. The mirror process of removing a meta-module from a boundary can be realized by running the construction process backwards—first, the active modules are removed, and then the skeleton is dismantled.

3 Prospects for hardware implementation

We discuss reconfiguration in an abstract setting—as a purely geometric problem on a square/cubic grid. We are restricted to numerical simulations for assessing the performance of reconfiguration algorithms, and do no hardware testing. We therefore provide below a short description of several applicable hardware solutions and obstacles which might be encountered in a real-life implementation.

One of module designs which could be employed as a hardware platform for the structures we propose is the spherical catom, advanced by the Claytronics Group (Reid et al. 2008; Campbell and Pillai 2008; Christensen et al. 2010)—this motivates the use of spherical modules in the figures of Sect. 2. Catoms have no moving parts and use electrodes or electromagnets, located around their surfaces, for attachment and actuation. Such modules have advantages and disadvantages from the viewpoint of volumetric reconfiguration on a cubic grid. They move by rolling, which is well suited to parallel tunneling of modules through a structure. Rolling modules need only to be attached to the sides of a tunnel—as required by the present reconfiguration scheme—and do not require support from other active modules along their streamline. In other words, the direction of movement of a module is perpendicular to its direction of attachment. This is in contrast to, for example, crystalline atoms (Rus and Vona 2001; Butler and Rus 2003) or telecubes (Vassilvitskii et al. 2002), whose direction of motion is parallel to their direction of attachment. Within the current reconfiguration scheme, this would require that consecutive modules along a streamline be attached to each other and result in problems with simultaneous motion around path corners, as shown in Fig. 3 and discussed in Sect. 2. On the other hand, the spherical shape itself is a disadvantage from the perspective of using a cubic grid. Cubic alignment is not a favored arrangement for spheres, and precise positioning of modules would be required to perform reconfiguration as presented here.

Another possibility is to use cubic modules with sliding capabilities, such as the EM-Cubes of An (2008). The attachment and actuation of neighbor cubes is effected by sets of permanent magnets and electromagnets placed under the modules’ surfaces. A similar linear propulsion mechanism was exploited by Piranda et al. (2013) to build a magnetic conveyor for transporting microparts. By being sequentially activated in a proper order, pairs of opposing electromagnets attract or repel each other, enforcing sliding motion between neighbor cubes. On the one hand, cubic shape is a natural candidate for building cubic-grid-based robots. On the other hand, precise positioning of modules is required in this case as well. The original EM-Cubes are designed to move over the surface of a robot. By contrast, the streamlines propagate through the volume of the robot in tightly-fit channels, which leaves less space for inaccuracies and might impede the movement of modules.

There may arise several implementation difficulties related to the geometry of the system and the proposed type of volumetric reconfiguration. They are connected with the fact that active modules flow through narrow channels inside a robot—a channel’s cross section is only one module wide. One source of problems was already mentioned, namely the imprecise positioning of modules. Another source is the deformation of the robot under gravity. Depending on the shape of the robot and the way in which it is supported, the flow channels may bend and shrink, preventing active modules from moving through—especially in the presence of friction. These problems may be avoided by widening the flow channels, for example making them $2\times 2$ modules wide. It would involve increasing the size of meta-modules and lowering the efficiency of reconfiguration by a constant factor, while preserving the volumetric character of reconfiguration. This solution would additionally provide space for cubic-shaped modules which move by rolling about their edges, like the momentum-driven M-Blocks (Romanishin et al. 2013). Another way of avoiding blockages to module flow would be to somewhat increase the spacing between modules which do not move, in particular—between the fixed modules. To that end, the bonds between static modules might slightly expand, in a manner employed by crystalline atoms or telecubes. This would provide active modules with the room to easily move through the tunnels.

Finally, large-ensemble modular-robotic structures, especially the porous ones, might tend to break or collapse under gravity if their inter-modular connections are not strong enough. We have discussed this issue in Hołobut et al. (2014, 2015) and Lengiewicz et al. (2017), where we suggested the use of two types of connections between modules—stronger ones for keeping modules together, and weaker ones for locomotion. This solution, if realized, would be well suited to forming the meta-modules for the present reconfiguration scheme. The fixed skeleton might be built using the strong connections, which would provide suitable mechanical strength to the robot, while the active modules might use the weak connections to move.

4 Shape transformation algorithm

4.1 Problem definition

The underlying meta-structure, presented in Sect. 2, allows us to express the problem of shape transformation and reconfiguration planning in a simple manner. First, we subdivide the space into cells of the size of a single meta-module. Meta-modules form some initial shape by occupying a connected set of cells. The final shape is specified by a different connected set of cells. The two sets can but do not need to overlap. The goal is to transform the ensemble from the initial to the final shape using the mechanisms introduced in Sect. 2.

Remark

The subdivision of space into discrete cells requires from each meta-module of a robot to determine its position in the system, which must be done in a distributed manner (the so-called internal localization problem). As discussed in Hołobut et al. (2016), it may in general pose a difficult task, but it greatly simplifies if the meta-structure of the present kind is considered.

Fig. 6

Three substeps of a single step of the reconfiguration procedure

4.2 Outline of the shape-transformation algorithm

The shape transformation is subdivided into discrete steps, repeated sequentially. At each step it is only required to (i) specify the source and target boundaries, (ii) connect them with disjoint streamlines and (iii) transport modules along the streamlines, removing meta-modules from the source boundary and creating them at the target boundary, see Fig. 6. Therefore, at each step the current ensemble boundary is only modified by a single meta-module layer.

Steps (i) and (ii) are viewed as global reconfiguration planning and step (iii) is understood as local reconfiguration control. In the present work, we mainly focus on steps (i) and (ii), while step (iii) is treated as a unit operation of moving meta-modules from respective sources to sinks, as discussed in Sect. 2.

For the purpose of global planning, the final shape is represented by a distance function $d(\mathbf{x})$ from that shape. For a cell located at $\mathbf{x}$, $d(\mathbf{x})$ is defined as the minimum number of horizontal and vertical unit moves that are needed to reach the final shape (Manhattan distance). In particular, cells forming the final shape are at a distance 0, see e.g. Fig. 13. It is assumed that each meta-module knows its current distance and the distance of its neighboring cells.

Step (i) The proposed rules for defining source- and target-boundary cells are related to the distance function. The idea is to choose source meta-modules at these parts of the boundary for which the outward normal is directed along the gradient of $d(\cdot )$, e.g., see red circles in Fig. 13a. Similarly, target-boundary cells are empty cells at the boundary for which the inward normal is directed along the gradient of $d(\cdot )$, e.g., see green circles in Fig. 13a. Additionally, target-boundary cells are always created at the boundary inside the final shape, e.g., see green circles in Fig. 13b.

Step (ii) Having the source and target boundaries defined, one needs to find a set of disjoint streamlines that link them. This can be done in many ways. In the present work, we transform that problem into a problem of finding a maximum flow in a special graph, see Fig. 4c. The occupied cells and target-boundary cells are vertexes of that graph, with edges representing adjacency of respective cells. Source-boundary vertexes are sources of the flow and target-boundary vertexes are sinks. In order to find disjoint paths of the maximum flow, both vertex- and edge capacities are set to 1. (A specific distributed version of the maximum-flow search algorithm applied in this work is presented in Sect. 5.)

Step (iii) After the streamlines are found, transport of modules along them is performed. That operation can be fully parallelized and takes the same amount of time regardless of the streamlines’ lengths. This is only possible because the algorithm combines three necessary ingredients. The first one is the maintained porosity, which allows undisturbed motion along zig-zag pathways; see the discussion in Sect. 2. The second one is the fact that the streamlines are non-intersecting, which gives collision-free pathways. The third one is the assumption that computation and message passing are much faster than physical motion, which allows the necessary synchronization of modules along each streamline.

It should be noted that the present algorithm, and especially its sub-step (ii) concerning the finding of the maximum flow, is computationally and communicationally intensive. We aim to increase the parallelism of motion at the cost of additional computation and communication. Therefore, for the algorithm to be advantageous in practice, computation and communication must be fast relative to movement. We assume this throughout the paper. In such a case, each transportation phase (iii), which is an “elementary step” in the sense that transport of modules along all streamlines is done in parallel and takes the same amount of time—as it was justified in Sect. 2, is followed by a relatively short computation phase; then the next transport begins.

Fig. 7

Organization of information exchange and processing in a meta-module

Remark

In the present work, the sub-steps (i) and (ii) are performed sequentially, i.e., source and target boundaries are first chosen to transform the shape in a desired way, and then the maximum flow between them is calculated. In general, however, the two sub-problems can be solved simultaneously, especially if one aims to find a reconfiguration scheme that is optimal in some sense, e.g., minimizing the overall number of reconfiguration steps.

Remark

It is, in general, impossible to link all sources with all sinks. Firstly, because their numbers may differ, see, e.g., Fig. 14b. Secondly, because there might be bottlenecks blocking the flow, see, e.g., Fig. 14c. The presented simple algorithm for choosing sources and sinks performs poorly in some cases and additional heuristics would be necessary if one wanted to improve the reconfiguration efficiency.

Remark

It is assumed that a modular robot subdivides into meta-modules ($2 \times 2 \times 2$ cells), each of which can act as a unit, i.e., it can perform computations, store internal data, and send/receive/enqueue messages, see Fig. 7. The assumed functionality of a meta-module requires synchronized work of its constituent modules. Implementation details are not further discussed.

Fig. 8

Reconfiguration procedure for a basic example. Max-flow search at the step 1 (Color figure online)

Fig. 9

Three different resolutions of the same geometry for a single reconfiguration step. Sources and sinks are marked with red and green color, respectively (Color figure online)

5 Distributed asynchronous maximum-flow algorithm

5.1 Preliminaries/problem classification

Finding the maximum flow in a graph is a well-known classical problem. As for its standard formulation, one can distinguish two leading approaches. The first of them derives from the earliest ideas of Ford and Fulkerson (1956), Dinic (1970) and Edmonds and Karp (1972), to perform gradual augmentation of the flow until it reaches the maximum. The second approach, sometimes called push-relabel algorithm, relies on the idea of Karzanov (1974) and Goldberg and Tarjan (1988) to allow the vertex inflow exceed the outflow, with further push and relabel operations to correct the flow in order to meet the network capacity constraints. The latter approach to finding the maximum flow is considered to produce algorithms of better time complexity, see e.g. Goldberg and Rao (1998) and Orlin (2013).

Within the aforementioned classification, there exist many possible variants of the maximum flow algorithms. Their properties, implementations and applicability depend on the type of the graph at hand but also are strongly related to a particular computer architecture that they are to be executed on. In our case, the max-flow problem derives from the problem of finding the maximum set of vertex-disjoint paths in a physical two- or three-dimensional distributed modular robotic ensemble. In that case, the number of edges is proportional to the number of vertexes (a graph with a sparse connection network), sources and sinks are located at the boundary, the flow is integral, and edge- and vertex capacity is 1. Regarding the computing architecture, our system can be classified as a distributed-memory Multiple Instruction Multiple Data (MIMD) parallel computing machine (Tanenbaum 2006), in which each meta-module is a separate node with its own CPU and memory and with capabilities to exchange messages with its direct neighbors (so-called mesh network), see Fig. 7. An algorithm utilizing the above special conditions is proposed and analyzed in this work.

5.2 Maximum-flow algorithm

We have found it most straightforward to develop and implement a special distributed version of the Edmonds–Karp max-flow algorithm (Edmonds and Karp 1972). In the standard (non-distributed) version, breadth-first search (BFS) is performed on the residual network in order to find the shortest augmenting path. The augmentation is repeated until no further improvement can be made. For the case of the many-sources-to-many-sinks integral flow of unit vertex capacity, each augmentation results in finding at least one new full streamline. This is much better than in the general case, in which each augmentation only guarantees the saturation of one new edge.

One of the main problems is how to maintain the general augmentation scheme in the distributed and asynchronous framework. Contrary to the synchronous case, in which one can schedule parallel BFS pulses without any significant computational or memory burden, in the asynchronous case it is not so straightforward. Instead of the synchronized pulses, we propose that source nodes sprout BFS-like non-intersecting trees on the residual network independently of each other (blue arrows in Fig. 8). Each tree is constructed on the basis of the quickest-wins rule, in which the growth of the branches is determined by the actual processing speed of nodes rather than the distance from the root. This is advantageous as it naturally promotes the computationally fastest track to link a source with a sink (however, this may violate the classical Edmonds–Karp condition that the augmenting path must be the shortest). Once the tree reaches the sink, a single unique path is backtracked (yellow arrows in Fig. 8) and the unused branches of the tree are cut off (gray crossed lines in Fig. 8), leaving the space for other trees to grow. After the backtracking reaches the source, the confirmation message is propagated along the already determined path, and the new streamline is established (red arrows in Fig. 8).

Every newly established streamline modifies the residual network by enabling the flow in reverse direction, which is an analogy to the standard Edmonds–Karp algorithm. This can also be seen as the possibility for the remaining BFS trees to continue their growth upstream along the existing streamlines (see the overlapping paths in Fig. 8, iteration 10 and further on). At the same time, because of the vertex-unit-capacity constraint, the algorithm prevents paths from simply crossing the streamlines; see e.g. iterations 9 and 10 in Fig. 8, in which the blue path $|11 \rightarrow 06|$ only turns left to become $|11 \rightarrow 06 \rightarrow 05|$ and does not branch into $|11 \rightarrow 06 \rightarrow 02|$.

If the flow can not be further augmented (i.e., the number of streamlines reaches its maximum), then the algorithm can proceed to the transportation sub-step (iii).

Remark

The proposed stepping and sub-stepping scheme, see Sect. 4.2 and Fig. 6, requires some sort of synchronization, e.g., to prevent starting the transportation sub-step (iii) before finalizing the maximum-flow sub-step (ii). For that purpose, in our approach each meta-module performs a countdown and only proceeds to a next sub-step if a given timeout is reached. And conversely, when a new streamline is established, a tick message is broadcast to restart the countdown.

Remark

As mentioned before, BFS trees grow independently; however, some level of interaction between them needs to be maintained. In particular, when a node becomes a part of a newly-established streamline or when an edge is cut off then such a change of the state needs to be communicated (and acknowledged) to the neighbors by sending a respective message. (The idea of acknowledgements is discussed in a similar context in Goldberg and Tarjan (1988).)

Remark

In the proposed scheme, sinks are virtual, i.e., they are located on the outer (empty) side of the boundary. Therefore, it is assumed that meta-modules located next to such a (virtual) sink are able to emulate its operation. To be able to do so, a local synchronization between the respective meta-modules is necessary, which may in turn require longer-distance communication to effectively secure the synchronization (see also discussion in Sect. 6.2).

5.3 Time-, memory- and CPU usage estimation for large ensembles

Below, we briefly analyze how the proposed distributed Edmonds–Karp algorithm performs with the increasing resolution of the system (decreasing module’s size). The main simplifying assumption here is that higher-resolution reconfiguration problems are “similar” to their low-resolution counterparts, see e.g. Fig. 9. (In a sense, we analyze the complexities individually for every possible generic coarse shape.) We also assume that a single operation, done by a meta-module, consists of the necessary computations and sending/receiving information, performed synchronously by all meta-modules.

We start with the lowest resolution $k=1$, for which we specify the coarse generic shape made of unit cubes (each cube corresponds to one low-resolution meta-module), see Fig. 9. In the analysis we increase the resolution, keeping the shape constant. For a given resolution k one can fit $k^{p}$ meta-modules into a unit cube in a p-dimensional space, $p\in \{2,3\}$ (k meta-modules per unit edge of the cube). We also assume the most unfavorable case in which the streamlines are constructed sequentially.

In the algorithm, for $k=1$, the number of iterations (time) needed to find a single streamline is proportional to the maximum distance $W_s$ between sources and sinks. For a given k it should be proportional to $W_s\cdot k$. The maximum number of streamlines to be found is related to the number of sources and sinks (located at the boundary) and the cardinality of the minimum cutting set (see the max-flow min-cut theorem, Ford and Fulkerson 1962). For the increasing k, this will be proportional to the number of modules occupying some $(p-1)$-dimensional area. Therefore, the number of streamlines should be proportional to $N_s\cdot k^{p-1}$, where $N_s$ is the maximum number of streamlines for $k=1$. Putting all together, the number of iterations for a single max-flow distributed search should be proportional to $N_s\cdot W_s\cdot k^{p}$.

As regards CPU usage, the number of operations per module needed to find a single streamline is bounded from above by a constant. Therefore, the number of operations per module for a single max-flow distributed search should be proportional to $N_s\cdot k^{p-1}$.

All the above assessments are made for a single reconfiguration step. The number of reconfiguration steps $N_R$ also increases with the increasing resolution, and in optimal scenarios it is proportional to k. This is because a higher-resolution flow can be easily generated by following low-resolution streamlines.

The assessment of memory usage per module is a little more involved. One could expect that it should be constant, regardless of the size of the ensemble. Here, it is not the case. The problem is with the cut-off operation, which is difficult to be controlled in a distributed manner without storing the history of the BFS trees that had been cut off in the current max-flow step. Such a history is necessary to prevent infinite loops (the tip of a branch is growing while the root is being cut off). The list length is proportional to the number of sources and sinks, i.e., $N_s\cdot k^{p-1}$ per module. Note that this is a pessimistic assessment as the growing BFS trees block one another—therefore only a limited number of trees pass through a given module. Also, we believe that the memory requirements can be significantly improved in future.

The obtained upper bounds are much lower than for the case of arbitrary graphs. This is mainly due to the specific type of graphs at hand and partially due to the applied parallelism. These bounds can be also further improved if better algorithms or additional heuristics are applied. One of such heuristics is demonstrated further in Sect. 5.4.

5.4 Reuse of max-flow search results

We propose a simple heuristic based on reusing streamlines from a previous max-flow search. Some streamlines can be reused and some can not. Everything depends on whether there is a source at the new step that is located along a streamline to be reused. If there is no such source present, see e.g. the streamline $|09 \rightarrow 10 \rightarrow 11 \rightarrow 12 \rightarrow 07|$ in Fig. 10, the path will be cut off. Conversely, if the source is present, the streamline is converted back into a normal branch of the BFS tree, and then the standard algorithm proceeds, as described in Sect. 5.2, see also Fig. 10. The advantage is that the streamline reuse can be mostly done simultaneously.

In order to take advantage of the presented heuristics, the streamlines can not change too frequently and abruptly, i.e., the sets of sources and sinks must in general follow the streamlines. This in turn strongly depends on the particular algorithm that is used to specify sets of sources and sinks, as well as on the particular reconfiguration problem at hand. Assuming that the algorithm is well adjusted/optimized, the frequency of streamline changes should mostly depend on how complex the initial and final shapes are. This is because, in that case, disruptions of the flow are mainly caused by the topology changes of the current shape and the interactions with the boundaries of the final shape. For the increasing resolution k, the number of such individual disruptions along the whole reconfiguration path scales with the number of meta-modules at the surface area, i.e., is proportional to $k^{p-1}$. Every individual disruption is followed by a single streamline search operation requiring $W_s\cdot k$ iterations, giving the total of $\sim k^p$ iterations, or $\sim k^{p-1}$ iterations per single reconfiguration step. This is one order of magnitude better than when no heuristics were used, see Sect. 5.3.

In Table 1 we summarize the assessed complexities. In general, the application of heuristics reduces the expected number of iterations and computations by the factor of k. This is not the case for the maximum memory usage per module, which theoretically can be the same even if the heuristic is applied. But again, in practice, BFS trees block one another, therefore the maximum memory usage should be much lower than in the presented rough predictions.

Fig. 10

Reconfiguration procedure for a basic example. Max-flow search at the step 2

Remark

One of the main drawbacks of our methodology to assess complexities is the assumption that intermediate shapes (the shapes of the intermediate stages of reconfiguration) can also be analyzed by just increasing the resolution of the coarse meta-modules, which is an idealistic assumption (but still possible). In general this assumption is incorrect, as the intermediate shapes strongly rely on the sources/sinks selection strategy and the results of the max-flow algorithm itself. For example, it is clearly visible in Fig. 17c that the topology of the intermediate shape becomes more complex because of the newly created hole. For higher resolutions, such effects can deteriorate the overall efficiency, which is not included in our rough complexity assessments. On the other hand, if one tried to assess the complexities purely as a function of the number of modules, the results would be less realistic. This is because, for higher resolutions, simple assessments would be skewed by the ensembles with very complex topologies and very unfavorable distribution of the sources and sinks, and would overestimate the typical complexities.

6 Extensions and improvements of the shape transformation algorithm

The proposed reconfiguration algorithm consists of a distributed and asynchronous subroutine for finding a maximum flow between source and target boundaries of a robot, and a complementary subroutine for choosing the appropriate boundaries. In its present form, the algorithm lacks many functionalities expected of a complete reconfiguration method. This is because our main purpose was to concentrate on the flow structure itself and its properties. In the present section, we sketch several additions which are necessary to make the algorithm complete and/or better behaved.

6.1 Connectedness preservation

Connectedness preservation is one of the most important features of any reconfiguration algorithm. In the present case, at each step of reconfiguration a source boundary is supplied, from which meta-modules are removed as selected by the max-flow procedure—with no regard for connectedness. Therefore, the problem reduces to such a choice of the source boundary that after removing any subset of its meta-modules the robot remains connected.

Table 1 Summary of the assessed complexities for the increasing resolution k in p dimensions

Fig. 11

Values of $s_i$ for an example ensemble of meta-modules. The meta-modules of ${\mathscr {S}}_0$ are red and those of ${\mathscr {S}}'_0$ are gray, with the origin meta-module $M_0$ in blue (Color figure online)

The method we propose is a modification of the distance function (gradient) approach used by Vassilvitskii et al. (2002) and Støy (2004, 2006). Let ${\mathscr {M}}$ be the set of all modules of a robot and ${\mathscr {I}}$ the set of their unique indices ($i\in {\mathscr {I}}\Leftrightarrow M_i\in {\mathscr {M}}$), ${\mathscr {S}}_0\subset {\mathscr {M}}$ be an initial set of source modules supplied by an external procedure, and ${\mathscr {S}}'_0={\mathscr {M}}-{\mathscr {S}}_0$. In general, removing some or all of the meta-modules of ${\mathscr {S}}_0$ may leave the robot disconnected. We shall therefore choose ${\mathscr {S}}\subseteq {\mathscr {S}}_0$ whose any portion can be removed without disconnecting the structure. ${\mathscr {S}}$ can then be safely used as the source boundary by the maximum flow procedure.

When selecting ${\mathscr {S}}$, we will use auxiliary quantities $s_i$, $i\in {\mathscr {I}}$. Basically, $s_i$ is equal to the minimum number of meta-modules of ${\mathscr {S}}_0$ which must be crossed when traveling from an “origin” meta-module $M_0\in {\mathscr {S}}_0'$ to $M_i$, taking any route inside the robot. In other words, $s_i$ is the distance between $M_0$ and $M_i$ measured in the meta-modules of ${\mathscr {S}}_0$ only. An example configuration, with the values of $s_i$ displayed on all meta-modules, is presented in Fig. 11. One can distinguish connected subsets of ${\mathscr {S}}'_0$ with equal values of $s_i$, separated by meta-modules of ${\mathscr {S}}_0$ with ascending/descending values of $s_i$. It can be deduced, for example, that if $s_i=1\Leftrightarrow M_i\in {\mathscr {S}}_0$ then removing any subset of ${\mathscr {S}}_0$ cannot disconnect the structure. In the opposite case, removing all $M_i\in {\mathscr {S}}_0$ whose $s_i=1$ separates the remaining $\{ M_i:\ s_i\geqslant 1 \}$ from $\{ M_i:\ s_i=0 \}$ and the structure loses connectedness.

We shall now provide more details. For simplicity, we restrict ourselves below to synchronous systems, in which all meta-modules update their internal states in parallel, but the results can be also extended to the asynchronous case. Furthermore, to shorten the descriptions, we depart from the present interpretation and write “modules” instead of “meta-modules” when referring to the basic units.

Let $M_0\in {\mathscr {S}}'_0$ be the “origin” module elected by the ensemble, s(P) be the number of modules which belong to ${\mathscr {S}}_0$ in a sequence of modules P, and $M_i|M_j$ mean that $M_i$ and $M_j$ are neighbors. A path of length n between $M_0$ and $M_i$ is a sequence $\{M_{i_0}, M_{i_1}, \ldots , M_{i_n}\}$ of not necessarily distinct modules, where $i_0=0$, $i_n=i$, and $M_{i_{k-1}}|M_{i_k}$ for $k=1,2,\ldots ,n$. Let finally ${\mathscr {P}}_i^n$ be the set of all paths of length at most n from $M_0$ to $M_i$ (possibly empty). We will now consider the minimum number of modules of ${\mathscr {S}}_0$ which must be crossed when traveling from $M_0$ to $M_i$ in at most n steps—a quantity denoted further by $s_i^n$. More precisely, $s_i^n=\min \{s(P):\ P\in {\mathscr {P}}_i^n\}$, with the convention that $s_i^n=\infty$ when ${\mathscr {P}}_i^n=\emptyset$. The values of $s_i^n$ allow one to compute $s_i$ since, as can be readily deduced, $s_i = \lim _{n\rightarrow \infty } s_i^n$. We will prove that $s_i^{n+1}$ can be computed by $M_i$ from local information using the formula

$$\begin{aligned} s_i^{n+1} = \min _{k:\ M_k|M_i} s_k^n + s(\{ M_i \}), \end{aligned}$$

(1)

with the boundary condition: $s_0^n=0$ for all $n\geqslant 0$, and the initial condition: $s_i^0=\infty$ for all $i\ne 0$.

Remark

We treat $\infty$ as a formal symbol processed by the modules alongside numbers when doing arithmetic operations. In particular, we assume that $\infty$ satisfies: $1<2<\cdots <\infty$, $\infty +0=\infty +1=\infty$, $\infty \leqslant \infty$, which allow $\infty$ to be correctly handled inside Eq. (1).

Proof

It can be seen that the boundary and initial conditions for Eq. 1 are correct: (a) the shortest path from $M_0$ to $M_0$—$\{ M_0 \}$, of length 0—is disjoint with ${\mathscr {S}}_0$, hence $s_0^n=0$ for all $n\geqslant 0$; (b) for all $i\ne 0$ there are no paths of length 0 between $M_0$ and $M_i$, ${\mathscr {P}}_i^0=\emptyset$, hence $s_i^0=\infty$ for all $i\ne 0$. As regards Eq. (1) itself, it can be observed that any path in ${\mathscr {P}}_i^{n+1}$, $i\ne 0$, must have one of the neighbors of $M_i$ as its last-but-one module. This is reflected by the bijection $^{*}:{\mathscr {P}}_i^{n+1}\rightarrow {\mathscr {N}}_i^n$, where ${\mathscr {N}}_i^n = \bigcup _{k:\ M_k|M_i}{\mathscr {P}}_k^n$, given by $\{ M_0,\ldots ,M_k,M_i \}^{*} = \{ M_0,\ldots ,M_k \}$. Using it, one can write:

$$\begin{aligned} s_i^{n+1}&= \min _{P\in {\mathscr {P}}_i^{n+1}} s(P) = \min _{P\in {\mathscr {P}}_i^{n+1}} s\left( P^{*}\right) + s(\{ M_i \}) \end{aligned}$$

(2)

$$\begin{aligned}&= \min _{P\in {\mathscr {N}}_i^n} s(P) + s(\{ M_i \}) \end{aligned}$$

(3)

$$\begin{aligned}&= \min _{k:\ M_k|M_i}\ \left[ \min _{P\in {\mathscr {P}}_k^n} s(P)\right] + s(\{ M_i \}) \end{aligned}$$

(4)

$$\begin{aligned}&= \min _{k:\ M_k|M_i} s_k^n + s(\{ M_i \}) \end{aligned}$$

(5)

where Eq. (2) comes from the definition of $s_i^{n+1}$ and the identity $s(P)=s(P^{*})+s(\{ M_i \})$ for $P\in {\mathscr {P}}_i^{n+1}$, Eq. (3) from passing from the domain to the codomain of the bijection, Eq. (4) from replacing the minimum over the union ${\mathscr {N}}_i^n$ by a repeated minimum over its component sets, and Eq. (5) from the definition of $s_k^n$. We have thus arrived at Eq. (1). It should be noted that the arithmetical rules assumed for $\infty$ guarantee that empty sets of paths are correctly handled. $\square$

It can also be deduced that in a structure composed of N modules all $s_i^n$ reach limit values, $s_i$, at step $n=N-1$ at the latest, i.e. $\forall _{i\in {{\mathscr {I}}}}\ s_i=\lim _{n\rightarrow \infty } s_i^n=s_i^{N-1}$.

Proof

In a structure composed of N modules, every non-self-intersecting path from $M_0$ to $M_i$ can be made of at most N modules, including $M_0$, so it must belong to ${\mathscr {P}}_i^{N-1}$. Since every path $P\in {\mathscr {P}}_i^n$ contains a non-self-intersecting subpath $R\in {\mathscr {P}}_i^n\cap {\mathscr {P}}_i^{N-1}$ and $s(R)\leqslant s(P)$, therefore $s_i^n=\min \{ s(P):\ P\in {\mathscr {P}}_i^n \}=\min \{ s(R):\ R\in {\mathscr {P}}_i^n\cap {\mathscr {P}}_i^{N-1} \}$. Taking into account that $\forall _{n\geqslant 0}\ {\mathscr {P}}_i^n \subseteq {\mathscr {P}}_i^{n+1}$ one finally obtains: $\lim _{n\rightarrow \infty } s_i^n = \min \{s(R):\ R\in {\mathscr {P}}_i^{N-1}\} = s_i^{N-1}$. The arguments were valid for any $i\in {{\mathscr {I}}}$, so the proposition is proved. $\square$

The above observations lead to the following example method of selecting ${\mathscr {S}}\subset {\mathscr {S}}_0$. A tree is formed, with the root at $M_0$ and spanning the entire structure, having the property that a path from $M_0$ to $M_i$ crosses exactly $s_i$ modules of ${\mathscr {S}}_0$. Within the tree, $M_k$ can be the parent of $M_j$ only if $s_k=\min \{ s_i:\ M_i|M_j \}$. Each module (except $M_0$) selects exactly one of its neighbors with the minimum value of $s_i$ as its parent. This is done during the Eq. (1)-based iteration and the parent is reset for $M_j$ at each step at which $s_j$ changes. Once the tree is formed, ${\mathscr {S}}$ is chosen as the set of those modules of ${\mathscr {S}}_0$ which have no children—the leaves of the tree.

One can get a useful lower bound on the number of modules in ${\mathscr {S}}$, as obtained by the above procedure, in the case when ${\mathscr {S}}'_0$ is connected. Then, $M_i\in {\mathscr {S}}'_0\Leftrightarrow s_i=0$. Let $n_k=\#\{ i:\ s_i=k \}$—the number of modules in ${\mathscr {M}}$ with $s_i=k$. Of course, $\sum _k n_k=\#{\mathscr {M}}$. Since every module belongs to only one tree-path, which originates at $M_0$ and passes through consecutive modules with non-decreasing values of $s_i$, one can conclude that

$$\begin{aligned} \#{\mathscr {S}} \geqslant \sum _{k=1}^m \max \{n_k-n_{k+1},0\}, \end{aligned}$$

(6)

where $m=\max \{ s_i:\ i\in {\mathscr {I}} \}$. Eq. (6) shows, in particular, that ${\mathscr {S}}$ is nonempty, because $n_m>0$ and $n_{m+1}=0$.

Remark

A reconfiguration strategy which aims to preserve connectedness on purely geometric grounds may not be realizable in practice. In the real physical setting, the robot must resist gravity, forces of inertia resulting from reconfiguration itself, and possibly an additional external loading. This problem affects mostly large-ensemble systems, in which the strength of individual intermodular connections is small compared with the weight of the entire system. Any realistic reconfiguration strategy must therefore take mechanical factors into account and guarantee that intermodular connections do not become overstressed during reconfiguration, that the robot does not lose balance about its support, and that the projected motion lies within the capabilities of the modules’ actuators. Otherwise the robot may collapse under gravity or fail to function as planned. Designing a mechanically-feasible reconfiguration path might require using methods of computational mechanics, examples of which for non-self-reconfigurable systems can be found in White et al. (2011) and Hiller and Lipson (2014). A possible approach to the distributed prediction of the mechanical overloading of connections due to a planned reconfiguration step has been presented in Hołobut and Lengiewicz (2017). Nevertheless, a full integration of mechanical constraints into reconfiguration planning seems to be a complicated issue which lies outside the scope of the present paper.

6.2 Avoiding “sink collisions”

The proposed algorithm computes streamlines between real source modules and virtual sink modules. In other words, sources are physically present, and sinks are not—they are empty spaces. Since such sinks cannot participate in the computation of streamlines, all respective operations must be handled by the modules in their neighborhood. In particular, the information about whether there is a streamline ending in a given sink module or not must be stored in the neighbors’ memories. This leads to problems, illustrated in Fig. 12, when several boundary modules simultaneously attempt to construct the same sink module. There are several possible solutions.

Fig. 12

Different streamlines leading to the same sinks. Each square represents a metamodule

The first option is to allow the streamlines to be constructed, even if their ends overlap. The subsequent movement of modules along such streamlines would eventually lead to module collisions, and the excessive modules would have to be withdrawn along the streamlines which brought them. This solution is unwelcome for several reasons, most notably for disturbing the simultaneity of movement which is the key feature of the present algorithm.

The second option is to algorithmically enforce uniqueness of streamline ends, using communication between neighbor modules only. This can either be done during target-boundary selection or in the runtime of the max-flow algorithm. The first way consists in assigning to each sink only one formal neighbor. This approach limits the number of possible flow patterns produced by the algorithm. The second way is based on checking and negotiating, during streamline construction, of the state of a sink by all of its neighbors. In general, this approach may be computationally prohibitive, since information has to be constantly passed between possibly distant modules—like at A in Fig. 12. A reasonable compromise between the two approaches might be to use single-neighbor assignment in the case when the neighbors of a given sink are far away from each other with respect to the robot’s internal metric, and to use realtime negotiation in the case when the neighbors are close—like at B in Fig. 12.

The third option, most advantageous from the computational point of view but more demanding of the modules’ hardware, is the use of a longer range of communication between modules—as was also assumed in Hurtado et al. (2015). The modules might have to be able to communicate at a distance of several module diameters, at least in the case when there are no other modules in between. In this way they could decide by direct communication the state of their common neighbor sink. Since the present algorithm deals with $2\times 2\times 2$ metamodules instead of individual modules, the communication range would have to be three module diameters—to cover a one-metamodule gap between metamodules.

6.3 Boundary selection—global planning

In the numerical examples presented in this paper, we have used a global planner based on the gradient of the Manhattan distance to the target shape, $d(\mathbf{x})$, as described in Sect. 4.2. This approach, like any other, has its strengths and weaknesses. On the one hand, it combines shape change and locomotion into one scheme, since the gradient can point to a target shape as well as to a distant object. Under certain circumstances, reconfiguration can also be quite efficient. On the other hand, modules need to know the values of the distance function around the target shape during the whole reconfiguration process. This requires that modules either store distance values over a potentially large area, or compute them, whenever needed, from the knowledge of the target shape and its relative position in space. The first approach is demanding memory-wise, the second—computationally. Moreover, there exist spatial arrangements of the initial and target shape, for which bottlenecks arise during reconfiguration which greatly reduce the parallelism of movement. Finally, when the source boundary is chosen based on the gradient information, it must also be verified that the structure will remain connected after the removal of the source modules, as discussed in Sect. 6.1.

There are other possible methods of choosing target and source boundaries. One of them is based on using an “internal” distance to the target shape, $d_i$, as opposed to the “external” distance $d(\mathbf{x})$. This is basically a reformulated and slightly modified version of the method used in Støy (2004, 2006) for attracting misplaced modules towards their destinations. Under the assumption that the current, ${\mathscr {C}}$, and target, ${\mathscr {T}}$, configurations meet or overlap, the target boundary is determined first as the empty cells of ${\mathscr {T}}$ lying at the border of ${\mathscr {C}}$. Next, $d_i$ is computed iteratively as the distance, measured inside ${\mathscr {C}}$, between every module $M_i\in {\mathscr {C}}-{\mathscr {T}}$ and the boundary of ${\mathscr {T}}$ as $d_i = \min \{ d_j:\ M_i|M_j \}+1$, where the modules at the outer boundary of ${\mathscr {T}}$ have fixed $d_i=0$. At the same time, a spanning tree is formed on the basis of $d_i$ in a similar fashion as in Sect. 6.1 with $s_i$. Finally, the source boundary is obtained as those modules of ${\mathscr {C}}$ which are leaves of the tree. This choice automatically guarantees that if ${\mathscr {C}}\cap {\mathscr {T}}$ is nonempty and connected then the structure will remain connected during reconfiguration. Advantages of this method are its lower memory/computational requirements and that reconfiguration proceeds entirely “in place”, i.e. the modules are always located inside the union of the initial and target configuration. Its disadvantages are that it does not directly address locomotion and that the parallelism of reconfiguration is limited by the capacity of the initial target boundary (all streamlines pass through it during the entire reconfiguration).

The final possibility which we wish to mention is reconfiguration considered not as a two-point process, between the initial and target shape, but reconfiguration along a “trajectory”. It is reasonable to assume that in many situations not only the endpoints of reconfiguration are important, but also the entire movement between them. This resembles path following in mechatronics, where desired configurations of a mechanical system are given as a function of time and the system is supposed to realize them through proper actuation. In the present case, the path consists of subsequent configurations of the ensemble of modules, with incremental changes of positions. In the discrete-time/discrete-space case, as considered in the present paper, the path is a sequence of configurations $C_0, C_1, \ldots , C_n$, with $C_i\subset {\mathbb {Z}}^3$, $\#C_i$ equal to the number of modules, and the Hausdorff distance between the sets $C_i$ and $C_{i+1}$ being 0 or 1. In the continuous-time/continuous-space case, which may be an approximation for large-ensemble systems, the path is given by a mapping $C:\ [t_0,t_1]\rightarrow P({\mathbb {R}}^3)$, from a time interval to the power set of ${\mathbb {R}}^3$. C should be continuous with respect to the Hausdorff metric in $P({\mathbb {R}}^3)$, and the sets C(t), $t\in [t_0,t_1]$, should be suitably regular and have equal volumes. When reconfiguration is defined in an incremental fashion as indicated above, the target and source boundaries are given by the set differences $C_{i+1}-C_i$ or $C(t+\varDelta t)-C(t)$, and $C_i-C_{i+1}$ or $C(t)-C(t+\varDelta t)$, respectively. If the flow capacity of the system is sufficient, the ensemble will approximately follow the prescribed reconfiguration path.

6.4 Quality control over intermediate shapes

It often happens during the run of the current version of the algorithm that convergence towards the target shape proceeds unevenly, in the sense that long “tails” of modules appear behind the structure (or in front of it), c.f. Fig. 14c. There are two possible reasons for this phenomenon. The first one is the “nearest first” approach during the construction of streamlines, which favors those source modules which lie closer to the target boundary. The second reason is related to the applied heuristics, which favor streamlines from the previous reconfiguration step. The resulting order of reconfiguration may be unsatisfactory from the mechanical point of view—thin elements may incur excessive stresses, resulting in overloading of connections between modules. Furthermore, uneven formation can impair the execution of other tasks which the system may have to perform during reconfiguration. Finally, as can be observed in Sect. 7.2, uneven selection of sources may increase the overall reconfiguration time.

The problem is broader and may be generally viewed as a problem of control of the quality of intermediate shapes (the shapes of the intermediate stages of reconfiguration). The resolution of this problem seems to be hard technically and even conceptually. A quality measure would have to be devised for the intermediate shapes. It seems reasonable to roughly assume that, in the absence of other constraints on reconfiguration, the shapes with smaller boundary areas are preferable—this disadvantages long, protruding elements, and uneven boundaries in general (probably the simplest measure would be just to promote the most distant sources). On the basis of this quality measure, the modules of the source and target boundaries would have to be ranked according to the influence on the quality of the boundary that their removal/formation would have. This ranking would take the form of weights assigned to individual source/target modules. Finally, a suitable weighted version of the max-flow algorithm would have to be applied, capable of finding the maximum flow among the several available possibilities which also constructs the boundary in the most favorable way. The development of such an algorithm is left for future research.

6.5 Extension to arbitrary modular robots

In this work, we restricted ourselves only to modular robots based on a cubic lattice, with two prescribed elementary moves. However, the presented methodology can be straight-forwardly extended to other, even non-lattice-based, systems. The only assumption is that it must be possible for the robot to create a rigid porous frame and that one can specify a scheme for melting the source boundary and forming the target boundary. In such a case, the pores in the structure generate the nodes of the corresponding graph, and open connections between the pores generate the respective edges in the graph. Once the source- and target boundaries are specified, the max-flow algorithm can be applied to find the maximum set of disjoint streamlines.

Fig. 13

Problem 1. The first, two intermediate, and the last reconfiguration step. a$t=1$, b$t=6$, c$t=8$, d$t=10$

Fig. 14

Problem 2. The first, two intermediate, and the last reconfiguration step. a$t=1$, b$t=6$, c$t=10$, d$t=16$

Fig. 15

Problem 3. The first, two intermediate, and the last reconfiguration step. a$t=1$, b$t=4$, c$t=7$, d$t=11$

7 Computer simulations

Three two-dimensional basic problems are presented to visualize the operation of the proposed methodology, to analyze the properties of the algorithm itself and to validate some of the complexity assessments done in Sect. 5. The simulations have been performed on a virtual machine which emulates the operation of the presented modular system. The emulator was implemented in the Wolfram Mathematica environment (Wolfram Research 2016). The implementation details, including the maximum flow algorithm, are provided in the “Appendix A”.

Remark

In the examples, we only analyze two-dimensional cases, despite the fact that the presented method is designed to work with three-dimensional ensembles equally well. The main reason why we limit ourselves to 2D is related to the max-flow streamline structure which we intended to emphasize—this is the main novelty of the algorithm and it is most clearly visible in 2D.

7.1 Three test problems

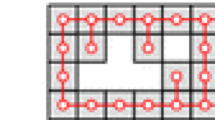
In the figures illustrating the test problems, arrows indicate streamlines, numbers are the values of the distance function from the desired shape, and red and green circles denote sources and sinks, respectively.

The first problem is a simple rectangle-to-rectangle transformation, where the initial rectangle is located vis-a-vis one of the sides of the final shape, see Fig. 13. While outside the desired shape, cf. Fig. 13a, the sources and sinks are always located at the opposite sides of the rectangle. This gives the maximum flow in the direction of the desired shape. While inside the desired shape, additional sinks appear and streamlines make turns in order to fill in that shape. The total number of reconfiguration steps is 10, and this is the minimal possible value.

In the second problem, see Fig. 14, a bottleneck appears, preventing the parallel flow of modules. For example, in Fig. 14c, despite the fact that there are two sources and five sinks, only one streamline can be found. This can be viewed as a drawback of the proposed algorithm for specifying sources and sinks, which is done on the basis of a very simple criterion, preventing outflow of modules from the final shape. Because of the lack of a full parallelism of flow, 15 steps are necessary to attain the goal shape.

One can make another observation about Fig. 14d. The calculated streamline is not optimal, in the sense that it makes unnecessary turns, engaging more modules in the flow. This drawback is related to the simplified criterion, requiring only finding the maximum set of disjoint streamlines, without any further preferences about the quality of the streamlines.

A slightly more complicated problem is shown in Fig. 15. Both the initial and the final shape have holes. This makes the flow more involved as the topology of the shape changes along the way—one of the holes closes as the flow becomes blocked, see Fig. 15c, and the final shape with two holes is attained at the end. Despite this complexity, the algorithm performs reasonably well.

Remark

In all analyzed problems, the initial shape is located in front of a flat wall belonging to the desired shape. Therefore, while away from the wall, the sources and sinks are always located at the left and right boundaries, respectively (the gradient of the distance function is uniform there). If the wall was not flat or the initial shape was placed lower and approaching the final shape from the corner, then one could expect the ensemble to tend to split into two separate bodies. Special techniques would then be necessary to prevent that unwanted behavior, e.g. the one discussed in Sect. 6.1, but we leave that problem for further research.

Table 2 Description of symbols used in figures

Fig. 16

Performance analysis. Dependence of the normalized number of reconfiguration steps on resolution

Fig. 17

Corresponding reconfiguration stages of the problem 2 for three different resolutions k. a$k=1$, step $t=10$ of 16, b$k=2$, step $t=20$ of 34, c$k=4$, step $t=40$ of 66

7.2 Performance check

In order to empirically check the performance of the presented approach we will analyze how the number of steps and computational effort changes with the increasing resolution k, keeping the initial and final shapes constant. The respective theoretical predictions have been provided in Sect. 5, Table 1. All the following results have been obtained using the heuristics described in Sect. 5.4. (See Table 2 for the description of symbols used in the following figures.)

Fig. 18

Problem 1, resolution $k=4$. Max-flow operations intensity per module at three subsequent steps. a Step $t=28, {\bar{t}}\simeq 0.69$, b step $t=29, {\bar{t}}\simeq 0.72$, c step $t=30, {\bar{t}}\simeq 0.74$

Fig. 19

Problem 1. Average number of max-flow operations per module during reconfiguration, for four resolutions k. a Two resolutions in the whole reconfiguration range, b all resolutions in a selected reconfiguration range

The most important performance factor is the scalability of the number of reconfiguration steps. In Fig. 16 it is demonstrated that the desired parallelism is maintained as the resolution increases, i.e., the number of reconfiguration steps $N_R$ is proportional to the resolution k. It means that $N_R$ increases only because the path is naturally subdivided into more steps. This is the most important expected result of the present work.

The observed proportionality is not obvious. In Fig. 17 we show selected intermediate steps of the problem 2 for three different resolutions. Steps are adjusted in such a way that they correspond more or less to the same reconfiguration stage. One can clearly see that for higher resolutions the reconfiguration is not following the patterns observed at lower resolutions. This is an expected behavior because the algorithm has freedom in choosing the preferred sets of sources and sinks to be connected by streamlines, which can differ for different resolutions (and even for two runs of the algorithm at the same resolution). This is one of the potential reasons why the predicted proportionality may not hold. In our case the observed small inclines of the curves in Fig. 16 are caused by a non-optimal choice of sources, done by our simplified algorithm, which results in a deficiency of sources at certain stages of reconfiguration.

In principle, the predicted proportionality should hold as long as the topologies of initial and final shapes are not changing with k. But if new holes/bottlenecks emerge at higher resolutions then reconfiguration may be hindered, at least when using the presented simplified criterion of source and sink selection (e.g., see the discussion of Example 2 in Sect. 7.1). However, it should be possible to greatly reduce the dependence on topology changes if a better source and sink selection strategy is applied. For example, this can be done by neglecting the topology complexities in the initial (rough) phase of reconfiguration and then refining the resultant shape in the final phase. We leave this topic for future work.

The second important performance factor is the amount of computation needed during reconfiguration. At a given step, this can be analyzed in terms of the number of operations performed by each meta-module (see Figs. 17, 18, 20, 22), but can also be expressed as an average over meta-modules (see Figs. 19, 21, 23). Finally, for a given resolution, one can take an average over all reconfiguration steps and modules, see Fig. 24.

Fig. 20

Problem 2, resolution $k=4$. Max-flow operations intensity per module at three subsequent steps. a Step $t=24, {\bar{t}}\simeq 0.35$, b step $t=25, {\bar{t}}\simeq 0.37$, c step $t=26, {\bar{t}}\simeq 0.38$

Fig. 21

Problem 2. Average number of max-flow operations per module during reconfiguration, for four resolutions k. a Two resolutions in the whole reconfiguration range, b all resolutions in a selected reconfiguration range

Fig. 22

Problem 3, resolution $k=4$. Max-flow operations intensity per module at three subsequent steps. a Step $t=16, {\bar{t}}\simeq 0.35$, b step $t=17, {\bar{t}}\simeq 0.37$, c step $t=18, {\bar{t}}\simeq 0.40$

Fig. 23

Problem 3. Average number of max-flow operations per module during reconfiguration, for four resolutions k. a Two resolutions in the whole reconfiguration range, b all resolutions in a selected reconfiguration range

Fig. 24

Performance analysis. Normalized number of max-flow operations per step per module for the increasing resolution k

In Figs. 18, 19, 20, 21, 22, 23 and 24 one can observe the expected advantageous effects of the applied heuristics. For example, in Figs. 18 and 19 it is shown that the peak of computation occurs at the first step after the streamlines reach the wall, and it is necessary to compute new directions. At the remaining steps, the amount of computation is low because only the confirmation of existing streamlines needs to be performed, and it is computationally cheap. In the two remaining problems, Figs. 20, 21, 22 and 23, the reduction of computational effort is clearly visible in the initial phase, prior to arriving at the first obstacle. After that, the situation becomes less clear, especially for higher resolutions. This is because the streamlines disperse, increasing the complexity of the shape and giving rise to new holes/boundaries. And this in turn usually creates the necessity of streamlines’ recalculation, see, e.g., a new hole that is created between steps 16 and 17 in Fig. 22.

Despite the increase of the flow complexity which can be observed for higher resolutions, Fig. 24 suggests that the overall computational effort tends to follow the predicted dependence (cf. Table 1). Without using the heuristics the plots in Fig. 24 would have a constant slope, because the number of max-flow operations would remain at some high level. When the heuristics are used, we only see spikes of computation intensity at “difficult” steps and low values otherwise. Ideally, the plots in Fig. 24 should be bounded by a constant, which would correspond to the predicted proportionality $\sim k^{p-2}$.

Remark

Note that the number of operations at the first step of Problem 1 is very low with respect to the peak value (cf. Fig. 19). The reason is that we start the first step simultaneously for all modules. Therefore, in such an idealized case, all streamlines are constructed in parallel (none of the BFS trees is able to block the others).

7.3 Comparison with other approaches

We will finally attempt to make a comparison between the characteristics and performance of the present algorithm and the ones of the two most closely related approaches—the algorithm of Støy (2004, 2006) and that of Butler and Rus (2003). All these algorithms are distributed, purely geometric with connectedness preservation (do not take mechanical constraints into account), formulated for cubic-lattice-based robots, and perform parallel volumetric reconfiguration. Since we do not possess directly comparable test data, we will resort to extrapolations and heuristic arguments.

The algorithm of Støy (2004, 2006) is designed for the same class of problems as the ones described in the present paper—the modules are not specified other that they are supposed to be able to slide and rotate with respect to their neighbors. Roughly speaking, the reconfiguration strategy is based on the modules at the boundary between the current and target shapes emitting limited-range attraction gradients, and misplaced modules following these gradients. A porous structure is maintained during the process to prevent blocking of the entire flow of modules.

The main difference between Støy’s algorithm and our algorithm is that the first one is entirely asynchronous, with intermixed computation and movement, while the second one proceeds in clearly defined stages, with a major computation phase separated from a movement phase. Both approaches result in volumetric transport of modules, but the present algorithm is in general more efficient in this respect. In Støy’s approach, many misplaced modules move simultaneously throughout the volume of the robot, which contributes to high parallelism of motion. However, the overall movement/flow is not optimized for maximum capacity, and the moving modules may also block one another during the motion. The present algorithm resolves these problems, at the cost of increased computation/communication load and complexity. Once the streamlines are determined, all active modules along all streamlines move simultaneously, which engages a volume of modules in motion. This is illustrated for one streamline in Fig. 4b, where the movements symbolized by black arrows are executed simultaneously; see also the description of step (iii) in Sect. 4.2. This fact combined with the max-flow property of the set of streamlines guarantees, as far as instantaneous transport between a chosen source and target boundary is concerned, that the parallelism of the proposed approach is never lower than that of Støy’s algorithm and should be higher in most cases.

In Støy (2006) two types of reconfiguration tests are made: reconfiguration from a plane of modules into a disc perpendicular to that plane, and reconfiguration from a plane into a sphere. As expected for a volumetric reconfiguration scheme, the number of time steps needed for reconfiguration to complete (most of which involve parallel movement of modules and are therefore reconfiguration steps) grows slightly sublinearly as a function of the number of modules N. By comparison, our algorithm would be expected to perform similar reconfiguration tasks in $\sim \sqrt{N}$ reconfiguration steps (provided that the N modules are arranged into metamodules). Generally, it should require less reconfiguration steps, but much more steps of communication and message processing.

The PacMan algorithm proposed in Butler and Rus (2003) is designed for unit-compressible modules, in which actuation is achieved through expansion and contraction. Suitable hardware platforms have been built and include crystalline atoms (Rus and Vona 2001; Butler and Rus 2003) and telecubes (Vassilvitskii et al. 2002). The algorithm is organized into stages, much like our algorithm: first, source and target boundaries are identified; then, reconfiguration paths are planned between the boundaries; finally, parallel movement of modules along the paths is performed.

There are three main differences between PacMan and our algorithm. Firstly, PacMan does not operate on metamodules, but on individual modules. Therefore, there arise numerous problems connected with module over-crowding—among them, reconfiguration along turning paths may be slowed down by the turns. Secondly, the paths are planned by a depth-first search from sinks to sources and established on a first-served basis. Thirdly, paths may intersect. The resulting paths do not form a max-flow structure, and when they intersect, the parallel movement of modules in the volume is disturbed. There are no simulation results which could be used for a direct comparison. Nevertheless it can be expected that, overall, the number of necessary reconfiguration steps for the PacMan algorithm will scale worse with N than for the present algorithm—even if PacMan is reformulated for another hardware platform.

8 Conclusions

The most pronounced conclusion of this work is that one can perform shape change of modular robots efficiently. This can be done by parallelizing the process of physical reconfiguration, which reduces the number of reconfiguration steps (reconfiguration time). It was demonstrated that, in the proposed framework, one can expect the number of necessary reconfiguration steps to be proportional to the resolution of the robot. The increase of the number of steps results solely from the refinement of the reconfiguration path itself. Therefore, this is actually the best that can be achieved if no other reconfiguration mechanisms are considered (such as monolithic motion of larger substructures of a robot).

We have given an interpretation of the reconfiguration as a problem of special flow through a porous meta-structure. The flow takes place between the source and the target surfaces of the modular ensemble, which can also be represented as sets of source and sink vertices of the corresponding graph. We have shown that the sources and sinks, as well as the desired maximal flow in the graph, can be determined by the modular robot itself in a distributed fashion. The presented approach allows one to split the problem of shape evolution into two, partially uncoupled, problems:

• the problem of planning the trajectory between current and desired shapes, only specified at the surface;

• the problem of finding an optimal flow of modules between source and target surfaces, specified in the whole volume;

Therefore, one can partially abstract from keeping control over modules’ flow (whose efficiency is to some extent assured), and focus more on higher-level shape-transformation planning. This technique seems promising as it may give rise to efficient reconfiguration scenarios.

A basic, simplified source and sink selection scenario has been shown in the present work. However, more advanced schemes need to be considered in future in order to increase the efficiency and alleviate some of the problems, as discussed earlier in this work. Undoubtedly, some interaction between high-level reconfiguration planning and low-level optimal flow search needs to be considered if a really robust reconfiguration scheme is to be developed.

We have proposed a suitable max-flow algorithm and analyzed it in terms of time-, memory- and computational complexity. The achieved time- and CPU complexities are significantly lower than those for the general case of arbitrary flow networks. Nevertheless, direct use of the max-flow search will probably be prohibitively expensive in very numerous ensembles. Therefore other (perhaps approximate) techniques need to be developed in future.

Appendices

Appendix A: implementation details

1.1 A.1 Emulator of the distributed system

Table 3 Description of variables, functions and constants used in the algorithm. All except modules are internal variables of meta-modules

A simplified emulator of a distributed robotic system has been implemented in the Wolfram Mathematica environment (Wolfram Research 2016), which enabled us to implement the distributed reconfiguration algorithms provided in Sect. A.2, and to run the analyses presented in Sect. 7.

In the emulator, each meta-module is represented as a separate data structure, consisting of the necessary internal variables and the message queue, cf. Fig. 7, see also Table 3. At each iteration, NextIteration() procedure (Proc. 2) is executed independently by each meta-module. At the end of each iteration, respective exchange of messages is done between neighboring modules.

In our implementation, all activity of the system, i.e., source/sink detection, maximum flow search and module transportation sub-steps are controlled in a distributed manner. Also a kind of distributed synchronization has been implemented, which assures that meta-modules switch to the next sub-step not earlier than when all messages from the current sub-step have been processed. However, for the sake of brevity and clarity, here we only present the max-flow-search part of the algorithm, in a version without heuristics and synchronization.

1.2 A.2 Distributed maximum flow algorithm

The distributed max-flow search routine is executed in the sub-step 2 of NextIteration() function (see the line 5 in Proc. 2). It implements the algorithm discussed in Sect. 5.2 and it consists of two parts (see MaxFlowSearch() procedure in Proc. 3). In the first part, lines 2–8, if the meta-module is an available source then it initiates a new BFS tree by sending a ”BFS” message to all neighbors. In the second part, the next message from the inbox (FIFO queue) is analyzed, and the respective procedure depending on the message type is executed (lines 9–22).

Remark

Lines 2–8 in Proc. 3 can also be seen as an initialization phase. It has been simplified here, and in its original implementation it also contains a part responsible for the heuristics (see Sect. 5.4). Implementation of the heuristics, performed in the first iteration of the sub-step 2, consists in analyzing the state of a meta-module and deciding whether to preserve the streamline by converting it into a BFS branch or whether to cut it off. It is not provided here for the sake of brevity and clarity.

Messages of type ”BFS” (Proc. 4) are responsible for spanning BFS trees (blue arrows in Fig. 8). As discussed in Sect. 5.2, there might be up to three paths that are flowing through a meta-module:

• main path (mainPath, lines 3–16);

• augmenting path that flows in from the outside of the existing streamline (aug1Path, lines 17–23, see blue arrow in meta-module 6 at iteration 9 in Fig. 8);

• augmenting path that flows in upstream the existing streamline (aug2Path, lines 24–30, see blue arrow in meta-module 5 at iteration 10 in Fig. 8).

Once a BFS path arrives at a sink it sends back a confirmation message (”ConfirmPath”, see lines 6–10).

Note here that a special edge confirmation protocol is necessary in order to properly establish a BFS edge. It is done by sending back a ”ConfirmEdge” message, and the respective output branch is made active only if edge confirmation has been received (see Proc. 5).

”ConfirmPath” messages (Proc. 6), combined with ”CutOff” messages (Proc. 7), are responsible for selecting (backtracking) a single path from the BFS tree, connecting the source located at the root with one of the sinks. It supports three path types, i.e., main path and two augmenting paths (lines 2–11, 12–15 and 16–20, respectively). While traveling the tree from leaf to root, it cuts off other branches, only leaving the current path. Once arriving at the root, it initiates the final streamline confirmation by sending back a ”ConfirmStreamline” message.

Note here that in order to use ”CutOff” mechanism safely, special precautions must be taken while growing the tree. As discussed in Sect. 5.3, a list of path ID’s which had passed the meta-module in a given step is stored (pathsOld), and this prevents processing a branch of the same tree twice in the step. Respective conditions are checked in Proc. 4 in lines 3, 17 and 24. Also, after cutting itself off, meta-module sends ”Available” message to the neighbors (line 16 in Proc. 7), which is the already discussed acknowledgment mechanism, see the remark in Sect. 5.2.

Streamline confirmation (Proc. 8), in the case of main paths, is necessary to allow other BFS trees to grow upstream a streamline. The use of a streamline can not be allowed earlier, i.e., just after path confirmation, because several concurrent branches of the tree may be building the path. We do not know in advance which path will become a streamline and which will be cut off. Again, acknowledgments are spread around after establishing the streamline—to make neighboring BFS trees know that there is new space for expansion.

In the case of augmenting paths, streamline confirmation has additional functionality. It crossbreeds the existing streamlines with the new augmenting path, see iterations 28 and further in Fig. 8. The operation can be viewed as a kind of symmetric difference on respective sets of edges—the set of main streamlines’ edges and the set of augmenting path edges. It removes the overlapping edges and reorganizes the flow accordingly.

Appendix B: supplementary material

In the electronic supplementary material we provide the complete results for the three problems discussed in Sect. 7.