1 Introduction

Since 1998 the phenomenon of the accelerated expansion of the Universe has attracted a great deal of interest among all astrophysicists, cosmologists, and astronomers. There are many models that refrained from investigating the behaviour of the Universe. In the past, before the discovery of the fast expansion of the universe, many scientists were interested in studying the evolution of the Universe with its constant deceleration parameter (Berman 1983; Berman and de Mello Gomide 1988). Consequently, a number of Cosmological models has been proposed. Some of these models have been obtained as particular solutions for the Einstein field equations; for instance, see (McVittie 1962; Sciama and Dodelson 1971). Researchers intended to study the expanding Universe after countless discoveries that were made by the Supernova Legacy Survey (SNIa); for instance, see Riess et al. (2004), Gold sample of Hubble Space, Telescope by Astier et al. (2006), and large scale structure (LSS) by Eisenstein et al. (2005). After that time, researchers began to study the Cosmological models with a variable deceleration parameter to explore the new theories about cosmic expansion; for instance, see (Choudhury and Padmanabhan 2005; Clark and Stephenson 2016; Akarsu and Dereli 2012; Sahoo et al. 2018; Bakry and Shafeek 2019; Sahni and Starobinsky 2000; Grøn and Hervik 2007). In addition, a substantial number of investigations of the models, with each cosmological term as a time variable, was proposed during the last two decades, see, e.g. (Chen and Wu 1990; Pavón 1991; Arbab and Abdel-Rahman 1994; Overduin and Cooperstock 1998; Carneiro and Lima 2005). The aim of the previous investigations was to generate a model that explains the phases of evolution of the Universe in line with modern observations. Cosmologists have tried to explain the expansion of the universe in two possible ways, the first of which is of dark energy, whereas the second is a set of modified theories of gravitation. Therefore, various alternative or modified theories of gravitation like bimetric theory, scalar-tensor theories, vector-tensor theories, Weyl theory (1918), \(f(R)\) theory (Sotiriou and Faraoni 2010), \(f(R,T)\) theory of gravity (Reddy et al. 2012), Brans Dickey theory (1961), and Lyra Geometry (Singh and Desikan 1997; Pradhan et al. 2001; Rahaman et al. 2005), etc., have been proposed. Among all these alternative theories we will discuss the Lyra’s geometry which is a modification of Riemannian geometry which is itself modified by introducing a gauge function into the structure-less manifold that bears a similar appearance to Weyl geometry. This resulted in the elimination of non-integrability of length transfer, which implies that the frequency of the spectral line emitted by atoms could not remain constant, but rather depends on their past history which is in direct contradiction to the observed uniformity of their properties. As known, Lyra’s geometry (Lyra 1951) can be considered as a candidate for modification of the contemporary cosmological models. In the consecutive investigations, Sen (1957) and Sen and Dunn (1971) proposed a new scalar tensor theory of gravitation and constructed a correlation among Einstein field equations based on Lyra’s geometry in a normal gauge function. The aim of this article is to study the behaviour and development of the universe in light of its successive acceleration, and to compare the results with astronomical observations in order to predict the future of the universe according to the current observations. In order to crystallize the organization of the current manuscript, the rest of the paper is organized as follows: Sect. 2 is devoted to investigating the modified Einstein’s field equations in Lyra’s geometry. The fundamental cosmological parameters are illustrated in a varying deceleration parameter. Finally, the concluding remarks are drawn in Sect. 5.

2 The modified Einstein’s field equations in Lyra’s geometry

Many Physicists have been investigating about gravitation in different contexts after Einstein. Hermann Weyl attempted to generalize the idea of geometrizing the gravitation and electromagnetism by applying different techniques and methods (Weyl 1918). He described both gravitation and electromagnetism geometrically by formulating a new kind of gauge theory involving metric tensor with an intrinsic geometrical significance. A scalar-tensor theory of gravitation proposed by Sen and Dunn (1971) is based on Lyra’s manifold rather than Riemannian’s (Lyra 1951). The results show that this new theory predicts the same effect within the scope of observation in Einstein’s theory. In the Lyra geometry, the connection is metric preserving as in the Riemannian geometry, which means length transfers are integrable. Also, in Lyra’s manifold, as obtained by Sen (1957), the Einstein field equations in a normal gauge are

$$ R_{\mu \nu } - (\frac{1}{2}R + \frac{3}{4} \phi _{\lambda } \phi ^{\lambda } ) g_{\mu \nu } + \frac{3}{2}\phi _{\mu } \phi _{\nu } = - T_{\mu \nu }, $$
(1)

where \(\phi _{\mu } = g_{\mu \nu } \phi ^{\nu } \) is the displacement vector field of Lyra geometry, \(T_{\mu \nu } \) is the energy-momentum tensor, \(R_{\mu \nu } \) is the Ricci tensor, and \(g_{\mu \nu } \) is the metric tensor. We assume that the gravity coupling constant \(8 \pi G = 1\). In the literature there are two choices for the displacement vector. First, the general time dependent displacement vector field is given by (Beesham 1988; Singh and Desikan 1997; Rahaman et al. 2005; Darabi et al. 2015)

$$ \phi ^{\mu } = (\beta (t), 0, 0, 0)), $$
(2)

where \(\beta (t)\) in the displacement field \(\phi ^{\mu } \). The physical meaning of the time component of the displacement vector was introduced by considering it as a part of the energy-momentum tensor as a viscosity (Hegazy and Rahaman 2019, 2020; Hegazy 2020).

Second, the constant displacement vector (Halford 1970) is as follows:

$$ \phi ^{\mu } = (\beta , 0, 0, 0)), $$
(3)

where \(\beta \) is a constant. In Lyra’s geometry, the constant displacement field \(\phi ^{\mu } \) plays the role of a cosmological constant in normal general relativistic treatment (Halford 1970).

In this work, in order to have a general form of field equations, we will consider its general time dependent form.

We may rewrite the field equations (1) in the mixed form as follows

$$ G_{\mu \nu } - \frac{3}{4} \phi _{\lambda } \phi ^{\lambda } g_{\mu \nu } + \frac{3}{2}\phi _{\mu } \phi _{\nu } = - T_{\mu \nu }, $$
(4)

where

$$ G_{\mu \nu } = R_{\mu \nu } - \frac{1}{2}R g_{\mu \nu }. $$
(5)

In the presence of creation of matter, the energy-momentum tensor \(T_{\mu \nu } \) can be written as follows (Bishi and Lepse 2021):

$$ T_{\mu \nu } = (\rho + P + P_{c}) u_{\mu } u_{\nu } - (P + P_{c}) g_{\mu \nu }, $$
(6)

where \(\rho \) is the energy density, \(p\) is the pressure of the fluid, \(p_{c}\) is the creation pressure, and \(u_{\mu } \) is the fluid-four velocity vector where \(u_{\mu } u^{\mu } = 1\).

In order to analyze the modified Einstein’s field equations based on Lyra’s geometry (1), it is necessary to make some simplifying assumptions, such as choosing a metric with a significant degree of symmetry. In the current paper, one may consider the Robertson-Walker metric with a maximally symmetric spatial section as follows (Robertson 1932):

$$ ds^{2} = dt^{2} - S^{2}(t)\left ( \frac{dr^{2}}{1 - k r^{2}} + r^{2}(d\theta ^{2} + \sin ^{2}\theta d\varphi ^{2}) \right ), $$
(7)

where \(S(t)\) is the Cosmic scale factor—which measures how much the Universe stretches as a function of time, and the spatial curvature index \(k \in \{ - 1, 0, 1\}\) corresponds to the spatially open, flat and closed Universes, respectively. For the metric (7), the energy-momentum tensor and Eq. (5) yield

$$ T_{0}^{ 0} = \rho ,\ T_{1}^{ 1} = T_{2}^{2} = T_{3}^{3} = - (P + P_{c}), $$
(8)

and

figure a

In a co-moving coordinate system, the modified Einstein field equations as given by Eqs. (8), (9) and (4) yield the following equations

$$ \rho = 3H^{2} + \frac{3 k}{ S^{2}} - \frac{3\beta ^{2}}{4}, $$
(10)

and

$$ P + P_{c} = - \left ( 3H^{2} + 2\dot{H} + \frac{k}{S^{2}} + \frac{3\beta ^{2}}{4} \right ), $$
(11)

where the over dot denotes the derivative with respect to Cosmic time \(t\), and the Hubble’s parameter is defined as

$$ H = \frac{\dot{S}}{S}, $$
(12)

it measures the expansion rate of the Universe as a function of time.

Equations (10) and (11) lead to the continuity equation

$$ \dot{\rho } + \frac{3}{2}\beta \dot{\beta } + 3H(\rho + P + P_{c} + \frac{3}{2}\beta ^{2}) = 0. $$
(13)

A record of the perfect fluids that are relevant to the Cosmology results in an equation of state (EoS) in the form

$$ p = \omega \rho . $$
(14)

The three greatest mutual examples of the Cosmological fluids with constancy \(\omega \) are the dust (\(\omega = 0\)), vacuum energy (\(\omega = - 1\)), and radiation (\(\omega = 1 / 3\)). It is known that fluids with (\(\omega < - 1 / 3\)) are usually considered in the setting of Dark Energy (DE) since they give rise to accelerating expansion. These cases will be discussed in depth in the Cosmological models proposed throughout this paper, with (\(- 1 \le \omega \le 1\)).

The creation pressure is given by (Bishi and Lepse 2021)

$$ P_{c} = - (1 + \omega ) \frac{\rho }{3H} \frac{\dot{N}}{N}, $$
(15)

where \(\frac{\dot{N}}{N}\) is the rate of change of the particle number in a co-moving volume \(V\).

The particular form of the particle source function is given by (Bishi and Lepse 2021)

$$ \frac{\dot{N}}{N} = b H, $$
(16)

where \(b \ge 0\) is a constant. Now, the elimination of \(\rho \) from (10) and (11) yields (Bishi and Lepse 2021)

$$\begin{aligned} P_{c} ={}& - \biggl( 2 \dot{H} + 3H^{2}(1 + \omega ) + \frac{ k}{ S^{2}}(1 + 3 \omega ) \\ &+ \frac{3\beta ^{2}}{4}(1 - \omega ) \biggr). \end{aligned}$$
(17)

Using Eqs. (10), (15)–(17), one obtains

$$\begin{aligned} \beta ^{2} ={}& - \frac{4}{(b + 3) + \omega (b - 3)} \biggl( 2 \dot{H} + H^{2}(1 + \omega ) (3 - b) \\ &+ \frac{ k}{ S^{2}}(1 + 3 \omega - b (1 + \omega )) \biggr). \end{aligned}$$
(18)

Substituting from Eq. (18) into Eqs. (11) and (17), the energy density and particle creation take the following form

$$ \rho = \frac{6}{(b + 3) + \omega (b - 3)} \left ( \dot{H} + 3H^{2} + \frac{ 2 k}{ S^{2}} \right ), $$
(19)
$$ P_{c} = - \frac{2b (1 + \omega )}{(b + 3) + \omega (b - 3)} \left ( \dot{H} + 3H^{2} + \frac{ 2 k}{ S^{2}} \right ). $$
(20)

Substituting from Eq. (19) and (20) into (11), the pressure of the resulting model is expressed as

$$ P = \frac{6 \omega }{(b + 3) + \omega (b - 3)} \left ( \dot{H} + 3H^{2} + \frac{ 2 k}{ S^{2}} \right ). $$
(21)

3 Fundamental cosmological parameters

At this stage, one may introduce some fundamental cosmological parameters that describe the kinematics of the Universe, namely the deceleration parameter, the Hubble parameter, and the scale factor. These parameters may be defined by the following mathematical equations:

The deceleration parameter is defined as

$$ q = \frac{dH^{ - 1}}{dt} - 1. $$
(22)

From Eq. (9), one can see that the Cosmological models with the variable deceleration parameter must go throughout the decelerating expansion if \(q > 0\), reach an expansion with the constant rate if \(q = 0\), and end at an accelerating power-law expansion if \(- 1 < q < 0\). The Cosmological model is the de Sitter expansion (exponential expansion) if \(q = - 1\).

Throughout this section, the linearly varying deceleration parameter is used as follows (Akarsu and Dereli 2012)

$$ q(t) = m - 1 - at, $$
(23)

where \(m\) and \(a\) are constants.

In the current paper, one may choose the coefficient value to match the observed kinematics of the Universe as follows (Katore and Shaikh 2015):

$$ m = 2\mbox{, and }a = 0.126. $$

For these reasons, one gets

$$ q(t) = 1 - 0.126 t, $$
(24)

where \(t:0 \to 2m / a = 31.8\).

Equations (23) and (24) lead to the following Hubble parameter and its derivative

$$\begin{aligned}& H(t) = \frac{2}{t (2m - at)} = \frac{2}{t (4 - 0.126 t)}, \\ \end{aligned}$$
(25)
$$\begin{aligned}& \dot{H}(t) = \frac{4(at - m)}{t^{2} (2m - at)^{2}} = \frac{4 (0.126 t - 2)}{t^{2} (4 - 0.126 t)^{2}}. \end{aligned}$$
(26)

The scale factor \(S(t)\) is obtained by integrating the Hubble parameter as follows:

$$ S(t) = S_{0}\left ( \frac{t}{2m - at} \right )^{1 / m} = S_{0} \left ( \frac{t}{4 - 0.126 t} \right )^{1 / 2}, $$
(27)

where \(S_{0}\) is the constant of integration and can be taken as a unity.

It is worth noting that the scale factor \(S(t)\) differs from that in the LVDP model; for instance, see (Akarsu and Dereli 2012).

We also solve the deceleration parameter \(q\) as a function of the redshift \(z + 1 = S_{z = 0} / S\) where \(S_{z = 0}\) is the present value of the scale factor

$$ q(z) = m - 1 - \frac{2ma S_{z = 0}^{m}}{(1 + z)^{m} + a S_{z = 0}^{m}} = 1 - \frac{3.1}{(1 + z)^{2} + 0.8}, $$
(28)

where \(S_{z = 0} = 2.46\) at \(t = 13.7\) Gyr.

In what follows, a set of diagrams will be plotted to show the influence of some important physical parameters on the model.

The previous figures may be illustrated as follows:

In Fig. 1, the deceleration parameter \(q(t)\) starts with deceleration \(q = 1\) at the Big Bang (\(t_{bb} = 0\)), and then moves to the acceleration \(q < 0\), until it eventually reaches the strong acceleration \(q < - 1\) at a Big Rip(\(t_{b r} = 31.8\)).

Fig. 1
figure 1

The deceleration parameter \(q(t)\) versus the cosmic time \(t:0 \to 31.8\)

Full size image

In Fig. 2, the scale factor \(S(t)\) starts with zero value at the Big Bang (\(t_{bb} = 0\)) and then it diverges at a Big Rip (\(t_{b r} = 31.8\)).

Fig. 2
figure 2

The Scale factor \(s(t)\) versus the cosmic time \(t:0 \to 31.8\). The Scale factor diverges at the Big Rip

Full size image

In Fig. 3, the Hubble parameter \(H(t)\) diverges at the beginning and the end of the universe.

Fig. 3
figure 3

The Hubble parameter \(H(t)\) versus the cosmic time: \(t:0 \to 31.8\)

Full size image

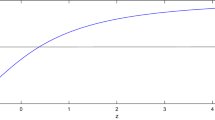
In Fig. 4, in general, the transition redshift of the accelerating expansion is given by \(0.3 < z_{t} < 0.9\). In our model, \(z_{t} \approx 0.51\), the value agrees with the \(\Lambda CDM\) model; for instance, see (Katore and Shaikh 2015).

Fig. 4
figure 4

The deceleration parameter \(q(z)\) versus redshift \(z:0 \to 2\)

Full size image

4 Big Rip model

By the two physically plausible relationships (10) and (17), one can solve the field Eqs. (10), (11). Substituting from Eqs. (25), (26) and (27) into Eqs. (19), (20) and (21), one gets

$$\begin{aligned} \beta ^{2} &= - \frac{4}{(b + 3) + \omega (b - 3)} \biggl( \frac{8 (at - m) + 4 (1 + \omega ) (3 - b)}{t^{2}(2m - at)^{2}} \\ &\quad + \frac{k(1 + 3 \omega - b (1 + \omega )) (2m - at)}{t} \biggr), \end{aligned}$$
(29)
$$\begin{aligned} \rho &= \frac{6}{(b + 3) + \omega (b - 3)} \biggl( \frac{4(3 - m + at)}{t^{2}(2m - at)^{2}} \\ &\quad+ \frac{2k (2m - at)}{t} \biggr), \end{aligned}$$
(30)
$$\begin{aligned} P_{c} &= - \frac{2b (1 + \omega )}{(b + 3) + \omega (b - 3)} \biggl( \frac{4(3 - m + at)}{t^{2}(2m - at)^{2}} \\ &\quad+ \frac{2k (2m - at}{t}) \biggr). \end{aligned}$$
(31)

Also, the pressure of the resulting model is expressed as

$$\begin{aligned} P &= \frac{6 \omega }{(b + 3) + \omega (b - 3)} \biggl( \frac{4(3 - m + at)}{t^{2}(2m - at)^{2}} \\ &\quad+ \frac{2k (2m - at)}{t} \biggr). \end{aligned}$$
(32)

Now, to demonstrate how the model matches the observed kinematics of the universe and makes additional predictions, we first plot the cosmological parameters by choosing \(m = 2\) and \(a = 0.126\), as before. In our model, the displacement vector component \(\beta ^{2}\) has the same behavior for closed, flat and open universe. From Figs. 5, 6 and 7, one may notice that \(\beta ^{2}\) evolves with the singularities at \(t = 0\) and 31.8, that is, at the Big Bang and the Big Rip, respectively. The displacement vector component \(\beta ^{2}\) evolves with a positive value at the Big Bang, then approaches zero with the evolution of time, and eventually reaches a negative value at the Big Rip for the flat, closed, and open universe, when \(\omega < - 0.5\) at \(b \ge 10\).

Fig. 5
figure 5

The displacement vector component \(\beta ^{2}(t)\) versus the cosmic time: \(t:0 \to 31.8\), and the state parameter \(\omega : - 1 \to 1\), \(b = 20\) for flat, open and closed universe

Full size image
Fig. 6
figure 6

The displacement vector component \(\beta ^{2}(t)\) versus the cosmic time: \(t:0 \to 31.8\), and the state parameter \(\omega : - 1 \to 1\), \(b = 10\) for flat, open and closed universe

Full size image
Fig. 7
figure 7

The displacement vector component \(\beta ^{2}(t)\) versus the cosmic time: \(t:0 \to 31.8\), and the state parameter \(\omega : - 1 \to 1\), \(b = 1\) for flat, open and closed universe

Full size image

In Fig. 8, we plot the energy density of the fluid \(\rho (t)\) versus cosmic time \(t\) and the state parameter \(\omega \). For the spatially closed, open and flat models, the energy density of the fluid diverges at the beginning and the end of the universe. One may observe that the spatially flat, open and closed models are possible since the positivity condition of the energy density is satisfied in these models. In Fig. 9, we plot the pressure of the fluid \(P(t)\) versus cosmic time \(t\) and the state parameter \(\omega \). One can notice that when \(\omega = 0\), the pressure diverges at the Big Bang and the end of the universe at the Big Rip. But when \(0 < \omega < 1\) has a positive value and when \(- 1 \le \omega < 0\), the pressure has an negative value. In Fig. 10, we plot the particle creation pressure \(P_{c}(t)\) versus cosmic time \(t\) and the state parameter \(\omega \). One may observe that the creation pressure \(P_{c}(t)\) has singularity at the Big Bang and the Big Rip. It has the value \(P_{c}(t) \le 0\) for all values of \(b > 0\).

Fig. 8
figure 8

The energy density \(\rho (t)\) versus the cosmic time: \(t:0 \to 31.8\), and the state parameter \(\omega : - 1 \to 1\), \(b > 0\) for open, closed and flat universe

Full size image
Fig. 9
figure 9

The pressure \(P(t)\) versus the cosmic time: \(t:0 \to 31.8\), and the state parameter \(\omega : - 1 \to 1\), \(b > 0\) for open, closed and flat universe

Full size image
Fig. 10
figure 10

The pressure \(P_{c}(t)\) versus the cosmic time: \(t:0 \to 31.8\), and the state parameter \(\omega : - 1 \to 1\), \(b > 0\) for open, closed and flat universe

Full size image

From Figs. 5-10, one may discuss all the stages, such as the Stiff matter model \(\omega = 1\), the Radiation dominated model \(\omega = 1/3\), the Dust filled model \(\omega = 0\), and the Vacuum energy model \(\omega = - 1\). From the previous figures, it is possible to accept flat, open and closed universes because these models fulfill the positive condition of the energy density. Also, the pressure begins with a positive value when the deceleration expands and turns into a negative value with a strong expansion, in line with the theory of dark energy.

Now we consider the energy conditions for our models. To consider the Energy Conditions, in Fig. 11, we plot \(\rho + P\) versus cosmic time \(t\) and the state parameter \(\omega \). We see that our models satisfy the Dominant Energy Condition \(\rho + P \ge 0\). Also, it satisfies the Null Energy Condition \(\rho - P \ge 0\) as shown in Fig. 12. Strong Energy Condition is achieved when \(- 0.3 \le \omega \le 1\), while it is violated when \(- 1 \le \omega < - 0.3\).

Fig. 11
figure 11

\(\rho + P\) versus the cosmic time: \(t:0 \to 31.8\), and the state parameter \(\omega : - 1 \to 1\), \(b > 0\) for open, closed and flat universe

Full size image
Fig. 12
figure 12

\(\rho - P\) versus the cosmic time: \(t:0 \to 31.8\), and the state parameter \(\omega : - 1 \to 1\), \(b > 0\) for open, closed and flat universe

Full size image
Fig. 13
figure 13

\(\rho + 3P\) versus the cosmic time: \(t:0 \to 31.8\), and the state parameter \(\omega : - 1 \to 1\), \(b > 0\) for open, closed and flat universe

Full size image

5 Concluding remarks

From the previous analysis of the linearly varying deceleration parameter and the particular form of the particle source function, we can solve the modified Einstein’s field equations in view of Lyra’s geometry. The solution is analysed for the Big Bang-Big Rip model. It starts with the Big Bang, then passes through the Stiff matter model, the Radiation dominated model, the Dust filled model, and the Vacuum energy model at the end of the universe when the Big Rip occurs. The physical behaviour of the displacement vector component \(\beta \), energy density \(\rho \), pressure \(P\) and particle creation pressure \(P_{c}\) is studied. The observations for the Big Bang-Big Rip model discussed in previous sections are as follows:

• The Big Bang-Big Rip model has singularity at \(t_{bb} = 0\) and \(t_{br} = 31.8\) Gyr.

• The transition redshift of the accelerating expansion occurs in our model when this value corresponds to the astronomical observations; see (Cunha and Lima 2008), and (Riess et al. 1998).

• Our model gives the present value of the deceleration parameter \(q_{day} = - 0.73\) at \(t_{day} = 13.7\) Gyr, see (Spergel et al. 2003).

• The pressure \(P > 0\) in the stiff matter model and radiation dominated model reaches \(P = 0\) in the dust filled model, while \(P < 0\) in the vacuum energy model.

• It is worth noting here, from Figs. 5-10, that the negative pressure accompanies the acceleration of the Universe, which leads to the Dark Energy. This argument would rule out almost all the usual suspects, such as cold dark matter, neutrinos, radiation, and kinetic energy because they have zero positive pressure; for instance, see Caldwell et al. (2003). A Dark Energy with a significant negative pressure will in fact cause the expansion of the Universe to speed up, so the supernova observations provide an empirical evidence of Dark Energy with a strong negative pressure; for instance, see Refs. (Garnavich et al. 1998; Padmanabhan 2003; Carroll et al. 2003; Silvestri and Trodden 2009).

• The particle creation pressure \(P_{c} \le 0\) for flat and closed models. In case of the open model, it starts with \(P_{c} < 0\) and reaches \(P_{c} = 0\) and ends \(P_{c} < 0\).

• In view of the positivity of the displacement vector component \(\beta ^{2}\), it evolves with a positive value at the Big Bang, then approaches zero with the evolution of time, and reaches to a negative value at the Big Rip for the flat, closed, and the open universe when \(\omega = - 1\) and \(b \ge 20\). This means that the displacement vector component \(\beta \) has imaginary values at the Big Rip. Pure imaginary values for \(\beta \) have already been considered by Sen (1957) and by Kalyanshetti and Waghmode (1982).

• One can notice that parameter \(b\) has a great influence on the behavior of the displacement vector component \(\beta ^{2}\). From Eqs. (16), (25), and (27), we can write the particular form of the particle source function as follows,

$$ N = (\frac{t}{4 - 0.126t)})^{b / 2}, $$
(33)

which gives \(N \to 0\) at the Big Bang and \(N \to \infty \) at the Big Rip.

It is worth noting here that all the results we have reached in this article are in full agreement with the previous literature, for example, the same case was studied using a quadratic deceleration parameter (Bishi and Lepse 2021), and also (Halford 1970; Beesham 1988). If \(\beta = 0\), our models are reduced to the linearly varying deceleration parameter (Akarsu and Dereli 2012).

• All the discussed models satisfy the Dominant Energy Condition and the Null Energy Condition, but the Strong Energy Condition is achieved when \(- 0.3 \le \omega \le 1\), while it is violated when \(- 1 \le \omega < - 0.3\) (Dark energy stage).

• It is worth noting here that all the results we have reached in this article are in full agreement with the previous literature, for example when the same case was studied using a quadratic deceleration parameter (Bishi and Lepse 2021), and also (Halford 1970; Beesham 1988). If \(\beta = 0\) our models are reduced to the linearly varying deceleration parameter (Akarsu and Dereli 2012).