Photometric analysis of the system Kepler-1

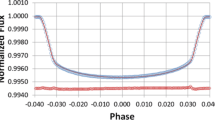
Abstract

We have applied the close binary system analysis program WinFitter to an intensive study of Kepler-1 (= TrES-2) using all the available photometry (14 quarters; 1570640 measures) from the NASA Exoplanet Archive (NEA) at the Caltech website http://exoplanetarchive.ipac.caltech.edu. The mean individual data-point error of the normalized flux values is 0.00026, leading to the model’s specification for the mean reference flux of the system to an accuracy of ${\sim} 0.5~\mbox{ppm}$. Completion of the analysis requires a number of prior quantities, relating mainly to the host star, that are adopted from relevant literature.

Our new results tend broadly to confirm those of previous authors, though there are a number of significant differences. Specifically, the applied photometric fitting function is more precise than those used before on the full Kepler data-set. The more complete discussion of the interdependent role of errors, using MCMC sampling, allows greater confidence in the obtained parameters themselves as well as understanding or their likely errors. Our photometrically derived values for the mass and radius of Kepler-1b are $1.18\pm 0.05~\mathrm{M}_{\mathrm{Jup}}$ and $1.21\pm 0.05~\mathrm{R}_{\mathrm{Jup}}$. The mass of this Safronov Class I planet is closer to published spectroscopic values than found from previous photometric analysis, which can be attributed to the improved fitting function.

The analysis determines a definite photometric Doppler effect from the orbit, but this is not independent of the tidal (‘ellipticity’) effect, and the two are consistently combined in our fitting function. A corresponding rotation-related Rossiter effect was not detected, allowing an upper limit on the rotation speed of ${\sim} 70~\mbox{km}\,\mbox{s}^{-1}$. The proportion of light coming from the known companion star is resolved, but turns out rather less than that inferred from the results of direct measurement. The fitting function also predicts a small secondary minimum (‘occultation’), when the light reflected by the planet is eclipsed. However, the occultation depth cannot be measured directly from the data to the relevant accuracy, and so models for the planet’s atmospheric properties based on this will be compromised by other assumptions and approximations in the light curve’s fitting function.

Suggestions of secular trends for the variation of parameters are considered, but the evidence of the Kepler data is not yet very persuasive.

Appendix: MCMC sampling, errors and correlations

We have used Monte Carlo techniques to further investigate uncertainties in fitting models to Kepler transit light curves. We implemented a Markov Chain Monte Carlo (MCMC) sampling method to explore parameter estimation for the case of Kepler 1b. A basic model for a single-planet, spherical body transiting system with a circular orbit was built in the Stan language. Stan was also used for Bayesian statistical inference using MCMC sampling. More information about Stan can be found in http://mc-stan.org. The model assumes that data-noise, as estimated from the residuals, is normally distributed as $N(0,\Delta l)$. The essential theory behind this model can be found in numerous sources: e.g. Russell (1912a, 1912b), Russell and Shapley (1912), Tsesevich (1936), Kopal (1941), Sobolev (1975), Charbonneau et al. (1999), Mandel and Agol (2002), and many others. Further details on our application of the model can be found in Ji (2016). We ran four independent Markov Chains in parallel, each of length 10,000 and with different starting values. We discarded the first half of each chain as ‘burn-in’. The remaining 20,000 samples were used for analysis.

Figure 8 presents fitting histograms and pairwise correlation diagrams for the following selected modelling parameters for Kepler 1: $k$, $r_{1}$, $u$, $\cos i$, $\Delta \phi_{0}$, $U$. These conventional binary system parameter designations retain the same meanings as in the rest of the paper. Also included in the diagram is $\Delta l$, the standard error of the (presumed) Gaussian white noise associated with the data. We initially selected the Quarter 1 data-set, which was folded by period and binned at 0.0002 d intervals. The histograms show derived parameter values, which are all unimodally distributed. Judging from the correlation plots and the Pearson correlation coefficients in Fig. 8, $k$, $r_{1}$, $u$ and $\cos i$ show stronger correlation effects than the other two modelling parameters. We later performed similar runs with the complete data-set discussed in Sect. 2. Our final summarized parameter results from these runs are given in Table 6. Small differences in $r_{1}$ and $u$ from those adopted in Table 4 can be associated with model differences, especially our use of the small planet approximation in calculating the light loss (Mandel and Agol 2002); but this does not seriously affect the correlations or general inferences from the MCMC technique.

Fig. 8

The pairwise correlation diagram is constructed from 20,000 sets of estimated parameters of the Kepler-1b system, obtained using MCMC sampling. Each sample involves the following parameters: $k$, $r_{1}$, $u$, $\cos i$, $\Delta \phi_{0}$, $U$ and $\Delta l$. The diagonal presents histograms of the 20,000 samples for each parameter. The lower triangular part of the array presents the pairwise correlation plots. The upper triangular part presents the Pearson correlation coefficient for each pair of parameters

Table 6 The table presents the point estimates (mean of 20000 samples) and 95 % confidence intervals ($2.5^{th}$ and $97.5^{th}$ percentiles of the samples) for each parameter of Kepler 1. These results may be compared with those given in the main section of the paper

A few standard MCMC convergence diagnoses such as the Gelman-Rubin statistics, trace plots and autocorrelation function (ACF) plots were applied to ensure fitting convergence was achieved and the results correspond to permissible parameters. Upon obtaining sufficient samples for each parameter, correlation diagrams could be constructed using R language tools (R Core Team 2014). The programming was adapted from the Github page.⁵

In order to help interpret the correlations found between the key parameters $k$, $r_{1}$, $u$ and $\cos i$, the separate effect of variation of each was studied, starting from parameter-sets obtained by taking mean values from the 20,000 MCMC sample results. Our findings are displayed in Fig. 9.

Fig. 9

These four diagrams are obtained by varying each parameter in turn from their optimal values, corresponding to the red curve. The step size is 0.005 for $k$, $r_{1}$ and $\cos i$ and is 0.06 for $u$. The blue curves corresponds to values smaller than the optimal ones and the green ones to larger values

According to Fig. 9a and b, smaller values of $k$ or $r_{1}$ push the transit level up and narrow its range. In panels c and d, smaller values of $u$ or $\cos i$ tend to lower the transit and widen it to some extent (more so for $\cos i$). So $k$ and $r_{1}$ have comparable effects, in the sense of a similar direction of change on the fitted model. Similarly with $u$ and $\cos i$, while these two pairs of parameters have opposite effects on the model. If two parameters with opposite effects (e.g. $r_{1}$ and $\cos i$) change in the same direction (increased from their starting values, say) their effects compensate each other and thus tend to leave the fitting unchanged. In this sense, they can be expected to show a positive correlation, since varying one and then the other in the same direction produces little, if any, improvement. Conversely, a negative correlation can be expected for a pair whose effects are in the same direction.

With prima facie impressions of the respective interactions, we could then expect $r_{1}$ vs. $\cos i$ to have relatively strong positive relationship, $r_{1}$ vs. $k$ to be more weakly negative, and $r_{1}$ vs. $u$ to be weakly positive. The first two of these expectations are borne out in the respective plots towards the upper left corner of the correlation array. The linear limb-darkening coefficient $u$ has a relatively weak effect on the light curve, however, and its response to the combined effects of varying the other parameters in the optimization results may be hard to predict. In any case, a negative correlation appears for the $r_{1}$, $u$ pair in the correlation array of Fig. 8.

For the other combinations we might expect $k$ vs. $\cos i$ and $k$ vs. $u$ to show a positive correlation with $\cos i$ vs. $u$ negative. Again, though the latter two of these expectations show up in Fig. 9, the first one appears contrary, apparently through mutual interactions of the other parameters. The strongest pair-correlations are between $r_{1}$ with $\cos i$, and $k$ with $u$, both positive, and fairly tight. The existence of such strong correlations, threatens the determinacy of the entire optimization and certainly limits the confidence with which we can estimate precise values of the geometric parameters.

These effects concur with the error matrix produced by WinFitter for an equivalent 6-parameter fitting to the transit region of the Kepler 1 light curve, as given in Table 7 and using the binned, complete data-set for the transit region. We should note that WinFitter deals with the inclination as the angle $i$ (in radians), which behaves in a closely similar way to $- \cos i$, the equivalent parameter in the MCMC samplings. The corresponding correlations to those shown in Fig. 8 correspond to the off-diagonal elements of the matrix. Thus $r_{1}$ has a positive correlation with $\cos i$ and a negative one with $k$, and so on. The scale of the off-axis elements compared with the matching products on the leading diagonal confirms $k$, $r_{1}$, $u$ and $\cos i$ as showing the main correlation effects.

Table 7 Error matrix for the 6-parameter WinFitter fitting corresponding to Fig. 8. The eigenvalues of the determinacy Hessian are listed below the matrix and under the first horizontal line in order of their increasing magnitude. The correlated error estimates are given on the line below that

Also given in Table 7 are the eigenvalues of the corresponding determinacy Hessian. These should be – and are – all positive for a unique optimum. However, the smallest, which inclines between the $r_{1}$ and $i$ axes, is seven orders of magnitude smaller than the largest, indicating the highly elongated nature of the $\chi^{2}$ hyper-ellipsoid in the vicinity of its minimum. Relative closeness to a breakdown of single-solution determinacy is thus implied for this 6-parameter fitting. The correlated error estimates are listed on the lowest line of the table. These (s.d.) errors may be compared with the 95 % confidence intervals given in Table 6. The corresponding formal errors, if correlations were neglected, are (in the order of Table 7) 0.000014, 0.000006, 0.000484, 0.000006, 0.000687 and 0.000002, respectively. In converting the radii to absolute units, however, the formal errors of the curve-fitting have little meaning, since the stellar mass, which determines the size of the orbit to which the relative radii are referred, is only known to a ${\sim} 5$ % accuracy.