1 Introduction

The nonlinear propagation of ion-acoustic (IA) solitary waves in space and laboratory plasmas has received considerable attention in the last few years. This IA wave arises due to delicate balance of nonlinearity and dispersion in plasma system. The structure of IA waves is investigated as theoretical and experimental in different plasma models. For example, one of these plasma systems is negative ion plasmas. Negative ion plasma can be defined as plasma that includes both negative and positive ion species, as well as electrons. This type of plasma can be created in the plasma processing reactors (Gottscho and Gaebe 1986) and low temperature laboratory experiments (Jacquinot et al. 1977; Nakamura et al. 1977; Weingarten et al. 2001; Ichiki et al. 2002). Also, negative ion plasmas are found in many space observations such as the D- and F-regions of the Earth’s ionosphere (Portnyagin et al. 1991). Linear and nonlinear propagation of IA waves in negative ion plasmas have been studied by many authors. Propagation and damping of IA waves have been investigated in a Q-machine plasma consisting of positive ions, negative ions and electrons by Song et al. (1991). Also, the propagation of electrostatic ion-cyclotron waves in a plasma with negative ions are investigated by Dangelo and Merlino (1986). The effects of negative ions on the amplitude and width of solitons are investigated by Das and Tagre (1975) and Das (1979). They have shown that in a critical density of negative ions the amplitude of the solitary waves becomes infinitely large. There are theoretical and experimental researches which show the existence of rarefactive solitary waves owing to the presence of negative ions in plasmas (Watanabe 1984; Tagare 1986; Cooney et al. 1991). Gill et al. (2004) have studied the IA soliton and double layers in plasma consisting of positive and negative ions with nonthermal electrons. It is seen that the nonthermal electrons have sufficiently large effects on the structures of ion-acoustic waves. Chattopadhyay et al. (2002) have shown that drift motion of ions has a significant contribution on the excitation of IA waves in the presence of negative ions in plasma. Also, Chattopadhyay et al. (2009) have been studied IA solitary waves in a drift negative ion plasma with two-temperature isothermal electrons using the pseudopotential method. They have found that the concentration of ions, drift velocities, mass ratios, equal temperature of ions (particular case) and presence of two groups of electrons modify the profiles of the Sagdeev pseudopotential curves of the solitary waves in the plasma. The K-dV and mK-dV equations for electrostatic waves in an unmagnetized negative ion plasma with two-temperature electrons is derived using reductive perturbation method by Mishra et al. (2012). It is shown that there exist two types of ion-acoustic modes, namely slow and fast IA modes in such plasma system and both compressive and rarefactive solitons coexist. Recently, IA solitary waves and IA double layers in a magnetoplasma with positive and negative ions and electrons are investigated by Das and Nag (2010), El-Labany et al. (2012), respectively. Ion-acoustic waves in complex (dusty) plasmas with negative ions as well as are investigated by many authors (Rosenberge and Merlino 2007; Mamun et al. 2009). However, in above mention references electrons are considered as isothermal and or nonthermal in which in many cases such as solar wind, magnetosphere and auroral zone plasmas electrons are often superthermal and characterized by kappa (κ) distribution function (Vasyliunas 1968; Formisano et al. 1973; Scudder et al. 1981; Marsch et al. 1982). The three-dimensional isotropic κ velocity distribution is given by (Leubner 2002; Pierrard and Lazar 2010)

$$ f_{k}(v) = \frac{n_{0}}{(\pi\kappa\theta^{2})^{3/2}}\frac{\varGamma (\kappa + 1)}{\varGamma(\kappa- 1/2)}\biggl(1 + \frac{v^{2}}{\kappa\theta^{2}}\biggr)^{ - (\kappa+ 1)}, $$
(1)

where n 0 is the species equilibrium number density, θ=[(1−3/(2κ))(2k B T/m)]1/2 is the characteristic velocity, T is the kinetic temperature and m is the species mass. Here \(v^{2} = v_{x}^{2} + v_{y}^{2} + v_{z}^{2}\) obviously denotes the square velocity norm of the velocity v, Γ(x) is the usual gamma function and κ is the spectral index that measuring deviation from Maxwellian equilibrium. We shall note that the effective thermal speed θ is only defined for κ>3/2, and thus when considering physical quantities derived from Eq. (1), such as the density, we shall use κ>3/2. For large values of κ (in limit κ→∞) kappa distributions reduces to Maxwellian distribution.

In the past few years, many researchers have studied the nonlinear structures such as solitons and shock waves in superthermal plasmas (Saini et al. 2009; Jung and Hong 2011; Chuang and Hau 2009; Sultana et al. 2010; Mehdipoor 2012), but there is not much investigation on propagation IA waves in negative ion plasmas with superthermal electrons. Recently, ion acoustic solitons in negative ion plasmas with superthermal electrons are investigated by Hussain et al. (2012). They have derived only the K-dV equation for solitary waves and found that different plasma parameters in the presence of superthermal electrons modify the IA solitary wave structure significantly. In this paper K-dV and mK-dV equations are derived for electrostatic solitary waves in multicomponent plasma containing of negative ions and superthermal electrons. It is well known that these types of plasmas can be present in space and in laboratory plasmas. For example, the (\(\mathrm{H}^{+},\mathrm{O}_{2}^{-}\)) and (H+,H−) plasmas have been found in the D- and F-regions of the Earth’s ionosphere, and the (\(\mathrm{Ar}^{ +},\mathrm{SF}_{6}^{-}\)) and (Ar+,F−) plasmas were used to study the IA wave propagation in laboratory experiments (Merlino and Loomis, 1990; Nakamura and Tsukabayashi, 1984, 1985). Also, the effects of spectral index of kappa distributed electrons; mass ratio and density ratio of the plasma species on IA solitary waves in negative ion plasmas with superthermal electrons are investigated. It is seen that both compressive and rarefactive solitons can be propagate in such plasma.

2 Basic equations

We consider an unmagnetized plasma with cold positive and negative ions (T i,±≪T e ) and superthermal electrons, which are described by a κ-type distribution function. Since we focus on low frequency waves, electron inertia is neglected by assuming v th,±≪v ph ≪v th,e , where v th,± (v th,e ) and v ph are the positive, negative ion (electron) thermal speed and the ion acoustic phase velocity, respectively. The ion dynamics is thus given as

$$\begin{aligned} &{\frac{\partial n_{ +}}{\partial t} + \frac{\partial(n_{ +} u_{ +} )}{\partial x} = 0, } \end{aligned}$$
(2)
$$\begin{aligned} &{\frac{\partial u_{ +}}{\partial t} + u_{ +} \frac{\partial u_{ +}}{ \partial x} = - \frac{1}{\mu} \frac{\partial\phi}{\partial x}, } \end{aligned}$$
(3)

for positive ions and

$$\begin{aligned} &{\frac{\partial n_{ -}}{\partial t} + \frac{\partial(n_{ -} u_{ -} )}{\partial x} = 0, } \end{aligned}$$
(4)
$$\begin{aligned} &{\frac{\partial u_{ -}}{\partial t} + u_{ -} \frac{\partial u_{ -}}{ \partial x} = \frac{\partial\phi}{\partial x}, } \end{aligned}$$
(5)

for negative ions. The Poisson’s equation is as

$$ \frac{\partial^{2}\phi}{\partial x^{2}} = n_{ -} - n_{ +} + n_{e}, $$
(6)

where the superthermal electrons density given by (Saini et al. 2009; Mehdipoor 2012)

$$ n_{e} = \alpha \biggl( 1 - \frac{\phi}{\kappa- 3/2} \biggr)^{ - \kappa+ 1/2}. $$
(7)

All physical quantities appearing in Eqs. (2)–(7) are normalized as follows:

The densities n +, n − and n e by the unperturbed negative ion density n −0; the time t by the ion plasma period of negative ions ω p−=(4πe 2 n −0/m −)1/2; the distance by the negative ion Debye length λ D−=(k B T e /4πe 2 n −0)1/2; ion velocity u + and u − by C s =(k B T e /m −)1/2 and the electric potential ϕ by k B T e /e. The neutrality condition implies as 1−β+α=0, where β=n +0/n −0 and α=n e0/n −0. Here, we have defined μ=m +/m − (where m + and m − are the positive and negative ion mass, respectively).

3 Derivation of the K-dV and mK-dV equation

For obtain K-dV equation according to reduce perturbation method the independent variables are stretched as

$$ \xi= \varepsilon^{1/2}(x - \lambda t)\quad\mbox{and}\quad \tau= \varepsilon^{3/2}t, $$
(8)

where ε is a small parameter and λ is the wave propagation speed. The dependent variables are expanded as

$$ \begin{aligned} &n_{ +} = \beta+ \sum_{i = 0}^{\infty} \varepsilon^{i + 1}n_{ +,i + 1},\\ &n_{ -} = 1 + \sum_{i = 0}^{\infty} \varepsilon^{i + 1}n_{ -,i + 1},\\ &u_{ \pm} = \sum_{i = 0}^{\infty} \varepsilon^{i + 1}u_{ \pm,i + 1},\\ &\phi= \sum_{i = 0}^{\infty} \varepsilon^{i + 1} \phi_{i + 1}. \end{aligned} $$
(9)

Using Eqs. (8) and (8) into Eqs. (2)–(7) and collecting the terms of various powers of ε, we obtain the following expressions to the lowest order of ε:

$$ \begin{aligned} &n_{ +,1} = \frac{\beta}{\lambda^{2}\mu} \phi_{1},\qquad u_{ +,1} = \frac{1}{\lambda\mu} \phi_{1},\\ & n_{ -,1}= \frac{ - 1}{\lambda^{2}}\phi_{1},\qquad u_{ -,1} = \frac{ - 1}{\lambda} \phi_{1}. \end{aligned} $$
(10)

From the lowest order ε of the Poisson equation the wave propagation speed λ can be written as

$$ \lambda= \sqrt{\frac{(\kappa- 3/2)(1 + \beta/\mu)}{\alpha(\kappa- 1/2)}}. $$
(11)

To the next order of ε, we get the required K-dV equation

$$ \frac{\partial\phi_{1}}{\partial\tau} + A\phi_{1}\frac{\partial \phi_{1}}{\partial\xi} + B \frac{\partial^{3}\phi_{1}}{\partial\xi ^{3}} = 0, $$
(12)

where the nonlinearity and the dispersion coefficients are respectively

$$A = \frac{3(\frac{\beta}{\mu^{2}} - 1)}{2\lambda(1 + \frac{\beta}{\mu} )} - \frac{\alpha(\kappa- \frac{1}{2})(\kappa+ \frac{1}{2})\lambda^{3}}{2(\kappa- \frac{3}{2})^{2}(1 + \frac{\beta}{\mu} )}, $$

and

$$ B = \frac{\lambda^{3}}{2(1 + \frac{\beta}{\mu} )}. $$
(13)

The stationary solution of (12) by introducing the variable η=ξ−Uτ is given as

$$ \phi_{1} = \phi_{0}\sec h^{2}\biggl( \frac{\eta}{\delta} \biggr), $$
(14)

where ϕ 0=3U/A, is the amplitude and δ=(4B/U)1/2, is the width of the ion acoustic solitons, respectively.

Now, it should be noted that the nonlinear coefficient A is a function of β, therefore based to Fig. 1 it is clear that the nonlinearity coefficient can have negative, zero and positive values. Thus, the ion acoustic waves are compressive (rarefactive) if A>0 (A<0). Also, we can conclude that the amplitude of solitons and the value of critical density dependence on negative ion plasma kind. On the other hand, the vanishing of the nonlinear coefficient in Eq. (12) (i.e., when A=0) determines the critical value of β=β c . Therefore, one must obtain the other type of nonlinear dynamical equation for description of these solitary waves when A=0.

Fig. 1
figure 1

The variation of nonlinear coefficient A, against β for κ=4, μ=0.03 (red line) for (\(\mathrm{H}^{+},\mathrm{O}_{2}^{-}\)) plasma, μ=1 (blue line) for (H+,H−) plasma and μ=2.1 (black line) for (Ar+,F−) plasma

Full size image

To derive the modified nonlinear equation, we use the stretched variables

$$ \xi= \varepsilon(x - \lambda t),\quad\tau= \varepsilon^{3}t. $$
(15)

Substituting relations (9) and (15) in the system of Eqs. (2)–(7) and equating coefficients of powers of ε, the lowest power of ε gives n ±,1, u ±,1 as given by relation (10) and λ is given by Eq. (11). To the next order of ε, we have

$$ \begin{aligned} &n_{ +,2} = \frac{3\beta}{2\lambda^{4}\mu^{2}}\phi_{1}^{2} + \frac{\beta}{ \lambda^{2}\mu} \phi_{2},\\ &n_{ -,2} = \frac{3}{2\lambda^{4}}\phi_{1}^{2} - \frac{1}{\lambda^{2}}\phi_{2},\\ &u_{ +,2} = \frac{1}{2\lambda^{3}\mu^{2}}\phi_{1}^{2} + \frac{1}{\lambda \mu} \phi_{2},\\ &u_{ -,2} = \frac{1}{2\lambda^{3}}\phi_{1}^{2} - \frac{1}{\lambda} \phi_{2}. \end{aligned} $$
(16)

Finally, from the next order of ε, we get the required modified K-dV equation

$$ \frac{\partial\phi_{1}}{\partial\tau} + \bar{A}\phi_{1}^{2}\frac {\partial \phi_{1}}{\partial\xi} + B\frac{\partial^{3}\phi_{1}}{\partial\xi ^{3}} = 0, $$
(17)

where the coefficient B is same with the dispersion coefficient in K-dV equation and the nonlinearity coefficient is as

$$ \bar{A} = \frac{15(1 + \frac{\beta}{\mu^{3}})}{4\lambda^{3}(1 + \frac{\beta}{\mu} )}. $$
(18)

The stationary solution of modified K-dV equation can be written as

$$ \phi_{1} = \pm\phi_{m}\sec h\biggl(\frac{\eta}{W} \biggr), $$
(19)

where \(\phi_{m} = (6U/\bar{A})^{1/2} \) and W=(B/U)1/2 are amplitude and width of the solitons, respectively. As it is seen from (17), \(\bar{A} > 0\), thus both compressive and rarefactive solitons are also allowed to coexist.

4 Conclusions

We have considered the nonlinear propagation of IA waves in non-Maxwellian (superthermal) plasmas with negative ions. Using the fluid model for ions and reductive perturbation technique, we have derived the K-dV equation to investigate small but finite amplitude solitons. As it has already been said, the coefficient A in K-dV Eq. (12) is zero for some critical value β=β c . Therefore there is a transition from compressive to rarefactive soliton for β>β c and β<β c , respectively (see Fig. 1). Also, for β=β c we obtain ion acoustic solitons which are the solutions of modified K-dV Eq. (17). In continue, we study the effects of different parameters on both K-dV and mK-dV solitons numerically for (\(\mathrm{H}^{ +},\mathrm{O}_{2}^{-}\)), (H+,H−) and (Ar+,F−) plasmas, where the mass ratios in these plasmas are, respectively, 0.03, 1 and 2.1.

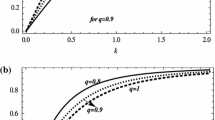
In Figs. 2, 3, 4 the variation of soliton amplitude with the spectral index κ for different values of β is illustrated. It should be noted, from these figures, that in all three different plasma compositions the compressive (ϕ 0>0) and rarefactive (ϕ 0<0) solitons can be propagated. In the other hand, for some fixed values of κ and μ, the compressive (rarefactive) solitary waves occur when the positive ion concentration is bigger (smaller) that critical value β c . In present plasma models the critical concentration value β c , based on Fig. 1, is 1.796, 4.791 and 12.257, respectively. For such types of plasmas the amplitude of rarefactive solitons increases as the value of spectral index κ increases while for compressive solitons the amplitude of the solitary wave’s decreases as the spectral index κ increases. This means that for some large population of superthermal electrons (smaller κ), the amplitude of ion acoustic waves is smaller (larger) when the positive to negative ion density ratio be smaller (larger) the critical value. (We can note that the structure of compressive solitons in this paper are same with Figs. 1 and 6 in Hussain et al. (2012)). It turned out that for given value of κ, with increasing (decreasing) the positive (negative) ion concentration, the amplitude of compressive (rarefactive) solitons decreases (increases). This is due to fact that the presence of negative ions causes significant electron density depletion, and consequently the shielding effect produced by electrons decreases. Also, Figs. 2, 3, 4 reveal that when negative ions are heavy (such as (\(\mathrm{H}^{+},\mathrm{O}_{2}^{ -}\)) plasma with μ=0.03) both the compressive and rarefactive solitons have smaller amplitude than plasmas with light negative ions (such as (Ar+,F−) plasma with μ=2.1). Therefore, the K-dV solitons can be propagated to higher velocities in plasmas with μ>1.

Fig. 2
figure 2

Variation of the rarefactive and compressive ion-acoustic soliton amplitude ϕ 0 with the spectral index of κ for different values of β in (\(\mathrm{H}^{+},\mathrm{O}_{2}^{ -}\)) plasma

Full size image
Fig. 3
figure 3

Variations of the rarefactive and compressive ion-acoustic soliton amplitude ϕ 0 with the spectral index of κ for different values of β in (H+,H−) plasma

Full size image
Fig. 4
figure 4

Variation of the rarefactive and compressive ion-acoustic soliton amplitude ϕ 0 with the spectral index of κ for different values of β in (Ar+,F−) plasma

Full size image

The variation of width of ion acoustic solitons with the spectral index κ and with positive ion concentration β is shown in Figs. 5, 6, 7. For these plasma models the width of the compressive and rarefactive solitons increases by increasing the spectral index κ. It is, also, found that for fixed value of κ as the positive ion concentration β increases, the width of the solitary wave’s decreases. The numerical calculations also have shown that the width decreases as the mass ratio μ=m +/m − increases. Thus, solitary waves are propagated with smaller width in (Ar+,F−) plasma rather than (\(\mathrm{H}^{+},\mathrm{O}_{2}^{-}\)) plasma.

Fig. 5
figure 5

Variation of the rarefactive and compressive ion-acoustic soliton width δ with the spectral index of κ for different values of β in (\(\mathrm{H}^{+},\mathrm{O}_{2}^{-}\)) plasma

Full size image
Fig. 6
figure 6

Variations of the rarefactive and compressive ion-acoustic soliton width δ with the spectral index of κ for different values of β in (H+,H−) plasma

Full size image
Fig. 7
figure 7

Variation of the rarefactive and compressive ion-acoustic soliton width δ with the spectral index of κ for different values of β in (Ar+,F−) plasma

Full size image

Also, the effect of superthermal electrons on the structure of solitary waves in the critical concentration of positive ions β=β c for a sample of negative ion plasmas such as (\(\mathrm{H}^{ +},\mathrm{O}_{2}^{-}\)) is given in Table 1. The values of the critical positive ion density β c , the nonlinear coefficient \(\bar{A}\), the dispersion coefficient B and the amplitude and the width for IA solitons of the modified K-dV equation (17) for different values of spectral index κ are given there. We record from Table 1, which the amplitude and the width of mK-dV ion acoustic soliton increase as κ increases. Also, β c decreases as the spectral index κ increases. Therefore, spectral index κ has significant effect on the form of solitary waves in negative ion plasmas. On the other word, for a large population of superthermal electrons (smaller κ), the critical value of density gets large. Interestingly, in a large population of superthermal electrons, the nonlinear (dispersion) term in the mK-dV equations is larger (smaller), and therefore ion acoustic waves should move slower (in the moving frame which moves with speed λ).

Table 1 The amplitude and width of ion-acoustic solitons when β=β c for different values of κ and μ=0.03
Full size table

Now, it should be remarked that the nonlinearity and dispersion coefficients in mK-dV equation also, are a function of the mass ratio μ=m +/m −. Therefore, we investigate the effect of this parameter on the amplitude and width of mK-dV solitons in Table 2.

Table 2 The amplitude and width of ion- acoustic solitons when β=β c for different values of μ and κ=4
Full size table

In Table 2, we observe that for given value of spectral index κ, by increasing the mass ratio of ion species, the value β c increases. Also, we found that the amplitude of mK-dV ion acoustic soliton firstly increases and then decreases when μ increases while increasing the mass ratio positive to negative ions the width of mK-dV solitons decreases. In the other word, for plasmas in which negative ions are heavier than positive ions, such as ((\(\mathrm{H}^{ +},\mathrm{O}_{2}^{ -}\)), (\(\mathrm{Ar}^{ +},\mathrm{SF}_{6}^{ -}\)) and (H+,H−), i.e., μ≤1), the amplitude of these waves increases, otherwise (μ>1), such as ((Ar+,F−) and (Cs+,Cl−)), the amplitude of solitary waves decreases as positive to negative ion mass ratio increases. From Table 2, it is shown that the nonlinear term firstly decreases and then increases while the dispersion term is decreasing with respect to μ.

In addition to above remarks, we note, for completeness, that results derived in this paper differ, essentially, from other works. For example in Hussain et al. (2012) only K-dV equation is derived for small amplitude of electrostatic waves in negative ion plasmas with superthermal electrons while, here, the author claims that this equation can not valid for the negligible of the nonlinear coefficient in the K-dV equation (i.e., A=0). The latter condition gives rise to infinitely large amplitude solitons which based on the reductive perturbation method they are invalid. Therefore, one looks for other type of nonlinear dynamical equation which can be valid for A=0.

Also, in latter reference the dependence of amplitude and width solitary waves on positive to negative ion mass ratio only for case μ≤1 is studied (μ, here, corresponds to γ in that work) in which the variations of ion acoustic solitons amplitude and width also are investigated, here, for μ>1. Furthermore, our work is essentially different from Mishra et al. (2012). They investigated the ion acoustic solitary waves in negative ion plasmas with two-electron temperature distributions. They pointed out that there are two types of ion acoustic modes and the parameter determining the compressive and rarefactive solitons is different for these modes.

To summarized, we have investigated the nonlinear properties of solitary waves in a plasma consisting of cold positive and negative ions and superthermal electrons. The basic set of equations is reduced to K-dV and mK-dV equation by using the reductive perturbation method and stationary solutions of these equations are obtained. These theoretical results may be directly useful in investigation of ion acoustic solitary waves in laboratory experiments plasmas, we are not aware of any experimental studies for comparing of these results, where two distinct groups of ions and superthermal electrons are present. Also, for better agreements between theory and experiments the effects of warm ions and magnetic field can consider in such plasmas. These effects are neglected in this paper but are under investigation.