1 Introduction

During the last two decades, there has been great deal of interest in the study of linear and nonlinear wave phenomena in electron–positron–ion plasmas. The electron–positron plasmas are thought to be generated naturally by pair production in high energy processes occurring in many astrophysical environments such as the early universe (Misner et al., 1973 and Rees, 1983) neutron stars, active galactic nuclei (Miller and Witta 1978) or pulsar magnetosphere (Goldreich and Julian 1969; Michel 1982) and in solar atmosphere (Tandberg-Hansen and Emslie, 1988). The electron–positron plasmas have also been created in the laboratory (Surko et al. 1989; Boehmer et al. 1995; Liang et al. 1998). Greaves et al. (1994) have reported that advances in the positron trapping technique have led to room-temperature plasmas of 107 positrons with lifetime of 103 s.

Because of long lifetime of the positrons most of the astrophysical and laboratory plasmas become an admixture of electrons, positrons, and ions. Therefore, the study of electron–positron–ion (EPI) plasmas is important to understand the behavior of both astrophysical (Surko et al. 1989; Tandberg-Hansen and Emslie 1988; Boehmer et al. 1995; Liang et al. 1998; Greaves et al. 1994; Piran 1999) and laboratory plasmas (Surko et al. 1986; Tinkle et al. 1994; Greaves and Surko 1995).

The study of linear as well as nonlinear wave phenomena in both unmagnetized and magnetized EPI plasmas has been attracted much attention (Rizzato 1988; Jammalamadaka et al. 1996; Popel et al. 1995; Farina and Bulanov 2001; Salahuddin et al. 2002; Tiwari 2007; Tiwari et al. 2007; Mahmood and Akhtar 2008; Gill et al. 2010; Masood and Rizvi 2011; Aoutou et al. 2012; Valiulina and Dubinov 2012).

Several authors have derived the nonlinear Schrödinger equation by either using the reductive perturbation method (Ichikawa et al., 1972; Shimizu and Ichikawa, 1972) or the KBM method (Kakutani and Sugimoto 1974) and have studied the stability of ion-acoustic waves against modulational instability in a collisional free plasma consisting of cold ions and hot electrons. Using the KBM method, the modulational instability of ion-acoustic waves in a collisionless plasma consisting of isothermal electrons and adiabatic ions is studied by Durrani et al. (1979). Using the standard reductive perturbation technique, a nonlinear Schrödinger equation is derived by Ju-Kui et al. (2002) to study the modulational instability of finite-amplitude ion-acoustic waves in a non-magnetized warm ion plasma. The effect of finite ion temperature on modulational instability of ion-acoustic waves is studied by Sharma et al. (1978) and effect of negative ions in plasma is investigated by Mishra et al. (1993). Timofeev (2013) found that the spectrum of modulational instability in the non-Maxwellian plasma narrows significantly, as compared to the equilibrium case, without change of the maximum growth rate and corresponding wave number.

Jehan et al. (2008) examined the effect of magnetic field on the stability behavior of low-frequency electrostatic ion waves in EPI plasmas. Zhang et al. (2009) studied the modulational instability of ion-acoustic waves, solitons and their interactions in nonthermal EPI plasmas. Bains et al. (2010) studied the modulational instability of ion-acoustic wave envelopes in magnetized quantum EPI plasmas. Mahmood et al. (2011) studied the nonlinear amplitude modulation of ion-acoustic wave in the presence of warm ions in unmagnetized EPI plasmas. However, in the course of their study, they have taken the same temperature for the electron and positron species. Therefore, their analysis cannot be used to study the modulational instability of ion-acoustic waves in electron–positron–ion plasmas in which electron and positron species are at different temperatures.

The aim of this paper is to study the modulational instability of ion-acoustic wave in unmagnetized electron–positron–ion plasma when electron and positron species have different temperatures. The results obtained in this study may be useful to explain the stable and unstable modulational of ion acoustic wave in the astrophysical environments where unmagnetized electrons, positrons and ions are present.

The paper is organized as follows: The basic sets of equations are given in Sect. 2. The nonlinear Schrödinger equation has been derived in Sect. 3. In Sect. 4 stability analysis has been discussed. The conclusions are summarized in Sect. 5.

2 Basic equations

We consider a collisionless unmagnetized plasma consisting of warm adiabatic ions and hot isothermal electrons and positrons. The normalized basic equations are:

(1)
(2)
(3)
(4)
(5)

where

$$\alpha= \frac{n_{p}^{(0)}}{n^{(0)}} $$

In the above equations, n and v are the density and fluid velocity of the ion species, E is the electric field, n e is the electron density and n p is the positron density, σ=3T i /T e , defines the temperature ratio of adiabatic warm ions to electrons of the plasma and γ=T p /T e , the ratio temperature of positron with electron fluid. We have normalized the quantities n, n e , n p with equilibrium density of electron fluid n 0 and space variable n with Debye shielding length \(\lambda_{D} = ( \frac {\varepsilon_{0}kT_{e}}{n_{0}e^{2}})^{1/2}\) and time variable t with inverse of ion plasma frequency. The electric field E is normalized with characteristic potential (kT e /e) divided by Debye shielding length λ D . Using the KBM perturbation method for nonlinear wave modulational, we expend all the dependent variable about their the equilibrium values as follows:

(6)

In order to consider the modulational instability of ion-acoustic waves in the system, we assume that the perturbed quantities of all orders depend on x and t through the complex amplitudes (\(a,\bar{a}\)) and phase factor (ψ). The phase factor is given by

$$ \psi= kx - \omega t $$
(7)

The complex amplitude a is a slowly varying function of x and t expressed as

(8a)
(8b)

together with the complex conjugate relations to Eqs. (8a) and (8b). The unknown functions A 1,A 2,… and B 1,B 2,… are determined so as to eliminate all secular terms in the perturbation solution.

3 Derivation of the nonlinear Schrödinger equation

On substituting the expression (6) into the set of Eqs. (1)–(5), using (8a) and (8b) and equating terms with the same power of ε, we obtain a set of equations for each order in ε. From the first-order equations, the first order solutions are given as

(9)

The condition for these solutions to be non-trivial is obtained in the form of linear dispersion relation

$$ \omega^{2} = \frac{k^{2} ( 1 - \alpha )}{ ( 1 + k^{2} + \alpha\gamma )} + \sigma k^{2} $$
(10)

The set of second order equations can be written as:

(11a)
(11b)
(11c)
(11d)
(11e)

with the help of first-order solutions and above set of equations, we find that second order v 2 is given by

(12)

where

(13)

and v g , represents the group velocity, given by

$$ v_{g} = \frac{d\omega}{dk} = \frac{\omega}{k}\frac{ [ 2k^{4}\sigma+ k^{2} ( 1 - \alpha ) + 2\sigma k^{2} ( \alpha\gamma+ 1 ) - \alpha\gamma k ( \sigma k^{2} - \omega^{2} ) - ( \sigma k^{2} - \omega^{2} ) + k^{2} ( \sigma k^{2} - \omega ^{2} ) ]}{ [ \sigma k^{4} + k^{2}\omega^{2} + k^{2} ( 1 - \alpha ) + ( \alpha\gamma+ 1 ) ( \sigma k^{2} + \omega^{2} ) ]} $$
(14)

We see that the solution of Eq. (12) would contain a secular term which is proportional to ψ unless the coefficient of exp(±iψ) term vanishes. For second solutions to be nonsecular this gives a condition:

$$ A_{1} + v_{g}B_{1} = 0 $$
(15)

In the lowest order of ε, using Eqs. (8a), (8b), A 1 and B 1 can be regarded as \(\frac{\partial a}{\partial t_{1}}\) and \(\frac{\partial a}{\partial x_{1}}\) where t 1=εt and x 1=εt. Thus Eq. (15) can be interpreted as

$$ \frac{\partial a}{\partial t_{1}} + v_{g}\frac{\partial a}{\partial x_{1}} = 0 $$
(16)

Which shows that, to the lowest order in ε, amplitude a is constant in a frame of reference moving with the group velocity. Under the condition (15), the non-secular solution of (12) is given by

(17a)

Where \(b_{1}(a,\bar{a})\) is assumed to be complex and \(\gamma _{1}(a,\bar{a})\) is assumed to be real and both are independent of ψ but depend on a and \(\bar{a}\). They are to be determined from the condition that higher order solutions should be free from secularity. Here α 1 is given by the relation \(\alpha_{1} = \frac{\omega A}{6k ( \omega ^{2} - \sigma k^{2} )}\).

Using the set of second order Eqs. (11a)–(11e), the remaining second order solutions can be expressed as:

(17b)
(17c)
(17d)
(17e)

where

Here γ 2,γ 3,γ 4 and γ 5 are function of a and \(\bar{a}\) only and are assumed to real. From Eqs. (11b) or (11d) we find that there should be no constant term in the expression for E 2. Therefore,

$$ \gamma_{2} ( a,\bar{a} ) = 0 $$
(18)

From Eq. (11e) we obtain another relation

$$ ( 1 - \alpha )\gamma_{3} + \alpha\gamma_{4} = \gamma_{5} $$
(19)

The set of third order equations can be written as:

(20a)
(20b)
(20c)
(20d)

The above equations can be used to obtain an equation for v 3 similar to Eq. (12) for v 2. We find that in the solution of v 3 there are resonant terms (proportional to exp(±i)) as well as constant terms with respect to ψ, which give rise to secular behavior. Therefore, in addition to the resonant terms, we must also require that the constant terms vanish. From the later conditions together with Eq. (19) we can determine the unknown constants γ 1,γ 3,γ 4 and γ 5. These are

(21a)
(21b)
(21c)
(21d)

where c 1,c 3,c 4, and c 5 are arbitrary constants independents of a, \(\bar{a}\) and ψ can be determined by the initial conditions.

In order that the solution v 3 be nonsecular, we equate to zero the coefficients of the resonant terms. Thus we obtain

(22)

Since

Equation (22) can be written as

$$ i\frac{1}{\varepsilon^{2}} \biggl( \frac{\partial a}{\partial t} + v_{g} \frac{\partial a}{\partial x} \biggr) + \frac{1}{\varepsilon^{2}}P\frac{\partial^{2}a}{\partial x^{2}} + Q\vert a \vert ^{2}a + Ra = 0 $$
(23)

Now using the coordinate transformation, defined by

$$ \xi= \varepsilon ( x - v_{g}t ),\qquad\tau= \varepsilon ^{2}t $$
(24)

Equation (23) reduces to

$$ i\frac{\partial a}{\partial\tau} + P\frac{\partial^{2}a}{\partial\xi ^{2}} + Q\vert a \vert ^{2}a + Ra = 0 $$
(25)

in the equation the linear interaction term Ra is not importance because R is real and this causes simply a phase shift. Using a simple substitution

$$ a \to a\exp(iR\tau) $$
(26)

Equation (25) modifies to

$$ i\frac{\partial a}{\partial\tau} + P\frac{\partial^{2}a}{\partial\xi ^{2}} + Q\vert a \vert ^{2}a = 0 $$
(27)

where

(28)
(29)
(30)

Here the dispersion coefficients P and the nonlinear interaction coefficient Q are given, respectively, by Eqs. (28) and (29). Note, that for simplicity, we have dropped the linear interaction term Ra as it is not much important and simply cause a phase shift.

4 Stability analysis and discussion

The linear stability analysis of Nishikawa and Liu (1976) shows that the wave is modulationaly stable for PQ<0, for PQ>0 the wave becomes modulationaly unstable for modulational wave number \(\tilde{K}_{m}\) in the region

$$ 0 < \tilde{K}^{2} < \frac{2Q\vert a_{0} \vert ^{2}}{P} $$
(31)

The maximum growth rate is obtained for

$$ \tilde{K}_{m} = \pm \biggl( \frac{Q}{P}\vert a_{0} \vert ^{2} \biggr)^{1/2} $$
(32)

and has a value

$$ y_{m} = \vert Q \vert \vert a_{0} \vert ^{2} $$
(33)

Where \(\tilde{K}_{m}\) is the wave number of modulational, which is assumed to less than the carrier wave number k and \(a_{0} = \vert \tilde{n} \vert /n_{0}\) is the normalized carrier wave amplitude. It is well known that the modulation instability depends on the sign of the product of the dispersive and nonlinear coefficient, i.e., PQ. This modifies the unstable region of the ion-acoustic waves which is defined by PQ>0 are and the stable region of the ion-acoustic waves which is defined by PQ<0. We find that the these waves are unstable only in the region k min<k<k max, which depends upon the ion temperature, positron concentration, and positron temperature of the plasma. For the case of cold ions and in the absence of positron, then we find the critical wave number k c =1.47.

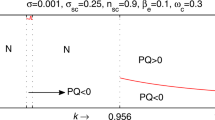
In Fig. 1, we have plotted the variation of PQ with respect to wave number k for different values of temperature ratio (T i /T e )=0 (solid line), 0.01 (dotted line), 0.05 (dashed line), and 0.1 (dash dotted line) at positron concentration (α)=0, and positron temperature (γ)=0. We also note from the figure that as the ion temperature (T i /T e ) increases, the values of k max and k min decreases at the same time the region of instability also decreases.

Fig. 1
figure 1

Plot of the product PQ versus wave number k for different values of temperature ratio (T i /T e )=0, 0.01, 0.05, and 0.1 at α=0, and γ=0

Full size image

In Fig. 2, we have plotted the variation of PQ with respect to wave number k for different values of ion temperature (T i /T e )=0 (solid line), 0.01 (dotted line), 0.05 (dashed line), and 0.1 (dash dotted line) at positron concentration (α)=0.01, and positron temperature (γ)=0.8. We also note from the figure that as the T i /T e increases, the values of k max and k min decrease at the same time the region of instability also decreases. From Figs. 1 and 2, we may conclude that on introducing the positrons, increases the values of k max and k min.

Fig. 2
figure 2

Plot of the product PQ versus wave number k for different values of temperature ratio (T i /T e )=0, 0.01, 0.05, and 0.1 at α=0.01, and γ=0.8

Full size image

In Fig. 3, we have plotted the variation of PQ with respect to wave number k for different values of positron temperature (γ)=0.01 (solid line), and 0.8 (dotted line) at ion temperature (T i /T e )=0.1, and positron concentration (α)=0.01. We also note from the figure that as the positron temperature (γ) increases, the values of k max and k min increases.

Fig. 3
figure 3

Plot of the product PQ versus wave number k for different values of γ=0.01 and 0.8 at T i /T e =0.1 and α=0.01

Full size image

In Fig. 4, we have plotted the variation of PQ with respect to wave number k for different values of positron concentration (α)=0.01 (solid line), 0.05 (dotted line) and 0.1 (dashed line) at ion temperature (T i /T e )=0.1, and positron temperature (γ)=0.8. We also note from the figure that as the positron concentration (α) increases, the values of k max and k min increases.

Fig. 4
figure 4

Plot of the product PQ versus wave number k for different values of α=0.01, 0.05 and 0.1 at T i /T e =0.1 and γ=0.8

Full size image

In Fig. 5, we have plotted the variation of PQ with respect to wave number k for different values of positron concentration (α)=0.01 (solid line), 0.05 (dotted line) and 0.1 (dash dotted line) at ion temperature (T i /T e )=0, and positron temperature (γ)=0.8. We also note from the figure that as the positron concentration (α) increases, the value of k min increases at cold ion case.

Fig. 5
figure 5

Plot of the product PQ versus wave number k for different values of α=0.01, 0.05 and 0.1 at T i /T e =0, and γ=0.8

Full size image

In Fig. 6, we have plotted the variation of PQ with respect to wave number k for different values of positron temperature (γ)=0.01 (solid line), 0.4 (dotted line) and 0.8 (dash dotted line) at T i /T e =0, and positron concentration (α)=0.01. We also note from the figure that as the positron temperature (γ) increases, the value of k min increases at cold ion case.

Fig. 6
figure 6

Plot of the product PQ versus wave number k for different values of γ=0.01, 0.4 and 0.8 at T i /T e =0, and α=0.01

Full size image

For the actual existence of instability, the following conditions must also be satisfied in addition to the requirement PQ>0. (i) The normalized wave number k must be less than one (k<K D ). (ii) The normalized modulational wave number, corresponding to the maximum growth rate of instability must also be less than one (\(\tilde{K}_{m}< K_{D}\)). (iii) The maximum instability growth rate must be greater than the Landau damping rate (y m =|Q||a 0|2>γ i ).

We have calculated the modulational wave number (\(\tilde{K}_{m}\)), the maximum growth rate (y m ) for the given values of k. For these given values of k, we also have PQ>0, in all cases. The calculations are made for two different values of carrier amplitude a 0 and we have assumed γ i ≃10−3 ω pi . The results of these calculations for difference situations are shown in Tables 1–6.

Table 1 Variation of the modulational wave number (\(\tilde{K}_{m}\)) and the maximum instability growth rate (y m ) with ion temperature (T i /T e ). α=0, γ=0, k=0.9
Full size table

From Table 1, it can easily be inferred that in absence of positron, for a finite wave number (k), on increasing the ion temperature (T i /T e ), modulational wave number (\(\tilde{K}_{m}\)), the maximum growth rate (y m ) increases, for carrier amplitude (a 0=0.01). The wave remains modulationaly stable, however on increasing the carrier amplitude (a 0=0.1). The wave remains stable for the comparatively lower value of ion temperature, on increasing the ion temperature, the wave becomes unstable.

Table 2, shows that in absence of positron, for a finite wave number (k), on increasing the ion temperature (T i /T e ), modulational wave number (\(\tilde {K}_{m}\)), the maximum growth rate (y m ) increases, for carrier amplitude (a 0=0.01). The wave remains modulationaly stable, however on increasing the carrier amplitude (a 0=0.1). The wave remains stable for the comparatively lower value of ion temperature, on increasing the ion temperature, the wave becomes unstable.

Table 2 Variation of the modulational wave number (\(\tilde {K}_{m}\)) and the maximum instability growth rate (y m ) with ion temperature (T i /T e ). α=0, γ=0, k=0.68
Full size table

In Table 3, the effect of positron, for a finite wave number (k), on increasing the ion temperature (T i /T e ), modulational wave number (\(\tilde {K}_{m}\)), the maximum growth rate (y m ) increases, for carrier amplitude (a 0=0.01). The wave remains modulationaly stable, however on increasing the carrier amplitude (a 0=0.1). The wave remains stable for the comparatively lower value of ion temperature, on increasing the ion temperature, the wave becomes unstable.

Table 3 Variation of the modulational wave number (\(\tilde {K}_{m}\)) and the maximum instability growth rate (y m ) with ion temperature (T i /T e ). α=0.01, γ=0.8, k=0.92
Full size table

From Table 4, it can easily be inferred that in presence of positron, for a finite wave number (k), on increasing the ion temperature (T i /T e ), modulational wave number (\(\tilde{K}_{m}\)), the maximum growth rate (y m ) increases, for carrier amplitude (a 0=0.01). The wave remains modulationaly stable, however on increasing the carrier amplitude (a 0=0.1). The wave remains stable for the comparatively lower value of ion temperature (T i /T e =0.05 and 0.08), on increasing the ion temperature (T i /T e =0.1), the wave becomes unstable.

Table 4 Variation of the modulational wave number (\(\tilde {K}_{m}\)) and the maximum instability growth rate (y m ) with ion temperature (T i /T e ). α=0.01, γ=0.8, k=0.7
Full size table

Table 5, shows in presence of finite positron concentration (α), for a finite wave number (k), on increasing the positron temperature (γ), modulational wave number (\(\tilde{K}_{m}\)), the maximum growth rate (y m ) increases, for carrier amplitude (a 0=0.01). The wave remains modulationaly stable and increasing the carrier amplitude (a 0=0.1). The wave remains unstable.

Table 5 Variation of the modulational wave number (\(\tilde {K}_{m}\)) and the maximum instability growth rate (y m ) with positron temperature (γ). α=0.01, T i /T e =0.1, k=0.7
Full size table

In Table 6, the effect of finite positron temperature (γ), for a finite wave number (k), on increasing the positron concentration (α), modulational wave number (\(\tilde{K}_{m}\)), the maximum growth rate (y m ) increases, for carrier amplitude (a 0=0.01). The wave remains modulationaly stable, however on increasing the carrier amplitude (a 0=0.1). The wave remains unstable for increasing the positron concentration (α).

Table 6 Variation of the modulational wave number (\(\tilde {K}_{m}\)) and the maximum instability growth rate (y m ) with positron concentration (α). T i /T e =0.1, γ=0.8, k=0.7
Full size table

5 Conclusion

Our main conclusions are as follows:

  1. (i)

    For the given set of parameter values with positron concentration (α), and positron temperature (γ), by increasing the ion temperature (T i /T e ), the value of k max and k min decreases, at the same time the region of instability also decreases.

  2. (ii)

    It is also found that the presence of positron concentration (α), and positron temperature ratio (γ), the value of k max and k min increases.

  3. (iii)

    For the given set of parameter values with the ion temperature (T i /T e ), and positron concentration (α), by increasing the value of positron temperature (γ), the value of k max and k min increases.

  4. (iv)

    For the given set of parameter values with ion temperature (T i /T e ), and positron temperature ratio (γ), by increasing the value of positron concentration (α), the value of k max and k min increases.

  5. (v)

    For the given set of parameter values with ion temperature ratio (T i /T e ), and positron temperature (γ), by increasing the value of positron concentration (α); the value of k min increases at cold ion case.

  6. (vi)

    For the given set of parameter values with ion temperature ratio (T i /T e ), and positron concentration (α), by increasing the value of positron temperature ratio (γ), the value of k min increases at cold ion case.

The exact extent of the regions of physical instability, the modulational wave number (K m ), the maximum growth rate (y m ) for a given set of values of a carrier amplitude (a 0), ion temperature (T i /T e ), wave number (k), positron concentration (α), and positron temperature ratio (γ) are shown clearly in the tables.

The results obtained in this study may be useful to explain the stable and unstable modulational of ion acoustic wave in the astrophysical environments where unmagnetized electrons, positrons and ions are present.