Effective potential energy in Størmer’s problem for an inclined rotating magnetic dipole

Abstract

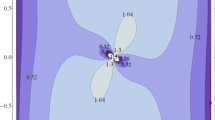
We discuss the dynamics of a charged nonrelativistic particle in electromagnetic field of a rotating magnetized celestial body. The equations of motion of the particle are obtained and some particular solutions are found. Effective potential energy is defined on the base of the first constant of motion. Regions accessible and inaccessible for a charged particle motion are studied and depicted for different values of a constant of motion.

Appendices

Appendix A: Relativistic equations of motion

Here we record relativistic equations of motion of a charged particle in the field of rotating magnetic dipole. Lagrangian (18) leads to the following equations of motion in a spherical coordinate system.

(A.1)

(A.2)

(A.3)

Appendix B: Stability of the orbit in the equatorial plane

It is easy to check that equations of motion (A.1)–(A.3) have partial solution

$$ r=R,\quad\theta=\frac{\pi}{2},\quad \varphi=\omega t+ \varphi_0 $$

(B.1)

with restriction on the initial phase φ ₀:

$$\cos(\rho_0+\varphi_0)+\rho_0\sin( \rho_0+\varphi_0)=0,\quad\rho _0=R\omega/c. $$

We assume now that the particle is a non relativistic one. Then ρ ₀≪1 and we have for the initial phase cosφ ₀=0. This solution corresponds to motion of a particle being at rest at the stationary points (43) and (44). Let us verify stability of this solution. We develop equations of motion as series in increments of coordinates in a neighborhood of the solution. Let us introduce the increments of coordinates as follows

$$ \theta=\frac{\pi}{2}+\delta\theta,\quad \varphi=\omega t+ \varphi_0+\delta\varphi,\quad r=R+\delta r. $$

(B.2)

We substitute these coordinates in Eqs. (A.1)–(A.3) and expand the equations up to first order of coordinates increments. Taking into account that for a non relativistic particle ρ≪1 we obtain a system of differential equations that describe the motion of a particle in a vicinity of a circle:

(B.3)

where ε=sinφ ₀=±1. We investigate the trivial solution of this system for stability. By Lyapunov’s theorem the trivial solution is stable when all roots of characteristic first-approximation equation of the system have negative real parts (Merkin 1996). We write Eq. (B.3) in the form:

(B.4)

where $x_{1}=\frac{\delta r}{R}, x_{2}=\delta\theta, x_{3}=\delta\varphi, T=\epsilon\operatorname{tg}\alpha$. Prime denotes ξ derivative , where ξ=ωt. Reduce the system (B.4) to a normal form:

(B.5)

A set of solutions of the system has the form d ₁=a ₁ e ^iνξ, d ₂=a ₂ e ^iνξ…x ₃=a ₆ e ^iνξ. This gives the characteristic equation:

(B.6)

where k=ν ².

Important criteria that give necessary and sufficient conditions for all the roots of the characteristic polynomial (with real coefficients) to lie in the left half of the complex plane are known as Routh-Hurwitz criteria (Gantmacher 1959).

Given a polynomial

(B.7)

where the coefficients a _i are real constants, i=1,2,3…,n. Define the n Hurwitz matrices using the coefficients a _i of the characteristic polynomial:

(B.8)

All of the roots of the polynomial P(λ) are negative or have negative real part if the determinants of all Hurwitz matrices are positive (Det H _j ≥0, j=1,2,…,n).

For the polynomials of degree n=3, the Routh-Hurwitz criteria simplify to

(B.9)

From (B.6) we get: a ₁=−(1+T ²), a ₂=−3(1+T ²), a ₃=−3T ². It is easy to see that conditions (B.9) of Routh-Hurwitz criteria are not satisfied. So, the trivial solution of system (B.3) is not stable.