1 Introduction

Shock-wave/turbulent boundary layer interactions (STBLI) are common in transonic, supersonic and hypersonic flows, such as supersonic engine inlets, over-expanded rocket nozzles and airfoils. In strong STBLI, shock waves impose an adverse pressure gradient on the boundary layer that leads to flow separation, which further results in other detrimental effects, such as total-pressure loss and reduced aerodynamic efficiency, unsteady mechanical and thermal loads on the structure, and engine inlet instability. To minimize these undesirable effects, a number of attempts have been made to control STBLI using both active and passive control strategies (Delery 1985).

Active control methods like active suction and pulsed jets are proven to be effective, but their implementation requires extra weight and energy (Babinsky and Ogawa 2008). Passive control methods, such as shock-control bumps (Ogawa et al. 2008), pressure-feedback ducts or secondary recirculation jets (Pasquariello et al. 2014; Wu et al. 2022), and vortex generators (Panaras and Lu 2015; Budich et al. 2013; Della Posta et al. 2023), are more energy-efficient and easier to install. Among passive control methods, micro-vortex generators (MVG) with a height of approximately 40% of the boundary layer thickness are highly successful in the suppression of shock-induced flow separation by introducing a pair of counter-rotating streamwise vortices that energize the boundary layer and thereby delay flow separation (Babinsky and Ogawa 2008). MVGs can also be combined with other control methods to achieve stronger control effects (Wu et al. 2022; Titchener and Babinsky 2013).

A common drawback of many active and passive flow control methods is that their control performance is very sensitive to the installation location (Gaitonde and Adler 2023). Although MVGs reduce parasitic drag compared to traditional vortex generators, they still lead to a substantial increase in drag when there is no flow separation (Rybalko et al. 2012), especially at high Reynolds number (Guo et al. 2022a). This is also the case for other passive methods such as local suction and injection through pressure feedback ducts (Pasquariello et al. 2014) and shock control bumps (Ogawa et al. 2008). Therefore, in high-speed applications, there is a compelling need for novel flow control methods that are insensitive to their installation location and have a low drag penalty.

For these reasons, we consider the utilization of surface roughness a promising research direction. Spanwise heterogeneous roughness can induce large-scale secondary flow structures, i.e., streamwise vortices, within a turbulent boundary layer. Secondary flows can be classified into Prandtl’s secondary flow of the first kind and the second kind (Nikitin et al. 2021). The former is driven by pressure gradients induced by streamwise geometry variations; examples are the streamwise vortices over MVGs or convergent-divergent (C-D) riblets (Nugroho et al. 2013). Secondary flow of the second kind, on the other hand, is generated by the imbalance between local production and viscous dissipation of turbulent kinetic energy and occurs only in turbulent flows.

Guo et al. (2022a) recently applied C-D riblets with a height less than 5% of the boundary layer thickness to control a Mach 2.9 compression-ramp STBLI flow. They found that C-D riblets are able to shrink the mean flow separation area by 56%, thus demonstrating that roughness-induced streamwise vortices are an effective way to control STBLI. However, C-D riblets also generate pressure drag and should therefore be applied only in a narrow region. The positioning of the riblets patch relative to the shock impingement point is arguably crucial for the control performance.

Prandtl’s secondary flow of the second kind can be induced by strip-type and ridge-type roughness (Kadivar et al. 2021). Strip-type roughness consists of alternating smooth/rough strips and the effects of the shear stress variation are predominant, while ridge-type roughness is formed by contouring a smooth wall and the effects of the wall elevation and wall-area increase are predominant. Ridge-type rough surfaces that are homogeneous along the streamwise direction do not suffer from increased pressure drag, unlike strip-type roughness and C-D riblets. Streamwise homogeneous ridge-type roughness can therefore be applied over large areas, such that the control effectiveness is less sensitive to the installation location. These advantages make the ridge-type roughness a promising method to study. Zampiron et al. (2020) experimentally demonstrate that ridge-type roughness can induce secondary currents, such as upwash over the ridges and downwash in the valleys, resulting in the formation of low-momentum and high-momentum pathways within the turbulent boundary layer. The same conclusions are confirmed numerically by Zhdanov et al. (2024). Wangsawijaya et al. (2020) point out the spacing between ridges, and the width and height of the ridge are the main contributing factors to the size of the secondary flows induced by the ridge-type roughness. Von Deyn et al. (2022a) have shown that the secondary motions exhibit a weak dependence on Reynolds number. Although extensive studies have investigated the properties of secondary flows induced by ridge-type roughness, no research has applied ridge-type roughness to control STBLI.

The goal of the present study is therefore to explore the control effects of streamwise homogeneous and spanwise heterogeneous ridge-type rough surfaces on a Mach 2.0 STBLI. The control principle is examined in detail and a parametric study is performed to understand the influence of the ridge spacing on boundary-layer turbulence, shock-induced flow separation, and the low-frequency unsteadiness of STBLI. This paper is organized as follows: Sec. 2 describes the test case, simulation setup, and numerical methods; Sec. 3 presents and discusses the observed effects on the incoming turbulent boundary layer and the interaction region, as well as low-frequency dynamics. Conclusions are drawn in Sec. 4.

2 Numerical Setup

2.1 Numerical Method

The three-dimensional, compressible Navier–Stokes equations are solved using our in-house finite volume solver INCA (https://www.inca-cfd.com/). We perform wall-resolved large eddy simulations (LES) using the adaptive local deconvolution method (ALDM). ALDM is a nonlinear solution-adaptive finite-volume scheme and follows a holistic approach for the subgrid-scale modeling of turbulence and shock waves, which enables the accurate propagation of smooth waves and turbulence without excessive numerical dissipation with a similar spectral resolution as provided by a six-order central difference scheme and the essentially non-oscillatory capturing of discontinuities through solution-adaptive stencil selection and an appropriate flux function (Hickel et al. 2014). An explicit 3rd-order Runge–Kutta-scheme is used for time marching. This solver has been extensively validated and successfully applied for various STBLI cases, including the compression ramp (Grilli et al. 2012), shock impingement (Pasquariello et al. 2017; Laguarda et al. 2024) and forward/backward facing step (Hu et al. 2021, 2022). A second-order cut-cell-based immersed boundary method (IBM) is utilized to represent the rough wall (Meyer et al. 2010; Örley et al. 2015). With this cut-cell method, the finite volume cells at the boundaries are re-shaped to locally conform to the wall boundary, which ensures the strict conservation of mass, momentum, and energy.

Fig. 1
figure 1

a Schematics of the computational domain (including streamwise velocity contours), and b schematic view of the investigated ridge-type rough walls with relevant definitions

Full size image

2.2 Problem Definition

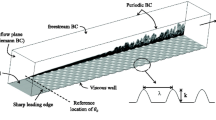
Six wall-geometry configurations are investigated in the present study. These include a baseline case, featuring a smooth wall, and five cases with different rough wall geometries. All configurations share identical inflow conditions: a Mach 2.0 turbulent boundary layer that interacts with an oblique impinging shock wave with a shock angle of \(\phi = 40.04^{\circ }\). This results in the STBLI flow depicted in Fig. 1a. The friction Reynolds number \(Re_{\tau ,0}=\delta _0/\delta _{\nu }\) is 250 based on the 99% boundary layer thickness at the inflow plane \(\delta _0\). The viscous length scale is \(\delta _{\nu }={\nu _w}/u_{\tau }\), where \(\nu _w\) is the kinematic viscosity at the wall, \(u_{\tau }=\sqrt{\tau _{w}/\rho _{w}}\) is the friction velocity; \(\tau _w\) and \(\rho _w\) are the drag per plane area and the density of the fluid at the wall, respectively. In the absence of shock wave, the 99% boundary layer thickness at the inviscid impingement point, which is located 32\(\delta _0\) downstream of the inlet, is \(\delta _{imp}=1.48\delta _{0}\) and the corresponding friction Reynolds number is \(Re_{\tau ,imp} = 355\). The dimensions of the computational domain for the smooth wall are \(L_x\times L_y\times L_z = 45.4\ \delta _{0} \times 16.5\ \delta _{0} \times 4 \ \delta _{0}\) as shown in Fig. 1a. The fluid is modeled as a perfect gas with the standard properties of air. Stagnation temperature and pressure are \(T_0=288.2\ \textrm{K}\) and \(p_0=355.6\ \textrm{kPa}\) at the inlet. Table 1 summarizes the dimensional and non-dimensional flow parameters.

Table 1 Summary of flow parameters adopted in the current research
Full size table

The spanwise heterogeneous roughness consists of sinusoidal ridges with non-dimensional spacing \(D/\delta _0\), width \(\lambda /\delta _0\), and height \(H/\delta _0\), see Fig. 1b. To better assess their efficacy for STBLI control, a parametric study on the ridge spacing \(D/\delta _0\) is performed, where considered values are \(D/\delta _0=\{2.0,1.0,0.5,0.25,0.125\}\), or \(D/\delta _{imp}=\{1.35,0.68,0.34,0.17,0.085\}\) if normalized with boundary layer thickness at the virtual impingement point, as shown in Fig. 1b. The normalized ridge spacing values are also included in Tab. 2 for convenience. The non-dimensional height of the ridges is \(H/\delta _0 = 0.1\) and their width is \(\lambda /\delta _0 = 0.2\) for all rough wall cases, except the case with \(D/\delta _0=0.125\) which does not have the flat bottom valley and only consists of continuous sinusoidal waves with \(D=\lambda\) due to the limited space in the spanwise direction. If scaled with the viscous length of the baseline case at the inlet, the non-dimensional width and height are \(\lambda ^+=\lambda /\delta _{\nu }=49.6\) and \(h^+=H/\delta _{\nu }=24.8\). Note that the crests of the ridges are at the plane of \(y=0\) and the geometry of the ridge-type roughness is homogeneous along the streamwise direction.

Fig. 2
figure 2

A zoomed-in view of the Cartesian mesh near the rough wall with \(D/\delta _0=0.25\) in the cross-stream plane. The mesh is uniform in the streamwise direction

Full size image
Table 2 Summary of STBLI cases parameters
Full size table

2.3 Boundary Conditions and Grid Distribution

Smooth and rough walls are modeled with adiabatic non-slip wall boundary conditions. A Digital Filter (DF) method (Laguarda and Hickel 2024) is employed at the inflow plane to introduce a synthetic turbulent boundary layer flow with well-defined space and time correlation in the computational domain. Unlike recycling/rescaling methods, DF methods can reproduce the first and second-order statistics of the turbulent boundary layer without introducing spurious correlations that may interfere with the low-frequency dynamics of STBLI (Touber and Sandham 2008). Non-reflecting boundary condition based on Riemann invariants is used at the top boundary, where the oblique shock is introduced using the Rankine–Hugoniont relations (Poinsot and Lele 1992). Linear extrapolation is used at the outlet and periodicity is imposed in the spanwise direction.

The Cartesian grid for the smooth-wall baseline case consists of \(N_x\times N_y \times N_z=512\times 192\times 128=12.6\cdot 10^6\) cells. The grid resolution in wall units is \(\Delta x^+=21.9\) and \(\Delta z^+=7.74\), with \(\Delta y^+_{wall} \le 0.93\). The mesh is coarsened in the streamwise and spanwise directions within the boundary layer above \(y\approx 0.7 \delta _0\) and within the freestream flow. For the rough wall cases, the mesh is locally refined near the wall to fully resolve the geometry and turbulent structures around the roughness ridges, see Fig. 2. Note that the shape of each sinusoidal ridge is well resolved with 14 cells and the mesh is stretched in the wall-normal direction with a very mild constant stretching factor of 1.02. For the controlled cases, the viscous-scaled grid resolution is \(\Delta x^+=5.49\), \(\Delta z^+=3.87\), \(\Delta y^+_{wall} \le 0.93\), which is much finer than what normally required in LES, resulting in \(58.7\cdot 10^6\) cells in total.

3 Results and Discussion

3.1 Upstream Turbulent Boundary Layer

The state of the incoming turbulent boundary layer (TBL) plays a pivotal role in the STBLI dynamics and organization, particularly in light of the working principle of the proposed flow-control method. Therefore, the analysis of the results is first focused on the upstream TBL. A probing station located \(20\delta _0\) upstream of the impingement point, which is free from the influence of the STBLI, is used for this purpose. Meanwhile, the probing station, situated \(12\delta _0\) downstream from the inflow plane, is appropriately positioned to ensure the turbulence reaches equilibrium (Laguarda and Hickel 2024; Morgan et al. 2011).

In order to better compare the characteristics of the TBL and to also assess the outer-layer similarity between the smooth wall and rough wall cases, a shifted wall-normal coordinate correction is considered. As explained by Chung et al. (Chung et al. 2021), this is necessary because the outer turbulent flow does not perceive its origin at \(y=0\) if the wall is rough. The origin of the wall-normal coordinate is thus shifted to the average roughness elevation height, or meltdown height, above the valley of the rough wall. The functional relation between \(y_s/\delta _0\) and \(y/\delta _0\) can be written as:

$$\begin{aligned} y_s/\delta _0 = (y+H-H_{md})/\delta _0 \end{aligned}$$
(1)

This is illustrated in Fig. 3, which shows the definition of the shifted wall-normal coordinate \(y_s\) and the non-dimensional roughness meltdown height \(H_{md}/\delta _0\). For the smooth wall case, \(y_s/\delta _0\) simplifies to \(y/\delta _0\).

Fig. 3
figure 3

Definition of the shifted wall-normal coordinate \(y_s\) and roughness meltdown height \(H_{md}\)

Full size image

Figure 4a shows the van Driest transformed mean velocity profile of the smooth-wall case. It is worth mentioning that intrinsic averaging is applied, considering only the fluid volume fraction of cells that are cut by the geometry as weights when calculating the flow statistics. The velocity profile agrees well with the classic law of the wall, confirming the accuracy of the incoming turbulent boundary layer. Reference DNS data of a Ma 2.0 TBL from Pirozzoli and Bernardini (2011) is also included in the figure and is in good agreement with the LES data. Note that the LES has a slightly higher friction Reynolds number (\(Re_{\tau } = 285\) at this station) than the DNS case (\(Re_{\tau } = 250\)), which is correctly represented by higher \(\langle u \rangle ^+_{vD}\) in the wake region. The density-scaled Reynolds stresses are shown in Fig. 4b and further highlight the very good agreement between the baseline LES and DNS results for a smooth wall. Small differences near the boundary-layer edge can be attributed to the difference in Reynolds number.

Fig. 4
figure 4

Comparison of present LES ( ) for the smooth wall case and DNS (\(\square\)) of Pirozzoli and Bernardini (2011); a van Driest transformed mean velocity profiles and b density scaled Reynolds stresses. Note: LES results are taken from \((x-x_{imp})/\delta _0=-20.0\), where \(Re_\tau =285\), and DNS data is at \(Re_\tau =250\)

Full size image
Fig. 5
figure 5

a van Driest transformed mean velocity profiles of the incoming turbulent boundary layer for: smooth wall; \(D/\delta _0=2.0\); \(D/\delta _0=1.0\); \(D/\delta _0=0.5\); \(D/\delta _0=0.25\); \(D/\delta _0=0.125\). b Roughness function for different non-dimensional ridge spacings. All results are taken at \((x-x_{imp})/\delta _0=-20.0\)

Full size image

A comparison of the van Driest transformed mean velocity profiles of the controlled cases is shown in Fig. 5a. A clear downshift of the profile is observed for all rough-wall cases except for the case with a ridge spacing of \(D/\delta _0=0.125\). The downshift indicates a drag increase and the corresponding momentum deficit due to the surface roughness, which can be quantified with the roughness function \(\Delta \langle u\rangle _{vD}^+=\langle u \rangle _{vD,S}^+-\langle u\rangle _{vD,R}^+\), where \(\langle u \rangle _{vD,S}^+\) and \(\langle u \rangle _{vD,R}^+\) represent the velocity profile over the smooth wall and the rough wall, respectively. The larger \(\Delta \langle u\rangle _{vD}^+\), the higher the added drag as a result of the roughness (Chung et al. 2021). Note that the downshift of velocity profiles is usually measured in the log-law region; however, \(\Delta \langle u\rangle _{vD}^+\) is measured here in the free stream because the investigated Reynolds number is low.

Figure 5b shows the relation between \(\Delta \langle u\rangle _{vD}^+\) and \(D/\delta _0\). Interestingly, when \(D/\delta _0\) decreases, \(\Delta \langle u\rangle _{vD}^+\) increases first (i.e., increased added drag) and then decreases. For the smallest spacing \(D/\delta _0=0.125\), \(\Delta \langle u\rangle _{vD}^+\) drops below zero indicating a decrease in drag compared to the smooth wall. This non-monotonic trend of \(\Delta \langle u\rangle _{vD}^+\) is consistent with previous studies (von Deyn et al. 2022b). The effect of the ridge spacing is expected to tend to diminish when the spacing approaches zero or infinity since – in both circumstances – the rough wall asymptotically tends towards an effectively smooth wall. For large finite ridge spacing, friction increases due to the larger wetted area compared to a smooth wall. As the spacing keeps decreasing, the ridge-type rough wall eventually transitions into the category of riblets and the skin friction reduces by exposing less surface area to high-velocity flow (Choi et al. 1993).

Profiles of the Reynolds stresses \(\tau _{ij}=\langle \rho \rangle \langle u_i'u_j'\rangle\) for the smooth-wall and rough-wall cases are compared in Fig. 6. The Reynolds stresses are normalized with the local wall shear at the probing station, whose value is obtained by integrating the wall shear stress in the spanwise direction over the wetted area and then normalizing it by the projected (plane) area. The profiles match well in the outer region of the TBL, while visible differences are found in the inner region up to approximately \(y_s^+=100\) due to different wall geometries. The peak of \(\tau _{xx}=\langle \rho \rangle \langle u'u'\rangle\) reduces when \(D/\delta _0\) decreases from 2.0 to 0.5 and then increases for \(D/\delta _0\) from 0.5 to 0.125. The Reynolds shear stress shows a similar trend when the ridge spacing varies.

Fig. 6
figure 6

Density scaled Reynolds stress profiles of the incoming turbulent boundary layer at \((x-x_{imp})/\delta _0=-20.0\) for smooth wall and rough wall cases: smooth wall; \(D/\delta _0=2.0\); \(D/\delta _0=1.0\); \(D/\delta _0=0.5\); \(D/\delta _0=0.25\); \(D/\delta _0=0.125\)

Full size image
Fig. 7
figure 7

Mean flow streamlines and Mach number distribution in a cross-stream plane at \((x-x_{imp})/\delta _0=-20\). The sonic line is shown in lime

Full size image
Fig. 8
figure 8

Mean vertical velocity in a cross-stream plane at \((x-x_{imp})/\delta _0=-20\) with superposed cross-stream velocity vectors. The sonic line is shown in lime

Full size image

The roughness-induced secondary flow is visualized in Fig. 7, which shows streamlines and Mach number distribution of the mean flow in the cross-stream plane at \((x-x_{imp})/\delta _0=-20\). Clear streamwise vortices induced by the roughness structure can be observed in the cross-stream plane, with upwash occurring at the ridges for all rough wall cases, consistent with findings from the incompressible flow experiment of Zampiron et al. (2020). The effect of rough walls on the Mach number distribution is confined within the thickness of the TBL, that is, the outer flow is only marginally affected by the rough wall upstream of the interaction region. The shape of the sonic line, see the lime line around 0.1 \(\delta _0\) above the wall in Fig. 7, is clearly altered by the wall shape. For larger ridge spacing cases, the sonic line basically follows the curvature of the rough wall structure. For the smaller ridge spacing cases, the sonic line remains at a distance of 0.1 \(\delta _0\) above the ridges and tends to recover a straight line. Note that this causes a larger subsonic cross-section area as compared to the smooth wall and the cases with wide ridge spacing. Figure 9a summarizes the spanwise-averaged height of the sonic lines expressed in the shifted wall normal coordinate. By measuring from the shifted wall origin, the spanwise-averaged height conveniently represents the subsonic area of the incoming boundary layer. When reducing the ridge spacing, the mean sonic height increases first, reaching for \(D/\delta _0=0.25\) the maximum value of 48% larger than the one in the smooth wall case, and then decreases.

Contours of the vertical velocity and velocity vectors in Fig. 8 also visualize the secondary-flow vortices. The maximum magnitude of the vertical velocity is observed to be around 3% of the freestream velocity, which agrees with the results reported by Vanderwel et al. (2019). From the streamline map of Fig. 7, it seems that another vortex pair adjacent to the vortex touching the ridges is induced in the cases \(D/\delta _0=2.0, 1.0\). However, this vortex pair is actually rather weak compared to the vortex pair near the ridges. Figure 8 shows that the magnitude of cross-stream velocity vectors in the valley is close to zero. The size of secondary flow vortices, which is here measured as the distance from the shifted wall origin to the highest location with secondary flow towards the wall, increases with \(D/\delta _0\) and reaches a maximum of around 0.5 local boundary layer thickness \(\delta _{99}\) in case \(D/\delta _0\)=1.0 as shown in Fig. 9b. This trend of size increase aligns with the findings of Zampiron et al. (2020) and Zhdanov et al. (2024), who indicate that in incompressible channel flow over ridges, the size of secondary vortices increases until they fill the entire channel.

Fig. 9
figure 9

a Spanwise-averaged height of the mean sonic line, b height of the secondary vortices induced by the rough wall structure, c maximum value of the mean vertical velocity, and d mean secondary flow intensity of such vortices at \((x-x_{imp})/\delta _0=-20\) as a function of the ridge distance \(D/\delta _0\). The corresponding value from the smooth wall case is indicated with a dashed line in a

Full size image

The intensity of the secondary flows can be evaluated both locally and globally. Locally, the intensity of the secondary motions can be represented by the maximum vertical velocity of the secondary flows before the interaction, as shown in Fig. 9c. The maximum vertical velocity increases with the ridge spacing from \(D/\delta _0=0\) to 1.0 and then remains almost constant regardless of the increase of the ridge spacing. However, the maximum downwash velocity in the valleys reduces with the larger ridge spacing as the vortices stretch wider. On the other hand, the global intensity of the secondary flow can be quantified by the variable introduced by Guo et al. (2022b), which is defined as:

$$\begin{aligned} I = \frac{1}{V}\int _V \sqrt{\langle v\rangle ^2+\langle w\rangle ^2}/u_{\infty } \textrm{d}x\textrm{d}y\textrm{d}z . \end{aligned}$$
(2)

As shown in Fig. 9d, the global intensity I peaks at \(D/\delta _0=0.5\), which is consistent with the observation in Fig. 8 that strong secondary vortices fully fill the whole span for the case with \(D/\delta _0=0.5\).

Fig. 10
figure 10

Mean pressure fluctuation distribution at \(z=0\) plane. Solid line color legend: zero mean streamwise velocity (red), mean sonic line (lime) and mean shock position (black)

Full size image

3.2 Interaction Region

Figure 10 shows contour plots of the mean pressure fluctuation distribution on the \(z=0\) plane for all cases. The shock system, sonic line, and separation lines are superimposed on the contours to provide a reference. It is clear that the most intensive pressure fluctuations appear along the separation shock, especially in the part above the intersection of incident shock and separation shock. Another region of high pressure fluctuations is found around the location where the incident shock impinges on the shear layer. Milder pressure fluctuations are found along the sonic line and expansion fan. Compared with the smooth wall case, cases \(D/\delta _0=2.0\) and \(D/\delta _0=1.0\) show a higher pressure fluctuation intensity at the separation shock. Contrarily, case \(D/\delta _0=0.25\) exhibits the weakest pressure fluctuations at the separation shock. It is also noticeable that case \(D/\delta _0=0.25\) is characterized by an elevated shock intersection point and the longest interaction length, and the separation region is clearly enlarged for this case.

Fig. 11
figure 11

Spanwise averaged a wall pressure and b wall pressure fluctuation c friction coefficient along streamwise direction for: smooth wall; \(D/\delta _0=2.0\); \(D/\delta _0=1.0\); \(D/\delta _0=0.5\); \(D/\delta _0=0.25\); \(D/\delta _0=0.125\)

Full size image

To better quantify the impact of wall roughness, the streamwise distributions of the spanwise averaged wall pressure \(\langle p_w\rangle /p_{\infty }\), wall-pressure fluctuation \(\sqrt{\langle p'p'\rangle }/p_{\infty }\), and skin friction coefficient \(C_f\) within the interaction region are discussed next. The wall pressure distributions are shown in Fig. 11a, where no significant difference is observed between the smooth wall and the \(D/\delta _0=2.0, 1.0\) cases. However, when \(D/\delta _0\) decreases from 1.0 to 0.25, the onset of the interaction moves upstream, resulting in an increase in the total interaction length. For \(D/\delta _0=0.125\), the onset location moves downstream instead. At the same time, the maximum wall pressure near the reattachment point first drops then rises with decreasing \(D/\delta _0\). A non-monotonic trend is evident, with the case \(D/\delta _0=0.25\) exhibiting the longest interaction length yet the smallest pressure increase, resulting in the most gradual pressure rise. Profiles of the wall-pressure r.m.s. fluctuation are shown in Fig. 11b. A typical feature of impinging STBLI is that the pressure fluctuation exhibits a local minimum in the middle of the separation bubble and local maxima near the separation and reattachment points (Pasquariello et al. 2017). However, we observe that the peak value in the case \(D/\delta _0=0.25\) is 12% lower than the baseline peak value, which hints at an attenuated separation shock unsteadiness. Therefore, it is worth investigating in more detail the behavior of the pressure fluctuations across different frequencies, which might provide additional insight on the reduction of the pressure peak and the mechanism responsible for this. This will be partially addressed in the upcoming sections. Case \(D/\delta _0=0.125\) shows a peak pressure fluctuation between the values for \(D/\delta _0=0.25\) and the smooth wall case. The location of the peak pressure fluctuation moves similarly to the onset of the interaction, with case \(D/\delta _0=0.25\) exhibiting the most upstream location, which is consistent with a substantial increase in the size of the reverse-flow region.

Figure 11c shows that the friction coefficient \(C_f\) upstream the interaction region changes in a non-monotonic fashion with increasing \(D/\delta _0\), reaching a maximum value for \(D/\delta _0=0.5\). This is consistent with the analysis of the upstream TBL. The \(C_f\) distribution also indicates that the separation region is divided into a primary separation zone and a secondary separation zone for large ridge spacing cases, i.e., \(D/\delta _0=2.0,1.0,0.5\). The total separation length increases when decreasing \(D/\delta _0\) from 1.0 to 0.25, while it remains almost unaffected for other values of \(D/\delta _0\) and slowly approaches the smooth wall case for further increased or decreased ridge spacing. The case \(D/\delta _0=0.125\) exhibits the lowest \(C_f\) in the separation region, especially right after the separation, indicating a stronger reverse flow in the separation bubble.

Figure 12 shows the local skin-friction coefficient distribution projected on the horizontal plane, thus including the effect of the increased wetted area. Before the interaction region, the skin friction shows the periodic pattern of the ridges, where higher friction appears due to the increased surface area. The separation and reattachment lines are highly spanwise corrugated in rough wall cases. This is because the ridges protrude into higher-speed flow, delaying separation and accelerating reattachment on top of the ridges relative to the flow in the valleys. The flow near the corners between ridges and valleys separates more easily due to corner effects. At corners, the wall-shear stress on the two adjacent walls reduces and it drops to zero right at the corner, giving rise to a less full boundary layer in this region, thus promoting separation. An interesting observation for cases with larger ridge spacing, such as \(D/\delta _0=2.0,1.0,0.5\), is that the flow over the valleys reattaches to the wall shortly after the initial separation, forming a locally attached region before the main separation bubble. A similar flow topology was also reported by Guo et al. (2022a). The flow over the valley for these three cases, \(D/\delta _0=2.0,1.0,0.5\), delays the mean-flow separation compared to the smooth wall case. This is believed to be the result of the downwash flow, which enhances momentum exchange brought about by the secondary vortices. For smaller ridge spacing, the subsonic region of the upstream turbulent boundary layer becomes thicker, promoting the upstream propagation of the adverse pressure gradient, making separation more likely.

Fig. 12
figure 12

Local skin friction coefficient distribution projected on the horizontal plane. Black lines denote the location where \(C_f=0\)

Full size image

Figure 13 summarizes how the separation length and separation area change with different ridge spacings. The separation length is calculated from the spanwise averaged \(C_f\) distribution, and measured as the distance between the first separation point to the final reattachment point. For cases \(D/\delta _0=2.0, 1.0\), the separation length is slightly larger than the smooth wall case, but the separation area reduces around \(15\%\) because the flow reattaches in the valleys. For the small ridge spacing case \(D/\delta _0=0.25,0.125\), the separation lengths increase by around 40% and the separation areas increase by 41% and 48% respectively.

Fig. 13
figure 13

a Spanwise-averaged separation length and b relative separation area as a function of \(D/\delta _0\). The dashed line denotes the corresponding value in smooth wall case

Full size image

The assessment of total pressure recovery holds critical importance in aero-engine inlet design. We therefore analyse the total pressure recovery at the \((x-x_{imp})/\delta _0=10\) plane, which is near the outlet of the computational domain. As shown in Fig. 14a, overall, the profiles for the smooth wall and two large ridge spacing cases \(D/\delta _0=\) 2.0, 1.0 are very similar and have the highest total pressure in the near-wall region \(y_s/\delta _0<2.0\). The total pressure recovery decreases as \(D/\delta _0\) reduces from 1.0 to 0.25, and subsequently increases as the ridge spacing decreases further. However, when the view is expanded to observe areas farther from the wall, as depicted in Fig. 14b, the trend in total pressure recovery with ridge spacing is inverted compared to the near-wall region. Case \(D/\delta _0=0.25\) exhibits the highest pressure recovery in a relatively large region from \(y_s/\delta _0=2.5\) until \(y_s/\delta _0=10.0\). Even though the curves show only small differences, the trend is significant and consistent with the observation that cases with higher friction suffer from more viscous loss in the near-wall region, while they also benefit from a more diffused shock, resulting in higher total pressure recovery. Since the mass flow away from the wall is significantly higher than the mass flow near the wall, the overall effect is that case \(D/\delta _0=0.25\) achieves an approximately 0.5% higher mass-flow averaged total pressure recovery than the smooth-wall case, see Fig. 14c.

Fig. 14
figure 14

Spanwise-averaged total pressure recovery profile at the \((x-x_{imp})/\delta _0=10\) plane a near the wall and b away from the wall for: smooth wall; \(D/\delta _0=2.0\); \(D/\delta _0=1.0\); \(D/\delta _0=0.5\); \(D/\delta _0=0.25\); \(D/\delta _0=0.125\). c Mass-flow averaged total pressure recovery at the same plane as a function of \(D/\delta _0\)

Full size image

3.3 Low-Frequency Dynamics

It is well known that STBLI are subject to large-scale low-frequency oscillations (Clemens and Narayanaswamy 2014). The streamwise distribution of the wall-pressure fluctuations indicated that streamwise-aligned ridges with a small ridge spacing (\(D/\delta _0=0.25\)) may be effective in attenuating the low-frequency motion of the separation shock. To further support this claim, we analyze the unsteady pressure probe data and perform a modal analysis of the flow field.

3.3.1 Spectral Analysis

We place 282 equally spaced pressure probes (\(\Delta /\delta _0 \approx 0.09\)) along the streamwise direction at \(y=0\) in the mid-plane, as indicated by the red dotted line in Fig. 1a, and samples have been collected over a time span around 4000 \(\delta _0/u_{\infty }\) with a sampling frequency of \(f_s\approx 46u_{\infty }/\delta _0\). This theoretically enables us to capture the flow unsteadiness within a very wide frequency range from \(2.5\times 10^{-4}\ u_{\infty }/\delta _0\) to \(23\ u_{\infty }/\delta _0\). We employ Welch’s method with Hann windows to compute the PSD employing eight segments with 50% overlap to achieve statistical convergence so that each time window has a length of \(889\delta _0/u_{\infty }\). The corresponding frequency range is \(1.12\times 10^{-3}u_{\infty }/\delta _0\) to \(23u_{\infty }/\delta _0\).

The separation length is selected as the characteristic length scale to define the Strouhal-number \(St=fL_{sep}/u_{\infty }\). Figure 15 shows the pre-multiplied power spectral density (PSD) of the wall-pressure signals. PSDs are normalized by the local pressure variance to highlight the relative local contributions to the variance at different frequencies, independent of the overall fluctuation strength.

Fig. 15
figure 15

Pre-multiplied power spectra density maps of wall-pressure signals at the mid-plane. The red lines denote the location where \(C_f=0\), i.e., separation and reattachment locations; the blue lines denote the location where maximum pressure fluctuation appears

Full size image

The PSDs of the upstream TBL in all cases show high amplitudes centered around \(fL_{sep}/u_{\infty }\approx 10\), which reflects the characteristic frequency of the turbulent boundary layer. Near the location of the separation line, an energetic low-frequency tone appears, approximately two orders of magnitude lower than the characteristic frequency in the upstream TBL. Because of the diffused character of the separation shock for the low Reynolds number case, the low-frequency content spreads over around two boundary layer thicknesses in streamwise direction. Correspondingly, the intensity is lower than typically observed in higher Reynolds number impinging STBLI (Pasquariello et al. 2017; Dupont et al. 2006). Comparing the smooth case with the rough cases, we observe that the low-frequency content for the three cases with the relatively large ridge spacing (\(D/\delta _0=2.0,1.0,0.5\)) is similar to the smooth-wall case, but it appears significantly weaker for \(D/\delta _0=0.25\) and 0.125.

Figure 15 also indicates that the location of low-frequency content appears near the separation point but does not necessarily coincide with the maximum pressure fluctuation point. The maximum pressure fluctuation appears downstream of the separation points, where the local pressure is mostly influenced by the detached shear layer vortices.

To better compare the low-frequency content at the separation line, we show the spectral content of the smooth-wall case and controlled cases with \(D/\delta _0=\{0.5,0.25\}\) in Fig. 16. We observe that all PSDs show significant content at \(St_{L_{sep}}\approx 10\) before the interaction, corresponding to the characteristic frequency of the TBL turbulence. However, the PSD of \(D/\delta _0=0.5\) case is higher than the smooth wall case near \(fL_{sep}/u_{\infty }\approx 0.05\), and the PSD for \(D/\delta _0=0.25\) drops significantly below the smooth wall case near this frequency. This provides additional evidence that the ridge-type roughness with \(D/\delta _0=0.25\) can attenuate the separation shock footprint on the wall.

Fig. 16
figure 16

Pre-multiplied power spectral density of wall-pressure signals at the mean separation lines of \(D/\delta _0=0.5\) ( ) and \(D/\delta _0=0.25\) ( ) compared to the smooth wall ( ). The averaged location of the separation line is at \((x_{sep}-x_{imp})/\delta _0=-8.56\) for the smooth wall; \((x_{sep}-x_{imp})/\delta _0=-9.18\) for \(D/\delta _0=0.5\); and \((x_{sep}-x_{imp})/\delta _0=-10.66\) for \(D/\delta _0=0.25\)

Full size image
Fig. 17
figure 17

Normalized amplitudes (black lines) of the DMD modes from the rough wall cases. The close-up view shows the eigenvalue distribution. The red color indicates a SPDMD subset of \(N_{sub}=17\) modes

Full size image

3.3.2 Dynamic Mode Decomposition

To better decouple different frequency dynamics and further validate our previous findings, a modal analysis was carried out based on Sparsity Promoting Dynamic Mode Decomposition (SPDMD). Dynamic Mode Decomposition (DMD) (Schmid 2010) is a purely data-driven decomposition technique that aims to extract coherent spatial-temporal structures from a sequence of snapshots. SPDMD is a variant of DMD that significantly simplifies the analysis and interpretation by automatically selecting the most relevant modes from the standard DMD solution (Jovanović et al. 2014). We apply SPDMD to 4101 2D snapshots of the pressure field at the \(z=0\) and \(y=0\) planes covering a time interval of \(tu_{\infty }/\delta _0 = 3997.5\) at a sampling frequency of \(f_s\delta _0/u_{\infty } \approx 1\) to conduct SPDMD. The corresponding frequency resolution range is \(2.5\times 10^{-4}<St_{\delta _0}<0.5\).

The mode amplitudes \(\psi _{i}\), which are normalized by the mean mode amplitude, from the DMD analysis are shown in Fig. 17 supplemented by a close-up view of eigenvalues \(\mu _i\) distribution. Since the input data is real-valued, modes appear as complex conjugate pairs but only the ones in the positive branch are shown here. SPDMD effectively selects modes that represent the dynamics at low and medium frequencies; modes selected by SPDMD are colored in red in Fig. 17. The distribution of the SPDMD selected modes indicates that case \(D/\delta _0=0.25\) shows attenuated low-frequency unsteadiness. Only one mode with \(St_{L_{sep}}<0.1\) is selected by SPDMD for this case.

Fig. 18
figure 18

Real part of selected mode \(\mathfrak {R}(\phi _p)\) at a \(St_{L_{sep}}=0.034\) b \(St_{L_{sep}}=0.537\) of smooth wall, c \(St_{L_{sep}}=0.028\) d \(St_{L_{sep}}=0.556\) of \(D/\delta _0=0.25\) case at initial phase. The mean shock system is superimposed by black solid lines

Full size image

Figure 18 shows the mode shape of selected low-frequency and high-frequency modes for the smooth-wall case (upper row) and for case \(D/\delta _0=0.25\) (lower row). Representative low-frequency modes from the smooth-wall and rough-wall case are shown in the left column, Fig. 18a, c, and clearly represent the motion of the separation shock. The impinging shock is steady and does not cause any fluctuation. The slightly less pronounced separation shock motion observed for case \(D/\delta _0=0.25\) is consistent with previous conclusions drawn from the wall-pressure fluctuations in Fig. 10. We also see that the shock-motion induced pressure fluctuation gradually diffuses when approaching the wall. The high-frequency modes shown in Fig. 18b, d primarily show pressure fluctuation caused by the shedding of shear-layer vortices. These fluctuations propagate further downstream and persist even after the interaction region.

4 Conclusion

The effect of spanwise heterogeneous roughness on the interaction between an impinging shock wave and a turbulent boundary layer at Mach 2.0 and \(Re_\tau \approx 355\) has been investigated. The structured roughness pattern is constituted by streamwise-aligned ridges, which induce secondary flow of Prandtl’s second kind. The size and intensity of the induced streamwise vortices increase with increasing non-dimensional ridge spacing and reach a maximum at \(D/\delta _0=1.0\). We found that a large ridge spacing (\(D/\delta _0=2.0,1.0\)) reduces the separation area by 15% but leads to stronger wall pressure fluctuation. A ridge spacing of \(D/\delta _0=0.25\) increases the separation area and decreases the peak value of the pressure fluctuation by 12% compared with the smooth wall case. Based on the analysis of wall-pressure spectra and a dynamic mode decomposition of 2D pressure fields, the reduction in pressure fluctuation is demonstrated to be associated with the attenuated low-frequency unsteadiness of the separation shock. To the best of our knowledge, this study presents the first observation that ridge-type roughness can reduce the wall pressure fluctuation peak near the separation point. The increase in total pressure recovery further underscores the potential of ridge-type roughness for engineering applications, such as in supersonic engine inlets.

The present study provides a proof-of-concept for a relatively low Reynolds number. We expect the control effect of the turbulence induced secondary flow will persist for high-Reynolds STBLI with a sharper separation shock and more pronounced low-frequency unsteadiness; however, this hypothesis needs to be corroborated with future studies.