Abstract
Wall-Modelled Large Eddy Simulations (LES) are conducted using a high-resolution CABARET method, accelerated on Graphics Processing Units (GPUs), for a canonical configuration that includes a flat plate within the linear hydrodynamic region of a single-stream jet. This configuration was previously investigated through experiments at the University of Bristol. The simulations investigate jets at acoustic Mach numbers of 0.5 and 0.9, focusing on two types of nozzle geometries: round and chevron nozzles. These nozzles are scaled-down versions (3:1 scale) of NASA’s SMC000 and SMC006 nozzles. The parameters from the LES, including flow and noise solutions, are validated by comparison with experimental data. Notably, the mean flow velocity and turbulence distribution are compared with NASA’s PIV measurements. Additionally, the near-field and far-field pressure spectra are evaluated in comparison with data from the Bristol experiments. For far-field noise predictions, a range of techniques are employed, ranging from the Ffowcs Williams–Hawkings (FW–H) method in both permeable and impermeable control surface formulations, to the trailing edge scattering model by Lyu and Dowling, which is based on the Amiet trailing edge noise theory. The permeable control surface FW–H solution, incorporating all jet mixing and installation noise sources, is within 2 dB of the experimental data across most frequencies and observer angles for all considered jet cases. Moreover, the impermeable control surface FW–H solution, accounting for some quadrupole noise contributions, proves adequate for accurate noise spectra predictions across all frequencies at larger observer angles. The implemented edge-scattering model successfully captures the mechanism of low-frequency sound amplification, dominant at low frequencies and high observer angles. Furthermore, this mechanism is shown to be effectively consistent for both \(M=0.5\) and \(M=0.9\), and for jets from both round and chevron nozzles.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The advent of modern high-bypass area-ratio turbofan engines in commercial aircraft led to a significant improvement in engine-fuel efficiency and reduction of jet noise due to the decrease in the nozzle exhaust velocity. However, the increase in bypass ratio also increased the engine diameter. In typical jet-under-the-wing configurations, this required the installation of engines in close proximity to the wing to maintain the required ground clearance. Altogether, this increased the interaction between the jet and the airframe, thereby leading to an increased low to mid-frequency noise referred to as the jet-installation (JI) effect. In a NASA study, Brown (2015) showed that jet installation noise for a canonical jet-flat-plate configuration depends on the vertical position of the jet centre line with respect to the solid surface as well as the horizontal distance between the end of the jet potential core and the flat plate edge.
In comparison to pure jet mixing noise, which primarily stems from turbulence-turbulence interactions, the jet installation noise is caused by the scattering of the hydrodynamic pressure field of the jet by a solid surface. While in isolated jets, the hydrodynamic pressure field is evanescent and decays exponentially in the radial direction (Lawrence et al. 2011), the presence of a solid surface in near-jet hydrodynamic field leads to its efficient propagation to the far-field, with notable scattering effects, particularly pronounced at the trailing edge of the surface. One of the earliest studies, conducted by Head (1976), identified the dipole nature of jet installation noise, a finding later validated by Way and Turner (1980), Shearin (1983), Mead and Strange (1998), underscoring the significant role played by scattering of surface pressure fluctuations. In accordance with Curle’s theory (Curle 1955), the surface pressure fluctuations induced by the jet can be represented by distributing acoustic dipoles on the surface. Ffowcs (Williams and Hall 1970) developed an analytical model of sound scattering by the trailing edge of a semi-infinite flat plate, assuming a quadrupole source close to the surface. An alternative sound scattering model was developed by Amiet (1976), wherein the effective acoustic source was identified as pressure fluctuations induced on the surface near the trailing edge. These fluctuations are then scattered to the far-field. Furthermore, compared to the Ffowcs (Williams and Hall 1970) model, the (Amiet 1976) trailing edge noise model is simpler, as it only requires a point source at the trailing edge to obtain far-field noise predictions and does not require the computation or measurement of the effective acoustic source in the volume. Using the underlying formulation of the Amiet model, Lyu et al. (2017) investigated the jet installation noise and formulated a semi-analytical model for its prediction. This model utilised near-field hydrodynamic evanescent waves as the acoustic source, derived from experimental data. The scattering of these waves by the trailing edge to the far-field is then described by an analytical transfer function. The research findings revealed that the model could accurately predict the mechanisms of edge-scattering noise generation for cases in which the edge of the plate was positioned within a linear hydrodynamic pressure field, i.e., at a location where the jet plume did not directly contact the surface. In addition, the accuracy of the model was closely associated with the accurate calculation of the hydrodynamic pressure field. However, the implementation was limited to considering the axi-symmetric azimuthal mode and round jets at a relatively low Mach number, which left a few open questions regarding the role of higher-order azimuthal modes for higher Mach numbers and asymmetric jets including chevrons.
In particular, the application of asymmetric nozzles such as chevrons offers an opportunity to enhance large-scale mixing in jet flow, thereby breaking the large-scale coherent structures and reducing the impact of the hydrodynamic waves on the solid surface. Consequently, this could lead to a reduction of jet installation noise. Along this line of thought, for isolated jets, Bridges and Brown (2004) analysed the factors influencing the acoustic benefits of chevron nozzles and showed that the number of chevrons, the length of the chevron, and the penetration angle strongly affect the peak jet noise associated with large-scale structures in the jet. More recently, Jawahar et al. (2021) performed a series of experiments to investigate the effect of chevrons on jet-installation noise for a jet-flat plate configuration at various Mach numbers and chevron geometries, when the flat plate was installed in a linear hydrodynamic jet region. Their findings demonstrated that the SMC006 chevron nozzle, identified as the most efficient for isolated jets, according to Bridges and Brown (2004), also leads to the best reduction of jet installation noise at least for the considered jet-plate configuration. At the same time, the study indicated that some of the fundamental mechanisms of jet installation noise, for example, the effect of high azimuthal pressure modes for chevron jets still remain unclear and merit further investigation. Addressing these effects is the main focus and novelty of the current work via high-resolution computational modelling.
In particular, the goal here will be to perform a series of Wall Modelled Large Eddy Simulations (WMLES) focusing on both installed and isolated, round and chevron jets from the experimental database of Jawahar et al. (2021). For validation in comparison with the Bristol experiment, the flow solutions are combined with the Ffowcs Williams and Hawkings method to obtain far-field noise spectra. Following this, the LES solutions of axi-symmetric and chevron jets are analysed in detail in terms of the noise sources by implementing the Amiet theory-based model of Lyu et al. (2017) and coupling it with the jet LES.
The WMLES calculations are based on the Compact Accurately Boundary Adjusting high-Resolution Technique (CABARET) solver (Karabasov and Goloviznin 2009; Chintagunta et al. 2018; Semiletov and Karabasov 2013), accelerated using Graphics Processing Units (GPUs) (Markesteijn and Karabasov 2018). The solver employs a GPU-optimised CABARET algorithm with asynchronous time stepping, aimed at minimising dispersion and dissipation errors by utilising the optimal local Courant-Friedrichs-Lewy (CFL) number for linear acoustic wave propagation (Semiletov and Karabasov 2013, 2014). In previous studies (Faranosov et al. 2013; Semiletov and Karabasov 2018; Markesteijn and Karabasov 2019; Markesteijn et al. 2020), the WMLES CABARET method has been validated for various jet flow and noise computations, as well as for aerofoil self-noise simulations (Abid et al. 2021a, b).
2 Numerical Setup
2.1 Installed Jet Configuration and Flow Condition
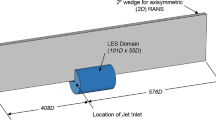
The installed jet setup and flow conditions are based on experiments conducted at the University of Bristol’s Jet Aeroacoustics Research Facility (B-JARF). In these experiments, the jets are positioned in a linear hydrodynamic region (outside jet plume) relative to a flat plate, where the flow velocity is much less than one per cent of the jet exit velocity (Jawahar et al. 2021). The performance of the anechoic test facility for a range of frequencies relevant for jet-installation-noise has been thoroughly validated in comparison with larger scale facilities including the NASA one for a wide range of jet flow Mach numbers (Jawahar et al. 2021a, 2021b; Jawahar and Azarpeyvand 2021, 2022). The experiments utilised a round convergent nozzle as well as chevrons. All of the nozzles considered in Bristol are scaled-down versions (3:1) of the baseline round SMC000 nozzle and its chevron derivatives employed in the NASA experiments (Brown 2015), so that the exit nozzle diameter was \(D_j=0.0169m\). The flat plate dimensions span \(10D_j\) axially and \(24D_j\) in the spanwise direction. To mitigate strong scattering effects from the leading and side edges, the nozzle exit was positioned \(3.5D_j\) downstream of the leading edge and is located at the mid-span. The jets are considered in static conditions so that there is no flow over the flat plate. The jet installation set-up is such that an axial distance from the jet exit plane to the trailing edge of the plate is \(L/D_j=6.5\), and the plate is positioned at a vertical distance of \(H/D_j=2\) from the jet centreline in a linear hydrodynamic jet region or outside the jet plume.
For the purpose of the present computational study, in addition to the baseline round jet, only the SMC006 chevron nozzle is considered. Two jet upstream conditions are considered, which correspond to the jet acoustic Mach numbers 0.5 and 0.9. For the Mach 0.5 jet, the corresponding total pressure and stagnation temperatures are 121,286 Pa and 273.74 K, while for Mach 0.9 the corresponding stagnation pressure and temperature are 188,566 Pa and 292.31 K. In all cases, the ambient pressure and temperature are \(P_{\infty }\)=101,325 Pa, \(T_{\infty }\)=288.15 K. Figures 1 and 2 illustrates the nozzle geometries and the setup of acoustic microphones for the installed jet case. The measurements are taken on the reflected side of the flat plate at a distance of 95 nozzle diameters from the nozzle exit. The observer polar angle is defined with respect to the jet downstream flow axis.
2.2 GPU CABARET LES Solver
Flow solutions of the isolated and installed jet cases are performed with the Wall Modelled LES method based on the Compact Accurately Boundary-Adjusting High-Resolution Technique (CABARET) (Faranosov et al. 2013; Semiletov and Karabasov 2018; Markesteijn and Karabasov 2019; Markesteijn et al. 2020). CABARET is a low-dispersion and low-dissipation finite-volume scheme for solving unsteady gas dynamics equations. As detailed in Semiletov and Karabasov (2013, 2014), an explicit asynchronous time-stepping algorithm is utilised to time-march the flow solution in an optimal manner with a Courant-Friedrichs-Lewy (CFL) number of CFL=0.5, which corresponds to exact solutions for the linear advection equation. The algorithm employs a hierarchy of local time steps that are distributed in several update groups in accordance with the cell sizes, making the algorithm highly efficient for non-uniform meshes. In the current LES calculations, 8 time update groups of the asynchronous time-stepping method were used, thereby covering a \(2^7=128\) range in terms of the time scale ratio between the smallest and largest grid cells. A wall model algorithm was implemented following the work of Park (2015). Within this algorithm, the cell-centred values of velocity (and density) are calculated at each time step within the boundary layer mesh. These computed values are then supplied to the wall model, which calculates the wall shear stress. This wall shear stress serves as the boundary condition for the LES calculation at the wall. The wall model is based on the algebraic method and uses Reichardt’s law, as described in Mukha et al. (2019). This law of the wall provides a relationship between the local \(u^+\) and \(y^+\) at the wall and assumes that the instantaneous velocity can be used as input for the wall law. The resulting nonlinear algebraic equation for the velocity profile is solved through a simple Newton iteration, yielding the wall shear stress. The CABARET LES solver is implemented on Graphics Processing Units (GPUs) with a low memory footprint to avoid computational bottlenecks due to GPU processes competing for the same memory. This implementation leads to a notable increase in computational speed in comparison with standard jet LES solvers.
2.3 Mesh Generation
The LES mesh for both isolated and installed jet cases was generated using the snappyHexMesh utility in OpenFOAM. Within this mesh generation method, the grid around the nozzle and plate geometry (for installed jets) was covered by a Cartesian grid. Near the wall boundaries, body-fitted hexahedral layers were added with controlling the layer thickness within an automated meshing procedure to merge the near-field body-fitted grid to the outer Cartesian mesh. During this process, the distance between the centre of the wall-nearest control volume and the boundary was maintained within predefined limits. The mesh topology was designed with a template prescribing several areas of grid refinement in the jet shear layers and the potential core.
The spatial domain of the numerical mesh encompassing both isolated and installed configurations spans from \(10 D_{j}\) upstream of the nozzle exit to \(100 D_{j}\) in the axial direction, and within a range of \(\pm 30 D_{j}\) in the vertical (y) and lateral (z) directions. The meshing topology incorporates six refinement zones, outlined in Fig. 3a and b. The location of these zones, in terms of the axial (x), vertical (y), and span-wise sizes (z), are detailed in Table 1 for the SMC000 and SMC006 mesh configurations. In these regions, Zone 1 corresponds to the early shear layers starting from the nozzle exit and extending \(2 D_j\) axially for \(\textrm{SMC000}\) nozzle and \(1.5 D_j\) for SMC006. Zones 2 and 3 denote areas where the jet’s potential core is prominent, while Zones 4 to 6 represent far-field regions.
The grid resolution \(dx/D_j\), \(dy/D_j\) and \(dz/D_j\) in each defined zone are adjusted to resolve relevant spatial and temporal (due to the use of the asynchronous time-stepping algorithm) scales of coherent flow structures. The resolution is coarsened from Zone 1 to 6, as shown in Fig. 3. Notably, the LES grid in Zones 1–3 is almost isotropic to properly resolve the 3D structure of developing jet shear layers. The grid in Zones 2–5 is kept sufficiently fine to resolve acoustic waves in the region around the jet, where acoustic control surfaces of the Ffowcs Williams and Hawking (FW–H) method are placed. The same mesh refinement strategy is applied for both the medium and the fine LES mesh considered for the isolated and installed, round, and chevron jet configurations.
2.3.1 Isolated Jet
The isolated round jet SMC000 was simulated at two grid resolutions: 40 and 110.7 million cells. On both grids, the resolution in Zone 1 (Fig. 3a) is \(dx/D_{j}=dy/D_{j}=dz/D_{j}\approx 0.006\). The refined LES mesh, consisting of 110.7 million cells, differs from the 40 million grid through a twice denser mesh in terms of the dx, dy, and dz in Zones 4 to 6 to better resolve the end of the jet potential core region. In particular, for numerical wave resolution of 8 points per acoustic wavelength (p.p.a.w.), the maximum resolved Strouhal number near the nozzle exit for the 40 million LES grid corresponds to \(St=9\), and the resolution up to \(St=2\) is achieved near the end of the jet potential core. For the 110.7 million LES grid, the resolution in the end of the jet potential core is increased to \(St=4\), while remaining the same grid density near the nozzle exit.
For the isolated chevron SMC006 jet, medium-fine 40 and fine 85 million cell LES were generated. The initial shear layers of the chevron jets are thicker in comparison with the round jets, hence the grid resolution at the nozzle lip of \(dx/D_{j}=dy/D_{j}=dz/D_{j}=0.01\) was deemed sufficient in this case. For both nozzles, to correctly represent the boundary layer profile upstream of the nozzle exit, the grid layers at the nozzle lip were adjusted to have 8 grid cells per boundary layer thickness, with the first off-the-wall cell corresponding to \(y^{+}\approx 60\). Assuming the numerical wave resolution of 8 points per acoustic wavelength (p.p.a.w.) in the FW–H surface region, the maximum resolved Strouhal number near the chevron nozzle corresponded to \(St=6\) and \(St=3\) near the end of the jet potential core for the 40 LES grid. Again, the resolution of the 85 million cell LES grid was twice finer and corresponded to \(St=6\). The improved resolution in the end of potential core region of the chevron jet in comparison with the round jet is due to a shorter potential core in the former case, where the end or the jet is located in a more refined mesh zone. Locations of the grid refinement zones around the round and chevron nozzles are shown in Fig. 4.
2.3.2 Installed jet
Two computational grids were generated for the installed SMC000 jet case, comprising 40 million and 125.8 million grid cells, respectively. The grid topology near the nozzle and in the downstream region was similar to that of the isolated SMC000 nozzle, with details presented in Fig. 3a and Table 1, and the corresponding zones depicted in Fig. 4. For the installed round jet on the 125.8 million cell mesh, in addition to the factor of two grid refinement in Zones 4–6 similar to the fine grid for the isolate nozzle, the grid cell sizes in zone 1 were reduced by another factor of two to reach \(dx/D_{j}=dy/D_{j}=dz/D_{j}\approx 0.003\), where the wall-normal cell size is closer to the grid refinement near the flat plate surface.
For the installed chevron jet SMC006, the medium-course and fine LES grids around the nozzle were the same as those generated for the isolated cases with the total cell count of 40 and 98 million cells, respectively. Similar to the grid setup for the installed round jet, the grid resolution in Zone 1 of the refined mesh for the installed jet case was also increased by a factor leading to \(dx/D_{j}=dy/D_{j}=dz/D_{j}=0.005\).
The grid on the flat-plate was generated with placing prism layers on the wall surface. The maximum thickness of the prism layer was set to \(0.06D_j\), and the expansion ratio of the cells from the plate wall surface to the outer prism layer was set to 1.4. Two resolutions for the flat plate grid were examined, involving 4 and 10 prism layers per the prism layer thickness. After the initial examination, it was noted that employing LES models with either 4 or 10 grid cells per the prism layer thickness did not yield any significant difference in the computed far-field noise spectra up to \(St=2\) relevant for the current jet-surface interaction noise study. Consequently, the LES grids with 4 grid layers per boundary layer thickness were employed to simulate the installed jet flow cases in all production runs reported in this publication.
For all considered jet cases, characteristic non-reflecting boundary conditions were used at all open-domain boundaries. The inlet boundary inside the nozzle was specified four nozzle diameters upstream of the nozzle exit, where the corresponding total pressure and temperature conditions were imposed to provide the required mass flow rate in accordance with the target acoustic Mach number. No turbulence measurements were available at the nozzle exit from the experiment, hence, similar to the previous CABARET LES of SMC000 jets by Markesteijn and Karabasov (2018), no synthetic turbulence inflow condition was imposed in the nozzle to avoid ambiguity. Notably, this strategy relies on a fast flow transition to turbulence in the jet early shear layers, which are known to be very thin for the SMC000 nozzle at considered jet Mach numbers 0.5\(-\)0.9.
2.3.3 Details of LES Runs and Computational Requirements
All simulations were initially run for a period of 300 convective time units to facilitate the initial-solution spin-out to a statistically stationary state. Here, a convective time unit, denoted as TU is defined as the characteristic time based on the nozzle exit diameter and the jet velocity at the nozzle exit, expressed as \(TU=\frac{\Delta t.U_{j}}{D_{j}}\), where \(\Delta t\) represents the physical flow through time of the numerical simulation.
After the initialisation, the production runs were performed for at least 1100 TUs to ensure sufficient statistical convergence. The computations were performed on JADE-2, which is a high-performance GPU computing facility equipped with NVIDIA TESLA V-100 (32GB) GPU cards. The simulations for both isolated and installed jets on 40 million LES grids were run on a single GPU card, while the fine grid simulations were performed on 2 GPUs to fit in the memory requirements. Computational run times for all performed GPU LES cases are summarised in Table 2.
3 Far-field Noise Modelling
This section outlines the method to compute the far-field noise for isolated and installed jet flows by first combining the LES flow solutions with the Ffowcs-Williams - Hawkings method and then the edge-scattering noise propagation model of Lyu and Dowling (2018).
3.1 Ffowcs Williams—Hawkings Models
In the first approach, the LES solution including velocity vector, density, and pressure were stored on a designated set of acoustic integration surfaces in accordance with required input for the retarded time formulation of the Ffowcs Williams–Hawkings (FW–H) method (Najafi-Yazdi et al. 2011) for far-field noise computation. Here, two variants of the FW–H method were considered: the permeable and impermeable formulations.
In the permeable FW–H formulation, the acoustic control surfaces were placed around the jet to confine all major noise sources such as turbulence-turbulence and jet pressure waves/flat plate interactions. To exclude numerical artefacts in the far-field acoustic predictions, such as caused by vorticity waves crossing the integration surfaces (Shur et al. 2005; Najafi-Yazdi et al. 2011), and following the previous jet LES CABARET calculations by Gryazev et al. (2023), 16 closing discs were used downstream of the end of the jet potential core. For the installed jets, in addition to the closing discs, several control integration surfaces confining the jet and a part of the flat plate were used. The locations of the FW–H surfaces around the isolated and installed jets are illustrated in Figs 5 and 6. The resulting far-field noise signal was computed as an average of noise predictions obtained using each of the individual control surfaces.
Additionally, for all installed jet cases, a second variant of the FW–H method was employed using the impermeable surface formulation. Here a single acoustic integration surface was selected to coincide with the flat plate wall, thereby only including the pressure fluctuations on the flat plate surface as the effective far-field noise sources. The comparison of the solutions of the permeable and the impermeable FW–H method formulations is useful for separating the contribution of volume jet noise from the jet-surface interaction effects. For unheated jets, such as considered in the current study, the former correspond to pure jet mixing, or turbulence-turbulence interaction noise, while the latter, predominantly, due to the interaction of jet pressure waves with the plate trailing edge, is associated with dipole noise.
3.2 Hydrodynamic Pressure Trailing Edge Scattering Model
In Lyu and Dowling (2018), an edge-scattering jet installation noise model was developed along the lines of the Amiet trailing edge noise theory. Unlike the planar boundary layer interacting with a semi-infinite plane originally considered by Amiet (1976), the acoustic source in the Lyu and Dowling (2018) model corresponds to the trailing edge scattering of azimuthal modes of the jet near-field hydrodynamic pressure. The flat plate is assumed to be located in a linear hydrodynamic region of the jet, so that the jet flow does not interact with the plate surface directly. Following this, the jet installation noise is modelled as dipole noise due to scattering of linear pressure waves, emanating from the jet, by the flat plate trailing edge, using the theories of Curle (1955).
Assuming that the far-field observer is located in mid span \(z=0\), the general expression for the farfield acoustic pressure \(S_{pp}\) at frequency \(\omega \) is given by:
where \(c_{o}\) is the speed of sound, \(U_{c}\) is the convection velocity of the hydrodynamic evanescent waves, \(\sigma \) is flow corrected far-field observation location defined as \(S_{0}^{2}=x^{2}+\beta ^{2}_{c}\left( y^{2}+z^{2}\right) \), \(\beta _{c}=\sqrt{1-M^{2}_{\infty }}\) is the compressibility correction. The coordinate x , y and z represents the observer coordinates in streamwise, vertical and spanwise direction of the jet-flat plate configuration. Additionally, \(\gamma _{c}\) signifies the radial decay function of hydrodynamic pressure, while H denotes the vertical distance between the nozzle exit and trailing edge of the plate.
In Eq. (1), \(\Pi _{s}(\omega , m)\) represents the azimuthal modal spectra characterising the near-field hydrodynamic pressure at radial frequency \(\omega \) and azimuthal mode m. As shown by Lyu et al. (2017), when the convection velocity of the hydrodynamic pressure does not depend on the mode number, the streamwise wave number, \(k_1=\omega /U_c\) is the same for each mode and the acoustic transfer function, \(\Gamma \left( c, \mu _{,} \mu _A\right) \) becomes independent of the azimuthal mode too. This simplifies the last term in the square brackets on the right-hand-side of Eq. (1), which involves \(\Pi _{s}(\omega , m)\) that can be evaluated as:
where \(K_{m}\) is defined as is the \(m-\)th modified Bessel function of the second kind and \(\Pi _{o}(\omega , m)\) is \(m-\)th harmonic single sided power spectral density measured at \(r_{0}\).
Previously, Lyu et al. (2017) demonstrated that the zeroth pressure mode is sufficient for capturing the jet installation noise of a round jet at M=0.5. However, the jet installation noise effect of the higher order azimuthal modes at Mach number 0.9 for chevron jets especially remained unexplored. Hence, in this work, the LES solutions obtained for different Mach numbers for the round and chevron nozzles are implemented with the Lyu and Dowling model using Eq. (1). For each mode, the pressure solution component from LES is used to compute the pressure spectrum \(\Pi _{o}(\omega , m)\), the radial decay function \(\gamma _c\), and the convection velocity \(U_c\). To compute the azimuthal mode spectrum, LES pressure–time signals are interpolated to a uniform cylindrical grid in the jet volume extending from \(x =1D_{j}\) to 16\(D_{j}\) downstream of the nozzle exit, with intervals (\(\Delta {x}/D_{j}\)) set at 0.1, corresponding to \(i=1,...,151\) points in the axial direction. The radial dimension of the grid ranges from \(r = 0.5 1D_{j}\) to \(r = 2.51D_{j}\), with intervals defined by (\(\Delta {r}/D_{j}\)) = 0.1, corresponding to \(j=1,..,101\) points. In the azimuthal direction, \(N_{\theta }\)=64 points are sampled with \(\Delta {\theta }=56.25\) degrees. The numerical calculation of the azimuthal pressure mode spectrum from LES is summarised as follows: First, the hydrodynamic pressure fluctuations are calculated in each cylindrical grid point \((x_i, r_j)\), \(p^{\prime }=p-\langle p \rangle \), where p is instantaneous pressure and \(\langle p \rangle \) is the local time-average. This is followed by the discrete Fourier transform in the azimuthal direction to extract the cylindrical modes,
Having transformed the pressure time signal to the frequency domain, the power-pectral density of each pressure mode is given by
The reference point is selected to coincide with the flat plate trailing edge, which in the case of the Bristol experiment corresponds to \(r=H=2D_{j}\) and \(x=L=6.5D_{j}\). In addition, the radial decay function \(\gamma _{c}\), is calculated in accordance with
where \(k_{1}\) is axial convective wave number defined as:
In the above, the frequency-dependent convection velocity, \(U_c(\omega )\) is computed from LES for each pressure mode to verify the assumption of convection velocity independence across modes for each jet case. The LES-informed implementation of the Lyu and Dowling model is then used to probe the sensitivity of far-field noise spectra predictions to higher order azimuthal modes for the installed round and chevron jets at acoustic Mach numbers 0.5 and 0.9.
4 Results and Discussion
4.1 Jet Velocity Solutions
Comparisons of the computed radial time-averaged and root-mean-square (RMS) profiles of the axial velocity with the experimental data for the isolated and installed SMC000 jets are shown in Figs. 7 and 8.
The experimental data correspond to the Particle Image Velocimetry (PIV) measurements performed by NASA (Brown 2015) for the isolated SMC000 jet at the same acoustic jet Mach number. Since the plate in the configuration of Jawahar et al. (2021) was located away from the jet, there is no difference between the isolated and installed jet flow solution profiles. While the NASA data correspond to a larger nozzle diameter (\(D_{j}\)=0.0508m) in comparison with the Bristol experiment (\(D_{j}\)=0.01693m), there is no appreciable difference expected between the isolated jet flows issuing from the same geometry nozzles at Reynolds numbers larger than \(\approx 300,000\) in line with the previous jet LES experience (Markesteijn and Karabasov 2018).
The mean flow velocity profiles of both the isolated and installed jets, obtained at fine grid resolutions of 110.7 million and 125.8 million cells, agree well with each other and align closely with experimental data across all distances from the nozzle exit. For the turbulent velocity fluctuation profiles, discrepancies between the isolated and installed flow solutions emerge near the nozzle exit, attributed to a higher grid density in this region of the 125.8 million cell LES grid. However, starting from a distance of \(x/D_{j}=2\), both the fine-grid installed and isolated jet LES solutions are in good agreement with each other, as well as with the measurements up to \(x/D_{j}=8-10\).
The medium-fine LES solutions at the 40 million cell resolution for the isolated and installed jet cases are in encouraging agreement with one another and the experiment within the main part of the jet potential core region up to \(x/D_{j}\)=4–6. Within the same jet region, both LES models reasonably well predict the mean flow velocity and turbulent velocity fluctuation profiles. Larger discrepancies between the two LES solutions and the experiment, which are especially notable downstream of \(x/D_{j}\)=6-8, are attributed to insufficient LES grid resolution at larger distances from the nozzle exit.
Overall, the above results suggest that the medium-fine LES grid resolution of 40 million should be sufficient to capture the major jet installation features, which are driven by relatively large-scale sources within the jet potential core region. A similar conclusion has been reached regarding the chevron SMC006 nozzle, where LES flow solutions on 40 million cell grids were compared against isolated and installed jet solutions employing 85 million and 98 million cells, respectively.
4.2 Pressure Solutions in the Linear Hydrodynamic Field
The near-field hydrodynamic pressure waves generated in the jet provide an effective source of jet installation noise due to the scattering by the trailing edge. Figs 9a and b visualise instantaneous pressure waves around the isolated and installed jet for the same acoustic Mach number, M=0.5. In comparison with the isolated jet, an additional source of acoustic waves can be noted at the plate trailing edge in the installed jet case. The acoustic waves generated by this source tend to propagated at large angles to the jet flow and are particularly prominent on the reflected side of the plate.
Figure 10 presents a comparison of the pressure spectra within the linear hydrodynamic field region. This comparison is between the LES solution for the isolated jet using a 40 million cell grid, and the experimental data on the reflected side of the plate, as obtained by Jawahar and Azarpeyvand (2022). The comparison includes results from both SMC000 and SMC006 nozzles at Mach numbers of 0.5 and 0.9. The hydrodynamic pressure measurements from the isolated jet experiment were conducted at two locations: near the flat plate trailing edge for the installed jet case at \(x/D_{j}=6.0, r/D_{j}=2.0\), and further downstream above the evolving shear layer in the self-similar jet region at \(x/D_{j}=14.0, r/D_{j}=3.0\).
It can be noted that the LES solution captures the shift of the peak of the hydrodynamic pressure spectrum to low frequencies with an increase of the jet velocity and an increase of the probe distance from the nozzle exit. The shift to low frequencies can be explained by an increase of the characteristic scales of the spatial-temporal coherent structures further downstream in the jet flow and also with an increased phase velocity of the higher Mach number jet.
For the \(x/D_{j}=6.0\) location, the LES prediction of the hydrodynamic pressure spectrum of the round jet is within 2dB from the experiment up to Strouhal numbers, \(St=\frac{\ fD_{j}}{U_{j}}=0.7-1\) for the \(M=0.5\) jet and \(St=0.4-0.6\) for the \(M=0.9\) jet. For the chevron jet at the same location, the LES resolves frequencies up to \(St=0.3-0.4\) for M=0.5 and \(St=0.2-0.3\) for \(M=0.9\). In all cases, even for the probe location in the self-similar jet region, \(x/D_{j}=14.0,~r/D_{j}=3.0\), the range of resolved frequencies of the hydrodynamic pressure from LES always larger than the frequencies relevant for jet-installation noise, \(St\approx 0.1\).
Figure 11 further compares the near-field hydrodynamic pressure spectra of the isolated and installed M=0.5 round jets. These spectra virtually overlap for a range of probe locations, \(x/D_{j}=2-6,~r/D_{j}=2\). The observed agreement indicates that not only the jet flow and turbulence remain unaffected by the considered flat plate installation but also the linear hydrodynamic waves emanated from the jet. Consequently, it can be inferred that the pressure field scattered by the flat plate trailing edge is a small byproduct of the incident evanescent pressure waves at the plate trailing edge location.
4.3 Far-field Noise Predictions
In this section, the results of the far-field noise spectra predictions for the isolated and installed SMC000 and SMC006 jets are presented. The acoustic results were obtained by coupling the LES solutions on 40 million cell grids with the FW–H method and compared with the acoustic microphone measurements in the Bristol experiment in terms of the Sound Pressure Levels (SPL),
4.3.1 Isolated Jet Noise
Figure 12 compares the predicted far-field noise spectra for isolated jets at Mach numbers 0.5 and 0.9 using the permeable FW–H formulation, which includes all noise sources. It can be seen that the noise spectra solutions are in good agreement with the experiment for both Mach numbers and a range of polar angles. In particular, for the round nozzle, the agreement with the experiment is within 2dB within a range of frequencies corresponding to Strouhal numbers from St= 0.03 to 1.5-2. For the chevron jet at \(M=0.5\), the current noise predictions are within 2–3dB in comparison with the experiment for frequencies corresponding to \(0.05< St < 1.5\).
It can be noted that for the round jet, the peak frequency of the noise spectra correspond to \(St=0.2-0.3\) in accordance with the standard jet mixing noise behaviour. At the same time, for the chevron jet at \(M=0.5\), the peak Strouhal number is shifted towards higher frequencies \(St=0.3-0.5\), consistent with the expected effect of the chevron nozzle to reduce jet noise at low frequencies. In most cases, the LES-FW–H solutions capture the peak noise frequency in agreement with the experiment.
For the high-speed chevron jet case at \(M=0.9\), the LES-FW–H solutions are in excellent agreement with the experiment for low frequencies. However, at high frequencies, the good agreement of the LES-FW–H predictions with the acoustic measurements is limited to \(St=0.8-1\), beyond which the experimental data show a rise, thereby leading to a flattening of the overall noise spectra with a broad peak shifted to around \(St=1\) for high observer angles. It should be pointed out that the unusual shape of the experimental noise spectra of the isolated round and chevron jets at \(M=0.9\) is due to the insufficient frequency resolution of the far-field microphones, used in the series of experiments by Jawahar et al. (2021). Hence, the differences with the LES results at frequencies \(St=1-2\) in this case can be attributed to the limitation of the experiment.
Overall, the above findings suggest that the considered LES grid resolution of 40 million cells is sufficient for the FW–H method to accurately capture jet mixing noise within frequencies \(St=0.05-1\), which is well beyond the range relevant for jet installation noise for all considered jet cases.
4.3.2 Installed Jet Noise
Comparison of the far-field noise spectra predictions for installed SMC000 and SMC006 jets with the experiment at Mach numbers 0.5 and 0.9 at observer angles of 30, 60, and 90 degrees. The datasets corresponding to different angles are offset by 30dB for clarity. Predictions of both permeable (PERM) and impermeable (IMPERM) control surface formulations of the FW–H method are included
Figure 13 shows results of the noise spectra predictions for installed jets in comparison with the experiment. The agreement between the permeable FW–H solutions with the experiment is within 2dB for all observer angles across the frequency range from \(St=0.03-0.4\) to \(1.5-2.0\). At the same time, the range of accuracy of the impermeable FW–H solutions, which exclude the effect of volume sources typical of jet mixing noise, is limited to low-mid frequencies and high observer angles. This is in agreement with the fact that jet mixing noise dominates over jet installation noise at high frequencies and shallow angles to the jet flow axis.
It can be noted that in comparison with the isolated jets (Fig. 12), the installed jets exhibit a significant noise amplification at low frequencies, \(St=0.08-0.1\) and high observer angles, in agreement with the previous experimental results in the literature (Head 1976). The amplification is attributed to additional noise generated due to the interaction between the hydrodynamic field of the jet and the plate trailing edge.
From comparison of the results for the round and chevron jets, it can be seen that the low-frequency noise amplification due to the installation effect is about 14–16 dB for the lower Mach number case, \(M=0.5\). For \(M=0.9\), the jet installation noise delta is reduced to 4–6 dB due to the increased effect of quadrupole-type turbulence-turbulence interactions, whose acoustic power rapidly increases at high acoustic Mach numbers, in accordance with Lighthil’s scaling law \(U_j^{8}\) of jet mixing noise (Semiletov and Karabasov 2017).
4.4 Trailing Edge Scattering Noise
The LES near-field pressure solution is substituted into the jet-installation model of Eq. (1) to analyse the far-field noise due to the mechanism of hydrodynamic pressure wave scattering by the plate trailing edge. The LES data were interpolated on a uniform cylindrical grid array as discussed in the methods section. Six azimuthal pressure modes were calculated, which were used to represent the incident pressure waves in Eqs (1), (2), (3), (4).
In accordance with Eqs (5), (6), and Lyu et al. (2017), the frequency-dependent convection velocity of the near-field pressure was computed for each azimuthal pressure mode for all nozzle geometries and Mach numbers. The LES data were analysed at the spatial location of the scattering edge, i.e. the trailing edge of the plate, \(x/D_{j}=6.5\) and \(r/D_{j}=2\).
Figure 14 shows the frequency-dependent convection velocity computed for SMC000 and SMC006 nozzles for first three modes at \(M=0.5\). The convection velocity increases with increasing the frequency and gradually converges to a constant at Strouhal numbers larger than 0.18. Different azimuthal modes correspond to a very similar behaviour of the convection velocity as a function of frequency. Trends obtained for the convection velocity of the chevron jet closely resembles those of the round one. The latter suggests that, despite the differences introduced by chevron due to breaking the symmetry of early shear layers of the round jet, the low-frequency pressure waves propagating to \(x/D_{j}=6.5\), \(r/D_{j}=2\) from the end of the potential core of both jets were generated by similar coherent flow structures.
After non-dimensionalising the convection velocity with respect to the jet velocity at the nozzle exit, it was found that the same dimensionless convection velocity function applies for the Mach 0.9 jets too.
The above results are in agreement with the previous experimental measurements reported in Kerhervé et al. (2006), who found that the convection velocity only weakly depends on the Mach number and stagnates to a constant at high frequencies.
Upon substituting the axi-symmetric pressure mode solution and the convection velocity at the plate trailing edge to the far-field noise model of Lyu et al. (2017), noise spectra predictions for the round and chevron Mach 0.5 and 0.9 jets are obtained. Results of the acoustic predictions for the 90 degree observer angle are shown in Fig. 15.
For the round jet, the LES-informed edge scattering model of the installed is able to predict the jet installation noise within 2dB in comparison to the experiment and the FW–H method solutions for all frequencies up to \(St=0.2-0.3\) for all Mach numbers and nozzle geometries considered. For the installed chevron jet, the agreement between the model predictions and the experiment (as well as the FW–H solutions) is less good for frequencies lower than St=0.06, where some 4–6dB noise amplification can be observed. Importantly, the edge-scattering model completely fails to predict high frequency noise in agreement with results reported in Lyu et al. (2017). At the same time, it can be noted that the impermeable surface solution of the FW–H model based on the same LES solution for the fluctuating pressure on the flat plate surface is in excellent agreement with the experiment for all frequencies and both jet Mach numbers. Since both the edge-scattering model and the FW–H model based on the impermeable surface formulation exclude volume sources, the difference in their predictions can be attributed to several factors such as: (1) the limitation of the Amiet’s (Amiet 1976) acoustic transfer function, which is known to lead to a rapid roll-off of the trailing edge noise spectra at high frequencies and (2) the induced effect of high-frequency quadrupole noise, which correspond to the acoustic waves generated at high angles to the jet flow and reflected from the flat plate surface upstream of the trailing edge. Some underprediction of high-frequency noise of the Lyu et al. (2017) model can also be associated with the contribution of high-order azimuthal modes excluded from the results of the edge-scattering model shown in Fig. 15, especially in the chevron jet case.
To further understand the effect of higher-order azimuthal models in the chevron jet case as well as the contribution of high-frequency jet mixing noise due to the pressure waves reflected from the flat plate surface, Fig. 16 compares predictions of the edge-scattering model for the first axi-symmetric mode, \(m=0\) only and the same for the first six pressure modes, \(m=0-5\) for the chevron and round installed jets at \(M=0.5\). The experimental results for the installed and isolated jets at the same conditions are also included in the plots for comparison.
Furthermore, It is noteworthy that the effect of higher-order azimuthal pressure modes for both the round and chevron jet is fairly marginal: the differences between the six-mode and the zero-mode solutions do not exceed 2–3dB. The lack of sensitivity for the chevron jet can be explained by the nature of low-frequency pressure waves, which are generated in the downstream part of the jet by largely axi-symmetric coherent structures propagating at a phase velocity similar to the round jet as discussed in the previous section. Secondly, it can be seen that despite the large amplification at low frequencies, the effect of jet installation in comparison with the isolated jet noise at high frequencies does not exceed 2 dB. This confirms that the high-frequency noise in predictions of the FW–H method based on the impermeable control surface is largely due to the wall pressure fluctuations induced by the quadrupole noise. Altogether, this underscores the predominant role of the axisymmetric pressure mode for low-frequency noise amplification of jet installation noise regardless of the jet Mach number and nozzle geometry.
5 Conclusion
Wall Modelled Large Eddy Simulations (LES) of isolated and installed jet flows using the high-resolution CABARET method accelerated on Graphics Processing Units have been performed for conditions corresponding to the University of Bristol experiment. The considered configurations include round and chevron nozzles corresponding to (3:1) versions of the NASA SMC000 and SMC006 nozzle geometries. Two acoustic Mach numbers, \(M=0.5\) and \(M=0.9\) are considered. For the installed case, a flat plate installed parallel to the jet in its linear hydrodynamic region is considered. The LES flow solutions are first analysed in terms of the grid sensitivity on meshes of 40–120 million cells, using the NASA PIV data for meanflow velocity and turbulent velocity fluctuations for the round jet as a reference. It is shown that the LES solutions are in encouraging agreement with the NASA data including the medium-fine LES grids of 40 million cells. In addition, the pressure spectra extracted from the LES solutions of the round and chevron jets in several locations of the linear hydrodynamic region are shown to agree with the University of Bristol measurements within 2dB for all frequencies relevant for jet installation noise. By comparison with the isolated jet solutions, it is also shown that, for the considered installation configuration, the effect of the flat plate on the jet flow and turbulence as well as the linear hydrodynamic field is negligible.
For far-field noise modelling, two approaches have been implemented. First, the LES solution is coupled with the Ffowcs Williams–Hawkings (FW–H) method, where both permeable and impermeable control surface formulations have been considered. Secondly, the LES solution is coupled with the edge scattering model of Lyu and Dowling based on the Amiet trailing edge noise theory. For the permeable-surface FW–H method, which fully includes all noise sources, a 2dB agreement with the round jet measurements up to \(St=1.5-2\) and a \(2-3\)dB agreement with the chevron jet experiment up to St=1–2 is reported for all observer angles and frequencies. The less good agreement with acoustic measurements at the high frequencies for the high Mach number chevron jet, which corresponds to an enhanced high-frequency noise spectrum, is attributed to the resolution limitation of the microphones used in the experiment in this case. The LES solution capture main features of the jet installation noise such as the strong low-frequency noise amplification in comparison with the isolated jet and the Mach number effect. While accurate for high observer angles, the acoustic predictions of the impermeable-surface FW–H method at shallow angles underestimate jet noise in accordance with the volume noise sources, whose contribution is mostly missing from the impermeable-surface formulation.
For implementation of the edge-scattering jet installation model, the LES pressure solution was interpolated on a cylindrical grid, and the corresponding amplitudes and convection velocities of first six azimuthal pressure modes were calculated. In agreement with the previous literature, the phase velocity dependence on frequency was shown to be largely independent of the mode and Mach number. Furthermore, it was shown to be the same in the round and the chevron jets. By using just the first axi-symmetric pressure mode, the far-field noise spectra predictions of the edge-scattering model at 90 degrees to the jet flow are found it capture the low frequency jet installation noise within 2dB for all Mach numbers and jet geometries considered. However, the model fails to resolve the high frequency noise, which was accurately predicted using the same LES dataset with either permeable or impermeable FW–H method. To further analyse the discrepancies at high frequencies, predictions of the edge-scattering model using just the first axi-symmetric mode and the same for the first six azimuthal modes are compared with the experimental measurements of the same round and chevron jets at Mach number 0.5. It is concluded that the edge-scattering model predictions are virtually independent of the high-order azimuthal modes due to the nature of low-frequency pressure waves, which are generated in the downstream part of the jet by largely axi-symmetric coherent flow structures. These structures have similar phase velocities for both chevron and round jets. In comparison with the edge-scattering model, noise predictions of the FW–H method based on the impermeable control surface coinciding with the flat plate include the pressure fluctuations due to the incident waves reflected by the hard wall, hence, incorporate the quadrupole noise effect at high frequencies. An important conclusion of this study is that the axisymmetric pressure mode may have a predominant role for the low-frequency noise amplification of jet installation noise not only for low Mach number round jets but also for Mach 0.9 jets and chevrons with a large penetration angle like SMC006.
References
Abid, H.A., Markesteijn, A.P., Karabasov, S.A.: Trailing edge noise modelling of flow over NACA airfoils informed by LES. https://doi.org/10.2514/6.2021-2233
Abid, H.A., Stalnov, O., Karabasov, S.A.: Comparative analysis of low order wall pressure spectrum models for trailing edge noise based in Amiet Theory. https://doi.org/10.2514/6.2021-2231
Amiet, R.: Noise due to turbulent flow past a trailing edge. J. Sound Vib. 47(3), 387–393 (1976). https://doi.org/10.1016/0022-460X(76)90948-2
Bridges, J., Brown, C.: Parametric testing of chevrons on single flow hot jets. https://doi.org/10.2514/6.2004-2824
Brown, C.: Jet-surface interaction test: Far-field noise results. Technical Memorandum NASA/TM–2015-218089, NASA (2015). https://ntrs.nasa.gov/api/citations/20150006729/downloads/20150006729.pdf
Chintagunta, A., Naghibi, S., Karabasov, S.: Flux-corrected dispersion-improved CABARET schemes for linear and nonlinear wave propagation problems. Comput. Fluids 169, 111–128 (2018). https://doi.org/10.1016/j.compfluid.2017.08.018
Curle, N.: The influence of solid boundaries upon aerodynamic sound. Proceed. R. Soc. Lond. Series Math. Phys. Sci. 231(1187), 505–514 (1955)
Faranosov, G.A., Goloviznin, V.M., Karabasov, S.A., Kondakov, V.G., Kopiev, V.F., Zaitsev, M.A.: CABARET method on unstructured hexahedral grids for jet noise computation. Comput. Fluids 88, 165–179 (2013). https://doi.org/10.1016/j.compfluid.2013.08.011
Gryazev, V., Markesteijn, A.P., Karabasov, S.A., Lawrence, J.L.T., Proença, A.R.: Jet flow and noise predictions for the Doak laboratory experiment. AIAA J. (2023). https://doi.org/10.2514/1.J062365
Head, F.M.R.: Jet/surface interaction noise—analysis of farfield low frequency augmentations of jet noise due to the presence of a solid shield. https://doi.org/10.2514/6.1976-502
Jawahar, H.K., Azarpeyvand, M.: On investigating the hydrodynamic field for jets with and without installation effects. https://doi.org/10.2514/6.2022-2907
Jawahar, H.K., Azarpeyvand, M.: Trailing-edge treatments for jet-installation noise reduction. https://doi.org/10.2514/6.2021-2185
Jawahar, H.K., Baskaran, K., Azarpeyvand, M.: Unsteady characteristics of mode oscillation for screeching jets. https://doi.org/10.2514/6.2021-2279
Jawahar, H.K., Markesteijn, A.P., Karabasov, S.A., Azarpeyvand, M.: Effects of chevrons on jet-installation noise. https://doi.org/10.2514/6.2021-2184
Jawahar, H.K., Meloni, S., Camussi, R. Azarpeyvand, M.: Experimental investigation on the jet noise sources for chevron nozzles in under-expanded condition. https://doi.org/10.2514/6.2021-2181
Karabasov, S., Goloviznin, V.: Compact accurately boundary-adjusting high-resolution technique for fluid dynamics. J. Comput. Phys. 228(19), 7426–7451 (2009). https://doi.org/10.1016/j.jcp.2009.06.037
Kerhervé, F., Fitzpatrick, J., Jordan, P.: The frequency dependence of jet turbulence for noise source modelling. J. Sound Vib. 296(1), 209–225 (2006). https://doi.org/10.1016/j.jsv.2006.02.012
Lawrence, J., Azarpeyvand, M., Self, R.: Interaction between a flat plate and a circular subsonic jet. https://doi.org/10.2514/6.2011-2745
Lyu, B., Dowling, A.P.: Experimental validation of the hybrid scattering model of installed jet noise. Phys. Fluids (2018). https://doi.org/10.1063/1.5036951
Lyu, B., Dowling, A.P., Naqavi, I.: Prediction of installed jet noise. J. Fluid Mech. 811, 234–268 (2017). https://doi.org/10.1017/jfm.2016.747
Markesteijn, A.P., Karabasov, S.A.: CABARET solutions on graphics processing units for NASA jets: Grid sensitivity and unsteady inflow condition effect. Compt. Rendus Mécanique 346(10), 948–963 (2018). https://doi.org/10.1016/j.crme.2018.07.004. (Jet noise modelling and control / Modélisation et contrôle du bruit de jet)
Markesteijn, A.P., Karabasov, S.A.: Simulations of co-axial jet flows on graphics processing units: the flow and noise analysis. Philos. Trans. R. Soc. A. 377(2159), 20190083 (2019). https://doi.org/10.1098/rsta.2019.0083
Markesteijn, A.P., Gryazev, V., Karabasov, S.A., Ayupov, R.S., Benderskiy, L.A., Lyubimov, D.A.: Flow and noise predictions of coaxial jets. AIAA J. 58(12), 5280–5293 (2020). https://doi.org/10.2514/1.J058881
Mead, C., Strange, P.: Under-wing installation effects on jet noise at sideline. https://doi.org/10.2514/6.1998-2207
Mukha, T., Rezaeiravesh, S., Liefvendahl, M.: A library for wall-modelled large-eddy simulation based on OpenFOAM technology. Comput. Phys. Commun. 239, 204–224 (2019). https://doi.org/10.1016/j.cpc.2019.01.016
Najafi-Yazdi, A., Brès, G.A., Mongeau, L.: An acoustic analogy formulation for moving sources in uniformly moving media. Proceed. R. Soc. Math. Phys. Eng. Sci. (2011). https://doi.org/10.1098/rspa.2010.0172
Park, I.G.: Wall-modeled large-eddy simulation of a separated flow over the NASA wall-mounted hump. Annual Research Briefs Center for Turbulence Research. pp. 145–160 (2015)
Semiletov, V., Karabasov, S.: CABARET scheme with conservation-flux asynchronous time-stepping for nonlinear aeroacoustics problems. J. Comput. Phys. 253, 157–165 (2013). https://doi.org/10.1016/j.jcp.2013.07.008
Semiletov, V., Karabasov, S.: CABARET scheme for computational aero acoustics: extension to asynchronous time stepping and 3D flow modelling. Int. J. Aeroacoustics 13(3–4), 321–336 (2014). https://doi.org/10.1260/1475-472X.13.3-4.321
Semiletov, V., Karabasov, S.: Similarity scaling of jet noise sources for low-order jet noise modelling based on the goldstein generalised acoustic analogy. Int. J. Aeroacoustics 16(6), 476–490 (2017). https://doi.org/10.1177/1475472X17730457
Semiletov, V.A., Karabasov, S.A.: A volume integral implementation of the goldstein generalised acoustic analogy for unsteady flow simulations. J. Fluid Mech. 853, 461–487 (2018). https://doi.org/10.1017/jfm.2018.572
Shearin, J.G.: Investigation of jet-installation noise sources under static conditions. Tech. Rep. 2181, NASA (1983). https://ntrs.nasa.gov/api/citations/19830025413/downloads/19830025413.pdf
Shur, M.L., Spalart, P.R., Strelets, M.K.: Noise prediction for increasingly complex jets part i: methods and tests. Int. J. Aeroacoustics (2005). https://doi.org/10.1260/1475472054771376
Way, D., Turner, B.: Model tests demonstrating under-wing installation effects on engine exhaust noise. https://doi.org/10.2514/6.1980-1048
Williams, J.E.F., Hall, L.H.: Aerodynamic sound generation by turbulent flow in the vicinity of a scattering half plane. J. Fluid Mech. 40(4), 657–670 (1970). https://doi.org/10.1017/S0022112070000368
Acknowledgements
The authors would like to acknowledge the Engineering and Physical Sciences Research Council (EPSRC) for supporting this research (Grant No. EP/S000917/1 and EP/S002065/1). The work of Sergey A. Karabasov was also supported by the grants from the Russian Science Foundation (No.19-12-00256) and the Ministry of Science and Higher Education of the Russian Federation (Grant agreement of May, 17, 2022 No. 075-15-2022-1023) within the program for the creation and development of the World-Class Research Center “Supersonic” for 2020–2025. The authors further acknowledge the use of Tier-2 high-performance computing (HPC) facility JADE-2, funded by the EPSRC on the grant (EP/T022205/1) and Queen Mary’s Apocrita HPC facility, supported by QMUL Research-IT. http://doi.org/10.5281/zenodo.438045
Funding
The authors declare they have no financial interests.
Author information
Authors and Affiliations
Contributions
HAA: Conceived and designed the study, analyzed and interpreted the data, and drafted the first version of the manuscript. Sergey A. Karabasov: Conceived and designed the study, interpreted the data, and revised the manuscript for important intellectual content. APM: Assisted with meshing the geometry and the LES CABARET Solver. HK. J: Conducted experimental data acquisition, analyzed the data, and revised the manuscript for important intellectual content. MA: Revised the manuscript for important intellectual content.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Abid, H.A., Markesteijn, A.P., Karabasov, S.A. et al. Jet Installation Noise Modelling for Round and Chevron Jets. Flow Turbulence Combust (2024). https://doi.org/10.1007/s10494-024-00559-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10494-024-00559-x