Improved Prediction of the Flow in Cylindrical Critical Flow Venturi Nozzles Using a Transitional Model

Abstract

Critical flow Venturi nozzles (CFVNs) are a state-of-the-art secondary standard widely used for gas flow measurements with high precision. The flow rate correlates with the type and thickness of the boundary layer (BL) inside the nozzle throat. In the cylindrical type—one of the two standard designs of CFVNs—the nozzle throat encompasses a defined axial length in which the BL develops. This numerical study is concerned with the BL effects in a cylindrical CFVN by means of two turbulence models. Compared to experimental data, the k-$\omega$ SST model predicts the discharge coefficient well for high and low Reynolds numbers, but not in the intermediate regime. The $\gamma$-$Re_{\theta }$ model, on the contrary, agrees well with experimental data in the entire flow range. Relevant quantities and profiles of the BL are separately investigated in the laminar, turbulent, and transitional region. The calculated laminar and turbulent BL thicknesses correspond to predictions based on integral methods for solving the BL equations. Simple representations are proposed for the Zagarola-Smits scaled laminar and turbulent deficit BL profiles removing the effects of axial position, Reynolds number, and pressure gradient. Furthermore, the shape factor is investigated as a characteristic parameter for determining the transitional region.

1 Introduction

Critical flow Venturi nozzles (CFVNs) are a state-of-the-art secondary standard widely used for measuring the mass flow rate of gases with high precision (EN ISO 9300 2005). For a sufficiently high pressure ratio across the nozzle, the incoming flow accelerates to the local speed of sound at the nozzle throat, namely the critical velocity. Once the nozzle is operated at critical condition, the mass flow rate is only a function of the upstream stagnation pressure and temperature, the gas properties, and the effective area of the throat. The mass flow rate is typically expressed dimensionlessly by the discharge coefficient $C_D$, as described by the ratio of the actual mass flow rate $\dot{m}$ (measured or simulated) to the mass flow rate under ideal conditions $\dot{m}_i$:

$$\begin{aligned} C_D = \frac{\dot{m}}{\dot{m}_i}. \end{aligned}$$

(1)

The ideal mass flow rate $\dot{m}_i$ depicts the mass flow rate under ideal conditions (one-dimensional, isentropic flow of a perfect gas):

$$\begin{aligned} \dot{m}_i = C_i^* \frac{p_0}{\sqrt{R_M T_0}} \frac{\pi }{4} d^2 \quad \text {with} \quad C_i^* = \sqrt{\kappa \left( \frac{2}{\kappa +1}\right) ^{\frac{\kappa +1}{\kappa -1}}}, \end{aligned}$$

(2)

where $p_0$ and $T_0$ are the upstream stagnation pressure and temperature, $C_i^*$, $R_M$, and $\kappa$ are the critical flow function, the specific gas constant, and the ratio of specific heat capacities, and d is the nozzle throat diameter. Due to viscous effects, a boundary layer (BL) develops in the nozzle throat that decreases the effective area of the throat and thus leads to a reduction of the discharge coefficient. Furthermore, the $C_D$ value depends on the predominant BL type (laminar or turbulent) that is mainly a function of the Reynolds number Re that is defined with respect to the nozzle throat diameter d as follows:

$$\begin{aligned} Re = \frac{4 \dot{m}}{\pi d \mu _0}, \end{aligned}$$

(3)

where $\mu _0$ depicts the upstream stagnation dynamic viscosity. Thus, a detailed analysis of the BL development and the prediction of the laminar-to-turbulent transition inside the nozzle throat are crucial for the characterization of the flow and, hence, for a reliable prediction of the mass flow rate of CFVNs.

In the literature, the development of turbulent BLs and the transition process have been extensively studied experimentally and numerically under numerous flow conditions. Zagarola and Smits (1998) experimentally investigated turbulent BLs in fully developed pipe flows and established a new outer velocity scale $U_{ZS} = U_e \left( \delta _1 / \delta \right)$, where $U_e$, $\delta _1$, and $\delta$ denote the velocity at the edge of the BL, the displacement thickness, and the BL thickness, respectively. Castillo and Johansson (2002) conducted experimental studies on turbulent BLs in a zero-pressure gradient (ZPG) using the laser Doppler anemometry (LDA) measurement technique. They showed that the mean normalized velocity deficit profiles $(U_e - U)/U_e$ at all streamwise locations collapse for constant upstream conditions. Cal et al. (2009) extended the work of Castillo and Johansson (2002) by investigating turbulent BLs also under the influence of favorable pressure gradients (FPG) and rough walls. Comparing different velocity scales, the velocity scale by Zagarola and Smits (1998) (ZS scaling) was successfully removing the roughness and pressure gradient effects in the mean velocity deficit profiles. In a comprehensive self-similarity analysis, Gibis et al. (2019) investigated the characteristics of turbulent BLs with pressure gradients obtained from compressible and quasi-incompressible direct numerical simulation (DNS) data by Wenzel et al. (2019). Among different scalings investigated, the edge and ZS scalings were able to collapse the mean deficit profiles in terms of velocity, mass flux, and total enthalpy. Recently, Parthasarathy and Saxton-Fox (2023) performed an experimental campaign to study a flat-plate turbulent BL opposed to a sequence of a streamwise favorable and adverse pressure gradient (APG) by using a variable convex curvature panel. They observed that due to the rapid change in pressure gradients an internal BL can grow within the turbulent BL containing the peak turbulent production.

Abu-Ghannam and Shaw (1980) experimentally investigated natural transition of BLs for a flat plate at different freestream turbulence intensities and pressure gradients. Based on their results, they proposed empirical correlations for the prediction of the start and end of transition in terms of the momentum thickness Reynolds number $Re_{\theta }$. Taghavi-Zenouz et al. (2008) carried out wind-tunnel tests on a flat plate at ZPG and various freestream turbulence intensities to study the transitional behavior of the BL. They observed a considerable drop in the streamwise shape factor $H_{12}$ and a substantial increase in the skin friction coefficient within the transitional region. Further, they found that the velocity profile becomes noticeably distorted due to an increase in the momentum in the inner region and a decrease in the outer region of the BL.

The compressible, transonic flow through CFVNs is intricate due to the exposure to different types of pressure gradients (FPG, APG, and ZPG) influencing the BL in the streamwise direction. Further, CFVNs are operated in a wide range of Reynolds numbers (between $10^4$ and $10^7$), in which the BL transitions from laminar to turbulent within the nozzle throat. According to the ISO 9300 standard (EN ISO 9300 2005), two nozzle designs can be differentiated, the toroidal and the cylindrical nozzle. The toroidal nozzle has its critical diameter in one location, whereas for the cylindrical type, the nozzle throat encompasses a defined axial length (typically of one throat diameter d).

In recent years, most of the studies addressed toroidal CFVNs. Cruz-Maya et al. (2006) provided a theoretical and numerical correlation for the determination of the discharge coefficient for turbulent BLs in toroidal CFVNs. The deviation of the derived correlation from measured discharge coefficients was below 0.2 %. Ünsal et al. (2016) numerically investigated the transitional effects of the BL for toroidal-shaped CFVNs at different nozzle diameters using Reynolds-averaged Navier–Stokes (RANS) turbulence models. Their results were in good agreement with the well-established correlation curve for toroidal nozzles by Ishibashi (2015), namely the so-called sCurve, which is based on calibration data of high-precision nozzles. However, they predicted the transitional range at higher Reynolds numbers and observed a diameter dependency on transition onset. Wang et al. (2019) conducted numerical simulations using the transitional $\gamma$-$Re_{\theta }$ turbulence model (Langtry and Menter 2009) to investigate the influence of wall roughness on BL transition in toroidal CFVNs. The transition occurred earlier (at lower values of Re) and the decrease of the discharge coefficient was stronger for higher values of relative roughness. Their computational fluid dynamics (CFD) curves were in good accordance with experimental data. Zebrowski et al. (2022) studied the laminar-to-turbulent BL transition in toroidal-shaped nozzles by means of a linear stability analysis. They showed that the BL is stable to modal disturbances due to the existence of a FPG, whereas transient growth of energy in the form of streamwise streaks is likely to occur within the throat region of the nozzle.

The cylindrical type of CFVNs is also frequently used in industry (Lambert et al. 2021) and recently gained attention in research. Mickan et al. (2006) developed a prediction model for the discharge coefficient of CFVNs based on their geometry and integral methods for solving the BL equations in the laminar and turbulent regime. Their results agreed well with experimentally determined $C_D$ values for both toroidal and cylindrical nozzles. Lambert et al. (2019) computationally studied the flow through cylindrical CFVNs in both laminar and turbulent regimes using a one-equation turbulence model. For lower Reynolds numbers, they observed the formation of a successive reflection of compression waves within the cylindrical section. They assumed that this shock-train flow pattern influences the growth of the BL within the cylindrical throat. However, in terms of cylindrical CFVNs no numerical data was found regarding the transitional behavior of the BL flow.

Hence, this numerical study is aimed at providing deeper insight into this topic by comparing two different turbulence models for the simulation of a cylindrical CFVN according to EN ISO 9300 (2005) in a wide range of Reynolds numbers (from $2.6\cdot 10^4$ to $1.3\cdot 10^7$). In Sect. 3.1, as a validation, the simulation results of the two turbulence models are compared with corresponding experimental data in terms of the discharge coefficient $C_D$. In Sect. 3.2, the general flow field within the nozzle is discussed for a representative flow case and the development of the pressure field is compared between the two turbulent models used. In Sect. 3.3 and Sect. 3.4, relevant quantities and profiles of the BL in the cylindrical part of the nozzle are separately analyzed and compared to data from the literature for the laminar and turbulent region, respectively. Furthermore, in Sect. 3.5, the shape factor $H_{12}$ is investigated as a potential measure of the extent of the transitional region and transitional BL profiles are addressed.

2 Methods

2.1 Geometry and Mesh

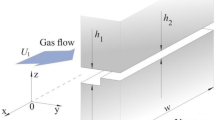
The computational domain of the cylindrical nozzle studied in this work is depicted in Fig. 1. It consists of a $5^\circ$ wedge sector of the nozzle to represent a two-dimensional axisymmetric flow. The inlet region encompasses a quarter circle with a radius of 2d, where the throat diameter d is 1 mm. The outlet region has an extension of 8d in the axial (z) and radial (y) direction. The geometry of the nozzle is according to the ISO 9300 standard (EN ISO 9300 2005) and can be divided into a convergent, cylindrical, and divergent part. Within the cylindrical part (highlighted in green), the flow becomes critical limiting the mass flow rate through the nozzle. Thus, the development of thickness and type of the BL in this throat area is extensively investigated in this numerical study. Therefore, results are evaluated at seven different axial positions z/d from 0.2 to 0.8. In this region, the pressure gradient stays relatively constant and BL profiles are reasonably unaffected by the geometry change towards the convergent (upstream) and divergent (downstream) part of the nozzle.

Fig. 1

Computational domain of the investigated cylindrical nozzle

The computational mesh constitutes approximately $3.5\cdot 10^5$ hexahedral cells that has been selected for all flow simulations as the best compromise between accuracy and computational runtime based on a grid independence study (see Appendix A). A schematic overview of the computational grid is displayed in Fig. 2. The mesh considers appropriate cell refinement towards the walls and flow regions where high gradients are expected, as in shock fronts. In addition, the non-dimensional wall distance $y^+$ is 1 or below at the walls in the cylindrical part of the nozzle, as recommended in (Langtry and Menter 2009).

Fig. 2

Schematic of the computational mesh

2.2 Numerical Settings

The numerical simulation is conducted in OpenFOAM v2012 (OpenCFD Limited 2020) using the transient, pressure-based, compressible Reynolds-averaged Navier–Stokes (RANS) solver sonicFoam. The RANS equations are solved with the PIMPLE algorithm, combining the SIMPLE (Semi-Implicit Method for Pressure-Linked Equations) (Patankar and Spalding 1972) and PISO (Pressure-Implicit with Splitting of Operators) (Issa 1986) algorithms. For the temporal discretization, the implicit Euler method is used, whereas for the spatial discretization, linear gradient schemes as well as linear and upwind divergence schemes are used. Two different RANS turbulence models are used (see Sect. 2.3).

For both models, a set of ten different throat Reynolds numbers is investigated, ranging from $2.6\cdot 10^4$ to $1.3\cdot 10^7$. The variation of the throat Reynolds number Re is realized by varying the total inlet pressure $p_0$, according to Eq. (3), where the mass flow rate $\dot{m}$ is calculated with respect to Eq. (1). The ratio of static outlet to total inlet pressure, also referred to as the back pressure ratio ($\text {BPR}$), is fixed to a value of 0.5 to allow for a critical flow through the nozzle and to keep the position of shocks located in the divergent part of the nozzle. The total inlet temperature $T_0$ is kept constant at 300 K and the inlet turbulence intensity TI is assumed to be 2 %. For all calculations, the flowing fluid is air considered as a perfect gas with a constant dynamic viscosity $\mu _0$ of $1.8\cdot 10^{-5}~\text {Pa\,s}$, specific gas constant $R_M$ of $287.7~\text {J/(kgK)}$, and ratio of specific heat capacities $\kappa$ of 1.4. These settings result in an inlet axial velocity $U_{z, in}$ of approximately $4.5~\text {m/s}$ and consequently in an inlet Mach number $M_{in}$ of 0.013 for all considered flow cases. At the walls, adiabatic no-slip boundary conditions are implemented. The pressures and the resulting throat Reynolds numbers for all simulated flow cases are listed in Table 1.

Table 1 Pressure boundary conditions and respective throat Reynolds numbers for the simulated flow cases

2.3 Turbulence Models

Two different turbulence models are investigated and compared with each other, namely the k-$\omega$ SST model (Menter 1994; Menter et al. 2003) and the $\gamma$-$Re_{\theta }$ model (Langtry and Menter 2009). The k-$\omega$ SST model is one of the most widely used two-equation eddy viscosity models, where two transport equations are solved for the turbulent kinetic energy k and the turbulent specific dissipation rate $\omega$.

The second model, the $\gamma$-$Re_{\theta }$ model, is a local correlation-based transitional model extending the classical SST model by solving two additional transport equations for the intermittency $\gamma$ and the transition momentum thickness Reynolds number $Re_{\theta t}$. The intermittency is used to trigger the transition process. It is directly coupled with the production term $P_k$ and destruction term $D_k$ of turbulent kinetic energy as follows:

$$\begin{aligned} P_k&= \gamma _{\text {eff}} P_{k, SST} \quad \text {with} \quad \gamma _{\text {eff}}=\max {\left( \gamma , \gamma _{\text {sep}}\right) }, \end{aligned}$$

(4)

$$\begin{aligned} D_k&=\min {\left( \max { \left( \gamma _{\text {eff}},0.1\right) }, 1.0\right) } D_{k, SST}, \end{aligned}$$

(5)

where $P_{k, SST}$ and $D_{k, SST}$ are the production and destruction terms of k of the classical SST model, respectively. Further, $\gamma _{\text {sep}}$ depicts a modification to the intermittency for predicting separation-induced transition. Hence, the effective intermittency $\gamma _{\text {eff}}$ might be higher than unity in separated BLs. The intermittency $\gamma$ can take values between 0 (fully laminar) and 1 (fully turbulent) based on empirical correlations for the length and onset of transition integrated in the production term of intermittency $P_{\gamma }$. Those correlations depend on the value of the second transported quantity, the transition momentum thickness Reynolds number $Re_{\theta t}$. The value of $Re_{\theta t}$ itself changes as a function of the turbulence intensity and a pressure gradient parameter of the flow via an empirical correlation derived from experimental studies investigating transition in numerous flat-plate test cases (Langtry and Menter 2009).

In this work, based on the aforementioned empirical correlation, the inlet value of $Re_{\theta t}$ is set to 260.25 to account for the assumed inlet turbulence intensity TI of 2 %. The turbulent parameters k and $\omega$ are set at the inlet in accordance to the assumed inlet turbulence intensity and the inlet axial velocity to constant values of 0.01215 m$^2$/s$^2$ and 1812.94 s$^{-1}$, respectively, throughout the considered flow cases. The simulations with the $\gamma$-$Re_{\theta }$ model are initialized with the flow field results of the k-$\omega$ SST model. The $y^+$ insensitive wall function nutkWallFunction of OpenFOAM that applies a turbulence viscosity wall condition based on the local $y^+$ value is employed for both models. The turbulence viscosity $\nu _t$ at the wall is determined as follows:

$$\begin{aligned} \nu _t&= {\left\{ \begin{array}{ll} 0 &{} \text {if } y^+ \le 11.53 \\ \nu \left( \frac{y^+ \kappa _w}{\ln {(E_wy^+)}}-1\right) &{} \text {if } y^+ > 11.53 \end{array}\right. } \end{aligned}$$

(6)

where $\nu$ is the kinematic viscosity of the fluid near the wall, and the wall function parameters $E_w$ and $\kappa _w$ are 9.8 and 0.41, respectively. However, the wall function only comes into effect in the outlet region, where the viscous sublayer is not resolved by the mesh. In the following, the two specific turbulence models will be referred to as “standard” and “transitional model”, respectively.

3 Results

3.1 Validation

For a validation of the numerical results, the discharge coefficients obtained from simulations of the standard and transitional model are compared with experimental data from primary standard flow measurements of a smooth (Mickan et al. 2016) and a rough (Lambert et al. 2019) cylindrical nozzle according to the ISO 9300 (EN ISO 9300 2005) for different Reynolds numbers, see Fig. 3. The rough nozzle has a machined roughness Ra of 0.7 $\upmu$m. Although the numerical models do not consider rough walls, a comparison with the tested nozzle is useful as the surface roughness has a negligible influence on the discharge coefficient in the laminar region (cf. Wang et al. (2019)) at which the rough nozzle was operated.

The experimental data indicates three distinguishable regimes of the nozzle flow. In the laminar range ($Re<8\cdot 10^5$), there is a steep increase in discharge coefficient with higher Reynolds numbers. In the transitional region, $8\cdot 10^5<Re<2\cdot 10^6$, the $C_D$ values slightly decrease until the discharge coefficients again increase in the fully turbulent range ($Re>2\cdot 10^6$), but with a smaller slope compared to the laminar part.

Fig. 3

Distribution of the discharge coefficient $C_D$ with Reynolds number Re for the standard ($\circ$) and transitional ($\diamond$) model of the numerical simulation in comparison with experimental data of two cylindrical CFVNs (Mickan et al. 2016)

The standard model ($\circ$) is able to predict the experimental data for higher Reynolds numbers above $2\cdot 10^6$. This is the expected behavior for a fully turbulent model. It also yields comparable results for the two smallest Reynolds numbers. For the lowest Reynolds number of $2.6\cdot 10^4$, the eddy viscosity is low in comparison to the molecular viscosity in the cylindrical part of the nozzle resulting in a laminar BL. This counter-intuitive observation is in accordance with the findings by Rumsey and Spalart (2009) investigating the behavior of turbulence models in low Reynolds number regions. For the second lowest Reynolds number of $1.3\cdot 10^5$, the BL in the cylindrical part is turbulent for the standard model as the eddy viscosity at the wall is high compared to the molecular viscosity. The predicted discharge coefficient is still comparable to the experimental data because the resulting displacement thickness is similar to that of the transitional model (where the BL is laminar) at this Reynolds number. However, the standard model fails in the intermediate range. In particular, the characteristic slope in the laminar region is not well captured. The results of the transitional model ($\diamond$), on the other hand, are in good agreement with the experiments throughout the entire Reynolds number range depicted. Especially in the laminar range ($Re<1\cdot 10^6$), the improvements of the transitional model towards the standard model become notable. The immediate decrease in discharge coefficient at around $Re=1\cdot 10^6$, as predicted by the transitional model, is a clear indication for the inherent change from laminar to turbulent behavior of the flow and is an estimate for the position of the transitional region. As will be discussed later in Sect. 3.5, only the thermal BL transitions to fully turbulent, whereas the velocity BL is still laminar. Due to the increased turbulent thermal BL (compared to the laminar one), the region of lower density close to the wall increases (compared to the core flow). As the global parameter of discharge coefficient $C_D$ can be understood as a deficit parameter of mass flux $\rho U$, the change in the density profile is responsible for this immediate decrease in $C_D$ and the good predictions of the transitional model at elevated Reynolds numbers. This correlates well with the experimental data, where the decrease of the $C_D$ value is not as steep as in the simulation, but it is also located in the same Reynolds number range.

3.2 General Flow Field

A representative depiction of the general flow field within the cylindrical nozzle is illustrated in Fig. 4 in terms of the Mach number (upper part) and normalized axial pressure gradient (lower part) distribution. The results shown are simulated with the transitional model for a throat Reynolds number of $2.6\cdot 10^5$.

Fig. 4

General flow field within the cylindrical nozzle (transitional model at a throat Reynolds number of $2.6\cdot 10^5$). Top: Mach number M. Bottom: Normalized axial pressure gradient $(\partial p / \partial z) / (p_0/d)$. Green lines indicate ZPG ($(\partial p / \partial z) / (p_0/d) = 0$) in the axial direction and white lines indicate critical flow condition ($M=1$). (Color figure online)

The flow is highly accelerated in the convergent part of the nozzle as indicated by the FPG region close to the wall. A small APG region forms wall-adjacently at the entry of the cylindrical part due to the sudden change in wall curvature. The green isoline (ZPG flow) indicates that the extent of the local APG region is up to approximately 20 % ($z/d = 0.2$) at the wall of the cylindrical part of the nozzle. This applies to all simulations conducted in this study. The air flow becomes critical, reaching a Mach number of 1, at circa 80 % ($z/d = 0.8$) of the cylinder length as indicated by the white isoline. For the flow cases considered, the critical condition is attained in the range between $z/d = 0.7$ and $z/d = 0.85$. The formation of a shock train within the cylindrical part, as described by Lambert et al. (2019), is not present for any of the flow cases considered. Since the sonic limit is reached, the flow is further accelerated in the expanding part of the nozzle forming a shock train in order to adapt to the prescribed outlet pressure condition. Further, the BL separates from the wall, which makes it inevitable to use a turbulence model even though the flow is laminar in the cylindrical part of the nozzle. The shock train arises from the interaction of the BL with the normal shock in the diffuser, as described by Matsuo et al. (1999). For all regarded flow cases, these shock structures are located inside of the divergent part due to the constant BPR of 0.5. The complex flow phenomena occurring in the divergent part have negligible influence on the mass flow rate through the nozzle as the critical state of the flow is already reached in the cylindrical part. However, the pressure field within the cylindrical part of the nozzle has an impact on the BL development upstream of the sonic line and thus affects the mass flow rate. Therefore, in the following, the analysis of the flow is focused on the cylindrical part of the nozzle as the relevant region for the determination of the mass flow rate.

Fig. 5

Contours of normalized axial pressure gradient $(\partial p / \partial z) / (p_0/d)$ for the standard and transitional model within the cylindrical part of the investigated CFVN at various Reynolds numbers. Green lines indicate ZPG ($(\partial p / \partial z) / (p_0/d) = 0$) in the axial direction and white lines indicate critical flow condition ($M=1$). *Flow cases used in Sect. 3.3 (Laminar region). **Flow cases used in Sect. 3.4 (Turbulent region). ***Flow cases used in Sect. 3.5 (Transitional region). (Color figure online)

Figure 5 shows the axial pressure gradients scaled by the ratio of total inlet pressure $p_0$ and throat diameter d of the standard model and of the transitional model for all Reynolds numbers investigated. The domains depicted have a radial extent from the nozzle wall ($y/d=0.0$) to the center ($y/d=0.5$) and an axial extent from the start ($z/d=0.0$) to the end ($z/d=1.0$) of the cylindrical part of the CFVN (as in the enlarged region in Fig. 4). For the standard model, the magnitude of the APG in the lower left corner increases more rapidly than for the transitional model for ascending Reynolds numbers (more intense red color). Due to this lower APG for the transitional model, the flow is able to accelerate faster. As a result, a small sonic region at the inlet corner (white line) is established for the Reynolds number cases from $5.2\cdot 10^5$ to $1.0\cdot 10^6$. At the next higher Reynolds number of $1.3\cdot 10^6$, the sonic region disappears for the transitional model since the magnitude of the APG is sufficiently strong so that the flow cannot further accelerate. As a consequence, the critical line ($M=1$) at the end of the cylinder inherently changes close to the wall indicating a transition process of the BL. At $Re=1.0\cdot 10^6$, the critical line is situated very close to the wall, whereas at $Re=1.3\cdot 10^6$, a deficit becomes visible resembling the isoline of the standard model at the same Reynolds number. Later in Sect. 3.5, it will be shown that this deficit results from the change of the thermal BL and the resulting decrease of the density close to the wall, whereas the velocity BL is still laminar for this Reynolds number and starts to transition at the higher Reynolds number of $5.2\cdot 10^6$. For Reynolds numbers above $1.3\cdot 10^6$, the strength of the APG further increases for both models. However, a small sonic region develops for the two highest Reynolds number cases, which can be explained by the fact that also the FPG in the convergent part of the nozzle further upstream gains in magnitude.

Furthermore, the axial position of the critical line changes depending on the Reynolds number and the turbulence model used. For the standard model, the critical line stays relatively constant above $z/d = 0.8$ (except for the lowest Reynolds number, where the position lies at ca. $z/d = 0.7$). For the transitional model, the $Ma=1$ line stays below $z/d = 0.8$ up to $Re = 1.0 \cdot 10^6$ and then increases above $z/d = 0.8$ towards the highest Reynolds number. This indicates that transition occurs when the critical line is located at ca. $z/d = 0.8$.

For a more detailed investigation of the BL characteristics, the following results will be presented separately for the three regions of the BL within the nozzle throat: laminar (Sect. 3.3), turbulent (Sect. 3.4), and transitional (Sect. 3.5). For the laminar region, the results of the transitional model are considered, as it is capable of demonstrating characteristic laminar BLs in comparison with the standard model. For the turbulent region, the results of the standard model are shown, as it considers turbulent flow independent of the Reynolds number. The results of the transitional model are not discussed in this section because although the thermal BL is already fully turbulent, the velocity BL is still laminar at a Reynolds number of $1.3\cdot 10^6$. Therefore, the direct comparison with data from the literature (where the velocity BL is fully turbulent) is not suitable. For the transitional region, first, the results of both models are compared in terms of the shape factor $H_{12}$ and second, the results of the transitional model are discussed regarding the aforementioned different transitional behavior of the thermal and velocity BLs.

3.3 Laminar Region

The displacement thickness $\delta _1$ can be understood as the distance by which a surrounding wall should be displaced into the flow in order to compensate the deficit of the mass flow rate owing to the formation of a BL at the wall. For a compressible flow, it is defined as follows:

$$\begin{aligned} \delta _1&= \int _0^{\delta } \left( \frac{\rho _e U_e - \rho U}{\rho _e U_e} \right) dy, \end{aligned}$$

(7)

where $\rho$ and U are the density and velocity and the upper integration limit $\delta$ is the BL thickness, defined as the local distance normal to the wall at which the velocity has a local maximum in the vicinity of the wall, referenced as $U_e$, and where $\rho _e$ is the corresponding density. Similarly, the momentum thickness $\delta _2$ is defined with respect to the deficit in flow momentum:

$$\begin{aligned} \delta _2&= \int _0^{\delta } \frac{\rho U}{\rho _e U_e} \left( \frac{U_e - U}{U_e} \right) dy. \end{aligned}$$

(8)

Both thicknesses are characteristic quantities for describing the BL development. In Fig. 6, they are displayed for the laminar region along the nozzle wall within the cylindrical part of the investigated CFVN for different Reynolds numbers up to $7.8 \cdot 10^5$.

Fig. 6

Development of the normalized displacement thickness $\delta _1$ and momentum thickness $\delta _2$ within the cylindrical part of the nozzle in the laminar region. The results of the transitional model (solid lines) are compared with a laminar approach by Mickan et al. (2006) (dashed lines)

The normalized axial start ($z/d=0.2$) and end position ($z/d=0.8$) are chosen in order to avoid the influence of nozzle curvature as expressed by the APG and FPG regions at the inlet and outlet of the cylindrical part, respectively (see Fig. 5). The computational results of the transitional model (solid line) are compared with a laminar approach (dashed line) by Mickan et al. (2006) . This approach is based on a predictive model for the determination of the discharge coefficient of CFVNs based on their geometry. The predictive model first transforms the compressible two-dimensional nozzle flow into an equivalent incompressible plane flow to which integral methods for solving the BL equations are applicable. In a second step, the characteristic quantities of the velocity BL, displacement and momentum thickness, are calculated and transformed back to the compressible two-dimensional nozzle flow. The resulting predictions for the discharge coefficient were validated with experimentally determined $C_D$ values for both toroidal and cylindrical CFVNs. Thus, also the predicted values of the displacement and momentum thickness are indirectly validated with respect to the velocity BL and are therefore suitable for a comparison with the computational results of the transitional model.

The curves of the transitional model and the laminar approach in the left-hand column (normalized by the throat diameter d) are in decent agreement. The values of the transitional model are slightly higher than predicted by the theoretical approach. All trendlines continuously increase within the nozzle throat with a tendency to stagnate or yet decrease towards the end at $z/d=0.8$ as the magnitude of the FPG starts to increase. For higher Reynolds numbers, the values for $\delta _1/d$ and $\delta _2/d$ become smaller, where the highest reduction is visible between the two lowest Reynolds numbers. This is in line with the rise in discharge coefficient for increasing Reynolds numbers in the laminar range, according to the proportional relation between the $C_D$ value and the effective reduction of the cross-sectional nozzle area by the displacement thickness:

$$\begin{aligned} C_D \sim \left( 1-\frac{2\delta _1}{d}\right) ^2. \end{aligned}$$

(9)

The curves collapse when multiplied by $\sqrt{Re}$ as can be seen in the right-hand column of Fig. 6. This correlation corresponds to the Blasius solution for a laminar BL of a flat plate (Blasius 1908).

As the formation of a BL causes a deficit in mass flux $F=\rho U$ close to the wall in comparison with an inviscid flow scenario, it often proves beneficial to investigate the BL in terms of the mass flux deficit profile $F_e - F$, where $F_e$ denotes the mass flux at the edge of the BL. For the characterization and comparison of those deficit profiles, three different scales are used in this study. These scales are listed in Table 2. The indices e, $\tau$, and ZS denote the edge, friction, and ZS (Zagarola and Smits 1998) scale, respectively. Furthermore, $\tau _w$ and $\rho _w$ are the wall shear stress and the density at the wall, respectively.

Table 2 Characteristic mass flux scales

Figure 7 depicts the laminar mass flux deficit profiles $F_e-F$ normalized by the different scales from Table 2.

Fig. 7

Laminar deficit BL profiles of mass flux $F_e-F$ using different scales: a edge scale $F_e$ (and y/d scale), b edge scale $F_e$ (and $y/\delta$ scale), c friction scale $F_{\tau }$ (and $y/\delta$ scale), and d ZS scale $F_{ZS}$ (and $y/\delta$ scale). Dashed lines indicate Blasius BL profiles (Blasius 1908)

The profiles of the transitional model are shown for different Reynolds numbers Re (indicated by specific colors) and normalized axial positions z/d in the nozzle (indicated by the opacity level). For the edge scaling in combination with the diameter-scaled wall coordinate y/d (see Fig. 7a), the deficit profiles are spread, where the area under the curve becomes smaller for increasing values of Re. For advancing axial positions z/d, the area under the curve slightly increases, equivalent to the rise in $\delta _1$ and $\delta _2$ in Fig. 6. The profiles collapse when the wall coordinate is scaled by the BL thickness (see Fig. 7b). This mutual curve also coincides with the Blasius BL deficit profile (black dashed line). The Blasius velocity profile (Blasius 1908) is an analytical self-similar solution of the incompressible BL equations for laminar flow over a flat plate at a ZPG. Although the flow in the cylindrical part of the nozzle encounters a weak FPG, it is still in decent accordance with the Blasius solution. The curves also fall onto a similarity line with the Blasius profile for the ZS scaling in Fig. 7d. This scaling was essentially proposed exclusively for turbulent outer BL flows. However, it is also a suitable choice for collapsing the laminar deficit profiles of this study. For the friction scaling in Fig. 7c the profiles clearly scatter for different Reynolds numbers up to a normalized wall distance of $y/\delta = 0.5$. The Blasius profiles have been created by considering the Reynolds number with respect to the axial distance $Re_z = Re \cdot z/d$, where $z/d=0.5$ (mid position of the cylindrical part). This scattering is thus also depicted by the Blasius profiles.

3.4 Turbulent Region

In this section, the BL characteristics within the nozzle throat are investigated in the turbulent region at elevated Reynolds numbers starting from $1.3\cdot 10^6$. The numerical results of the standard model are compared with fully turbulent BL profiles from the literature. The results of the transitional model are not chosen for a comparison with the data from the literature in this section as only the thermal BL is fully turbulent at Reynolds numbers above $1.3\cdot 10^6$ but the velocity BL is still laminar and transitions at a higher Reynolds number. The data from the literature is related to the fully turbulent velocity BL and therefore the results of the standard model are not suitable for a direct comparison. However, the results of the transitional model for the global parameter of discharge coefficient $C_D$ agree well with the experimental data (see Fig. 3) at high Reynolds numbers because the thermal BL is already fully turbulent, which increases the region of lower density (compared to the core flow) close to the wall. As the discharge coefficient $C_D$ can be understood as a deficit parameter in mass flux $\rho U$, the change of the density $\rho$ is responsible for the good predictions of the transitional model, despite the fact that the velocity BL is still laminar. The behavior of the transitional model at high Reynolds number flows will therefore be discussed in more detail in the following Sect. 3.5.

Figure 8 shows the normalized displacement thickness $\delta _1$ and momentum thickness $\delta _2$ curves for Reynolds numbers Re starting from $1.3\cdot 10^6$ in the turbulent region. Similarly to Fig. 6 for the laminar region, the thicknesses are evaluated along the nozzle wall within the cylindrical part in the range from $z/d=0.2$ to $z/d=0.8$. The numerical results of the standard model (solid line) are compared with a turbulent approach (dashed line) by Mickan et al. (2006) . This approach is based on the same predictive model as presented in the previous Sect. 3.3 that is adapted for the calculation of the displacement and momentum thickness in CFVNs with respect to the fully turbulent velocity BL. The predictions of the discharge coefficient by the model were also validated with experimental results of toroidal and cylindrical CFVNs. Hence, the model results are appropriate for the assessment of the numerical results of the standard model.

Fig. 8

Development of the normalized displacement thickness $\delta _1$ and momentum thickness $\delta _2$ within the cylindrical part of the nozzle in the turbulent region. The results of the standard model (solid lines) are compared with a turbulent approach by Mickan et al. (2006) (dashed lines)

The curves of the standard model and the turbulent approach in the left-hand column (normalized by the throat diameter d) show similar trends in the same order of magnitude. The values of the standard model are slightly below the theoretical prediction, except for the normalized displacement thickness at $Re=1.3\cdot 10^6$. As in the case for the laminar curves, the turbulent BL thicknesses steadily grow within the nozzle throat. However, they do not yet show the tendency to stagnate, which correlates with the later position of the $M=1$ line for the turbulent flow cases compared with the laminar flow cases (cf. Fig. 5). For rising Reynolds numbers, the BL thickness diminishes. However, the reduction is smaller compared to the laminar curves for the same Reynolds number increase. This corresponds to the smaller slope for higher Reynolds numbers in the discharge coefficient diagram in Fig. 3. In the right-hand column of Fig. 8, the trendlines are multiplied by $Re^{0.139}$, as used by Mickan (2021) in order to estimate $C_D$ values for turbulent BLs cases in CFVNs. Thus, the curves of the turbulent approach approximate to a smaller range, whereas the curves of the standard model successfully collapse on a mutual line.

In Fig. 9 the turbulent deficit mass flux BL profiles are shown for different scalings (as listed in Table 2). The results of the standard model for various Reynolds numbers (colored circles) and axial positions (opacity level) are compared with data from the literature. Black squares ($\square$) and crosses ($\times$) indicate experimental data by Cal et al. (2009) and Castillo and Johansson (2002) for incompressible turbulent FPG and ZPG flows over a flat plate, respectively. Black triangles ($\triangle$) are linked to DNS data by Gibis et al. (2019) of quasi-incompressible flat-plate turbulent BLs at ZPG. The edge scaling combined with the diameter-scaled wall distance y/d in Fig. 9a reveals a clustering of the curves for the standard model with a wide spread depending on the Reynolds number and the axial position. The area below the curves becomes bigger for decreasing Re values and increasing z/d positions (similar to the laminar profiles in Fig. 7a). When the wall distance is scaled by the BL thickness (see Fig. 9b), the curves tend to collapse with a smaller scatter width. They are sorted with respect to the Reynolds number and the effect of the axial position is removed compared to Fig. 9a.The experimental data by Cal et al. (2009) and Castillo and Johansson (2002) and the DNS data by Gibis et al. (2019) are in decent accordance with the numerical results for the CFVN flow of this study. The ZPG cases are oriented towards the upper limit of the curves of the CFVN, whereas the FPG case coincides with curves at the lower end. For the friction scaling in Fig. 9c the numerical curves virtually collapse perfectly also removing the influence of the Reynolds number in comparison with the edge scaling in Fig. 9b. The data from the literature again is sorted from ZPG to FPG cases, where the FPG case forms a lower bound and the ZPG cases directly lie on the numerical curves. This is in line with the conformity of the laminar curves with the Blasius profile in Fig. 7b and Fig. 7d indicating that the pressure gradient in the cylindrical nozzle throat is low enough to be considered quasi ZPG. The best collapse of the curves is achievable using the ZS scaling in Fig. 9d. Here, all curves, including the FPG case by Cal et al. (2009), fall onto a common line removing the effect of the pressure gradient. This scaling, as proposed by Zagarola and Smits (1998), has been successfully demonstrated by numerous authors to show self-similar behavior for a wide range of outer turbulent deficit BLs with pressure gradients.

Fig. 9

Turbulent deficit BL profiles of mass flux $F_e-F$ using different scales: a edge scale $F_e$ (and y/d scale), b edge scale $F_e$ (and $y/\delta$ scale), c friction scale $F_{\tau }$ (and $y/\delta$ scale), and d ZS scale $F_{ZS}$ (and $y/\delta$ scale). Black symbols ($\square$, $\times$, $\triangle$) indicate data from Cal et al. (2009), Castillo and Johansson (2002), and Gibis et al. (2019), respectively

3.5 Transitional Region

The shape factor $H_{12}=\delta _1/\delta _2$ is defined as the ratio of displacement thickness $\delta _1$ to momentum thickness $\delta _2$ of a BL. Figure 10 illustrates the $H_{12}$ variation for different Reynolds numbers Re at different normalized axial positions z/d in the cylindrical part of the nozzle.

Fig. 10

Shape factor $H_{12}$ in the cylindrical part of the nozzle for different Reynolds numbers Re and normalized axial positions z/d. Results of the standard ($\circ$) and transitional model ($\diamond$) are compared with laminar ($\triangle$) and turbulent ($\triangledown$) approaches by Mickan et al. (2006). Light red and light blue areas highlight characteristic regions for fully laminar and turbulent BLs of the flow around a flat plate, respectively, according to Abu-Ghannam and Shaw (1980)

The diagram shows the characteristic values of the theoretical approaches for laminar ($\triangle$) and turbulent ($\triangledown$) flows (Mickan et al. 2006) as well as the values of the standard ($\circ$) and transitional model ($\diamond$). Different opacity levels of the curves indicate different normalized axial positions z/d in the nozzle, where the position ranges from $z/d=0.2$ (lightest color) to $z/d=0.8$ (darkest color). Experimental investigations by Abu-Ghannam and Shaw (1980) on the transition of the flow around a flat plate indicated characteristic regions for fully laminar and fully turbulent BLs in a range of 2.5 to 3.0 and 1.4 to 1.6, respectively. As a reference, these regions are highlighted in Fig. 10 as light red and light blue areas.

The laminar approach predicts shape factors of ca. 2.7 to 3.2 with an increase towards higher Reynolds numbers. Comparing different axial positions z/d in the nozzle throat, there is drop in values of $H_{12}$ in the flow direction. The turbulent approach, on the other hand, estimates values of 1.7 for all Reynolds numbers and axial positions. These values are comparable with the measured data of a flat plate by Abu-Ghannam and Shaw (1980). Thus, the shape factors of the laminar and turbulent approach indicate an upper and lower bound for the CFVN flow. The shape factor, as calculated with the standard model, starts at values comparable with the laminar approach and then rapidly decreases, already for Reynolds numbers in the range of $10^5$. It stagnates at a value of approximately 1.8, which is slightly higher than in the turbulent approach. The trend is similar for all z/d positions, where the values slightly decrease for later positions in the CFVN. The transitional model starts to follow the tendency of the shape factors as predicted by the laminar approach until a Reynolds number of $10^6$. For Reynolds numbers above, a clear decline in shape factor is visible approaching values comparable to those of the standard model and turbulent approach. For ascending axial positions, the $H_{12}$ values drop, where the highest deviation between start and end position is at Reynolds numbers from $10^6$ to $10^7$. In their experimental study of transitional BLs on a flat plate using hot-wire anemometry, Taghavi-Zenouz et al. (2008) also showed this considerable decrease in the shape factor in a specific Reynolds number region. They identified this as the transitional region of the BL. Thus, the transitional region for the investigated cylindrical nozzle can be estimated between $Re=1\cdot 10^6$ and $5\cdot 10^6$. This region extends to a higher Reynolds number in comparison with the transitional regime estimated from the discharge coefficient in Fig. 3 (only up to $Re = 2\cdot 10^6$).

As the discharge coefficient represents a deficit in mass flux $\rho U$, the distribution of both quantities, density and velocity, close to the wall becomes relevant regarding the assessment of the transitional region. Figure 11 therefore shows the edge-scaled density and velocity distribution of the transitional model separately in (a) and (b) in combination with the intermittency $\gamma$ (c) at Reynolds numbers starting from $1.0\cdot 10^6$ at the normalized axial position z/d of 0.8. At this Reynolds number, the start of the transitional region can be identified based on results of the transitional model for both the discharge coefficient $C_D$ in Fig. 3 and for the shape factor $H_{12}$ in Fig. 10.

Fig. 11

Edge-scaled BL profiles of density $\rho$ a and velocity U b and profiles of intermittency $\gamma$ c of the transitional model at the normalized axial position z/d of 0.8

The edge velocity $U_e$ depicts the local maximum of the velocity in the vicinity of the wall, which defines the thickness of the velocity BL $\delta$. Similarly, a thermal BL thickness $\delta _T$ can be defined as the local distance normal to the wall at which the temperature has a local minimum $T_e$. As the density is calculated based on the equation of state for an ideal gas, it is directly dependent on the temperature distribution. Hence, the edge density $\rho _e$ is defined with respect to the thermal BL.

Between the two flow cases at Reynolds numbers of $1.0\cdot 10^6$ and $1.3\cdot 10^6$, the edge-scaled density profile in Fig. 11a inherently changes regarding the extent of the increasing range indicating a growth of the thermal BL thickness. This change correlates with the disappearance of the sonic region at the inlet corner of the cylindrical part of the nozzle and the inherent change of the critical line ($M=1$) close to the wall between those two Reynolds numbers in Fig. 5. For higher Reynolds numbers, the density profiles do not alter significantly. The profiles of the edge-scaled velocity in Fig. 11b show a distinct change from laminar to turbulent and a resulting increase of the velocity BL thickness between the Reynolds numbers of $2.6\cdot 10^6$ and $5.2\cdot 10^6$. This is in line with the sudden increase of intermittency from 0 to 1 close to the wall in Fig. 11c. Thus, the thermal BL thickness $\delta _T$ increases prior to the velocity BL thickness $\delta$. There are no relevant experimental or numerical data available in the literature that support or refute this finding. The modification of the density profile between the two lowest depicted Reynolds numbers also affects the velocity profiles in the vicinity of the edge velocity position as shown in the zoomed section in (b). They exhibit a marginal descent after reaching their peak value. Further, the intermittency profiles in (c) evidently alter at a distance from the wall ($y/d>0.005$) at the lowest Reynolds numbers, which presumably correlate with the change of the density profile and thus the thermal BL. In order to further investigate this, detailed experimental studies of the transitional BL in cylindrical CFVNs are necessary.

In Fig. 12, the ZS scaled deficit BL profiles of mass flux are depicted. The ZS scaling has been shown to successfully collapse both laminar (as predicted by the transitional model in Fig. 7d) and turbulent profiles (as predicted by the standard model in Fig. 9d) onto a respective similarity line. These profiles are displayed in Fig. 12a and b, respectively. As a simple representation, two approximation curves are proposed as follows:

$$\begin{aligned} \frac{F_e - F}{F_{ZS}} \left( \frac{y}{\delta }\right) = {\left\{ \begin{array}{ll} 5 \left( \frac{y}{\delta } - 1\right) ^4 &{} \text {(Laminar region)}\\ \left( \frac{y}{\delta }\right) ^{-\frac{1}{3}} - \frac{y}{\delta } &{} \text {(Turbulent region),} \end{array}\right. } \end{aligned}$$

(10)

which are also plotted alongside the laminar and turbulent profiles. The area below both curves in the range of $y/\delta =0$ and $y/\delta =1$ is equal to unity, respectively, which is typical for the ZS scaling. In Fig. 12c, both approximation curves are compared with the transitional profiles as predicted by the transitional model for Reynolds numbers Re starting from $1\cdot 10^6$ and different axial positions z/d. By the intersection of the approximation curves two regions are formed that are highlighted in light green color. The transitional profiles of the lowest Reynolds number ($Re=1\cdot 10^6$) stay well on the laminar profile. For ascending values of Re, the profiles start to move towards the turbulent profile in the lower intersection area (denoted as 1), whereas they stay unchanged in the upper intersection area (denoted as 2). This corresponds to the transition of the thermal BL thickness $\delta _T$. At the Reynolds number of $5.2\cdot 10^6$, the profiles transition in the intersection area 2 from the laminar profile at the beginning of the nozzle throat ($z/d=0.2$) to the turbulent profile towards the end of the nozzle throat ($z/d =0.8$). This corresponds to the transition of the velocity BL thickness $\delta$. This is not visible in the distribution of the discharge coefficient in Fig. 3, as the transition of $\delta _T$, influencing the density in the product of $\rho U$, manifests an earlier turbulent character of the flow and is responsible for the drop in the $C_D$ value starting at the Reynolds number of $1.3\cdot 10^6$. At the highest Reynolds number investigated ($Re = 1.3\cdot 10^7$), all profiles follow the turbulent profile. The Reynolds number at which the profiles start to change in intersection area 1 and the Reynolds number at which the profiles reach the turbulent profile in intersection area 2 conform with the estimated transitional region based on the shape factor $H_{12}$ in Fig. 10.

Fig. 12

Deficit BL profiles of mass flux $F_e-F$ using the ZS scale $F_{ZS}$ for the a laminar region (transitional model), b turbulent region (standard model), and c transitional region (transitional model)

4 Summary and Conclusion

This computational work described the investigation of two different turbulence models, namely the k-$\omega$ SST model (standard model) and the $\gamma$-$Re_{\theta }$ model (transitional model), for the simulation of the flow through a cylindrical CFVN according to the ISO 9300 standard. The objective of this study was to gain an understanding of the BL effects inside the nozzle throat depending on the Reynolds number and the axial position in the cylindrical part of the CFVN, which is crucial for a precise prediction of the mass flow rate.

As a validation of the numerical results, the discharge coefficients of the standard and transitional model were compared with those of primary standard flow measurements for different Reynolds numbers. The results of the standard model were in good agreement with the experimental data only for high and low Reynolds numbers, but not in the intermediate regime. For the transitional model, on the other hand, the $C_D$ values were in good accordance with the experiments for the entire Reynolds number range. Further, the significant drop in discharge coefficient at a Reynolds number of around $10^6$—characteristic for the laminar-to-turbulent transition—correlated well with the experimental data. Hence, the transitional model is essential in numerical analyses of cylindrical CFVNs and superior to the standard model in terms of the prediction of the discharge coefficient.

Within the cylindrical part of the nozzle, the flow field was compared between the standard and transitional model for all simulated flow cases. For lower Reynolds numbers, the magnitude of the APG region grew more rapidly for the standard model, whereas the flow of the transitional model exhibited a higher acceleration. This affected the position and the shape of the respective critical line indicating an inherent change from laminar to turbulent. This transition was identified to occur when the critical line was located at ca. 80 % of the cylindrical part. For higher Reynolds numbers, the flow field of both models resembled each other.

Relevant quantities and profiles of the BL in the nozzle throat were separately investigated in the laminar, turbulent, and transitional region, respectively. The curves of displacement and momentum thickness successfully collapsed when multiplied by $\sqrt{Re}$ and $Re^{0.139}$ in the laminar (using the transitional model) and in the turbulent (using the standard model) regime, respectively. The laminar deficit BL profiles collapsed for the edge and ZS scale and compared well with the Blasius profile. The turbulent deficit BL profiles collapsed for the friction and ZS scale and were in alignment with pertinent data from the literature. Moreover, it was shown that the edge scale removed the effect of axial position z/d, the friction scale removed the effect of Reynolds number Re, and the ZS scale removed the effect of pressure gradient for the turbulent deficit BL profiles. Simple representations for laminar and turbulent ZS scaled deficit BL profiles in cylindrical CFVNs were introduced in this study to facilitate the comparison to other BL flow scenarios.

The transitional region was estimated based on the drop of the shape factor in the nozzle throat (using the transitional model) from typical laminar to typical turbulent values according to respective literature. This predicted region extended to a higher Reynolds number than the $C_D$ curve suggested. A separate investigation of density and velocity in the vicinity of the wall revealed that the thermal BL thickness increased prior to the velocity BL thickness denoting the start and end of the transitional region, respectively. Numerical or experimental data are necessary to support or to refute this finding. This transitional range, however, corresponded to the range predicted by the shape factor. Hence, the shape factor is potentially more appropriate for estimating the transitional region than the global parameter of discharge coefficient. In many studies regarding transitional models, often only global parameters are considered for the assessment of the Reynolds number range, where transition occurs. Therefore, detailed experimental data of the BL in CFVNs is essential for a more detailed investigation of the transitional behavior in CFVNs. This could help to assess the predictive qualities of the transitional model in the transitional region. Based on that, the transitional model could be further improved by adjusting the model parameters to the experimental data.

In future studies, the influence of the inlet turbulence intensity on the onset of transition should be investigated to account for realistic inflow conditions. Therefore, it is also advisable to provide this quantity in experimental campaigns as each measurement setup entails an individual inlet turbulence intensity. Moreover, different relevant effects, e.g. wall roughness, non-ideal wall contours, or heat transfer, should be treated to gain further insight into more realistic configurations.

Appendix: Grid Independence Study

The mesh refinement level in this study is chosen based on a grid independence study conducted for the cylindrical CFVN nozzle in Fig. 1 using the transitional model. The study is performed for three different quality meshes of the computational domain of the nozzle geometry. The fine, medium, and coarse meshes consist of $N_1=1.4\cdot 10^6$, $N_2=3.5\cdot 10^5$, and $N_3=8.8\cdot 10^4$ cells, respectively. The procedure for estimation and reporting of discretization uncertainty in CFD applications by Celik et al. (2008) is followed in this study. It is based on the grid convergence index (GCI) derived from the Richardson extrapolation (RE) (Richardson 1910; Richardson and Gaunt 1927). The discharge coefficient $C_D$ is calculated at the inlet patch of the nozzle domain for each mesh type and for two different Reynolds numbers, namely $2.6\cdot 10^4$ and $1.3\cdot 10^7$. Table 3 provides the parameters of the discretization error analysis where the fine, medium, and coarse meshes are denoted by the indices 1, 2, and 3, respectively.

Table 3 Discretization parameters for grid independence study conducted for two Reynolds numbers

The approximate relative errors between the medium and coarse grid $e_a^{32}$ are 0.1595 % and 0.1007 % for the low and high Reynolds number, respectively. The errors between the fine and medium grid $e_a^{21}$ reduce to 0.0002 % and 0.0247 %. Other relevant quantities are the grid refinement factors $r_{32}$ and $r_{21}$, the differences of discharge coefficient between the grids $\epsilon _{32}$ and $\epsilon _{21}$, the apparent order p, and the extrapolated discharge coefficients $C_{D,ext}^{32}$ and $C_{D,ext}^{21}$. The extrapolated relative errors $e_{ext}^{32}$ and grid convergence indices $GCI^{32}$, comparing the medium and coarse meshes, are both below 0.0002 % and 0.0410 % for the low and high Reynolds number, respectively. They further decrease between the fine and medium mesh ($e_{ext}^{21}$ and $GCI^{21}$) to values below 0.0000002 % and 0.0101 %, which are sufficiently small. Furthermore, the extrapolated discharge coefficients $C_{D,ext}^{32}$ and $C_{D,ext}^{21}$ conform up to the fifth decimal place for each Reynolds number case, respectively, indicating a mesh convergence. Therefore, based on this study, the medium mesh is selected for all further flow simulations as it yields similar results to the fine mesh requiring only one fourth of its number of cells.