1 Introduction

The lifting of a flame has two key advantages over an attached flame. Firstly, once the flame is lifted, the risk of flashback is largely eliminated, which is crucial for injection systems operating in partially or fully premixed regimes. Secondly, the distance between the burner rim of an injector and the flame base creates a separation layer that protects the burner from thermal stresses or, in the case of hydrogen combustion, from hydrogen corrosion as well. On the other hand, when the flame is lifted, the risk of flame blow-out increases, particularly when the combustion process occurs under lean conditions.

The stabilization mechanism of lifted flames is largely dependent on large-scale vortical structures (Lawn 2009). These structures play a crucial role in enhancing the mixing process of fuel and oxidizer, thereby facilitating combustion and strengthening flame stabilization (Renard et al. 2000). In non-premixed systems where fuel and oxidizer are injected as separate, neighbouring streams, a high level of mixing of the fuel and oxidizer is a necessary condition for efficient combustion. This is achieved through the formation of a mixing layer (shear layer) in which fuel and oxidizer mix through both diffusive and convective transport processes. A typical injection system is composed of a circular nozzle supplying fuel surrounded by a co-flowing oxidizer (Cabra et al. 2002, 2005; Markides and Mastorakos 2005). In such a configuration large vortices can be created by applying suction to the periphery of the jet (annular counterflow) (Strykowski and Niccum 1991). The modification of the inflow pattern induced by suction is relatively small, but in some cases, it can trigger a global instability mechanism (Jendoubi and Strykowski 1994). Depending on the strength of the suction, two types of global instability exist: Mode I and Mode II (Jendoubi and Strykowski 1994; Lesshafft and Huerre 2007). The former, also known as the shear layer mode, occurs when the suction is strong, causing a counterflow that engulfs the main jet. In such regimes, global oscillations originate from the shear layer. Mode II, called the jet column mode, occurs in conditions with a moderate suction intensity or even without suction when the density of the jet is much lower than the density of the ambient flow (Monkewitz et al. 1989). In the global instability regimes characterized by Mode II, the flow disturbance spreads throughout the entire jet region. It has been demonstrated that both instability modes can exist indefinitely and over a wide range of operating conditions, including different Reynolds numbers and shear layer thicknesses (Jendoubi and Strykowski 1994; Strykowski and Niccum 1991; Strykowski and Wilcoxon 1993; Lesshafft and Huerre 2007; Lesshafft et al. 2007; Wawrzak et al. 2021; Wawrzak and Boguslawski 2022). The essential feature of global instability is the rapid growth of perturbations that saturate into large coherent toroidal vortices (Strykowski and Niccum 1991). These vortices vary periodically in time, in close vicinity to the nozzle. The formation of these vortices is characterized by a distinct peak in the velocity spectra (Boguslawski et al. 2016; Lesshafft et al. 2007; Wawrzak et al. 2021; Wawrzak and Boguslawski 2022). A striking feature of jets experiencing global instability is a large spreading rate of the main jet stream and a radial ejection of thin fluid streams in the form of the ‘side-jets’ inclined to the main flow direction (Monkewitz et al. 1989; Wawrzak and Tyliszczak 2022). This contributes to enhanced mixing, characteristic of the corresponding combustion process.

The large potential of counter-current flow as a ‘tool’ for controlling the flame dynamics has been noted already in the 1990 s (Lourenco et al. 1997; Chan et al. 2002). It has been reported that the counter-current flow can effectively stabilize flames and prevent blowout. This stabilizing effect has been attributed to the presence of large-scale vortices in the near field region, which enhances the fuel-oxidizer mixing by inducing transport of oxidizer into the jet region and frequent outward ejections of fuel from the main jet to the oxidizer stream. An important observation made by Lourenco et al. (1997) and Chan et al. (2002) was that the reverse flow induced by the counter-current flow system contained only a negligible amount of fuel. This indicates that the mechanism of flame stabilization is not related to changes in the fuel mass flow rate, but rather to the dynamics of the flow in the vicinity of the injection nozzle. While these studies shed some light on the mechanism of flame stabilization, they failed to unambiguously identify the criteria that should be met to trigger global instability. Specifically, it is unclear why toroidal vortices favour flame stabilization. Moreover, these studies did not provide fundamental insight into the developing flame structure.

Within this study, an analysis of hydrogen-diluted flame dynamics in a counter-current configuration is carried out with the help of the large eddy simulation (LES) method. LES has been proven to be a reliable numerical method for studying complex combustion processes (Stanković et al. 2013; Tyliszczak et al. 2014; Tyliszczak 2015; Brauner et al. 2016; Tyliszczak and Wawrzak 2022; Tyliszczak et al. 2023; Fredrich et al. 2021; Giusti and Mastorakos 2019) as well as hydrodynamic instability problems, including flow connected to global instability (Foysi et al. 2010; Boguslawski et al. 2016; Wawrzak et al. 2021; Wawrzak and Boguslawski 2022). Specifically, we investigate the transition process between convective and absolute instability and analyze how this change in flow regimes affects the flame. We also focus on the suction required to trigger global instability in cases with significantly different turbulence levels. It is shown that in the absence of suction or with weak suction, the flame remains attached to the nozzle, with a typical non-premixed flame shape observed at low Reynolds numbers. However, when the suction is strong enough, it induces global instability, the flame is lifted and exhibits a complex and strongly turbulent character with both premixed and non-premixed zones.

The lifted flame condition appears to persist indefinitely as long as the suction strength remains sufficiently large. The exact flow mechanism responsible for this observed global instability phenomenon has not yet been conclusively determined in the literature. Nevertheless, our computational demonstration of the qualitative modification of the flow due to suction points at a robust self-maintained process. In fact, the suction near the nozzle alters the flow such that it may even induce global instability that can dynamically lead to a lifted flame. For example, a significant difference induced by the lifting of the flame is in the amount of unburned fuel, which is high in attached flame conditions but significantly reduced for lifted flames, due to the more intense mixing above the flame stabilization zone. These main findings of this paper have also practical implications, as they could enable the design of more compact combustion chambers.

The paper is organized as follows. The next section outlines the numerical approach and the specific problem considered. Section 3 presents the results of the study, including the ignition process, flame propagation and stabilization, and the relationship between flame lift-off and global instability. Finally, Sect. 4 offers conclusions based on the presented findings.

2 Mathematical Model

The numerical model employed in this study utilizes the low Mach number approximation (Majda and Sethian 1985) of the momentum, reactive scalars, and energy equations. In the framework of LES, these equations are defined as follows:

$$\begin{aligned} \partial _t {\bar{\rho }}+\nabla \cdot ({\bar{\rho }}\widetilde{{\textbf{u}}})=0 \end{aligned}$$
(1)
$$\begin{aligned} \bar{\rho }\partial _t\widetilde{{\textbf{u}}} +(\bar{\rho }\widetilde{{\textbf{u}}}\cdot \nabla )\widetilde{{\textbf{u}}} +\nabla {\bar{p}}=\nabla \cdot \ (\varvec{\tau }+\varvec{\tau }^{SGS}) \end{aligned}$$
(2)

where the bar symbol denotes LES filtered quantities and tilde its density weighted counterpart (Geurts 2004) defined through the convolutions:

$$\begin{aligned} \bar{f}({\textbf{x}},t)={\mathcal {G}}({\textbf{x}};\Delta )*f({\textbf{x}},t)=\int _\Omega {\mathcal {G}}({\textbf{x}}-{\textbf{x}}';\Delta )f(\mathbf {x'},t)\text {d}{\textbf{x}}' \end{aligned}$$
(3)
$$\begin{aligned} {\widetilde{f}}({\textbf{x}},t)=\overline{\rho ({\textbf{x}},t)f({\textbf{x}},t)}/{{\bar{\rho }}}=1/{\bar{\rho }}({\textbf{x}},t)\int _\Omega {\mathcal {G}}({\textbf{x}}-{\textbf{x}}';\Delta )\rho ({\textbf{x}}',t)f(\mathbf {x'},t)\text {d}{\textbf{x}}' \end{aligned}$$
(4)

where f stands for a general variable and \({\mathcal {G}}\) is the filter kernel such that \(\int _\Omega {\mathcal {G}}({\textbf{x}};\Delta )\text {d}{\textbf{x}}=1\). The symbol \(\rho\) refers to the mass density, \({\textbf{u}}\) is the velocity vector, p is the hydrodynamic pressure, \(\varvec{\tau }=2\mu {\textbf{S}}\) represents the viscous stress tensor where \({\textbf{S}}\) is the rate of strain tensor of the resolved velocity field (\(S_{ij}=1/2(\partial {\widetilde{u}}_i/\partial x_j+\partial {\widetilde{u}}_i/\partial x_j - 2/3\delta _{ij}\partial {\widetilde{u}}_k/\partial x_k)\)) and \(\mu\) is the molecular viscosity calculated from the Sutherland law. The term \(\varvec{\tau }^{SGS}=2\mu _t{\textbf{S}}\) is the sub-grid stress tensor with \(\mu _t\) representing the sub-grid viscosity calculated applying the model proposed by Vreman (2004). The transport equations of \(N_{\tiny {\text {species}}}\) species mass fractions \({Y}_{\alpha }\) (\(\alpha =1,2,\dots ,N_{\tiny {\text {species}}}\)) and enthalpy h are given as:

$$\begin{aligned} \bar{\rho }\partial _t{\widetilde{Y}}_{\alpha }+(\bar{\rho }{\widetilde{{\textbf{u}}}\cdot \nabla ){\widetilde{Y}}_{\alpha }} =\nabla \cdot \left( {\bar{\rho }({D}_{\alpha }+{D}_{\alpha }^{SGS}) {\nabla {\widetilde{Y}}_{\alpha }}}\right) + \overline{\dot{w}_{\alpha }} \end{aligned}$$
(5)
$$\begin{aligned} \bar{\rho }\partial _t\widetilde{{h}}+(\bar{\rho }{\widetilde{{\textbf{u}}}\cdot \nabla ){\widetilde{h}}}=\nabla \cdot \left( {\bar{\rho }({D}_h+D_h^{SGS}) {\nabla {h}}}\right) \end{aligned}$$
(6)

where \({D}_{\alpha }\) and \(D_{h}\) stand for the mass and heat diffusivities. While assuming unity Lewis numbers and equal diffusivity for all species can oversimplify hydrogen combustion (see e.g., Maragkos et al. (2014); Berger et al. (2022)), the common practice is to neglect the importance of thermo-diffusive effects. In the present work, following (Jones and Navarro-Martinez 2007; Stanković et al. 2013), the mass diffusivities of all species are assumed to be the same \({D}_{\alpha }=D=\mu /({\bar{\rho }}\,\text {Sc})\) where \(\text {Sc}=0.7\) is the Schmidt number and the Lewis number is \(\text {Le}=D_{h}/{D}=1\). The same applies for the sub-grid diffusivities which are computed as \({D}^{SGS}=\mu _t/({\bar{\rho }}\,\sigma )\), where \(\sigma\) represents turbulent Schmidt and Prandtl numbers, which are assumed to be equal to 0.7 (Jones and Navarro-Martinez 2007; Stanković et al. 2013; Triantafyllidis and Mastorakos 2009). The equation of state is defined as:

$$\begin{aligned} p_0=\overline{\rho } R {\widetilde{T}} \end{aligned}$$
(7)

where \(p_0\) is a constant thermodynamic pressure (\(p_0=101325\) Pa), T stands for the temperature, and R is the gas constant.

2.1 Combustion Model

The source term \(\overline{\dot{w}_\alpha ({\textbf{Y}},h)}\) in Eq. (5) stands for the filtered production/consumption rate of the species due to the chemical reactions. In the present work, a ‘no model’ approach is employed, in which \(\overline{\dot{w}_\alpha ({\textbf{Y}},h)}\) are calculated using filtered variables, i.e., \(\overline{\dot{w}_\alpha ({\textbf{Y}},h)}\approx {\dot{w}_\alpha (\widetilde{{\textbf{Y}}},{\widetilde{h}})}\). The ‘no model’ assumption would lead to inaccurate solutions in the Reynolds Averaged Navier–Stokes (RANS) framework where the fluctuations around mean values are generally large. On the other hand, in laminar flow simulations and direct numerical simulations (DNS), where all turbulent flow scales are resolved, the ‘no model’ approach is valid. Therefore, one can reasonably expect that solutions obtained without modelling of the reaction terms are not affected by significant errors if either a sufficiently dense computational mesh is used or the flow is characterized by sufficiently low Reynolds number and relatively low turbulence levels. The suitability of the ‘no model’ approach for problems of similar complexity as the present work has been demonstrated in several studies (Duwig and Fuchs 2008; Duwig et al. 2011; Prasad et al. 2014; Tyliszczak and Wawrzak 2022; Tyliszczak et al. 2023). It is important to note that the formation of large coherent structures, which is an essential feature of global instability, does not necessarily require very dense computational meshes for accurate resolution (Boguslawski et al. 2016; Wawrzak et al. 2021). Nevertheless, to ensure the reliability of the obtained solutions, the selected cases have also been simulated using the Eulerian stochastic fields method (ESF) to model turbulence-chemistry interactions (Valino et al. 2016).

2.1.1 Eulerian Stochastic Fields Method

In the ESF method, the scalar transport equations (5) and (6) are replaced by an equivalent evolution equation for the density-weighted filtered PDF function (Brauner et al. 2016; Hansinger et al. 2020), which is solved using the stochastic field method (Valino et al. 2016). Each scalar \({\tilde{\phi }}_\alpha\) is represented by \(1\le n\le N_s\) stochastic fields \(\xi _\alpha ^n\) such that

$$\begin{aligned} {\tilde{\phi }}_\alpha =\frac{1}{N_s}\sum _{n=1}^{N_s}\xi _\alpha ^n \end{aligned}$$
(8)

The stochastic fields evolve according to:

$$\begin{aligned} \begin{aligned} \text {d}\xi _\alpha ^n=&-\widetilde{{\textbf{u}}}\cdot \nabla \xi _\alpha ^n \text {dt} + \nabla \cdot \left( \left( {D}_{\alpha }+{D}^{SGS}_{\alpha }\right) \, \nabla \xi _\alpha ^n\right) \text {dt}\\&+\sqrt{2{D}^{SGS}_{\alpha }}\, \nabla \xi _\alpha ^n\cdot \text {d}{\textbf{W}}-0.5\tau ^{-1}\left( \xi _\alpha ^n - {\tilde{\phi }}_\alpha \right) \text {dt}\\&+{\dot{w}}_{\alpha }(\xi _\alpha ^n )\text {dt} \end{aligned} \end{aligned}$$
(9)

where the micro-mixing time-scale equals to \(\tau ={{\bar{\rho }}\Delta ^2}/({\mu +\mu _{\textrm{t}}})\) (Jones and Navarro-Martinez 2007) with \(\Delta =(\Delta x\times \Delta y\times \Delta z)^{1/3}\) being the LES filter width, and \(\text {d}{\textbf{W}}\) represents a vector of Wiener process increments different for each field (Valino et al. 2016). The results obtained applying the ESF method are discussed in Sec. 3.3 for cases that significantly differ in flow regime. These test cases include conditions where the flow is in convective and absolutely unstable regimes.

2.2 Solution Algorithm

The LES code used in this study is an in-house solver called SAILOR. The Navier–Stokes and continuity equations are discretized using the sixth-order compact difference method on half-staggered meshes (Tyliszczak 2014, 2016). The scalar transport equations for species and enthalpy are discretized using the 2nd order TVD (Total Variation Diminishing) scheme with Korens’ (Koren 1993) limiter. The time integration is performed by means of an operator-splitting approach where the transport in physical space and chemical terms are solved separately. The predictor-corrector technique with the 2nd order Adams-Bashforth / Adams-Moulton methods is used to integrate in time the convective and diffusive terms of the governing equations, and a fully implicit 1st order method is applied to integrate the chemical terms. VODPK (Brown and Hindmarsh 1989) procedure is used to solve a stiff system of equations that arises in this step. The chemical reactions are modeled by a detailed mechanism of hydrogen combustion involving 9 species and 21 reactions (Mueller et al. 1999). To calculate the chemical source terms \(\overline{\dot{w}_\alpha ({\textbf{Y}},h)}\), the CHEMKIN interpreter (Kee et al. 1980) is employed. Several studies, including those on combustion in jet-type configurations (Tyliszczak 2013; Wawrzak and Tyliszczak 2016; Wawrzak et al. 2021; Tyliszczak and Wawrzak 2022; Tyliszczak 2015; Rosiak and Tyliszczak 2016) and mixing layers (Wawrzak and Tyliszczak 2019, 2020), as well as those investigating global instability (Boguslawski et al. 2016; Wawrzak et al. 2021), have demonstrated the reliability of results obtained using the SAILOR code.

2.3 Counter-Current Jet Configuration

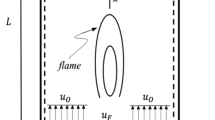
The computational configuration used in this work is shown schematically in Fig. 1. It comprises a rectangular domain with dimensions \(L_y=30D,L_x=L_z=15D\) into which fuel (nitrogen-diluted hydrogen) is injected through a central nozzle (\(D=2.25\) mm) surrounded by a larger co-axial nozzle (\(D_{suc}=2D=4.5\) mm) that sucks fluid from its vicinity. The combustion process is initiated by the contact of fuel with hot oxidizer (air) co-flowing outside of the co-axial nozzle. Table 1 shows flow parameters and compositions of the fuel and oxidizer streams. They are adopted from an experimental work devoted to study an auto-ignition process (Markides and Mastorakos 2005), which was later also modeled using the SAILOR code with good results (Tyliszczak 2015). In the present study, the original configuration is modified by adding the co-axial nozzle.

Fig. 1
figure 1

Schematic of the inlet nozzles and the computational domain

Full size image
Table 1 Parameters describing the simulated hydrogen jet flames
Full size table

2.3.1 Boundary Conditions and Simulation Parameters

In the simulations, we do not explicitly consider the nozzles, but instead, we impose an appropriate inlet velocity profile to mimic their presence. The mean velocity profile issuing from the central nozzle is described by the Blasius profile, which is based on the centreline velocity of the fuel jet (\(U_j\)) and the assumed shear layer thickness characterized by the parameter \(D/\theta =40\) (\(\theta =\int _0^{\infty } { U}/{ U_j}(1-{ U}/{ U_j})\text {d}r\) - momentum thickness). The velocity profile is obtained by solving the Blasius equation by the power series method, which leads to the following formula:

$$\begin{aligned} U_{Bl}(r) = \frac{U_j}{2}\sum _{n=1}^{\infty }\frac{np_n}{(n-1)!} \left[ 0.5 \left( r-\frac{D}{2} \right) \frac{0.664}{\theta } -1 \right] ^{n-1} \end{aligned}$$
(10)

where r is the inner radius of the nozzle and the factors \(p_n\) are defined as:

$$\begin{aligned} p_{0}&=0.6499,\, p_{1}=1.2594,\, p_{2}=1.0668 \\ p_{n}&= \sum _{i=1}^{n-3} p_{i}p_{n-1-i},\quad n\ge 3 \end{aligned}$$

The axial inlet velocity profile (\(U_y\)) plays a significant role in the study of the global instability phenomenon (Jendoubi and Strykowski 1994; Lesshafft et al. 2007; Boguslawski et al. 2016; Wawrzak et al. 2021, 2015). For the present case, the Blasius profile was selected as it suits well for relatively low Reynolds number jets (Boguslawski et al. 2013; Pawlowska and Boguslawski 2020), here \(\text {Re}=U_jD/\nu =1500\) (\(\nu\) - kinematic viscosity of the fuel jet at \(T_j=691\) K). Moreover, it has been shown in past that the use of the Blasius velocity profile at the inlet leads to more accurate results than a tangent hyperbolic profile, which is often used for jet flow simulations at higher Reynolds numbers (Wawrzak et al. 2015, 2021). In the present configuration, the Blasius profile is combined with a flat velocity profile (\(U_{suc}\)) in the co-axial suction nozzle and a flat velocity profile of the co-flowing air (\(U_{cf}\)). Therefore, the mean velocity profile defined on the bottom side of the computational domain is \(U_{y}=U_{Bl} + U_{suc} + U_{cf}\), which is shown in Fig. 2.

Fig. 2
figure 2

Mean inlet velocity profile in the central fuel jet, the co-axial suction nozzle and co-flow at the inlet boundary

Full size image

The remaining components of the inlet velocity are assumed to be zero \(U_x=U_z=0\). The suction velocity is defined by the suction strength parameter \(I=-U_{suc}/U_j\). In this study, we assume I to be in the range of \(0.0-0.2\), in which the instability character changes between the convectively and absolutely unstable regimes, as shown in previous studies (Strykowski and Niccum 1991; Jendoubi and Strykowski 1994; Wawrzak et al. 2021). It should be noted that the case with \(I=0.0\) represents the configuration with a solid collar placed around the fuel nozzle.

To trigger the laminar-turbulent transition, fluctuating velocity components (\(u'_{x,y,z}\)) are introduced in the region of the central fuel jet. These velocity components are computed using the method proposed by Klein et al. (2003), which enables an accurate representation of a real turbulent velocity signal with appropriately correlated fluctuations. Combined with the mean inlet velocity, they serve as the boundary condition. The necessary condition for the occurrence of the global instability is a low level of turbulence intensity, as turbulent fluctuations at high levels suppress the formation of large vortical structures inducing the global instability phenomenon. In this research, we consider two values of the turbulence intensity \(T_i=u'_y/U_j=1\%\) and \(5\%\), which are in the range of commonly used values in numerical simulations and also found in practical applications or experimental studies (Ball et al. 2012). The global instability phenomenon in jet flows can occur due to a density difference between the jet and the ambient flow. The critical density ratio \(S=\rho _{j}/\rho _{cf}\) (\(\rho _{j}\) - jet density, \(\rho _{cf}\) - co-flow density) below which global oscillations emerge can vary between 0.5\(-\)0.72 (Monkewitz and Sohn 1988; Strykowski and Niccum 1991; Russ and Strykowski 1993; Boguslawski et al. 2016), depending on the flow parameters such as the inlet jet velocity profile, turbulent intensity, and momentum thickness. In the present configuration, \(S=0.53\), however, this value alone is insufficient to generate global instability, and suction is a crucial factor for its occurrence. Most likely, the reason why the global instability does not occur for \(S=0.53\) is due to the Reynolds number being too low and \(T_i\) being relatively large compared to the range of \(T_i=0.05\%-0.2\%\) reported in experimental research (Monkewitz et al. 1990; Kyle and Sreenivasan 1993), where the global instability phenomenon was observed.

At the lateral boundaries of the computational domain, the axial velocity is assumed to be equal to \(U_{cf}\), and the remaining velocity components are equal to zero. The pressure is computed from the Neumann condition \({\textbf{n}}\cdot \nabla p = 0\), and the same applies to \(Y_{\alpha },\, h\). At the outlet plane, \(p=p_0\) and all velocity components and scalars are computed from a convective boundary condition \(\partial \phi /\partial t + U_{out}\partial \phi /\partial n = 0\) (\(\phi\) - a general variable) with the convection velocity calculated every time-step as the mean velocity over the outlet plane, limited such that \(U_{out} = \text {max}(U_{mean}, 0)\) (Orlanski 1976), where \(U_{mean}\) is the mean velocity on the outlet plane.

The computational domain was discretized by \(N_y=288\), \(N_x=N_z=192\) nodes in the axial and radial directions, respectively. The computational mesh was stretched radially and axially towards the nozzles so that in the region \(x,\,z \le 2D\) the cell had an almost uniform size \(\Delta x=\Delta z=0.03D\). In the axial direction, in the direct vicinity of the inlet, the cell size was equal to \(\Delta y=0.06D\). The shear layer thickness of the mean velocity profile within the region \(U_{suc} < U_y \le 0.99U_j\) was covered by 7 nodes. It should be noted that a coarser mesh (\(N_y=192\), \(N_x=N_z=160\)) was previously used in Tyliszczak (2015) to simulate a similar flow configuration (Markides and Mastorakos 2005) without suction, which yielded accurate solutions. Here, the number of nodes was increased in order to resolve both nozzle sections with cells of the same size, and to account for locally higher instantaneous velocity gradients that may potentially arise in the global instability regimes. All simulations were performed using a constant time step \(\Delta t=1\times 10^{-7}\) s, which corresponded to the Courant number in the range 0.25\(-\)0.5. The time-averaging procedure began once the flames were fully developed, i.e., after \(t=4\) ms from the beginning of the simulation, and continued over the time \(t_{ave}=7\) ms. After this time, the mean values and RMS of time-averaged quantities remained virtually unchanged. The simulations were run on 48 processors (Intel Xeon E5-2697 v3), and the real-time for a single simulation was approximately one month.

Fig. 3
figure 3

Instantaneous temperature at the main cross-section for flames at various suction strengths and turbulence intensities. Nine different cases are presented: \(\mathrm {Ti1\_I00}\) (a), \(\mathrm {Ti1\_I01}\) (b), \(\mathrm {Ti1\_I017}\) (c), \(\mathrm {Ti1\_I018}\) (d), \(\mathrm {Ti1\_I02}\) (e), \(\mathrm {Ti5\_I017}\) (f), \(\mathrm {Ti5\_I018}\) (g), \(\mathrm {Ti5\_I019}\) (h), \(\mathrm {Ti5\_I02}\) (i). The self-excited global oscillations involve (d, e, h, i)

Full size image
Fig. 4
figure 4

Side-jets visualized by instantaneous temperature for case \(\mathrm {Ti1\_I018}\). Subfigures show iso-surfaces (\(T=880,\,1500,\,2000\) K) and contours in the cross-section perpendicular to the jet axis at two different downstream positions from the inlet (\(y/D=4\) and \(y/D=7\)), marked by the horizontal lines in the figure on the left

Full size image

3 Results

In the following sections, we investigate the auto-ignition process, flame propagation, and stabilization phases in cases with different turbulence intensities and suction strengths. The cases are labeled as \(\textrm{Ti}T_i\_\textrm{I}I\), for instance, \(\textrm{Ti}1\_\textrm{I}01\) denotes the case with \(T_i=1\%\) and \(I=0.1\). The simulations start with the computational domain filled by the oxidizer. The fuel jet, the suction and the co-flowing stream are impulsively turned on simultaneously. The fuel jet then evolves freely in the domain and auto-ignites after mixing with the oxidizer. The flame then spreads in the domain and stabilizes in the direct vicinity of the inlet or as lifted, depending on the values of \(T_i\) and I. The difference between these two states is shown in Fig. 3 presenting contours of temperature in the main cross-section plane. These results were obtained in simulations of nine different cases \(\textrm{Ti}T_i\_\textrm{I}I\) and correspond to a time moment of \(t=4\) ms, when the flames were fully developed. It can be seen that applying sufficiently strong suction (Fig. 3d, e, h, i) can create flow regimes that prevent upstream flame propagation. The suction causes a counter-current flow around the fuel jet, which induces the global instability phenomenon. One can readily see that the picture of the flow is significantly different when this happens. A common sign of the global instability phenomenon is the formation of the side-jets (Monkewitz et al. 1989; Kyle and Sreenivasan 1993; Wawrzak and Tyliszczak 2022) well visualized in Fig. 4. They appear as streaks of low temperature iso-surfaces developing from the main jet. They are inclined to the main jet axis at various angles and their number can be different depending on the inlet conditions and time moment (Wawrzak and Tyliszczak 2022). In Fig. 4, there are seven side-jets randomly distributed along the azimuthal direction. According to Monkewitz et al. (1989), the main mechanism of the side-jets formation is the azimuthal instability deforming the toroidal vortical structures emerging near the inlet in the mixing layer region. They mutually interact and eject fluid away from the main jet stream.

Fig. 5
figure 5

Isosurfaces of the Q-parameter: \(Q=0.02\) s\(^{-2}\) (a, d), \(Q=2\) s\(^{-2}\) (b, c, e, f), colored by the mixture fraction. The axial velocity contours are presented in the central cross-section plane ‘x-y’. The white isolines denotes \(U_y=0\) m/s

Full size image

3.1 Coherent Toroidal Vortical Structures

Figure 5 displays the instantaneous flow fields near the inlet plane for a few representative cases. The results are presented as instantaneous iso-surfaces of the Q-parameter (\(Q=0.5(\vert \mathbf {\Omega }\vert ^2-\vert {\textbf{S}}\vert ^2)\), \(\mathbf {\Omega }\) - the vorticity tensor, \({\textbf{S}}\) - the rate of strain tensor), coloured by the mixture fraction \(\xi\), as well as contours of the streamwise velocity (\(U_y\)) in the central cross-section plane ‘x-y’. The Q-parameter is often used as an indicator of vortical structures (Hunt et al. 1988; Gohil et al. 2015; Tyliszczak 2015). The mixture fraction is computed following Bilger’s definition:

$$\begin{aligned} \xi =\frac{(Y_{\tiny {\text {H}}}-Y_{\tiny {\text {H,o}}})/2W_{\tiny {\text {H}}} -(Y_{\tiny {\text {O}}}-Y_{\tiny {\text {O,o}}})/W_{\tiny {\text {O}}}}{(Y_{\tiny {\text {H,f}}}-Y_{\tiny {\text {H,o}}})/2W_{\tiny {\text {H}}}-(Y_{\tiny {\text {O,f}}} -Y_{\tiny {\text {O,o}}})/W_{\tiny {\text {O}}}} \end{aligned}$$
(11)

where Y’s are the elemental mass fractions, W’s are the atomic weights, and the subscripts, f and o, correspond to fuel and air, respectively.

The white iso-lines in Fig. 5 represent the instantaneous axial velocity equal to zero, which can be roughly interpreted as a border of the region from which the fluid is sucked out of the computational domain. The analysis of the mass fractions of the sucked flow shows that it contains a negligible amount of fuel, less than \(0.2\%\) by mass, which is consisted with Lourenco et al. (1997) and Chan et al. (2002). Hence, one can convincingly assume that the change in the flow character does not stem from the alteration of the fuel-to-oxidizer ratio. The results in Fig. 5 represent solutions in regimes of convective (\(\mathrm {Ti1\_I017}\), \(\mathrm {Ti5\_I018}\)) and global instability (all other subfigures). In the latter case, coherent toroidal vortices close to the nozzle are clearly visible. It should be noted that for \(T_i=5\%\), the generated vortices are not as strong and well-formed as in the cases with \(T_i=1\%\). However, in both cases, the presence of these vortices, in addition to the side-jets, is a manifestation of the occurrence of the global instability phenomenon (Strykowski and Niccum 1991; Wawrzak et al. 2021). When moving downstream, the vortices rotate and a close analysis of the mixture fraction distribution on their surfaces shows that they transport fuel from the main jet stream outside of it, while the oxidizer is pushed towards the jet core. One can infer that this coincides with the change of the flame position. Fuel ejection by the side-jets and rotational motion of the toroidal vortices cause the mixture to become leaner. At the same time, local turbulence intensity increases, and these two factors prevent the flame development close to the inlet.

Fig. 6
figure 6

Amplitude spectra of the axial velocity at two locations from the inlet plane

Full size image

The interactions between the subsequent toroidal vortices occur mainly through longitudinal rib-like streamwise vortices, whose shapes are very similar to the ones obtained in excited jets (Kantharaju et al. 2020; Tyliszczak et al. 2022; Tyliszczak and Wawrzak 2022). As a result of these interactions, the large toroidal vortices become highly distorted and break up at an axial distance of approximately \(4-6D\). In Kantharaju et al. (2020); Tyliszczak et al. (2022); Tyliszczak and Wawrzak (2022), the toroidal vortices resulted from external excitation and appeared with a frequency defined by the excitation frequency. Here, they have a self-excited character without a priori defined frequency. However, their periodic occurrence is evidenced by the analysis of the temporal evolution of the axial velocity along the fuel jet axis. Figure 6 shows the amplitude spectra as a function of a non-dimensional frequency defined through the Strouhal number \(St_D=fD/U_j\). These spectra were calculated based on the time signals registered at \(y/D=1\) and \(y/D=4\). The well-defined and distinct peaks observed in the amplitude spectra immediately above the inlet plane indicate self-excited global oscillations (Strykowski and Niccum 1991; Wawrzak et al. 2021). One can find that the critical velocity ratio \(I_{GI}\), for which these oscillations appear at \(St_{D,GI}\approx 0.4\), is weakly dependent on \(T_i\). Specifically, it places within the range \(0.17<I_{GI}<0.18\) for \(T_i=1\%\) and \(0.18<I_{GI}<0.19\) for \(T_i=5\%\). Worth noticing is that the localization of \(St_{D,GI}\) and its harmonics remain unchanged along the jet. Additionally, for \(T_i=1\%\) also the magnitude of the observed peaks does not significantly change and strong oscillations are observed even downstream of \(y/D=4\). This agrees well with the results presented in Figs. 5b, c where large vortices are seen even around \(y/D=6\).

In cases with \(I<I_{GI}\), the spectra at \(y/D=1\) do not show any characteristic frequency. Such frequencies appear only at \(y/D=4\), but not as a clear peak, rather as a broadband increase in fluctuations at a level approximately two orders of magnitude smaller than for \(I>I_{GI}\).

Fig. 7
figure 7

Time-averaged axial velocity (mean and fluctuations) and mixture fraction. Contours (a) are shown for case \(\mathrm {Ti1\_I02}\). Profiles (b) are gathered along the white vertical/horizontal line marked in the subfigure (a)

Full size image

The periodic shedding of strong toroidal vortices is manifested in the time-averaged velocity distribution. Figure 7a shows the contours of the mean axial velocity and its fluctuations for case \(\mathrm {Ti1\_I02}\). The large fluctuations observed throughout the entire jet region suggest that the observed absolute instability mode can be classified as Mode II (Strykowski and Niccum 1991; Strykowski and Wilcoxon 1993; Jendoubi and Strykowski 1994; Lesshafft and Huerre 2007). The differences in the velocity distribution in the convective and globally unstable flow regimes are presented in Fig. 7b. It shows the profiles of the time-averaged axial velocity and its fluctuations along the centreline and along radial direction at \(y/D=2\) marked in Fig. 7a the white line perpendicular to the jest axis. Additionally, the profiles of the mixture fraction along this line are also presented. For cases \(\mathrm {Ti1\_I00}\) and \(\mathrm {Ti1\_I01}\), the mean velocity is almost equal to the inlet jet velocity up to a distance of \(y/D=10\). The long potential core observed in these cases is a consequence of the low level of fluctuations present across the jet. At a distance of \(y/D=2\), the fluctuations only reach a value of \(\langle u'_y\rangle /U_j\approx 0.01\). In this case, the mixing process between the fuel and oxidizer is very ineffective and holds mainly through molecular diffusion in the thin shear layer. On the contrary, for cases \(\mathrm {Ti1\_I02}\) and \(\mathrm {Ti5\_I02}\) when the flow becomes globally unstable, the mean jet velocity drops almost immediately behind the inlet. Referring to the results presented in Fig. 5, we can infer that the changes in the inclination of the velocity profiles at \(y/D=2\) and \(y/D=6\) are related to the formation and destruction of the large toroidal vortices. At \(y/D=2\), the occurrence of local maxima of fluctuations in the shear layer in the region \(0.3<x/D<0.7\) implies intense mixing, making the mixture in the central part of the flow significantly leaner. As will be shown in the next section, fluctuations at the level of \(\langle u'_y\rangle /U_j\approx 0.2\) lead to large values of the scalar dissipation rate (\(SDR=2D(\nabla \xi \nabla \xi )\)) that, according to Mastorakos (2009), prevent flame development.

Fig. 8
figure 8

Instantaneous distributions of the H\(_2\) and OH mass fraction, heat release rate (HRR), scalar dissipation rate (SDR), and the normalized Takeno index (TI) for cases: \(\mathrm {Ti1\_I02}\) during the ignition (a) and in fully developed state (b), \(\mathrm {Ti5\_I02}\) (c), \(\mathrm {Ti5\_I018}\) (d). Results along the green line marked in subfigure (b) are shown in Fig. 9

Full size image
Fig. 9
figure 9

Profiles of H\(_2\), O\(_2\), OH mass fractions, HRR, SDR and TI across the reaction zone (green line in Fig. 8b) for case \(\mathrm {Ti1\_I02}\)

Full size image

3.2 Flame Structure

Figure 8 shows instantaneous flame topology represented by H\(_2\) and OH species mass fractions, heat release rate (HRR), scalar dissipation rate (SDR), and the normalized Takeno index (TI), which is defined as \(TI=\nabla Y_\text {H2}\cdot \nabla Y_\text {O2}/\vert \nabla Y_\text {H2}\vert \vert \nabla Y_\text {O2}\vert\) (Yamashita et al. 1996). The Takeno index value of \(TI=1\) indicates perfectly aligned fuel and oxidizer gradients, corresponding to fully premixed combustion regimes, while \(TI=-1\) corresponds to non-premixed combustion. In Fig. 8, the flame front is represented by the heat release rate \({HRR}>1\times 10^8\) J/m\(^3\)s. Subfigures 8a, b show the solutions for case \(\mathrm {Ti1\_I02}\) obtained shortly after ignition and when the flame is fully developed. The results presented in subfigures 8c, d refer to cases \(\mathrm {Ti5\_I02}\) and \(\mathrm {Ti5\_I018}\), respectively. They illustrate how a subtle change in suction strength (\(I=0.2\rightarrow 0.18\)) can alter the flame dynamics and position. Analysis of the instantaneous results shows that the time when the first flame kernels appear is weakly dependent on I (see Sect. 3.4). Furthermore, their spatial localizations downstream of the inlet are almost independent of I, and occurr around \(y/D=10\). This agrees quite well with the results obtained by Markides and Mastorakos (2005) and Tyliszczak (2015), suggesting that, in the present flow configuration, the auto-ignition process is mostly related to the rate of proceeding of the chemical reactions rather than suction strength. However, suction strength has a huge impact on the subsequent flame evolution phase, as previously presented. When \(I>I_{GI}\) (cases \(\mathrm {Ti1\_I02}\) and \(\mathrm {Ti5\_I02}\), Figs. 8a – c), the initial flame kernels spread downstream and propagate upstream only up to \(y/D\approx 6\). Apparently, intensified mixing does not necessarily mean more favorable regimes for flame development. The leaning of the mixture and large local values of SRR upstream of the spreading flame prevent its downstream evolution. Instantaneous solutions show that freshly ignited “pockets” of the mixture that could potentially propagate towards the inlet flow part are extinguished by streams of a very lean mixture introduced into local reaction zones by axially traveling toroidal vortices. In effect, the flame eventually stabilizes at \(y/D\approx 6\) and manifests a very complex behavior with a wavy reaction zone spreading radially in between \(-1.2<r/D<1.2\). The mixture approaching this zone is rich with an equivalence ratio locally varying in the range \(\phi =1-5\). Unlike as in case of a lifted flame studied by Domingo et al. (2005), a tribrachial flame base in which both premixed and non-premixed combustion regions coexist, does not occur here. A variability of instantaneous values of H\(_2\), O\(_2\), OH mass fractions, HRR, SDR and TI across the reaction zone (green line in Fig. 8b) is presented in Fig. 9. The Takeno index indicates that at the beginning of the reaction zone, i.e., where \({HRR}>1\times 10^8\) J/m\(^3\)s and the OH species appears, the combustion process has a non-premixed character (\(TI<0\)). In the center of the reaction zone, however, it changes to an almost perfectly premixed regime (\(TI\approx 1\)) that again changes to a non-premixed regime (\(TI\approx -1\)) in the region of the developed flame. The reason for that is the rich mixture upstream of the reaction zone. The level of H\(_2\) mass fractions decreases twice passing through the premixed flame front, while the amount of O\(_2\) drops almost to zero. It flows into the region above the reaction zone from the radial direction, and as a result, \(\nabla Y_\text {O2}\) is not aligned with \(\nabla Y_\text {H2}\) as H\(_2\) passes through the reaction zone in the axial direction. The highly turbulent flow character causes very intense combustion, and almost all of the H\(_2\) is consumed. This demonstrates that although the global instability phenomenon shifts the flame far from the inlet, it enhances the mixing process to a level that ensures the burning of all fuel in a compact domain. On the contrary, in regimes of convective instability, when \(I<I_{GI}\) (case \(\mathrm {Ti5\_I018}\), Fig. 8d), the flame is long and appears laminar, with an elongated diffusive reaction zone located in the shear layer. In this case, a large amount of unburned fuel leaves the computational domain.

3.3 Lift-Off Height, Flame Volume, and Maximum Temperature Evolutions

Significant differences in the instantaneous flame dynamics in the convective and global instability regimes are scrutinized based on the evolutions of lift-off heights, the flames volumes, and maximum temperature inside the computational domain, which are presented in Fig. 10. The lift-off height was determined as the distance from the inlet where the temperature is larger 1% above the co-flow, i.e., \(L_H=\min (y^{T\ge 1.01T_{cf}})\). This measure of \(L_H\) has been used in previous studies, such as Stanković et al. (2013), among others. The flame volume can be roughly calculated as the sum of the volumes of the computational cells in which the temperature is larger than some threshold value, here we arbitrarily took 1200 K and define \(V_{flame}=\sum V_{cell}^{T\ge 1200\textrm{K}}\). The reported maximum temperature is the highest temperature found in the computational domain, regardless of where it occurs. The results obtained using the ESF method are also shown in Fig. 10. As mentioned in Sect. 2.1, these results aim to demonstrate that the ‘no model’ approach is not biased by significant errors resulting from neglecting the temperature and species mass fraction fluctuations in the calculation of chemical reaction terms. The simulations employing the ESF model have been performed for only selected cases as they are much more costly in the sense of computiational time. These test cases include conditions where the flow is in convective (\(\mathrm {Ti1\_I01}\)) and absolutely unstable (\(\mathrm {Ti1\_I02}\)) regimes. Obtaining the solutions with 4 and 8 stochastic fields (results denoted in Fig. 10 as 4ESF and 8ESF ) took almost two and four months, respectively. It can be observed that differences between the results obtained with the ‘no model’ approach and the ESF model are small and only quantitative, i.e., when using the ESF model, the flame remains attached/lifted, as it did with the ‘no model’ approach. Additionally, for the lower suction strength case (\(\mathrm {Ti1\_I01}\)), where the flame approaches the inlet plane and the lift-off height \(L_H\) decreases, the differences between the ‘no model’ approach and the ESF model are more pronounced than for the lifted flame case \(\mathrm {Ti1\_I02}\). The discrepancies between the ‘no model’ approach and the ESF model observed in Fig. 10 are primarily due to differences in auto-ignition times. As can be deduced from the profiles of the maximum temperature, the flame appears earlier when the ESF model is employed. This discrepancy arises because the ESF approach considers micromixing effects associated with the small scales that contribute to the ignition process. The influence of this micromixing term becomes more noticeable under reduced suction conditions, where overall mixing is less intensive compared to flows in global instability regimes at higher I. It is very important to remark that increasing the number of stochastic fields (\(N_s=4\rightarrow 8\)) does not significantly change the solution. Especially, taking into account the lifted flame in the global instability regimes.

Fig. 10
figure 10

Evolution of the lift-off height of the flame (\(L_H\)), the flame volume (\(V_{flame}\)), and the maximum temperature (\(T_{max}\)) for inlet turbulence intensity \(T_i=1\%\) (a) and \(T_i=5\%\) (b)

Full size image

Regarding the auto-ignition phase, it can be seen that it is weakly dependent on the suction strength, as mentioned in the previous section. The \(V_{flame}\) for \(I=0.2\) starts to increase only slightly later, but the rate of its step increase is virtually the same for all cases. Similarly, during the stabilization phase, the flames attain their final positions at approximately \(t=2\) ms. When \(I<I_{GI}\), the \(L_H\) drops down quickly, but the moment when it happens depends on I. The larger I is, the longer the flame remains away from the inlet. On the other hand, for \(I>I_{GI}\), the flame stabilizes at a distance of \(y/D\approx 6\), and \(L_H\) changes slightly depending on the flow variations upstream of the flame front. In these cases, the maximum temperature is approximately 100 K higher, and \(V_{flame}\) is approximately three times larger than the flame volume for \(I<I_{GI}\). Worth noticing is that \(T_i\) has small impact on the solution when the flame is lifted. This is consisted with findings reported in Monkewitz et al. (1990), where it was observed that the impact of the inlet fluctuation level on a behavior of the jet in the globally unstable regime is small, since perturbation growing in time are limited only by non-linear interactions. However, the initial turbulence intensity has the impact on I needed to trigger the globally unstable regimes. For \(T_i=1\%\), the suction with \(I=0.18\) is sufficient, while for \(T_i=5\%\), it must be larger (\(I=0.2\)). An interesting result is obtained for \(T_i=5\%\) and \(I=0.19\), where the flame remained lifted for a relatively long time but eventually propagated upstream. The mechanism of this propagation is discussed in the next section.

Fig. 11
figure 11

Evolution of the temperature during transition from the lifted to attached flame in case \(\mathrm {Ti5\_I019}\)

Full size image

3.4 Transition from Lifted to Attached Flame

Thus far, two distinct scenarios have been discussed in which flames quickly stabilized as either lifted or attached depending on I. However, the \(\mathrm {Ti5\_I019}\) case presents an exception from this rule, as the flame remained lifted for an extended period of time (as shown in Fig. 10) before suddenly propagating upstream. We note that a change from \(I=0.19\) to \(I=0.2\) can have quite large consequences. In fact, referring to \(I=0.19\) the change \(\Delta I=0.01\) corresponds to about 5% change in I. At the flame and flow conditions considered here the response of the dynamics to changes in the suction parameters is found to be highly sensitive - the modest change in I turns out to have a qualitative effect on the final flame position. We hypothesize that this is a characteristic of a bifurcation in which crucial parameters appear to traverse a critical value, inducing major changes.

The transition from lifted to attached state is illustrated in the time sequence of the temperature field presented in Fig. 11, which occurs between \(t=4.6\) ms and \(t=6.5\) ms. As shown in the previous sections, the lift-off mechanism involves the combined effects of (i) enhanced mixing with a continuous supply of a large amount of oxidizer through the large coherent structures induced by the global instability, and, (ii) modulation of the flame surface area via interaction with these vortices. In lifted flames, the auto-ignition process occurring at a nearly constant spatial localization has a crucial impact on the flame position and its stability. In the case \(\mathrm {Ti5\_I019}\), a well-mixed pocket of fuel and oxidizer travels towards the flame front, initiating the transition at \(t=4.6\) ms. Once this pocket of trapped reactants is consumed by the flame front, there is a temporal decrease in the lift-off height. Subsequently, at \(t=4.8\) ms, a flame tail emerges on the left side of the primary combustion zone, propagating towards the nozzle. As shown in Fig. 8a–c, lifted flames exhibit a premixed-type flame front. In these regimes, the flame propagation speed is substantial. If it exceeds the velocity of the incoming mixture, the flame propagates upstream. This is most likely observed in the case \(\mathrm {Ti5\_I019}\) soon after a stronger flame tail develops. The temperature close to the inlet rises, which leads to an increase in molecular viscosity, almost entirely damping the impact of suction. This is followed by flame anchoring as can be seen at the time moment \(t=6.5\) ms (right subfigure in Fig. 11). As a result, the flame appears similar to those in which the suction is significantly lower than \(I_{GI}\).

4 Conclusions

LES studies have been carried out to analyze the dynamics of nitrogen-diluted hydrogen flames in the counter-current configuration with co-axial nozzles, at different levels of suction strength (\(I=0.0-0.2\)) and two inflow turbulence intensities (\(T_i=1\%\) and \(T_i=5\%\)). It has been shown that the critical velocity ratio between the flow in the two nozzles necessary to trigger the global instability is sensitive to the turbulence intensity and increases with \(T_i\). Additionally, it is shown that increasing \(T_i\) can lead to re-attachment of already lifted flames. Flame lifting, resulting from the global instability regime formed upstream of the flame base, was found for \(I\ge 0.18\) and \(I\ge 0.2\), respectively for \(T_i=1\%\) and \(T_i=5\%\).

During the transition to global instability, large toroidal structures form immediately above the inlet plane. Their coherent motion was confirmed in the velocity spectra registered at the fuel jet axis. These self-excited oscillations tend to enhance mixing and lead to a leaner mixture in the central flow. This, along with a high level of scalar dissipation, alters qualitatively the flame character (attached/lifted) but also causes significant changes in the flame characteristics.

Analysis of the flame index in the flame stabilization zone revealed that the flame front is mainly premixed and followed by a very intense combustion zone. Consequently, a significant radial widening of the flame and a much quicker consumption of fuel were found when comparing the lifted to the attached flame. This may have important practical implications. The global instability generated in the region of relatively strong counter-current flow could allow for a significant shortening of combustion chambers and hence novel design opportunities.