Kinetic Energy Budget in Turbulent Flows of Dilute Polymer Solutions

Abstract

Direct numerical simulation of a turbulent pipe flow of a realistic solution of $10^8$ polymers, modelled as finitely extensible nonlinear elastic (FENE) dumbbells, and directly momentum coupled with the incompressible Navier–Stokes equations, are performed by means of an Eulerian-Lagrangian approach. Besides the drag reduction, the polymers significantly modify mean and turbulent kinetic energy budgets. The polymer backreaction to the solvent reduces the Reynolds stress and thus decreases the turbulent production and, at large Weissenberg number, the polymers act as a source of turbulent kinetic energy for $y^+> 40$, leading to an increase in the dissipation. This effect is peculiar to large Weissenberg polymers and it is particularly apparent at a small Reynolds number. At a smaller Weissenberg number, the effect of the polymers remains confined in the buffer layer, with the kinetic energy budget not significantly altered elsewhere.

1 Introduction

After the experiments of Toms (1949), who showed that the addition of a tiny amount of long polymer chains in a turbulent flow of a Newtonian solvent can drastically reduce the drag, the drag reduction (DR) phenomenon gained large interest, both from the experimental and the numerical point of view. Experiments demonstrated that drag reduction (DR) is due to the mechanical interaction between the polymer chains and the turbulent flow (Xi 2019), and can reach large amounts, up to $80\%$ (Procaccia et al. 2008). Since the experiments cannot show the actual interaction between polymer chains and turbulent flow dynamics, direct numerical simulations (DNS) of the Navier-Stokes equations have been performed since the pioneering work of Sureshkumar et al. (1997), using the viscoelastic FENE-P (finitely extensible nonlinear elastic with Peterlin’s approximation) model (Bird et al. 1987) to account for polymer dynamics and the polymer effect on turbulence. Numerical simulations with the FENE-P model (Dimitropoulos et al. 1998; De Angelis et al. 2002) helped to capture insights into the polymer drag reduction phenomenon, showing qualitative accordance with the experimental observations.

Both experiments and numerical simulations agree that the polymer effect on the solvent is to reduce the momentum flux to the wall. The main modification of turbulence occurs in the buffer layer (Virk 1975) where the Reynolds stress peaks. The reduction of the Reynolds stress causes a consistent decrease in the production term in the turbulent kinetic energy budget, meaning that less energy is transferred from the mean flow to the fluctuating flow field. By analysing the fluctuating fluid velocity - polymer force correlation, De Angelis et al. (2002) suggested that the polymers extract energy from the turbulent fluctuations in most of the flow field (negative correlation), while the viscoelastic forces perform a positive work to the fluid velocity (positive correlation) within the viscous sublayer.

Despite the phenomenon of drag reduction being known since the ’40 s, the mechanism at its basis is not fully understood. From the numerical point of view, it is recognised that the FENE-P model presents some shortcomings (Graham 2004; Keunings 1997), that did not allow to reproduce realistic polymer systems (Dubief et al. 2022). In fact, DNSs of realistic polymer solutions require a Lagrangian description of the polymer phase to overcome the FENE-P model limitations (see Peters and Schumacher 2007; Watanabe and Gotoh 2013 for two applications in unbounded 3D turbulence). Such simulations have been performed only recently in wall-bounded turbulence, see (Serafini et al. 2022, 2022) for numerical simulations in pipe flows at different friction Reynolds numbers, thanks to massive MPI-GPUs parallelization and physically consistent approaches to account for the polymer back-reaction on the Newtonian solvent (Gualtieri et al. 2015). In particular, it is shown that, at large Weissenberg number $\textrm{Wi}$ (ratio of the polymer relaxation time and the fluid time scale), DR is entirely induced by the polymers elongated to their maximum extension, and has a weak dependence on the Reynolds number. Instead, at a fixed Reynolds number and increasing Weissenberg number, DR grows up to an asymptote (Serafini et al. 2023).

In this paper, we investigate the polymer modification to the kinetic energy path by analysing spatial fluxes, production, and dissipation of kinetic energy associated with both the mean flow and the velocity fluctuations. We present a comparison between two different Reynolds numbers, namely $\textrm{Re}_{\tau }=180$ and $\textrm{Re}_{\tau }=320$ in the asymptotic Weissenberg number range, i.e $\textrm{Wi}> 10^3$, and a comparison between two different Weissenberg number, namely $\textrm{Wi}=10$ and $\textrm{Wi}=10^4$, at fixed friction Reynolds number $\textrm{Re}_{\tau }=180$. At the smallest Weissenberg number, we compare the results given by the Eulerian-Lagrangian FENE model with those provided by the classical FENE-P model.

2 Methodology

The turbulent flow is considered in a pipe geometry. It is described by the (dimensionless) incompressible Navier–Stokes equations in cylindrical coordinates $(\theta ,r,z)$, completed with the no-slip condition at the wall $\varvec{u}(t,\theta ,r=1,z)= \textbf{0}$. The Navier-Stokes system is coupled with the evolution of $N_p$ polymer macromolecules, modelled as finitely extensible nonlinear elastic (FENE) dumbbells (two massless beads at the chain ends $\varvec{x}_{1/2}^{(j)}$, connected by an entropic nonlinear spring).

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \varvec{\nabla }\cdot \varvec{u}= 0 \\ \displaystyle \frac{\partial \varvec{u}}{\partial t} + \varvec{\nabla }\cdot (\varvec{u}\otimes \varvec{u}) = -\varvec{\nabla }p + \frac{1}{\textrm{Re}} \varvec{\nabla }^2 \varvec{u}+ \varvec{F}\\ \displaystyle \frac{d \varvec{x}_{c}^{(j)}}{d t} = \frac{\varvec{u}_{1}^{(j)}+\varvec{u}_{2}^{(j)}}{2} + \frac{L\, h_{eq}}{\sqrt{3\textrm{Wi}}} \frac{\varvec{\xi }_{1}^{(j)}+\varvec{\xi }_{2}^{(j)}}{2} \\ \displaystyle \frac{d \varvec{h}^{(j)}}{d t} = \frac{{\check{\varvec{u}}}_{2}^{(j)}-{\check{\varvec{u}}}_{1}^{(j)}}{L} - \frac{\varvec{h}^{(j)}}{\textrm{Wi}(1-H^{(j)2})} + \frac{h_{eq}\left( \varvec{\xi }_{2}^{(j)} -\varvec{\xi }_{1}^{(j)}\right) }{\sqrt{3\textrm{Wi}}} \\ \end{array}\right. } \, \end{aligned}$$

(1)

The system (1) is made dimensionless using the following reference quantities (with asterisks denoting dimensional quantities): the pipe radius $\ell _{0}^*$, the solvent density $\rho ^*$, the bulk velocity $U_{b}^*=Q_{b}^*/(\pi \ell _{0}^{*2})$ of the Newtonian case ($Q_b^*$ is the volumetric flow rate), and the solvent viscosity $\mu ^*$. In eq. (1), $\varvec{u}(t,\theta ,r,z)$ is the fluid velocity, $p(t,\theta ,r,z)$ the hydrodynamic pressure, $\varvec{x}_{c}^{(j)}=(\varvec{x}_1^{(j)}+\varvec{x}_2^{(j)})/2$ is the coordinate of polymer centre, $\varvec{h}^{(j)}=(\varvec{x}_{2}^{(j)}-\varvec{x}_{1}^{(j)})/L$ the end-to-end vector that connects the two beads of the dumbbell, normalised by the polymer contour length L. Finally, $H^{(j)}=\Vert \varvec{h}^{(j)}\Vert$ is the dumbbell length, and $h_{eq}$ is the equilibrium size of the chain determined by the Brownian forces $\varvec{\xi }_{1/2}^{(j)}$ in a quiet solvent.

The back-reaction of the polymers to the solvent is accounted for by the polymer forcing term

$$\begin{aligned} \nonumber \varvec{F}&= - \sum \limits _{j=1}^{N_{p}} \varvec{D}_{1}^{(j)} \delta (\varvec{x}-\varvec{x}_{1}^{(j)}) + \varvec{D}_{2}^{(j)} \delta (\varvec{x}-\varvec{x}_{2}^{(j)}) \\&\simeq \frac{1}{2\textrm{Wi}\, \textrm{Re}_p} \sum _{j=1}^{N_{p}} \frac{\varvec{h}^{(j)}}{1-H^{(j)2}} \frac{\delta (\varvec{x}-\varvec{x}_{1}^{(j)})-\delta (\varvec{x}-\varvec{x}_{2}^{(j)})}{c_o L} \, , \end{aligned}$$

(2)

given the friction forces $\varvec{D}_{1/2}^{(j)} = \gamma ({\check{\varvec{u}}}_{1/2}^{(j)}-{\varvec{v}}_{1/2}^{(j)})$ mutually exchanged by the polymer beads with the Newtonian solvent.

In the previous expression of the friction force ${\varvec{v}}_{1/2}^{(j)}$ is the velocity of the bead, ${\check{\varvec{u}}}_{1/2}^{(j)}$ the velocity of the fluid at the position of the bead, deprived of the bead’s self-interaction contribution (Maxey and Riley 1983), and $\gamma$ is the friction coefficient of the beads. For a dumbbell, the dimensional friction coefficient can be related to the other polymer parameters as follows Serafini et al. (2022)

$$\begin{aligned} \gamma ^* = 2\, \tau ^* \, \frac{3 k_B^* \theta ^*}{L^{*2} h_{eq}^{*2}}, \end{aligned}$$

(3)

where $\tau ^*$ is the relaxation time of the macromolecule, $k_B^*$ the Boltzmann constant and $\theta ^*$ the absolute temperature.

Neglecting the Brownian contribution, the feedback force can be rewritten as a function of the end-to-end vector $\varvec{h}$. In eq. (2) $c_o$ is the polymer concentration. The friction forces $\varvec{D}_{1/2}$ are localised at the instantaneous position occupied by the beads $\varvec{x}_{1/2}$ and they need to be regularised to be accounted for in the Navier–Stokes system. The regularisation is provided by the Exact Regularised Point Particle method (ERPP) (Battista et al. 2019; Motta et al. 2020).

Finally, we describe the dimensionless parameters appearing in eqns. (1) and (2). $\textrm{Re}=\rho ^*U_{b}^*\ell _{0}^*/\mu ^*$ is the bulk Reynolds number, $\textrm{Wi}=\tau ^*/(\ell _{0}^*/U_{b}^*)$, is called Weissenberg number, and $\textrm{Re}_p=\rho ^*U_{b}^*\ell _{0}^*/\mu _p^*$ is the polymer Reynolds number, built with the quantity $\mu _p^*=c_o^*\gamma ^* L^{*2}$ which is dimensionally a viscosity.

Simulations are performed with periodic boundary conditions in the axial/tangential direction, and at imposed pressure gradient, i.e. fixed friction Reynolds number $Re_\tau =u_\tau ^* \ell _0^* / \nu ^*$ (where $u_\tau ^*=\sqrt{\tau _w^*/\rho ^*}$ is the friction velocity). The drag reduction appears as a flow rate increase and can be evaluated in terms of friction coefficients $c_f^{(0)/(p)}$ (with $^{(0)}$ and $^{(p)}$ denoting Newtonian and polymer case respectively),

$$\begin{aligned} DR = \frac{c_{f}^{(0)} - c_{f}^{(p)}}{c_{f}^{(0)}} = 1 - \left( \frac{Q_{b}^{(0)}}{Q_{b}^{(p)}}\right) ^2. \end{aligned}$$

(4)

For the Eulerian-Eulerian FENE-P model (Bird et al. 1987), the polymers are modelled according to the conformation tensor ${\textbf{C}}= \langle \varvec{h}\otimes \varvec{h}\rangle$ that represents the covariance of the local polymer population. The corresponding equation for ${\textbf{C}}$ is

$$\begin{aligned} \frac{d {\textbf{C}}}{d t} = {\textbf{C}}\cdot \varvec{\nabla }\varvec{u}+ ({\textbf{C}}\cdot \varvec{\nabla }\varvec{u})^T - \frac{2}{\textrm{Wi}} \left[ \frac{1-3\, h_{eq}^2}{1^2-\textrm{Tr}({\textbf{C}})} {\textbf{C}}-\frac{h_{eq}^2}{3}\tilde{\textrm{I}} \right] . \end{aligned}$$

(5)

Equation (5) can be derived by performing an ensemble average over the local polymer population (here denoted by the angular brackets) after the following hypotheses are made: i) uniform polymer concentration $c_o$, ii) the velocity of the beads ${\check{\varvec{u}}}_{1/2}^{(j)}$ can be linearised around the polymer centre $\varvec{x}_c$, iii) the diffusion of the polymer centre is neglected and the polymers are simply advected by the fluid velocity. Finally, Peterlin’s approximation needs to be considered as a closure assumption to constrain the average polymer extension $\textrm{Tr}({\textbf{C}})$ to the polymer contour length L. This assumption is known to introduce artefacts in turbulent flows, as polymers are allowed to overcome their maximum length, being only the polymer extension variance constrained. The polymer forcing is evaluated as the divergence of the extra-stress tensor, $\varvec{F}= \varvec{\nabla }\cdot T_p^{FP}$, whose expression is

$$\begin{aligned} {\textbf{T}}_p^{FP} = \frac{1}{2 \textrm{Wi}\textrm{Re}_p} \left[ \frac{1^2-3\, h_{eq}^2}{1^2-\textrm{Tr}({\textbf{C}})} {\textbf{C}}-\frac{h_{eq}^2}{3}\tilde{\textrm{I}} \right] . \end{aligned}$$

(6)

The system of equations is numerically solved (Direct Numerical Simulation) on a staggered grid in cylindrical coordinates ($\theta ,r,z$) using a projection method to enforce velocity solenoidality. All the time integrations are performed using a four-step, third-order, Runge–Kutta low-storage scheme. The domain dimensionless size is $(2\pi \times 1 \times 6\pi )$, while the number of grid points are reported in tab. 1. In the radial direction, a minimum grid size $\Delta r^+ \simeq 0.5$ at the wall and a maximum grid size $\Delta r^+ \simeq 2$ at the pipe centre are obtained by means of a coordinate transformation. The high resolution in the axial and tangential directions is employed in the polymer-laden simulations to ensure an accurate regularisation of the back-reaction of the beads (Gualtieri et al. 2015; Battista et al. 2019). The momentum equation and the conformation tensor equation, apart from the convective term of the latter, are discretized in space with a second-order centred scheme. The BCDS scheme (Waterson and Deconinck 2007) is used to treat the convective term of the equation for ${\textbf{C}}$, to avoid the addition of artificial diffusion. The numerical solution is accelerated using a hybrid MPI+GPUs approach, using the 2DECOMP & FFT library (Li and Laizet 2010). Simulations are run on the CINECA Marconi100 cluster. Concerning polymer-laden simulations, 32 GPUs were used for each simulation for approximately 20000 core-hours to collect 200 statistically steady-state uncorrelated fields, while all FENE-P simulations ran on 8 GPUs for approximately 7200 core-hours to collect 200 statistically steady-state uncorrelated fields.

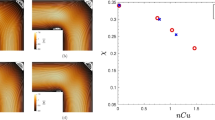
Table 1 summerises the simulation parameters, while an illustrative example of the flow configuration is reported in Fig. 1 where the instantaneous field of the turbulent kinetic energy is shown as a contour plot for the FENE and FENE-P simulations.

Table 1 Simulation parameters. From left to right: simulation codename; grid size in azimuthal, radial and axial directions respectively; friction Reynolds number $\textrm{Re}_\tau$, and Weissenberg number $\textrm{Wi}$. N denotes the Newtonian simulations, D the FENE dumbbell simulations, and FP the FENE-P simulation

Fig. 1

Example of the flow configuration and snapshot of turbulent kinetic energy field for the Eulerian-Lagrangian FENE simulation (left) and for FENE-P simulation (right) at $\textrm{Re}_{\tau }=180$ and $\textrm{Wi}=10$

3 Results

Fig. 2

Mean square velocity fluctuations and turbulent kinetic energy at $\textrm{Re}_\tau = 180$, panel a, and $\textrm{Re}_\tau = 320$, panel b. Solid line: $\langle u_z'^2 \rangle$, dashed line: $\langle u_r'^2 \rangle$, dot-dashed line: $\langle u_\theta '^2 \rangle$, solid line with circles: $k_T$

As shown in previous works the drag reduction, defined in eq. (4), increases up to about $27\%$ with the Weissenberg number, and it is not significantly affected by an increase in the Reynolds number. As also captured by simulations with the FENE-P model, DR is mainly due to the depletion of the Reynolds stress. Here we address how the polymers alter the dynamics of the kinetic energy of the mean velocity ($k_M = \langle \varvec{u}\rangle ^2/2$) and fluctuating velocity ($k_T = \langle \varvec{u}'^2 \rangle /2$), respectively,

$$\begin{aligned} \begin{aligned} \varvec{\nabla }\cdot {\varvec{\Phi }}_M&=-\mathcal{P} - \varepsilon _M + \langle \varvec{F}\rangle \cdot \langle \varvec{u}\rangle + P_w\\ \varvec{\nabla }\cdot {\varvec{\Phi }}_T&= \mathcal{P} - \varepsilon _T + \langle \varvec{F}' \cdot \varvec{u}' \rangle . \end{aligned} \end{aligned}$$

(7)

On the left-hand side of Eq. 7, we find the divergence of the spatial fluxes $\varvec{\Phi }_M$ and $\varvec{\Phi }_T$, whose expressions are the following:

$$\begin{aligned} \begin{aligned} {\varvec{\Phi }}_M&= \langle \varvec{u}\rangle k_M + \langle \varvec{u}\rangle \langle p \rangle - \frac{1}{\textrm{Re}}\varvec{\nabla }k_M +\langle \varvec{u}\rangle \cdot \langle \varvec{u}' \otimes \varvec{u}' \rangle \\ {\varvec{\Phi }}_T&= \langle \varvec{u}\rangle k_T +\langle \varvec{u}' p' \rangle - \frac{1}{\textrm{Re}} \varvec{\nabla }k_T + \frac{1}{2}\langle \varvec{u}' \varvec{u}'^2 \rangle \\ \end{aligned}. \end{aligned}$$

(8)

Due to the symmetry of the pipe flow, the divergence of the fluxes $\varvec{\nabla }\cdot (\langle \varvec{u}\rangle k_M)$, $\varvec{\nabla }\cdot (\langle \varvec{u}\rangle k_T)$, and $\varvec{\nabla }\cdot (\langle \varvec{u}\rangle \langle p \rangle )$ are statistically zero and they are not reported in the budget.

On the right-hand side of Eq. 7 we find the production term $\mathcal{P}=-\langle \varvec{u}' \otimes \varvec{u}' \rangle : \varvec{\nabla }\langle \varvec{u}\rangle$, the dissipation $\varepsilon _{M}=\varvec{\nabla }\langle \varvec{u}\rangle :\varvec{\nabla }\langle \varvec{u}\rangle /\textrm{Re}$ of the mean flow, the dissipation of the fluctuating field $\varepsilon _{T}= \langle \varvec{\nabla }\varvec{u}':\varvec{\nabla }\varvec{u}'\rangle /\textrm{Re}$, and the energy source/sink $\langle \varvec{F}\rangle \cdot \langle \varvec{u}\rangle$ and $\langle \varvec{F}' \cdot \varvec{u}' \rangle$ associated with the mean $\langle \varvec{F}\rangle$ and fluctuating $\varvec{F}'$ polymer coupling term. Finally, $P_w = -dp/dz \Vert _0 \langle \varvec{u}\rangle$ accounts for the power injected into the system via the imposed pressure gradient $dp/dz \Vert _0$.

Figure 2 reports the mean square velocity fluctuations and the turbulent kinetic energy $k_T$, for the FENE simulations at $\textrm{Re}_{\tau }=180$, panel (a), and $\textrm{Re}_{\tau }=320$, panel (b). As a common factor in the polymer-laden case, streamwise velocity fluctuations increase above $y^+\simeq 10$ with respect to the Newtonian case while tangential and radial components decrease in the entire pipe cross-section. These modifications result in a slight increase in turbulence kinetic energy, especially at the larger Reynolds number $\textrm{Re}_\tau = 320$. An interesting difference between the profiles at different Reynolds numbers appears close to the pipe centre, where at $\textrm{Re}_\tau =180$ axial velocity fluctuations are decreased with respect to the Newtonian case, with a companion decrease of the turbulence intensity. Besides the modification of the turbulent kinetic energy profile, another consequence of the reduced axial fluctuations is the decrease of large-scale anisotropy in the bulk region, reported in Fig. 3. The large-scale anisotropy is measured in terms of the parameter $b = \Vert \textbf{b} \Vert$ where $\textbf{b}$ is the (normalised) deviatoric part of the Reynolds stress tensor

$$\begin{aligned} b_{ij} = \frac{\langle u'_i u'_j \rangle }{\langle u'_k u'_k \rangle } - \frac{1}{3} \delta _{ij}. \end{aligned}$$

(9)

Fig. 3

Large scale anisotropy parameter b as function of the wall-normal distance

Fig. 3 shows that the large-scale anisotropy is maximum in the near-wall region, where the mean square axial velocity fluctuations peak. The effect of polymers is to increase the anisotropy in most of the pipe. However, at the smallest Reynolds number $\textrm{Re}_\tau = 180$, and thus the smallest polymer Reynolds number $\textrm{Re}_p$, the anisotropy of the flow is reduced close to the pipe centre. The previous observations, i.e. the difference both in turbulent kinetic energy and large-scale anisotropy in the bulk region, suggest that the turbulent second order statistics are affected by $\textrm{Re}$ (or $\textrm{Re}_p$), despite the overall amount of drag reduction is not.

Fig. 4

Panel a: Budget of mean kinetic energy at $\textrm{Re}_\tau = 180$ and $\textrm{Wi}=10^4$. Panel b: Budget of turbulent kinetic energy. Dashed lines in panel b represent Newtonian quantities. All the terms in the budget are normalised by the total injected power

In order to get more insights into the way the polymers modify turbulence, let us now discuss the budget of mean and turbulent kinetic energy at $\textrm{Re}_{\tau }=180$. Figure 4a shows the budget of kinetic energy associated with the mean velocity. The term $P_w$ injects power into the system through the mean imposed pressure gradient, mainly in the bulk of the flow. The injected power is essentially moved into the buffer layer by the term $\langle \varvec{u}\rangle \cdot \langle \varvec{u}' \otimes \varvec{u}' \rangle$, which represents the flux of the Reynolds stress. In the buffer layer, the flux of viscous stress $\varvec{\nabla }k_M /\textrm{Re}$ has a negative peak, meaning that it removes energy from the buffer layer to inject it in the near wall region, where the $\varepsilon _M$ dissipates the kinetic energy of the mean flow. Still in the buffer layer, the energy that is not transferred to the wall by $\varvec{\nabla }k_M /\textrm{Re}$, besides being partially dissipated locally by $\varepsilon _{M}$, is gathered by the production term $\mathcal P$, that takes energy from the mean flow to feed the turbulent velocity fluctuations. The polymer term $\langle \varvec{u}\rangle \cdot \langle \varvec{F}\rangle$ acts as a source of mean kinetic energy in the near wall region ($y^+<30$), whilst it is a sink in the bulk ($y^+>30$). Its contribution is however smaller than the other terms in the budget.

The budget of turbulent kinetic energy is shown in Fig. 4b. The peak of the production $\mathcal{P}$ in the polymer case is significantly lower than the corresponding one for the Newtonian flow (dashed blue line), with a peak slightly shifted further from the wall. Less of the power injected to sustain the mean flow is thus transferred, and then dissipated, from the mean to the fluctuating field, explaining the lower drag of the polymer-laden flow. Velocity fluctuations are mainly fed in the buffer layer, where the production $\mathcal{P}$ peaks. Part of the available energy is locally dissipated, while the other part is mainly transferred towards the wall by the fluxes, namely $\langle p'\varvec{u}' \rangle$, $\varvec{\nabla }k_T/\textrm{Re}$, $\langle \varvec{u}\, \varvec{u}'^2/2)$, where the energy is dissipated by $\varepsilon _T$. It is worth highlighting that the turbulent dissipation at the wall in the polymer-laden case is lower than in the Newtonian case. The part of the available energy that is not moved towards the wall is transferred towards the pipe centre by the turbulent flux $\langle \varvec{u}\, \varvec{u}'^2/2)$ that feeds turbulent fluctuations, and thus the dissipation, also in the bulk region. In Newtonian flow, this effect is however almost negligible, being the dissipation in the bulk very small (dashed red line). Conversely, in the polymer case, the dissipation is not negligible in the bulk, because turbulent fluctuations are directly sustained by the polymers via the correlation $\langle \varvec{u}' \cdot \varvec{F}' \rangle$, which behaves as a local source of turbulent kinetic energy in the region $y^+>40$. Below $y^+<40$ the contribution of the polymers is small with respect to the other terms and acts as a source of turbulent kinetic energy for $y^+<15$ and as a sink for $15<y^+<40$.

Fig. 5

Budget of turbulent kinetic energy at $\textrm{Re}_\tau = 320$ and $\textrm{Wi}=2\cdot 10^4$. Dashed lines represent Newtonian quantities. All the terms in the budget are normalised by the total injected power

The noticeable effect of the polymers in the bulk, and the consequent increase of the dissipation, is peculiar to a high Weissenberg number flow and is enhanced at the smaller Reynolds number $\textrm{Re}$, i.e. smaller $\textrm{Re}_p$, as shown by the budget of turbulent kinetic energy at $\textrm{Re}_{\tau }=320$ in Fig. 5. Despite the scenario being qualitatively similar to the one described at $\textrm{Re}_{\tau }=180$, the effect of the polymers is apparently less intense in the bulk, and the dissipation is not significantly increased by the polymer back-reaction.

The phenomenon of enhanced dissipation completely disappears at a smaller Weissenberg number $\textrm{Wi}=10$, as reported by the turbulent kinetic energy budget in Fig. 6. In this case, we compare the results of the FENE dumbbell model, panel (a), and the FENE-P model, panel (b). Both models capture a qualitatively similar scenario, with quantitative discrepancies either in terms of turbulent production, and thus drag reduction, or in terms of turbulent dissipation, especially far from the wall. Turbulent fluctuations take energy from the mean flow via the production term $\mathcal{P}$ whose peak is significantly lower than the corresponding one for the Newtonian flow (dashed-blue line). The production peaks in the buffer layer with effect enhanced in the FENE-P simulation predicting a larger DR measured (Serafini et al. 2023). The path of the energy is qualitatively similar to the one observed at the large Weissenberg number. Again, consistently with the lower drag measured, the turbulent dissipation at the wall in the polymer case is lower than in the Newtonian case (dashed red line), and the effect is amplified in the FENE-P simulation. The correlation between the polymer forcing and the velocity fluctuation $\langle \varvec{u}' \cdot \varvec{F}' \rangle$, behaves as a local source of turbulent kinetic energy very close to the wall $y^+<10$, although its contribution is significantly smaller than the other terms in the budget. In contrast, far from the wall at $y^+>10$, the correlation $\langle \varvec{u}' \cdot \varvec{F}' \rangle$ behaves as a sink of turbulent kinetic energy; the effect predicted by the FENE model is small and decays above $y^+=70$. The same effect is amplified by the FENE-P model, which predicts an apparent larger amplitude of the correlation $\langle \varvec{u}' \cdot \varvec{F}' \rangle$ in the buffer layer, with a slight reduction going towards the pipe centre up to finite not null value. Since the FENE-P model predicts that the polymers act as a sink of energy in the bulk, the model predicts a lower dissipation of turbulent kinetic energy with respect to the Newtonian flow. This effect is however an artefact of the FENE-P model, and its simplifying assumptions, since the more accurate Lagrangian FENE dumbbell model does not predict significant changes of dissipation in the region $y^+>70$, with respect to the Newtonian case.

Fig. 6

Turbulent kinetic energy budget. Panel a: Lagrangian-Eulerian FENE model. Panel b: Eulerian-Eulerian FENE-P model. In both panels, dashed lines represent data for the reference Newtonian case. All the terms in the budget are normalised by the total injected power

4 Conclusions

A hybrid Eulerian-Lagrangian approach has been exploited to investigate the mean and turbulent kinetic energy budgets of a polymer-laden turbulent pipe flow at friction Reynolds number $\textrm{Re}_{\tau }=180$ and $\textrm{Re}_{\tau }=320$ and Weissenberg number $\textrm{Wi}=10^4$ and $\textrm{Wi}=2\cdot 10^4$. The population of FENE dumbbells is evolved alongside the incompressible Navier–Stokes system and the backreaction of the polymers on the flow field is accounted for by means of the Exact Regularised Point Particle (ERPP) method for wall-bounded turbulent flows. Besides a drag reduction of about $27 \%$ at both Reynolds numbers, the budgets of mean and turbulent kinetic energy show that the polymers significantly reduce the turbulent production, thus the transfer of kinetic energy from the mean flow to the velocity fluctuations. The dissipation of turbulent kinetic energy is significantly reduced at the wall and is increased above the buffer layer where the polymers act as a direct source of velocity fluctuations. This remarkable effect is particularly apparent at small Reynolds number $\textrm{Re}_\tau =180$, where the turbulent dissipation is significantly increased and reduces with increasing Reynolds number, despite the amount of drag reduction being unaffected.

The budget of turbulent kinetic energy is also accounted at a smaller Weissenberg number $\textrm{Wi}=10$, at $\textrm{Re}_\tau =180$, where the FENE-P model is also considered. The dissipation is considerably reduced at the wall, and the FENE-P model amplifies the effect consistently with the predicted larger drag reduction. Above the buffer layer, the effect of the polymer force-velocity correlation on the kinetic energy budget is insignificant and the dissipation is not affected. The FENE-P model, as a consequence of the restrictive assumptions on the polymer population, predicts that the polymers act as a sink of turbulent kinetic energy above the buffer layer, and predicts a lower dissipation with respect to the Newtonian flow.

As a final comment, we stress the importance of investigating a wide range of Weissenberg numbers when characterising turbulent flows of dilute polymer solutions, as the parameter varies a lot depending on the specific polymer and its molecular weight (Doi and Edwards 1988; Harnau and Reineker 1999). For instance, for $20 \, \mu \textrm{m}$ DNA molecule the relaxation time is of the order of $1 \, \textrm{s}$, while for a PEO chain of equal length, the relaxation time is approximately $10^{-3} \, \textrm{s}$. Such a large difference explains the importance of investigating very high $\textrm{Wi}$, up to the asymptotic range, as both polymers and turbulence dynamics are largely influenced by the Weissenberg numbers.