1 Introduction

Heat release rate fluctuations in lean premixed combustion are likely to couple with pressure fluctuations leading to combustion instabilities. These instabilities pose challenges for burner development since uncontrolled pressure oscillations can cause significant structural damage leading to complete engine failure. The Flame Describing Function (FDF), commonly used to study thermoacoustic oscillations, allows to quantify the flame response to incoming acoustic perturbations. The FDF, denoted by H, is defined as the ratio of temporal fluctuation of heat release, \(\dot{Q}'\), to the streamwise velocity fluctuations \(u'\) at the combustor inlet, normalised by their respective time averaged values. It is a function of both forcing (velocity) amplitude and frequency and is written as (Palies et al. 2010; Balachandran et al. 2005)

$$\begin{aligned} H(f, \mid \! u' \! \mid ) = \frac{\dot{Q}'(f, \mid \! u' \! \mid )/\langle \dot{Q} \rangle }{ \mid\!u'\!\mid / \langle u \rangle }, \end{aligned}$$
(1)

where \(\dot{Q}\) is the volume integrated heat release rate \(\dot{Q}(t) = \int _{V_c} \dot{q}({\textbf{x}}, t) dV\) with \(V_c\) as the combustor volume and \(\dot{q}\) as the local heat release rate per unit volume at a given location \({\textbf{x}}\) and time t. The angle brackets \(\langle \ \rangle\) denote a time averaged quantity and the fluctuating heat release rate is defined as \(\dot{Q}' = \dot{Q} - \langle \dot{Q} \rangle\). Typically, the dominant frequency of the flame response is the same as that of the acoustic forcing frequency. A Flame Transfer Function (FTF), H(f), which is a function of f only, is defined in exactly the same way as Eq. (1) but assumes a linear flame response. This FTF/FDF is used as an input for low-order system level modelling to study thermoacoustic characteristics of gas turbine combustors (Dowling and Stow 2003; Stow and Dowling 2009; Han et al. 2015).

There are ample studies in the past investigating the characteristics of FTF/FDF in premixed combustion. Early analytical models tracked the motion of the flame surface in two dimensions to predict the response of flames in simple flow configurations (Fleifil et al. 1996; Dowling 1999; Schuller et al. 2003; Preetham et al. 2008; Hemchandra et al. 2011). The flame surface modulations were highlighted to be the significant source of heat release oscillations in past experimental works (Balachandran et al. 2005; Durox et al. 2009). The FTFs/FDFs have also been studied computationally using URANS (Armitage et al. 2006; Ruan et al. 2016) and LES (Han and Morgans 2015; Han et al. 2015; Lee and Cant 2017; Cheng et al. 2021) paradigms in the past. However, most of these studies considered non-swirling flames and there are fewer computational investigations of swirling flame FDFs (Pampaloni et al. 2019; Chatelier et al. 2019; Dupuy et al. 2020).

The heat release oscillations in swirling premixed flames, also manifest through flame area modulations (Külsheimer and Büchner 2002; Liu et al. 2022), but swirl introduces additional complexities. Thermoacoustic characteristics of swirling flames have been widely investigated under premixed (Palies et al. 2010; Gatti et al. 2019; Acharya et al. 2012; Bellows et al. 2006; Dupuy et al. 2020) and non/partially premixed configurations (Dinesh et al. 2009; Chen et al. 2019; Chen and Swaminathan 2020; Rajendram Soundararajan et al. 2022). The non-swirling flame acts as a low pass filter for incoming pressure perturbations and its FTF gain has, typically, a single peak whereas minima and maxima are frequently observed in the measured FTFs of swirling flames (Gentemann et al. 2004; Palies et al. 2010, 2011; Bourgouin et al. 2013; Kim and Santavicca 2013; Dupuy et al. 2020). Many works have also investigated the factors influencing the location and magnitude of these extrema in the FTF. The influence of the swirler location on the time delays related to vorticity and acoustic waves was suggested to affect the FTF shape (Hirsch et al. 2005; Komarek and Polifke 2010; Kim and Santavicca 2013; Albayrak et al. 2017). Longitudinal disturbances travel at the speed of sound while the azimuthal disturbances created at the downstream tip of the swirler travel at convective speed creating swirl number fluctuations (Palies et al. 2010, 2011). Based on this principle, a time-lag model was used to capture a swirling flame FTF (Komarek and Polifke 2010). However, the time delays may not be readily available for a given combustor configuration.

Some studies (Palies et al. 2011; Bunce et al. 2014; Gatti et al. 2019) suggested that the FTF trough occurred when the swirl number fluctuations at the flame base were maximum. These large swirl number oscillations were linked to flame angle oscillations which could dampen the vortex formation and hence, decrease the FTF gain (Bunce et al. 2014; Gatti et al. 2019).

The geometrical characteristics of burners were also found to influence the FTF shape suggesting that the FTF variation with forcing frequency might not be universal. The combustor enclosure also influences the location and magnitude of the FTF extrema (Cuquel et al. 2013; De Rosa et al. 2016; Nygård and Worth 2021; Ånestad et al. 2022) by changing the flame length. Furthermore, the response of an aerodynamically stabilised flame was shown to be significantly different from that of a bluff body stabilised flame although the same swirler was employed (Gatti et al. 2019). Kim and Santavicca (2013) measured the FTF at various operating conditions and found that the locations of the peaks and troughs are related to a flame length scale (to be defined later). However, a single forcing amplitude and swirl number was used (Kim and Santavicca 2013).

The swirl number was also shown to influence the FTF but with some conflicting results. The flame response was shown to be augmented with increasing swirl number by Külsheimer and Büchner (2002), whereas an opposite behaviour was noted by Palies et al. (2011) which was attributed to the flame confinement used in their study. Furthermore, it was also observed (Palies et al. 2011) that axial swirlers produced a response with higher maxima and lower minima than radial swirlers and a similar behaviour was also reported by Durox et al. (2013).

The objective of this paper is to understand the effect of swirl number on the flame response by performing a series of Large Eddy Simulations (LES) and experiments, and comparing the computational results to measurements. Four configurations with different swirl numbers and two forcing amplitudes are considered. The Flame Describing Functions are then scaled using flame length scales estimated through two different ways. FDF scaling of swirling flames is important as the effect of swirl to dominant modes and limit cycle amplitudes in a low order model can be assessed without the need to compute the FDF for multiple flames at different swirl numbers.

This paper is organised as follows. Section 2 describes the burner configuration used and the experimental techniques employed. A summary of the LES model and the details of the computational setup used are discussed in Sect. 3. The results are presented in Sect. 4. First, the model is validated by comparing the computed and measured flow and flame features for the unforced swirling flames. Then, the FTF analysis is presented and discussed. The conclusions are summarised in the final section.

2 Experiments

2.1 Burner Detail

A schematic of the bluff body burner used for this study is shown in Fig. 1. Details of this burner have been described previously in Ajetunmobi et al. (2019), Kallifronas et al. (2022). The 300 mm long burner plenum has convergent and divergent sections that house the loud speakers for acoustic excitation of the flow. Downstream of the plenum is a 400 mm long duct with 35 mm internal diameter. A conical bluff body with a diameter \(D_0=25\) mm and a \(45^\circ\) angle produces a blockage ratio of \(51 \%\) and is located at the entry to the chamber as shown in Fig. 1. Two axial swirlers with \(45^\circ\) and \(60^\circ\) vane angles were used that were placed 42 mm upstream of the bluff body base (dump plane). A square enclosure with 100 mm quartz walls was used to prevent the entrainment of ambient air. Fully premixed fuel and air enter this chamber through a pipe of radius \(R_p=17.5\) mm and the hot products exit through a circular hole of 79.5 mm in a 8 mm thick metal plate located at the exit of the chamber. A premixed ethylene-air mixture is used for all cases at an equivalence ratio of \(\phi =0.52\) at atmospheric pressure and room temperature. The bulk mean axial velocity at the dump plane is fixed at \(u_0=10\) m/s.

Fig. 1
figure 1

Schematic of the bluff body burner (Ajetunmobi et al. 2019). The red box represents the field of view in the experiments

Full size image

2.2 Experimental Methods

Compressed air was used as the oxidiser and \(C_2H_4\) was provided from BOC gas cylinders at room temperature and pressure. The air and \(C_2H_4\) flow rates were controlled using a mass flow meters (Bronkhorst MASS-VIEW, accuracy up to ± 1.5% at full scale division) and were premixed upstream of the plenum. An amplified sinusoidal wave was provided to the loud speakers for acoustic excitation. Simultaneously dynamic acoustic pressures in the duct were recorded at 170 mm and 302 mm upstream of the bluff body base using two high-sensitivity KuLite pressure transducer (Model XCS-093) microphones with sensitivities \(4.075 \cdot 10^{-3}\) mv/Pa and \(3.67\cdot 10^{-3}\) mv/Pa respectively. Global OH* chemiluminescence measurements were carried out using a highly sensitive Photomultiplier tube, PMT (Hamamatsu R3788) using band pass filters with peaks at 307±10 nm, (at FWHM). The signal from the PMT was amplified and recorded on an oscilloscope along with the reference input acoustic signal. All these signals were acquired at a sampling rate of 50 kHz for a time period, \(t_p\), of 2 s for post-processing. Measurements using OH* chemiluminescence imaging were conducted using a high speed VEO710 camera and Lambert Intensifier at an imaging frequency of 100 Hz. A Sodern UV 100 mm f/2.8 Cerco objective lens was used. The field of view was \(\sim 71.5 \times 59.5\) mm with a pixel resolution of   94 \({{\mu m}}\)/pixel. Gain and gate widths were varied to get a reasonable signal.

3 Numerical Modelling

3.1 Modelling Framework

The compressible Favre-filtered transport equations for mass, momentum and energy are solved. These equations for mass and momentum are

$$\begin{aligned}{} & {} \frac{\partial \overline{\rho }}{\partial t} + \frac{\partial }{\partial x_j} (\overline{\rho } \widetilde{u}_j) = 0 , \end{aligned}$$
(2)
$$\begin{aligned}{} & {} \frac{\partial \overline{\rho } \widetilde{u}_i}{\partial t} + \frac{\partial }{\partial x_j} (\overline{\rho } \widetilde{u}_i \widetilde{u}_j) = \frac{\partial \overline{p}}{\partial x_i} + \frac{\partial \overline{\tau }_{ij}}{\partial x_j}-\frac{\partial }{\partial x_j}(\overline{\rho u_i u_j} - \overline{\rho } \widetilde{u_i} \widetilde{u_j}) . \end{aligned}$$
(3)

The fluid mixture density is \(\rho\), \(u_i\) is the \(i^{th}\) velocity component, p is the pressure and \(\tau _{ij}\) is the molecular shear stress. The residual stress tensor \(( \overline{\rho u_i u_j}-\overline{\rho } \widetilde{u}_i \widetilde{u}_j )\) is modelled using the dynamic Smagorinsky model (Germano et al. 1991; Lilly 1992) For reacting flows, the total enthalpy \(\widetilde{h}\) (the sum of sensible and chemical enthalpies), mixture fraction \(\widetilde{\xi }\), the reaction progress variable \(\widetilde{c}\) and its sub-grid variance \({ \sigma }_{c, \, \text { sgs } }^{ 2 }\) are also solved along with the momentum and continuity equations. The mixture fraction as defined by Bilger (1988) is used as a marker for combustor stream in order to treat the mixing of burnt products with ambient air at the combustor outlet. The progress variable is defined as \(c=(Y_{\text {CO}}+Y_{\text {CO}_2}) / (Y_{\text {CO}}+Y_{\text {CO}_2})_b\), where the subscript ‘b’ denotes the burnt conditions. This definition implies a zero and and unity for the reactants and products respectively. These transport equations are written in the compact form, with \({ \widetilde{ \varvec{ \varphi } } = \lbrace \widetilde{ h } \,, \, \widetilde{ c } \,, \, { \sigma }_{ c, \text { sgs } }^{ 2 } \,, \, \widetilde{ \xi } \rbrace }^{ \intercal }\), as

$$\begin{aligned} \frac{\partial \overline{\rho } \widetilde{ \varvec{ \varphi } }}{\partial t} + \frac{\partial }{\partial x_j} (\overline{\rho } \widetilde{u}_j \widetilde{ \varvec{ \varphi } }) = \frac{\partial }{\partial x_j} \left( \overline{ \rho { {\mathcal {D}} }_{ \text { eff } } } \frac{ \partial \widetilde{ \varvec{ \varphi } } }{ \partial x_j } \right) + \overline{ { {\varvec{S}} }_{ \varvec{ \varphi } }^{ + } } - \overline{ { {\varvec{S}} }_{ \varvec{ \varphi } }^{ - } } . \end{aligned}$$
(4)

The effective diffusivity is modelled as \(\overline{ \rho { {\mathcal {D}} }_{ \text { eff } } } = {\mathcal {D}}_{ \varvec{ \varphi } } + { \nu }_{ T }/ Sc_T\), where \({ \nu }_{ T }\) is the turbulent viscosity and \({\mathcal {D}}_{ \varvec{ \varphi } }\) is the molecular diffusivity for \(\varvec{ \varphi }\). The turbulent Schmidt number of \(Sc_T=0.4\) is used (Pitsch and Steiner 2000; Chen et al. 2017)(see Table 1). It would be ideal to evaluate this parameter dynamically, which is an on-going activity. This molecular diffusivity is taken to be the thermal diffusivity, \(\alpha\), for the enthalpy. For the other scalars, \({\mathcal {D}}_{ \varvec{ \varphi } } \equiv \nu / \text { Sc }\), where \(\text { Sc } = 0.7\) is the molecular Schmidt number (Pitsch and Steiner 2000; Chen et al. 2017). For the enthalpy equation, the turbulent Prandtl number \(Pr_T=0.4\) is used. The density is obtained using the state equation \(\overline{ \rho } = \overline{ p } \widetilde{ M } / { \Re }^{ 0 } \widetilde{ T }\), where \(\widetilde{ M }\) and \({ \Re }^{ 0 }\) are the molecular mass and the universal gas constant respectively. The filtered temperature \(\widetilde{ T }\) is obtained from the total enthalpy transport equation using \(\widetilde{ T } = T_0 + ( \widetilde{ h } - \widetilde{ \Delta h }_{ f }^{ 0 } ) / \widetilde{ c }_p\), where \(\widetilde{ \Delta h }_{ f }^{ 0 }\) and \(\widetilde{ c }_p\) are the enthalpy of formation and an effective specific heat capacity as defined by Ruan et al. (2014) respectively, and \(T_0 = 298.15 \, \text { K }\). The sources \(\overline{ { {\varvec{S}} }_{ \varvec{ \varphi } }^{ + } }\) and sinks \(\overline{ { {\varvec{S}} }_{ \varvec{ \varphi } }^{ - } }\) in Eq. (4) are respectively written as

$$\begin{aligned} \overline{ { {\varvec{S}} }_{ \varvec{ \varphi } }^{ + } }&= { \left\{ \frac{D \overline{p}}{Dt} \, , \, \overline{ { {\dot{\omega }} } }_{ c } \, , \, 2 \overline{ \rho } \frac{ { \nu }_{ T } }{ { \text { Sc } }_{ T } } \, { |\, \nabla \widetilde{ c } \, |}^{ 2 } + 2 \left( \overline{ c \, { {\dot{\omega }} }_{ c } } - \widetilde{ c } \, \overline{ { {\dot{\omega }} } }_{ c } \right) \, , \, 0 \right\} }^{ \intercal } \, , \end{aligned}$$
(5)
$$\begin{aligned} \overline{ { {\varvec{S}} }_{ \varvec{ \varphi } }^{ - } }&= { \left\{ 0 \, , \, 0 \, , \, 2 \, \overline{ \rho } \, { \widetilde{ \chi } }_{ c , \text { sgs } } \, , \, 0 \right\} }^{ \intercal } \, . \end{aligned}$$
(6)

The expression proposed in Dunstan et al. (2013) is used for the sub-grid scalar dissipation rate (SDR) term \({ \widetilde{ \chi } }_{ c, \text { sgs } }\) in the transport equation for \({ \sigma }_{ c, \text { sgs } }^{ 2 }\):

$$\begin{aligned} { \widetilde{ \chi } }_{ c , \text { sgs } } = \mathscr {F} \left[ 2K_c \frac{s_l}{\delta _l} + \left( C_3- \tau C_4 Da_\Delta \right) \left( \frac{2u'_\Delta }{3\Delta } \right) \right] \frac{\sigma ^2_{c,sgs}}{\beta _c} \end{aligned}$$
(7)

where the constants and parameters are selected and modelled as described by Chen et al. (2017) and Langella et al. (2018). The tunable parameter \(\beta _c\) has been tuned based on the cases used in the present work and ranges between 4 and 7.5. A presumed probability density function (PDF) approach is used to calculate the filtered reaction rate in Eq. (5)

$$\begin{aligned} \overline{{\dot{\omega }}}_c = \overline{\rho } \int _{0}^{1} \frac{\dot{\omega }_c \left( \zeta \right) }{\rho \left( \zeta \right) } \widetilde{P} \left( \zeta \right) \, d\zeta , \end{aligned}$$
(8)

where \(\dot{\omega }_c \left( \zeta \right)\) and \(\rho \left( \zeta \right)\) are the flamelet reaction rate for the progress variable calculated using \(\dot{\omega }_c \left( \zeta \right) = ( \dot{ \omega }_{\text { CO }} + \dot{ \omega }_{\text {CO}_2 } ) / (Y_{\text {CO}}+Y_{\text {CO}_2})_b\) and the flamelet mixture density respectively. The density-weighted PDF is obtained using a \({\upbeta }\)-distribution \(\widetilde{ P } (\zeta ) = P_\beta ( \zeta ; \widetilde{ c }, { \sigma }_{ c, \text { sgs } }^{ 2 } )\) to construct a look-up table for the filtered reaction rate. The flamelet is computed using one-dimensional unstrained laminar premixed flame with USC chemical mechanism for ethylene-air combustion (Wang and Laskin 1998). The mechanism involves 529 elementary reactions and 75 species. This flamelet is computed using the Cantera software (Goodwin et al. 2017). The thermochemical parameters, \(\widetilde{ M }\), \(\widetilde{ \Delta h }_{ f }^{ 0 }\) and \(\widetilde{ c }_p\), are also stored in the look-up table along with \(\overline{\dot{\omega }}_c\) following (Ruan et al. 2014). The source term \(\overline{ c \, { \dot{ \omega } }_{ c } }\) required for the \({ \sigma }_{ c, \text { sgs } }^{ 2}\) equation is determined in a similar form as Eq. (8) following previous studies (Langella and Swaminathan 2016; Chen et al. 2017).

3.2 Computational Setup

The computational model for the burner is an accurate representation of the experimental case including a 2 mm purge gap between the central support rod and swirler (not shown in Fig. 1). The cases with the \(45^\circ\) and \(60^\circ\) swirlers are referred as S-S45 and S-S60 respectively. Two additional cases are considered for LES. For case S-S60NP, the purge gap is closed which leads to an increase in the swirl number as described by Kallifronas et al. (2022). For the second one, C-S60, a modified version of the burner developed by Balachandran (2005) is employed which features a cylindrical enclosure of 100 mm diameter and 80 mm height, hence the prefix ‘C’ is used. A different axial swirler design is used for this case which produces a higher swirl number compared to the rest of the cases. More information about this modified burner can be found in previous work by Kallifronas et al. (2023).

In the experiments, the flames are forced at an amplitude \(A=u'/ \langle u \rangle =7\%\) which is measured using the two microphone method described in Sect. 2.2. This is the highest allowable amplitude in the experimental setup for a wide range of frequencies. Forcing amplitudes larger than this are not achievable in the experimental setup due to the limitations of the speakers used for the acoustic forcing. Hence they are explored only computationally in this study. The amplitude of \(7\%\) is considered for LES cases S-S45, S-S60, S-S60NP and an additional amplitude of \(A=25\%\) is considered for all four cases. However, the computed amplitude is measured using the surface averaged axial velocity at the dump plane. As noted earlier, different values of \(\beta _c\) in Eq. (7) have been chosen for each case. This parameter does not unduly affect the location of the minima and maxima of the FDF in the frequency space, however, the gain magnitude is affected. It has been found that \(\beta _c=7.5\) and 4 are suitable values for S-S45 case and the rest of the cases respectively. A summary of the cases studied is given in Table 1:

Table 1 Details of the cases studied
Full size table

The swirl number in Table 1 is calculated using the LES results at the dump plane employing (Beer and Chigier 1972):

$$\begin{aligned} SN = \frac{\int _{0}^{R_p}u_xu_\theta r^2\,dr}{R_p\int _{0}^{R_p}u_x^2r\,dr} \end{aligned}$$
(9)

where \(u_x\) and \(u_\theta\) are the axial and azimuthal velocity components respectively and \(R_P\) is the radius of the inlet pipe as shown in Fig. 1.

Unstructured meshes ranging between 2.3 and 2.8 million cells are used for the cases studied which include the entire swirler geometry. The grid size and distribution for cases S-S60 and S-S60NP is chosen based on a mesh sensitivity study for case S-S45 to maintain consistency. A similar sensitivity study was performed for case C-S60 (Kallifronas et al. 2023). At the outlet of the combustor the domain has been extended by adding a cylindrical domain of 500 mm length and 700 mm diameter as shown in Fig. 1. This extended domain allows to specify clear boundary conditions since the flame is observed to occasionally extend beyond the combustor length of 100 mm in some cases.

Adiabatic no-slip conditions are applied at the wall boundaries and wall functions are used for the boundary layers following earlier studies (Massey et al. 2018; Kallifronas et al. 2022). A wave transmissive boundary condition is employed for pressure at the outlet to prevent acoustic reflection. The inlet turbulence intensity is set to be about 5% at the inlet which is upstream of the swirler as shown in Fig. 1. However, the contribution of this turbulence to the turbulence level inside the combustor is not significant compared to those produced by the swirler wake. For this reason, the swirler geometry is included in the computational model. The acoustic forcing is simulated by superimposing a sinusoidal variation of a given amplitude and frequency to the velocity boundary condition at the inlet.

A first order implicit Euler and second-order accurate numerical schemes are used for the time and spatial derivatives respectively. The Courant-Friedrichs-Lewy (CFL) number is kept below 0.4 in the entire computational domain which maintains a time step of the order of \(10^{-7}\)s. A modified PIMPLE algorithm is used with the density coupling to handle the full compressibility effects (rhoPimpleFoam solver).

After allowing 3 flow-through times based on the bulk velocity and the computational domain length of \(L_D\) (see Fig. 1) for initial transients to escape the computational domain, statistics are collected for 10 flow-through times for unforced flames.The data collected over at least 25 cycles after the initial transients is used to construct the FTF through the fast fourier transform (FFT).

All simulations are performed with open-source package OpenFOAM 7 using the ARCHER2 UK national high performance computing facility.

4 Results and Discussion

4.1 Unforced Flow and Flame Characteristics

The unforced flames and their characteristics are used to validate the LES model, numerical setup and boundary conditions. Figure 2 shows the streamlines and axial velocity contours under reacting conditions for cases S-S45 and S-S60. The central recirculation zone (CRZ) behind the bluff body of both cases consists of an inner and outer toroidal vortices. The height of the outer vortex extends to approximately \(2D_0\) (50 mm) in both cases and the the inner vortices up to approximately \(0.8D_0\) (20 mm) for case S-S45 and \(0.4D_0\) (10 mm) for case S-S60. A vortex breakdown bubble (VBB) appears in cases S-S45 near the burner outlet in the computations which suggests that the VBB and CRZ are not merged. A small VBB can also be observed in case S-S60 at a lower height compared to S-S45. This is expected as an increase in the swirl number leads to a shift of the VBB upstream (Sheen et al. 1996; Ranga Dinesh and Kirkpatrick 2009; Kallifronas et al. 2022). The VBBs are not visible in the experiments as they are located outside the interrogation window.

Fig. 2
figure 2

Comparisons of measured (left half) and computed (right half) time-averaged velocity streamlines and axial velocity contour for case S-S45 are shown in (a) and (b) respectively, and for case S-S60 in (c) and (d) respectively. The white lines are for zero axial velocity. Dimensions are in mm

Full size image

There is very good agreement between the measured and computed CRZ height in both cases with a small overestimation for S-S45 in the computations. There is also good agreement in terms of jet spread for case S-S45, while for case S-S60 the jet is wider in the computations at 50 mm height. The uncertainty is large for PIV in the region (within few mm) closer to the bluff body base due to laser light reflection. A further comparison is shown in Fig. 3 for the axial and radial velocities for case S-S45. There is a very good agreement between the measured and computed mean velocities and a satisfactory agreement for rms velocities. Similar agreement is observed for case S-S60 as well and hence it is not shown here. A more detailed study of the flow fields is reported in Kallifronas et al. (2022). As shown in previous studies (Han and Morgans 2015; Lee and Cant 2017), small differences in the rms velocities do not affect the prediction of FDFs.

Fig. 3
figure 3

Comparison of measured and computed mean and rms velocity profiles at three different axial positions for reacting flow of case S-S45

Full size image
Fig. 4
figure 4

Comparisons of the computed time-averaged axial velocity and velocity streamlines for a case S-S60NP and b C-S60. The white lines are for zero axial velocity. Dimensions are in mm

Full size image

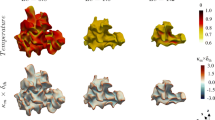
The flowfields for cases S-S60NP and C-S60 are presented in Fig. 4. There is a much larger CRZ for both cases as the vortex breakdown bubble is merged with the CRZ behind the bluff body due to the high levels of swirl. This leads to a highly unsteady CRZ and its instantaneous structure can vary significantly from the time-averaged structure (Kallifronas et al. 2022).

Fig. 5
figure 5

Power spectral density of the azimuthal velocity at the three probe locations shown in Fig. 4a for cases a–c S-S60 and d–f S-S60NP. The red curves represent moving averages

Full size image

Figure 5 shows the power spectral density (PSD) of the azimuthal velocity at three probe locations as shown in Fig. 4a for cases S-S60 and S-S60NP. While some peaks can be observed for case S-S60 at probe 2 in Fig. 5b at approximately 300, 400 and 500 Hz, their amplitude around is small compared to the noise levels. This suggests that there are no flow instabilities present. On the other hand, for case S-S60NP a distinct peak can be observed at all three locations with the amplitude being particularly high at probes 1 and 3, in Fig. 5d and f respectively, which implies the existence of a flow instability. However, no helical structures suggesting the presence of a precessing vortex core were identified. Probe 1 is located at the dump plane and the high amplitude of the oscillation there implies that the instability is generated near the swirler. Similar PSDs were observed for the rest of the velocity components as well.

This flow instability in case S-S60NP can be visualised using contours of the instantaneous azimuthal velocity at the dump plane at four instances 8 ms apart as shown in Fig. 6a. The figure reveals three regions of high azimuthal velocity (shown using arrows at \(t=0\) ms). These three regions are displaced clockwise through time as it can be seen between 8 and 24 ms. The rotation frequency is approximately 160 Hz, which explains the peak shown in Fig. 5d and f at 480 Hz. A 3D isosurface of \(u_\theta =13\) m/s depicting a \(m=3\) mode is shown in Fig. 6b. Finally, a similar flow instability was observed for case C-S60, but not for case S-S45.

Fig. 6
figure 6

a Time sequence of the azimuthal velocity at the dump plane for case S-S60NP. b Isosurface of \(u_\theta = 13\) m/s

Full size image

Figure 7 shows a comparison of the measured and computed flame surface density (FSD) for the 4 cases studied. The measured FSD comes from OH* as explained in Sect. 2.2 whereas its value from the LES is calculated through:

$$\begin{aligned} \Sigma = \frac{\dot{q}}{\Delta H_{c} \rho _u s_l} \approx \frac{ \overline{\dot{\omega }}_c Y_{f,u}}{\rho _u s_l} \end{aligned}$$
(10)

where \(\Delta H_{C}\) is the lower calorific value of ethylene, \(\rho _u\) is the unburnt mixture density, \(s_l\) is the unstrained laminar flame speed and \(Y_{f,u}\) is the fuel mass fraction in the unburnt mixture.

Fig. 7
figure 7

Time averaged FSD for the four cases considered. For cases a S-S45 and b S-S60, the left and right halves are from the experiments and computations respectively

Full size image

There is good agreement between the measured and computed flame shapes for case S-S45 in Fig. 7a. The region of high FSD is between approximately 25 mm to 45 mm in the measurements and between 30 mm and 50 mm in the computation. For case S-S60, a relatively shorter flame can be observed as increasing swirl shortens the flame region with thicker flame brush arising due to the stronger turbulence. The highest reaction rate is observed between 20 and 45 mm and it matches well with the flame shape suggested by the measured OH*. While in both flames the peak reaction rate is computed correctly near the tip of the inner flame, there is an outer flame in the computations which is absent in the experiments. This is due to the use of adiabatic boundary conditions for the walls. The precense of this outer flame was shown to not influence the FDF estimates in a similar burner, but with no swirl (Han and Morgans 2015; Ruan et al. 2016; Cheng et al. 2021). However, this may not be the case when there is swirl and hence it is assessed carefully by calculating the integrated heat release rate by considering the flame portion to the left of the dashed line shown in Fig. 7b for the S-S60 case. The results will be discussed in Sect. 4.2.

For cases S-S60NP and C-S60 in Fig. 7c and d respectively, which are considered for LES only, the flame angle becomes larger with respect to the flow axis with increasing swirl and the heat release rate distribution is also changed. For case S-S60NP, the flame is not significantly shorter, but it is thinner than flame S-S60. The flame height is similar and the peak heat release rate is higher than S-S60. For case C-S60, the flame is observed to be shorter and the peak heat release rate higher compared to the rest of the cases.

Fig. 8
figure 8

Time-averaged heat release rate per unit length as a function of axial distance for the four cases studied

Full size image

To understand the flame behaviour further, the heat release rate distribution for the four flames can be seen in Fig. 8 where \(\delta {\mathcal {Q}}/\delta x\) is the heat release rate per unit length calculated by splitting the combustor into N segments of height \(\delta x\) such as \(\langle \dot{Q} \rangle = \sum _{i=1}^{N} \delta \mathcal {Q}_i\). The quantity \(\delta \mathcal {Q}_i\) is calculated as \(\delta \mathcal {Q}_i = \int _{V_i} \langle \dot{q} \rangle dV\) where \(V_i\) is the \(i^{th}\) segment’s volume. For case S-S45, it can be observed that the flame extends along the entire combustor length. However, the height at which \(\delta \mathcal {Q} /\delta x\) drops to approximately zero is reduced monotonically with increasing swirl. The peak value of \(\delta \mathcal {Q} /\delta x\) is increasing with the level of swirl and there is a shift upstream when the swirl is increased from 0.44 to 0.56 for cases S-S45 and S-S60 respectively and also from 0.8 to 0.97 for cases S-S60NP and C-S60. However, the peak location does not change significantly when swirl is increased from 0.56 to 0.8 for cases S-S60 and S-S60NP respectively. This may be attributed to the significantly different flow structure between those two cases and the merging of the VBB and CRZ which may alter the flame characteristics as observed in Figs. 2b and 4a. These results suggest that the flame becomes convectively compact (spatially) as the swirl number increases.

Following previous studies (Kim and Santavicca 2013; De Rosa et al. 2016), FDFs obtained using various operating conditions may be scaled using an appropriate flame length scale. In this study two length scales are considered, the flame height \(\ell _1\) which can be calculated from the computations using the isocontour of \(\widetilde{c}=0.9\). However, estimating \(\ell =\ell _1\) from the isocontour of the progress variable is challenging as the choice of \(\widetilde{c}\) value is somewhat arbitrary. A second and less ambiguous length scale, \(\ell _2\), can be defined as the axial distance of peak heat release rate per unit length as observed in Fig. 8. This is similar to the length scale used in Kim and Santavicca (2013), De Rosa et al. (2016) which is based on the axial location of peak OH* intensity. These length scales can be used to calculate Strouhal numbers \(St=f \ \ell /u_0\) required in the next subsection. Table 2 lists these two length scales for the flames studied.

Table 2 Typical flame length scales for the two unforced flames
Full size table

Figures 9a-c show time variations of the fluctuating volume integrated heat release rate for cases S-S45, S-S60 and S-S60NP. These fluctuations, normalised by the time-averaged volume integrated heat release rate \(\langle \dot{Q} \rangle\), have approximately up to \(15\%\) peak-to-peak amplitude for case S-S45 as observed in Fig. 9a. This range of fluctuations agree well with the experimental data shown in the same figure. For case S-S60, the range of fluctuations is up to \(20\%\) and up to \(17\%\) for case S-S60NP. Despite these large fluctuation levels, the spectral contents shown in Fig. 9d–f are quite low and have broad-band characteristics suggesting that these fluctuations are arising from turbulence-chemistry rather than thermoacoustics. For case S-S60NP no peak can be observed at the frequency at which the flow instability was observed around 480 Hz. This implies that the flame is thermo-acoustically stable.

Fig. 9
figure 9

The heat release as a function of time for cases a S-S45, b S-S60 and c S-S60NP and the corresponding power spectral density with its moving average d–f

Full size image

4.2 Flame Describing Functions

Figure 10 compares the measured and computed FDF gain and phase for the case S-S45 for frequencies up to 300 Hz and forcing amplitudes \(A=7\%\) and \(25\%\). The shape of the gain in Fig. 10a is typical for swirling flames and involves two maxima at a low and high frequency and a minimum in between them (Hirsch et al. 2005; Palies et al. 2010, 2011; Kim and Santavicca 2013). The computed FTF gain agrees quite well with the measured values, but with a shift to the left of approximately 20 Hz as seen in Fig. 10a. The measured first maximum is located at 70 Hz and the second one is between 180 and 210 Hz (160 Hz for LES). The gain for the first maximum is about 1.4 while for the second one is around unity. The minimum is located at 130 Hz (110 Hz for LES) with a gain approximately 0.4 to 0.5 as seen in Fig. 10a. The shift between the measured and computed FTF could be related to the overprediction of the flame height in the LES as seen in Fig. 7a. The longer flame affects the convective timescales which influence the location of the extrema as one shall see later in Sect. 4.3. The gains at the extrema are estimated quite well in LES. The gain decays for frequencies higher than 240 Hz exhibiting a typical low pass filter behaviour (Ducruix et al. 2000).

Fig. 10
figure 10

FTF gain a and phase b for case S-S45 forced at \(A=7\%\) and \(25\%\)

Full size image

The phase shown in Fig. 10b is decreasing with increasing frequency. While the slope of the computed curve matches the measured one well at \(A=7\%\), there is a large offset of approximately \(0.5\pi\) to \(0.6\pi\) between these two curves. This difference arises because of the difference in the approach used to estimate \(u'/\langle u \rangle\) in the experiments and LES. As noted earlier, an acoustic velocity derived using a two microphone method is used in the experiments, while in the simulations, a surfaced averaged axial velocity directly calculated at the dump plane is used. In both the measured and computed curves there is a local minimum which is located around 130 Hz for the measured curve and 110 Hz for the computed one and coincides with the respective minima.

For an amplitude of \(A=25\%\), a similar gain curve shape is observed in Fig. 10a with the extrema remaining at the same frequencies. However, there is a smaller gain difference between the minimum and the maximum at 160 Hz compared to \(A=7\%\). There are also small differences in gain at frequencies between 100 and 160 Hz and a reduction in gain at 80 Hz and higher than 160 Hz. This suggests that the flame operates in the linear region between 100 and 160 Hz, while some non-linearities exist at other frequencies. The phase is also unaffected by the increase in forcing amplitude for frequencies up to 160 Hz. An increase is visible at frequencies higher that 160 Hz as seen in Fig. 10b.

The FDF for S-S60 is shown in Fig. 11. The variation of gain with frequency shown in Fig. 11a is similar to S-S45, but with different extrema and their corresponding frequencies. The minimum for \(A=7\%\) is predicted to be at 140 Hz which agrees well with the measurements and the second peak is located at approximately 190 Hz. The gain at the minimum is underpredicted in the simulations as the computed value is 0.5 while the measured one is 0.7. The gain at the second maximum is correctly predicted and it is approximately 1. The phase in Fig. 11b shows a similar behaviour to that for S-S45, but with a shallower slope. While the slope is correctly predicted by LES there is still an offset of approximately \(0.5 \pi\) to \(0.6\pi\).

To assess the role of the outer flame branch, a separate FTF calculation has been performed by considering only the inner branch of the flame as described in Sect. 4.1 (see Fig. 7 and its discussion). The results are shown in Fig. 11 and it is clear that the shape and, the locations of the peak and the minimum are not affected by excluding the outer branch, although there are some minor differences in the gain. This is expected as the most of the heat release occurs near the tip of the inner flame as seen in Figs. 7 and 8.

For \(A=25\%\) in Fig. 11a, the minimum and second maximum remain at approximately the same frequencies as for \(A=7\%\). As observed for case S-S45 as well, there is a smaller gain difference between those two extrema compared to \(A=7\%\). However, for \(A=25\%\), the gain is higher compared to \(A=7\%\) between 140 and 160 Hz and very similar for all other frequencies. An increase in the gain with amplitude has also been observed in the past studies (Liu et al. 2022; Rajendram Soundararajan et al. 2022) for some frequencies. Similarly to case S-S45, the phase remains mostly unaffected at lower frequencies and is increased for frequencies higher than 190 Hz.

Fig. 11
figure 11

FTF gain a and phase b for case S-S60 forced at \(A=7\%\) and \(25\%\)

Full size image

The FDF for cases S-S60NP and C-S60 are presented in Fig. 12. For case S-S60NP, a notable increase in gain near the maximum at 190 Hz can be observed in Fig. 12a for \(A=7\%\) compared to cases S-S45 and S-S60 in Figs. 10a and 11a respectively. It reaches a value of 1.6 at the maximum, while it remains low around 0.6 near the minimum. The minimum has also shifted to a lower frequency (100 Hz) compared to S-S60 (140 Hz). For an amplitude of \(A=25\%\), the shape of the curve is significantly different with the minimum being shifted to 130 Hz and the gain at the maximum being considerably lower. This highlights the role of swirl in altering the non-linear characteristics of the flame (Kallifronas et al. 2023). Similarly to cases S-S45 and S-S60, the phase is also increased when the amplitude is increased for frequencies above 130 Hz..

For case C-S60, the gain at the minimum and the maximum at 240 Hz in Fig. 12a is lower compared to case S-S60NP and the curve is shifted significantly towards the higher frequencies. The phase is similar to that of case S-S60NP in Fig. 12b for frequencies up to 100 Hz while some differences are observed at higher frequencies.

In summary, increasing the level of swirl can alter the frequencies at which the extrema in the gain curves occur and also affect the gain magnitude at those extrema. While the former effect can be linked to flame length scales as it will be explained in the next subsection, the correlation of swirl and gain magnitude at the extrema is less clear. Increasing the forcing amplitude has been found to affect the location of the minimum for only one case, but appears to smoothen the curve for all cases, reducing the difference in gain value between the minimum and second maximum. It also increases the phase at higher frequencies.

Fig. 12
figure 12

FTF gain a and phase b for case S-S60NP forced at \(A=7\%\) and cases S-S60NP and C-S60 forced at \(25\%\)

Full size image

4.3 FDF Scaling

Earlier studies have found that the extrema may be collapsed by plotting the FTF as a function of a Strouhal number based on a flame length scale and bulk velocity (Kim and Santavicca 2013; De Rosa et al. 2016). In this study, two Strouhal numbers are defined based on the length scales noted earlier as \(St_1=f \ell _1/u_0\) and \(St_2=f \ \ell _2 /u_0\). Following previous studies by Palies et al. (2011), Kim and Santavicca (2013), a Strouhal number may also be defined by considering the distance between the swirler exit and the dump plane. However, this distance is kept the same for all cases featuring the square enclosure (42 mm) and approximately the same for C-S60 (46 mm) which means that there would be no benefit in assessing it further.

Figure 13 shows the FTF for the cases S-S45, S-S60 and S-S60NP as a function of \(St_1\) for \(A=7\%\). In Fig. 13a, the gain curve shows a poor collapse for the three cases as the minimum is shifted to lower \(St_1\) with increasing swirl number. The maxima are also imperfectly collapsed. For the phase in Fig. 13b, cases S-S60 and S-S60NP collapse well, but there is a significant shift to the right for case S-S45. This suggests that \(\ell _1\) is not a suitable length scale for the cases studied at low forcing amplitude.

Fig. 13
figure 13

FTF gain and phase as a function of strouhal number based on \(\ell _1\) for \(A=7\%\)

Full size image

On the contrary, the S-S45 and S-S60 FTFs for \(A=7\%\) collapse well when they are plotted as a function of \(St_2\) as shown in Fig. 14. The minima are found at \(St_2 \approx 0.5\) and the maxima at \(St\approx 0.7\). This is consistent with a previous work (Kim and Santavicca 2013) suggesting that the minima collapse at \(St \approx 0.6\) and the maxima at \(St \approx\) 0.8. However, for case S-S60NP there is a shift of the minimum to \(St \approx 0.35\). This is related to the flow instability noted in Sect. 4.1 and will be discussed further. In terms of phase, there is a better collapse by using \(\ell _2\) rather than \(\ell _1\) with an almost perfect collapse for cases S-S45 and S-S60NP and a small shift to the left for case S-S60.

Fig. 14
figure 14

FTF gain and phase as a function of strouhal number based on \(\ell _2\) for \(A=7\%\)

Full size image

The same procedure is followed for the FTFs at \(A=25\%\). The FTF gain curves scaled using \(\ell _1\) are presented for this amplitude in Fig. 15a, and suggest an imperfect collapse for both the minima and the maxima of the gain. The minima range between \(St_1 \approx 0.7\) and 1.1 and the maxima between 1.05 and 1.5. Better collapse can be observed for phase in Fig. 15b as cases S-S60, S-S60NP and C-S60 scale well. However, the curve for S-S45 remains shifted to the right compared to the rest.

Fig. 15
figure 15

FTF gain and phase as a function of strouhal number based on \(\ell _1\) for \(A=25\%\)

Full size image

For \(\ell _2\), there is a very good collapse of the gain minima and the high frequency maxima for all four cases as shown in Fig. 16a. The minima are encountered at \(St_2 \approx 0.5\) and the maxima at \(St_2 \approx 0.7\). For the phase in Fig. 16b, while the curves do not collapse perfectly, the inflection points appear to collapse at \(St_2 \approx 0.5\).

Fig. 16
figure 16

FTF gain and phase as a function of strouhal number based on \(\ell _2\) for \(A=25\%.\)

Full size image

It is now investigated why the FDF scaled well using \(\ell _2\) for \(A=25\%\), but not well for \(A=7\%\). In Sect. 4.1, the existence of a flow instability arising near the swirler is discussed. The same PSDs of the azimuthal velocities from Probes 1 and 3, shown in Fig. 4a are now presented for cases S-S60 and S-S60NP and a forcing frequency of 190 Hz (200 Hz for case S-S60NP and \(A=25\%\)). In Fig. 17a at Probe 1 for case S-S60, no peaks can be observed for \(A=7\%\) and two peaks for \(A=25\%\) which correspond to the forcing frequency at 190 Hz and the first harmonic at 380 Hz. At Probe 3 in Fig. 17b, there is a peak at 190 Hz for both \(A=7\%\) and \(A=25\%\) and a noticeable first harmonic for \(A=25\%\). This is expected as at higher harmonics tend to be excited at higher forcing amplitudes (Balachandran et al. 2005).

For case S-S60NP and \(A=7\%\), at both Probes 1 and 3 in Fig. 17c and d there is a distinct peak at the frequency of the flow instability near 480 Hz. A small peak of low amplitude compared to the flow instability is observed at 190 Hz at Probe 1 and no peak at Probe 3. When A is increased to \(25\%\) in Fig. 17c and d, the flow instability is completely suppressed at both Probes 1 and 3 and there is a distinct peak only at the forcing frequency of 200 Hz. In the absence of the flow instability at \(A=25\%\), case S-S60NP scaled well with the rest of the cases using \(\ell _2\). It is therefore suggested that flow instabilities can alter the behaviour of the FDF because they can interact with time delays related to vorticity waves and is responsible for the local minima and maxima in the FDF as described in Komarek and Polifke (2010).

Fig. 17
figure 17

Power spectral density of the azimuthal velocity at the three probe locations shown in Fig. 4a for cases S-S60 (a–b) and S-S60NP (c–d) forced at 190 Hz (200 Hz for case S-S60NP at \(A=25\%\))

Full size image

Overall, it is found that calculating a Strouhal Number using a length scale related to the height of maximum heat release per unit length is effective for scaling the FDF minima and maxima at various swirl numbers and amplitudes. Present flow instabilities may affect the scaling and lead to imperfect collapse by interacting with the relevant time delays of the flow.

5 Conclusion

In this paper, experiments and Large Eddy Simulations have been performed on a bluff body burner to assess the effect of swirl on the FTF. Four configurations with swirl numbers ranging between 0.44 and 0.97 have been considered by placing an axial swirler in the inlet pipe. The validation of the unforced flame features is observed to be good with the computed flow and flame features matching the measured ones.

The flames are then forced at two amplitudes \(A=0.07\) and 0.25 for a range of frequencies up to 300 Hz. The LES was generally capable of correctly capturing the shape and magnitude of the gain in the two cases with available experimental data. The phase trend is also captured correctly, however, with a significant offset. This is attributed to the different methods of calculating the axial velocity signal between experiments and computations.

The FDF gain curves for all cases exhibit a typical behaviour with a low frequency maximum, a minimum and a higher frequency maximum followed by decay at higher frequencies. It is found that changes in the swirl number lead to a shift in the gain curve. While no clear relationship has been established between the swirl number and the gain magnitude at the extrema, it is observed that an increase in forcing amplitude leads to a smoothened gain curve for all the cases considered. When the forcing amplitude is increased, an increase in the phase is also observed at higher frequencies compared to the low amplitude case.

Two flame length scales are used to scale the FDFs. The first one, defined using an isocontour of the progress variable, leads to an imperfect collapse in all cases. The second one linked to the height of maximum heat release per axial unit length has been found effective in scaling the gain curves and collapsing the minima. Only one of the cases studied does not scale well and this is attributed to the existence of a flow instability which affects the associated time delays.