Probabilistic Modeling and Uncertainty Quantification of Detailed Combustion Simulation for a Swirl Stabilized Spray Burner

Abstract

To enable risk informed decisions in the simulation-based design and development of novel combustors, uncertainties in the simulation results must be considered. However, due to the high computational costs for their quantification, these uncertainties are commonly not taken into account. Therefore, this work aims at applying an efficient methodology for uncertainty quantification based on Polynomial Chaos Expansion to a semi-technical spray burner reflecting characteristics typically found in modern aeroengine combustors. This requires accurate treatment of the multicomponent liquid fuel, a combustion model relying on finite rate chemistry and a scale resolving hybrid turbulence model to account for highly unsteady flow features and combustion. To overcome the need for costly experimental data for the spray boundary conditions, an algebraic primary breakup model is utilized. The resulting reduction in a priori information is compensated through probabilistic modeling and uncertainty quantification. Due to their importance in the design process, temperature distribution in the gas phase as well as the flame position are considered as the primary quantities of interest. For these quantities of interest, moderate uncertainties are found in the probabilistic simulation results. Further, the predictive capability of the simulation model under uncertainties is quantitively assessed by defining accurary metrics for the gas phase temperature prediction. The study further reveals that the imposed input uncertainties affect quantities of interest in both the dispersed and the gas phase through phase coupling effects.

1 Introduction

Anthropogenic emissions from combustion systems are widely recognized as a leading contributor to global climate change. To mitigate the environmental impact of aviation and comply with increasingly strict regulatory policies, improving the performance of combustion systems in aeroengines has become a key challenge. In this regard, virtual simulation tools play an important role for the efficient exploration of the design space when considering novel combustor concepts in the design process. As such design processes are inherently exploratory, many input parameters to the simulation tools are uncertain or even unknown beforehand due to lack of knowledge regarding the final design. This induces uncertainties in the simulation results which should be quantified and taken into consideration. Only on the basis of this additional information, risk-informed decisions can be made to ensure optimal and safe operation.

A key aspect regarding aeroengine safety and emissions is fuel injection and distribution in the combustor (Dryer 2015; Hubbard and Denny 1975; Lefebvre 2010), i.e. the reliable atomization of the liquid fuel into a spray of droplets. Subsequent processes from evaporation up to pollutant formation strongly depend on the quality of the spray (Lefebvre 1988). In simulations, this must be reflected in accurate boundary conditions regarding droplet size, velocity and local volume flux. However, this data is difficult to acquire from experiments (Tropea 2011) and often relies on expert opinion and experience in early stages of the design process. The influence of incomplete knowledge regarding the spray boundary condition on simulation results was mentioned for example by Eckel and Grohmann (2019), Ruoff et al. (2019), or Pei and Davis (2015), but no systematic assessment in terms of uncertainties in the simulation results was reported.

For this purpose, uncertainty quantification (UQ) aims at quantitatively characterizing the uncertainties in simulation results. In recent times, probabilistic methods have become increasingly popular for the treatment and quantification of uncertainties (Loeven et al. 2007; Red-Horse and Benjamin 2004). In this approach, uncertain input quantities are treated as random variables which can be characterized by probability density functions or intervals to portray their probabilistic behavior. Uncertainties in the output, i.e. the simulation results, are then derived as random variables. As a result, minimum/maximum or confidence intervals can be reported in addition to the simulation results to support the decision makers.

While Monte Carlo simulations are a straightforward method for analyzing the complex mapping between input and output uncertainties, the computational cost of each simulation run in the case of reacting multiphase flows is prohibitively high. Therefore, surrogate models must be used in lieu of the high fidelity simulation model for the propagation of the input uncertainties. An adequate representation of the forward model observables as well as computational efficiency are the main characteristics of such surrogate models. Among the various models proposed in the literature (Forrester and Keane 2008; Yondo and Andrés 2018), Polynomial Chaos Expansion (PCE) in combination with sparse quadrature approaches (Le Maître and Knio 2010) have drawn increasing attention for the use in UQ (Najm 2009; Sheen and Wang 2011; de Souza and Colaço 2014). While the prediction accuracy of data-driven approaches such as Gaussian process regresssion depends on the underlying sampling strategy of the high fidelity simulation model, the PCE and sparse quadrature combination already dictates the most efficient sampling strategy through the quadrature points for PCE construction. Although the PCE methodology is applicable for both intrusive and non-intrusive UQ, the work at hand is focused on the latter approach, in which an existing simulation code is treated as a black box rather than reformulating the governing equations in a stochastic framework.

Early results of UQ studies for reacting flow simulations were reported for example by  Reagan and Najm (2003) and  Duraisamy and Alonso (2012), but were limited to gas phase combustion. Pei and Davis (2015) investigated the sensitivity of spray distribution in the Engine Combustion Network (ECN) experimental configuration on parameters of the spray boundary condition under non-reacting conditions. In a similar study, Van Dam and Rutland (2016) analyzed the uncertainties in the LES results for liquid and vapor penetration from a multi-hole gasoline injector. They considered selected parameters for the primary breakup model as input uncertainties to the LES. Further UQ results from the field of combustion simulation covering sub-phenomena such as thermoacoustic (Guo et al. 2018), chemical kinetics (Mueller and Iaccarino 2013) and droplet evaporation (Ruoff et al. 2020) are available in the literature. The use of PCE in detailed combustion simulations for a laboratory-scale turbulent methane/hydrogen bluff-body flame was demonstrated by Khalil and Lacaze (2015), focusing on uncertainties in LES modeling parameters. Furthermore, Masquelet et al. (2017) reported PCE-based UQ results for an industrial scale aviation gas turbine combustor. However, due to the assumption of fast evaporation of the fuel, the multiphase spray regime was not explicitly simulated. A comprehensive UQ study of spray combustion simulations including detailed modeling of the multiphase regime with a distinct focus on the specification of spray boundary conditions is available from (Enderle and Rauch 2020). In this work, a well characterized laboratory-scale spray flame for liquid ethanol was studied. Uncertainties and sensitivities in temperature profiles over the reaction zone were analyzed using PCE. It was shown that these uncertainties mainly arise from the imprecise knowledge concerning the spray cone angle in the spray boundary condition.

The objective of this study is to extend the PCE-based UQ methodology to a complex, semi-technical use case of spray combustion, which is critical for developing innovative aeroengine combustors. The approach employs uncertainty quantification and probabilistic modeling to improve the accuracy of a simulation model when only limited information is available on the spray boundary condition. Hence, this work addresses the aforementioned challenges in the design process, where some inputs to the simulation model are uncertain due to the lack of knowledge regarding the final design, thereby demonstrating the practical applicability of the proposed methodology. Resolving unsteady and non-linear features in flow fields is crucial for (semi)-technical use cases, which necessitates a scale-resolving simulation approach. To this end, the present study aims to demonstrate the feasibility of the proposed UQ methodology in dealing with simulation problems that have high computational costs, thus highlighting its practical utility in such cases.

The remainder of this paper is organized as follows. A brief summary of the methodology for the simulation of turbulent spray combustion is given in Sect. 2, followed by the methods used for PCE-based uncertainty quantification in Sect. 3. These methods are then applied to the DLR Standard Spray Burner (Grohmann and Rauch 2017) in Sect. 4 in which the simulation setup is briefly validated against experimental data for the non-reacting case, followed by detailed UQ results for the reacting multiphase flow. Finally, concluding remarks are drawn in Sect. 5.

2 Methodology for the Simulation of Turbulent Spray Combustion

For the simulation of turbulent spray combustion a computational platform consisting of separate simulation codes for the gaseous and dispersed phase is utilized. Data is exchanged online via two-way coupling of both phases.

2.1 Gas Flow Solver

The Favre filtered transport equations for mass, momentum, enthalpy and species mass fractions in the gas phase are solved by means of the DLR in-house code THETA (Turbulent Heat Release Extension of the TAU Code) (Di Domenico et al. 2011; Domenico 2008). THETA is an incompressible 3D finite volume solver for structured and unstructured dual grids. A second order accurate solution method is achieved by combining the Crank-Nicolson time discretization scheme with central differencing for the convective and diffusive fluxes. The pressure–velocity coupling is based on a projection method.

To account for the complex three-dimensional and unsteady flow features typically found in swirling flames, a hybrid URANS/LES method based on the Scale Adaptive Simulation (SAS) approach as introduced by Menter et al. (2003a) is utilized. The general SAS concept relies on dynamic transitioning between URANS and LES based on the ratio of turbulent lenth scale $\mathscr {L}_t$ to the von Karman length scale $\mathscr {L}_{vK}$. The transition is achieved by introducing a source term to the transport equation of the dissipative turbulence scale in the underlying URANS turbulence model. The SAS model for the work at hand relies on the $k-\omega$-SST turbulence model (Menter and Egorov 2005; Menter et al. 2003b). The additional source term $F_{SST-SAS}$ for the $\omega$ transport equation reads

$$\begin{aligned} F_{SST-SAS} = \text {max} \left[ C_{F_1} k \varvec{S}^2 \frac{\mathscr {L}_t}{\mathscr {L}_{vK}} - \frac{2}{C_{F_2}}k~\text {max} \left( \frac{1}{\omega ^2} \frac{\partial \omega }{\partial x_j} \frac{\partial \omega }{\partial x_j}, \frac{1}{k^2} \frac{\partial k}{\partial x_j} \frac{\partial k}{\partial x_j} \right) , 0 \right] . \end{aligned}$$

(1)

$C_{F,i}$ are modeling constants, $\mathscr {L}_t=\sqrt{k}/\omega$ is the turbulent length scale, $\varvec{S}$ denotes the norm of the strain tensor and $\mathscr {L}_{vK}$ is the von Karman length scale with

$$\begin{aligned} \mathscr {L}_{vK} = \text {max} \left( \kappa \frac{\sqrt{2S_{ij}S_{ij}}}{\sqrt{ \frac{\partial ^2 u_i}{\partial x^2_k} \frac{\partial ^2 u_i}{\partial x^2_j}}}, C_s\sqrt{\frac{\kappa \hat{\zeta }}{\beta _{\omega _2/\beta _k}-\gamma _2}} \varDelta \right) . \end{aligned}$$

(2)

This formulation allows $\mathscr {L}_{vK}$ to adjust to the already resolved scales in a simulation (Menter and Egorov 2005) and provides a length-scale which is proportional to the size of the resolved eddies with consideration of the local grid spacing $\varDelta$. In high turbulence regions, the source term $F_{SST-SAS}$ therefore increases and the modeled turbulent viscosity is damped by $\omega$. Ultimately, the dissipating effect of the turbulent viscosity on the resolved fluctuations is reduced.

2.1.1 Combustion Modeling

Chemical reactions of the gas phase species are modeled by a finite-rate combustion (FRC) approach in which a separate transport equation is solved for each species $\alpha$ (Gerlinger 2005). Reaction rate coefficients are calculated during the simulation instead of a priori tabulation. The chemical source term from the FRC model is given by

$$\begin{aligned} \omega _\alpha (T,Y)=M_\alpha \sum _{r=1}^{N_r}\left( \nu _{\alpha ,r}'' - \nu _{\alpha ,r}'\right) \left[ \left\langle k_{f,r} \right\rangle \prod _{\beta =1}^{N_{sp}}C^{\nu '_{\beta ,r}}_\beta - \left\langle k_{b,r} \right\rangle \prod _{\beta =1}^{N_{sp}}C^{\nu ''_{\beta ,r}}_\beta \right] . \end{aligned}$$

(3)

$M_\alpha$ is the molar mass of species $\alpha$, $N_r$ the number of reactions and $\nu$ are the stochiometric coefficients. Terms in square brackets denote sources of reactions which are controlled by the forward and backward rate coefficients $k_f$ and $k_b$. They are calculated using the Arrhenius law (Poinsot and Veynante 2005).

For the application of the FRC model in the context of hybrid URANS/LES, a filtered formulation of the source term from Eq. (3) and a closure for the subgrid contribution is required. For this purpose, subgrid-scale turbulence-chemistry interaction is included using an assumed PDF model (APDF) following Girimaji (1991). This requires the solution of two additional transport equations for the temperature variance and the sum of species variances, as detailed in the work of Gerlinger (2005). The filtered chemical source term then reads

$$\begin{aligned} \overline{\omega }_\alpha ^{FRC-APDF}=\int _{-\infty }^\infty \int _{-\infty }^\infty \omega _\alpha (\hat{T},\hat{Y}) P(\hat{T}) P(\hat{Y})~\text {d}\hat{T} \text {d}\hat{Y}, \end{aligned}$$

(4)

where P is an assumed PDF and $\hat{\bullet }$ denotes a random variable. It is assumed that the temperature fluctuation follows a clipped Gaussian PDF while the species’ mass fraction fluctuations follow a multivariate $\beta$-PDF (Domenico 2008). For further analysis of the APDF model in the context of Scale Adaptive Simulations, the reader is referred to the work of Lourier et al. (2015).

2.1.2 Chemical Reaction Mechanism

After vaporization, species from the CTM fuel families are mapped to equivalent species in the gas phase. Normal-alkanes, cyclo-alkanes and mono-aromatics are assigned to normal-decane, iso-octane and toluene, respectively. These species form the main fuel species in a detailed reaction mechanism comprising 49 species and 300 reactions. The mechanism is based on the work of Slavinskaya (2008) and has been optimized for enhanced stability and computational speed using a linear transformation method (Methling 2017). Furthermore, a sub-mechanism for the formation of the ${\hbox {OH}}^*$ radical by Kathrotia (2011) is included.

2.2 Dispersed Phase Solver

The dispersed phase, i.e. the evaporating fuel droplets, is computed using the DLR in-house simulation code SPRAYSIM which is based on particle tracking in a Lagrangian reference frame. Subsets of physical fuel droplets with equal properties are approximated by numerical particles and treated as point sources. In this simplification, particles are assumed to be discrete points providing point sources and point forces to the gas field (Jenny and Roekaerts 2012). The coupled ordinary differential equations for the particles’ position $\vec {x}_p$, velocity $\vec {u}_p$, diameter $d_p$, and temperature $T_p$ along their trajectories are solved by a predictor-corrector scheme.

Secondary breakup of the particles is modeled by the Cascade Atomization and Breakup (CAB) model (Tanner 2003). Unresolved subgrid scale velocity fluctuations of the particles are accounted for using the droplet dispersion model proposed by Bini and Jones (2008).

2.2.1 Multicomponent Vaporization Model

In order to capture the complex composition of aviation fuels (Dryer 2015), a multicomponent vaporization model based on Continuous Thermodynamics (CTM) (Doué et al. 2006) is selected. It approximates the properties of the wide range of liquid species typically found in Jet A-1 via distribution functions and representative fuel families. A $\varGamma$-PDF is chosen as distribution function and three species families are considered, namely normal-alkanes, cyclo-alkanes and mono-aromatics. The three PDFs were calibrated to match the corresponding two-dimensional gas chromatography (GCxGC) data for Jet A-1. A comparison between experimental data (bars) and CTM approximation (lines) is shown in Fig. 1 for the distribution of mole fraction over the normal boiling point. By this approach, the number of degrees of freedom which need to be calculated in the vaporization model reduces by orders of magnitude. The underlying vaporization model resembles the model by Abramzon and Sirignano (1989) in which rapid mixing within the droplet is assumed. Transformed equations of the vaporization model for the use with CTM are detailed in the work of  Eckel and Grohmann (2019).

Fig. 1

Continuous description of Jet A-1 composition using three $\varGamma$-PDFs. GCxGC data (bars), CTM fuel families (lines)

The mass change due to evaporation leads to mass source terms in the gas field equations which are exchanged between the solvers at each time step.

2.2.2 Modeling of Prefilming Airblast Atomization

The PAMELA (Primary Atomization Model for prEfilming airbLAst injector) model as introduced by Chaussonnet and Vermorel (2016) and Chaussonnet (2014) provides a droplet size distribution characteristic for the spray from prefilming airblast atomizers. An overview of such an atomizer is given in Fig.  2a.

In this phenomenological model, a Rosin-Rammler (RR) function

$$\begin{aligned} F_{3,RR}(D) = 1 - \text {exp} \left[ -\left( \frac{D}{m} \right) ^q \right] , \end{aligned}$$

(5)

is assumed for the distribution of the droplet diameter. More specifically, Eq. (5) denotes the cumulative volume distribution function for a Rosin-Rammler distribution with the two parameters m and q being the mean value and its spread. These parameters are calculated from geometrical features of the atomizer, namely the thickness $h_a$ of the atomizing edge, the film length $L_f$ and the mean air velocity $U_G$ alongside the film. Figure 2b illustrates these parameters as a detail of the pre-filming airblast atomizer. For the work at hand, the global formulation of the PAMELA model is utilized, i.e. calculations based on steady-state mean values.

Fig. 2

Typical airblast atomizer as considered in the PAMELA model

Constitutive equations for the PAMELA model were derived from the analysis of an academic experiment of liquid film breakup at an atomizing edge (Müller and Meier 2004) consisting of a planar wing-shaped pre-filmer over which a liquid film was atomized. Simultaneous measurements of the film length, air velocity and resulting spray established a database for a wide range of operating conditions (Gepperth et al. 2010).

In this database, a correlation between $D_{32}/h_a$ and $\text {We}_{h_a}$ is observed:

$$\begin{aligned} \frac{D_{32}}{h_a} = \frac{C_{1}}{\sqrt{\text {We}_{h_a}}}. \end{aligned}$$

(6)

$We_{h_a}$ denotes the Weber number with respect to the atomizing edge $h_a$

$$\begin{aligned} \text {We}_{h_a} = \frac{\rho _g h_a (r_{\rho } U_G)^2}{\sigma } \end{aligned}$$

(7)

and $r_{\rho }$ is the ratio of liquid and gas densities:

$$\begin{aligned} r_{\rho } = \frac{\sqrt{\rho _l}}{\sqrt{\rho _l}+\sqrt{\rho _g}}. \end{aligned}$$

(8)

As aforementioned, it is assumed that the spray after the atomizing edge follows a Rosin-Rammler distribution with parameters $q_{\text {PAM}}$ and $m_{\text {PAM}}$. In this case, a relation between $D_{32}$ and the distribution parameters is given by

$$\begin{aligned} D_{32}^{RR} = m \frac{\varGamma (3/q+1)}{\varGamma (2/q+1)} \end{aligned}$$

(9)

see Lefebvre (2010). Combining Eqs. (9) and (6) yields:

$$\begin{aligned} m_{\text {PAM}} = C_1 \frac{h_a}{\sqrt{\text {We}_{h_a}}} \frac{\varGamma (2/q+1)}{\varGamma (3/q+1)}, \end{aligned}$$

(10)

in which $C_1$ is a calibration constant. As mentioned before, q describes the dispersion of the drop size in the spray. Therefore, this parameter cannot be formally linked to a single measurement value (Chaussonnet 2014). A correlation function for q is obtained from fitting of the Rosin-Rammler distribution to the sprays from the database and comparison with the aerodynamic Weber number $\text {We}_\delta$ based on the boundary layer thickness $\delta$ at the atomizing edge,

$$\begin{aligned} \text {We}_\delta = \frac{\rho _g \delta U_G^2}{\sigma }. \end{aligned}$$

(11)

The thickness $\delta$ is defined according to the work of  Gepperth et al. (2010) as

$$\begin{aligned} \delta = 0.16 \frac{L_{f}}{\text {Re}^{\frac{1}{7}}_{L_{f}}} \quad \quad \text {with} \quad \quad \text {Re}_{L_{f}}=\frac{U_G L_{f}}{\nu _g}. \end{aligned}$$

(12)

The correlation for $q_{\text {PAM}}$ finally reads

$$\begin{aligned} q_{\text {PAM}} = \frac{C_2}{\sqrt{\text {We}_\delta }} + \left( \frac{h_a}{C_3}\right) ^2 + C_4 . \end{aligned}$$

(13)

Again, $C_2,C_3$ and $C_4$ are calibration constants. Constants for the PAMELA model from fitting against the experimental database are summarized in Table 1.

Table 1 Fitting constants in the PAMELA model

3 Methodology for Uncertainty Quantification

Uncertainty quantification aims at identifying the variance in the vector of quantities of interest ${\varvec{q}}=\{q_1, q_2, q_3,.. \}$ calculated from a simulation model $\mathscr {M}$ with

$$\begin{aligned} {\varvec{x}}: \mapsto {\varvec{q}}=\mathscr {M}({\varvec{x}}). \end{aligned}$$

(14)

Equation (14) describes the deterministic mapping of the inputs ${\varvec{x}}=\{x_1, x_2, x_3,..,x_{n_x}\}$ to the quantities of interest. In practical applications, $\mathscr {M}$ may have arbitrary complexity, including several sub-models $\mathscr {M}_{s,i}$ with $\mathscr {M}_{s,i} \subset \mathscr {M}$.

Possible sources of uncertainties in the mapping from Eq. (14) are generally subdivided into model form uncertainties, numerical uncertainties and input uncertainties (Roy and Oberkampf 2011). While model form uncertainties stem from the approximation of the physical system by $\mathscr {M}$, numerical uncertainties are introduced by the numerical solution methods for the underlying set of non-linear differential equations. Finally, input uncertainties describe variations in the vector ${\varvec{x}}$ comprising initial and boundary conditions as well as model parameters. The present work exclusively focuses on the latter type of uncertainties, since input uncertainties are the dominant type in the design process of aeroengine combustors.

For this purpose, a probabilistic approach is adopted in which uncertainties in ${\varvec{x}}$ and ${\varvec{q}}$ are characterized by random variables ${\varvec{X}}$ and ${\varvec{Q}}$ over a sample space $\varOmega$. Statistical measures regarding the simulation results can then be derived from ${\varvec{Q}}$. Hence, the probabilistic formulation of Eq. (14) reads

$$\begin{aligned} {\varvec{X}}: \mapsto {\varvec{Q}}=\mathscr {M}({\varvec{X}}). \end{aligned}$$

(15)

A straight-forward technique to explore this mapping is the well established Monte Carlo method (Fishman 2013), in which Eq. (15) is reconstructed from a series of deterministic model evaluations

$$\begin{aligned} {\varvec{x}}^{(i)}: \mapsto {\varvec{q}}^{(i)}=\mathscr {M}({\varvec{x}}^{(i)}). \end{aligned}$$

(16)

In this approach, the evaluation points ${\varvec{x}}^{(i)}$ are drawn at random from $\varOmega$ or placed following sampling strategies such as Latin Hypercube Sampling (McKay and Beckman 1979) or low discrepancy series (Sobol and Asotsky 2011). Major drawbacks of these sampling-based methods are the relatively low convergence rate of higher moments in ${\varvec{Q}}$ (Le Maître and Knio 2017) and the curse of dimensionality (Bengtsson et al. 2008) when facing high dimensional random variables for ${\varvec{X}}$. This requires a large set of model evaluations which may be infeasible for computationally expensive models. As an alternative to the direct sampling approach, stochastic spectral methods based on non-intrusive polynomial chaos expansion (PCE) are utilized in the work at hand for the evaluation of Eq. (15).

3.1 Polynomial Chaos Expansion

In contrast to the direct sampling approach, PCE aims at directly reconstructing the functional dependence of the output quantity ${\varvec{Q}}$ on the stochastic input ${\varvec{X}}$ (Sudret 2007) making it popular for the use in uncertainty quantification and probabilistic modeling (Najm 2009; Reagan and Najm 2004).

PCE utilizes the fact that the random variable Q can be expressed as a spectral expansion in terms of orthogonal functions of a vector of standard random variables ${\varvec{\xi }}=\{\xi _1,\xi _2,..,\xi _n\}$ conditional on ${\varvec{X}}$ (Ghanem and Spanos 1991). The polynomial chaos expansion of Q then reads

$$\begin{aligned} Q({\varvec{\xi }}) = \sum _{k=0}^\infty \alpha _k {\varvec{\varPsi }}_k\left( \xi _1,\xi _2,...\right) , \end{aligned}$$

(17)

where $\alpha _k$ are deterministic expansion coefficients and ${\varvec{\varPsi }}_k$ are multivariate polynomials of ${\varvec{\xi }}$, forming a complete orthogonal basis with respect to the measure on ${\varvec{\xi }}$ (Khalil and Lacaze 2015). For practical computations, the infinite series from Eq. (17) is typically truncated to a certain order, hence

$$\begin{aligned} Q = \mathscr {M}({\varvec{\xi }}) \approx \sum _{k=0}^P \alpha _k {\varvec{\varPsi }}_k\left( \xi _1,\xi _2,...,\xi _n\right) = \sum _{k=0}^P \alpha _k {\varvec{\varPsi }}_k\left( {\varvec{\xi }}\right) . \end{aligned}$$

(18)

Applying a projection method (Ghanem and Ghiocel 1998) and taking advantage of the orthogonality constraint on ${\varvec{\varPsi }}_k$, the expansion coefficients are given as

$$\begin{aligned} \alpha _k = \frac{1}{\langle {\varvec{\varPsi }}_k, {\varvec{\varPsi }}_k \rangle } \int _{{\varvec{\varOmega }}} \mathscr {M}({\varvec{\xi }}) {\varvec{\varPsi }}_k({\varvec{\xi }}) \mathscr {P}({\varvec{\xi }})~\text {d}{\varvec{\xi }}. \end{aligned}$$

(19)

Since the inner product $\langle {\varvec{\varPsi }}_k, {\varvec{\varPsi }}_k \rangle$ is known analytically from the choice of $\varPsi _k$, the primary computational effort resides in evaluating the multidimensional integral over $\varOmega$. The order of accuracy of the numerical integration directly provides a measure for the accuracy of the PCE. For the work at hand, multidimensional numerical integration based on the Smolyak sparse grid tensorization method (Le Maître and Knio 2010) in combination with a nested Gauss-Patterson quadrature rule (Davis and Rabinowitz 2007) is used. This involves evaluating Eq. (14) at each integration point, i.e. running the actual CFD simulation.

While expectation $\mathbb {E}$ and standard deviation $\mathbb {V}$ of Q can be directly computed from the expansion coefficients by

$$\begin{aligned} \mathbb {E}\left[ Q \right] \approx \alpha _0 \quad \text {and}\quad \mathbb {V}\left[ Q\right] \approx \sum _{k=1}^P\alpha _k^2\left\langle \varPsi _k^2\right\rangle , \end{aligned}$$

(20)

the full posterior distribution $\mathscr {P}(Q)$ is inferred from space filling sampling of the PCE following the density assumed for $\xi _i$.

3.2 Accuracy Metrics for Uncertain Predictions

The quantitative comparison of observations and uncertain predictions, i.e. experimental data and uncertain simulation results, demands for validation metrics which take into account the probabilistic structure of the uncertain predictions. Two validation metrics are utilized to evaluate the quality of uncertain predictions:

3.2.1 Deterministic Observations

In the case of deterministic observations, for example experimental data without measurement uncertainties, the Continous Rankend Probabibilty Score (CRPS) (Gneiting and Raftery 2007) evaluates the difference between the CDF of the uncertain prediction and the idealized perfect observation. The CRPS is defined as

$$\begin{aligned} \text {CRPS} = \int _{-\infty }^\infty \left( \mathscr {C}_Q(\chi ) - \mathbb {H}(\chi -q_{obs}) \right) ^2 \text {d}\chi , \end{aligned}$$

(21)

where $\mathscr {C}_Q$ is the CDF of the uncertain prediction of a QoI q, $q_{obs}$ is the certain observation of q and $\mathbb {H}$ denotes the Heaviside function. Therefore, the CRPS yields a generalized mean absolute error in case of uncertain predictions.

3.2.2 Uncertain Observations

In contrast, the $\textit{Wasserstein-1}$ metric $W_1$ is utilized to compare the probability structure of an uncertain prediction Q with an uncertain observation $Q_{obs}$. A typical example for an uncertain observation could be experimental data with measurement errors. In the Euclidian space, the quantity $W_1 \left( Q, Q_{obs} \right)$ can be interpreted as the minimum amount of work that is required to turn the respective distribution $\mathscr {C}_Q$ into $\mathscr {C}_{Q_{obs}}$ (Johnson and Wu 2017). In case of one-dimensional distributions on the real line, $W_1$ can be written in explicit form as

$$\begin{aligned} W_1 = \int _0^1 |\mathscr {C}_{Q}^{-1}(\varXi )- \mathscr {C}_{Q_{obs}}^{-1}(\varXi )| \text {d}\varXi . \end{aligned}$$

(22)

In this equation $\mathscr {C}_{Q}^{-1}$ and $\mathscr {C}_{Q_{obs}}^{-1}$ are the corresponding inversions of $\mathscr {C}_Q$ and $\mathscr {C}_{Q_{obs}}$. For further derivations, the reader is referred to the work of Bobkov and Ledoux (2014).

3.3 Sensitivity Analysis: Sobol’ Indices

Variance-based sensitivity methods such as Sobol’ indices (Sobol 1993) offer insight into the sensitivity structure of a given quantity of interest Q. Through this approach, the sensitivity of the simulation results to the different uncertainties in the input can be assessed. Sobol’ indices are based on the decomposition of the total variance $\mathbb {V}$ of a model output $\mathscr {M}({\varvec{\xi }})$ into contributions from the different inputs $\mathbb {V}[\mathscr {M}({\varvec{\xi }})|\xi _{i}]$. We consider the first order indices $S_i$ which account for the direct contribution to the variance of $\mathscr {M}$ from $\xi _i$, and the total-effect index $S_i^{T}$ (Homma and Saltelli 1996) which also includes interaction effects of $\xi _i$ with $\xi _{\ne i}$:

$$\begin{aligned} S_{1,i} = \frac{\mathbb {V}\left[ \mathbb {E}\left[ \mathscr {M}\left( {\varvec{\xi }}\right) |\xi _i\right] \right] }{\mathbb {V}\left[ \mathscr {M}\left( {\varvec{\xi }}\right) \right] }, \quad S_i^T=\frac{\mathbb {V}\left[ \mathscr {M}\left( {\varvec{\xi }}\right) |{\varvec{\xi }}_{\sim i}\right] }{\mathbb {V\left[ \mathscr {M}\left( {\varvec{\xi }}\right) \right] }}. \end{aligned}$$

(23)

Note that $S_{1,i}\le S_i^T$. In the case of a Polynomial Chaos Expansion for Q, first order and total Sobol’ indices can be computed directly from the expansion coefficients $\alpha _k$ exploiting Eq. (20).

4 Application

4.1 Test Case

The DLR Standard Spray Burner (SSB) (Grohmann and Rauch 2017) reflects characteristics typically found in aero-engine combustors, while keeping the geometrical complexity on a semi-technical level. These characteristics include, among others, a complex multi-component fuel, pre-filming airblast atomization, flame confinement through combustor walls and a swirl-dominated flow field for the purpose of flame stabilization. Grohmann and Rauch (2017) and Cantu and Grohmann (2018) reported detailed experimental results for a variety of single component fuels as well as conventional Jet A-1.

Figure 3 provides an overview of the experimental apparatus and a detail of the airblast atomizer. The combustor consists of two distinct components: an air nozzle equipped with a pre-filming airblast atomizer and a rectangular combustion chamber with a cross section of $85~\hbox {mm} \times 85~\hbox {mm}$ and a height of $169~\hbox {mm}$ facilitating optical access to the reaction zone through four quartz glass windows. At the top, the cross section of the combustion chamber reduces to a duct (chimney) with $40~\hbox {mm}$ in diameter to ensure well defined outflow conditions. In the air nozzle, an inner and outer swirler consisting of quadratic swirl vanes provide air for atomization and the formation of a co-rotating swirling flow inside the combustion chamber. Geometrical swirl numbers of $\text {Sw}_i = 1.17$ and $\text {Sw}_o = 1.22$ were reported for the inner and outer swirler, respectively (Grohmann et al. 2016). In the center of the air nozzle, a primary pressure-swirl injector (Schlick Mod. 121) ejects fuel droplets onto the pre-filmer surface on which a liquid film evolves and finally disintegrates into a fine spray at the atomizing edge. At the exit plane, the inner and outer air nozzles have a diameter of $D_i = 8~\hbox {mm}$ and $D_o = 11.6~\hbox {mm}$, respectively.

The comprehensive experimental database for the SSB includes a characterization of the flow field from PIV, temperature profiles over the reaction zone obtained by CARS and dispersed phase data from PDA. Furthermore, a qualitative portrayal of the reaction zone is available from the line-of-sight integrated signal of ${\hbox {CH}}^*$ chemiluminescence. Due to the challenges for PIV in the presence of additional fine fuel droplets, PIV was only conducted for the non-reacting flow field. For the work at hand, the baseline case for Jet A-1 as summarized in Table 2 is considered.

Fig. 3

Sketch and detail of the swirl-stabilized Standard Spray Burner

Table 2 Operating conditions of the baseline Jet A-1 case

4.2 Computational Domain and Numerical Setup

The computational domain for the simulation comprises the air nozzle, the quadratic combustion chamber and the outlet chimney. In addition, the air plenum from which the preheated air is fed to the swirler stages is included to obtain a well defined inflow region at the plenum inlet.

An unstructured grid consisting of approximately 1.2 million nodes, corresponding to 5.7 million cells, provides the spatial discretization of the aforementioned computational domain. The grid mainly consists of tetrahedral cells augmented with 4 prismatic layers alongside the walls and hexahedron cells in regions with a distinct flow region (inlet plenum, swirler vanes, outlet duct). Cell sizes range between $0.4~\hbox {mm}$ in the swirler region and $3.0~\hbox {mm}$ towards the outlet. The flame zone contains a mesh refinement in the magnitude of $0.75~\hbox {mm}$. Figure 4 provides an overview of the grid in a central plane including a detail at the atomizing edge of the air nozzle.

Fig. 4

Distribution of cell sizes in a central plane

Inlet boundary conditions for the gas phase are given in Table 2. Wall temperatures of the combustion chamber were experimentally determined by phosphor thermometry (Nau et al. 2019). Following the results of Eckel and Grohmann (2019), the bottom plate of the combustion chamber is divided into three zones. According to the measured temperatures in these zones, the temperatures are set to a constant value of $T=717~\hbox {K}$, $T=901~\hbox {K}$ and $T=831~\hbox {K}$ in the central part, the glowing ring and the corners of the bottom plate, respectively. Based on the thermometry data, a temperature profile in dependence of the axial direction is imposed at the combustor sidewalls. Resulting temperature profiles for the axial and lateral direction of the combustion chamber and a detail of the baseplate from the experiments are shown in Fig. 5. At the outlet of the chimney, an outflow boundary condition is imposed. Here, velocity and all transport equations are extrapolated whereas the pressure is fixed to atmospheric conditions.

Fig. 5

Temperature profiles for the isothermal boundary condition in the combustion chamber

A constant time step $\varDelta t= 5\times 10^{-6}~\hbox {s}$ is set ensuring CFL numbers below unity. For all cases, the simulation is initialized over $\tau _{init} = 0.1~\hbox {s}$ before temporal statistics are collected over consecutive $\tau _{avg} = 0.1~\hbox {s}$. This is based on an estimation of the mean residence time $\overline{\tau }_{res} \approx 0.005~\hbox {s}$ inside the combustor and previous test simulations which analyzed the convergence of statistical moments in the gaseous and the dispersed phase during averaging.

4.3 Spray Boundary Condition from the PAMELA Model

The PAMELA primary breakup model as detailed in Sect. 2.2.2 is used for the definition of the spray boundary condition. Droplets start from an annulus with $r_i=3.5~\hbox {mm}$ and $r_o=4.5~\hbox {mm}$, placed at an axial offset $\varDelta z =1.5~\hbox {mm}$ with respect to the atomizer edge. The PAMELA model provides an SMD $D_{32}$ and a spread factor q for a Rosin-Rammler distribution as defined in Eq. (5). Inputs to the model are the atomizer edge thickness $h_a$, the length of the liquid film $L_f$ along the prefilmer and the mean gas velocity $U_G$ parallel to the liquid film.

For the SSB, the atomizer edge thickness is reported as $h_{a,SSB}=0.1~\hbox {mm}$ Grohmann (2019). Based on the geometry of the prefilmer (see right part of Fig. 3) and the nominal opening angle of the primary pressure-swirl atomizer ($\theta =60^{\circ }$), the location where droplets from the primary atomizer impinge the prefilmer surface can be reconstructed and hence the liquid film length estimated as $L_{f,SSB}=3.8~\hbox {mm}$. Mean gas velocity $U_{G,SSB}$ alongside the liquid film is extracted from preliminary simulations of the mean gas field and ranges between 70 and $85~\hbox {ms}^{-1}$ as the air flow is accelerated within the inner air nozzle.

The PAMELA model does not provide data for the velocity components of the droplets after primary atomization. Therefore, it is assumed that the droplets rapidly couple to the local gas flow at the starting annulus. This is supported by findings from previous simulations. It was found that close to the starting annulus, most droplets had a Stokes number below 10. Therefore, the velocity vector $\vec {U}_D$ of a droplet starting at the boundary condition is derived from the local vector of the gas velocity. The definition of $\vec {U}_D$ is depicted in Fig. 6: In the local polar coordinate system of the droplet, $\vec {U}_D$ is determined by the axial angle $\varphi _D$, the swirl angle $\psi _D$ and the velocity magnitude $U_D$.

Fig. 6

Definition of the velocity vector $\vec {U}_D$ at the spray boundary condition. Black system: Global coordinate system. Green system: Local coordinate system. Blue dots: Droplet starting annulus

4.4 Identification of Input Uncertainties

Sources of uncertainties are identified by analyzing the simulation model for the SSB with respect to input uncertainties. They might arise from uncertainties in the geometry, the modeling constants, as well as boundary conditions for the continuous and dispersed phases.

4.4.1 Geometry

All geometric dimensions and quantities of the SSB, e.g. the combustor length or the dimensions of the channels in the swirler, are documented in the work of Grohmann (2019). Furthermore, the reduced complexity of the geometry in comparison to a full-scale aero-engine enables the resolution of all geometric features in the computational grid.

The atomizer edge thickness $h_a$ serves as an input to the primary atomization model. As detailed in Sect. 4.3, this parameter is known for the SSB. In a preliminary study using the PAMELA model, uncertainties within the reported manufacturing tolerance have shown to have no significant effect on the droplet size distribution calculated by the PAMELA model. For example, the SMD varied by $\pm 1 \%$ due to $h_a=0.1\pm 0.05~\hbox {mm}$, which is the reported manufacturing tolerance for $h_a$.

4.4.2 Modeling Constants

The simulation case under consideration involves a number of sub-models and thus numerous modeling constants which might affect the simulation results. For example, the choice of the Smagorinsky constant $C_s$ in the SAS turbulence model influences the turbulent damping in the LES regions (Ivanova 2012).

In the present study, all modeling constants are set to their respective reference values for which they were validated. This includes modeling constants for the CTM vaporization model, the hybrid turbulence model and the PAMELA primary breakup model. Since uncertainties in modeling constants are beyond the scope of this study, impact of uncertainties in these parameters are not further investigated.

4.4.3 Initial and Boundary Conditions of the Gas Phase

Regarding the boundary condition for the gaseous phase, a simplification applies to the inlet at the plenum, at which the turbulence intensity $I_t$ was not measured in the experiments. Therefore, a uniform inlet velocity rather than synthetic turbulence (Klein and Sadiki 2003) is imposed. In view of the fact that the flow undergoes a strong contraction and most of the turbulence is generated in the swirler stages, this uncertainty should not affect the flow inside the combustion chamber. Measurement uncertainties below $1.2\%$ have been reported for the mass flow rate of the air (Grohmann 2019).

Mercier and Schmitt (2015) demonstrated that uncertainties in wall temperatures and associated heat losses can have a significant impact on local and global temperature distribution. In the present study, temperature profiles from thermometry measurements are utilized. For this data, Grohmann (2019) estimated an error of $\pm \,2\%$.

4.4.4 Initial and Boundary Conditions of the Dispersed Phase

Since the velocity vector of the droplets at the dispersed phase boundary condition is derived from the gas field trajectories, uncertainties are introduced from the variation of the trajectory angle $\psi$ and $\varphi$ over the starting annulus. In the flow field, $\psi$ ranges between $55^{\circ }$ and $63^{\circ }$ while $\varphi$ varies between $26^{\circ }$ and $29^{\circ }$. Furthermore, by applying the absolute velocity $U\approx 60~\hbox {ms}^{-1}$ of the gas phase at the starting annulus to the dispersed phase, droplets start with a significantly too high momentum and mostly impinge at the combustion chamber walls. Therefore, the droplets’ absolute velocity $U_D$ is assumed to be between 25 and $30~\hbox {ms}^{-1}$. This is inferred from similar atomizer configurations (Setzwein et al. 2019; Jones and Marquis 2014). As mentioned in the previous section, the mean gas velocity $U_G$ alongside the liquid film ranges between 70 and $80~\hbox {ms}^{-1}$.

Finally, uncertainties exist regarding the temperature of the liquid droplets at the boundary condition. In the experiments, the temperature of the fuel in the supply system was measured at a location close to the primary pressure-swirl atomizer ($T_{liq,exp}=303~\hbox {K}$). However, the fuel might undergo additional heating during pre-filming atomization due to the surrounding air flow ($T_{air}=323~\hbox {K}$) as well as radiative heat transfer from the reaction zone. Accordingly, the droplets’ temperature is estimated to range between $T_{liq,exp}=303~\hbox {K}$ and $T_{air}=323~\hbox {K}$.

Table 3 provides an overview of the most relevant sources of input uncertainties as identified in this section. Note that depending on the scope of the analysis, additional quantities could be included.

Table 3 Relevant sources of input uncertainties in the simulation model

4.5 Probabilistic Modeling and PCE Construction

From the possible uncertainties identified in the previous section, only the uncertainties in the spray boundary condition will be analyzed in detail, since these parameters play a key role in the early stage design process of novel combustor systems. In a previous study (Enderle and Rauch 2020), uncertainties in the spray boundary condition demonstrated a significant effect on the flame position and temperature distribution over the reaction zone. Thus, the input parameters to the PAMELA model are seen as uncertain inputs to the simulation model.

For simplicity, they are all interpreted as uncorrelated uncertainties and characterized by a joint uniform distribution function with the respective minimum and maximum from the previous analysis. The choice of uniform distribution functions for the marginal distributions in case of minimum/maximum data is derived from the principle of maximum entropy (Kapur and Kesavan 1992; Sudret 2007). Thus, precise probability theory is applied, resulting in a probabilistic simulation model of the SSB, enabling insight into the probabilistic structure of the uncertainties in the simulation results. Table 4 provides a summary of the uncertain input parameters which form the input space $\varOmega _{\text {SSB}} = [\varphi _D \times \psi _D \times U_D \times U_G \times T_{liq}]$. Note that the uncertainty in the mean gas velocity $U_G$ results in SMDs $D_{32}=29-35~{\upmu }\hbox {m}$ and MMDs $D_{50}=35-41~{\upmu }\hbox {m}$ calculated by the PAMELA model.

Table 4 Parameter space $\varOmega _{\text {SSB}}$ of the input uncertainties

Output uncertainties in the probabilistic simulation model are quantified through PCE. The present study specifically focuses on gas phase temperature as quantity of interest, since its accurate prediction plays a crucial role in combustor design (Lefebvre 2010). However, additional quantities of interest from the gas phase as well as the dispersed phase are considered in order to get insight into the phase-coupling dynamics under the given uncertainties. Formally, the truncated PC expansion of a Quantity of Interest Q from the probabilistic simulation model reads:

$$\begin{aligned} Q = \sum _{k=0}^P \alpha _k {\varvec{\varPsi }}_k\left( {\varvec{\xi }}\right) = \sum _{k=0}^P \alpha _k {\varvec{\varPsi }}_k\left( \xi _{\varphi _D},\xi _{\psi _D},\xi _{U_D},\xi _{U_G},\xi _{T_{liq}}\right) . \end{aligned}$$

(24)

Since all uncertainties in Table 4 follow a uniform distribution function, Legendre polynomials form the basis ${\varvec{\varPsi }}_k$ (Xiu and Karniadakis 2002). Multidimensional integration on a Smolyak sparse grid is utilized for the computation of series coefficients $\alpha _k$. A Level-2 expansion is considered, requiring 71 evaluations of the simulation model. The distribution of the integration points over the the parameter space $\varOmega _{SSB}$ is shown exemplarily for the $\varphi _D$ subspace in Fig. 7. Since a single model evaluation requires approximately 22000 CPU hours, the total computational cost for this study is in the order of $1.5\times 10^6$ CPU hours.

Fig. 7

Level-2 PCE quadrature points ( 

 ) of a Smolyak sparse grid over the parameter space $\varOmega _{SSB}$ using a Gauss-Patterson rule

The fact that precise distribution functions are assigned to all input uncertainties allows for a computation of probability distribution functions for the Quantities of Interest from space filling sampling of $\varOmega _{\text {SSB}}$. For this purpose, $10^5$ samples are drawn from the respective PC expansion.

4.6 Results and Discussion

4.6.1 Cold Flow Validation

In order to validate the modeling setup, a deterministic simulation of the cold flow is conducted. Only main features for which experimental data is available are discussed. For a thorough analysis of the SSB baseline case, the reader is referred to the work of Eckel (2018) and Grohmann (2019).

Since the quality of Scale Adaptive Simulations strongly depends on the ability of the grid to locally resolve turbulent fluctuations and thereby switch into LES mode, the local spatial resolution must be reassessed for each problem under consideration. For this purpose, a first criterion is given by the ratio $r_k$ of resolved to total turbulent kinetic energy. It is defined as

$$\begin{aligned} r_{k} = \frac{\overline{k}_{res.}}{\overline{k}_{res.}+\overline{k}_{mod.}} = \frac{\frac{1}{2}\overline{u_i'u_i'}}{\frac{1}{2}\overline{u_i'u_i'}+\overline{k}_{mod}}, \end{aligned}$$

(25)

where $\overline{u_i'u_i'}$ denotes the time-averaged product of velocity fluctuations $u_i'$, whereas $\overline{k}_{mod}$ is the modeled turbulent kinetic energy from the SST turbulence model. According to Pope (2004), in a well-resolved LES this ratio should be at least 0.8, meaning that $80\%$ of the local turbulent kinetic energy budget is being resolved. The criterion is satisfied for the most parts of the computational domain, with exception of the inlet plenum and the swirler vanes, where a URANS solution is obtained.

As a further criterion, the ratio of turbulent to molecular viscosity $r_\mu = \overline{\mu _t}/\overline{\mu }$ is calculated. In LES regions, this ratio should not exceed $\mathscr {O}(10^1)$ (Ivanova 2012; Menter 2012). Similar to the turbulent kinetic energy criterion this is not the case for the core region of the air nozzle, whereas in the combustion chamber, the criterion is met.

An overview of the structure of the non-reacting flow field is given in Fig. 8 by means of contours of absolute velocity in the central $y-z$ plane. In the transient snapshot (Fig. 8a), highest velocities are found inside the air nozzle, specifically at the nozzle exit where the flow reaches a maximum of $|U|_{\text {max}}\approx 120~\hbox {ms}^{-1}$. This corresponds to a local Mach number of $\text {Ma}\approx 0.34$ which is close to the limit of the incompressibility assumption (Poinsot and Veynante 2005). The superimposed streamlines (gray lines) display a strongly turbulent and three-dimensional flow field with vortices shedding from the shear layer caused by the high local velocities at the exit of the air nozzle.

Fig. 8

Simulation results for absolute velocity and streamtraces of the non-reacting flow field

Figure 8b displays the flow field averaged over the simulation runtime. Flow patterns typical for confined swirling flows (Lucca-Negro and O’Doherty 2001) are observable: A small central recirculation zone (CRZ) is formed around $z=0~\hbox {mm}$ reducing the effective outflow area of the inner nozzle. As a consequence, velocity is increased along the prefilmer. Furthermore, a negative pressure gradient along the $z\text {-axis}$ causes a backflow and thus a large inner recirculation zone (IRZ) with a stagnation point at $z\approx 110~\hbox {mm}$. Finally, the back-pressure of the walls and the strong shear layer from the air nozzle establish a counter-rotating outer recirculation zone (ORZ).

Radial profiles of the velocity components from PIV enable a quantitative validation of the simulation results. Figure 8b indicates the region for which PIV data is available in the $y-z$ plane. A comparison of the time-averaged axial velocity and the respective RMS fluctuation is given in Fig. 9 by means of profiles along the lateral y-axis. Axial positions between $z=5~\hbox {mm}$ and $40~\hbox {mm}$ are considered as this region contains the main reaction zone in the following simulation of the reacting flow. For the mean velocity $\overline{w}$, simulation and experiment are in excellent agreement regarding magnitude and radial distribution. As aforementioned, a backflow along the z-axis ($y=0~\hbox {mm}$) is visible. Regarding fluctuations $\overline{w'}$, the simulation overestimates the fluctuation intensity, specifically at $z=5~\hbox {mm}$, $z=10~\hbox {mm}$ and $z=20~\hbox {mm}$. Note that for the simulation, the displayed fluctuation is the total budget of resolved and modeled fluctuations:

$$\begin{aligned} \overline{w'}_{\text {sum}} = \overline{w'}_{res} + \overline{w'}_{mod} = \overline{w'}_{res} + \sqrt{\frac{2}{3}\overline{k}_{mod}}. \end{aligned}$$

(26)

Thus, the overestimation could be a potential imbalance between resolved and modeled fluctuations as a result of the transition from URANS to LES mode of the SAS model, which was identified in the previous section, especially since the resolved part of the fluctuations agrees well with the experimental data.

Further comparison between experiment and simulation is shown in Figs. 20 and 21 in the appendix for the v and u velocity components, respectively. Again, mean data is accurately reproduced by the simulation, while fluctuations are slightly too low, especially at the first axial position.

From the inspection of the two criteria $r_k$ and $r_\mu$ as well as the comparison with PIV data for the flow field, it is concluded that the spatial resolution of the simulation setup is sufficient for a Scale Adaptive Simulation of the SSB.

Fig. 9

Time-averaged profiles of axial (w) velocity component at different axial positions from cold flow measurements and simulation. Mean (left column) and RMS (right column)

4.6.2 Reacting Flow Under Uncertainties—Gas Phase

At first, a single realization from the probabilistic simulation model is considered to provide an overview of the combustion process. For this purpose, the central point of the PC expansion over $\varOmega _{SSB}$ with $\varphi _D=22.5~^{\circ }, \psi _D=59~^{\circ }, U_D=27.5~\hbox {ms}^{-1}, U_G=77.5~\hbox {ms}^{-1}, T_{liq}=311.5~\hbox {K}$ is analyzed. An impression of the combustion process is given by means of contours of gas phase temperature in Fig. 10. The transient snapshot in Fig. 10a shows a wrinkled flame front, indicated by gray contour lines of heat release. In this flame front, fuel that has been transferred to the gas phase is consumed and local temperature increases significantly. The reaction zone extends from $z=5~\hbox {mm}$ up to $z=40~\hbox {mm}$. Hot gases from the flame front accumulate in the outer recirculation zone and are partly transported back to the centerline by large eddies from the inner recirculation. Close to the exit of the air nozzle, these hot gases mix with the cold air flow. With increasing axial distance from the reaction zone, the temperature field becomes more homogeneous. Maximum temperature ranges in the magnitude of $T_{max}=2000~\hbox {K}$ which is well below the theoretical maximum temperature $T_{max}^{adi}\approx 2250~\hbox {K}$ in case of an adiabatic equilibrium. To further illustrate the influence of heat losses due to the isothermal walls and the influence of finite rate chemistry, Fig. 11 displays the different states of the reacting system in the mixture fraction - temperature space. Each scatter represents a positions within the computational domain with its respective mixture fraction Z and transient temperature T. Scatter color corresponds to the axial position. The black line represents the limit of infinitely fast chemistry under adiabatic conditions calculated by an adiabatic equilibrium computation with CANTERA (Goodwin et al. 2018). This limit cannot be reached as the system suffers from heat losses at the isothermal walls. Instead, an upper limit is found approximately $250~\hbox {K}$ below the adiabatic limit (gray line). This new upper limit can be met in the equilibrium computation with CANTERA by reducing the thermal input by $1.75~\text {kW}$ or $17\%$. This value can be seen as an approximation of the heat loss due to the isothermal walls. As also evident from Fig. 11, a significant number of states in the main reaction zone (red and purple dots) deviate from the gray equilibrium line, indicating that these states are governed by a finite rate chemistry. In such states, fuel and oxidizer can coexist since the diffusion and flow timescales are significantly larger than the chemical timescales.

In the time-averaged field of gas phase temperature (Fig. 10b), an M-shaped cold inner zone with axially increasing temperature is visible as well as local hot spots in the outer recirculation zone. In the vicinity of the walls, the influence of the isothermal boundary condition is observable.

Fig. 10

Deterministic simulation results for gas phase temperature of the reacting flow field at the central point of $\varOmega _{SSB}$. Gray lines indicate heat release

Fig. 11

Transient state of the reacting multiphase flow characterized by mixture fraction and temperature. Colors indicate axial position

In the following, probabilistic results from space filling sampling of the PC expansion over $\varOmega _{SSB}$ are taken into consideration. Hence, the full probabilistic strucuture of all quantities of interest can be investigated. Gas phase temperature from the probabilistic simulation is investigated by means of axial and radial profiles over the combustion chamber in the $y-z$ plane, following the CARS measurement locations as indicated in Fig. 8b. Resulting temperature profiles from the PCE over $\varOmega _{\text {SSB}}$ are shown in Fig. 12a–e. The probability structure of the uncertain simulation results is characterized by probability intervals: light gray areas indicate regions with $5\%<\text {Pr}(T)<95\%$, whereas dark gray areas represent $25\%<\text {Pr}(T)<75\%$. The median realization is given by cyan lines. Red squares show the mean temperature $\mu (T_{exp})$ from the CARS measurements while the error bars indicate the corresponding standard deviation $\sigma (T_{exp})$. Most notably, the probability intervals clearly reveal a non-uniform distribution of output uncertainties, despite the fact that all input uncertainties were defined as uniformly distributed. This highlights the non-linear propagation of uncertainties through the simulation model.

Fig. 12

Non-deterministic simulation results for time-averaged profiles of gas phase temperature. Error bars (

) indicate standard deviation of the experimental measurements

Over all positions, moderate uncertainties in the magnitude of $100{-}200~\hbox {K}$ regarding the $[5\%;95\%]$ intervals are visible. In the z-profiles (Fig. 12d, e), highest uncertainties are located at the high temperature regions $(y\approx \pm 30~\hbox {mm})$ where most of the combustion reactions take place. These processes are closely connected to the supply of fuel components through spray evaporation, which is ultimately linked to the input uncertainties at the spray boundary conditions. At the first two axial positions, the non-deterministic simulation is able to bracket almost all experimental data. However, at $z=35~\hbox {mm}$ (Fig. 12c) the temperature profile is still overestimated in the simulation results.

Although the spray boundary condition is symmetric with respect to the z-axis, the uncertain simulation results in the z-profiles appear slightly asymmetric, especially regarding the $[5\%;95\%]$ intervals. This could be caused by noisy data for the construction of the PCE due to incomplete time-averaging in the numerical simulation, insufficient PCE accuracy or an insufficient sample size for the precise computation of the local PDF. Since the influence of time-averaging was investigated in detail for the reference simulation, the asymmetry is most likely due to local PCE accuracy. In Enderle and Rauch (2020) it was identified that the quality of the PC expansion can vary along a profile of QoIs for a complex simulation problem.

Along the axial profile at $y=0~\hbox {mm}$ (Fig. 12d), all measurement data except for the last one are included in the uncertainty region. However, the fact that the axial gradient in the experimental data is almost zero over the last few measurement positions whereas the temperature in the simulation still rises up to $1800~\hbox {K}$ indicates that the temperature in the upper half of the combustor is systematically overestimated in the simulation. This could be caused by deficient thermal losses at the combustor walls due to the thermal boundary condition. Furthermore, it could also stem from a general modeling error.

A significant increase in local uncertainty in the $y=0~\hbox {mm}$ profile (Fig. 12d) is found between $z=40$ and $z=80~\hbox {mm}$. This coincides with the axial position of possible spray-wall impingement after which the droplets are reflected back towards the centerline region. Presumably, this impingement depends on the droplets’ starting velocity $U_D$ and their axial angle $\varphi _D$. Hence, uncertainties in these quantities might influence the spray impingement location and finally the temperature profiles downstream of the respective location.

The tendency in the z-profiles that highest uncertainties are found in the high temperature regions is also reflected in the $y=-20~\hbox {mm}$ profile (Fig. 12e). Here, the mean of the experimental data is within or below the $5\%$ quantile at all positions.

For a quantitative comparison of the non-deterministic simulations and the experimental data, the accuracy metrics Continous Rankend Probabibilty Score (CRPS) from Eq. (21) and Wasserstein-1 ($W_1$) from Eq. (22) are calculated. In the calculation of the CRPS, the mean of the experimental data $\mu _{exp}$ at each location is interpreted as a certain observation. The CRPS yields a generalized mean absolute error in case of uncertain predictions and certain experimental observation. Thus, the measurement error from the experiment is not taken into account and the CRPS is calculated from the local cumulative distribution function of the temperature from the non-deterministic simulation and the mean temperature from the experiment. The local CRPS for the temperature predictions from the non-deterministic simulation is given in Fig. 13a–e. Note that the CRPS is only calculated at radial and axial positions for which experimental data is available. In order to compare the probability structure of the non-deterministic simulation results and the experimental data including measurement errors, the Wasserstein-1 metric for the temperature results is calculated at the same positions as the CRPS. For this purpose, the measurement uncertainty and hence the uncertain observation is assumed to follow a normal distribution $\mathscr {N}(\mu _{exp}, \sigma _{exp})$. The standard deviation $\sigma _{exp}$ is available from the experimental database Cantu and Grohmann (2018). Results for $W_1$ are also included in Fig. 13a–e. At all positions, $W_1 > \text {CRPS}$ stemming from the fact that $W_1$ compares the full probability structure of experiment and simulations, thereby including additional degrees of freedom compared to the point estimate in the CRPS. Key findings from the previous qualitative comparison are confirmed by the metrics: highest values for both metrics, and therefore highest uncertainties, are found around $y=-20~\hbox {mm}$ and $y=0~\hbox {mm}$ for the radial profiles. Uncertainties in the simulation results increase along the axial profile. The mean absolute error under uncertainties given by the CRPS stays between $50~\hbox {K}$ and $200~\hbox {K}$ at all positions. The observation that W1 greatly exceeds CRPS at certain positions, such as $y=-20~\hbox {mm}$, $z=20~\hbox {mm}$ in Fig. 13e, implies that these positions not only exhibit an absolute deviation between the experimental and uncertain simulation results, but also a substantial disparity in the probability distribution’s shape.

Fig. 13

CRPS ( 

 ) and Wasserstein metric $W_1$ ( 

 ) for the probabilistic temperature predictions

Results for the axial component of gas phase velocity in Fig. 14a–e demonstrate that uncertainties in the temperature distribution couple with uncertainties in the gas phase velocity. As in the temperature profiles, highest uncertainties in the z-profiles are found around the reaction zone. Moreover, the width of the $[5\%, 95\%]$ interval increases with increasing axial distance. This tendency is also present in the axial profiles ($y=0~\hbox {mm}$, $y=-20~\hbox {mm}$; Fig. 14d–e) and might be an indicator that the backflow of hot combustion products is affected by the variations in the temperature field due to the input uncertainties with respect to the spray boundary condition. Since experimental data for the velocity field in the reacting flow is not available, a final statement wether the varations in the velocity field are mainly driven by the input uncertainties or an amplification of the effect of general modeling choices is prohibitive.

Fig. 14

Non-deterministic simulation results for time-averaged profiles of axial velocity in the gas phase

4.6.3 Reacting Flow Under Uncertainties—Dispersed Phase

Statistics of the dispersed phase are collected in a two-dimensional registration plane at $z=15~\hbox {mm}$ which is parallel to the $x-y$ plane. Hence, particles from the dispersed phase passing through the registration plane are registered with its respective properties (e.g. velocity, diameter) and time-averaged over the simulation runtime using a cartesian grid over the registration plane for spatial discretization. For each quantity of interest (e.g. droplet velocity components, liquid volume flux) a PCE is then constructed and sampled over $\varOmega _{SSB}$ as decscribed in Sect. 4.5. Figure 15 provides a comparison between the non-deterministic results and PDA data (experiment). The three velocity components are defined with respect to the global coordinate system. Thus, the axial, radial and tangential velocity is derived from the global z, y and x velocity, respectively. The droplets experience a swirling motion in the mathematical positive direction with respect to the z-axis, as they couple to the gas flow. Droplet data from the probabilistic simulation is subdivided into three distinct diameters ($10, 30, 50~{\upmu }\hbox {m}$) to display the droplet dispersion. A $\pm \,10\%$ margin is added for a better statistical convergence. Therefore, the three size classes are defined as $10~{\upmu }\hbox {m}<d<11~{\upmu }\hbox {m}$ (small), $27~{\upmu }\hbox {m}<d<33~~{\upmu }\hbox {m}$ (medium), and $45~{\upmu }\hbox {m}<d<55~{\upmu }\hbox {m}$ (large). In contrast, from the PDA measurements only averaged data regarding the droplet diameter is available. Note that probabilistic simulation results are only shown for locations at which sufficient time-averaged droplet data is available from all 71 simulations. Otherwise, the PC expansion would be prone to high local approximation errors. As for the temperature profiles, the probability structure is characterized by the two probability intervals $[5\%;95\%]$ and $[25\%;75\%]$ as well as the median realization.

Fig. 15

Non-deterministic simulation results for time averaged profiles of droplet velocity components at $z=15~\hbox {mm}$. Simulation data is split into small (

), medium (

), and large droplets (

). Experimental data (

) is averaged over all diameters

Despite the fact that all input uncertainties from Table 4 are directly linked to the dispersed phase, output uncertainties in the components of droplet velocity are low, especially for the medium (blue) and large (green) droplets. The fact that the magnitude of uncertainty increases towards lower droplet diameters can be explained by their low Stokes number and thus higher tendencies to couple to the local gas velocity. As aforementioned, output uncertainties are also present in the velocity components of the gas field. Hence, these uncertainties might be passed on to the small droplets. In contrast, uncertainties in the velocity components of the large droplets simply reflect the input uncertainty in the absolute velocity $U_D$ of $5~\hbox {ms}^{-1}$.

In general, magnitude and profile of the velocity components are well reproduced by the probabilistic simulation. A slight dispersion in axial velocity is observable over the three size classes. Overall, the probabilistic simulation results for the droplet velocity verify the assumption made in the definition of the spray boundary condition that the droplet starting trajectories can be derived from the local gas velocities.

Figure 16 provides probabilistic simulation results for Sauter Mean Diameter and normalized liquid volume flux through the registration plane at $z=15~\hbox {mm}$. Although experimental data for the SMD ranges between $17~{\upmu }\hbox {m}$ and $32~{\upmu }\hbox {m}$, the probabilistic simulation predicts a maximum SMD in the magnitude of $40~{\upmu }\hbox {m}$ and a minimum below $15~{\upmu }\hbox {m}$. However, the SMD profiles must be interpreted with respect to the volume flux data for which simulation and experiment are in good agreement and uncertainties in the simulation are low (see Fig. 16a). Close to the z-axis ($y=0~\hbox {mm}$), the SMD in the simulation reaches its minimum while the volume flux drops to almost zero. Therefore, these droplets relate to a very low volume flux. In contrast, at the radial position of maximum volume flux ($y\approx \pm 17.5~\hbox {mm}$) the uncertainty level with respect to the $[5\%; 95\%]$ interval is in the magnitude of $5~{\upmu }\hbox {m}$ which is the range of SMDs provided by the PAMELA model under the given uncertainty for $U_G$. The radial position of maximum volume flux in Fig. 16b appears almost unaffected by the input uncertainties, confirming that the distribution of droplets is dominated by the gas field in the SSB case.

Fig. 16

Non-deterministic simulation results for time averaged profiles of Sauter Mean Diameter (SMD) and normalized liquid volume flux at $z=15~\hbox {mm}$

For brevity, additional plots for droplet velocities and mean diameter at $z=25~\hbox {mm}$ are given in Figs. 22 and 23 in the appendix. Similar phenomena and tendencies as discussed for $z=15~\hbox {mm}$ can be identified.

4.6.4 Reacting Flow Under Uncertainties—Reaction Zone

Insight into the probability structure of integral quantities of interest under the given uncertainties is provided by the examples of mean flame lift-off height $h_{\text {LO}}$ and mean flame length $L_{\text {F}}$, since most other quantities are highly correlated with the location of the reaction zone in the combustor. Both quantities are derived from the line-of-sight (here: y-axis) integrated and time-averaged ${\hbox {OH}}^*$ concentration in the $\overline{Y}_{{\textrm{OH}}^*}$ simulations, as the ${\hbox {OH}}^*$ radical is primarily found in the reaction zone. Therefore, $h_{\text {LO}}$ is defined as the mean axial distance between the contour $\upsilon \cdot \text {max}(\overline{Y}_{{\textrm{OH}}^*})$ and the exit plane of the air nozzle, while $l_F$ is defined as the difference between the mean extent of this contour minus $h_{LO}$. In this definition, $\upsilon$ is a threshold value which is set to $70\%$. A depiction of the parameters’ definition is available from Fig. 17a–c.

Figure 18 summarizes results from space filling sampling of the PCE over $\varOmega _{\text {SSB}}$ through histograms and the corresponding empirical CDFs $\hat{\mathscr {C}}_{L_{\text {F}}}$ and $\hat{\mathscr {C}}_{h_{\text {LO}}}$. As evident from the histograms, both QoIs follow a distribution function that resembles a normal distribution, despite the fact that all input uncertainties are uniformly distributed. As already discussed for the temperature profiles, this points out that the flame stabilization in the SSB follows a highly non-linear mechanism regarding the injection of liquid fuel droplets.

Experimental results are indicated by orange dashed lines. In case of $L_{\text {F}}$ (Fig. 18b), the experimental value coincides with the mode of $\hat{\mathscr {P}}_{L_{\text {F}}}$, i.e. the most probable realization from the simulation. This should not be confused with the mean realization $\mu _{L_{\text {F}}}=16~\hbox {mm}$, which is greater than the experimental value. Regarding $h_{\text {LO}}$ most realizations underestimate the true lift-off height from the experiment (Fig. 18a). From $\hat{\mathscr {C}}_{h_{\text {LO}}}$ it can be inferred that $80\%$ of the realizations are below the experimental value.

Fig. 17

Definition and extraction of flame lift-off height $h_{LO}$ and flame length $l_F$ from line of sight intergrated ${\hbox {OH}}^*$ simulation results

Fig. 18

Non-deterministic simulation results for flame lift-off height and flame length with respect to a threshold value $\upsilon =50\%$

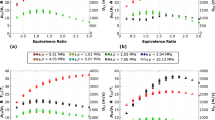
To asses the sensitivity of the two global flame parameters $h_{\text {LO}}$ and $L_{\text {F}}$ to the uncertainties in the input parameters, Sobol’ indices are derived from the Polynomial Chaos Expansion. Figure 19 summarizes the first order Sobol’ indices $S_{1,i}$ and total Sobol’ indices $S_i^T$ with respect to the five uncertain input parameters. Note that total order indices are indicated by hatched color bars.

Fig. 19

First order and total Sobol’ indices for flame lift-off height and flame length. Hatched bars indicate total indices

The flame lift-off height exhibits the most prominent first order indices, and hence the highest sensitivities, for two factors: the liquid fuel temperature $T_{liq}$, and the swirl angle of the droplets $\varPsi _D$. The temperature of the liquid fuel droplets is closely linked with the time it takes for them to evaporate, affecting the transfer of fuel from the liquid to gaseous state. This impacts the axial position at which the flame becomes stable above the atomizer. The swirl angle of the droplets determines wether the droplets are injected in a wider or narrower swirl movement around the z-axis (see Fig. 6) and hence influcences the distribution of liquid and evaporated fuel in the reaction zone. This could explain the high sensitivity of the flame lift-off to this quantity. Although a similar effect should apply to the droplet’s axial angle, the first order index for $\varphi _D$ with respect to the lift-off height is significantly lower then for $\varPsi _D$. However, this could be a result of the smaller uncertainty in $\varPsi _D$ then in $\varphi _D$ (see Table 4). Mean gas velocity along the prefilmer $U_G$ and especially the doplet’s injection velocity $U_D$ show a minor direct contribution to the variation in the flame lift-off height. The degree to which interaction between the input parameters contribute to this variation is indicated by the total Sobol’ indices. For all parameters, $S^T,i>>S_{1,i}$ and $S^T,i-S_{1,i}\approx \text {constant}$, indicating that there is a substantial but equal degree of interaction between all input parameters.

Regarding the flame length, first order Sobol’ indices in the right hand part of Fig. 19 indicate that this quantify is mainly influenced by the two droplet inject angles $\varphi _D$ and $\varPsi _D$. Although the degree of uncertainty is distinctly different between the two inputs, $S_{1,\varphi _D}=S_{1,\varPsi _d}$ as well as $S^T_{\varphi _D}=S^T_{\varPsi _d}$. Hence, the sensitivity and the degree of interaction is the same for both inputs (Fig. 19).

5 Summary and Conclusions

The present study succesfully demonstrated the application of probabilistic modeling to quantify uncertainties in the simulation of a complex, semi-technical combustor burning a multicomponent liquid fuel. The DLR Standard Spray Burner (SSB) constituted a simulation problem reflecting characteristics typically found in modern aeroengine combustors. In order to resolve the complex three-dimensional and unsteady flow structure, hybrid URANS/LES was utilized. To overcome the dependency from the experimental data for the spray phase—i.e. the need for calibration against existing data, an algebraic primary breakup model was incorporated. The resulting reduction in prior knowledge was compensated through probabilistic modeling and uncertainty quantification methods. The breakup model provided data for the mean diameter in the spray, but no information regarding the droplet velocities. The velocity vector of the droplets at the boundary condition was estimated from the local gas field and treated as uniformly distributed uncertainties. Further uncertainties regarding the spray boundary condition resulted in a six-dimensional parameter space of uncertain inputs. Due to their importance in the design process, temperature distribution and flame position were considered as the main quantities of interest. Output uncertainties in the simulation were then quantified through Polynomial Chaos Expansion. Moderate uncertainties were found in the results for the gas phase temperature as well as the droplet velocities. This was further confirmed by accuracy metrics comparing the probabilistic simulation results with the experimental data. A thorough analysis of the dispersed phase under uncertainties verified the assumption made in the definition of the spray boundary condition that the droplet starting velocities can be derived from the local gas velocities. Finally, a sensitivity analysis utilizing Sobol’ indices revealed that the variation in the flame lift-off height is mainly induced by the uncertainties in the temperature of the liquid droplets as well as the swirl angle of the droplets, while the flame length is mostly sensitive to the uncertainties in the droplet’s axial and swirl angle at the spray boundary condition.

On the basis of these results, the following conclusions are drawn:

• Propagation of uncertainties through coupling effects: The present work focused on input uncertainties in the spray boundary conditions. Hence, input uncertainties were primarily introduced to the dispersed phase of the reacting multiphase system. However, it was identified that these uncertainties affect quantities of interest in the dispersed and the continuous phase (e.g. gas phase temperature and velocity or flame position). This highlighted the propagation of input uncertainties through coupling effects throughout the entire thermo-chemical process of multiphase combustion. In view of this fact it is important to note that other input uncertainties which were not considered in the present study should be analyzed. For example, uncertainties in the chemical reaction rates would alter the temperature field and thus influence the local evaporation of droplets.

• Interpretation of uncertain simulation results: Uniformly distributed uncertainties were presumed in the SSB case which enabled the calculation of probability intervals for the uncertain simulation results. This yielded a best estimated prediction of the quantities of interest under the given uncertainties. It should be pointed out that this best estimate purely relied on the assumption of uniform input uncertainties. In contrast, probability bounds from Probabibilty Bounds Analysis as demonstrated in Enderle and Rauch (2020) are known to be larger (Oberkampf 2010) but always reflect the state of knowledge without further assumptions. Therefore, the impact of the application of different UQ frameworks needs to be further studied.

• Potential of UQ in the simulation of spray combustion: The present study clearly demonstrated the added value of uncertainty quantification when only limited data regarding the spray boundary conditions is available. With the additional information concerning the uncertainties in the simulation results, risks can be quantified by comparing the uncertainties with the performance targets. Thereby, decision-making in the design and development process can be supported and advanced towards risk-informed decision-making.

A: Additional Figures

See Figs. 20, 21, 22 and 23.

Fig. 20

Time-averaged profiles of v velocity component at different axial positions from cold flow measurements and simulation. Mean (left column) and RMS (right column)

Fig. 21

Time-averaged profiles of u velocity component at different axial positions from cold flow measurements and simulation. Mean (left column) and RMS (right column)

Fig. 22

Non-deterministic simulation results for time averaged profiles of droplet velocity components at $z=25~\hbox {mm}$. Simulation data is split into small ( 

 ), medium ( 

 ), and large droplets ( 

 ). Experimental data ( 

 ) is averaged over all diameters

Fig. 23

Non-deterministic simulation results for time averaged profiles of Sauter Mean Diameter (SMD) and normalized liquid volume flux at $z=25~\hbox {mm}$