Effects of Fuel Concentration Gradient on Stabilization of Oblique Detonation Waves in Kerosene–Air Mixtures

Abstract

The transition structures and wave stabilization features of the wedge-induced oblique detonation wave (ODW) affect the combustion of the hypersonic air-breathing detonation engine, which is associated with the inhomogeneity of the inflow mixture. This study numerically investigates the influence of inhomogeneous kerosene–air mixtures on the stabilization of ODW for the first time, considering the inter-phase heat and mass transfers and focusing on the flow structure. The multiphase reacting flows are solved by the two-way coupling Eulerian–Lagrangian method. The inhomogeneous degree of fuel–air premixing is represented by the gradient of the liquid fuel equivalence ratio. A new pattern of transition wave structure from the shock-induced deflagration to oblique detonation is found. Under the fuel-rich condition before the shock-induced deflagration wave, a diamond-shaped wave structure is generated due to the large fuel concentration gradients. This flow structure is formed on the wedge without oscillations and is expected for a well-stabilized ODW. The initiation length of ODW is used to value the combustion performance. Its dependence on the inhomogeneous premixing degree displays a W-shaped curve. The chemical heat release influences the initiation length more obviously than the evaporative cooling in the fuel-lean conditions before the shock-induced deflagration. The ODW stabilization is enhanced by the heat released from the fuel-rich chemical reaction. Generally, the two-phase oblique detonation is determined by the competitiveness between the evaporative heat loss and chemical heat release. A uniform fuel–air mixture may not be optimal for detonation initiation based on the results of the present study.

1 Introduction

An oblique detonation wave (ODW) is a combustion wave stabilized on a solid wedge as the supersonic reactive flow interacts with the wedge. This combustion organization method can be harnessed to be promising for the future high-speed propulsion system due to the intrinsic pressure gain features and fast burning rate. The research on oblique detonation wave engines (ODWE) using ODW to produce thrust has grown over the past few decades (Desai et al. 2023; Yao et al. 2023; Yao and Lin 2023; Zhang et al. 2022; Bachman and Goodwin 2021). However, the organization of the well-stabilized ODW in engineering applications is still challenging. In particular, the flow structures and stabilization features of the ODW under various flight conditions should be studied to understand and then design a reliable combustion chamber. For the application of oblique detonations for hypersonic propulsion, the initiation locations and stabilization wave structures must be predicted in the combustion chamber to facilitate the engineering design. To form an ODW, a transition process from a deflagration wave, which is induced by an oblique shock wave (OSW) attached to the wedge, usually occurs during the formation of ODW (Viguier et al. 1996). A triple point connects the OSW, deflagration wave and ODW, and this is named an abrupt transition pattern. Other types of transition structures have also been numerically studied. A smooth transition without the triple point (Teng and Jiang 2012) and other transition patterns with complex wave configurations were found under different inflow conditions (Liu et al. 2015; Bhattrai and Tang 2017).

From the point view of the practical operation of the combustor, the incoming flow and the fuel–air mixing are inhomogeneous during the flight. Research on the ODW formed in fuel concentration gradients is rare. Sislian et al. (2000) analysed the incomplete mixing of fuel and air, and used a Gaussian function to distribute the equivalence ratio. They found the distortion of deflagration waves during the transition process. Iwata et al. (2016) considered a supersonic spherical projectile and numerically studied the effects of inhomogeneous mixing conditions on the patterns of combustion induced by a bow shock wave. Then they studied the ODW stabilized a solid wedge and considered a non-uniform distribution of the equivalence ratio (Iwata et al. 2017). A delegation wave with a V-shape and the Mach stem structures with a shape of V + Y are found due to the effects of the non-uniform fuel–air mixing. Fang et al. (2017) simulated the ODW using hydrogen and compared the results of the initiation length for the ODW under different conditions of the composition inhomogeneity. They found that the distribution of the equivalence ratio during the initiation has a main influence on the initiation length. Iwata et al. (2021) extended their study (Iwata et al. 2016) on the ODW stabilized on the spherical projectile and analysed the ODW formed in a inhomogeneous hydrogen/oxygen/argon mixture. They indicated that the fuel-rich mixture resulted in the decoupling of shock and flame due to the slow chemical reaction.

Previous research has mostly concerned gaseous hydrogen fuel (Zhang et al. 2020) and more recent gaseous acetylene fuel (Zhang et al. 2019). Due to the high density and liquid state for storage, the liquid hydrocarbon fuel has its advantage for aviation and aerospace propulsion. The liquid fuel from the tank usually needs to be injected into the combustor to form reactive mixtures. Because of the injection position of liquid fuel and the interaction between unsteady flow and atomization, the spatial mixing of sprayed droplets and the air is usually inhomogeneous, resulting in high fuel concentration near the injector and low concentration far from the injector. This premixing inhomogeneity affects the performance of the ODWE combustor, but there is a lack of study on the stabilization features of the ODW formed in an inhomogeneous two-phase reactive mixture.

In this study, we investigate ODW created by an inhomogeneous kerosene–air premixed mixture formed on a solid wedge through a parametric numerical study. A linear distribution of liquid fuel equivalence ratios from the incoming supersonic flow is introduced, generating various fuel-lean or fuel-rich inflow mixtures and representing the premixing inhomogeneity. The wave structures of the oblique detonations and their associated initiation features are analysed.

2 Mathematical and Physical Models

The present numerical simulations solve the conservative equations of mass, momentum, and total energy as well as the transport equations of species needed for the combustion process. Each dispersing droplet is tracked individually along its Lagrangian path. The inter-phase interactions, considering the exchanges of mass, momentum, and energy between the Eulerian reacting flow and the Lagrangian droplets, are described by a point-source in cell (PSIC) method (Crowe et al. 1977). The point-force approximation is adopted for the droplets and the droplet diameter is smaller than the Eulerian cell size. Considering the mesh size of 30 μm, the droplets with the diameter of 2 μm are sub-grid and the size ratio of mesh to droplet is 15. The initial mean distance between two neighbour droplet is 20 μm and a sparse dispersion of the droplet-phase system is assumed. Droplet interactions are not considered.

The mathematical equations used in the present simulations are as below,

$${\text{gas - phase}}\;{\text{equations}}\left\{ {\begin{array}{*{20}l} {\frac{\partial }{\partial t}(\rho ) + \frac{\partial }{{\partial x_{j} }}\left( {\rho u_{j} } \right) = S_{{\text{m}}} } \hfill \\ {\frac{\partial }{\partial t}\left( {\rho u_{i} } \right) + \frac{\partial }{{\partial x_{j} }}\left( {\rho u_{j} u_{i} + P\delta_{ij} - \tau_{ij} } \right) = S_{{{\text{F,}}i}} } \hfill \\ {\frac{\partial }{\partial t}\left( {\rho e_{{\text{t}}} } \right) + \frac{\partial }{{\partial x_{j} }}\left( {\left( {\rho e_{{\text{t}}} + P} \right)u_{j} - u_{i} \tau_{ij} - q_{j} } \right) = S_{{\text{Q}}} } \hfill \\ {\frac{\partial }{\partial t}\left( {\rho Y_{k} } \right) + \frac{\partial }{{\partial x_{j} }}\left( {\rho Y_{k} u_{j} } \right) + \frac{\partial }{{\partial x_{j} }}\left( {\rho Y_{k} \left( {V_{k,j} + V_{j}^{{\text{c}}} } \right)} \right) = S_{{{\text{combustion}},k}} + S_{{Y_{k} }} } \hfill \\ \end{array} } \right.$$

(1)

$${\text{droplet - phase}}\;{\text{equations}}\left\{ {\begin{array}{*{20}l} {\frac{{{\text{d}}x_{{{\text{d}},i}} }}{{{\text{d}}t}} = u_{{{\text{d}},i}} } \hfill \\ {\frac{{{\text{d}}u_{{{\text{d}},i}} }}{{{\text{d}}t}} = \frac{{F_{{{\text{d,}}i}} }}{{m_{{\text{d}}} }} = \frac{{F_{{{\text{sg,}}i}} + F_{{{\text{qs,}}i}} + F_{{{\text{am,}}i}} + F_{{{\text{vu,}}i}} }}{{m_{{\text{d}}} }}} \hfill \\ {\frac{{{\text{d}}T_{{\text{d}}} }}{{{\text{d}}t}} = \frac{{Q_{{\text{d}}} + \dot{m}_{{\text{d}}} L_{{\text{V}}} }}{{m_{{\text{d}}} c_{{\text{L}}} }} = \left( {\frac{{f_{{\text{Q}}} \left( {{\text{Re}}_{{\text{d}}} } \right)}}{{\tau_{{\text{a}}} }}} \right)\left( {\frac{{{\text{Nu}}}}{3\Pr }} \right)\left( {\frac{{c_{p} }}{{c_{{\text{L}}} }}} \right)\left( {T_{{\text{@d}}} - T_{{\text{d}}} } \right) + \left( {\frac{{\dot{m}_{{\text{d}}} }}{{m_{{\text{d}}} }}} \right)\frac{{L_{{\text{V}}} }}{{c_{{\text{L}}} }}} \hfill \\ {\frac{{{\text{d}}m_{{\text{d}}} }}{{{\text{d}}t}} = \dot{m}_{{\text{d}}} = - m_{{\text{d}}} \left( {\frac{1}{{\tau_{{\text{a}}} }}} \right)\left( {\frac{{{\text{Sh}}}}{{{\text{3Sc}}}}} \right){\text{In}}\left( {1 + B_{{\text{M}}} } \right)} \hfill \\ \end{array} } \right.$$

(2)

$${\text{inter - phase}}\;{\text{coupling}}\;{\text{terms}}\left\{ {\begin{array}{*{20}l} {S_{{\text{m}}} = - \frac{1}{\Delta V}\sum\limits_{{N_{{\text{c}}} }} {\left( {\dot{m}_{{\text{d}}} } \right)} } \hfill \\ {S_{{{\text{F,}}i}} = - \frac{1}{\Delta V}\sum\limits_{{N_{{\text{c}}} }} {\left( {F_{{{\text{d,}}i}} + \dot{m}_{{\text{d}}} u_{{{\text{d}},i}} } \right)} } \hfill \\ {S_{{\text{Q}}} = - \frac{1}{\Delta V}\sum\limits_{{N_{{\text{c}}} }} {\left( {Q_{{\text{d}}} + \dot{m}_{{\text{d}}} \left( {\frac{{u_{{{\text{d}},i}} u_{{{\text{d}},i}} }}{2} + h_{{{\text{V}},{\text{sf}}}} } \right)} \right)} } \hfill \\ {S_{{Y_{k} }} = \left\{ {\begin{array}{*{20}l} { - \frac{1}{\Delta V}\sum\limits_{{N_{{\text{c}}} }} {\left( {\dot{m}_{{\text{d}}} } \right)} } \hfill & {{\text{for}}\;{\text{fuel}}} \hfill \\ {0{\kern 1pt} } \hfill & {{\text{for}}\;{\text{other}}\;{\text{species}}} \hfill \\ \end{array} } \right.} \hfill \\ \end{array} } \right.$$

(3)

The density, velocity vector, static pressure, static temperature, and total energy of the gas-phase are represented by ρ, u_i, P, T, and e, respectively, in the above equations. The Y_k indicates the mass fraction of species k in the mixture. The kinetic theory (Poling et al. 2001), which is an accurate method, is applied to model the transportation parameters including the dynamics viscosity, heat conductivity coefficient, and mass diffusion coefficient. In particular, the Lennard–Jones potentials are used to calculate the inter-molecular forces. The heat conductivity of each species is calculated by using the modified Eucken model. The dynamic viscosity and the binary diffusion coefficient are computed according to the Chapman-Enskog theory. The semi-empirical expressions proposed by Wake and Wassiljewa are used to calculate the dynamic viscosity, μ, and heat conductivity, λ, of the gaseous mixture. The unsteady forces, such as stress-gradient, quasi-steady, added-mass, and viscous-unsteady forces (Ling et al. 2016), are added on the droplet, and the definitions of these parameters in the above governing equations can be found in Ren et al. (2018a).

The two-phase reacting flow is solved by an in-house CFD code, and this code has been applied for the numerical investigation of two-phase reacting flow (Ren et al. 2018a) and detonation (Ren et al. 2018b). The high-order numerical scheme of WENO-CU6 (Hu et al. 2010) is coupled with the code to obtain a sixth-order accuracy for the convection term. The diffusion term is discretized by a six-order compact scheme. A third-order Runge–Kutta integration is utilized to get the new physical information of the droplet-phase. A fourth-order Lagrangian interpolation method is applied to pick up the physical information at the droplet’s position from the flow field. The time integration for the droplet-phase is a third-order Adams–Bashforth method.

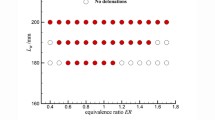
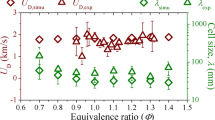
A two-step reduced chemical reaction model of kerosene proposed by Franzelli et al. (2010) is used in the present calculation. The velocities of detonation waves and cell sizes are obtained by a series of two-dimensional simulations on the propagation of detonation waves in the kerosene–air mixture with different equivalence ratios, and the set-up of the simulations can be found in Huang et al. (2021). The detonation velocities are recorded and the cell sizes are measured by the distributions of the maximum pressure. The results are compared with the experimental data (Schauer et al. 2005; Austin and Shepherd 2003), as shown in Fig. 1. It is found that the numerical predictions reasonably agree with the experimental measurement.

Fig. 1

The comparison of detonation velocity, U_D, and cell size, λ, predicted by present numerical simulations (round scatters) and experiments (square scatters)

A sketch of the oblique detonation wave engine (ODWE) with simple components is shown in Fig. 2a. At the combustor’s wall, the liquid fuel is injected to form small dispersing droplets, resulting in an inhomogeneous spatial fuel concentration. A local enlargement of the combustor in ODWE is depicted in Fig. 2b. The droplets evaporate to form vapours and the momentum balance between droplets and surrounding gas is considered to be achieved in the downstream region from the injection. The computational domain is bounded by the dashed line. The supersonic flow containing fuel droplets is from left to right. The flow passes the solid wedge with an angle of θ_w, which induces an oblique shock wave has an angle of θ_s. After a transition process, a detonation wave is generated downstream with an angle of θ_d. A supersonic inlet boundary is used. The wedge surface is treated as a non-slip wall and is modelled using an immersed boundary method (IBM), which is constructed by two layers of ghost cells across the surface. The rest boundaries are modelled as zero-gradients.

Fig. 2

Schematic of ODWE and wedge-induced oblique detonation formed in inhomogeneous two-phase mixtures

The two-dimensional computation domain has a rectangle size of L_x × L_y, where L_x is the streamwise length and L_y is the transverse length. The length and height of the wedge are L_w and H_w, respectively. L_x is three times H_w and L_y is 1.75 times H_w. In particular, L_x equals 0.06 m and L_y is 0.03 m. The wedge angle is set as θ_w = 20°. The computational domain is kept the same as the previous studies on the ODW of hydrogen fuel to make a comparison (Iwata et al. 2021).

The flight condition of hypersonic air-breathing aircraft will affect the inlet conditions of the combustor. A typical flight condition is studied in the present paper. The flight altitude is 30 km and the flight Mach number is 10. In the inlet of the ODWE, the supersonic inflow is compressed by the oblique shock waves, and then the Mach number at the combustor inlet is M₀ = 5.1. The static pressure (referred to as P₀) and the static temperature (T₀) are 0.05 MPa and 1000 K, respectively. P₀ and T₀ are then chosen as the inflow parameters for the computation. The droplet-phase is considered a well-atomized mist. Each droplet has the same initial diameter of 2 μm with the temperature of T_d = 298.15 K. The initial Stokes number, St₀, is St₀ = t_a0/t_flow = 0.18. The initial velocity of the droplet equals the velocity of the surrounding gas. The breakup process is not considered in the present study since the Weber number based on the velocity difference of the droplet and gas is very small. The kerosene (C₁₀H₂₀) fuel is a linear combination of the C₁₀H₂₂, C₉H₁₂, and C₉H₁₈ species (Hu et al. 2010).

The fuel can be injected from upper or lower walls in a combustor to obtain well mixing from the interaction of supersonic flow and spray, as depicted in Fig. 3, resulting in a non-uniform distribution of fuel concentration. To study the concentration gradient of the equivalence ratio, the liquid fuel equivalence ratio, Φ_l, is applied and is assumed as a linear distribution along the transverse direction as the first step to model the inhomogeneous fuel–air mixture. The Φ_l is represented by $\Phi_{{\text{l}}} \cdot \left( {F/O} \right)_{{{\text{st}}}} = \dot{m}_{{{\text{fuel}}}} /\left( {\dot{m}_{{{\text{air}}}} Y_{{{\text{O}}_{2} }} } \right)$. (F/O)_st is the stoichiometric value of the fuel-to-oxidizer ratio and equals 3.42. $\dot{m}_{{{\text{fuel}}}}$ and $\dot{m}_{{{\text{air}}}}$ are the mass flow rates of fuel and air, respectively. $Y_{{{\text{O}}_{2} }}$(= 0.23) is the mass fraction of oxygen in the air. The inflow distributions of Φ_l are justified by measuring the number of dispersed kerosene droplets injected into supersonic airflows according to the function Φ_l (y),

$$\Phi_{{\text{l}}} \left( y \right){ = }\left( {\Phi_{{L_{y} }} - \Phi_{0} } \right)/L_{y} \cdot y + \Phi_{0}$$

(4)

Fig. 3

Schematic of the fuel injection pattern

Here, $\Phi_{{L_{y} }} = 1 + \Delta \Phi_{{\text{l}}}$ is the liquid fuel equivalence ratio at y = L_y, and $\Phi_{0} = 1 - \Delta \Phi_{{\text{l}}}$ is the liquid fuel equivalence ratio at y = 0, as shown in Fig. 2. The liquid fuel equivalence ratio at the transverse centreline of the inlet, Φ_l(L_y/2), maintains the unity. The value of the parameter, ΔΦ_l, represents the inhomogeneous degree of fuel–air premixing and is chosen to maintain the unity of the total equivalence ratio by the integration over the region 0 < y < L_y of the inlet. Six levels of the fuel concentration gradients for the inhomogeneous distributions are chosen from the above limitation. In particular, the SR cases represent the scenarios where the fuel is injected from the lower wall to form a fuel-rich mixture near the wedge side. The SL cases refer to the situations for the fuel injected from the upper wall, as seen in Fig. 3, resulting in a fuel-lean condition near the wedge.

The cases for simulating the detonation wave formed in the two-phase flows are summarized in Table 1, and Case SU for a uniform fuel–air mixture is also applied as a comparison. The simulation cases with the number SL correspond to the fuel-lean conditions and those with the number SR to the fuel-rich conditions in the lower half of the inlet. The Φ_l(y) is varied along the transverse direction of the inlet, and other initial conditions remain unchanged. The resulting distributions of Φ_l(y) at the inlet for each case are depicted in Fig. 4.

Table 1 Summary of simulation cases

Fig. 4

Distributions of liquid fuel equivalence ratio at the inflow boundary

3 Results and Discussion

3.1 Uniform Mixture and Grid-Independence Resolution

The Case SU with a uniform fuel–air mixture is firstly simulated, and the grid-independence study is applied based on Case SU. Three sizes of grids (40, 30, and 20 μm) are utilized and the results are shown in Fig. 5. The streamwise profiles of fuel mass fraction (Y_F) are shown in Fig. 5a. It is found that a constant value is reached after an increasing stage, which means that the droplet finished evaporation. The fuel mass profile of the 30 μm case overlaps with that of the 20 μm case, and the grid-independence for the droplet evaporation is achieved for the 30 μm grid. Figure 5b, c provide the pressure distributions across the OSW and the ODW, respectively. The curves of the simulation using a 30 μm grid are almost the same as those of the 20 μm grid. It indicates that the 30 μm grid can obtain a grid-independence study to mimic the shock wave and detonation wave in the present study.

Fig. 5

Grid dependence for Case SU: a fuel mass fraction Y_F for droplet evaporation, b dimensionless pressure P/P₀ across ODW along y = 1.5 H_w, and c dimensionless pressure P/P₀ across OSW along y = 0.5 H_w

3.2 Wave Structure

Firstly, the Case SU with a uniform fuel concentration is analysed. The fuel droplets with a small initial diameter evaporate quickly and finish the evaporation before they pass through the detonation wave. The interaction between droplet and detonation wave does not occur. An oblique shock wave (OSW) stabilizes on the wedge and the OSW induces a deflagration wave downstream. The transition from the deflagration to an oblique detonation wave (ODW) is achieved in a downstream region. This is a typical abrupt transition (Teng and Jiang 2012) with a multi-wave point connecting the OSW, deflagration wave and ODW, as shown in Fig. 6b. It is found that the transition point has a much higher pressure than the oblique detonation. Several transverse waves are also formed in the transition regime.

Fig. 6

Distributions of dimensionless temperature T/T₀ along the droplet living boundary where the droplets finish evaporation (a) and distributions of dimensionless pressure P/P₀ (b–h). Here, the black regimes refer to the fuel droplets

The droplets are released in the supersonic flow with a higher temperature. The evaporation of droplets decreases their surrounding temperature due to the cooling effects. The increase in the liquid fuel equivalence ratio results in more droplets with a higher fuel concentration and hence a lower gaseous temperature around the droplets because of the evaporative cooling. It is therefore necessary to discuss the thermal features of the two-phase flows affected by the inhomogeneous fuel concentration. Figure 6a shows the distributions of the gaseous temperature along the boundary where the fuel droplets finish evaporation, as scaled by the white dashed line in Fig. 6c. The y-axis starts around y/L_y = 0.2 where the OSW begins to affect the droplet evaporation and increase their temperature. For the SR cases (fuel-rich mixture in the lower half of the inlet), the gaseous temperature T/T₀ decreases linearly as the y/L_y decreases, and the increase in the liquid fuel equivalence ratio, Φ_l(y), results in a reduction of temperature. It should be noted that the Φ_l(y) and their associated distribution patterns affect the initiation of detonation. Although the SR cases could have enough fuel droplets for the shock-induced deflagration in the initiation region, the relatively low gaseous temperature due to the evaporative cooling effects may decrease the chemical reaction rate during the detonation initiation process. The influence of the fuel concentration gradient on the formation of oblique detonations is discussed in the following section.

Figure 6c–h shows the instantaneous distributions of the dimensionless pressure, P/P₀, of the simulation cases with the inhomogeneous distributions of Φ_l(y). The black regimes indicating the evaporating fuel droplets. The increase in Φ_l(y) results in a longer droplet living distance, as depicted by the white dashed lines for Case SL-1, which is mainly due to the decreasing ambient gaseous temperature around the droplets because of the cooling effects from evaporation. The overall characteristics indicate that the inhomogeneous premixing not only influences the initiation length of ODW but also alters the transition pattern from the OSW to ODW. For Case SL-1, the lower half of the incoming flow is a lean fuel–air mixture where ΔΦ_l = 1.0, which means that the Φ_l(y) before the OSW has a minimum value of 0. The fuel-lacking condition before the OSW and the associated shock-induced deflagration suppress ODW formation. The initiation of oblique detonation is delayed with a low transition pressure for Case SL-1. The ODW is initiated smoothly from a curved shock wave around x/H_w = 3.0. When ΔΦ_l decreases for the SL cases, the inflow fuel concentration becomes uniform. It is found that the initiation position of the ODW moves upstream and the ODW formation is accelerated with a higher transition pressure. This is because more fuel droplets are injected from the lower half of the incoming flow, and the evaporated fuel vapours contribute to the deflagration, which accelerates the chemical reaction rates and increases the amount of heat released. The occurrence of ODW changes from x/H_w = 3.0 in Case SL-1 to x/H_w = 2.5 in Case SL-3 (ΔΦ_l = 0.2). The transition also varies from smooth to abrupt patterns with a strong transverse wave in Case SL-3. In addition, the smooth detonation surface appears at first but then destabilizes to generate the local cellular structures on the ODW front. However, as ΔΦ_l further decreases to 0, the initiation position of ODW approaches downstream, as shown in Fig. 6b. The temperature reduction from the evaporative cooling tend to be obvious, which suppresses the deflagration and then has a negative influence on the transition to ODW.

For the fuel-rich mixture from the lower half of the inflow, the decrease in ΔΦ_l from Case SR-3 (ΔΦ_l = − 0.2) to Case SR-2 (ΔΦ_l = − 0.6) results in the accelerated formation of oblique detonations, associated with an increasing transition pressure. For Case SR-2, the transition from the OSW to ODW is coupled with a series of transverse compression waves. With a further decrease in ΔΦ_l from Case SR-2 to Case SR-1 (ΔΦ_l = − 1.0), the initiation of the oblique detonations is delayed, and the initiation position moves downstream. The transition pattern from the OSW to ODW becomes smooth and is associated with a curved shock as well as a low transition pressure. Although more fuel droplets are injected into the upstream flow of the shock-induced deflagration, the initiation cannot be accelerated. This is mainly attributed to the fact that, for a two-phase detonation, the thermal energy of the incoming flow is used not only for the initiation of the chemical reaction but also for droplet gasification. The evaporation of fuel droplets depends on the heat transferred from the surrounding gas, and the decrease in the ambient gaseous temperature results in a reduction of the chemical reaction rates for the initiation process. For Case SR-1, it is notable that the transition zone connecting the OSW and ODW contains a complex wave structure, and the shape looks like a diamond, and its analysis will be discussed later.

The local enlarged snapshot of the gaseous pressure around the transition zone for Case SR-1 is shown in Fig. 7, and the white dashed lines in the contours correspond to the fuel mass fraction of the stoichiometric mixture, Y_F,st. Y_F,st equals 0.063 for the kerosene–air mixture. A schematic of the complex wave structure is also given in Fig. 7. It is clear that the transition from the OSW to ODW is smooth with a curved shock and a transverse wave with relatively weak strength, denoted as W3 in the schematic. The reactive mixture is fuel-lean on the up-side of Y_F,st and is fuel-rich on the down-side before the oblique shock. The inhomogeneous premixed fuel–air mixture results in a V-shaped flame front after the OSW, which was also observed in previous research on hydrogen-air oblique detonation (Fang et al. 2017). The V-shaped deflagration wave consists of two compression waves, namely W1 and W2, which are shown in the schematic diagram in Fig. 7. The W2 interacts with the wedge surface and reflects to form a compression wave W4. The W4 then intersects with the W3 in the downstream regime, and the interaction of the two compression waves results in a local pressure peak, as depicted in the pressure contours. For a large gradient of fuel concentration in the two-phase mixture, the stabilization wave structure during the transition from the OSW to ODW displays a diamond-shaped structure, and this structure is stable.

Fig. 7

Distributions of dimensionless pressure P/P₀ (a) and fuel mass fraction (b) around the transition zone for Case SR-1. Here, the white dashed lines refer to the fuel mass fraction for a stoichiometric mixture, Y_F,st., and the black dashed lines indicate the wave structure. A schematic of the diamond-shaped stabilization structure is shown on the right side of (a)

Figure 8 shows the streamwise evolutions of the pressure and temperature profiles along the transverse lines y/H_w = 0.85 and y/H_w = 0.90, respectively. The line along the y/H_w = 0.85 crosses the V-shaped flame (W1 and W2) and the compression wave W4, as depicted in Fig. 7. The OSW, located at x/H_w = 2.5, results in high pressure and high temperature. The V-shaped flame forms in the post-shock flow, and it is due to the inhomogeneous fuel concentration with a large gradient. The combustion products of the deflagration have a local high temperature. Then the reflection of W2 on the wedge surface leads to a compression wave, W4, with much higher pressure, as shown in Fig. 8a. Figure 8b displays the line along the y/H_w = 0.90 that passes the deflagration wave W1 and the compression wave W3. W1 leads to high pressure in the post-OSW flow and is associated with an increasing temperature from the chemical reaction heat release. The reactants are consumed across W1, and the pressure decreases in the downstream regime. The W3 intersects with the reflection wave W4 around x/H_w = 3.1 and results in higher pressure. W3 further propagates and reflects on the wedge surface, forming a weak compression wave, as indicated in Fig. 8b. In general, there are complex interactions of the compression waves and deflagration waves in the transition regime connecting the OSW and ODW. The fuel-rich concentration with large gradients leads to the diamond-shaped stabilization wave structure.

Fig. 8

Streamwise profiles of dimensionless pressure P/P₀ (blue lines) and dimensionless temperature T/T₀ (red lines) along: a y/H_w = 0.85 and b y/H_w = 0.90 for Case SR-1

3.3 Initiation Length of ODW

To further investigate the inhomogeneous premixing effects, the characteristic initiation length, L_i, is considered (Ren et al. 2018b). L_i is measured along the streamwise direction, which starts from the tip of the wedge and ends at the formation of the ODW, as shown in Fig. 2. The initiation length is obtained by a time average during 10 flow circles for a steady condition. A series of additional simulation cases are applied to analyse the dependence of oblique detonation initiation on the inflow premixing inhomogeneity. To achieve a comprehensive scenario, the inhomogeneous degree of the liquid fuel equivalence ratio, ΔΦ_l, is chosen as − 0.8, − 0.4, 0.4, and 0.8, and the associated cases are simulated. It is interesting to find that a diamond-shaped wave structure is found during some fuel-rich concentration conditions, as shown in Fig. 9. For the ΔΦ_l with values of − 0.8 and − 0.7, the fuel concentration before the OSW has a large gradient, as shown in Fig. 10, and a V-shaped deflagration wave is initiated after the OSW. The V-shaped deflagration wave, combined with a transverse wave from the transition point and a reflection wave, forms the stabilization structure with the diamond shape. The difference is the transition with a higher ΔΦ_l (− 0.7) and a smaller fuel concentration gradient displays an abrupt pattern with higher pressure and a stronger transition wave, compared with those of the ΔΦ_l = − 0.8 case and a smooth transition. Therefore, the intersection of the W3 and W4 leads to a higher pressure peak, as shown in Fig. 9b. When the ΔΦ_l increases to − 0.6 (Case SR-2), this typical wave structure cannot be formed, as seen by Fig. 6f.

Fig. 9

Distributions of dimensionless pressure P/P₀ for the ODWs fuelled with droplets: a ΔΦ_l = − 0.8 and b ΔΦ_l = − 0.7. Here, the white dashed lines indicate the distribution of Y_F,st

Fig. 10

Distributions of fuel mass fraction for the ODWs fuelled with droplets: a ΔΦ_l = − 0.8 and b ΔΦ_l = − 0.7. Here, the white dashed lines indicate the distribution of Y_F,st

Figure 11 displays the dependence of the time-averaged initiation length $\overline{L }$_i, on the ΔΦ_l. The negative value of ΔΦ_l means that the reactive mixture is fuel-rich in the lower half of the inlet (SR) and is fuel-lean in the upper half. The fuel concentrations of the cases with positive ΔΦ_l (SL) have opposite situations. When the ΔΦ_l equals 0, the case has a stoichiometric fuel–air mixture with a uniform fuel concentration. The overall dependence features of the initiation length on the degree of inhomogeneity display a W-shaped distribution. In particular, for the fuel-rich mixture in the lower half of the inlet, the increasing ΔΦ_l from − 1.0 to 0.0 results in a V-shaped $\overline{L }$_i to ΔΦ_l distribution with a minimum $\overline{L }$_i around ΔΦ_l = − 0.4. As shown in Fig. 2, the deflagration induced by the OSW occurs in the lower half of the flow field, which contributes to the transition from deflagration to detonation, and neither a large nor a small gradient of fuel-rich concentration will have a negative influence on the ODW initiation under the present simulations. The degree of gradient inhomogeneity with − 0.4 induces a minimum initiation length, meaning the relatively fuel-rich mixtures in the lower half of the fuel injection could be the best from the viewpoint of oblique detonation initiation. However, the initiation length increases drastically when the ΔΦ_l is larger than − 0.4. For the SR cases, the ODWs are formed in the fuel-rich mixtures as ΔΦ_l equals − 0.6 and − 0.4, which also have a short $\overline{L }$_i, and are initiated in fuel-lean conditions for other cases.

Fig. 11

Dependence of the initiation length, $\overline{{\varvec{L}} }$_i, on the inhomogeneity of the liquid fuel equivalence ratio, ΔΦ_l

The dependence of $\overline{L }$_i on ΔΦ_l also shows a V-shaped curve, as the ΔΦ_l is higher than 0.0 for a fuel-lean mixture before the OSW and associated shock-induced deflagration. When increasing the ΔΦ_l from 0.0 to 1.0, the initiation length of ODW first decreases and then increases, and the $\overline{L }$_i has a minimum value corresponding to the ΔΦ_l = 0.4. The ODWs are formed in a fuel-rich mixture for the SL cases. In particular, as ΔΦ_l decreases from SL-1 (ΔΦ_l = 1.0) to SL-2 (ΔΦ_l = 0.6), the equivalence ratio at y = 0 increases from 0 to 0.4, and the effect of heat release from the chemical reaction is larger than that of evaporative cooling in these fuel-lean conditions. However, the variation range of $\overline{L }$ _i from ΔΦ_l = 1.0 to 0.0 is much smaller than that of ΔΦ_l from − 1.0 to 0.0. The heat release can promote the initiation of ODW. The cooling from evaporation decreases the thermal energy of the inflow and reduces the capacity for ODW formation.

A series of gas-phase simulation cases using pre-evaporated kerosene vapours as the fuel is applied to quantify the effects of chemical reaction on the initiation of ODW. The utilization of fuel vapor can neglect the influence of droplet evaporation. The range of fuel concentration gradient is the same as that in the two-phase cases, and the inhomogeneity of the equivalence ratio, ΔΦ, varies from − 1.0 to 1.0. The pressure contours indicating the stabilization wave structure of ODW are shown in Fig. 12. In general, it is found that the ODWs are formed in the fuel-rich mixtures for the SR cases. The figures in the left column show the cases with ΔΦ lower than 0. For the fuel-rich mixture at the lower half inlet with a large concentration gradient, the transition from the shock-induced deflagration wave to the ODW has a complex structure. A V-shaped deflagration wave is formed during the transition as the ΔΦ equals − 1.0, as seen in Fig. 12a. The deflagration wave intersects with a transverse wave initiated from the transition point and reflects from the wedge surface, leading to a reflection wave propagating downstream. When the ΔΦ decreases to − 0.8 with a lower fuel concentration gradient, the ODW is formed at an upstream position, and the wave structure becomes more complex. An abrupt transition occurs around the streamwise position x/H_w = 1.6, leading to a curved detonation wave (CDW) and a strong transverse wave. The CDW develops downstream and another ODW with higher pressure and a straight surface is formed at x/H_w = 1.8. This is mainly due to the inhomogeneous distribution of fuel concentration, resulting in a spontaneous occurrence of the flame-shock coupling. The transverse waves propagate towards the wedge and the shock decouples with the flame near the wedge (at the streamwise location x/H_w = 1.7). The decoupled flame then attaches to the wedge surface. The local fuel-rich mixture results in this decoupling. Similar to the Case ΔΦ = − 1.0, a transverse wave reflects from the wedge surface and approaches downstream. As the fuel concentration gradient decreases, the initiation length of the ODW is further decreased, as shown in Fig. 12e. In particular, a V-shaped deflagration wave with a sharp tip towards the incoming flow is formed, and an abrupt transition with a strong transverse wave is observed. The shortest initiation length of the ODW occurs for the Case ΔΦ = − 0.4. The ODW is formed through a smooth transition with relatively low pressure. However, as the fuel concentration gradient further decreases to ΔΦ = − 0.2 and ΔΦ = 0, the ODW initiation positions move downstream continuously and the transition pressure increases. These phenomena demonstrate that a uniform fuel distribution could not contribute to the early initiation of the ODW under the present configuration. In particular, the right column in Fig. 12 shows the stabilization wave structures with a fuel-lean mixture near the wedge. It is found that the initiation position of the ODW approaches continuously as the ΔΦ decreases from 1.0 to 0.2, and there are no complex wave structures, compared to the cases with ΔΦ lower than 0. The smooth transitions occur for the cases with ΔΦ equalling 1.0, 0.8, and 0.6. The decoupling of the shock and flame occurs under the large fuel concentrations, as shown in Fig. 12b, d. The fuel-lean mixtures lead to the decoupling in the downstream region from x/H_w > 2.9. For the cases with a more uniform fuel concentration (ΔΦ = 0.4 and ΔΦ = 0.2), the transition pattern tends to be abrupt with high pressures.

Fig. 12

Distributions of dimensionless pressure P/P₀ with different inhomogeneity of the equivalence ratio, ΔΦ, from − 1.0 to 1.0. Here, the white dashed line refers to the distribution of Y_F,st

The dependence of the initiation length on the inhomogeneity of the equivalence ratio for the ODW fuelled with kerosene vapours is shown in Fig. 13. The dependence of the length $\overline{L }$_i on the inhomogeneity degree of the equivalence ratio, ΔΦ, is generally distributed as a V-shaped curve for the gas-phase reactive mixture. The minimum $\overline{L }$_i occurs around ΔΦ = − 0.4, which corresponds to a relatively fuel-rich mixture in the lower half of the inlet near the wedge, as depicted in Fig. 12g. The increase in the fuel concentration gradient from ΔΦ = − 1.0 to − 0.4 results in the acceleration of the shock-induced chemical reactions and contributes to the coupling between the shock and the post-shock flame. For the SR cases, in particular, the length-to-ratio curve for the gaseous reactive flow is similar to that of the two-phase flow, displaying a V-shaped distribution. For the SL cases with the fuel-lean mixture at the lower half of the inlet, the decrease in ΔΦ from 1.0 to 0.0 leads to a continuous decrease in the initiation length, which trend is different from the two-phase cases. It means that the shock-induced chemical reaction, depending on the equivalence ratio with a fuel-lean condition, plays an important role in ODW formation.

Fig. 13

Dependence of the initiation length, $\overline{{\varvec{L}} }$_i, on the inhomogeneity of the equivalence ratio, ΔΦ, for a gas-phase mixture

To have an overall comparison of the ODW initiation features fuelled with kerosene droplets or vapours, the disparities in the initiation length for the gas-phase and two-phase detonations are further plotted in Fig. 14. In general, the $\overline{L }$_i of the ODW formed in the gas-phase flow is shorter than that of the two-phase ODW. It is because the fuel droplets for the two-phase detonation need to evaporate to form reactive mixtures for chemical reaction, associated with a decrease in the local ambient temperature due to the evaporative cooling. The obvious differences of $\overline{L }$_i exist as the ΔΦ_l (or ΔΦ) between − 0.2 and 0.2, which represents a relatively uniform fuel concentration. However, for a larger fuel concentration gradient, the disparity becomes small. The evaporative cooling and reaction heat release counterbalance each other during the two-phase detonation. In particular, for the same ΔΦ_l (or ΔΦ) with the same heat release, the evaporative cooling effect becomes significant as ΔΦ_l (or ΔΦ) is smaller than 0.4, and the fuel evaporation is more influential on the initiation of ODW.

The disparities in $\overline{{\varvec{L}} }$_i for the gas-phase and two-phase detonations

Because the inflow inhomogeneity of the fuel concentration is unavoidable in the combustor, the transverse jet of liquid fuel from the wall results in an inhomogeneous spatial distribution of fuel vapours (fuel-rich mixtures near the wall and fuel-lean mixtures far from the wall). The results of this study can help design ODWE combustors. It is concluded that either fuel-rich (ΔΦ_l = − 0.4) or fuel-lean (ΔΦ_l = 0.4) reactive mixtures injected before the wedge or the wedge-induced OSW can contribute to the short ODW initiation length, and a uniform inflow fuel–air mixture may not be the best solution. For the detonation formed in supersonic two-phase flows, the competition between the exothermal reaction (mainly depending on the fuel–air equivalence ratio and ambient temperature) and evaporation (mainly depending on ambient temperature) is shown to be complex.

4 Conclusions

This paper numerically analysed the stabilization features of oblique detonation waves (ODWs) on a wedge in a droplet-laden supersonic flow, considering the effects of inflow premixing inhomogeneity. The gas-droplet reacting flow is simulated using a hybrid Eulerian–Lagrangian method. The inhomogeneous two-phase mixture is formed due to the injection scheme in a combustor and is introduced by assuming a linear distribution of the liquid fuel equivalence ratio, Φ_l, at the inlet, and the degree of inhomogeneity, ΔΦ_l, is proposed. The analyses focus on the fuel concentration gradient and combined effects of chemical heat release and evaporative cooling.

The results indicate that the fuel concentration gradient not only affects the initiation length of ODW but also has an influence on the stabilization wave structures during the transition from OSW to ODW. The dependence of the initiation length of ODW, $\overline{L }$_i, on the ΔΦ_l exhibits a W-shaped curve. As the Φ_l before the OSW and shock-induced deflagration is in a fuel-lean condition, the variation in ΔΦ_l results in a V-shaped $\overline{L }$_i to ΔΦ_l distribution with a minimum $\overline{L }$_i around ΔΦ_l = 0.4, and the effects of heat release from the reaction on the initiation of ODW are more obvious. As ΔΦ_l is lower than unity, the $\overline{L }$_i to ΔΦ_l curve also displays a V-shaped distribution with a larger variation steepness. The minimum initiation length occurs at ΔΦ_l = − 0.4 for a fuel-rich mixture before the OSW. In particular, for a fuel-rich mixture with large fuel concentration gradients, the premixing inhomogeneity distorts the stabilization wave structures. The V-shaped deflagration, wave reflection from the wedge, and the diamond-shaped wave structure are confirmed. From the point of view of engineering application, the injection of liquid fuel at the same side as the wedge (SR cases in the present study) to form a fuel-rich mixture could contribute to a short initiation distance of ODW.

In this study, although the linear distribution of fuel concentration gradient is an ideal consideration, it benefits the quantitative analysis and comparison by eliminating nonlinear effects, compared to Gaussian distribution for instance. This is an attempt to study the inhomogeneous oblique detonation using liquid fuel from a point of view of fundamental research. The results from this research are expected to contribute to future studies, reaching a rigorous theory to guide the fuel injection patterns regarding the stabilization of ODW using liquid fuel for hypersonic propulsion. The future study will consider the dynamics of large droplets closer to the actual atomization process, the atomization of liquid fuel, and three-dimensional simulations.