Abstract
Due to the proprietary nature of modern motorsport and Formula 1, current scientific literature lacks relevant studies and benchmarks that can be used to understand flow physics in this area, as well as to test and validate new simulation methodology. With the release of a new, open-source geometry (the Imperial Front Wing), we present a computational study of a multi-element aerofoil at a ride height of 0.36h/c and a Reynolds number of \({\mathbf{2}}{\mathbf{.2 \times 10}}^{{\mathbf{5}}}\). A 0.16c slice of the Imperial Front Wing has been examined using high-order spectral/hp element methods. Time averaged force data is presented, finding lift and drag coefficients of \(-\)8.33 and 0.17 respectively. Unsteady analysis of the force and surface pressure data has allowed salient feature identification with respect to the transition mechanisms of each element. The mainplane and flap laminar separation are studied and the cross-spectral phase is presented for the lower frequency modes. At \(\varvec{St = 40}\) an in-phase relationship is identified between mainplane and flap laminar separation bubbles, whilst at \(\varvec{St = 60}\) a distinct out-of-phase relationship is observed. Wake results, including wake-momentum deficit and turbulent kinetic energy are presented, which show wake meandering and subsequent breakdown due to a Kelvin–Helmholtz instability. These results, in particular the transition mechanisms, will allow for the construction of a dataset to validate novel methods in this area.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
1 Introduction
Aerodynamic performance is a pivotal aspect of motorsports, with leading racing classes such as Formula 1 (F1) having average speeds which have increased by a factor of 1.5 over the pre-aerodynamic era in the 1960’s (Zhang and Zerihan 2003) despite strict engine architecture and weight restrictions. The major aerodynamic focus has been the increase of negative lift or downforce, with any increase in downforce positively impacting performance in any traction limited zone such as braking, cornering, acceleration, or any combination of these. Whilst downforce has been the major concern, the impact of drag on top speed has been known since the 1920 s (Bettes 1982), with the power required to overcome drag increasing the with cube of vehicle speed.
Front wings are one of the key aerodynamic elements of a modern F1 car. They are of major importance, not only shaping overall aerodynamic performance as the frontmost structure of the vehicle, but also in generating 20-30% of the total vehicle load. Whilst generating one of the more significant loads on vehicle, they are also particularly sensitive to vehicle attitude (i.e. roll, pitch and yaw), with these factors impacting total load more disproportionately than other aerodynamic components due to ground effect.
However, front wings in ground effect have been studied to a limited degree in recent times. A number of experimental (Buscariolo et al. 2019; Roberts et al. 2017, 2016; Zhang and Zerihan 2003) and numerical (Buscariolo et al. 2019; Lombard 2017) studies have been conducted, which focus mainly on time-averaged and integral phenomena, such as forces and mean flow effects including on- and off-surface flows. Furthermore, investigation into effect of the underlying geometry has been limited, due to the closed and proprietary nature of modern F1. Consequently, there are only a small number of case studies and benchmarks, and more complex analysis into flow phenomena, including transition and salient unsteady feature identification and analysis, has not been performed. In this work, we aim to overcome this gap through the detailed study of a multi-element wing in ground effect.
2 Background
2.1 Imperial Front Wing
The Imperial Front Wing (IFW) shown in Fig. 1 was a model given to Imperial College London based on an unraced front wing specification of the McLaren MP4-17D. The IFW is a representative geometry of modern motorsports, and in particular F1 front wing geometries. With new regulations introduced in 2022 demanding relatively simpler front wings than in previous years, the IFW represents a further opportunity for a benchmark case that demonstrates salient flow phenomena.
It has been the subject of two experimental campaigns at Imperial College London (Buscariolo et al. 2019; Pegrum 2006) and a further two computational campaigns (Buscariolo et al. 2019; Lombard 2017). The experiments of Pegrum (2006) analysed the ride height and influence of a rotating wheel on the vortex system created by the outboard section of the geometry. Buscariolo et al. (2019) performed similar investigations at a normalised ride height of \(h/c=0.36\), in particular comparing high-order computational results against their own experimental campaign including planar flows, surface flow visualisations and computational forces for a number of polynomial orders.
The purpose of this study is to continue to build upon the current literature and expand upon this growing dataset of results around the IFW. A limiting factor in the current set of experiments and computational studies is the high-level analysis presented, predominantly due to the complexity and resolution requirements of these campaigns. The specific focus of this study is to consider a multi-element wing in ground effect, taken from a cross-section of the IFW geometry. This will allow the study of aerodynamic properties in far greater detail, such as identifying and presenting transition classifications, salient flow phenomena and their underpinning mechanisms. This will address a broader gap in the literature pertaining to the experimental and numerical studies of this area, and will also provide a part of a highly-resolved benchmark for these configurations. To provide context, this will be contained within a hierarchical set of benchmarks from the same geometry that will allow the extensive validation of models against problems of increasing complexity, whilst still maintaining industrial relevance to motorsports aerodynamics and F1 in particular.
3 Numerical Methods
In this study, and following the approaches of Buscariolo et al. (2019) and Lombard (2017), implicit large-eddy simulations (iLES) are utilised, where no sub-grid scale (SGS) model to models the under-resolved turbulent stresses. This is combined with stabilisation methodologies for numerical robustness that will be presented later. We note that although these play a similar role and are somewhat analogous to a sub-grid scale model, the dissipation characteristics are not matched to any known phenomena and are a pure characteristic of the numerical scheme. With iLES, the assumption is that the SGS stresses are of the order of magnitude as the truncation error of the discretisation. In the sections below, we outline specifically the discretisation choice in terms of space, and outline the various properties used in the setup and running of the simulations.
3.1 Spectral/hp Element Methods for Industrial Simulations
Simulations have been performed using the open-source Nektar++ framework presented in Moxey et al. (2020). Nektar++ utilises a spectral/hp element discretisation, which combine the geometric flexibility of the finite element method in the ability to represent complex geometries, together with desirable numerical properties, such as the low dissipation and diffusion that is broadly seen in spectral methods. In this study, since the geometry focuses on a small cross-section in which the wing can be seen to be homogeneous, we opt to further select a hybrid Fourier-spectral/hp discretisation (Blackburn and Sherwin 2004), where two-dimensional planar meshes are used to represent the wing cross-section using the spectral/hp element method, and the spanwise homogeneous direction is discretised using a Fourier basis. The incompressible Navier-Stokes solver has been utilised with the velocity-correction or operator-splitting scheme of Guermond and Shen (2003), allowing the decoupling of pressure and velocity in the momentum equations whilst retaining higher-order time integration accuracy. A second order in time implicit-explicit time-stepping scheme is chosen, which evolves the advection terms explicitly, whilst the diffusion term is discretised implicitly.
A further advantage of the hybrid discreisation is that it permits solution of many smaller 2D equations for each plane, rather than a large coupled 3D system. This allows a wider choice of solution strategies for the underlying matrix systems (Bolis et al. 2016). In this study, we use a direct solver with multi-level static condensation for the solution of the discretised system in each plane. Multi-level static condensation reduces the size of the linear system to be solved by recursively decomposing the global matrix into boundary and interior nodes. By selecting an optimal ordering of the ndoes, it is possible to promote block-diagonal matrices that can be trivially inverted by using the Schur complement, significantly enhancing computational efficiency (Vos 2011).
3.1.1 Stability Considerations
Unlike traditional applications of the finite element method, where linear shape functions are used within each element, the spectral/hp element method permits high-order polynomial expansions within an element. For industrial-type simulations, typical polynomial orders of the range of 3-8 are used, as can be seen from the range of previously successfully applied geometries (Hambli et al. 2022; Buscariolo et al. 2019). In selecting the discretisation orders for the velocity and pressure fields, to ensure the inf-sup condition is satisfied we employ a Taylor-Hood approach, where the polynomial expansion for velocity variables is one higher than for pressure (Ferrer et al. 2014). Other sources of instabiity can arise from aliasing (Mengaldo et al. 2015), owing to the lack of sufficient quadrature order to resolve either the nonlinearity of the underlying equations, or the higher-order mapping terms arising from the curved elements that are required to represent the geometry. Stabilisation of aliasing-type errors in under-resolved simulations is also usually required for industrial simulations.
In previous works, the spectral vanishing viscosity (SVV) method of Tadmor (1989) has proven to be a robust stabilisation technique to identify and suppress oscillatory effects observed in higher-order simulations. However, as discussed in Moura et al. (2022), the use of SVV at lower polynomial orders can be overly diffusive, resulting in a significant loss in resolution. This disproportionately impacts industrial simulations, which are limited to lower polynomial orders due to the large resolution requirements needed for complex geometries. To overcome this, a new approach is proposed in Moura et al. (2022) named gradient-jump penalisation (GJP), which introduces artificial dissipation through a penalty term that is based on observed discontinuity of the derivative of the solution fields between elemental boundaries.
A further contribution of this work is that the GJP approach has outperformed the SVV approach on canonical cases, but has yet to be applied to more complex geometries. For these studies, the use of a hybrid discretisation means that we employ a hybrid stabilisation strategy, where GJP is used to stabilise the in-planar flows, and the SVV approach using the exponential kernel of Karniadakis and Sherwin (2005) is used in the Fourier direction. The exponential kernel activates purely on expansion modes greater than the product of the cut-off ratio and the polynomial order.
3.2 Boundary Conditions and Domain
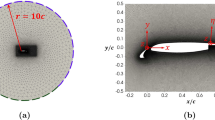
A visualisation of the computational domain can be seen in Fig. 2. The domain is approximately 39c long, where c refers to the mainplane chord length of 0.25 m. The domain is designed to accommodate 10c of length upstream of the leading edge, and 28c behind. It is around 10c in height, resulting in an approximate blockage of 5%. As in previous cases (Pegrum 2006; Buscariolo et al. 2019; Lombard 2017), a ride height of 0.36h/c has been chosen, set from the footplate of the full geometry. To construct the wing cross-section, a slice is taken through the plane defined by \(Y=250\)mm in CAD to create the full geometry. A spanwise length of \(L_z = 0.16c\) has been chosen, the justification for which we outline in section 3.4.2.
Boundary conditions are also shown in Fig. 2, which are specified fully here for completeness. Parameters in Nektar++ are nondimensionalised, and thus velocity boundary conditions are set to a unit value, with the viscosity then being scaled according to the Reynolds number Re. The following boundary conditions are used:
-
Inlet Dirichlet velocity using a freestream condition \(U = 1.0\)
-
Outlet: A high-order convective boundary condition (Dirichlet) of Dong et al. (2014), which permits the stable convection of high-energy structures through the outlet.
-
Walls (pressure) The Neumann pressure boundary condition of Karniadakis and Orszag (1991) and Guermond and Shen (2003) is used to ensure the pressure Poisson equation preserves high-order time integration.
-
Wing (velocity) no-slip condition.
-
Floor (velocity) Dirichlet condition with value U.
-
Floor (velocity) Slip Boundary Condition (Neumann).
3.3 Computational Setup
The case has a Reynolds number \(Re = 2.2 \times 10^{5}\) based on the mainplane chord length c. In the spanwise direction, 64 Fourier modes are used to discretise the domain with periodic boundary conditions imposed by the Fourier discretisation. Polynomial orders for velocity and pressure of 6 and 5 are used in the current investigation. In combination with the mesh within each two-dimensional cross-section which we discuss below, the domain contains 72,580,160 degrees of freedom in total. A non-dimensional time \(t^{*} = tU/c\) based on the far-field velocity U and chord length c. The non-dimensional time step is then presented as \(dt^{*}\) =\(1.6 \times 10^{-6}\) or 625,000 time steps per convective length. The solution is allowed to develop for \(\approx 40 t^{*}\) before averaging and averaging is conducted over \(8 t^{*}\).
3.3.1 Initial Conditions
Simulations are started from homogeneous initial conditions, with the velocity components (u, v, w), which act in the (x, y, z) directions respectively, set to inlet values of \((u,v,w) = (1.0,0.0,0.0)\), and the pressure set to 0.0 (gauge). Normally-distributed noise is added to all three velocity directions with mean of 0.0 and variance of 1.0, which is then scaled by a factor of 0.05.
3.4 Mesh Generation
In the spectral/hp discretisation, accurate representation of the geometry requires the use of curvilinear high-order meshes, in order to minimise geometric error. The additional degrees of freedom this introduces means that larger element sizes h should be used to avoid an unnecessary increase resolution. This process requires a different pipeline of mesh generation strategies that most commercial software do not yet provide.
Following the strategy laid out in Mengaldo et al. (2020), we adopt an a posteiori approach, which converts a coarse, straight-sided linear mesh into a curvilinear high-order mesh. The linear mesh is generated in Star-CCM+, which is conformal, contains only triangles and quadrilaterals, and utilises only a single inflation/quadrilateral layer around relevant surfaces which will be refined in the high-order conversion steps. Three wake refinement regions are created, which are shown in Fig. 3.
The linear mesh is then processed by NekMesh, the high-order mesh generation utility for the Nektar++ framework. Projection of the CAD boundary information onto the high-order element is performed, which transforms the mesh from a linear one to a high-order curvilinear mesh. To achieve this, high-order nodes are inserted on edges, faces and elemental interiors to deform the mesh to the underlying CAD boundary representation. The single prismatic inflation layer is clearly insufficient for simulation purposes; however, the aim of this initial linear element was to allow sufficient room for the curvature of the grid to be incorporated into the mesh without any self-intersection.
To generate the final boundary layer grid, we split this element using the isoparametric approach of Moxey et al. (2015), in order to refine the boundary layer to the desired thickness and distribution. Since the curvilinear element is defined through a mapping from a reference element to the Cartesian element, we can apply a simple technique to split the reference element, and then apply the original mapping to yield a refined Cartesian element. This permits the generation of a boundary layer to any desired thickness of distribution, which is guaranteed to be valid so long as the original element is valid.
Layers are typically distributed according to a geometric series. The mesh used in the current study contains 10 prism layers around the aerofoil elements at a growth rate of 1.4, to resolve both the thin laminar boundary layer and the turbulent boundary layer. Five layers at the same growth rate are used for the floor pseudo-boundary layer, which does not require the same degree of resolution due to the lack of a thinner laminar boundary layer preceding the separation.
3.4.1 Resolution Verification
The mesh resolution is presented in wall-units in Fig. 4, where wall units are \(\Delta (x^{+},y^{+},z^{+}) = \frac{u_{\tau }(x,y,z)}{\nu }\) and x, y, z refers to the nominal spacing divided by the chosen polynomial order. In terms of wall resolution, standard guidance that \(y^+ < 1\) is typically adopted for the first cell height when using traditional lower-order discretisations. However, since we are using higher-order elements, which contain many degrees of freedom within them, we instead consider the position of the first quadrature point within the element. These spacings are also only estimates, taken from the Star-CCM+ specified mesh spacings, and not the explicit arc lengths. Limits presented are those from Georgiadis et al. (2010). All x-y planar spacings are smaller than those recommended, apart from two small sections on the mainplane, at the leading edge and at mid-chord, where the \(y^{+}\) value is slightly above one.
The spanwise resolution in wall-normal units is not presented due to the use of a Fourier expansion in the z-direction, although we note that the spanwise resolution is \(L_z/64\). We do present however a modal energy analysis, to quantify the spanwise resolution more explicitly. The energy contained in each mode is calculated via the expression
where \(\hat{u}_k(x,y)\) is the k-th Fourier mode represented on 2D cross-sections of the domain. The modal energy is recorded every 10 time steps. The subsequent discrete time-series is then averaged at each mode, and is presented in Fig. 5. The energy quickly decays to \(10^{-7}\), with two decades after the mean mode or mode 0, before hitting the SVV filter-width, which damps the energy contained within the high-frequency modes. The plot shows the decay of modal energy with respect to increasing number of modes to a relatively insignificant level, suggesting that the spanwise resolution is sufficent.
3.4.2 Spanwise width Sensitivity Study
In order to evaluate the effects of selecting a narrow spanwise width, a sensitivity study has been undertaken with respect to the lift force with increase spanwise length. Several spanwise lengths were considered ranging from 0.16z/c to 2z/c. Examining the integral quantities such as lift and drag, shows that these only vary by around 5% across the spanwise length range.
An auto-correlation study was undertaken to examine the implications of the reduced spanwise length on the key flow phenomena. Two points A and B were chosen in the near- and the far-wake, as shown in Fig. 6 with precise locations given in Table 1. Using the spanwise velocity measured at these locations, auto-correlations are integrated up until the first zero-crossing for a variety of. Numerically, integrating this measure and multiplying by the mean velocity gives an estimated integral length-scale, as per the method in O’Neil et al. (2004). The auto-correlations for Point A at 0.16z/c and 0.5z/c are presented in Fig. 7 and for Point B in Fig. 8.
Figure 7 shows the auto-correlations at Point A do not change significantly between both spanwise lengths. In particular, the zero crossing does not change significantly. However, in contrast, Fig. 8 shows a significant change in the zero crossing between spanwise lengths.
Using the method described previously, integral length scale are presented in Table 1. At Point A, as also shown in the auto-correlation plots, limited difference is seen in the length scale, whereas at Point B, there is a rather marked difference.
This suggests that the force variation is a result of the wake breakdown mechanism in the farfield. As this is of less interest than the near-wall flows and as these wake breakdown modes are unlikely to exist in reality, the smaller domain of 0.16z/c was chosen given the perhaps more prevalent industrial relevance.
4 Results
The results of the study are grouped and presented in the following order. Firstly, the average flow field is presented. Following this, the force coefficients are presented and examined. The unsteady properties of the force coefficient are investigated and mode identification from power-spectral density (PSD) plots of the lift coefficient of each of the aerofoils is presented. The transition properties are presented through boundary layer profiles, a mid-plane time-space contour, a cross-spectral phase relationship between the mainplane and first flap lift coefficients and surface line integral convolution plots. Finally, the wake structure, meandering, and subsequent breakdown are presented through examination of vorticity contours, Q-criterion iso-surfaces, wake momentum deficit and line turbulent kinetic energy.
4.1 Average flow field
Looking closely at the average flow field in Fig. 9, a number of key flow-features can be seen. Firstly, laminar separation bubbles (LSB) can be seen on the mainplane and the first flap suctions surfaces. These appear to be extremely thin, due to the thin oncoming laminar boundary layer. This is a consequence of the higher local Reynolds numbers due to ground effect. The floor sees a similar LSB due to the significant expansion aft of the mainplane. This bubble seems to be significantly larger and thicker than the two on the suction sides of the first two wing elements. Finally, a similar transition mechanism can be seen on the pressure side of the upper flap. Similarly to the floor bubble, it is not thinned, and hence is relatively larger than the others.
Figure 10 shows the average pressure coefficient over each of the elements of the aerofoil, defined as
Stagnation pressure is predicted well at the leading edge of each element. A maximum value of \(|C_{p}|\) occurs on the suction side very close to the leading edge of the mainplane at \(C_{p} \sim -11\). Steep adverse pressure gradients can be seen on the suction side of all elements with the pressure increase monotonically along the streamwise direction, except for small regions on the mainplane between \(0.46 \le x/c \le 0.50\). The second flap is seemingly misaligned to local flow seen by the stagnation points location not at the leading edge. A subsequent flip in magnitude of \(C_{p}\) aft of the stagnation point is seen on both surfaces.
The skin friction coefficient is further shown in Fig. 11, which is defined by
where \(U_{\infty }\) is the free-stream velocity. The figure shows the evolution of wall shear across the aerofoils. Firstly, the skin friction is constant over the pressure side of the mainplane and the first flap, affirming the laminar nature of the pressure side flows. This changes for the second flap, however, in which a transition can be seen through the significant increase in wall shear on the pressure side.
The suction surfaces in Fig. 11 highlight that the peak skin-friction coefficient occurs around the leading edge on all three elements. On the first and second flap, this decreases to a minimum equivalent to the laminar suction side before steeply increasing, suggesting a transition mechanism. Again, the second flap is different, where the spike in skin friction coefficient towards the trailing edge on the suction surface is a lot less significant and the gradient is far more gradual.
The next series of figures examine the surface line integral convolution (LIC), which is described in Cabral and Leedom (1993). Across the suction sides of the three wing elements in Fig. 12, we see additional confirmation and detail further the extent of the LSBs on the mainplane and the first flap. Two bifurcation lines can be seen on both the mainplane and first flap, between which are the recirculation regions for the LSB. Critically, no bifurcation lines are seen on the second flap, suggesting a differing transition mechanism than on previous elements.
Figure 13 shows a surface LIC of wall shear for the pressure side of the second flap. The LSB on the pressure side is clearly shown, as it is contained at the leading edge within the two bifurcation lines, similar to those on the mainplane and first flap suction side bubbles. This bubble, however, is significantly longer relative to the length of the aerofoil in comparison to the suction side bubbles, suggesting the length of the others is impacted through the adverse pressure gradient, and possibly the interaction with the wake shed from upwind elements.
Re-examining the \(C_{p}\) plots shown in Fig. 10 confirms this assertion. The LSBs on the suction side are evident in the pressure distribution on the suction side of both the first and second flaps. Between \(0.45 \le x/c \le 0.50\) on the mainplane, the \(C_{p}\) distribution flattens and then sharply increases across the length of the bubble. Whilst this is increasingly obvious on the mainplane, the first flap is far less prominent than the mainplane. The LSB is also relatively longer in the case of the first flap, spanning almost the same distance, whilst the second flap has a significantly shorter element length.
With regards to the suction side of the second flap, no evidence of a LSB is present agreeing with the LIC. This points again to a differing transition mechanism on this flap. A type of bypass transition is described in Serdar et al. (2012) called wake transition, whereby the windward blade’s wake causes bypass transition in the downstream blades, where otherwise a differing transition mechanism would be expected. The instantaneous x-velocity contour shown in Fig. 14 suggests that a similar process occurs on the final flap. The wake from the trailing edge shedding, and the shear layer from the first flap and mainplane, interact with the laminar boundary layer on the second flap. This causes a bypass-like mechanism, rather than the LSB seen on the upwind elements.
The boundary layer profiles in Fig. 15 show that the inflection point occurs at around 0.4x/c. The reversed flow region exists until around 0.5x/c in line with the LIC plot. The reversed region exists up until \(y/c \approx 0.001\) from the wall suggestion, again showing the extensive thinning caused by the steep adverse pressure gradient.
4.2 Force Coefficients
Both time-averaged and unsteady force coefficient results have been examined to further investigate the salient flow phenomena. The average lift and drag coefficients are \(C_{L} = -8.33\) and \(C_{D} = 0.17\) respectively, with forces sampled every 10 timesteps. A similar interrogation window was used to create PSD visualisations of the \(C_{L}\) time series, which is shown in Fig. 16. These are computed using Welch’s method, outlined in Jwo et al. (2021). Each PSD, one for each element and one for the summation, has been vertically scaled to ensure they are visible.
Strikingly, at \(St=60\) a narrow-band dominant mode exists on all three elements. On the mainplane, higher narrow-band modes exist at \(St=140\) and \(St=200\) which are not as visible on the other elements. A lower frequency mode at \(St=40\) on all elements, with this being most dominant on the first flap. On the second flap a equally dominant mode exists at \(St=30\) that does not exist on the other flaps.
4.3 Spectral Analysis
The unsteadiness is now investigated in conjunction with an attempt to identify and present mechanisms for several flow features. Firstly, the unsteady properties of the surface pressure fluctuations are considered. These are sampled after the initial \(40t^{*}\) at the linear mesh locations every 10 timesteps over an averaging period of \(8t^{*}\). This allows the examination not only the average states, but the statistical distributions observed at each station. In Fig. 17, the suction side pressure coefficient \(C_{p}\) is presented, with each point’s interquartile range shown as error bars. In the right-hand side figures, the root mean square (RMS) of \(C_{P}\), denoted by \(C_{P,RMS}\), is presented to investigate the main areas of pressure fluctuation across the suction side of both the mainplane and the first flap.
Mainplane and flap 1 laminar separation bubble PSDs at starred locations in Fig. 17
Examining the interquartile range, the variance seems to be greatest within and around the LSB. Given the sharp increase in skin friction coefficient in the same area, transition to turbulence in this region is expected aligning with the increase in pressure variance, suggesting generation and/or presence of turbulent kinetic energy in this region. Upwind of the LSB, the variance seems to be significantly smaller, and downwind of the LSB, some elevated level of variance persists on the mainplane.
On the flap however, some variance exists upwind of the LSB, suggesting some mainplane/flap interactions. This could be due to the shedding off the trailing edge or the boundary layer, and subsequent separated shear layer interacting with the flap laminar boundary layer. Again, similarly to the mainplane, the maxima in interquartile range occurs across the range of the LSB, and the interquartile range returns to somewhat of an elevated level aft of it suggesting transition again.
The variation of the RMS of the pressure coefficient plots are also presented in Fig. 17, where \(C^{\prime }_{P,RMS} = \sqrt{C_{P}-\overline{C_{P}}}\). These figures give further fidelity to degree of unsteadiness of the surface pressure at each particular probe, and the results confirm the previous assertions that the maximum surface pressure fluctuations occur in the LSB. Using these figures, further maxima can be determined: for example, maxima surface pressure fluctuations occur at around 0.55x/c and 0.61x/c on the mainplane and flap respectively. These locations are marked by a star and are used and referred to in subsequent sections.
Looking at the PSD of the \(C_{p}\) time histories at these two starred locations on the mainplane and flap, and by comparing these against the force coefficient PSDs, the relevant flow features can be identified from the spectra as shown in Fig. 18. In looking at the dominant spectral peaks, the PSD of the starred location on the mainplane coincides with the peaks at \(St=60\), \(St=140\), and \(St=200\). This suggests that there is a relationship between these features and the LSB. Figure 19 shows the comparison between the spectra at the trailing edge and the lift spectra, which highlights that these spectra peaks do exist at the trailing edge. Whilst a feedback mechanism between the trailing edge and the LSB is a possibility, it is less likely due to the lower energy in these frequencies at the trailing edge. Additionally, the instantaneous velocity field around the suction side in Fig. 20 demonstrates that upstream propagation is the less likely mechanism. However, this could be the source of any transition instability. Ruling this out would require physical isolation through a splitter (or similar device) at the trailing edge, as instability analysis at this Reynolds number remains infeasible at present.
Whilst the mainplane contains no fluctuations upwind of the LSB, the first flap does. Therefore, it is not immediately possible to say that these two features are causal. However, there are no other obvious dominant frequencies other than the ones at \(St=60\), \(St=140\) and \(St=200\), and thus it is reasonable to infer that these are inter-related. The fact that the frequencies are locked for both LSBs, despite the difference in scale, is something that warrants further investigation and discussion.
Figure 21 shows the same lift PSD plots on the mainplane and first flap, but also shows the cross-spectral phase between the two signals. The plot uses a vector of roughly 35,000 samples long (again sampled every 10 time-steps) using a segment of 16,052 elements. Reduced variance in the provided spectra could be obtained through a larger time sample (e.g. common to experimental results). However, the results afforded in Fig. 21 show significant clustering of phase relationships coincident with the spectral peaks previously observed. Examining the first peak at \(St=40\), we see an in-phase relationship between the two signals with a clustering of points around \(\phi = 0\). At \(St=60\), the more energetic narrow-band feature, a distinct out-of-phase relationship between the two signals, can be seen due to the clustering of points at \(\phi \approx 180\).
A mechanism in Serdar et al. (2012) is discussed where LSB vortices occurred from Kelvin-Helmholtz (K-H) type instabilities causing the shear layer to roll up. These vortices tended to burst and dissipate quickly, releasing and ejecting low momentum flow away from the surface and into the flow freestream. Figures 22a–c shows this process, with three contour plots of the instantaneous flow field which are spaced at time intervals of \(t^{*} = 4.16 \times 10^{-5}\). The subplot visualised in Fig. 22a shows the reattachment of the LSB and the downstream ejection of the low-momentum flow. The next image in Fig. 22b shows the stretching of this system in both the wall-normal and wall-tangential directions. Finally, Fig. 22c shows this flow ejected into the freestream and away from the wall.
The impacts of this phenomenon can be further seen in the time-space contour presented in Fig. 23. A cut of the aerofoil is taken at the mid-plane at \(z=L_{z}/2\). History points are taken at each of the linear mesh locations and are sampled every 10 time steps. These are then discretised and interpolated onto a regular grid of size \(N_{points} \times N_{time steps}\) and displayed as the contour shown. The transition location is visible, with quasi-periodic streaky structures emanating from this region towards the trailing edge. Whilst not continuously regular, these streaks do seem to be of similar wavelength and period when they do occur - suggesting some regularity.
Figures 24 and 25 shows a similar technique, investigating the \(C_{P,RMS}\) then using key points to investigate within the frequency domain. However, with the second flap the pressure surface is investigated. In comparison, the pressure fluctuation is a lot more consistent over the element with three defined peaks at the leading edge, the transition location at \(x/c \approx 0.35\) and the trailing edge. PSDs at each of these locations are presented, shown by coloured stars, with the colour corresponding to the PSD in Fig. 25.
Flap 2 pressure side PSD at starred locations from Fig. 24
Figure 25 shows the \(St=60\), \(St=140\), and \(St=200\) peaks exist in each of the three series at each location. These series are vertically shifted to allow for ease of visualisation. The trailing edge location, however, shows the presence of the feature at \(St=30\), suggesting that it could be related to the trailing edge shedding. The feature at \(St=40\), however, cannot be seen on these plots. Further investigation could look for the location to determine the maximum energy within that frequency bin, which could help to identify this feature.
4.4 The Wake
Figure 26a shows an instantaneous velocity magnitude contour on the mid-plane. The wake is clearly visible, with the most significant velocity deficit visible above the mainplane and behind the first flap. The wake extends downstream, before meandering about 1c downstream of the second flap, before breaking up a few chords downstream. The wake from the floor pseudo-boundary layer is also visible, with the shear layer growing along the length of the floor. No clearly visible interactions between the floor boundary layer and the wake are visible within the a few chords downstream.
Streamwise and spanwise vorticity contours are presented in Fig. 26b, c respectively. The streamwise vorticity is relatively well mixed and homogeneous across the near wake. About 1.5c downstream of the trailing edge instability is obvious from the Kelvin-Helmholtz type shedding and meandering of the wake.
Isosurfaces of Q-criterion with value of \(Q=100\) are shown in Fig. 27a and b. Figure 27a shows the detail of the wake, where the wake meandering is clearly visible downstream. The isosurface also details the LSB on the upper surface of the second flap with no visible transition on the pressure surfaces of the mainplane and first flap. The mainplane view of the Q criterion isosurfaces in Fig. 27b details the LSB mechanism. A spanwise homogenous K-H mode propagates from the start of the LSB, before breaking down very quickly into turbulence. The exact method of breakdown of these 2D structures is unclear, though further discussion is presented in following sections. From previous theory, LSBs are amplifiers of other instabilities and mechanisms, such as K-H rollup in the shear layer around the edge of the recirculation region, which often leads to transition in these cases (Serdar et al. 2012).
The wake momentum deficit plots at stations of \(x/c =2,2.5,4,6\) are presented in Fig. 28. The results are overlaid with error bars corresponding to the interquartile range. The wake in the \(x/c=2\) plot appears stratified, with more unsteadiness in the bottom portion of the wake, and in the upper section of the wake a stair-step exists. The shear layer on the floor only exhibits a 15% velocity deficit over less than 0.07c in height at this station.
Moving downstream at \(x/c=2.5\), the wake appears more uniform, but still has larger variance in the velocity magnitude on the lower portion of the wake than the upper. The wake has shifted upwards relative to the \(x/c=2\) station and the shear layer on the floor has thickened in comparison to the upstream location.
The further downstream stations at \(x/c=4\) and \(x/c=6\) show significant unsteadiness and mixing in the middle and upper portion of the wake at both stations. The wake at \(x/c=4\) is lower than both its upwind and downwind neighbours respectively. The velocity deficit in the floor shear layer looks similar for all stations; however, the interquartile range has significantly increased in comparison to the upwind station. Outside of the wake, the velocity has returned to freestream values in comparison to the near-field, which had significant acceleration in the lower portion of the wake. Minimal differences, other than the location of the peak velocity change, can be found between \(x/c=4\) and \(x/c=6\).
a \(x/c=2\) b \(x/c=2.5\) c \(x/c=4\) d \(x/c=6\). Wake turbulent kinetic energy at the same stations \(x/c = 2,2.5,4,6\) as in Fig. 28
Visualisation of turbulent kinetic energy (TKE) defined as \(k = \frac{1}{2}(\overline{u'}+\overline{v'}+\overline{w'})\) are presented in Fig. 29 at the same stations as the wake momentum deficit of Fig. 28, where TKE is half the sum of the variances of the velocity components. From the near-field stations in Fig. 29a and 29b, it is clear to see a wake with 3 distinct peaks and layers in k in the wake at \(y/c=0.75\), \(y/c=0.8\), and \(y/c=1.0\), corresponding to the separate wakes of each of the 3 wing elements. In Fig. 29b, the peak TKE in the wake is at a similar location and value.
In the farfield at \(x/c=4\), the wake and turbulence are more thoroughly mixed with no significant layers existing or visible in the TKE profile. There is generally a lower amount of TKE in this region with a maximum value of \(k= 0.008\), in comparison to the value of \(k=0.012\) found at the \(x/c = 2.5\) station. However, the wake is wider than in previous stations, and the floor shear layer continues to dissipate in comparison to the near field.
At \(x/c = 6\), the K-H mode must generate significant turbulent kinetic energy. This is highlighted by the maximum value of TKE being 50% larger than recorded 2c upstream, and is closer to the levels in the near-field. The wake has moved vertically by a significant amount compared against the previous station, and is far wider than even in the near-field. This is most likely a result of the meandering of the wake due to the K–H mode.
5 Conclusions
This study presents a study on a multi-element wing in ground effect using a spectral/hp element method. We present average pressure coefficient \(C_{p}\) plots, force data both time-averaged, unsteady and spectral analysis. The time-averaged force coefficients are \(-\)8.33 and 0.17 for lift and drag respectively. Spectral peaks were found at \(St=40\), \(St=60\), \(St=140\) and \(St=200\) on all flaps, with the \(St=140\) mode being significantly less visible on the second flap. Mode identification was undertaken, with these spectral peaks likely corresponding to modes associated with the LSB. However, a lower frequency mode at \(St=30\) exists only on the second flap which likely corresponds to the LSB on the pressure surface.
Secondary effects, including the ejection of lower momentum flow into the freestream, have been discussed and presented through contour plots, along with isosurfaces of Q-criterion and a time-space contour at the midplane of the mainplane that details the primary transition mechanism on the mainplane in fair detail. Through the cross-spectral phase, the phase relationship at \(St=40\) and \(St=60\) were shown, with the \(St=40\) mode showing an in-phase relationship, whilst the \(St=60\) mode shows an out-of-phase relationship. Although initial phase relationships were found, further investigations into the coupling of these mechanisms could be undertaken and would be of interest for future studies.
The wake structure has been discussed and presented through isosurfaces of Q-criterion, streamwise and spanwise vorticity contours, wake momentum deficit and turbulent kinetic energy line plots at various near- and far-field stations. The wake appears to be stratified in the near-field, with three distinct zones. In particular, this can be seen in the visualisation of the turbulent kinetic energy, where three distinct local maxima are present. Moving further downstream, this wake mixes through a primary K-H type instability that causes the wake to meander and eventually break down.
The results presented are the initial findings for the creation of a benchmark dataset, which can act as the calibration of lower fidelity models with respect to transition mechanisms, as well as for near-wall flows relevant to motorsport and F1, with a particular focus on downforce-producing elements in ground effect. The final uploaded dataset will contain more specific data required for this, and will be useful for the calibration of novel methodologies and reduced order models. Field data, such as time- and spatially-averaged velocities, first-order statistics such as turbulent kinetic energy and vorticity will also be presented in full.
Finally, the mesh and session (setup) files, a restart field, and the utilised version of the code will be provided, to allow for researchers to repeat and extend these results in the future.
References
Bettes, W.H.: The aerodynamic drag of road vehicles past, present, and future. Eng. Sci. 45, 4–10 (1982)
Blackburn, H.M., Sherwin, S.J.: Formulation of a galerkin spectral element-fourier method for three-dimensional incompressible flows in cylindrical geometries. J. Computat. Phys. 197(2), 759–778 (2004). https://doi.org/10.1016/j.jcp.2004.02.013
Bolis, A., Cantwell, C.D., Moxey, D., Serson, D., Sherwin, S.J.: An adaptable parallel algorithm for the direct numerical simulation of incompressible turbulent flows using a Fourier spectral/hp element method and MPI virtual topologies. Comput. Phys. Commun. 206, 17–25 (2016). https://doi.org/10.1016/j.cpc.2016.04.011
Buscariolo, F.F., Hoessler, J., Moxey, D., Jassim, A., Gouder, K., Basley, J., Murai, Y., Assi, G.R.S., Sherwin, S.J.: 9. Spectral/hp element simulation of flow past a formula one front wing: validation against experiments (2019)
Cabral, B., Leedom, L. Imaging vector fields using line integral convolution. Proceedings of the 20th annual conference on Computer graphics and interactive techniques: 263–270 (1993). https://doi.org/10.1145/166117.166151
Dong, S., Karniadakis, G.E., Chryssostomidis, C.: A robust and accurate outflow boundary condition for incompressible flow simulations on severely-truncated unbounded domains. J. Comput. Phys. 261, 83–105 (2014). https://doi.org/10.1016/j.jcp.2013.12.042
Ferrer, E., Moxey, D., Sherwin, S.J., Willden, R.H.J.: Stability of projection methods for incompressible flows using high order pressure-velocity pairs of same degree: Continuous and Discontinuous Galerkin formulations. Commun. Comp. Phys. 16(3), 817–840 (2014). https://doi.org/10.4208/cicp.290114.170414a
Georgiadis, N.J., Rizzetta, D.P., Fureby, C.: Large-eddy simulation: current capabilities, recommended practices, and future research. AIAA J. 48, 1772–1784 (2010). https://doi.org/10.2514/1.J050232
Guermond, J.L., Shen, J.: Velocity-correction projection methods for incompressible flows. SIAM J. Num. Anal. 41, 112–134 (2003). https://doi.org/10.1137/S0036142901395400
Hambli, W., Slaughter, J., Buscariolo, F., Sherwin, S.: Extension of spectral/hp element methods towards robust large-eddy simulation of industrial automotive geometries. Fluids (2022). https://doi.org/10.3390/fluids
Jwo, D.J., Chang, W.Y., Wu, I.H.: Windowing techniques, the welch method for improvement of power spectrum estimation. Comput. Mater. Continua 67, 3983–4003 (2021). https://doi.org/10.32604/cmc.2021.014752
Karniadakis, G., Sherwin, S. 6. Spectral/hp Element Methods for Computational Fluid Dynamics. Oxford University Press (2005)
Karniadakis, G.E., Orszag, S.A.: High-order splitting methods for the incompressible navier-stokes equations. J. Comput. Phys. 97, 414443 (1991)
Lombard, J.E.W.: A high-fidelity spectral/hp element LES study of Formula 1 front-wing and exposed wheel aerodynamics. Ph. D. thesis, Imperial College London (2017)
Mengaldo, G., de Grazia, D., Moxey, D., Vincent, P.E., Sherwin, S.J.: Dealiasing techniques for high-order spectral element methods on regular and irregular grids. J. Comput. Phys. 299, 56–81 (2015). https://doi.org/10.1016/j.jcp.2015.06.032
Mengaldo, G., Moxey, D., Turner, M., Moura, R.C., Jassim, A., Taylor, M., Peiro, J., Sherwin, S.J.: Industry-relevant implicit large-eddy simulation of a high-performance road car via spectral/hp element methods. SIAM Rev. 63, 723 (2019)
Moura, R.C., Cassinelli, A., da Silva, A.F., Burman, E., Sherwin, S.J.: Gradient jump penalty stabilisation of spectral/hp element discretisation for under-resolved turbulence simulations. Comput. Methods Appl. Mech. Eng. (2022). https://doi.org/10.1016/j.cma.2021.114200
Moxey, D., Cantwell, C.D., Bao, Y.: Nektar++: Enhancing the capability and application of high-fidelity spectral/hp element methods. Comput. Phys. Commun. 249, 107110 (2020). https://doi.org/10.17632/9drxd9d8nx.1
Moxey, D., Green, M.D., Sherwin, S.J., Peiró, J.: An isoparametric approach to high-order curvilinear boundary-layer meshing. Comput. Methods Appl. Mech. Eng. 283, 636–650 (2015). https://doi.org/10.1016/j.cma.2014.09.019
O’Neil, P., Nicolaides, D., Honnery, D., Soria, J.: Autocorrelation functions and the determination of integral length with reference to experimental and numerical data. 15th Australasian Fluid Mechanics Conference (2004)
Pegrum, J.M.: Experimental Study of the Vortex System Generated by a Formula 1 Front Wing. Ph. D. thesis, Imperial College London (2006)
Roberts, L.S., Correia, J., Finnis, M.V., Knowles, K.: Aerodynamic characteristics of a wing-and-flap configuration in ground effect and yaw. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering 230, 841–854 (2016). https://doi.org/10.1177/0954407015596274
Roberts, L.S., Finnis, M.V., Knowles, K. (2017) Forcing boundary-layer transition on a single-element wing in ground effect. Journal of Fluids Engineering, Transactions of the ASME. Journal of Fluids Engineering. https://doi.org/10.1115/1.4037036
Serdar, M., Karasu, lyas, Hakan, H., Turul, M.: Low reynolds number flows and transition. Low Reynolds Number Aerodynamics and Transition (2012). https://doi.org/10.5772/31131
Tadmor, E.: Convergence of spectral methods for nonlinear conservation laws. SIAM Journal of Numerical Analysis 26, 30–44 (1989)
Vos, P.: From h to p efficiently: optimising the implementation of spectral/hp element methods. Ph. D. thesis (2011)
Zhang, X., Zerihan, J.: Aerodynamics of a double-element wing in ground effect. AIAA Journal 41, (2003)
Acknowledgements
The authors acknowledge the efforts of Julien Hoessler and Francesco Bottone, who provided the CAD geometries as well as provided advice and assistance during the duration of these studies. This work primarily used the ARCHER2 UK National Supercomputing Service (https://www.archer2.ac.uk). This work was supported by the Engineering and Physical Sciences Research Council [EP/R029326/1]. Some calculations were performed using the CSD3 Tier 2 HPC platform hosted by the University of Cambridge.
Author information
Authors and Affiliations
Contributions
James Slaughter ran the simulations, prepared the data and wrote the first draft. David Moxey, Spencer Sherwin are responsible for the code development, editing and supervision of James Slaughter. All authors have read and agreed to the final version.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no pertinent conflict of interests related to this work or its publication.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Slaughter, J., Moxey, D. & Sherwin, S. Large Eddy Simulation of an Inverted Multi-element Wing in Ground Effect. Flow Turbulence Combust 110, 917–944 (2023). https://doi.org/10.1007/s10494-023-00404-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10494-023-00404-7