Flame Self-interaction and Flow Topology in Turbulent Homogeneous Mixture n-Heptane MILD Combustion

Abstract

Moderate or Intense Low-oxygen Dilution (MILD) combustion has potential to achieve both high energy efficiency and ultra-low emissions. This analysis adopts the critical point theory to characterise the Flame-Self Interaction (FSI) events and flow topologies in turbulent, homogeneous mixture, n-Heptane MILD combustion using Direct Numerical Simulations (DNS) with reduced chemical mechanism. The local flame geometry has also been categorised using the mean and Gauss curvatures. It was found that the Tunnel Formation (TF) and Tunnel Closure (TC) topologies are the most probable FSI events at all values of the reaction progress variable c, while the Unburned Pocket (UP) and Burned Pocket (BP) topologies were mostly present towards the unburned and burned mixtures of the flame, respectively. Moreover, increasing the turbulence intensity did not result in any significant changes in the distribution of FSI events. Investigation of the flow topology distribution showed that the features associated with non-zero dilatation rate did not exist in the MILD cases considered. This is a consequence of the negligible thermal expansion effect due to the small temperature rise in MILD combustion cases. Increasing the dilution factor caused a reduction in the frequency of FSI events for all c levels. The distributions of flame self-interaction events in homogeneous mixture MILD combustion have been found to be significantly different from previously reported distributions for conventional turbulent premixed combustion.

1 Introduction

The ever more stringent environmental regulations in response to climate change necessitate the development of novel combustion techniques that are simultaneously energy efficient and environmentally friendly. One such technique is the Moderate or Intense Low-oxygen Dilution (MILD) combustion which has shown potential to achieve both high energy efficiency and ultra-low emissions (Wünning and Wünning 1997; Cavaliere and de Joannon 2004). A combustion process is considered to be under MILD conditions if the fuel-oxidiser mixture is preheated above its autoignition temperature ($T_r > T_{ign}$), while the maximum temperature rise remains smaller than the autoignition temperature ($\varDelta T|_{\textrm{max}} < T_{ign}$) (Wünning and Wünning 1997; Cavaliere and de Joannon 2004). Such conditions could potentially be achieved by recirculating exhaust gases (i.e. Exhaust Gas Recirculation, EGR) back to the combustor in furnaces and boilers, or in Jet in Hot Co-flow (JHC) type combustors. However, the low oxygen concentrations required to achieve the MILD combustion conditions may lead to difficulties in ignition and flame stabilisation. Thus, in order to take advantage of the potential of this combustion technique, it is important to improve our fundamental understanding of the flame behaviour under MILD combustion conditions.

Experimental investigations of MILD combustion using Planar Laser-Induced Fluorescence images of OH radicals (OH-PLIF) have shown the presence of flame fronts, and indications of distributed burning were revealed through temperature measurements (Plessing et al. 1998; Özdemir and Peters 2001). These findings were confirmed by Minamoto, Swaminathan and co-workers who conducted 3D Direct Numerical Simulations (DNS) of EGR-type, homogeneous mixture, MILD combustion (Minamoto et al. 2013, 2014b; Minamoto and Swaminathan 2014; Minamoto et al. 2014a), and investigated the distribution of species, temperature, and reaction rate fields (Minamoto et al. 2013; Minamoto and Swaminathan 2014), morphological and topological structures (Minamoto et al. 2014a) and scalar gradient statistics in terms of temperature and equivalent OH-PLIF signal (Minamoto and Swaminathan 2014). Minamoto et al. (2014a) concluded that the distributed nature of combustion seen in OH-PLIF visualisation (Plessing et al. 1998; Özdemir and Peters 2001) can be attributed to the interaction of thin reaction zones. Thus, these interactions (of reaction zones or flame surfaces) play a key role in MILD combustion. Moreover, further DNS investigations suggested that modified flamelet-based models can be applied to gaseous fuel MILD combustion (Minamoto and Swaminathan 2015). However, when the conventional flamelet and eddy dissipation approaches were applied under MILD conditions in Reynolds Averaged Navier–Stokes (RANS) and Large Eddy Simulations (LES) type studies, they provided good predictions for the mean velocity and temperature fields, but discrepancies with experiments have been reported in terms of peak temperature and minor species concentrations (Aminian et al. 2011; Christo and Dally 2005). Thus, further investigations are needed to fully understand the behaviour of flamelet-based approaches in MILD combustion.

In order to extend flamelet based modelling approach (e.g. the generalised Flame Surface Density, FSD (Boger et al. 1998)) for homogeneous mixture MILD combustion, an improved understanding of the geometry of the reaction zone and the topologies of Flame Self-Interactions (FSI) can potentially play an important role. The local topology of FSI influences events such as pocket burnout and cusp formation, which can significantly affect the balance of flame area production and destruction and thus can influence the overall burning rate (Griffiths et al. 2015). Trivedi et al. (2019) and Malkeson et al. (2021) have discussed the implications of the FSI events’ distribution in the context of FSD-type modelling approaches. These implications on modelling are also presented in this paper for completeness.

Different approaches have been used in the literature to characterise the FSI events. These include a critical point theory based method (Griffiths et al. 2015), automatic feature extraction technique using complex wavelet transform (Dunstan et al. 2013), and Minkowski functional based approach (Minamoto et al. 2014a). In MILD combustion, Minamoto et al. (2014a) used Minkowski functional to study the morphology of the reaction zones in methane-air mixtures, which resulted in a shapefinders map based on planarity and filamentarity parameters for the convenient classification of the reaction zone morphological structures. The reaction zones in MILD combustion showed a variety of shapes including blobs, pancakes and ribbons. However, the pancake-like shapes were found to be the most probable. This confirms the experimental finding first reported by Dally et al. (2004). These shapes are associated with autoignition events and propagating-flames in mixtures of reactants, products and intermediate species (Minamoto et al. 2014a).

While the previous analyses provided useful physical insights into MILD combustion, it is also useful to categorise the flow topologies present in MILD combustion flames, particularly those influencing the FSI topology. This could help in the design of experimental setups, which can potentially isolate, or increase the probability of a certain FSI event by controlling the dominant flow topology. Thus, the present analysis adopts the critical point theory to investigate the influence of turbulence intensity and dilution level on FSI and flow topologies in turbulent, homogeneous mixture, n-heptane MILD combustion. For this purpose, a DNS dataset of EGR-type, homogeneous-mixture, n-Heptane/air MILD combustion cases at two dilution levels (mole fraction of oxygen $X_{O_2} = 4.5, 3.0\%$) and two root-mean-square turbulent velocity fluctuations ($u' = 2.0, \, 4.0$ m/s) has been considered. In this study, n-heptane was chosen as the fuel, since it is a better representative of the heavier hydrocarbons used in industrial applications.

2 Mathematical Background

2.1 Flame Self-interaction

For this analysis, the reaction progress variable c has been defined based on the oxidiser mass fraction ($Y_{O_2}$) as follows:

$$\begin{aligned} c= & {} \frac{Y_{O_2} - Y_{O_2,u}}{Y_{O_2,b} - Y_{O_2,u}} \end{aligned}$$

(1)

where the subscripts u and b refer to the values of $Y_{O_2}$ in the unburned and fully burned gases, respectively. While the critical point theory approach for FSI was shown to be insensitive to the choice of progress variable species (Griffiths et al. 2015) as long as the resulting c is continuous and monotonic, defining c based on oxygen is justified since larger hydrocarbons, like n-heptane, break down to smaller ones at high temperatures, and thus a fuel based progress variable may not represent the entire combustion process.

At the critical points in the flame, the gradient of c goes to zero, and thus a Taylor series expansion around a critical point can be written as:

$$\begin{aligned} c (\textbf{a} + \textbf{x})= & {} c (\textbf{a}) + \frac{{\textbf{x}}^T}{2} \underline{\underline{H}}(c(\textbf{a}))\textbf{x} + \dots \end{aligned}$$

(2)

where $\textbf{x}$ is the position vector and $\textbf{a}$ the position vector at the critical point. In Eq. (2), the Hessian $\underline{\underline{H}}(c)$ gives a second order accurate representation of the local field. Since $\underline{\underline{H}}(c)$ is symmetric, its eigenvalues ($\lambda _1, \, \lambda _2, \, \lambda _3$) are real. These eigenvalues describe the curvature along the three principle axes and thus fully characterize (with second order accuracy) the local topology as long as the orientation of structures remains irrelevant (Griffiths et al. 2015). More insights can be obtained by converting the principle axes to spherical coordinates. Following Griffiths et al. (2015) and for $\lambda _1> \lambda _2 > \lambda _3$, the longitude ($\theta$) about the vector $[e_{\lambda _1}, \, 0, \, -e_{\lambda _3}]$ is written as:

$$\begin{aligned} \theta= & {} \frac{6}{\pi } \arctan \left( \frac{(\lambda _1 -2\lambda _2 + \lambda _3)/6^{1/2}}{(\lambda _1 - \lambda _3)/2^{1/2}} \right) \end{aligned}$$

(3)

while the latitude ($\varphi$) about the pole vector $[e_{\lambda _1}, \, e_{\lambda _2}, \, e_{\lambda _3}]$ is given by:

$$\begin{aligned} \varphi= & {} \frac{2}{\pi } \arctan \left( \frac{(\lambda _1 + \lambda _2 + \lambda _3) \cos \left( \frac{\theta \pi }{6} \right) /3^{1/2}}{(\lambda _1 - \lambda _3)/2^{1/2}} \right) \end{aligned}$$

(4)

The magnitude of the eigenvalues ($\kappa = {[\lambda _1^2 + \lambda _2^2 + \lambda _3^2]}^{1/2}$) provides an overall measure of curvature. Hence, $\varphi$ and $\theta$ are considered as shaping factors which define a continuous domain describing the various feasible local topologies of FSI, as shown in Fig. 1.

Fig. 1

Various types of FSI topologies

It can be seen from Fig. 1 that the eigenvalues of the Hessian $\underline{\underline{H}}(c)$ take the signs ($---$), ($--+$), ($-++$) and ($+++$) from left to right. These signs correspond to Burned Pocket (BP), Tunnel Formation (TF), Tunnel Closure (TC) and Unburned Pocket (UP) topologies, respectively. The BP (UP) topologies represent a spherical flame propagating outward (inwards), while the TF and TC topologies correspond to cylindrical flames propagating away from (TF) or towards (TC) a common axis. In this analysis the critical points associated with the FSI events are identified based on the methodology adopted by Griffiths et al. (2015).

It is also useful to classify the local flame geometry based on the local mean curvature $\kappa _m = (\kappa _1 + \kappa _2)/2$ and the Gauss curvature $\kappa _g = \kappa _1 \kappa _2$, where $\kappa _1$, $\kappa _2$ are the principle curvatures (Dopazo et al. 2007). Excluding the complex curvature region ($\kappa _g > \kappa _m^2$), positive (negative) value for $\kappa _m$ suggests that the flame surface is convex (concave) towards the reactant side, while the sign of $\kappa _g$ indicates the topology type (positive $\kappa _g$ for an elliptic topology, and negative for a hyperbolic, saddle-like structures).

Fig. 2

Schematic of the various flow topologies, S1-S8

2.2 Flow Topology

Chong et al. (1990) used the invariants $P, \, Q$ and R of the velocity gradient tensor $A_{ij}=\nabla \textbf{u}$ to classify all possible local small turbulent structures into eight categories S1 - S8. The velocity gradient tensor can be written as:

$$\begin{aligned} A_{ij}= & {} S_{ij} + W_{ij} \end{aligned}$$

(5)

where $S_{ij}$ and $W_{ij}$ are the symmetric and antisymmetric components, respectively. The eigenvalues $\lambda _1^F, \, \lambda _2^F$ and $\lambda _3^F$ of $A_{ij}$ are found from the characteristic equation

$$\begin{aligned}{} & {} {\lambda ^F}^3 + P {\lambda ^F}^2 + Q {\lambda ^F} + R = 0 \end{aligned}$$

(6)

Where

$$\begin{aligned} P =&-(\lambda _1^F + \lambda _2^F + \lambda _3^F) \end{aligned}$$

(7)

$$\begin{aligned} Q =&0.5( P^2 - S_{ij}S_{ij} + W_{ij}W_{ij}) \end{aligned}$$

(8)

$$\begin{aligned} R =&(-P^3 + 3PQ - S_{ij}S_{jk}S_{ki} -3 W_{ij}W_{jk}S_{ki})/3 \end{aligned}$$

(9)

Depending on the discriminant of the characteristic equation and the type of the eigenvalues (complex or real), the $P-Q-R$ space is divided into eight flow topologies, as shown in Fig. 2. The first four topologies S1 - S4 exist in both compressible and incompressible flows, while S5 - S8 are associated with non-zero dilatation rate (i.e. $\nabla . \textbf{u} \ne 0$), and for that they show up exclusively in compressible flows. More details about the above procedure can be found in Chong et al. (1990).

3 Numerical Implementation

In the current analysis, a DNS dataset of turbulent homogeneous EGR-type n-Heptane/air mixture under MILD conditions at two dilution levels and two turbulent intensities has been considered. For these simulations, a cubic domain ($L = 20 \, mm$) has been discretised by a uniformly spaced Cartesian grid comprising of 216 nodes in each direction. This grid resolution ensures that the thermal flame thickness ($\delta _{th} = (T_p - T_r)/\max |\nabla T |_L$ where $T,\, T_p$ and $T_r$ are the instantaneous, products and reactants temperatures and the subscript L refers to the 1D unstretched laminar flame) has been resolved by a minimum of 15 grid points, while the Kolmogorov length scale ($\eta$) has been resolved using 1.1 grid points. Turbulent inflow boundary condition with specified density, velocity and species mass fractions has been imposed at the inlet, while a partially non-reflective outflow boundary condition has been utilised for the outlet. All other boundaries have been treated as periodic.

Table 1 shows the thermochemical and turbulent conditions used for the generation of the simulation’s initial field. These include the mole fractions of the oxidiser stream, unstretched laminar burning velocity and Zeldovich flame thickness (i.e. $\delta _f = \alpha _T/S_L$ where $\alpha _T$ is the thermal diffusivity of the mixture). The fuel-oxidiser mixture has an equivalence ratio $\phi = 0.8$. The turbulence levels used in this study are comparable to those reported by Oldenhof et al. (2011), while the unburned gas temperature of $T_r = 1100$K is close to that used in the experimental investigation by Ye et al. (2017). The mean inflow velocity $U_{\textrm{mean}}$ was chosen to be 6.0 m/s for all cases. The simulations have been sampled starting at two flow-through times (i.e. $\tau _{\textrm{sim}}=2.0L/U_{\textrm{mean}}$), which amounts to 6.67 and 13.34 initial eddy turnover times for the low (HM-A1, HM-B) and high (HM-A2) turbulence cases, respectively, and for a period of one flow-through time.

The process for creating the initial scalar and turbulence fields was described in detail by Minamoto et al. (2013) and briefly consists of:

• 1) The generation of a homogeneous isotropic field to initialize the turbulent velocity fluctuations. This is done using the pseudo-spectral method of Rogallo (1981). The initial turbulence intensity $u'$ and turbulent length scale $\ell _{{}_0}$ for the generated isotropic turbulence field has been given in Table 1 for all cases.

• 2) For each case, a corresponding one-dimensional unstretched freely propagating laminar premixed flame simulation was carried out using the thermochemical conditions shown in Table 1 and $\phi =0.8$. The resulting species mass fractions of this simulation were parameterised as functions of the oxygen based reaction progress variable (i.e., $Y_{\alpha ,L} = f_\alpha (c_{O2,L})$)

• 3) An initial bimodal distribution of c (i.e., corresponding to a of mean of $\langle c \rangle=0.5$ with peaks at $c=0$ and $c=1.0$) with length scale $\ell _c$ (here $\ell _c/\ell _{{}_0} = 1.225$) was generated using the methodology by Eswaran and Pope (1988).

• 4) The functions $Y_{\alpha ,L} = f_\alpha (c_{O2,L})$ generated in step 2 are then used to create the initial scalar field using the bimodal c field from step 3 as an input parameter. Here, atmospheric pressure and an unburned gas temperature $T_r = 1100$K were also used.

• 5) The resulting scalar field was allowed to evolve with turbulence for about one turnover time in a periodic domain mimicking the mixing of fuel and oxidiser in an EGR-type combustor. The mixing time here is well below the ignition delay time.

• 6) Finally, the evolved scalar field was then used as an initial field as well as being fed into the domain through the inlet with a mean velocity $U_{\textrm{mean}} = 6.0$ m/s.

The simulations in this study have been conducted using the compressible, finite difference DNS code SENGA2 (Cant 2012). In this code, the dimensional form of the compressible mass, momentum, energy and species mass fractions transport equations are solved with chemical reaction and temperature dependent thermo-physical properties (viscosity, thermal conductivity, specific heat capacities and mass diffusivities). A reduced chemical mechanism comprising 22 species and 18-steps has been taken to represent the chemical kinetics of combustion (Liu et al. 2004). A constant Lewis number approach has been used to model the molecular transport effects. In this approach, the mass diffusion constant for each species $D_\alpha$ is calculated using its Lewis number $Le_\alpha$. Further details about this approach can be found in Cant (2012). A $\mathrm {10{th}}$ order central difference scheme is used for spatial discretisation at the internal grid points, which reduces to a one-sided fourth-order accurate scheme at the non-periodic boundaries. For time stepping, a fourth-order explicit low storage Runge–Kutta scheme is used. Due to the stiffness of the chemical mechanism, the species mass fractions equations have been solved using the fractional step method where the linear system of ODEs in the second step (which includes the chemical source term) was solved using a variable-coefficient solver with preconditioned Krylov iteration as implemented in the VODPK package (Byrne 1992). The boundary conditions are specified according to the Navier–Stokes Characteristic Boundary Condition (NSCBC) methodology.

Table 1 Initial conditions for turbulence and scalar fields in n-Heptane MILD combustion simulations

4 Results and Discussion

4.1 View of the Instantaneous Scalar Field

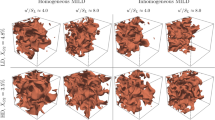
The instantaneous views of c iso-surfaces for all cases are shown in Fig. 3. These c iso-surfaces were chosen to represent the reaction progress variable value at which the maximum heat release is obtained in the corresponding unstretched laminar premixed flame used to initialise each case (Here, $c = 0.71$ for HM-A1, HM-A2 and $c=0.75$ for HM-B), and thus it can be considered to represent the flame surface. Moreover, while the c iso-surfaces in Fig. 3 are taken at one time snapshot (two flow-through times), they remain representative of the c iso-surfaces at all snapshots between $2.0 - 3.0\,L/U_{\textrm{mean}}$. The distributed nature of the flame in MILD combustion, observed in OH-PLIF visualisations by Plessing et al. (1998), is evident in Fig. 3, which also illustrates the potential for a considerable amount of flame self-interactions in these cases. It can also be seen that increasing the turbulence intensity (case HM-A2) gives rise to a noticeably more wrinkled c iso-surfaces. Comparing Fig. 3a and c shows that increasing the dilution factor resulted in the c iso-surfaces generally covering smaller portion of the domain. This is substantiated quantitatively in Table 2, which shows the ratio of flame area for cases HM-A2 and HM-B to the flame area in case HM-A1. A possible explanation for this observation is that the higher dilution rate means less oxygen in the domain, and thus the combustion process is completed in a smaller portion of the domain.

Fig. 3

The iso-surfaces of c at the location of maximum heat release for the equivalent lamniar flames ($c = 0.71$ for HM-A1, HM-A2 and $c=0.75$ for HM-B). The isometric view is from the outlet side

Table 2 The surface area (A) of the c iso-surface shown in Fig. 3 for cases HM-A2 and HM-B normalised by that from case HM-A1

4.2 Flame Self-interaction

The frequency of FSI topologies and their percentages at different values of c are shown in Fig. 4. For the cases at low turbulence intensity (HM-A1, HM-B), the frequency of FSI events peaks just below $c=0.5$, while the peak frequency is shifted to $c \approx 0.6$ for the case at high turbulence intensity (HM-A2). It should be noted that this is not an artefact of the $\langle c \rangle \approx 0.5$ for the initial field, due to the bimodal nature of the initial c field which has its PDF peaks around $c=0$ and $c=1$. Furthermore, to completely discard the effect of the simulation initialisation, the FSI analysis have been conducted on the initial field and the resulting number of FSI events was subtracted from the total FSI counts. After doing so, the exact same trend is maintained. The FSI distribution in all cases is significantly different to that previously reported for turbulent premixed flames, which exhibit high frequencies of FSI events only towards the unburned and burned gas sides of the flame front (Griffiths et al. 2015; Trivedi et al. 2019) in contrast to the middle of the reactive region in the case of MILD combustion. Interested readers can refer to Griffiths et al. (2015); Trivedi et al. (2019) for an in-depth description of FSI events distribution in turbulent premixed flames. Thus, the main findings in Griffiths et al. (2015); Trivedi et al. (2019) will be referred to in this paper without reproducing the results in these studies.

Griffiths et al. (2015) showed that decreasing the Damköhler number (i.e. $Da = (\ell _{{}_0} S_L)/(\delta _{th} u')$) in a slot jet configuration led to an increase in FSI event frequency towards the middle of the flame. Thus, the high frequency of FSI events at the interior of the flame front under MILD conditions for which Damköhler number is typically low (here $Da = 0.26, 0.13$ and 0.095 for HM-A1, HM-A2 and HM-B, respectively) is qualitatively consistent with previous findings by Griffiths et al. (2015). From the percentages of FSI events at different c values shown in Fig. 4, it can be seen that the unburned pocket topology (UP) has higher likelihood near the unburned gas side, and becomes rare towards the burned gas side. By contrast, the opposite is true for the burned pocket topology (BP) which exhibits very low probability towards the unburned gas side but becomes more frequent as c increases. In all cases, the most probable FSI events are the cylindrical tunnel closure (TC) and tunnel formation (TF). Figure 4 shows that for $c < 0.5$ tunnel closure (TC) events are the most likely FSI events to occur. However, as the value of c increases, the tunnel formation (TF) topologies increase in frequency and become the most probable towards the burned gas side of the flame front.

Fig. 4

Histogram of the number of samples and their percentage for the four FSI topologies at different values of c

Figure 4 also shows that, with the same number of snapshots analysed, increasing the dilution factor reduces the frequency of FSI events across the entire range of c values. A possible explanation for this behaviour is that the reduced oxygen concentration makes it more difficult to progress the chemical reaction, and thus reduces the overall flame volume and with it the frequency of FSI events. The above comparison is meaningful when using the same number of snapshots (i.e. the same sample size) which has only been possible in cases HM-A1 and HM-B, since these cases share the same initial turbulence characteristics. For case HM-A2, the higher initial turbulence intensity necessitate a smaller solution time step and give rise to larger number of snapshots within the analysed time frame (one flow through time). Hence, comparing the frequency count for case HM-A2 with the other case can potentially be misleading. In general, the frequency count plots are only useful to illustrate the qualitative distribution of FSI events in the c space. The relative weights of each FSI event can be better understood from the percentage plot in Fig. 4.

4.3 Flow Topologies

Fig. 5

Histogram of the flow topologies in the whole domain for all three MILD combustion cases

Figure 5 shows the flow topologies present in the simulation domain for all three MILD combustion cases. It can be seen from Fig. 5 that the topologies S5-S8 have negligible frequencies in the domain and the flow field only contains S1-S4 topologies in similar fashion to what is seen in incompressible flows. This is also visually illustrated from the contours of flow topologies shown in Fig. 6, which also shows the smaller flow structures associated with an increased level of turbulence in case HM-A2.

Fig. 6

Contours of the flow topology field at the $x-y$ midplane

The lack of S5-S8 topologies in the domain is due to the small temperature rise characteristic of MILD combustion which leads to insignificant levels of thermal expansion in the domain. This can be substantiated from the profiles of the mean values of $P= -\nabla \cdot \textbf{u}$ shown in Fig. 7, which shows that the invariant P (and consequently $\nabla \cdot \textbf{u}$) have very small mean values compared to the turbulent straining (i.e. $\ell _{{}_0}/u'$).

Fig. 7

Profiles of the first invariant of the velocity gradient tensor normalised by the turbulent straining ($P= - \nabla \cdot \textbf{u} \times (\ell _{{}_0}/u')$) and conditioned upon c

Moreover, similar to the distribution of flow topologies in incompressible flows, where the S4 topology is the most dominant, while S1 and S2 have comparable probabilities (Suman and Girimaji 2010), Fig. 5 shows that in the current MILD setup results in comparable S1 and S2 probabilities as well, while S4 and S3 remain the most dominant and least likely flow topologies, respectively. Hasslberger et al. (2019) have presented a theoretical framework for estimating the volume fraction of the various flow topologies in incompressible, isotropic turbulence. They found that the percentage volume fraction for nodal (S2 and S3) and focal (S1 and S4) topologies is expected to be 20 and 80%, respectively. In contrast, The current MILD simulations has a percentage volume fraction of approximately 30% for nodal (S2 and S3) and 70% for focal (S1 and S4) topologies in all case. Thus, while seeming to revert to a pure mixing problem (due to the low heat release), the current MILD configuration quantitatively deviates in the nodal-to-focal topologies distribution from the idealized incompressible, isotropic turbulence state but qualitatively the results obtained in this analysis is consistent (i.e. more focal topologies than nodal ones) with the distribution proposed by Hasslberger et al. (2019). Figure 5 also shows that changing the turbulence and dilution levels within the parameter range considered in this study has little impact on the distribution of the flow topologies.

4.4 Flow Topologies Conditioned upon FSI

Fig. 8

Histogram of the percentages of the available flow topologies for each FSI event at different values of c

Figure 8 shows the percentages of the various flow topologies present in the domain at different c values for each FSI event. It can be seen from Fig. 8 that at the spherical FSI events (Burned Pocket BP and Unburned Pocket UP) the focal flow topologies (S1, S4) are the most likely to be present. On the other hand, S2 becomes significant in the cylindrical FSI events (Tunnel formation TF and closure TC) with similar probability to that of S1, while S4 remains the most frequent flow topology. This is similar to what is expected in the incompressible flows (Suman and Girimaji 2010) which may indicate particularly low levels of $\nabla \cdot \textbf{u}$ at the locations of the tunnel formation and closure FSI events. It can also be seen from Fig. 8 that changing the turbulence and dilution levels within the values considered in this study does not have a significant effect on the distribution of flow topologies at each FSI event.

4.5 Mean and Gauss Curvatures

Fig. 9

Scatter of $\kappa _g \times \delta _{th}^2$ with $\kappa _m \times \delta _{th}$ in the region $0.01 \le c \le 0.99$. Scatter is coloured by the different FSI topologies

Figure 9 shows the scatters of FSI events in the $\kappa _m-\kappa _g$ space. It can be seen from Fig. 9 that, in all cases, the spherical FSI events are associated solely with elliptic structures with the Burned Pocket (BP) topology predominantly showing convex structures, while the opposite is true for the Unburned Pocket (UP) topology (i.e. showing concave elliptic structures). The cylindrical FSI events are present across all types of structures with tunnel formation FSI events associated with convex elliptic and inverted saddle-like structures, while tunnel closure events showing concave elliptic and convex saddle-like structures. It can be seen from Fig. 9 that increasing the turbulence intensity or the dilution level did not lead to any noticeable changes in the mean and Gauss curvature values within the parameter range explored in the current work.

4.6 Modelling Implications

From a modelling perspective, physical insights into FSI can be achieved by considering the statistical behaviours of the displacement speed, $S_d$, of the reaction progress variable and the surface density function, $| \nabla c |$. For this purpose, it is worthwhile to present the transport equation of the reaction progress variable:

$$\begin{aligned} \rho \frac{\partial c}{\partial t} + \rho u_j \frac{\partial c}{\partial x_j}= & {} \frac{\partial }{\partial x_j} \left( \rho D \frac{\partial c}{\partial x_j} \right) + \dot{\omega }_c \end{aligned}$$

(10)

where $\dot{\omega }_c$ is the reaction rate of c and D is the reaction progress variable diffusivity. The transport equation of c can be recast in kinematic form for a given c-isosurface in the following manner

$$\begin{aligned} \frac{\partial c}{\partial t} + u_j \frac{\partial c}{\partial x_j}= & {} S_d | \nabla c | \end{aligned}$$

(11)

Here, $S_d$ is the displacement speed and can be expressed in the following manner based on Eqs. (10) and (11):

$$\begin{aligned} S_d= & {} \frac{ \dot{\omega }_c + \nabla \cdot (\rho D \nabla c)}{ \rho | \nabla c |} \end{aligned}$$

(12)

The transport equation of the surface density function (SDF), $| \nabla c |$, can be derived based on Eq. (11) as Trivedi et al. (2019):

$$\begin{aligned} \frac{\partial | \nabla c |}{\partial t} + \frac{\partial (u_j | \nabla c |)}{\partial x_j}= & {} a_T | \nabla c | - \frac{\partial \left( S_d N_j | \nabla c | \right) }{\partial x_j} + 2 S_d \kappa _m | \nabla c | \end{aligned}$$

(13)

In Eq. (13), $a_T = (\delta _{ij} - N_i N_j ) \partial u_i/ \partial x_j$ is the tangential strain rate. The four principal FSI topologies (i.e. UP, TF, TC and BP) can be represented based on the scaled local coordinates x, y and z for small deviations from a critical point in the following manner (Trivedi et al. 2019).

$$\begin{aligned} c(x,y,z)= & {} c_0 + \frac{1}{2} x^2 + \frac{1}{2} y^2 + \frac{1}{2} z^2 \; \quad \textrm{for} \quad \textrm{UP} \nonumber \\ c(x,y,z)= & {} c_0 + \frac{1}{2} x^2 - \frac{1}{2} y^2 - \frac{1}{2} z^2 \; \quad \textrm{for} \quad \textrm{TF} \nonumber \\ c(x,y,z)= & {} c_0 - \frac{1}{2} x^2 + \frac{1}{2} y^2 + \frac{1}{2} z^2 \; \quad \textrm{for} \quad \textrm{TC} \nonumber \\ c(x,y,z)= & {} c_0 - \frac{1}{2} x^2 - \frac{1}{2} y^2 - \frac{1}{2} z^2 \; \quad \textrm{for} \quad \textrm{BP} \end{aligned}$$

(14)

Here $c_0$ is the reaction progress variable value at the critical point. Based upon Eq. (14), it can be appreciated that an UP will correspond to a local minimum (i.e. a central low value of the reaction progress variable with surrounding higher values), whereas a BP corresponds to a local maximum (i.e. a central high value of the reaction progress variable with surrounding lower values). For the unburned gas pocket (UP), the flame normal vector $\textbf{N}$ is given by: $\textbf{N} = (-x/r,-y/r,-z/r)^{\textrm{T}}$ according to Eq. (14), where the radius $r=\sqrt{x^2 + y^2 + z^2}$, and twice the curvature of the flame surface, $2\kappa _m$, can be given as $2\kappa _m=-2/r$. For the burned gas pocket (BP), $\textbf{N}$, can be expressed as $\textbf{N} = (x/r,y/r,z/r)^{\textrm{T}}$ and the curvature of the flame surface, $\kappa _m$, can be given as $\kappa _m=1/r$. A TF FSI event corresponds to a local saddle point with a minimum on the central axis of the tunnel (taken as the x direction) and a maximum in the two other directions whereas a TC event is obtained at a local saddle point with a maximum on the central axis of the tunnel (taken as the x direction) and a minimum in the two other directions. Thus, for the TF FSI events one gets: $\textbf{N} = (-x/r,y/r,z/r)^{\textrm{T}}$ and $\kappa _m = x^2/r^3$, whereas $\textbf{N} = (x/r,-y/r,-z/r)^{\textrm{T}}$ and $\kappa _m = -x^2/r^3$ for the TC FSI events. Extending this analysis further, it is possible to evaluate the terms in the SDF transport equation using the expressions $\textbf{N}$ and $\kappa _m$ in the case of FSI events (Trivedi et al. 2019; Malkeson et al. 2021). It can be appreciated from Eq. (13) that the first two terms on the right-hand side identically vanish at the critical point but the expressions for $\textbf{N}$ and $2\kappa _m$ reveal that the last term does not exhibit a singularity even when r approaches zero (i.e. critical point). It has been found that the term $-{\partial \left( S_d N_j | \nabla c | \right) }/{\partial x_j}$ indeed assumes vanishingly small values for the critical points (not shown explicitly because it only shows the numerical noise). This further suggests that the SDF transport equation and the terms of transport equations of the quantities such as FSD and Scalar Dissipation Rate, which depend on the SDF, remain bounded even at the critical points.

Finally, the considerably different distributions of FSI topologies in homogeneous mixture MILD combustion from the reported distributions for conventional premixed flames (Griffiths et al. 2015; Trivedi et al. 2019) may have significant implications on the modifications needed to the flamelet combustion models (e.g. FSD methodology), which depend on the flame surface topology, to make them applicable for MILD combustion. Moreover, any such attempt to extend the flame surface based modelling methodology for MILD combustion needs to include the effects of dilution (e.g. $\mathrm {O_2}$ concentration).

5 Summary and Conclusions

The flow topologies and the topologies associated with the Flame Self-Interaction (FSI) events were investigated using the critical point theory for turbulent, homogeneous mixture n-Heptane/air MILD combustion. The local flame geometry has also been categorised using the mean and Gauss curvatures. It was found that the peak frequencies of FSI events were in the range $c=0.5 - 0.6$ and that the cylindrical FSI topologies (tunnel formation TF and tunnel closure TC) are the most probable FSI events across the whole range of c values in the cases considered, while the spherical FSI topologies were mostly present at the leading (Unburned Pocket UP) and trailing (Burned Pocket BP) edges of the flame. Moreover, increasing the turbulence intensity and dilution level did not result in any significant changes in the distribution of FSI events. It was also found that the flow topologies associated with non-zero dilatation rate did not exist in the MILD cases considered here. This is due to the small temperature rise under MILD conditions, which led to negligible thermal expansion effect. Increasing the dilution factor caused a reduction in the frequency of FSI events for all c levels. The qualitative nature of the distributions of the FSI events for homogeneous mixture MILD combustion has been found to be significantly different from the previously reported distributions in conventional premixed turbulent flames (Griffiths et al. 2015; Trivedi et al. 2019), which may have important implications on the possibility of extending of flame surface based flamelet modelling methodologies for turbulent MILD combustion.