LES and ILES Simulations of Free-Jets

Abstract

A systematic numerical study was performed to investigate the influence of subgrid-scale (SGS) treatments on the simulation of turbulent free-jets. Large eddy simulations (LES) of such flows were performed to assess the accuracy of two SGS approaches: the detached eddy simulation and the dynamic Smagorinsky model (DSM). The Non-oscillatory Forward in Time-Multidimensional Positive Definite Advection Transport Algorithm (NFT-MPDATA) numerical scheme was employed to integrate the Navier–Stokes equations for incompressible flows. MPDATA due to its self-regularisation property is used to implicitly provide SGS effects. Two options of implicit LES (ILES) are investigated: ILES-NS, which solves the Navier–Stokes equations without an explicit SGS model, and ILES-EU that solves the Euler equations where viscous terms are absent. The performance of each approach was evaluated focusing on key global characteristics of jets, self-similar properties, and energy spectra. Quantitative and qualitative comparisons showed that all simulations were in good agreement with laboratory experiments, prior numerical studies, and each other, thus confirming the validity of the numerical approach and suitability of ILES for this class of flows. Additionally, energy spectra analysis revealed that ILES can reproduce the $-5/3$ and $-7$ gradients that signify the universal inertia subrange and dissipation range for turbulent free-jets.

1 Introduction

There is a continuing interest in advancing LES and ILES methodologies alongside associated SGS treatments for turbulent jets. The turbulent free-jet is a type of free shear flow that plays an integral role in many engineering applications, ranging from fuel-jet mixing in a combustion engine to elements of a drug delivery system in medical applications. Such jet flows are related among others to the spreading rate and turbulent mixing characteristics, often dictated by the large turbulent structure exhibited in the jet itself. LES and ILES are particularly well suited to capturing the large scale evolution of jets since they resolve large turbulent scales.

The LES approach has been previously applied to study physics of turbulent jets. For instance, Bogey and Bailly (2006) and Salkhordeh et al. (2019) employed LES to investigate Reynolds number effects for compressible and incompressible jets respectively. Some numerical studies explored various SGS treatments for LES in simulating free-jets. For example, Gohil et al. (2014) assessed the shear-improved Smagorinsky model for predicting higher-order flow statistics of a $Re = 1.0 \times 10^4$ jet. Ghaisas et al. (2015) tested the Sigma model and employed it to simulate both non-buoyant and buoyant horizontal free-jets. Recently, Pinho and Muniz (2021) compared the accuracy of classical Smagorinsky model, dynamic Smagorinsky model, and velocity structure functions in predicting mean axial velocities and axial velocities fluctuations on the centreline of a $Re = 2.0 \times 10^4$ jet. An alternative to SGS treatments for simulating turbulent free-jets that has recently gained attention is the ILES approach. In ILES, SGS effects are implicitly achieved through the numerical scheme itself rather than explicit modelling. Among them, DeBonis (2018) employed ILES to simulate a series of hot jets at various Mach numbers previously studied experimentally by NASA; Margnat et al. (2018) simulated incompressible turbulent round free-jet with ILES and further performed an acoustic analysis of the ILES data; Loppi et al. (2018) assessed their developed code for ILES capabilities by validating it against the turbulent round free-jet data experimentally obtained by Panchapakesan and Lumley (1993), while Tai et al. (2021) demonstrated that for subsonic and supersonic planar jets ILES is capable of reproducing velocity and passive scalar fields obtained with DNS.

The earliest work comparing the LES and ILES approaches for turbulent free-jets belongs to Fureby and Grinstein (1999) who investigated vortex dynamics of compressible square free-jets with the monotonically integrated LES (MILES) schemes based on the Flux-Corrected Transport (FCT) method. In this work, the authors employed MILES to carry out conventional LES simulations, ILES simulations without explicit SGS models, and ILES simulations without both SGS and viscous molecular terms. They showed that all three approaches yield very similar results including capturing the inertial subrange and the dissipation range on the velocity spectra as well as being capable to achieve almost identical cumulative distribution function of the vorticity magnitude. Similarly, Karaca et al. (2012) compared LES and ILES based on a 5th order Weighted Essentially Non-Oscillatory (WENO) scheme in simulating high-speed turbulent jets. They concluded that the conventional LES did not show any superiority against the ILES results and they even showed that the LES with the classical Smagorinsky model yield unsatisfactory results owing to its overly dissipative nature (Karaca et al. 2012).

These earlier investigations concentrated on the applicability of ILES to free-jet flows and comparing its performance to LES and experiments in the context of compressible flows. In contrast, to the best of our knowledge this work provides the first such investigation for incompressible free-jets.

Herein, we report a systematic study that compares simulations of the turbulent free-jet using the LES and ILES approaches based on MPDATA. MPDATA, originally proposed by Smolarkiewicz (1984), applies the first-order upwind scheme in an iterative manner such that the subsequent iterations compensate for the implicit viscosity of the preceding steps. In that respect, it resembles similarity models where an estimate of the full unfiltered Navier–Stokes velocity entering the subgrid-scale stress tensor is obtained by an approximate inversion of the filtering operation, i.e. deconvolution (Domaradzki and Adams 2002; Smolarkiewicz and Szmelter 2005a). Presented developments employ the infinite gauge option of MPDATA using an edge-based data structure, which is second-order accurate, conservative, sign-preserving, and fully multidimensional free of directional splitting errors (Smolarkiewicz and Szmelter 2005b). The ILES properties of MPDATA based high Reynolds number solvers were widely documented in the context of stratified geophysical flows, e.g. (Smolarkiewicz et al. 2013, 2016) where MPDATA acts as a non-linear advector operator in the framework used by NFT solvers, c.f. (Szmelter and Smolarkiewicz 2010). More recent developments of MPDATA based schemes have included a finite volume formulation (Szmelter and Smolarkiewicz 2006) allowing the governing equations to be integrated over arbitrary shape cells beneficial for simulating turbulent flows over complex geometries, thus facilitating an extension of applications of the finite volume NFT-MPDATA solvers to engineering problems (Szmelter and Smolarkiewicz 2006; Smolarkiewicz and Szmelter 2008; Szmelter et al. 2019; Cocetta et al. 2021). The MPDATA capabilities have also been utilised in the effective conservative remapping for Arbitrary Lagrangian–Eulerian (ALE) schemes (Szmelter and Gillard 2020). In this paper we document the NFT-MPDATA solver for incompressible flows with its new extensions incorporating the implementation of the dynamic Smagorinsky model (Piomelli and Liu 1995) and the dynamic outlet convective boundary conditions (Orlanski 1976) suitable for jet problems. Furthermore, the reported study expands the portfolio of NFT-MPDATA engineering applications to jet flows.

In the presented comparative study of the NFT-MPDATA based LES and ILES approaches, closure for LES is achieved by employing two different SGS models, namely the Smagorinsky-like SGS model within the Spalart-Allmaras DES turbulence model (denoted as LES-SA) (Spalart et al. 1997) and the dynamic Smagorinsky model (Piomelli and Liu 1995) (denoted as LES-DSM). In ILES approaches, the self-regularisation property of MPDATA provides the necessary viscous dissipation implicitly, either by integrating the governing equations without explicit SGS modelling (denoted as ILES-NS) or through integrating the governing equations with the complete omission of the viscous terms (denoted as ILES-EU). The latter is employed in the limit of high Reynolds number flows.

The study focuses on simulating the turbulent free-jet in its axial region most relevant to engineering applications, namely the near- to intermediate- fields (Ball et al. 2012; Fellouah et al. 2009) (depicted in Fig. 1). Many experimental and theoretical studies have been devoted to the axial region beyond the intermediate-field (also commonly known as the far-field) to understand the fundamental behaviour of turbulence. However, the influence of upstream conditions on the heat, mass, and momentum transfer are often observed in the near- and intermediate-fields which are more important for engineering applications (Ball et al. 2012; Fellouah et al. 2009).

The paper is organised as follows. The governing equations including the SGS treatments and the employed numerical scheme are provided in Sect. 2. Section 3 describes the numerical set-up used to simulate the turbulent round free-jet. Results comparing different SGS treatments are presented and discussed in Sect. 4 and the work is concluded in Sect. 5.

2 Governing Equations and Numerical Methodology

2.1 Semi-implicit NFT-MPDATA for Incompressible Flows

The turbulent free-jets are simulated by seeking the solutions to the isothermal, homogeneous, incompressible Navier–Stokes equations. The set of LES grid-filtered governing equations assuming the Boussinesq hypothesis for SGS turbulence modelling is given by

$$\frac{{\partial \rho _{o} V_{I} }}{{\partial t}} + \nabla \cdot ({\mathbf{V}}\rho _{o} V_{I} ) = - \rho _{o} \frac{{\partial \varphi }}{{\partial x_{I} }} + \frac{\partial }{{\partial x_{J} }}\left\{ {\left( {\mu + \mu _{\tau } } \right)\left( {\frac{{\partial V_{I} }}{{\partial x_{J} }} + \frac{{\partial V_{J} }}{{\partial x_{I} }}} \right)} \right\}~,{\text{ }}$$

(1)

$$\begin{aligned} \nabla \cdot ({\mathbf {V}}\rho _o)&=0~, \end{aligned}$$

(2)

where $V_I$ denotes the velocity components in Cartesian coordinates $x_I$ with $I=1,2,3$; $\varphi = (p-p_\infty )/\rho _o$ is the pressure perturbation with respect to the static pressure $p_\infty$ that has been normalised against the constant reference density $\rho _o$; $(\mu + \mu _\tau )$ is the effective viscosity consisting of the molecular dynamic viscosity $\mu$, and the SGS viscosity $\mu _\tau$. Herein we adopt the repeated index summation convention and same notation like in Szmelter et al. (2019). Note that the tilde symbol commonly used to denote LES grid-filtered variables has been dropped for conciseness. The governing equations are integrated using the NFT framework. The detailed derivation of the NFT-MPDATA scheme for incompressible flows can be found in Sect. 3 of Szmelter et al. (2019). Similarly like in Szmelter et al. (2019), the NFT integration is applied to (1), at every node, giving

$$\begin{aligned} {V_I}^{n+1}=\widehat{V_I} -0.5{\delta }t\,\frac{\partial \varphi }{\partial x_I}^{n+1}~, \end{aligned}$$

(3)

where n indicates the time-level. MPDATA advects the auxiliary field $\widetilde{V_I}$ with ${\varvec{{\mathcal {V}}}}^{n+1/2}$ to yield the explicit part of the solutions $\widehat{V_I}$, as

$$\begin{aligned} \widehat{V_I} = MPDATA(\widetilde{V_I},\varvec{{\mathcal {V}}}^{n+1/2},\rho _o)~, \end{aligned}$$

(4)

where a division of the discrete integral of (1) by $\rho _o$ is taken into account in the MPDATA operator. The auxiliary fields $\widetilde{V_I}$ are given by

$$\begin{aligned} \widetilde{V_I} = V_I^n + 0.5{\delta }t\, \left( -\frac{\partial \varphi }{\partial x_I}^n + { \frac{2}{\rho _o}\frac{\partial }{\partial x_J} \Bigg \{(\mu + \mu _\tau ) \Bigg ( \frac{\partial V_I}{\partial x_J} + \frac{\partial V_J}{\partial x_I}} \Bigg ) \Bigg \}^n \right) ~, \end{aligned}$$

(5)

while the required advector $\varvec{{\mathcal {V}}}^{n+1/2}$ is an ${{\mathcal {O}}}(\delta t^2)$ estimate of $\rho _o\mathbf{V}$ at $t+0.5\delta t$, linearly extrapolated from $\varvec{{\mathcal {V}}}^{n-1}$ and $\varvec{{\mathcal {V}}}^n$. Solenoidality of the estimated $\varvec{{\mathcal {V}}}^{n+1/2}$ is ensured given that the velocity fields at the current and previous time-steps are also divergence-free.

A discretised in time form of mass continuity Eq. (2), for every node at $t^{n+1}$ can be written as

$$\begin{aligned} \frac{\partial \rho _o V^{n+1}_I}{\partial x_I} = 0~. \end{aligned}$$

(6)

A discrete Poisson boundary-value problem can be now formulated by applying the discrete divergence operator to both sides of (3) and enforcing the continuity constraint (6). The resulting equation for $\varphi ^{n+1}$ takes the form

$$\frac{\partial }{{\partial x_{I} }}\left( {\rho _{o} \left\{ {\widehat{{V_{I} }} - 0.5\delta t\frac{{\partial \varphi }}{{\partial x_{I} }}|^{{n + 1}} } \right\}} \right) = 0~.$$

(7)

The adopted numerical scheme is designed around a median-dual finite volume spatial discretisation with an edge-based formulation, providing flexibility to integrate partial differential equations over arbitrary shape cells. The spatial discretisation implemented here is based on a dual cell constructed around a node by joining centres of the edges connected to this node with the barycentres of polyhedra and faces of the primary mesh elements sharing these edges. Reference (Smolarkiewicz et al. 2013) provides details of such finite volume discretisation where the evaluation of all spatial derivative operators follows the principles of the Gauss divergence theorem. A collocated arrangement is used for all flow variables; this arrangement is computationally less intensive than a staggered mesh and allows for a more direct implementation of the NFT integrator and the associated numerical components. Furthermore, the presented numerical scheme does not require any form of artificial dissipation since MPDATA in combination with the elliptic solver mitigates the numerical instabilities that arise from the odd-even decoupling problem typically associated with a collocated arrangement.

The solution procedure takes the following steps. After formulating auxiliary variables according to (5), the advection operator MPDATA (Smolarkiewicz and Szmelter 2005b) is used to obtain explicit velocity fields $\widehat{{\mathbf {V}}}$. The infinite gauge MPDATA option is used in all presented here calculations with FCT-like limiting ensuring monotonocity of the scheme (Smolarkiewicz and Szmelter 2005b; Szmelter et al. 2019). A generalized conjugate-gradient residual Krylov-subspace elliptic solver (Smolarkiewicz and Szmelter 2011) is then employed to obtain the normalised pressure perturbation at the next time-step, $\varphi ^{n+1}$ from (7), subject to the Neumann boundary conditions for $\phi ^{n+1}$ implied by the Dirichlet boundary conditions to the velocity fields¹, ${\mathbf {V}}^{n+1}$. Once the pressure perturbation $\varphi ^{n+1}$ is obtained at the time-level $n+1$, the velocity fields ${\mathbf {V}}^{n+1}$ are updated from (3).

The resulting NFT algorithm is second-order-accurate in space and time, with the exception of the viscous term which is integrated explicitly to first-order accuracy in time - a common treatment to the viscous terms when employing the NFT framework (Smolarkiewicz and Charbonneau 2013; Szmelter et al. 2019). Further details on the semi-implicit NFT scheme as well as its associated numerical components such as the spatial discretisation, MPDATA and the Krylov solver can be found in Smolarkiewicz and Szmelter (2005b, 2011); Szmelter et al. (2019) and references therein. The quality of simulations benefits from an MPI parallelisation of the code and an auxiliary bespoke OpenMP parallelised code (Cocetta et al. 2021) providing the halo definition with a halo depth of one. The MeTis package (Karypis and Kumar 1998) provides the multilevel graph partitioning of the computational domain.

2.2 Subgrid-scale (SGS) treatments

2.2.1 Spalart–Allmaras DES Model

The Spalart-Allmaras DES turbulence model implemented in Szmelter et al. (2019) is adopted in this work. However, as there are no solid walls in presented simulations of the turbulent free-jet problem, only the LES-part of this DES turbulence model (i.e. the Smagorinsky-like SGS model (Spalart et al. 1997)) is activated. The turbulent viscosity required for closure is given by,

$$\begin{aligned} \mu _\tau =\rho _o{\hat{\nu }}f_{v1}~,~~\mathrm{with}~~f_{v1}=\frac{\chi ^3}{\chi ^3+c_{v1}^3}~, ~~\chi =\frac{{\hat{\nu }}}{\nu }~,~~\mathrm{and}~~\nu =\frac{\mu }{\rho _o}~, \end{aligned}$$

(8)

where the working variable ${\hat{\nu }}$ is transported with the following equation,

$$\begin{aligned} \frac{\partial {\hat{\nu }}}{\partial t} + {\mathbf {V}} \cdot \nabla {\hat{\nu }} = c_{b1} {\hat{S}} {\hat{\nu }} + \frac{1}{\sigma } \nabla \cdot [(\nu +{\hat{\nu }})\nabla {\hat{\nu }}] + \frac{c_{b2}}{\sigma } (\nabla {\hat{\nu }})^2 - c_{w1} f_w \Bigg (\frac{{\hat{\nu }}}{d}\Bigg )^2~. \end{aligned}$$

(9)

The term ${\hat{S}}$ in (9) is defined by

$$\begin{aligned} {\hat{S}}={\bar{S}}+\frac{{\hat{\nu }}}{\kappa ^2d^2}f_{v2}~,~~\mathrm{with}~~f_{v2}=1-\frac{\chi }{1+\chi f_{v1}}~, ~~\mathrm{and}~~{\bar{S}}=(2\Omega _{IJ}\Omega _{IJ})^{1/2}~, \end{aligned}$$

(10)

where $\Omega _{IJ}$ is the rotation tensor given by $\Omega _{IJ}=\frac{1}{2}\left( \frac{\partial {V}_I}{\partial x_J} -\frac{\partial {V}_J}{\partial x_I}\right)$. The remaining model functions in (9) are defined as

$$\begin{aligned} f_w=\gamma \left( \frac{1+c_{w3}^6}{\gamma ^6+c_{w3}^6}\right) ^{1/6}~,~~ \gamma =r+c_{w2}(R^6-R)~,~~R=\frac{{\hat{\nu }}}{{\hat{S}}\kappa ^2d^2}~, \end{aligned}$$

(11)

and all other model constants appearing in (8–11) are set to

$$\begin{aligned}&c_{b1}=0.1355~,~~\sigma =2/3~,~~c_{b2}=0.622~,~~\kappa =0.41~,\nonumber \\&c_{w1}=c_{b1}/\kappa ^2+(1+c_{b2})/\sigma ~,~~c_{w2}=0.3~,~~c_{w3}=2.0~,~~c_{v1}=7.1~. \end{aligned}$$

(12)

To activate the LES-part only, the characteristics length scale d in (9) has been set to $d=C_{DES}\Delta _g$ throughout the entire computational domain where $C_{DES}$ is a model constant and $\Delta _g$ is the cut-off length defined by the grid-filter formally defined as the cubic root of the cell volume, $\Delta _{g} = \sqrt[3] {{\mathcal{V}}_{{\mathcal{P}}} }$. $C_{{DES}}=0.65$ is set for all presented cases based on other numerical studies of turbulent jets (Kapadia et al. 2003; Lyubimov 2012)² and past experience with this turbulence model (Szmelter et al. 2019). The solution of (9) is detailed in Szmelter et al. (2019) and also uses the NFT integration.

2.2.2 Dynamic Smagorinsky Model (DSM)

A commonly applied SGS model for turbulent free-jet simulations is the dynamic Smagorinsky model (DSM) (Bogey and Bailly 2006; Kim and Choi 2009; Ranga Dinesh et al. 2010; Salkhordeh et al. 2019; Zhang and Chin 2020). The DSM is based on the standard Smagorinsky model which can be given by

$$\begin{aligned} \mu _\tau = \rho _o C (\Delta _g)^2 |S |~, \end{aligned}$$

(13)

where $|S |$ is the magnitude of the filtered strain rate tensor

$$\begin{aligned} |S |= (2 {S_{IJ}}{S_{IJ}})^{1/2} ~,~~\mathrm{with}~~ {S_{IJ}}=\frac{1}{2}\left( \frac{\partial {V}_I}{\partial x_J} +\frac{\partial {V}_J}{\partial x_I}\right) ~, \end{aligned}$$

(14)

and $C = {C_{Smag}}^2$ where $C_{Smag}$ is the Smagorinsky constant in the classical Smagorinsky model. The dynamic formulation is then introduced to (13) by computing the required square of the Smagorinsky constant C locally at each time step rather than prescribing it a priori, allowing it to dynamically adjust to different flow regimes. This is particularly useful for turbulent free-jets considering the differences in the flow physics between the potential core in the near-field and the fully turbulent intermediate-field. Moreover, sensitivity studies of $C_{Smag}$ for the turbulent free-jet performed by several authors (Uzun et al. 2003; Ilyushin and Krasinsky 2006; Pinho and Muniz 2021) indicate that there is no consensus about the preferred value for $C_{Smag}$. The current work implements the DSM for the first time in the context of NFT-MPDATA class of schemes. It adopts the localised DSM proposed by Piomelli and Liu (1995) in which C in (13) is computed using

$$\begin{aligned} C = -\frac{1}{2}\frac{({\mathcal {L}}_{IJ}-2\widehat{\widehat{C^* \beta _{IJ}}})\alpha _{IJ}}{\alpha _{mn}\alpha _{mn}}~, \end{aligned}$$

(15)

where

$$\begin{aligned} {\mathcal {L}}_{IJ} = \widehat{\widehat{{V_I}{V_J}}} - \widehat{\widehat{{V_I}}}\widehat{\widehat{{V_J}}} ~,~~ \alpha _{IJ} = \Delta _{t}^2 |\widehat{{\widehat{S}}}|\widehat{\widehat{S_{IJ}}} ~,~~\mathrm{and}~~ \beta _{IJ} = \Delta _{g}^2 |S |S_{IJ}~. \end{aligned}$$

(16)

The double caret symbol indicates test-filtering operation in (15) as well as (16) and $\Delta _{t}$ is the coarser sub-test filter’s cut-off length. Here, we implemented the test-filtering operator described in Park and Mahesh (2007). The test-filtering operation for computing an arbitary test-filtered variable $\widehat{\widehat{{\phi _P}}}$ at node P is defined by

$$\begin{aligned} \widehat{\widehat{{\phi _P}}} = \frac{1}{N_{e}} \sum ^{N_{e}} \frac{1}{2}(\phi _P + \phi _Q)~, \end{aligned}$$

(17)

where $\phi _P$ and $\phi _Q$ are the arbitary grid-filtered variables at nodes P and Q respectively and Q is the node connected to node P by an edge. Furthermore, $N_e$ is the number of edges connected to node P. For the estimated value of the square of the Smagorinsky constant $C^*$ in (15), the current work follows the first suggestion by Piomelli and Liu (1995) whereby the square of the Smagorinsky constant from the previous time-step is taken as the estimated square of the Smagorinsky constant, i.e. $C^*=C^{n-1}$. Finally, like in Pope (2000) and Sagaut (2002), to avoid any form of numerical instabilities arising from the dynamic computations of C, C has also been clipped such that the locally computed value $0 \le C \le {C_{Smag,max}}^2$ with $C_{Smag,max} = 0.18$. This is equivalent of setting $C_{Smag}=0.18$ in the classical Smagorinsky model for the upper limit. These limits differ between implementations e.g. (Pinho and Muniz 2021) and (Sagaut 2002).

2.2.3 Implicit Large Eddy Simulations

Alternatively, the contribution of the necessary SGS dissipation or even the overall viscous effects can be implicitly delegated to the numerical scheme itself rather than explicitly modelled. In the present work, the MPDATA, through its self-regularisation property, is used to implicitly provide the SGS effects (ILES-NS) or the overall viscous effects (ILES-EU). In particular, ILES-NS is achieved simply by setting $\mu _\tau =0$ when computing the viscous term in (5). This effectively leads to a set of governing equations akin to the unfiltered incompressible Navier–Stokes equations. On the other hand, in the limit of high Reynolds number flows, ILES-EU is achieved by the complete omission of the viscous terms in (5) which subsequently reduces (1) to a set of incompressible Euler equations. In the absence of either the SGS term or the overall viscous terms, the filtering process of the low order upwinding in MPDATA is reversed by the self-regularisation property within the iterative apparatus of MPDATA, effectively prompting the leading-order truncation terms to behave as a higher-order filter within the limit of grid resolution (Szmelter et al. 2019). The suitability of MPDATA in the context of ILES is supported not only by multiple successful applications (Smolarkiewicz et al. 2013, 2016) but also by theoretical considerations. Notably, in Margolin et al. (2006) modified equation analysis showed that the truncation terms of MPDATA contain nonlinear terms comparable to the self-similar Clark model and dissipative stress terms akin to the tensor version of the classical Smagorinsky model.

3 Problem Formulation

3.1 Physical Characterisation of Free-jet flows

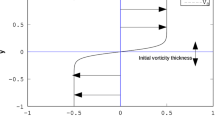
To facilitate further discussion, Fig. 1 depicts the generic regions and the typical mean axial velocity profile $<W(r,z)>$ exhibited by a free-jet with a jet velocity $W_0$ issued into a parallel co-flowing stream of velocity $w_\text{cf}$, c.f. (Ball et al. 2012).

Fig. 1

Schematic of a free-jet characterisation in a parallel co-flowing stream

Here, the free-jet has been characterised along the axial-axis corresponding to the direction $x_3$ and the radial-axis corresponding to the radial distance evaluated from the centreline, $r = \sqrt{x_1^2 + x_2^2}$. It is also convenient for comparisons with the literature to define z as the axial distance measured from the inlet plane of the jet $L_z$, Fig. 1. The evolution of the jet in the axial direction can be categorised into the near-field, the intermediate-field, and the far-field while the flow field in the radial direction is composed of three distinctive concentric layers that can be identified as: the centreline layer, the shear layer, and the outer layer. As the jet is issued into the near-field, the velocity gradient between the jet and the surrounding fluid generates an unstable thin shear layer. The flow instabilities form vortical structures that eventually evolve, roll up and/or pair up as the jet propagates further downstream to the intermediate- and far-fields (Ball et al. 2012). This leads to the entrainment of ambient fluid into the free-jet that subsequently thickens the shear layer, or in other words, spreads the jet. As the shear layer thickens, the time-averaged radial flow profile in the centreline layer of the jet begins to lose its initial shape at the nozzle exit. It eventually disappears when the shear layers from all sides merge (Ball et al. 2012). The point at which the time-averaged centreline velocity $<W_c(z)>$ is no longer equal to the nozzle value is known as the end of the potential core of the jet and the start of the intermediate field. In the intermediate-field, the jet will further spread and decay whilst transitioning into a fully developed self-similar state at the far-field. Once the jet has developed into the far-field, it continues to decay to the point where its initial momentum is completely lost to the dissipative viscous action (Ball et al. 2012).

3.2 Problem Domain

In this study, the turbulent free-jet simulations are computed in a cuboidal domain $[-6,6] \times [-6,6] \times [0,30]$ m$^{3}$. The use of a cuboidal computational domain is also commonly seen in other simulations of turbulent round free-jets (Bogey and Bailly 2006; Taub et al. 2013; Gohil et al. 2014; Ghaisas et al. 2015). The jet is discharged from a round inlet with reference diameter $D = 1.00$ m and the centre positioned at $[x_1,x_2,x_3] = [0,0,30]$ m and propagates out of the computational domain at the boundary plane located at $x_3 = 0$ m. The axial length $L_z$ is selected to be sufficiently long to enable the jet transition into its intermediate-field and to develop radial profiles that are nearly close to their self-similar states. It can also accommodate the absorber used as part of the outlet boundary condition strategy. Details of their implementation will be provided in Sect. 3.3. It should be stressed that computations taking into account the long axial range processed in experiments such as Panchapakesan and Lumley (1993) and Hussein et al. (1994) to attain true self-similar profiles would be beyond the allocated computing resources available for the present work as more points would be needed in the axial direction. Additionally the lateral lengths of the domain would also need extensions to allow further radial dispersion of the jet. Moreover, numerical studies (Boersma et al. 1998; Taub et al. 2013; Gohil et al. 2014; Ghaisas et al. 2015; Loppi et al. 2018; Zhang and Chin 2020) showed that the jet profiles in the intermediate-field closely resemble the self-similar states reported in experiments (i.e. (Hussein et al. 1994; Panchapakesan and Lumley 1993)).

This study focuses on simulations performed on Cartesian meshes; however, to demonstrate the flexibility of the NFT-MPDATA scheme initial simulations using different mesh topologies for the LES-SA option are also included. Three different prismatic meshes have been tested based on: a uniformly distributed 2D Cartesian mesh (MT-CART-UF), a uniform triangular-based mesh (MT-PRIZ-UF), and a triangular-based mesh with coarsening towards the lateral boundaries (MT-PRIZ-CS). All current three-dimensional meshes are generated from two-dimensional bases extruded in the axial direction to the required length. Cross-sections of generated base meshes are shown in Fig. 2.

Fig. 2

Two-dimensional base of the employed meshes

The Cartesian mesh is constructed using a spacing of $dx_1 = dx_2 = 0.100$ m. The triangular meshes use the same background size discretisation. For the mesh MT-PRIZ-CS, the region between $x_1=x_2=\pm 4.00$ m and the lateral boundary planes has the mesh resolution coarsened to be approximately $dx_1=dx_2=0.220$ to 0.250 m near the lateral boundaries. The two-dimensional base Cartesian and triangular meshes are then extended with the uniform spacing of $dx_3 = 0.125$ m which is similar to the axial mesh resolution used for the intermediate and far-field in Salkhordeh et al. (2019). Preliminary simulations using coarser meshes did not allow for an adequate shear layer development and did not capture the linear centreline velocity decay characteristics in the intermediate-field. The time-step has been set to $dt = 1.25 \times 10^{-2}$ s in all simulations and corresponds to a typical maximum CFL number of 0.4 for all meshes. The turbulent free-jets are simulated for a total time of $t = 1500$ s in all cases.

3.3 Boundary Conditions

Numerical and experimental studies have shown that the turbulent free-jets are sensitive to the mean velocity profile and the background disturbance at the inlet (Boersma et al. 1998; Mi et al. 2001; Xu and Antonia 2002; Kim and Choi 2009). Different mean velocity profiles could change the jet characteristics such as the centreline velocity decay constant (Mi et al. 2001; Xu and Antonia 2002). The most accurate way of capturing the inlet profile is to include the nozzle geometry, such as the long pipe or a contracting duct, as part of the computation (Salkhordeh et al. 2019; Zhang and Chin 2020). This procedure would certainly allow to capture the influence of boundary layers forming on the nozzle wall and the flow fluctuation accurately but at a higher computational cost. Therefore, the presented results follow another approach adopted for turbulent free-jets which applies a suitable mean velocity profile at the inlet and introduces random noise profiles. These profiles differ slightly depending on the literature source (Ranga Dinesh et al. 2010; Taub et al. 2013; Gohil et al. 2014; Ghaisas et al. 2015).

On the inlet plane (i.e. boundary plane at $x_3=30$ m), a uniformly distributed jet velocity of $W_0 = -1.00$ $\text{ms}^{-1}$ (with respect to the $x_3$-axis depicted in Fig. 1, ${\mathbf {V}}=[0,0,-1]$ $\text{ms}^{-1}$) is applied in the jet inlet region where $r \le 0.5$ m. It mimics the top-hat velocity profile produced by a smooth contracting nozzle typically seen in experiments such as Panchapakesan and Lumley (1993), Hussein et al. (1994), Mi et al. (2001), Shiri et al. (2008). The typical hyperbolic tangent profile used in Bogey and Bailly (2006), Gohil et al. (2014) and Loppi et al. (2018) that accounts for and also controls the amount of the momentum thickness was not implemented in the presented computations since the grid-sensitivity study of the inlet presented by Kim and Choi (2009) suggested that the mesh resolution near the inlet of the current set-up is certainly not fine enough to capture the effects of the momentum thickness. However, the prescribed mean inlet profile is still representative of the inlet profile observed in the experiment of Panchapakesan and Lumley (1993) in which the boundary-layer thickness of the top-hat velocity profile was minimised by discharging the jet through a nozzle with a very large contraction ratio. To trigger earlier transition into the intermediate-field, the jet is perturbed by normally distributed random noises that are continuously added at the round jet inlet and the mesh nodes located at a small distance perpendicularly away from the inlet. This is done by superimposing the velocity fields at the required mesh nodes with random velocity perturbation in the following manner

$$\begin{aligned} V_{I}^n= V_{I,\text {(No Noise)}}^n + A_I \epsilon _{ran}~, \end{aligned}$$

(18)

where $A_I$ controls the amount of added noise and $\epsilon _{ran}$ is a standard normally distributed random number. Herein, $A_3$ has been set to 0.01 $\text{ms}^{-1}$ in the axial direction and $A_1 = A_2 = 0.005$ $\text{ms}^{-1}$ in the tangential directions for all presented cases. Transverse turbulence intensity at the inlet was also observed in some experiments, (e.g. (Fellouah et al. 2009)) and the tangential noise was found to better promote the development of the shear layers in the near-field region. Furthermore, a weak co-flow of $w_{cf}=-0.04$ $\text{ms}^{-1}$ parallel to the $x_3$-axis, i.e. ${\mathbf {V}}_{cf} =[0,0,-0.04]$ $\text{ms}^{-1}$, is also prescribed as the boundary velocity on the remaining parts of the inlet plane where $x_3=30$ m and $r > 0.5$ m. The application of a weak co-flow has been seen in numerical studies (Pinho and Muniz 2021; Ghaisas et al. 2015; Naqavi et al. 2018; Margnat et al. 2018) as it is needed to provide entrainment fluid for the jet and to suppress any large scale vortices near the outlet. Free-slip boundary conditions are imposed on all four lateral boundary planes.

The outflow specification include the use of an absorber which artificially attenuates vortical structures near the boundary and the Convective Boundary Conditions (CBC) (Orlanski 1976) to propagate the weakened jet out of the computational domain at the boundary plane $x_3 = 0$ m. Implementation of the absorber is achieved by adding an extra term to the right-hand side of the momentum Eq. (1),

$$\begin{aligned} {\mathcal {F}}_I = - \alpha (x_3)\rho _0 (V_I- V^T_{I})~, \end{aligned}$$

(19)

where $\alpha (x_3)$ is a modulation function that activates the absorber in the proximity of the outlet boundary plane. The modulation function $\alpha (x_3)$ is chosen to exponentially attenuate a given flow variable $V_I$ into their target form $V^T_{I}$ (described later) such that,

$$\begin{aligned} \frac{d \rho _0 V_I}{dt} = -\alpha (x_3) \rho _0 V_I~, \end{aligned}$$

(20)

with

$$\begin{aligned} \alpha (x_3) = \frac{1}{\tau } \frac{l_1-x_3}{l_1-l_0}~, \end{aligned}$$

(21)

where $\tau$ controls the absorber’s strength. The absorber attenuates wave from the spatial position $x_3 = l_1$ to the boundary at $x_3 = l_0 = 0$ m. Note that $l_1 > l_0$ given that the jet is propagating from the positive $x_3$ to the negative $x_3$ direction, i.e. $W_0 < 0~\text{ms}^{-1}$. In the numerical implementation, the NFT integrator (3) and the auxiliary field (5) have been augmented with (19) yielding the following respectively:

$$\begin{aligned} {V_I}^{n+1} = \widehat{V_I} - 0.5\delta t \frac{\partial \varphi }{\partial x_I}^{n+1} + \frac{0.5\delta t}{\rho _o} {{\mathcal {F}}_I}^{n+1}~, \end{aligned}$$

(22)

and

$$\begin{aligned} \widetilde{V_I} = V_I^n + 0.5{\delta }t\, \left( -\frac{\partial \varphi }{\partial x_I}^n + { \frac{2}{\rho _o}\frac{\partial }{\partial x_J} \Bigg \{(\mu + \mu _\tau ) \Bigg ( \frac{\partial V_I}{\partial x_J} + \frac{\partial V_J}{\partial x_I}} \Bigg ) \Bigg \}^n \right) + \frac{0.5\delta t}{\rho _o} {{\mathcal {F}}_I}^{n} ~, \end{aligned}$$

(23)

where ${\mathcal {F}}^{n+1}_I$ is estimated using linear extrapolation from fields evaluated at previous time-levels. This form of absorbing boundary conditions have been successfully applied in the context of external flows (Szmelter et al. 2019; Cocetta et al. 2021) where the absorber targeted free-stream conditions. In the current application, the absorber has been designed to attenuate towards the spatially³ varying target solution prescribed for the axial velocity component and as 0 $\text{ms}^{-1}$ for the tangential velocity components. For consistency with CBC described below, we choose $\mathbf {V^T}= [0,0,W_{con}]$ where $W_{con}$ is the convective velocity acting in the normal direction to the outlet plane (i.e. $x_3$-axis).

The CBC provides values of $V_I$ at the boundary nodes on the outlet plane $\Gamma _{\text {out}}$ and takes the form of the 1D convective equation (Orlanski 1976),

$$\begin{aligned} \frac{\partial V_I}{\partial t} + W_{con} \frac{\partial V_I}{\partial x_3} = 0 \; \; \; \text {on } \; \Gamma _{\text {out}}~, \end{aligned}$$

(24)

where the spatial derivative is evaluated in the normal direction to the outlet. The solution of (24) is evaluated based on the values of $V_I$ from the preceeding time-step. The outlet boundary values are computed for each velocity components, $I=1,2,3$. $V_1$ and $V_2$ are not necessary completely attenuated to the target form $V^T_1 = V^T_2 = 0$ $\text{ms}^{-1}$ in the case where a weak absorber is applied (i.e. $\tau \ne 1$), therefore, on the boundary $\Gamma _{\text {out}}$, values of $V_1$ and $V_2$ are updated with (24). The key aspect when implementing the CBC is the choice of convective velocity, $W_{con}$, which should be representative of the velocity at the outlet (Gresho 1991). The simplest option is to prescribe the mean normal velocity expected at the outlet (Gresho 1991), however Ol’shanskii and Staroverov (2000) postulated that upstream influence can be better suppressed if the specified convective velocity has a spatial distribution representative of the flow solution; in their case, they applied a Poiseuille profile for the convective velocity for channel flow simulations. For turbulent round free-jets, the most natural choice of convective velocity distribution is a Gaussian profile as it is representative of a self-similar mean axial velocity profile in a fully developed turbulent round free-jet (Panchapakesan and Lumley 1993; Hussein et al. 1994). More importantly, the Gaussian profile allows advection to occur at a higher speed in the core layers (centreline layer and shear layer) and lower speed in the outer layer. This is a better representation of the local flow acceleration compared to assuming a constant uniform velocity (Walchshofer et al. 2011). Similarly to Dai et al. (1994), the following Gaussian profile for the convective velocity has been applied,

$$\begin{aligned} W_{con}(r) = (w_{max} - w_{cf}) \exp { \left\{ - \left( \frac{r}{r_g} \right) ^2 \right\} } + w_{cf}~, \end{aligned}$$

(25)

where $r_g$ controls the spread of the Gaussian profile, and $w_{max}$ is the maximum velocity component $V_3$. $w_{max}$ is prescribed at the centreline at the outlet (i.e. the maximum amplitude of the Gaussian profile), is tunned for a problem at hand, and usually is based on the centreline velocity decay characteristics of the simulated jet. Where applicable, the selection of $w_{max}$ also follows the advice of Walchshofer et al. (2011) in which a narrower Gaussian profile is applied to avoid unphysical spreading and stability issues. The spreading term $r_g$ is selected such that the overall Gaussian velocity profile satisfies the global continuity equation when integrated over the outlet plane with the specified maximum amplitude of the Gaussian velocity $w_{max}$ and the specified co-flow $w_{cf}$ at the inlet. The final computed mass flow rate at the outlet is also checked at every single time step to ensure that the global continuity is conserved.

The parameters set for the outflow boundary strategy for all presented simulations are listed in Table 1.

Table 1 Parameters set for the outflow strategy

All cases use the same setting to achieve a moderately weak absorber where the flow is allowed to gradually attenuate to the target over a 6 m distance (i.e. $l_1 - l_0 = 6$ m in (21)). The current outflow boundary strategy is similar to those in Margnat et al. (2018); Zhao and Wang (2018) but there are several differences including the modulation function $\alpha$ in (19) and its overall strength. Here, a moderately weak absorber is preferred to minimise the upstream influences and to prevent any potential reflection on the absorber interface (where $x_3=l_1$) due to the sudden changes in the flow field. Systematic studies on coarser meshes found that co-flow smaller than 4% of the jet velocity was insufficient to suppress the vortical structures downstream of the jet even with the applied absorber. It was observed that the computed jet will attempt to draw in fluid from outside of the domain through the outlet and induce axial velocities with opposite signs to the prescribed jet velocity near the outflow plane. Furthermore, setting a small positive value of co-flow to maintain identical signs between the flow field and the convective velocity in the outer layer region of the jet on the outlet plane is numerically beneficial since the CBC is a form of the advection equation. To further minimise the effect of the absorber in the LES-DSM approach, the DSM has been deactivated in the absorber region as its activation in this region produced centreline velocity decay characteristics akin to lower Reynolds number jets in the upstream region of the absorber. Such unphysical centreline velocity decay characteristics would most likely be caused by the DSM responding to the weakened, less turbulent jet resulting from the artificial viscous forcing.

4 Results

4.1 Preamble

The presented numerical results are primarily validated against experimental data of Panchapakesan and Lumley (1993) and Hussein et al. (1994) through comparing the centreline velocity decay, the spreading behaviour, and the self-similar profiles obtained in the intermediate-field of the jet. For a round jet issued into a quiescent environment, self-similarity principles and momentum balance from theoretical derivations imply that the time-averaged centreline axial velocity $<W_c(z)>$ (defined in Fig. 1) will decay inversely proportional with the axial distance, i.e. $<W_c(z)>\sim (z - z_0)^{-1}$. The jet will spread linearly with the axial distance, $dr_{0.5}/dz = \text {constant}$ (Pope 2000; Hussein et al. 1994). $z = 30 - x_3$ m based on the current computational domain and $z_0$ is known as the virtual origin to be determined from the centreline velocity decay expression (shown later in (26) (Hussein et al. 1994)); angle brackets $<.>$ denote time-averaging. The current work adopts the same self-similar coordinates convention $\eta = r/(z-z_0)$ as Hussein et al. (1994), where the characteristic lengthscale that normalises the radial coordinates is $(z-z_0)$. The adoption of the self-similar coordinates $\eta$ is also seen in several numerical studies (Boersma et al. 1998; Gohil et al. 2014; Loppi et al. 2018; Salkhordeh et al. 2019; Zhang and Chin 2020). A key difference between the current numerical set-up and the experiments is that we assume that the jet is discharged into a weak parallel co-flowing stream. Herein, the weak co-flow is chosen by selecting the excess centreline mean velocity $(W_c(z) - w_{cf})$ as the characteristic velocity scale.

The presented results are based on solutions collected from several probed points and between $t = 250$ to 1500 s when the jet is in quasi-steady state. The probed points used to establish the centreline velocity decay characteristics include all points on the centreline ($x_1 = x_2 = 0$ m). To assess the radial variation of the flow field probe points are selected at every increment of $dx_3$ = 1.00 m, and at every $90^\circ$ degrees. Points located in the absorber region are excluded from post-processing.

4.2 Comparison of Different SGS Treatments

The results of the LES-SA, LES-DSM, ILES-NS, and ILES-EU approaches computed using the Cartesian mesh (MT-CART-UF) are presented here. To facilitate comparisons with experiment in Panchapakesan and Lumley (1993), LES-SA, LES-DSM, and ILES-NS of free jets are performed at $Re = 1.1 \times 10^4$. In addition to the global jet behaviour and self-similar profiles, trends of centreline velocity are evaluated through the energy spectra for all four approaches.

4.2.1 Global Characteristics

The centreline velocity decay characteristics and the evolution of the half-width of the jet obtained from all four approaches are first compared against data available in the literature. The expression for the centreline velocity decay characteristics takes the following form,

$$\begin{aligned} \frac{W_0 - w_{cf}}{<W_c(z)>- w_{cf}} = \frac{1}{k_u} \left (\frac{z}{D}- \frac{z_0}{D}\right )~, \end{aligned}$$

(26)

where the centreline velocity decay rate $k_u$ and the virtual origin $z_0$ are found through linear curve fitting. Zhang and Chin (2020) carried out a systematic LES study of the influence of co-flow of up to 33% of the prescribed jet velocity⁴ on single-phase jets issued from a pipe (parabolic profile) and demonstrated that the decay rate of the centreline velocity only varies slightly between the tested co-flows ($1/k_u = 0.147$ to $1/k_u = 0.143$). Based on this study, it is expected that the free-jet discharged into a weak co-flow will yield a $k_u$ within the range established in experiments for jets issued from contraction nozzle, (i.e. Panchapakesan and Lumley 1993; Hussein et al. 1994; Abdel-Rahman et al. 1997; Shiri et al. 2008; Quinn 2006). However, a high amount of co-flow will still affect the behaviour of the jet, such as the self-similar profiles. The results in Zhang and Chin (2020) showed that increasing the amount of co-flow will shift the maximum peak of the axial velocity fluctuations towards the centreline and enhance the overall magnitude of the peak axial velocity fluctuation. Thus, the application of a weak co-flow minimises these effects.

For the spreading behaviour, the spreading rate is commonly measured using the half-width of the jet, $r_{0.5}$. The full width of the jet is harder to quantify considering the turbulent to non-turbulent interface between the jet and the surrounding fluid. The half-width of the jet at a given axial distance, $r_{0.5}$, is defined as the radial position where the local axial velocity is half of the local centreline velocity at the given axial position, i.e. $<W(r_{0.5 },z)>= 0.5<W_c(z)>$, visualised in Fig. 1, while the spreading rate $k_r$ is obtained by measuring the linear gradient in the intermediate-field of the jet,

$$\begin{aligned} k_r = \frac{dr_{0.5}}{dz}. \end{aligned}$$

(27)

The centreline velocity decay characteristics and the evolution of the jet’s half-width are shown in Figs. 3a and b respectively. Both figures are accompanied by the empirical experimental data fit reported in Panchapakesan and Lumley (1993). Following Panchapakesan and Lumley (1993), the virtual origin for experimental centreline velocity decay characteristics is assumed at the origin. A similar assumption is made for the experimental fit of the evolution of the half-width in Fig. 3b. The key parameters of the centreline velocity decay characteristics in (26) and the spreading rate $k_r$ computed from (27) are listed in Table 2 which also compares the presented results with other similar free-jet studies available in the literature⁵. These only include turbulent round free-jets discharged through a contracting nozzle (i.e. top-hat velocity profile at the efflux) at Reynolds number equal and above $Re = 1.0 \times 10^4$.

Fig. 3

Global jet’s characteristics for $Re = 1.1 \times 10^{4}$ and ILES-EU

Table 2 Comparison of centreline velocity decay characteristics and spreading rates among LES, ILES and the data available in the literature

The key comparison is conducted in the intermediate-field of the jet represented by the inclined lines in both Figs. 3a and b where the jet begins to become fully turbulent and starts to develop into its self-similar state in the far-field. For all presented numerical results, the centreline velocity decay constant $k_u$ shown in Fig. 3a and the spreading rate $k_r$ displayed in Fig. 3b are found to be within the consensus range established in the literature. In particular, the results yield the centreline velocity decay constant $k_u$ that lies within the range of $k_u = 5.80$ and 6.10, while the spreading rate $k_r$ lies within the range of $k_r=0.093$ and 0.102. The comparison of $k_u$ and $k_r$ for $\text{Re} = 1.1 \times 10^4$ results against free-jets’ data at higher Reynolds number can be considered valid given that these two quantities have been experimentally observed to tend towards asymptotic values with increasing Reynolds number beyond $\text{Re} = 1.0 \times 10^4$ (Mi et al. 2013). Dimotakis (2000) referred to this critical Reynolds number as the mixing transition Reynolds number and stated that it falls between $\text{Re} \in [1.0 \times 10^4, 2.0 \times 10^4]$ whereas Mi et al. (2013) identified it to be around $\text{Re} = 1.0 \times 10^4$ for turbulent round free-jets. This also allows $k_u$ and $k_r$ obtained with ILES-EU to be compared against the numerical results evaluated at $\text{Re} = 1.1 \times 10^4$ in Table 2, since ILES-EU is a representation of high Reynolds number flows. The values of $k_u$ and $k_r$ obtained with ILES-EU are also found to be in good agreement with the other numerical results and the validation data. Slight variations of $k_u$ and $k_r$ between the numerical results and validation data in Table 2 could be attributed to the small variation within the transition between the near-field and intermediate-field. These values were also found to vary due to post-processing of the results over different time-periods. Salkhordeh et al. (2019) highlighted that different curve-fitting techniques and even the enclosure size for the jet can also influence the computation of the centreline velocity decay constant, therefore comparisons are traditionally conducted against the consensus range of $k_u$ and $k_r$.

More pronounced differences between the results can be observed in the length of the horizontal straight line in Fig. 3a, related to the potential core length and representing the near-field development of the jets. Similarly to Bogey and Bailly (2006), herein the potential core length $L_{PC}$ is formally defined at the normalised axial position where the excess mean centreline velocity ratio is 0.95, i.e.

$$\begin{aligned} \frac{<W_c(z/D=L_{PC})>- w_{cf}}{W_0 - w_{cf}} = 0.95~. \end{aligned}$$

(28)

The excess mean centreline velocity ratio on the left-hand side of (28) is the inverse of the left-hand side function of the centreline velocity decay expression in (26). This allows $L_{PC}$ to be obtained from directly reading the corresponding z/D for $(W_0 - w_{cf})/(<W_c(z/D=L_{PC})>- w_{cf}) = 1/0.95$ in Fig. 3a, although in practice $L_{PC}$ is computed by linearly interpolating the excess mean centreline velocity ratio between the two nearest points. $z/D = L_{PC}$ also represents the point of transition between the near and intermediate-fields measured from the inlet as well as the length of the near-field development region. The computed $L_{PC}$ is included in Table 2. For ILES-EU, ILES-NS, and LES-DSM, values of $L_{PC}$ are consistent with observations in the literature that near-field is usually expected to fall within the range of $0 \le z/D \le 7$ (Ball et al. 2012). Subsequently, the centreline velocity decay characteristics in the intermediate-field obtained with these three approaches compare better with the experimental data (Panchapakesan and Lumley 1993) than results obtained with LES-SA, as seen in Fig. 3a. The latter yields a longer potential core length of $L_{PC}=9.15$ which is outside the expected range stated in Ball et al. (2012). Additionally, random noises were added to the inlet to promote transition into the intermediate-field. These indicate that LES-SA could not predict the near-field development region as well as LES-DSM and ILES-NS. It is also anticipated that the potential core length will decrease slightly with increasing Reynolds number (Fellouah et al. 2009; Bogey and Bailly 2006). This was indeed observed when comparing the ILES-EU results that represented the higher Reynolds number jets and the results obtained with ILES-NS performed at $Re = 1.1 \times 10^4$. The small difference in the potential core length between ILES-EU and ILES-NS is also consistent with literature findings for higher Reynolds number jets (Fellouah et al. 2009; Bogey and Bailly 2006), for instance, the LES data in Bogey and Bailly (2006) showed that there is only a small difference in potential core length between a $Re = 1.0 \times 10^4$ jet and a $Re = 4.0 \times 10^5$ jet whereas there is a larger difference between the potential core length of jets at $Re = 1.7 \times 10^3$ and $Re = 2.5 \times 10^3$.

4.2.2 Spectral Analysis

Further insights into the centreline velocity decay could be observed through the trends exhibited by the energy spectra. The presented analysis follows closely that performed by Fellouah and Pollard (2009) whereby one-dimensional energy spectra based on the autocorrelation function of axial velocity fluctuations $E_{11}$ at various axial positions on the centreline are computed to reproduce trends observed experimentally in Fellouah and Pollard (2009). Following Fellouah and Pollard (2009), the one-dimensional energy spectra $E_{11}(\kappa _1)$ is taken as the absolute square of the Fourier transform of the time-series of the probed data $H(\kappa _1)$, i.e. $E_{11}(\kappa _1) = |H(\kappa _1)|^2$ where $\kappa _1$ is the wavenumber $\kappa _1= 2\pi f/<W(r,z)>$ and f is the sampling frequency. Considering that the probed data is discrete and finite, the time-series data has also been tapered with the Hanning window prior to the Fast Fourier Transformation with the aim of reducing the spectra lobe leakage (Bendat and Piersol 2010). Lastly, similarly to Fellouah and Pollard (2009), a running average filter is applied to further reduce noise within the computed energy spectra. The dimensional energy spectra $E_{11}(\kappa _1)$ are presented instead of their conventional non-dimensional form (Pope 2000) since quantifying viscosity needed to compute the Kolmogorov scales for ILES-EU is non-trivial. One-dimensional energy spectra $E_{11}$ plotted against the wavenumbers at various axial positions on the centreline for the LES and ILES cases are displayed in Figs. 4 and 5 respectively.

Fig. 4

Energy spectra $E_{11}$ at various centreline points ($r = 0~\text{m}$) for LES cases

Fig. 5

Energy spectra $E_{11}$ at various centreline points ($r = 0~\text{m}$) for ILES cases

Figure 4 shows that the LES-DSM approach (right panel) produces spectra of higher values at the dominant wavenumber than the LES-SA approach (left panel). This indicates that LES-SA could not evolve the jet in its near-field region as quickly as LES-DSM which is consistent with the centreline velocity decay curves obtained with the two approaches; see Fig. 3a. Notably, similar energy spectra were obtained from LES-DSM (Fig. 4b) and ILES-NS (Fig. 5a). The discernible peaks at $z = 5.00$ m for both simulations have a comparable magnitude of $E_{11}$ and occur at very close values of wavenumber $\kappa _1$. This confirms that MPDATA can provide a similar SGS effect to that explicitly applied by the dynamic Smagorinsky model in the potential core, owing to the fact that the implicit SGS tensors in MPDATA take a form consisting of terms akin to the Smagorinsky and Clark SGS model (Margolin et al. 2006). Similarly to other computations at $\text{Re}=1.1 \times 10^4$, the ILES-EU approach also captures the discernible peak in the energy spectra at $z = 5.00$ m. Overall, the ILES-EU’s energy spectra are observed to be more energetic than those obtained for other cases, including their values at the lower wavenumbers. This is most likely due to ILES-EU transitioning the jet into its intermediate-field earlier than the other approaches.

Figures 4 and 5 also show that once the jet has become fully turbulent in the intermediate-field (i.e. at $z \ge 10$ m for LES-SA and $z \ge 8$ m for the rest), all approaches produce energy spectra with similar gradients. For all presented cases, the minor differences among the energy spectra evaluated at different axial positions in the intermediate field are also observed by Taub et al. (2013) in their DNS study and can be seen in the experimental data of Fellouah and Pollard (2009). Moreover, energy spectra evaluated in the intermediate-field from the four numerical approaches exhibit the $-5/3$ and $-7$ gradients. The $-5/3$ gradient signifies the universal inertia sub-range that is observed in various flow configurations (Pope 2000). On the other hand, gradients steeper than $-5/3$ would characterise the viscous dissipation regime. More specifically, viscous dissipation subrange in momentum driven round free-jets has been experimentally shown to manifest itself as the $-7$ gradient of the energy spectra (Fellouah and Pollard 2009). The existence of these two trends in all presented cases adds to the validation of all four approaches. More importantly, the analysis illustrated that the inertia subrange and dissipation range are captured by both ILES approaches due to MPDATA self-regularisation property.

4.2.3 Self-Similar Profiles

This section evaluates the capabilities of the four approaches to capture the self-similar radial profiles by comparing the conically averaged radial profiles in the intermediate region against the self-similar profiles obtained from experiments of Panchapakesan and Lumley (1993) and Hussein et al. (1994). For the conical averaging, the processed axial region is chosen from where the flow statistics begin to approach the self-similar solution. In the case of LES-DSM, ILES-NS, and ILES-EU, the processed axial region stretches from $z=10$ to $z=22$ m, while it is taken between $z=13$ and $z=22$ m in the case of LES-SA. The offset accounts for the delay of the jet transition from the near-field to the intermediate-field. The post-processed axial region was also selected to avoid the minor upstream influence of the absorber that would occur slightly before the jet reaches the absorber. All radial profiles are plotted with the self-similar coordinates, $\eta$. The mean axial profiles obtained from the four approaches are shown in Fig. 6.

Fig. 6

Mean axial velocity

As expected, all four approaches produce the mean axial velocity that fits well a Gaussian distribution and the profiles were found to be in good agreement with both sets of experimental data (Panchapakesan and Lumley 1993; Hussein et al. 1994). The mean axial velocity tending towards a Gaussian fit is a common characteristic of a turbulent round free-jet even in the lower Reynolds number regime (Boersma et al. 1998; Taub et al. 2013). The discrepancies between the numerical data and the experimental data in the outer shear layer and beyond may be a result of evaluating the self-similar profiles in the intermediate-field rather than the far-field as it is expected that jets would exhibit true self-similar states beyond $z/D = 70$ onwards (Ball et al. 2012). The underestimation of mean axial velocity at the outer layer of the jet also appears to be consistent with other numerical studies (Loppi et al. 2018; Ghaisas et al. 2015). A similar tendency is seen in Salkhordeh et al. (2019) for individual mean axial velocity radial profiles evaluated in the intermediate field (i.e. $z/D = 20$ and $z/D = 50$).

The second-order turbulent statistics produced by all four approaches are assessed next. The results corresponding to LES-SA, LES-DSM, ILES-NS, and ILES-EU computations are presented in terms of the profiles of the axial velocity fluctuations (Fig. 7), the radial velocity fluctuations (Fig. 8), and the Reynolds stresses (Fig. 9) where $w'$ and $v_r'$ denote axial velocity fluctuation and radial velocity fluctuation respectively. The graphs include the conically averaged profiles as well as the azimuthally averaged radial profiles at $z=16$ m and $z=20~\text{m}$ axial positions plotted alongside the experimental data (Panchapakesan and Lumley 1993; Hussein et al. 1994).

Fig. 7

Profiles of axial velocity fluctuations

The profiles of axial velocity fluctuations generally compare well with the experimental data of Panchapakesan and Lumley (1993). In all cases, the off-axis peak was found to be very close to the experimental data. The overall magnitude of the conically averaged axial velocity fluctuations obtained from LES-DSM, ILES-NS, and ILES-EU is slightly higher than that obtained with LES-SA. This was expected for ILES-EU but not for LES-DSM and ILES-NS since these approaches simulate jets at the same Reynolds number as LES-SA. Such tendency can possibly be attributed to the noise treatment. The off-axis peak is also more prominent in LES-SA than in LES-DSM and ILES-NS simulations. A closer inspection of the LES-SA results shows that in comparison to the experimental data of Panchapakesan and Lumley (1993) the off-axis peak is slightly shifted towards the centreline and the presence of a small underprediction in the shear layer region (i.e. from the off-axis peak to $\eta \approx 0.13$) in comparison to the experimental data of Panchapakesan and Lumley (1993). Both effects are most likely a result of the weak co-flow and have also been observed by Zhang and Chin (2020) in their systematic study of co-flow effects. They further showed that these effects become more prominent for larger values of the co-flow. All simulations underpredict experimental values of the axial velocity fluctuations reported in Hussein et al. (1994).

Fig. 8

Profiles of radial velocity fluctuations

In terms of the radial velocity fluctuations, numerical solutions are generally in quite good agreement with the experimental findings in Hussein et al. (1994). LES-SA results were observed to tend towards the experimentally derived values in Panchapakesan and Lumley (1993) whereas the radial velocity fluctuations obtained with LES-DSM and ILES-NS are found to be marginally higher. The overprediction of both axial velocity fluctuations and radial velocity fluctuations in LES-DSM and ILES-NS simulations in Figs. 7 and 8 respectively is arguably related to the noise treatment. Various noise treatments are used by other studies. For example, the agreement of LES results with Hussein et al. (1994) is also seen in Gohil et al. (2014) which employed normally distributed random noises. Notably, similarly as documented in Zhang and Chin (2020), the presented results indicate that a small amount of co-flow has negligible effects on the radial velocity fluctuations.

Fig. 9

Profiles of Reynolds stresses

As can be seen in Fig. 9, Reynolds stresses obtained from all simulations are higher than experimental values documented in Panchapakesan and Lumley (1993) and Hussein et al. (1994) although they are quite close to the latter. Furthermore, some local differences can be noticed between the azimuthally averaged Reynolds stresses and the conically averaged self-similar profiles. Data from experiments (Panchapakesan and Lumley 1993; Hussein et al. 1994) indicate that it is difficult to attain convergence for self-similarity of Reynolds stresses even at axial positions in the jet’s far-field. The original data measured at selected axial locations in Panchapakesan and Lumley (1993); Hussein et al. (1994) displayed a significant amount of scattering when compared to reported there conically averaged self-similar Reynolds stress profiles. These averaged results are reproduced in Fig. 9. Noteworthy, in the current results, the addition of noise may have promoted higher values of Reynolds stress resulting in profiles consistent with trends observed in the radial velocity fluctuations. The fact that all numerically obtained Reynolds stresses for the processed axial range are still close to the bounds of the experimental data and that the location of Reynolds stress peaks are in agreement with the experiments suggests that all investigated numerical approaches can adequately capture the Reynolds stresses in the jet’s far-field and can be further improved with better inlet conditions such as noise profiles.

The presented results confirmed the suitability of both the LES and ILES options of the NFT-MPDATA scheme for predicting the turbulent free-jet using the Cartesian mesh. All four approaches yield results that are in general agreement with the experimental findings documented in Panchapakesan and Lumley (1993); Hussein et al. (1994); Fellouah and Pollard (2009). Impressively, ILES-NS proved to be able to reproduce the results of LES-DSM and additionally, ILES-EU predicted jet behaviour that follows trends of higher Reynolds number jets. This is particularly useful as ILES-EU enables the representation of high Reynolds number flows without the need for explicit SGS modelling and viscous treatments. LES-DSM and ILES-NS showed the ability to predict a transition of the jet into the intermediate-field quicker, while the LES-SA approach combined with the proposed noise treatment produced results that agree well with the experimental data of Panchapakesan and Lumley (1993), especially in the intermediate-field of the jet.

4.2.4 Near-Field Evolution

The evolution of the turbulent round free-jet in the near-field is evaluated next. This is achieved by analysing the individual radial profiles of the flow statistics at various axial positions $z = 2,4,6,8~\text{m}$. This region encompasses the potential core of the turbulent round free-jet. The evolution of the mean axial velocities, axial velocity fluctuations, radial velocity fluctuations, and Reynolds stresses is plotted in Figs. 10, 11, 12, and 13 respectively. The individual radial profiles are normalised with the jet inlet velocity $W_0$⁶.

Fig. 10

Radial Profiles of the mean axial velocity $<W>$. Each profile is shifted by 1 unit

Fig. 11

Radial Profiles of the axial velocity fluctuations $<w'w'>$. Each profile is shifted by 0.3 units

Fig. 12

Radial Profiles of the radial velocity fluctuations $<v_r' v_r'>$. Each profile is shifted by 0.3 units

Fig. 13

Radial Profiles of the Reynolds stresses $<w'v_r'>$. Each profile is shifted by 0.03 units

Figure 10 shows that all four approaches yield very similar mean axial velocities for $z = 2~\text{m}$ and $z = 4~\text{m}$, however, for $z=6~\text{m}$ and $z=8~\text{m}$, the mean axial profiles predicted by LES-DSM, ILES-NS, and ILES-EU begin to approach a Gaussian profile, whereas LES-SA results show a delay in transition. The centreline velocity (at $r = 0~\text{m}$) for LES-DSM, ILES-NS, and ILES-EU has already decayed at $z = 8~\text{m}$ consistently with the centreline velocity decay characteristics shown in Fig. 3a, however, the velocity profile for $z=6~\text{m}$ still resembles a top-hat profile for LES-SA. Such trends of the mean flow can be inferred from the statistics in Figs. 10, 12, and 13. The statistics obtained from LES-DSM, ILES-NS, and ILES-EU at a given axial position are relatively similar but differ from LES-SA results. The small discrepancy between the second-order statistics of LES-DSM, ILES-NS, and ILES-EU is also reflected in close values of the potential core length $L_{PC}$ (Table 2).

The values of the second-order flow statistics predicted by LES-DSM, ILES-NS, and ILES-EU are generally higher than those obtained for LES-SA, particularly in the shear layer region where LES-SA seems to lag behind by at least 2 m when compared to the results of LES-DSM, ILES-NS, and ILES-EU. This is compatible with the difference in the computed potential core length $L_{PC}$ (Table 2). These observations imply a more efficient turbulent mixing in LES-DSM, ILES-NS, and ILES-EU simulations that subsequently decays the jet faster, consistently with the centreline velocity decay characteristics shown in Fig. 3a.

Additionally, Figs. 10, 11, 12 and 13 show that the mean axial velocity approaches the self-similar state faster than the second-order flow statistics. This has also been suggested in Fellouah et al. (2009). In contrast, in the case of second-order flow statistics predicted by LES-DSM, ILES-NS, and ILES-EU, the discernible sharp peak at about $z = 2$ m and at the interface of the jet and co-flowing environment, at about $r \approx 0.5$ m, can be observed at least until $z = 6$ m. This peak becomes less prominent at $z = 8$ m where also the radial profiles start to approach the self-similar states, as illustrated in Figs. 7, 8, and 9 for axial velocity fluctuations, radial velocity fluctuations, and Reynolds stresses respectively as the jet spreads in the intermediate-field. This does not occur for LES-SA due to the delay in transition of the jet. The spreading of the second-order flow statistics in the shear layer and outer layer of the jet beyond the peak also correlates with the spreading phenomena of the mean axial velocity seen in Fig. 10.

4.3 Comparison of Simulations Using Different Types of Meshes

The flexibility of the NFT-MPDATA scheme operating on unstructured meshes has been preliminary explored using the LES-SA option. The LES-SA simulations are repeated using similar boundary conditions as before but this time they are performed on the two different triangular-based prismatic meshes described in Sect. 3.2. A similar procedure as before is applied for the post-processing of results, however, the field variables were linearly interpolated from the closest nodes, to provide values in the same points which were used to collect data in the simulations using Cartesian mesh.

4.3.1 Global Characteristics

The centreline velocity decay characteristics and the half-width evolution of the jet obtained using different types of meshes are compared against experiment (Panchapakesan and Lumley 1993) in Figs. 14a and b. All related parameters are summarised in Table 3.

Fig. 14

Global jets characteristics — effects of using different mesh types

Table 3 Comparison of centreline velocity decay characteristics and spreading rates

Figure 14a and Table 3 show that the computations using three different meshes produce similar gradients for the centreline velocity decay characteristics in the intermediate-field with the centreline velocity decay constant $k_u$ that lies within the expected range ($k_u = 5.8$ to 6.1). The almost identical centreline velocity decay characteristics for both triangular prismatic meshes are expected given that the coarsening in MT-PRIZ-CS occurs only close to the lateral sides of the computational domain. For both triangular prismatic meshes, the transition of the jet into its intermediate-field at a slightly earlier location than for the Cartesian mesh. For all meshes, the evolution of half-width, Fig. 14b, is found to be similar and the spreading rate $k_r$ is within the expected range ($k_r = 0.093$ to 0.102). All simulations are in good agreement with the references listed in Table 2.

4.3.2 Self-similar profiles

The profiles of mean axial velocity, axial velocity fluctuations, radial velocity fluctuations, and Reynolds stresses obtained on different meshes are documented in Fig. 15.

Fig. 15

Comparison of the self-similar profiles

The mean axial velocity and axial velocity fluctuations predicted using all three meshes are very close which could be expected since all meshes are axially extended in a similar manner. However, discernible differences in radial velocity fluctuations and the Reynolds stresses can be detected between computations using both triangular prismatic meshes and the Cartesian mesh, with the triangular prismatic meshes producing slightly higher radial velocity fluctuations and a slightly higher Reynolds stress in shear layer region ($0.085 \le \eta \le 0.15$). These differences alongside the centreline velocity decay characteristics seen in Fig. 14 are most likely due to triangular prismatic cells inducing some form of flow solution perturbation akin to random noise that could have promoted the shear layer development of the jet rather than a reduction in molecular diffusion.

5 Conclusions

We demonstrated the accuracy that can be achieved using ILES for incompressible flow free-jets, and compared ILES results against LES and experimental data. The new implementation of the LES option with the dynamic Smagorinsky model and the incorporation of dynamic outlet convective boundary conditions provide an extension to the previously documented MPDATA based NFT integrators for incompressible viscous flows. These numerical developments are reported and verified against notable laboratory and numerical experiments that capture the key aspects of canonical turbulent free-jet flows.

The extended NFT-MPDATA scheme enables a range of the explicit and implicit large eddy simulations. Two options for explicit SGS treatments were considered: LES-DES and LES with the newly implemented dynamic Smagorinsky model. The implicit large eddy simulation capability of the NFT-MPDATA has already been extensively proven in the context of geophysical stratified flows (Smolarkiewicz et al. 2013, 2016). In these applications the anelastic system of equations is solved where the stress tensor accounting for viscous effects is absent. It maybe of interest to note that the NFT-MPDATA scheme uses efficient collocation of all dependent variables. In many schemes this would support nontrivial null spaces of the discrete differential operators and would require a form of stabilisation. In the NFT-MPDATA schemes such stabilisation is not required, owing to the self-regularisation properties of MPDATA.

The presented simulations confirm MPDATA ILES property for turbulent free-jet flows. In this study, the NFT-MPDATA solver was employed to solve either the Navier–Stokes equations (ILES-NS) with viscous terms but without the SGS model or the Euler equations (ILES-EU). In the intermediate-field of the jet, comparisons of the centreline velocity decay constant and spreading rates showed that all SGS treatments implemented in the NFT-MPDATA scheme for free-jet flows yield values in good agreement with experimental findings documented in Panchapakesan and Lumley (1993), Hussein et al. (1994), Abdel-Rahman et al. (1997), Shiri et al. (2008), Quinn (2006) and are within the consensus ranges established in the literature. Moreover, all four presented approaches yield self-similar flow statistics that compare well with the experimental data of Panchapakesan and Lumley (1993) and Hussein et al. (1994). The validity of both LES and ILES approaches based on NFT-MPDATA are further supported by the observation made in the computed energy spectra, specifically all approaches produce the $-5/3$ gradient signifying the universal inertia subrange as well as the $-7$ gradient characterising the dissipation range typically observed for free-jets (Fellouah and Pollard 2009).

The ILES-EU approach was found to be particularly useful, as it enables the representation of high Reynolds number flows without the need for explicit SGS models. In comparison with traditional LES the omission of viscous terms reduces the number of required numerical operations making it also more efficient. ILES-EU achieved up to 17% and 21% computational cost savings when compared to both LES-SA and LES-DSM respectively. The comparisons between the ILES-EU and ILES-NS show also that the inherent dissipation of MPDATA does not add but adapts to the physical dissipation present in the system. Furthermore, ILES-NS yields similar results to LES-DSM showing promise for using ILES-NS for lower Reynolds number jets.

The study identifies and validates NFT-MPDATA with associated I/LES turbulence treatments as an accurate numerical tool for researching turbulent jet flows. It also discusses such aspects as a specification of boundary conditions, required for successful simulations of this class of problems. This information opens avenues for further investigations of other jet flows. Turbulent jet flows are important to many applications including internal combustion engines, cooling flows (for example for electronics), sprays, aerosol delivery, water jets for cleaning and machine processes, food processing, and weather, to mention just a few. Some of these applications involve complex geometries for which flexible unstructured meshes are beneficial. Our study shows that quality simulations for jets can be achieved on both, Cartesian and unstructured meshes.