The Wall-Jet Region of a Turbulent Jet Impinging on Smooth and Rough Plates

Abstract

The study reports direct numerical simulations of a turbulent jet impinging onto smooth and rough surfaces at Reynolds number Re = 10,000 (based on the jet mean bulk velocity and diameter). Surface roughness is included in the simulations using an immersed boundary method. The deflection of the flow after jet impingement generates a radial wall-jet that develops parallel to the mean plate surface. The wall-jet is structured into an inner and an outer layer that, in the limit of infinite local Reynolds number, resemble a turbulent boundary layer and a free-shear flow. The investigation assesses the self-similar character of the mean radial velocity and Reynolds stresses profiles scaled by inner and outer layer units for varying size of the roughness topography. Namely the usual viscous units $u_\tau$ and $\delta _\nu$ are used as inner layer scales, while the maximum radial velocity $u_m$ and its wall-normal location $z_m$ are used as outer layer scales. It is shown that the self-similarity of the mean radial velocity profiles scaled by outer layer units is marginally affected by the span of roughness topographies investigated, as outer layer velocity and length reference scales do not show a significantly modified behavior when surface roughness is considered. On the other hand, the mean radial velocity profiles scaled by inner layer units show a considerable scatter, as the roughness sub-layer determined by the considered roughness topographies extends up to the outer layer of the wall-jet. Nevertheless, the similar character of the velocity profiles appears to be conserved despite the profound impact of surface roughness.

1 Introduction

The impingement of turbulent jets onto solid surfaces is a common flow phenomenon encountered in many different flow scenarios, ranging from industrial applications to geophysical flows. Directing a jet of fluid toward a solid object is a relatively cheap and convenient strategy for enhancing the transfer of heat and mass away from the surface of the object. Hence, impinging jets are of widespread use in cooling systems, even for critical applications such as the internal cooling of turbine blades of turbo-jet engines (Bunker et al. 2014). Impinging jet burners are used to study flame-wall interaction which is of increasing importance in the development of modern combustion devices (Jainski et al. 2017).

The flow phenomena involved with impinging jets are also important in the context of vertical take-off and landing (VTOL) aircraft and helicopters. In this regard, the study of jet impingement is particularly relevant for assessing the impact that near-ground operations of such aircraft have on the surrounding environment (Wu et al. 2016; Cárdenas et al. 2020). Impinging jets play also a significant role in geophysical phenomena such as the scouring due to liquid streams impacting on a solid bed (Dong et al. 2020).

It is apparent that the topography of the impingement surface always includes the presence of geometrical irregularities, from invisible-to-the-eye surface grooves inside turbine blades, to obstacles of size comparable to the largest length scales involved in the considered problem. Well-established results on the impact of surface roughness on canonical turbulent flows show that roughness affects the flow as long as the characteristic length scale k associated with the roughness topography is comparable to (or larger than) the viscous length scale $\delta _\nu$ of the flow (Chung et al. 2021; Kadivar et al. 2021). In such scenario, the flow is strongly modified by the presence of roughness, especially within a thin layer that is usually termed roughness sub-layer.

For impinging jets, a limited number of studies exists about the effects of random surface roughness. In Wu et al. (2016), an investigation of such effects is carried out using large eddy simulations (LES) at a relatively large Reynolds number. Other studies experimentally investigate impinging jets to determine the effects of surface roughness on heat transfer (Nevin 2011) or on noise generation (Dhamanekar and Srinivasan 2014). On the other hand, other works focus more specifically on engineered rough surfaces, mostly designed with the objective of maximizing the heat transfer of the configuration (Nagesha et al. 2020; Van Hout et al. 2018). Relatively few investigations in the literature report direct numerical simulations (DNS) of impinging jet configurations, and most of them limit the study to smooth impingement plates (Dairay et al. 2015; Wilke and Sesterhenn 2017; Magagnato et al. 2021). In our recent work (Secchi et al. 2022), we assess the novel parametric forcing approach (PFA) (Busse and Sandham 2012; Forooghi et al. 2018) for the inclusion of surface roughness effects in the simulation of turbulent impinging jets.

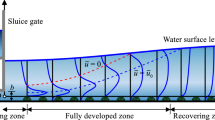
After the deflection of the flow in the impingement region, the flow develops into a radial wall-jet. The latter is traditionally identified as a boundary layer in which the velocity over some region of the shear layer exceeds that in the outer region of the flow (Launder and Rodi 1979, 1983). Plane and radial wall-jets have been intensively studied in the past decades experimentally and numerically (Gupta et al. 2020; Dejoan and Leschziner 2005; Eriksson et al. 1998; Fairweather and Hargrave 2002; Knowles 1998; Jaramillo et al. 2008). For fully developed wall-jets over smooth walls, great attention has been directed into detecting the proper scaling variables that allow to evidence self-similarity of mean velocity profiles in the inner and outer regions of the wall-jet. Many investigations have evidenced non universality in the log-law region of the friction-scaled mean velocity profiles of fully developed wall-jets (Schwarz and Cosart 1961; Launder and Rodi 1983; Wygnanski et al. 1992; Guerra et al. 2005); a consistent number of works reports that self-similarity of mean velocity profiles can also be attained by using outer region flow quantities as scaling variables (Eriksson et al. 1998; Tachie et al. 2004; Rostamy et al. 2011). The theoretical study of George et al. (2000) suggests that viscous units and outer flow variables are both appropriate sets of scaling variables in, respectively, the inner and outer layers of the jet. However, perfect collapse of the profiles onto a single curve is to be expected only in the limit of local infinite Reynolds number. For finite Reynolds numbers, the interaction of inner and outer layers is predominant and possibly induces the scattering of the data (Banyassady and Piomelli 2015).

In the present work, the immersed boundary method resolved DNS (Secchi et al. 2022) are used to directly investigate the influence that random surface roughness has on the radial wall-jet region of the impinging jet configuration. The results for three different roughness geometries of increasing size are compared to the reference case of a jet impinging on a smooth plate. The local low Reynolds numbers attainable along the impingement plate via the current DNS framework and the presence of random roughness on the plate surface undermine the possibility of observing strong separation of scales between the inner layer and the outer layer of the wall-jet at any radial location. Nevertheless, the scaling strategies traditionally applied for plane and radial wall-jets are tested to assess the existence of self-similar flow regions and the degrading of self-similarity for increasing size of the roughness topography.

2 Methods

2.1 Flow Configuration

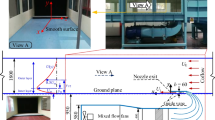
The configuration of an axisymmetric impinging jet is sketched in Fig. 1. A jet issues from a fully developed turbulent pipe flow and impinges on a plate placed 2D away from the jet exit section (D represents the pipe diameter). The particular choice of the nozzle-to-plate distance follows the work of Dairay et al. (2015) which is used as a reference to validate the present numerical setup. In addition, the same configuration has also been studied by several other experimental and large eddy simulation investigations [for instance (Lee and Lee 1999; Uddin et al. 2013; Hadẑiabdić and Hanjalić 2008)]. The flow is incompressible, and the fluid properties are considered uniform and constant everywhere. The bottom surface of the computational domain is placed at $x_3/D=0$ and surface roughness is overlaid on top of it and accounted for by using an immersed boundary method (IBM). Further details about the adopted IBM and computational approach are provided in Sect. 2.2.

Fig. 1

Impinging jet flow configuration. Left, top view; right, front view. Color map of an instantaneous snapshot of the velocity magnitude aids the visualization of the flow. Note that the confinement plate is not shown in the top view representation

Near-wall features of jet impingement flows are known to be sensitive to inflow boundary conditions prescribed at the jet exit section (Forooghi et al. 2016). Existing numerical studies on turbulent impinging jets (Dairay et al. 2014, 2015; Wilke and Sesterhenn 2017) recur to the superposition of sinusoidal disturbances to a top-hat type velocity profile at the inlet section of the jet. This particular choice of the inflow velocity profile usually aims to mimic the non-fully-developed turbulent conditions found at the exit section of a slightly convergent nozzle. Although selecting such a specific inflow profile is of practical relevance for many industrial applications, the present study prescribes a fully developed-turbulent inflow profile at the inlet section of the jet computational domain due to its unequivocal definition.

At the inlet boundary, inflow is generated using a precursor simulation of a fully-developed turbulent pipe flow. The precursor simulation is preferred to applying a synthetic eddy method to generate fully-developed turbulent inflow conditions. The main advantage of synthesizing turbulence with, for instance, the synthetic eddy method (Poletto 2015) or the turbulent spot method (Kröger and Kornev 2018), usually resides in the relatively cheap computational cost associated with these methods. Nonetheless, synthesizing realistic fully-developed turbulence, up to high-order statistical moments, requires sufficiently long spatial development lengths. Thus, applying either one of these methods to the present configuration leads to a computational cost comparable to that associated with the precursor-type strategy.

At $x_3/D=2$, the computational domain is confined by an additional plate that allows avoiding the entrainment of the fluid from the outside of the domain, hence considerably simplifying the task of modeling the configuration, which would otherwise need to include an additional inflow/outflow boundary.

The cylindrical lateral surface constitutes the outflow boundary of the computational domain and has a diameter of 20D. The large distance separating the jet axis and the lateral surface is chosen to minimize the influence of outflow boundary conditions on the region of interest of the flow which, in the present investigation, is restricted to $r/D<6$. On the lateral surface of the computational domain, the outflow boundary condition presented by Dong (2015) is prescribed. Note that this particular treatment of the outflow boundary condition allows to avoid the application of a buffer region near the outflow boundary.

2.2 Governing Equations and Numerical Approach

The incompressible Navier–Stokes equations:

$$\begin{aligned}&\frac{\partial u_j}{\partial x_j} = 0 \end{aligned}$$

(1)

$$\begin{aligned}&\frac{\partial u_i}{\partial t} + u_j\frac{\partial u_i}{\partial x_j} = -\frac{\partial p}{\partial x_i} + \frac{1}{Re} \frac{\partial ^2 u_i}{\partial x_j \partial x_j} + f_i \end{aligned}$$

(2)

are spatially discretised in the computational domain through the use of the spectral element method of Patera (1984). In particular, the numerical integration of the governing equations is performed using the flow solver Nek5000 (Fisher et al. 2008-2020).

In Eqs. 1 and 2, summation is implied over repeated indices and $i,j=1,\,2,\,3$. In the form appearing above, the equations are made dimensionless using the mean bulk velocity $U_b$ in the pipe and the pipe diameter D. Hence, the Reynolds number appearing in Eq. 2 is $Re=U_b D/ \nu$, where $\nu$ is the kinematic viscosity of the fluid. The Reynolds number is set to Re = 10,000 for all the simulations reported in this study.

A volume force $f_i$ is added to the momentum equation 2 to account for solid boundaries using an IBM. In particular, $f_i =0, \, i=1,\,2,3$ in the fluid region, while $f_i \ne 0$ in the solid region, where the forcing is tuned to enforce the non-slip and non-penetration boundary conditions at the fluid-solid interface. In particular, the volume force is prescribed following the feedback loop approach presented by Goldstein et al. (1993). According to this strategy, the forcing acts as a proportional-integral controller which aims at keeping the velocity to zero within the solid wall. More precisely,

$$\begin{aligned} f_i=-\alpha \int _0^t u_i \textrm{d}t' - \beta u_i \end{aligned}$$

(3)

where $\alpha$ and $\beta$ are constants that need to be adjusted for the specific case to have a fast enough controller given the stability limits of the adopted time integration method.

The application of the present forcing strategy coupled with a pseudo spectral method is reported in several works (Forooghi et al. 2017, 2018; Vanderwel et al. 2019; Stroh et al. 2020; Yang et al. 2022). We validated our implementation by comparing our results with experimental measurements for turbulent jets impinging on smooth and rough surfaces. Details about the experimental data and results of the comparison can be found in our previous work (Secchi et al. 2022).

The simplicity of implementation of the forcing strategy of Eq. 3 and the associated straightforward identification of the fluid-solid interface are chosen in spite of the loss of spectral accuracy in the near wall region. An often adopted remedy to the latter problem consists in applying a suitable filter to avoid jump discontinuities in the forcing distribution across the fluid-solid interface. Nonetheless, the choice of a proper filter kernel is not trivial, especially in the case of non-uniform grid spacing as in the present case.

Despite the limitations associated with the adopted immersed boundary strategy, such as the appearance of spurious oscillations in the approximated solution (Goldstein et al. 1995) and the loss of accuracy (Lai and Peskin 2000; Griffith and Peskin 2005), the grid resolution employed in the present study appears to allow for a physically meaningful resolution of the roughness details into the simulations. As an example Fig. 2 represents the time-averaged radial velocity distribution in the core of the rough surface at three different wall-normal heights for one of the investigated roughness topographies. In the figure, roughness elements are evidenced by white solid contours. In all the three slices reported in the figure, the mean radial velocity field does not show evident spurious fluctuations that could be attributed to the presence of a discontinuous forcing across the fluid-solid interface. At sufficiently large wall-normal heights (i.e. as seen in Fig. 2b, c), the wake behind and above single roughness elements appears to be well represented by the IBM. In particular, notice that the slice in Fig. 2c does not cut any roughness elements, but it is sufficiently close to the roughness crests for their wakes to be visible.

Fig. 2

Color maps of the time averaged radial velocity component at different wall-normal heights. a $x_3/D=0.05$; b $x_3/D=0.07$; c $x_3/D=0.09$

The present computational framework uses two concurrent simulations: one precursor simulation for generating inflow boundary conditions, and one for the jet flow domain. Consequently, two different meshes are necessary. For the precursor pipe flow simulation, the mesh consists of 608,175 spectral elements, while the mesh of the jet flow domain consists of 2,034,995 elements. To increase the spatial resolution, a p-type refinement approach is used (i.e. the resolution is increased by increasing the polynomial degree of the Lagrange polynomials basis on each element.) In particular, all the cases presented in this study were obtained using polynomials of 7th degree for both the velocity and pressure fields (i.e. a $\textrm{P}_n - \textrm{P}_n$ formulation was used).

The grid resolution is checked by inspecting the ratio between the local grid size to the Kolmogorov length scale $\tilde{\eta }=(\nu ^3/\epsilon )^{1/4}$, where $\nu$ indicates the kinematic viscosity of the fluid, and $\epsilon$ the turbulent dissipation. The local grid size is estimated to be $\Delta = (\Delta x_1 \Delta x_2 \Delta x_3)^{\frac{1}{3}}$, where $\Delta x_i$ indicate the local grid spacing in the ith coordinate direction. The comparison between the two length scales for a typical solution based on 7th degree polynomials (shown in figure 3 (A) of Secchi et al. (2022)) shows that the local grid size attains values $\Delta < 2 \tilde{\eta }$ in every region of interest of the flow.

A grid independence study was also performed by comparing mean flow quantities between two solutions based on polynomials of 3rd and 5th degree (in addition to the 7th degree based solution used for the results shown in the present work). Although the comparison between these two cases did not show any visible discrepancy between the computed mean flow quantities in any region of interest of the flow, it was decided to rely on a 7th polynomial degree solution in order to have a finer resolution of the roughness topography. Further details about the computational meshes, grid resolution and grid independence study are reported in our previous work (Secchi et al. 2022).

2.3 Surface Roughness

Surface roughness at the bottom plate of the computational domain consists of a wall height random distribution in the $x_1 - x_2$ plane, $h=h(x_1,x_2)$. The analysis is restricted to wall height distributions such that $h>0$ everywhere to reproduce the surface roughness determined by the deposition of sediments over an otherwise smooth bed.

Fig. 3

Samples of the investigated rough surfaces. Color maps of the wall height distribution in the unit square $[0,\,1] \times [0,\,1]$. a $k_{99}/D=0.05$; b $k_{99}/D=0.12$; c $k_{99}/D=0.15$

The procedure by which the wall height distribution is designed is based on the algorithm presented by Pèrez-Ràfols and Almqvist (2019). It is an iterative algorithm that generates roughness topologies having prescribed power spectrum (PS) and probability density function (PDF). Starting from the input PDF and PS, the method first generates two surfaces: the first one with the prescribed PDF (but unknown PS), and the second one having the desired PS (but unknown PDF). Then, an iterative procedure corrects successively the PS of the first surface and then the PDF of the second one in order to match the desired input. Convergence is reached when both surfaces are characterized by the prescribed PDF and PS (although the two will always slightly differ for surfaces of finite size). In the context of turbulent flow research, the same approach for generating random rough surfaces is also used, for instance, in the work of Yang et al. (2022).

Further scaling of the wall height distribution designed with the method described above allows the characterization of various rough surfaces. In particular, three Gaussian surfaces (i.e. characterized by a Gaussian wall height distribution) are distinguished by the $99\%$ confidence interval of their PDF distribution of roughness height; namely, $k_{99}=0.05D, \, 0.12D, \, 0.15D$. The effective slope parameter (ES) (Napoli et al. 2008) is kept constant $ES=0.41$ for the three surfaces. Samples of the three rough surfaces are displayed in Fig. 3 and main statistical properties of the roughness topographies are reported in Table 1.

Table 1 Surface roughness statistics

2.4 Averaging

The DNS are performed integrating the Navier–Stokes equations 1 and 2 in Cartesian coordinates, with $x_i$ and $u_i$ ($i=1, \, 2, \, 3$) indicating the space coordinates and the velocity components respectively. The numerical framework adopted in this study has been validated against experimental and numerical data for the smooth wall case in Dong (2015), and with novel experimental measurements for the case of surface roughness (Secchi et al. 2022). The collection of time statistics starts after the flow has reached a statistically stationary state and it is carried out during run-time of the simulations for approximately $60 \, D/U_b$.

During post-processing, the acquired time-averaged variables are first interpolated onto a cylindrical coordinates grid ${r, \, \theta , \, z}$. In this new reference system, $u_r$, $u_\theta$ and $u_z$ indicate the radial, the circumferential and z velocity components, respectively (note that the wall-normal distance z is interchangeably used in place of the $x_3$ coordinate throughout the text). Subsequently, averaging is performed in the circumferential direction such that the resulting mean flow field depends only on two independent directions; namely the radial distance from the jet axis r, and the wall-normal distance z. In what follows, an over-line $\overline{\left( \, \cdot \, \right) }$ will be used to indicate the time and circumferential averaging performed on the considered quantity. Since only the mean flow field away from the roughness core is addressed in the present study, for all the cases averaging in the circumferential direction is performed including fluid and solid regions. This particular way of computing statistics is known as extrinsic averaging and it is further detailed in appendix A of this work, where also a comparison with intrinsic averaging (i.e. performed considering only the fluid region of the computational domain) is shown.

3 Results and Discussion

3.1 Mean Velocity Field

Depending on the geometric parameters of the configuration and the Reynolds number of the pipe flow issuing the jet, several markedly different regions can be distinguished in the flow originated by the jet impingement (Jambunathan et al. 1992). Namely, the jet area can be divided into a free jet region and an impinging region. The former can be further split into its core part [sometimes referred to as potential core (Jambunathan et al. 1992)] and a shear layer region. Figure 4 shows a color map of the mean turbulent kinetic energy distribution $0.5(\overline{u'_i u'_i})/U_b^2$ for all the simulated cases. From the figure it can be appreciated how turbulence fluctuations in the shear layer region of the free jet are much more intense compared to the fluctuations in the core region of the free jet. The impinging jet region constitutes the region where the flow gets deflected by the strong adverse wall-normal pressure gradient that originates from the presence of a stagnation point at $r/D=0$. The flow deflection in the impingement region gives rise to a developing flow along the radial direction parallel to the impingement plate. For small radial distances, approximately $r/D<1$, the favourable radial pressure gradient and the momentum injected from the incoming free jet determine an intense radial acceleration of the flow. The wall-jet radially develops growing in thickness as the flow slows down. From Fig. 4, it also appears that surface roughness is responsible for magnifying turbulence intensities near the wall for $0.5< r/D < 2$. Furthermore, the thickness of this region of intensified turbulence fluctuations seems to increase with the characteristic roughness size.

Fig. 4

Color maps of the mean turbulent kinetic distribution $0.5(\overline{u'_i u'_i})/U_b^2$. a Smooth wall; b $k_{99}/D=0.05$; c $k_{99}/D=0.12$; d $k_{99}/D=0.15$

Fig. 5

Color-maps of the mean radial velocity component. a Smooth wall; b $k_{99}/D=0.05$; c $k_{99}/D=0.12$; d $k_{99}/D=0.15$. Iso-lines: $\overline{u_r}/U_b=0.1$, ; $\overline{u_r}/U_b=0.25$, white curve; $\overline{u_r}/U_b=0.5$, ; $\overline{u_r}/U_b=1$,

Compared to the smooth wall case, the most immediate consequence of surface roughness is that a greater resistance is felt by the flow occurring next to the rough surface. The greater drag exerted by the roughness on the fluid strongly reduces the radial development of the flow along the plate when compared to the smooth wall case. This is exemplified in Fig. 5, where color maps of the mean radial velocity component are depicted for all the considered cases. In particular, panel (a) represents the smooth-wall reference case, while panels (b), (c) and (d) refer to the cases $k_{99}/D= 0.05, \, 0.12, \, 0.15$ respectively. In the figure, selected iso-lines aid the visualization of the radial development of the mean flow. Cases with surface roughness are characterized by a faster decay of the radial flow. The greater the roughness size, the smaller is the region where the global peak of radial velocity occurs. Nonetheless, the location of such maximum remains approximately constant in a neighbourhood of $r/D\approx 1$.

Another apparent effect determined by the presence of surface roughness is the upward wall-normal shift of the mean flow. Note that this upward shift is not an artifact introduced by the particular way of computing averages in the circumferential direction. A comparison between the adopted extrinsic averaging and intrinsic averaging of the radial velocity component is reported in Fig. 21 of appendix A. From the analysis of the figure, it is evident that both strategies lead to a prediction of the same wall-normal displacement of the mean flow field. A question that naturally arises is how to quantify the observed shift or, equivalently, where is it physically meaningful to locate the virtual origin perceived by the turbulent flow occurring next to a rough surface. Different solutions have been proposed in the past for various drag-altering textured and rough surfaces (Jackson 1981; Luchini et al. 1991; Jiménez 1994; Ibrahim et al. 2021). In the present work, we identify the upward wall-normal shift of the mean flow field with the mean roughness height k, as it is a convenient (a priori definable) quantity which does not depend on the local flow properties. Further, it is also noted that, for $z < k$, surface roughness appears to be almost impermeable to the fluid for all the investigated cases. In fact, Fig. 21 shows that the mean radial velocity is essentially zero or has very low values for $z < k$.

The sketch reported in Fig. 6 visualizes the wall-normal shift that is used throughout the present work to assess comparisons between the rough and smooth cases.

Fig. 6

Sketch of a typical mean radial velocity profile at a fixed radial location for the smooth and a rough case. For the rough wall case, $z=k$ identifies the virtual origin of the wall-normal distance

Fig. 7

Mean radial velocity profiles at different radial locations. a Smooth wall; b $k_{99}/D=0.05$; c $k_{99}/D=0.12$; d $k_{99}/D=0.15$.   Inner layer thickness $z_m/D$;  Outer layer thickness $z_{1/2}/D$

Figure 7 reports various mean radial velocity profiles at different radial locations for all the three cases. The profiles that correspond to rough cases have been shifted downward by their mean wall height in order to enable the comparison with the smooth wall case. It is noted that a slip velocity exists for the rough cases at $z=k$, as the virtual origin of the wall-normal coordinate is not a physical boundary where a no-slip boundary condition is applied. For all the investigated cases, the slip velocity at $z=k$ reaches a maximum (in the order of $\overline{u_r}\approx 15\%U_b$) around $r/D = 0.5$ and then decreases quickly for larger radial distances. In particular, the slip velocity is $\overline{u_r} < 10\%U_b$ for any radial location $r>1.5D$. The observation of the mean radial velocity profiles reported in Fig. 7 is instructive to understand the development of the flow in the radial direction. For $r/D>1$, the velocity develops an inner boundary layer due to the presence of the solid wall, and an outer free-shear boundary layer with the external quiescent fluid. As typically done in the analysis of wall-jets (Banyassady and Piomelli 2015), the thickness of the inner and outer layers can be identified, respectively, by $z_m$ and $z_{1/2}$. The former represents the wall-normal distance at which the radial velocity reaches its maximum $u_m$ at a certain radial location; the latter is the greatest distance from the wall at which the radial velocity is $0.5u_m$.

The development of the inner and outer layers can be envisaged from Fig. 7, where the height of the two layers is depicted at each radial location by black symbols. For the rough cases, the thicknesses of the two layers are not displayed in the figure for approximately $r/D >6$, as at these radial locations the weak radial velocities and the presence of radial back-flow in the top part of the computational domain do not allow a meaningful definition of the two thicknesses. Better comparison between the examined cases of the growth of inner and outer layers is displayed in Fig. 8. As already noted by Secchi et al. (2022), the major effect of surface roughness on the development of the inner and outer layers is to provoke an upward shift of such layers at a given radial location. The entity of the upward shift increases as the size of the roughness topography increases. Nevertheless, the growth rate of both layers does not appear to change due to the presence of surface roughness. For all the examined cases, a linear growth of the inner layer $z_m/D$ is observed in the range $0.5< r/D < 4.5$, while a linear growth of the outer layer thickness $z_{1/2}/D$ is limited to the range $1.5< r/D < 4$.

Fig. 8

Radial wall-jet growth. a Inner layer thickness $z_m/D$; b Outer layer thickness $z_{1/2}/D$ Smooth plate,; $k_{99}/D=0.05$, ; $k_{99}/D=0.12$, ; $k_{99}/D=0.15$,

3.2 Wall-Jet Region: Outer Layer Scaling

Some authors indicate that mean velocity profiles of plane and radial wall-jets exhibit a self-similar character when scaled with $u_m$ and $z_m$ (Schwarz and Cosart 1961). It is noted that $z_m$ is a possible measure of the boundary layer thickness at a certain radial position, while $u_m$ is an appropriate velocity scale for the outer layer of the wall-jet.

With this particular choice, for the smooth wall case self-similarity requires that the mean radial velocity can be written as:

$$\begin{aligned} \overline{u_r}(r,z) = u_m f\left( \eta (z)\right) \end{aligned}$$

(4)

where the similarity variable $\eta =z/z_m$. Assuming equation 4 to hold, it is straightforward to conclude that:

$$\begin{aligned} \frac{Re_m \overline{\tau _w}}{\rho u_m^2} = f'(0). \end{aligned}$$

(5)

where $Re_m=u_m z_m / \nu$ is the local Reynolds number based on $u_m$ and $z_m$, and $\overline{\tau _w}$ is the mean stress at the wall. For the rough cases, the lack of a precise definition of fluid-solid interface in the mean flow field poses a serious challenge in the accurate evaluation of the total wall-stress. In particular, the presence of a slip-velocity at the virtual origin $z=k$ makes the selection of such location questionable when it comes to the evaluation of the wall shear stress. While it would be possible to extract this information from the mean distribution of the volume force introduced by the IBM, within the present framework this possibility is compromised by the severe fluctuations present in the mean volume force distribution (caused concurrently by the random nature of the roughness topography and, as discussed in Sect. 2.2, by the application of a discontinuous forcing distribution within the spectral discretization of the governing equations). Hence, an estimate for the total wall-stress is deduced from the peak value of the mean wall-normal radial velocity gradient at each radial location. Consistent to this approach, Eq. 5 can be rewritten for the cases with roughness as:

$$\begin{aligned} \frac{Re_m \overline{\tau _w}}{\rho u_m^2} = f'(\eta _w). \end{aligned}$$

(6)

where, according to the wall-normal shift of the mean flow field discussed in Sect. 3.1, the similarity variable $\eta$ is modified to $\eta = (z-k)/(z_m-k)$ and $\eta _w$ represents the value of the similarity variable for which the wall-normal derivative of the mean radial velocity is maximum.

Equations 5 and 6 indicate that scaling the wall-stress by $\rho u_m^2 / Re_m$ should yield to a constant value in the regions where self-similarity in Eq. 4 holds.

Fig. 9

$f'(0)$ and $f'(\eta _w)$ (see Eqs. 5 and 6) distributions along the impingement plate. a Smooth plate; b $k_{99}/D=0.05$; c $k_{99}/D=0.12$; d $k_{99}/D=0.15$

This argument is tested in Fig. 9 for all the simulated cases. From the figure, it is apparent that there is not a range of radial locations where $f'(0)$ or $f'(\eta _w)$ attain truly a constant value for any of the simulated cases. However, for the smooth and $k_{99}/D=0.05$ cases, the variation of, respectively, $f'(0)$ and $f'(\eta _w)$ in the interval $2 \le r/D \le 4$ is sufficiently weak to consider $f'(0)$ and $f'(\eta _w)$ to be approximately constant in that range. All the roughness cases show a peak of $f'(\eta _w)$ at approximately $r/D=1.5$; the magnitude of this peak appears to be larger for increasing the characteristic roughness size $k_{99}/D$. For greater radial distances, a consistent decreasing behavior of $f'(\eta _w)$ is observed for all the roughness cases in the range $1.5< r/D < 5$. The relative variation of $f'(\eta _w)$ in this range of radial distances is greater for increasing size of the roughness topography.

The approximately constant value of $f'(0)$ and $f'(\eta _w)$ observed for the smooth and $k_{99}/D=0.05$ cases suggests that self-similarity of mean radial velocity profiles could be sought in the range $2 \le r/D \le 4$.

Fig. 10

Outer units scaled mean radial velocity profiles in the range $2 \le r/D \le 4$. a Smooth plate; b $k_{99}/D=0.05$; c $k_{99}/D=0.12$; d $k_{99}/D=0.15$

Outer units scaled mean radial velocity profiles (i.e. scaled according to Eq. 4) are reported in figure 10. The profiles are taken in the interval $2 \le r/D \le 4$ with a spacing between each sampled profile of approximately 0.1D. Reasonable collapse of the curves is observed for all the cases for approximately $z/z_m < 5$ (or $(z-k)/z_m < 5$ for the cases with surface roughness). For increasing size of the roughness topography, larger scattering of the profiles is observed, especially very close to the wall. Although self-similarity of the mean radial velocity profiles scaled by outer units cannot be formally expected (based on the results shown in Fig. 9), all the profiles depicted in Fig. 10 indicate a self-similar character. In addition, the latter appears to be rather insensitive to the presence of surface roughness, as only minor scattering of the velocity profiles is observed for the roughness cases.

Similarly to Eq. 4, self-similar profiles for the Reynolds stress components are sought in the form:

$$\begin{aligned} \overline{u'_i u'_j}(r,z) = u_m^2 g_{ij}\left( \eta (z)\right) \end{aligned}$$

(7)

where the similarity variable $\eta$ is $\eta =z/z_m$ for the smooth case and $\eta =(z-k)/(z_m-k)$ for the rough cases. Figure 11 reports the normal Reynolds stresses profiles $\overline{u'_r u'_r}$, $\overline{u'_\theta u'_\theta }$ and $\overline{u'_z u'_z}$ at the same radial locations used for the mean radial velocity profiles in Fig. 10 (i.e. $2 \le r/D \le 4$). Very good collapse of the profiles is observed for the smooth wall case for all the normal Reynolds stress components. On the other hand, scattering of the profiles is observed for all the rough cases. In the two cases having the largest roughness characteristic size (i.e. $k_{99}/D=0.12$ in Fig. 11c and $k_{99}/D=0.15$ in Fig. 11d), a significant scatter of the data is observed in the near-wall region within the inner layer for $(z-k) < 0.5 (z_m-k)$. On the contrary, the self-similar character of the outer units scaled normal Reynolds stress components is less affected in the outer layer for $(z-k) > (z_m-k)$. Differently, for the $k_{99}/D=0.05$ case, $\overline{u'_r u'_r}$ shows a visible deviation from the similarity of the outer units scaled profiles in the range of wall-normal distances $0.2< (z-k)/(z_m-k) < 3$, whereas a good collapse is observed at all other locations.

Fig. 11

Normal Reynolds stresses profiles scaled by outer units in the range $2 \le r/D \le 4$. a Smooth plate; b $k_{99}/D=0.05$; c $k_{99}/D=0.12$; d $k_{99}/D=0.15$. Solid lines, $\overline{u'_r u'_r}/u_m^2$; dashed lines, $\overline{u'_\theta u'_\theta }/u_m^2$; dash-dot lines, $\overline{u'_z u'_z}/u_m^2$

Fig. 12

Reynolds shear stress profiles scaled by outer units in the range $2 \le r/D \le 4$. a Smooth plate; b $k_{99}/D=0.05$; c $k_{99}/D=0.12$; d $k_{99}/D=0.15$

From Fig. 11 it also transpires that surface roughness greatly affects the radial normal Reynolds stress component $\overline{u'_r u'_r}$. In the smooth case, $\overline{u'_r u'_r}$ is characterized by the presence of a single global maximum located in the outer layer of the wall-jet around $z \approx 2.5 z_m$. The location of such maximum and its value do not seem to be strongly influenced by surface roughness. In addition, the outer units scaling results in a reasonable collapse of the curves around this maximum. Increased turbulence fluctuations of the radial velocity component characterize the inner layer region for all the turbulent cases. In particular, for a sufficiently large roughness characteristic size (i.e. for the cases $k_{99}/D=0.12$ and $k_{99}/D=0.15$), this increased turbulence activity manifests itself with the appearance of a secondary peak in the $\overline{u'_r u'_r}$ profiles around $(z-k) \approx 0.3(z_m-k)$. The intensity of the secondary peak overshoots the primary peak present in the outer layer region. While the location of the secondary peak scales reasonably well with $(z_m - k)$, the same does not appear to apply for its magnitude scaled with $u_m^2$.

Despite the scattering of the data observed in the inner region for the cases $k_{99}/D=0.12$ and $k_{99}/D=0.15$, the normal Reynolds stress components $\overline{u'_\theta u'_\theta }$ and $\overline{u'_z u'_z}$ do not show significant effects of the surface roughness. Especially, the profiles are characterized by approximately the same shape in the inner region of the wall-jet. In such a scenario, it is likely that the appearance of the secondary peak in the $\overline{u'_r u'_r}$ profiles can be ascribed to the wakes produced by surface roughness elements. The clear increase of turbulence intensity in the near-wall region of the rough cases was also observed in the analysis of the mean turbulent kinetic energy distribution reported in Fig. 4.

The outer units scaled Reynolds shear stress profiles $\overline{u'_r u'_z}$ in the wall-jet region are displayed in Fig. 12. Overall, the Reynolds shear stress profiles are not greatly affected by surface roughness. The Reynolds shear stress is negative in almost all the inner layer and it is positive in the outer layer. The zero crossing of the profiles occurs slightly beneath the location of the local maximum radial velocity. At the wall-normal distance where the mean radial velocity is maximum (i.e. at $z=z_m$), the Reynolds shear stress attains the value $\overline{u'_r u'_z}=0.01u_m^2$. A reasonable collapse of the outer units scaled profiles is observed for all the investigated cases. However, it is noted that, even the smooth wall case shows minor scattering of the profiles in the neighbourhood of the outer layer peak around $z\approx 2.5z_m$. In the range of wall-normal distances $0.8<(z-k)/(z_m-k)<2$, all the rough cases show very good scaling of the profiles.

Fig. 13

Distribution along the impingement plate of the mean roughness height k scaled by the local inner layer thickness $(z_m-k)$. $k_{99}/D=0.05$, ; $k_{99}/D=0.12$, ; $k_{99}/D=0.15$,

The relative size of the characteristic roughness size k with respect to the scaling length $z_m$ is visualized through the ratio $k/(z_m-k)$ in Fig. 13. Naturally, the relative size of the surface roughness to the inner layer thickness decreases with increasing radial distances, as the boundary layer grows along the plate. Within the range of radial positions $2 \le r/D \le 4$ (i.e. within the region where self-similarity of outer units scaled radial velocity is observed), the smallest roughness size case has $k/(z_m-k)<1$, while the same feature is observed for the other cases for approximately $r/D>3$. Then, in the considered interval, the surface roughness is sufficiently small not to affect sensibly either $u_m$ or $z_m$ and, ultimately, the collapse of the velocity profiles.

Based on theoretical arguments, George et al. (2000) suggest that, for fully developed wall-jets,

$$\begin{aligned} u_o \sim \delta ^n \end{aligned}$$

(8)

where $u_o$ and $\delta$ are outer layer velocity and length scales, respectively, and n is an exponent that can depend, at most, on source conditions of the wall-jet. Here $u_o$ and $\delta$ are identified with $u_m$ and $z_{1/2} - z_m$ respectively. Figure 14 shows that for an extended range of radial locations, the relationship in Eq. 8 is observed also in the present case. Moreover, the figure confirms the mild influence that the considered surface roughness has on the outer layer units.

Fig. 14

Log-log plot of $u_m/U_b$ and $(z_{1/2}-z_m)/D$. Smooth plate, ; $k_{99}/D=0.05$, ; $k_{99}/D=0.12$, ; $k_{99}/D=0.15$, ; , $u_m/U_b=0.065(z_{1/2}-z_m)^{-1.06}$

3.3 Wall-Jet: Inner Layer Scaling

According to George et al. (2000), for plane wall-jets at infinite local Reynolds numbers, the appropriate characteristic velocity and length scales in the inner layer of the jet are, respectively, the friction velocity $u_\tau =\sqrt{ \tau _w / \rho }$ and the viscous length scale $\delta _\nu =\nu /u_\tau$. Banyassady and Piomelli (2015) further argue that, for very large Reynolds numbers, the separation of scales between the inner and outer layers should allow the appearance of a universal logarithmic-law in the inertial range for the mean radial velocity profiles.

The presence of surface roughness complicates the problem, as it determines a new range of length scales (those comparable to the characteristic size of the roughness topography) at which the flow is, possibly, directly influenced.

Based on well-established results on surface roughness effects in canonical shear flows (Chung et al. 2021; Kadivar et al. 2021), it is expected that similarity of friction-scaled velocity profiles subsists provided that, at the same time, $k \ll z \le \delta$ and $\delta _\nu \ll z \le \delta$ (here $\delta$ indicates a suitable characteristic length of the outer layer). In addition, the universal logarithmic behavior of the mean velocity profile appears when sufficient separation with the outer length scale $\delta$ exists (i.e. when $k \ll z \ll \delta$ and $\delta _\nu \ll z \ll \delta$).

The comparison of the roughness size k with the viscous length scale $\delta _\nu$ is displayed for all the rough cases in terms of the roughness Reynolds number $k^+=k/\delta _\nu$ in Fig. 15 (from now on, a $+$ superscripts is used to indicate inner units scaled quantities). After the rapid increase of $k^+$ for $0<r/D<1$, a monotonically decreasing behavior is observed for increasing radial distances. As the wall-jet develops, the viscous length $\delta _\nu$ increases because of the decrease in total stress experienced at the wall by the fluid.

Fig. 15

Roughness Reynolds number $k^+=k/\delta _\nu$ distribution along the impingement plate. $k_{99}/D=0.05$, ; $k_{99}/D=0.12$, ; $k_{99}/D=0.15$,

Mean radial velocity profiles scaled by inner units are depicted in Fig. 16 for all the simulated cases. The profiles plotted in the figure are taken within the interval $2\le r/D \le 4$ where also the mean radial velocity profiles scaled by outer units showed a self-similar character (as discussed in Sect. 3.2). All the plotted smooth wall case profiles collapse consistently well for approximately $z^+<200$. On the other hand, the presence of roughness deteriorates the self-similar character of the inner units scaled mean radial velocity profiles, with the decline becoming more significant for increasing size of the roughness. Nevertheless, it must also be considered that the roughness size in the three cases is large relative to the local values of the viscous length scale $\delta _\nu$, as it can be appreciated in Fig. 15. Therefore, it is expected that, for all the three cases, the roughness sub-layer extends to wall-normal distances comparable to $z_m^+$. With this perspective, it is in fact remarkable to observe that the similar character of the velocity profiles is not completely compromised.

Fig. 16

Inner units scaled mean radial velocity profiles in the range $2 \le r/D \le 4$. a Smooth plate; b $k_{99}/D=0.05$; c $k_{99}/D=0.12$; d $k_{99}/D=0.15$

In each plot reported in Fig. 16, a black dashed line represents the linear behavior for $z^+<10$ and the logarithmic law:

$$\begin{aligned} u_r^+=\frac{1}{\textrm{k}}\log (z^+) + B \end{aligned}$$

(9)

in the range $10<z^+<100$. In Eq. 9, $\textrm{k}=0.41$ is the von Kármán constant and $B=5.2$ is the intercept of the logarithmic law at $z^+=1$ (Pope 2000). Even for the reference smooth wall case, the interaction between the inner and the outer layers of the wall-jet appears to be predominant to such a degree that the logarithmic behavior cannot be established. George et al. (2000) suggest that, for plane wall-jets, sufficient scale separation between the inner and outer layers of the wall-jet can be assumed roughly for $z_{1/2}^+>3000$. When this condition is met, the inner and outer layers of the wall-jet become actually very similar to, respectively, a turbulent boundary layer and a free-shear flow. In this regime, a universal logarithmic behavior of the mean radial velocity can then be expected to appear in the inertial range of wall-normal distances (Banyassady and Piomelli 2015).

For the presented cases, $(z_{1/2}-k)^+$ distributions are reported in Fig. 17. From the figure, it can be seen that, for all the cases, $(z_{1/2}-k)^+$ attains a value far below the aforementioned suggested threshold at all radial locations. Consistently, no clear evidence of universal logarithmic behavior is seen in Fig. 16.

The inner units scaling of the Reynolds stresses in the wall-jet region is tested in Fig. 18 for the normal stresses and in Fig. 19 for the shear stress. The greatest scattering of the data is observed in the $\overline{u'_r u'_r}^+$ profiles, while a somewhat better collapse of the curves is seen for $\overline{u'_\theta u'_\theta }^+$, $\overline{u'_z u'_z}^+$ and $\overline{u'_r u'_z}^+$. It should be noted that the scattering of the inner units scaled data could be potentially ascribed to the uncertainties associated to the computation of the total wall-stress by means of the procedure discussed in Sect. 3.2. Nevertheless, inner units scaled mean radial velocity and Reynolds stresses profiles show a fairly good collapse over extended ranges of wall-normal distances, and visible deviations from self-similarity are encountered similarly to what was observed in the analysis of the outer units scaled statistics, where the uncertainties related to the computation of the mean wall-stress do not play a role.

Fig. 17

Distribution along the impingement plate of the outer layer thickness measure $z_{1/2}$ scaled with the local viscous length scale $\delta _\nu$. Smooth plate, ; $k_{99}/D=0.05$, ; $k_{99}/D=0.12$, ; $k_{99}/D=0.15$,

Fig. 18

Normal Reynolds stresses profiles scaled by inner units in the range $2 \le r/D \le 4$. a Smooth plate; b $k_{99}/D=0.05$; (c) $k_{99}/D=0.12$; d $k_{99}/D=0.15$. Solid lines, $\overline{u'_r u'_r}^+$; dashed lines, $\overline{u'_\theta u'_\theta }^+$; dash-dot lines, $\overline{u'_z u'_z}^+$

Fig. 19

Reynolds shear stress profiles scaled by inner units in the range $2 \le r/D \le 4$. a Smooth plate; b $k_{99}/D=0.05$; c $k_{99}/D=0.12$; d $k_{99}/D=0.15$

4 Conclusions

The work presented DNS of a turbulent impinging jet over smooth and rough plates. In the considered flow configuration, the jet originates from a fully developed turbulent pipe flow at $Re_b=10 \, 000$ and impinges normally onto a plate positioned at 2D distance from the jet exit section. Surface roughness is distributed homogeneously over the impingement plate and is described by a surface height distribution $h=h(x_1,x_2)$. Three different surfaces were selected, each one featuring a Gaussian wall height distribution characterized by a different roughness size $k_{99}$ (i.e. the $99\%$ confidence interval of the PDF of the roughness height distribution); namely, $k_{99}=0.05D, \, 0.12D, \, 0.15D$.

The presented results show a significant impact of the surface roughness on the mean flow field, especially in the wall-jet region of the flow. The latter is identified as the two-layers shear flow occurring next to the impingement plate after the deflection of the flow near the impingement region. Compared to the smooth wall case, the presence of surface roughness induces a greater drag on the flow and limits the development of the radial wall-jet. This effect gets more evident for roughness topographies of larger characteristic size. Within the wall-jet region, the impact of surface roughness on the self-similar character of the mean radial velocity profiles and Reynolds stresses has been addressed by scaling these quantities using two different sets of characteristic velocity and length scales for the inner and outer layers of the wall-jet.

Outer layer characteristic velocity and length scales were identified with the maximum radial velocity $u_m$ and its wall-normal location $z_m$ respectively. A reasonable collapse of the mean radial velocity profiles scaled by outer units is observed for all the cases in the range of radial locations $2\le r/D \le 4$. The presence of surface roughness introduces a weak scattering of the velocity profiles, especially in the near-wall region. The mild effect of surface roughness on the self-similar character of the mean radial velocity profiles is ascribed to the rather weak influence that surface roughness has on the outer units. Nonetheless, a greater scatter of the profiles is observed in the outer units scaled Reynolds stress components profiles in the same range of radial locations.

Characteristic velocity and length scales in the inner layer of the wall-jet were identified with the friction velocity $u_\tau$ and the viscous length scale $\delta _\nu$. The mean radial velocity profiles scaled by inner units show a good collapse in the range of radial locations $2\le r/D \le 4$ for the smooth and $k_{99}/D=0.05$ cases. On the other hand, larger roughness sizes are shown to produce a stronger impact on the self-similar character of the mean velocity profiles up to approximately $z^+=z_m^+$. Similarly to the outer units scaling, a broader scatter of the inner units scaled data is observed in the Reynolds stress profiles in the same range of radial locations. It is also noted that part of the observed scattering could be ascribed to the uncertainties stemming from the specific approach adopted to compute the total wall-stress.

The relatively low local Reynolds numbers attainable along the impingement plate within the present DNS framework prevent the possibility of reaching sufficient scales separation between the inner and the outer layers of the jet. Accordingly, significant interactions between the two layers occur among the two layers at any radial location for all the investigated cases and the inner units scaled mean radial velocity profiles do not display any range of wall-normal distances where a logarithmic behavior can be distinguished.

Appendix A Extrinsic Averaging

For the cases with surface roughness on the impingement plate, the spatial averaging in the circumferential direction is performed over both fluid and solid regions of the domain. This way of computing averages is known as extrinsic (or also superficial or comprehensive spatial average) averaging. Conversely, considering only fluid regions in the computation of averages is usually termed intrinsic averaging. Extrinsic averaging is widely used in the literature regarding flows through porous media (Wood et al. 2020), atmospheric boundary layer over vegetation and urban canopies (Böhm et al. 2013; Castro 2017; Cheng et al. 2021) and turbulent shear flows over stream-wise aligned ridges (Stroh et al. 2020; Castro et al. 2021) and rough surfaces (Yuan and Piomelli 2014; Stroh et al. 2020). The usually adopted justification in favor of using extrinsic averaging is that the solid regions represent a small fraction of the total volume. In such a scenario, the differences between the two averaging approaches can be deemed negligible. Introducing the porosity $\epsilon$ as the ratio of the volume occupied by the fluid to the total volume, it is possible to check whether the aforementioned hypothesis holds (i.e. $\epsilon \approx 1$).

Fig. 20

Porosity of the investigated rough surfaces. $k_{99}/D=0.05$, ; $k_{99}/D=0.12$, ; $k_{99}/D=0.15$,

The considered surface roughness is statistically homogeneous in the $x-y$ plane, but not in the wall-normal direction. Hence, the porosity is a function of the wall-normal direction and can be defined as $\epsilon (z) = A_f(z)/A_{tot}$, where $A_f(z)$ is the area occupied by the fluid at a wall-parallel slice cutting the surface at z, and $A_{tot}$ is the total area at the same wall-normal height (i.e. $A_{tot} = A_f(z) + A_s(z)$, where $A_s(z)$ represents the area occupied by the solid at the same wall-normal height). Figure 20 represents the wall-normal variation of the porosity for the three investigated rough surfaces. In the figure, the wall-normal coordinate is scaled by the height of the maximum peak of the roughness distribution $k_{max}$. It is observed that for approximately $z > 0.6 k_{max}$, the porosity is close to unity. Moving closer to the bottom plate (i.e. decreasing z), the porosity drops quickly to very small values, meaning that surface roughness tends to be almost impermeable for approximately $z < 0.3 k_{max}$.

Accordingly, it is expected for extrinsic averaging to provide reliable predictions of the mean flow properties sufficiently far away from the roughness core (i.e. for approximately $z>0.6k_{max}$; nonetheless, we note that intrinsic averaging should be employed whenever the mean flow properties within the roughness core are addressed. The comparison between extrinsic and intrinsic averaging of the time-averaged radial velocity component is reported in Fig. 21 for the three investigated rough cases.

Fig. 21

Color maps of the mean radial velocity component: left column, extrinsic space averaged field; right column, intrinsic averaged field. a, b $k_{99}/D=0.05$; c, d $k_{99}/D=0.12$; d, e $k_{99}/D=0.15$. A white dashed line represents the $0.6k_{max}/D$

In addition, as it is further discussed in Sects. 3.1 and 3.2, the extrinsic averaging results in a homogenization of the flow region where surface roughness is present. This fact is conveniently used for two important aspects. First, it suggests a possible way of defining a zero wall-height which allows the comparison of the mean flow over the surface roughness with the reference smooth wall case; second, the homogenization of the wall allows to estimate the total wall-stress by assessing the wall-normal mean radial velocity gradient at the interface between the homogenized wall and the fluid region.