An Empirical Wall Law for the Mean Velocity in an Adverse Pressure Gradient for RANS Turbulence Modelling

Abstract

An empirical wall law for the mean velocity in an adverse pressure gradient is presented, with the ultimate goal of aiming at the improvement of RANS turbulence models and wall functions. For this purpose a large database of turbulent boundary-layer flows in adverse pressure gradients from wind tunnel experiments is considered, and the mean velocity in the inner layer is analysed. The log law in the mean velocity is found to be a robust feature. The extent of the log-law region is reduced in ratio to the boundary layer thickness with increasing strength of the pressure gradient. An extended wall law emerges above the log law, extending up to the outer edge of the inner layer. An empirical correlation to describe the reduction of the log-law region is proposed, depending on the pressure-gradient parameter and on the Reynolds number in inner viscous scaling, whose functional form is motivated by similarity and scaling arguments. Finally, there is a discussion of the conjecture of the existence of a wall law for the mean velocity, which is governed mainly by local parameters and whose leading order effects are the pressure gradient and the Reynolds number, but whose details can be perturbed by higher-order local and history effects.

1 Introduction

Significant uncertainties are still associated with predicting of turbulent boundary-layer flows over smooth surfaces subjected to an adverse pressure gradient (APG) and flow separation using statistical turbulence models based on the Reynolds-averaged Navier-Stokes (RANS) equations. The lack of knowledge about an empirical wall law for the mean velocity in an adverse pressure gradient is a primary hurdle for the improvement of RANS turbulence models.

For turbulent boundary-layer flows at zero pressure gradient, there is a wide consensus that the mean velocity U in the inner part of the boundary layer at sufficiently large Reynolds numbers can be described by the log law (see Marusic et al. 2013)

$$\begin{aligned} u^+=\frac{1}{\kappa }\log (y^+)+B\,. \end{aligned}$$

(1)

Here y is the wall-distance, and inner viscous scaling $u^+=U/u_\tau$, $y^+=y u_\tau /\nu$ is used with the wall shear stress $\tau _w$, the density $\rho$, the friction velocity $u_\tau =\sqrt{\tau _w/\rho }$, and the kinematic viscosity $\nu$. The outer edge of the region occupied by the log law is near $y=0.15\delta$, with $\delta$ being determined from a fit of the composite law-of-the-wall/law-of-the-wake (Marusic et al. 2013). The region $y<0.15\delta$ will be referred to as the inner layer.

The resilience of the log law for the mean velocity in an APG is widely reported in Coles and Hirst (1969), Galbraith et al. (1977), Perry et al. (1966), Alving and Fernholz (1995), and Johnstone et al. (2010). The region occupied by the log law in ratio to $\delta$ is found to be reduced, compared to the zero-pressure-gradient case, as the effect of the APG, e.g., the pressure-gradient parameter in inner viscous scaling

$$\begin{aligned} \Delta p_s^+=\nu /(\rho u_\tau ^3)\mathrm {d}P/\mathrm {d}s \end{aligned}$$

(2)

becomes stronger (see Alving and Fernholz 1995; Knopp 2016). Here P is the pressure and s is the wall-tangential direction of the mean velocity as $y\rightarrow 0$ (see Sect. 2.1). Some researchers report that a so-called half-power law or square-root law (abbreviated: sqrt-law) emerges above the log law (see Perry et al. 1966; Kader and Yaglom 1978, and Telbany and Reynolds 1980). To be more precise, these authors used the half-power law for zero-skin-friction flow by Stratford (1959) (given in equation (15) in Sect. 2.3). Note that the half-power law is related to the y-scaling of the mixing length (see Stratford 1959). This distance-from-the-wall scaling was recently found for the turbulent structures of the APG flow by Romero et al. (2022). Alternatively, an extended wall law was applied in the entire inner layer above the buffer layer (see Szablewski 1960; Townsend 1961, and Afzal 2008), which is asymptotic to the log law at low values of $\Delta p_s^+$ and asymptotic to the half-power law at large values of $\Delta p_s^+$. (The extended wall law is given in equation (14) in Sect. 2.3). The extended wall law was used in Knopp et al. (2021) to describe the mean velocity above the log law in an APG. (In Knopp et al. (2021) and in the present work, the designation ”half-power law” is used loosely for the extended wall law (14)).

Regarding the breakdown of the log law in an APG, the work by Alving and Fernholz (1995) supports the idea of a breakdown if $\Delta p_s^+$ exceeds some threshold, e.g., $\Delta p_s^+>0.05$, rather than the onset of instantaneous reverse flow. The breakdown of a region where $u^+$ grows linearly with $\log (y^+)$ needs to be distinguished from a change of $\kappa$ and B. Regarding the latter, some theoretical results and experimental observations indicate that the values for $\kappa$ and B could change for strong values of $\Delta p_s^+$ (see Nickels 2004; Dixit and Ramesh 2008, and Knopp et al. 2021). This question is not studied in the present work, mainly due to the significant effect of the accuracy to determine $u_\tau$ on the values inferred for $\kappa$ (see Knopp et al. 2021).

The great question is the existence of a wall-law region in which the mean-velocity profile depends only on local flow quantities. Such a region was proposed, among others, by Perry et al. (1966), who divided the boundary layer into a wall region and a historical region. In the wall region, only the local flow quantities/variables $(1/\rho )\mathrm {d}P/{\mathrm {d}s}$, $\tau _\mathrm {w}/\rho$, $\nu$, and y govern the mean-velocity profile, and higher derivatives of $(1/\rho )\mathrm {d}P/{\mathrm {d}s}$ and $\tau _\mathrm {w}/\rho$ could be involved above a certain wall-distance. In the historical region, the mean-velocity profile is influenced by upstream events. The existence of a local wall law can be motivated by and is related to the concept of moving equilibrium. Following Kader and Yaglom (1978), a boundary-layer flow is in moving equilibrium if the free-stream velocity $U_\infty$ and the kinematic pressure gradient $(1/\rho )\mathrm {d}P/\mathrm {d}s$ are varying only slowly with the streamwise coordinate s so that the boundary layer adjusts to these variations and its structure at any value of s depends essentially on the relevant local parameters (at the same s) only, not on the upstream history of the flow.

Similar results were found for Couette-Poiseuille (CP) flow by Telbany and Reynolds (1980), reporting that the logarithmic layer is eroded, and ultimately vanishes, as the stress gradient increases in importance. Here the wall-normal stress gradient is given by the streamwise pressure gradient. Moreover, a correlation is reported for the $y^+$-location of transition between the logarithmic layer and the so-called gradient layer (being the half-power law region), i. e., $y^+= 90 \lambda ^{-1/2}$ using the parameter $\lambda =\Delta p_s^+ Re_{\tau ,h}$, with $Re_{\tau ,h}$ based on $u_\tau$ and on the channel half-width h. The systematic reduction of the log-law region and the appearance of a half-power law for CP flow can therefore be seen as a consequence of the pressure gradient and not a history effect, as CP flow is a self-similar flow in dynamic equilibrium in the sense of Gungor et al. (2016). The findings for CP flow are seen to support the conjecture of a local wall law.

The present approach to find a wall law in an APG uses a combination of data analysis and theoretical arguments. A large database from wind tunnel experiments was analysed. The initial preliminary results were presented in Knopp (2016). The core of the database is the famous test case collection (Coles and Hirst 1969) published at the seminal 1968 Stanford conference on turbulent boundary layers.

Analysis of the database prompts the following hypotheses about an empirical wall law for the mean velocity in an adverse pressure gradient:

• The log law in the mean-velocity profile is a robust feature in an APG;

• The log-law region is thinner than its zero-pressure-gradient counterpart at the same $Re_\tau$ and does not extend up to $y=0.15\delta$;

• The extent of the log-law region in ratio to $\delta$ is decreasing with increasing $\Delta p_s^+$;

• An extended wall law (designated loosely as ”half-power law”) emerges above the log law in a large part of the region the log law occupies at zero pressure gradient.

Note that an additional hypothesis states that the von Kármán constant $\kappa$ changes with $\Delta p_s^+$ and that this can be described by the model by Nickels (2004); however, this is not considered in the present work. In the present paper, the focus is directed at the mean velocity in the inner part of turbulent boundary layers. Recent work focusing mainly on the outer part of the boundary layer in an adverse pressure gradient can be found in Maciel et al. (2018), Bobke et al. (2017) and Vila et al. (2017).

This work is restricted to turbulent boundary-layer flows. Internal flows with streamwise pressure gradients like Couette-Poiseuille flows (Telbany and Reynolds 1980) or flows in divergent channels are not considered. The analysis is restricted to the case of plane-wall, two-dimensional flow. Effects of streamwise curvature are ignored. The effects of three-dimensional boundary-layer flows with sweep and cases with a three-dimensionality of the flow due to a spanwise expansion of the geometry or spanwise surface curvature are excluded. Streamwise curvature leads to a departure from the log law which is increasing with increasing $y^+$. The profile for $u^+$ turns below the log law in the case of a concave wall and above in the case of a convex wall (see Kim and Rhode 2000). In three-dimensional turbulent boundary layer flows, a streamwise and a spanwise component of the mean velocity arise (defined in a local coordinate system with the x-axis aligned with the freestream or with the wall shear stress vector), and a spanwise pressure gradient results in flow skewing (see Devenport and Lowe 2022). A wall law for the mean-velocity component aligned with the wall shear stress and the transverse component perpendicular to it is described in van den Berg (1973), van den Berg (1975), which accounts for streamwise and spanwise pressure gradients.

The paper is organized as follows. The theoretical background is described in Sect. 2. The database is presented in Sect. 3. The methods used for the evaluation of the mean-velocity profiles are described in Sect. 4. The results are presented in Sect. 5. The correlations for the wall law in an APG are given in Sect. 6. An attempt to discuss the issues of a local wall law, the moving-equilibrium concept, history effects, and effects of the measurement accuracy is given in Sect. 7. The conclusions are given in Sect. 8.

Finally, as implied in the title, the connection between the present analysis and RANS turbulence models is briefly described. A preliminary APG modification was presented in Knopp (2016). The idea is to use a model augmentation term in conjunction with a blending function. The augmentation term is added to the transport equation for the specific rate of turbulent dissipation $\omega$. It is designed to obtain the assumed solution for the mean velocity and the turbulence quantities in the half-power law region. The blending function is used to activate the augmentation term only in the half-power law region. It is based on the correlations that describe the regions of the log law and the half-power law as functions of $y^+$, $Re_\tau$, $\Delta p_s^+$ and $y/\delta$ (see Sect. 6).

2 Boundary-Layer Theory

This section presents the theoretical results used for the design and the calibration of the wall law.

2.1 Boundary-Layer Approximation

Two-dimensional, incompressible turbulent boundary-layer flow in a wall-fitted coordinate system with streamwise wall-parallel direction s, wall-normal direction y and corresponding velocity components U, V is assumed (see Hinze 1975)

$$\begin{aligned} \nu \frac{\partial ^2 U}{\partial y^2} - \frac{\partial \overline{u'v'}}{\partial y} = \frac{1}{\rho }\frac{\mathrm {d} P_\mathrm {w}}{\mathrm {d} s} +U\frac{\partial U}{\partial s} +V\frac{\partial U}{\partial y} + \frac{\partial }{\partial s}\left( \overline{u'^2}-\overline{v'^2}\right) \,. \end{aligned}$$

(3)

The subscript w indicates values at $y=0$. Integration of (3) from the wall to the wall-distance y gives the following relation for the total shear stress $\tau$

$$\begin{aligned} \frac{\tau }{\rho } \equiv \nu \frac{\partial U}{\partial y}- \overline{u'v'} =\frac{\tau _w}{\rho } +\frac{1}{\rho }\frac{\mathrm {d} P_\mathrm {w}}{\mathrm {d} s} y +I_\mathrm {cu}(y)+I_\mathrm {cv}(y)+I_\mathrm {r}(y) \end{aligned}$$

(4)

where $\tau _w$ denotes the wall shear stress and with the following notation

$$\begin{aligned} I_\mathrm {cu}(y)=\int _{0}^yU\frac{\partial U}{\partial s}\,\mathrm {d}{\tilde{y}}\,, \quad I_\mathrm {cv}(y)=\int _{0}^yV\frac{\partial U}{\partial {\tilde{y}}}\,\mathrm {d}{\tilde{y}}\,, \quad I_\mathrm {r}(y)=\int _{0}^y \frac{\partial }{\partial s}\left( \overline{u'^2}-\overline{v'^2}\right) \,\mathrm {d}{\tilde{y}} \end{aligned}$$

(5)

for the integrated convective term and the Reynolds normal stress term.

Note that in the three-dimensional case, the direction s used in (2) is defined by the direction of the wall-parallel velocity as $y\rightarrow 0$ (being the direction of the skin friction vector).

2.2 A Local Model for the Total Shear Stress

The next step is to motivate local surface parameters to characterise the different terms in the mean momentum balance and hence the mean-velocity profile in the inner layer. A first-order local model for the total shear stress was proposed by Coles (1956) and Perry (1966). It is based on the following ansatz for the mean-velocity profile in the inner layer

$$\begin{aligned} U(s,y)=u_\tau (s) \,f(y^+(s,y))\,,\quad y^+(s,y)=u_\tau (s)y/\nu \,. \end{aligned}$$

(6)

As described in van den Berg (1973) and Knopp et al. (2015), the mean-inertia term can be written as

$$\begin{aligned} \int _0^yU \frac{\partial U}{\partial s}\,\mathrm {d}{\tilde{y}} + \int _0^yV \frac{\partial U}{\partial {\tilde{y}}}\,\mathrm {d}{\tilde{y}} =\nu \frac{\mathrm {d} u_\tau }{\mathrm {d} s}\int _0^{y^+} f^2\,\mathrm {d}{\tilde{y}}^+\,. \end{aligned}$$

(7)

By substitution of (7) into (5) and neglecting the contribution of the Reynolds normal stress term $I_\mathrm {r}^+(y^+)$ in (5), the result for $\tau ^+=\tau /\tau _w$ is

$$\begin{aligned} \tau ^+(y^+) =1 + \Delta p_s^+ y^++\Delta u_{\tau ,s}^+ I_1^+\,, \quad \Delta u_{\tau ,s}^+= \frac{\nu }{u_\tau ^2}\frac{\mathrm {d} u_\tau }{\mathrm {d} s}\,\quad I_1^+=\int _0^{y^+} f^2\mathrm {d}{\tilde{y}}^+ \end{aligned}$$

(8)

showing that the total shear stress in the inner layer not only depends on $\Delta p_s^+$ but also on the wall-shear-stress-gradient parameter $\Delta u_{\tau ,s}^+$, which describes the local flow deceleration. The approximation to neglect $I_\mathrm {r}^+(y^+)$ if the flow is far from incipient separation is supported by the DLR/UniBw experiment II (see Figs. 7.1 and 7.2 in Knopp 2019). Note that in the $y^+$-region where the mean-velocity profile follows the log law $I_1^+$ can be approximated by Eq. (8) in Galbraith et al. (1977)

$$\begin{aligned} \tau ^+=1+\Delta p_x^+y^+ + \Delta u_{\tau ,x}^+\left[ y^+\left( k_1\left( \log y^+\right) ^2+k_2\log (y^+)+k_3\right) +k_4\right] \end{aligned}$$

(9)

for $y^+>30$ with constants $k_1,\ldots ,k_4$ depending only on $\kappa$ and B. The total shear stress is approximated by a linear relation in e.g. McDonald (1969)

$$\begin{aligned} \tau ^+=1 + \alpha ^+y^+\,,\quad \quad \alpha ^+\equiv \lambda \Delta p_s^+\,, \end{aligned}$$

(10)

where $\lambda$ is a constant smaller than one, and $\alpha ^+\equiv \lambda \Delta p_s^+$ is called the effective pressure gradient. The linear approximation (10) can be inferred from (9) for small values of $\Delta u_{\tau ,s}^+$ and $y^+$.

A higher-order model for $\tau ^+$ can be obtained by extending (6), motivated by the dependence of f on $\Delta p_s^+$ in the half-power law

$$\begin{aligned} U(s,y)=u_\tau (s) \,f(y^+(s,y), \Delta p_s^+(s))\,,\quad y^+(s,y)=u_\tau (s)y/\nu \end{aligned}$$

(11)

to account for higher-order effects on $\tau ^+$. The extended model for $\tau ^+$, which is described in detail in Knopp et al. (2015), includes the additional local flow parameter $\Delta ^2 p_s^+$ which involves $\mathrm {d}^2P/\mathrm {d}s^2$. This higher-order local parameter will be used in the discussion of the conjecture of a local wall law in Subsects. 7.1 and 7.2.

2.3 Log Law/Half-Power Law

For the mean-velocity profile in an adverse pressure gradient, a log-law/half-power-law structure is assumed, motivated by the findings described in the introduction

$$\begin{aligned} u^+={\left\{ \begin{array}{ll} u_{\mathrm {log}}^+ &{} \quad \text {if}\quad y^+ \in (y^+_{\mathrm {log,min}}, \,y^+_{\mathrm {log,max}})\\ u_{\mathrm {sqrt}}^+ &{} \quad \text {if}\quad y^+ \in (y^+_{\mathrm {sqrt,min}}, \,y^+_{\mathrm {sqrt,max}}) \end{array}\right. } \end{aligned}$$

(12)

with the log law

$$\begin{aligned} u_{\mathrm {log}}^+=\frac{1}{\kappa }\log (y^+)+B \end{aligned}$$

(13)

and the extended wall law (involving the parameter $\alpha ^+$ defined in (10))

$$\begin{aligned} u_{\mathrm {sqrt}}^+=\frac{1}{K}\left[ 2\left( (1+\alpha ^+ y^+)^\frac{1}{2}-1\right) + \log (y^+) +2\log \left( \frac{2}{(1+\alpha ^+ y^+)^\frac{1}{2}+1}\right) \right] + B_{\mathrm {o}}\,. \end{aligned}$$

(14)

The designation ”half-power law” is used loosely for the extended wall law.

Note that there is an intermediate region in which neither the log law nor the half-power law describes the mean velocity. The important parameters for the calibration are $y^+_{\mathrm {log,max}}$ and $y^+_{\mathrm {sqrt,min}}$. They describe the reduction of the log-law region, and are supposed to depend, among other effects, on the pressure gradient and on the Reynolds number. They will be calibrated using the database. The half-power law is assumed to extend up to the outer edge of the inner layer. The value for $\kappa$ is assumed to be constant with $\kappa =0.41$, and K will be studied in Sect. 6.4. The value of $y_\mathrm {log, min}^+$ is expected to depend on the Reynolds number and possibly on the pressure gradient, but is not considered in this work. Note the alternative form of the half-power law by Stratford (1959) for zero-skin-friction flows

$$\begin{aligned} U(y)=\frac{2}{K}\left( \frac{1}{\rho }\frac{\mathrm {d}P}{\mathrm {d}s}\right) ^{1/2}y^{1/2} + C \end{aligned}$$

(15)

which was recently confirmed by the DNS of Coleman et al. (2017).

2.4 A Velocity Scale for the Inner Layer

The classical velocity scale for the inner layer $u_\tau$ leads to well-known issues as the flow approaches separation. As $u_\tau \rightarrow 0$, the profile $u^+$ versus $y^+$ is not defined. Moreover, boundary-layer parameters involving $u_\tau$, e.g.,

$$\begin{aligned} Re_\tau \equiv \delta ^+=\frac{\delta u_\tau }{\nu }\,,\quad \quad \beta _\mathrm {RC}=\frac{\delta ^*}{\rho u_\tau ^2}\frac{\mathrm {d}P_w}{\mathrm {d}s} \end{aligned}$$

(16)

and $\Delta p_s^+$, are approaching zero or infinity. In particular, the Reynolds number $\delta ^+$ is found to give decreasing values as the flow approaches separation, whereas $Re_\theta$ and $Re_\delta ^*$ are increasing, and $\Delta p_s^+$ and $\beta _\mathrm {RC}$ can reach high values mainly due to the small values of $u_\tau$.

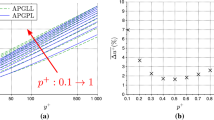
A modified velocity scale for the inner layer was devised in Nickels (2004) as a part of an analytical model for the mean velocity depending on the local value of $\Delta p_s^+$. It involves the quantity $y_c^+$, which is associated with the thickness of the viscous sublayer and related to a critical value of the local Reynolds number based on the total shear stress (cf. (8), neglecting the convective term)

$$\begin{aligned} Re_c=\frac{u_\mathrm {T}y_c}{\nu },\quad \quad u_\mathrm {T}=\left( \frac{\tau \vert _{y=y_c}}{\rho }\right) ^{1/2}\, , \quad \quad \tau ^+\vert _{y=y_c}=1+\Delta p_s^+y_c^+\, . \end{aligned}$$

(17)

The assumption that $Re_c$ has a universal value for all wall-bounded flows ($Re_c=12$) leads to a cubic equation for $y_c^+$, which can be interpreted as the critical value above which the viscous sublayer becomes unstable,

$$\begin{aligned} \Delta p_s^+\left( y_c^+\right) ^3+\left( y_c^+\right) ^2-Re_c^2=0\,. \end{aligned}$$

(18)

The physically relevant solution for $y_c$ is the smallest positive root of (18).

The exact solution for $y_c$ follows from the formula by del Ferro, Tartaglia, and Cardano (see Nickels 2004). For large $\Delta p_s^+$ this solution may be approximated by

$$\begin{aligned} y_c^+ = \frac{Re_c^{2/3} (\Delta p_s^+)^{2/3}-\frac{1}{3}}{\Delta p_s^+} \end{aligned}$$

(19)

(see also eq. (10.1) in Nickels (2004)). As $u_\tau \rightarrow 0$ (and $\Delta p_s^+\rightarrow \infty$)

$$\begin{aligned} u_\mathrm {T}=u_\tau (1+\Delta p_s^+ y_c^+)^{1/2}\rightarrow Re_c^{1/3}u_p\,, \end{aligned}$$

(20)

i.e., $u_\mathrm {T}$ converges to the non-zero value $Re_c^{1/3}u_p$. Here $u_p=\vert \nu /\rho \mathrm {d}P_\mathrm {w}/\mathrm {d}s\vert ^{1/3}$ is the so-called pressure-viscosity velocity by Stratford (1959) with $\Delta p_s^+=(u_p/u_\tau )^3$.

For $0<\Delta p_s^+<0.1$, the analytical solution of (18) can be approximated by

$$\begin{aligned} y_c^+\approx Re_c (1+ y_{c,0}^+\Delta p_s^+)^{-1/3}\,,\quad \quad y_{c,0}^+=16\,. \end{aligned}$$

(21)

Figure 1 provides some illustration for $y_c^+$ (left) and for $u_\mathrm {T}/u_\tau$ (right).

Fig. 1

Behaviour of $y_c^+$ (left) from (18), (19), (21) and modified velocity scale $u_\mathrm {T}$ (right)

The above model could require modification for large values of $\Delta p_s^+$. Then the mean-inertia term can become important and needs to be accounted for in the approximation of $\tau ^+$ in (17).

2.5 Self-Similarity

The existence of a wall law is related to the question of self-similarity of the mean-velocity profile in the inner layer. The classical approach is to seek a similarity solution of the form

$$\begin{aligned} U(s,y)=U_e(s)f'(\eta )\,,\quad \overline{u'v'}= u_t^2(s)\, t(\eta )\,,\quad \eta (s,y)=\frac{y}{\delta (s)}\,. \end{aligned}$$

(22)

Note that the choice for $u_t$ for a self-similar scaling of the Reynolds stresses is still open in the literature (see Elsberry et al. 2000). Then consider (3), with the streamwise gradients of the Reynolds stresses being neglected. Substitution of (22) yields (see e.g. Dixit and Ramesh 2008)

$$\begin{aligned} -\frac{\delta U_e}{\nu }\frac{\mathrm {d}\delta }{\mathrm {d}s}\left[ f''f \right] + \frac{\delta ^2}{\nu }\frac{\mathrm {d} U_e}{\mathrm {d}s} \left[ (f')^2 -f''f - 1 \right] = f''' +\frac{U_e \delta }{\nu }\,\left( \frac{u_t}{U_e}\right) ^2\,t'\,. \end{aligned}$$

(23)

A similarity solution exists only if the coefficients are independent of s

$$\begin{aligned} \beta _1\equiv \frac{\delta U_e}{\nu }\frac{\mathrm {d}\delta }{\mathrm {d}s}=\mathrm {const}\,,\quad \beta _H\equiv \frac{\delta ^2}{\nu }\frac{\mathrm {d} U_e}{\mathrm {d}s}=\mathrm {const} \,,\quad \beta _3\equiv \frac{U_e \delta }{\nu }\,\left( \frac{u_t}{U_e}\right) ^2=\mathrm {const}\,. \end{aligned}$$

(24)

Note that $\beta _H$ is the Hartree parameter in the laminar case. It can be written as

$$\begin{aligned} \beta _\mathrm {H} = \frac{\delta ^2}{\nu }\frac{\mathrm {d} U_e}{\mathrm {d}s} = -\Delta p_s^+ \,Re_\tau ^2 \,\left( \frac{u_\tau }{U_e}\right) \,. \end{aligned}$$

(25)

and alternatively in the form $\beta _\mathrm {H}=- \beta _\mathrm {RC}\,Re_\tau ^2 \,Re_{\delta ^*}^{-1}$. Traditionally, $\beta _\mathrm {RC}$ is seen to be the governing parameter of the similarity solution.

3 Database

A database study was performed to account for the variety of turbulent boundary-layer flows in an APG and the richness of the parameter space. Based on the assumption that an asymptotic structure of the mean velocity profile arises only for sufficiently large Re, the focus is on mean-velocity profiles at $Re_\theta >8000$.

3.1 Experimental Data

The database covers the famous test-case collection Coles and Hirst (1969). Additionally, the more recent experiments by Samuel and Joubert (1974), Skare and Krogstad (1994), Marusic and Perry (1995), and Romero et al. (2022) are used. For the data in the collection by Coles and Hirst (1969), their identifiers (IDENTs, abbreviated IDs) are used. The flows by Clauser and by Bradshaw are equilibrium flows. Moreover, two joint DLR/UniBw turbulent boundary-layer experiments are considered. They were designed to achieve large values of $\Delta p_s^+$ and $Re_\theta$.

Two data sets at small Re are included. For the wind tunnel experiment by Nagano et al. (1991) the mean-velocity profiles are for $481 \le Re_\tau \le 639$, $1290\le Re_\theta \le 3350$ and $0.009\le \Delta p_s^+\le 0.025$. For the DNS of a turbulent boundary layer with separation and reattachment by Coleman et al. (2018), $Re_\tau$ is up to 880 and $2000\le Re_\theta \le 6400$ in the APG region, and $\Delta p_s^+$ is increasing from 0.001 to values exceeding 1 as the flow is approaching separation. Note that the low-Re data are used only in Sect. 7.3 to assess the validity of the wall law for small Re. The test cases and their acronyms are summarised in Table  1.

3.2 Boundary-Layer Characterisation

The characterisation of turbulent boundary-layer flows in adverse pressure gradients using suitable boundary-layer parameters is still open (cf. Vila et al. 2017). The parameter space is much wider than for the zero-pressure-gradient case. Figure 2 (left) shows $\beta _\mathrm {RC}$ versus $Re_\theta$. Each symbol corresponds to a mean-velocity profile. The number of data points for $Re_\theta >30000$ is small. The strength of the APG felt in the inner layer can be described by $\Delta p_s^+$. The values of $\Delta p_s^+$ plotted against $Re_\tau$ are shown in Fig. 2 (right). Only in a small number of experiments are values of $\Delta p_s^+>0.02$ reached.

Fig. 2

Characterisation of the turbulent boundary-layer flows in the database

4 Methods for Data Evaluation

This section describes the methods used for the evaluation of the data. The methods to determine the friction velocity $u_\tau$ and the boundary-layer thickness $\delta$ are described in Sect. 4.1. Section 4.2 describes the methods used to identify the regions of the log law and the half-power law. Finally, the assessment of the data in the region of the half-power law is described in Sect. 4.3.

4.1 Fit to the Law-of-the-Wall/Law-of-the-Wake

In the collection by Coles and Hirst (1969), the boundary-layer thickness $\delta$, the wake factor $\Pi$, and the friction velocity $u_\tau$ were determined such that the root-mean-square (r.m.s.) deviation of the data from the law-of-the-wall/law-of-the-wake

$$\begin{aligned} u^+=\frac{1}{\kappa }\log (y^+) + B + \frac{2\Pi }{\kappa }\left( \sin \left( \frac{\pi \eta }{2}\right) \right) ^2\,,\quad \eta =\frac{y}{\delta } \end{aligned}$$

(26)

is minimised. The values $\kappa =0.41$ and $B=5.0$ by Coles & Hirst were used for all cases throughout this work, except for the experiments by DLR/UniBw experiments and by UNH and the two flows at small Re, for which almost direct values for $u_\tau$ are provided. A similar evaluation as in Coles and Hirst (1969) was provided for the flows by Skare and Krogstad (1994) and Marusic and Perry (1995). Note that the recently proposed methods to determine the boundary-layer thickness by Coleman et al. (2018) and Vinuesa et al. (2016) are not used in the present method, as they require additional data which are not available for most of the old data sets in the database.

The first step was a review of the values reported for $\delta$, $\Pi$, and $u_\tau$. First, the mean-velocity profiles were plotted in viscous units and compared with the log law to assess $u_\tau$. The original values for $u_\tau$ could be supported and were used for the data analysis. This concurs with the result by Patel (1965), reporting an uncertainty within $6\%$ for $\Delta p_s^+<0.015$ for the Preston tube. This was seen to be acceptable, given the different sources of uncertainties.

The next step was to review the values for $\delta$. The aim was to ensure comparable and consistent values for $\delta$ among all test cases. The mean-velocity profiles in viscous units were compared with (26) in the law-of-the-wake region, and overall, the values reported for $\delta$ and $\Pi$ were found to give a good agreement. For some data sets, minor adjustments in $\delta$ by visual inspection were applied to obtain a similar matching between the experimental data and (26) near the boundary-layer edge. This is summarised in Table  1, which is explained at the end of this section.

Fig. 3

Comparison of $\delta _{99.5}$ and $\delta$ (left) and $y^+_\mathrm {log,max}/\delta$ versus $\beta _\mathrm {RC}$ (right)

The evaluation of $u_\tau$ and $\delta$ was different for the UNH experiment Romero et al. (2022) and for the DLR/UniBw experiments Knopp et al. (2015) and Knopp et al. (2021). For the UNH flow, the values for $u_\tau$ were determined by matching the hot-wire data for the mean velocity with the LES mean-velocity profiles by Bobke et al. (2017) for $y^+<40$. Note that the values for $u_\tau$ were confirmed by the author using the Clauser-chart method (CCM). The relative deviation in $u_\tau$ was found to be below $1.5\%$. Regarding the boundary-layer thickness, the values by Romero et al. (2022) are used, which were determined using an indirect method involving the profile for $\overline{{u'}^2}$ (see Romero et al. 2022). The values were supported by the evaluation of $\delta _{99.5}$ by the author.

For the DLR/UniBw experiment II at $x=9.944\,\mathrm {m}$, $u_\tau$ was determined using oil film interferometry (OFI) and from the 2D $\mathrm {\mu }\hbox {PTV}$ and 3D LPT data using an (almost) direct method based on a least-squares fit of the data with the mean-velocity profile by Nickels for $y^+<20$ (see Knopp et al. 2021). For the other positions, $u_\tau$ was determined from the 2D2C PIV data using the standard CCM. For the boundary-layer thickness $\delta _{99.5}$ was used, as a close matching with (26) could not be obtained, possibly due to history effects. Note that for all flows, $\delta _{99.5}$ was found to be in close agreement with $\delta$ (see Fig.  3 (left)).

The data evaluation is summarised in Table  1. The fourth column gives the source for the value used for $u_\tau$. In the fifth column, the method used to determine the boundary-layer thickness is specified. Here $\delta$ denotes the approach by Coles and Hirst (1969). The values used for $\delta$ are given in the sixth column. These are mainly the values by Coles and Hirst (1969), although the recomputed values (denoted by re) are used for some of the streamwise evolving flows. For the flow by Marusic & Perry, the recomputed values are used. For the flow by Samuel & Joubert, $\delta$ was determined by the author. The next column gives the maximum deviation for $\delta$ in percent between the original value and the recomputed value. The number in brackets gives the number of mean-velocity profiles for which the deviation is greater than 1%. This shows that the deviation between the values by Coles and Hirst (1969) and the recomputed values is small compared to the other sources of uncertainties. Note that for the flow by Marusic & Perry, the deviation between the original values for $\delta$ and the recomputed values was smaller than 8% for the last four profiles in the region of the strongest APG. The next column specifies the values for $\kappa$ and B used to determine the extent of the log-law region $y^+_\mathrm {log,max}$ (see the next subsection). The log-law with $\kappa =0.41$ and $B=5.0$ by Coles & Hirst is denoted by ” Coles and Hirst (1969)”, whereas ”fit” indicates that $\kappa$ and B are fitted to the mean-velocity profile, which is described in detail in the next section. The last column summarises the assessment for the calibration of the half-power law using the criteria C1 - C4 described in Subsect. 4.3.

Table 1 Summary of the data evaluation and the acronyms used in the figure legends

4.2 Identification of Log Law and Half-Power Law

The next step was the identification of the log-law and the half-power law region. The log-law region is referred to as the region in which the mean-velocity profile can be fitted by a log law. The half-power law region is defined analogously. The notation introduced in Sect. 2.3 is used. For illustration, Fig.  4 shows the mean-velocity profiles for the flow by Ludwieg & Tillmann (1108) at $\Delta p_s^+=3.05\times 10^{-3}$, $Re_\theta =25870$ and $Re_\tau =5031$ (left) and for the flow by Samuel & Joubert at $\Delta p_s^+=0.00735$, $Re_\theta =13804$ and $Re_\tau =2990$ (right).

Fig. 4

Left: Ludwieg & Tillmann, mild APG (1108) at $\Delta p_s^+=3.05\times 10^{-3}$ and $Re_\tau =5031$. Right: Samuel & Joubert, mild APG at $\Delta p_s^+=7.35\times 10^{-3}$ and $Re_\tau =2990$

For the evaluation of $y^+_\mathrm {log,max}$, for each mean-velocity profile, the maximum wall-distance was determined up to which the experimental data for $u^+$ follow the log law (13). The method to determine $y^+_\mathrm {log,max}$ was based on visual inspection and the determination of the $y^+$-position, where a best-approximation polynomial through the data points above the log-law region smoothly joins the log law. The results for $y^+_\mathrm {log,max}$ are plotted against $\beta _\mathrm {RC}$ in Fig.  3 (right). Here $\kappa =0.41$ and $B=5.0$ was used in (13) for all flows, except for the flows by DLR/UniBw and UNH. Note that the influence of using a fitted value for $\kappa$ versus a constant value is discussed below for the DLR/UniBw experiment and in Sect. 7.3.

For the flows by DLR/UniBw and UNH, $u_\tau$ was determined independently of the assumption of the log law. The profiles for $u^+$ show a departure from the log law with $\kappa =0.41$ and $B=5.0$. An iterative method was used to determine the fitted values for $\kappa$ and B and $y^+_\mathrm {log,max}$ simultaneously under the constraint to minimise the least-squares error in the $y^+$-interval used for the fit, which was successively adjusted.

For the DLR/UniBw experiment, a study was made to assess the sensitivity of $y^+_\mathrm {log,max}$ on details of the method used. The details are given in appendix B. The main conclusion is that the sensitivity of $y^+_\mathrm {log,max}$ on details of the evaluation is small for the DLR/UniBw flow compared to the uncertainties of the older flows in the data base (see Sect. 6.5).

The outer edge of the half-power law is assumed to extend up to $y=0.2\delta$. The motivation for this assumption is the observation that the half-power law, if fitted up to $y=0.15\delta$, describes the mean-velocity profile even up to $y=0.2\delta$. The choice of $y=0.2\delta$ has the advantage of increasing the number of data points for the half-power law fit compared to $y=0.15\delta$.

The inner edge of the half-power law, denoted by $y^+_\mathrm {sqrt,min}$, is determined iteratively. In the first step, the two data points below and above $y=0.15\delta$ are chosen and a preliminary fit is computed. Then this stencil is extended successively above and below $y=0.15\delta$. The points with the smallest $y^+$ value are removed if such improves the overall fit; alternatively additional points are included successively if they are in agreement with the fit. For the final evaluation of the half-power law and after a comparison among all test cases, the outer edge is set to the constant value $y=0.21\delta$. For the inner edge, the value determined by the iterative method described above is employed. The results are shown in Fig.  5. In case the above method does not identify two points for the half-power law fit below $y=0.21\delta$, the outer edge is increased, but these data sets are then used with special care (see criterion C1 in Sect. 4.3).

Fig. 5

Inner edge (left) and outer edge (right) used for the fit to the half-power law

4.3 Data Assessment for the Half-Power Law Region

For the calibration of the half-power law, the individual mean-velocity profiles need to be assessed, so that only the suitable ones are considered for the calibration. The number of data points in the half-power law region $N_\mathrm {sqrt}$ is an important quantity for the assessment, and is shown in Fig.  6 (left). This number can become large if $Re_\theta$ is large, if $y^+_\mathrm {sqrt,min}$ is significantly smaller than $0.15\delta ^+$, or if the wall-normal spacing between adjacent data points $\Delta y^+$ is small. The largest values for $N_\mathrm {sqrt}$ are reached for the DLR/UniBw experiment II, exceeding 80 for the 2D2C PIV measurements and 250 for the 3D LPT measurement technique. For some mean-velocity profiles, the number of data points for the half-power law fit is only two. These profiles are considered with special care (see criterion C2 below) for the calibration of the wall law in Sects. 5 and 6.

A theoretical criterion for a half-power law in the form (15) was proposed by Yaglom (1979). Based on the three length scales $\delta _\nu =\nu /u_\tau$, $\delta _p=\rho u_\tau ^2/(\mathrm {d}P/\mathrm {d}s)$, and $\delta$, the criterion can be written in the form $\delta _\nu \ll \delta _p\ll \delta$ (cf. Kader and Yaglom (1978), Yaglom (1979)), or alternatively in the form $\Delta p_s^+\ll 1$ and $\delta ^+\Delta p_s^+\gg 1$ (see Alving and Fernholz (1995)). The values of $\delta ^+\Delta p_s^+$ versus $\Delta p_s^+$ are shown in Fig.  6 (right) for the mean-velocity profiles in the database. From Fig.  6 (right) the downstream profiles of most data sets are meeting the criterion $\delta ^+\Delta p_s^+>15$ (see criterion C3 below), albeit a value of several tens is not considered to be very high by Yaglom (1979). However, $\delta ^+\Delta p_s^+>100$ is reached only for a few mean-velocity profiles.

Fig. 6

Number of data points $N_\mathrm {sqrt}$ in the half-power law region (left) and $\delta ^+\Delta p_s^+$ versus $\Delta p_s^+$ (right)

To summarise: for the assessment of the half-power law region, the following criteria are used:

• C1: Two data points in the half-power law region below $y/\delta =0.21$ and $y_\mathrm {sqrt,max}/\delta \le 0.21$ in Fig.  5 (right);

• C2: $N_\mathrm {sqrt}\ge 3$ for most of the mean-velocity profiles (see Fig.  6 (left));

• C3: $\delta ^+\Delta p_s^+>15$ for at least two mean-velocity profiles (see Fig.  6 (right));

• C4: No significant history effects in the APG region.

The assessment of these criteria is given in the last column of Table  1. An additional minor criterion is the smoothness of the data. The calibration of the half-power law relies mainly on the data sets that satisfy all criteria. The mean-velocity profiles by Perry, Skare & Krogstad, and Schubauer & Klebanoff are at a high Re, exhibit a relatively thick half-power law region and match all criteria C1 - C4. Among them, the lowest number of data points is for the case by Schubauer & Klebanoff, being only between three and five due to the large $\Delta y^+$-spacing. Note that some of the mean-velocity profiles by Perry, by Schubauer & Klebanoff, and by Skare & Krogstad show some wiggles.

Some of the flows are not considered for the final calibration of the half-power law (see Table 1), violating already criteria C1 and C2. An additional difficulty is caused by the substantial wiggles in the data observed for the flows by Clauser and by Schubauer & Spangenberg. Nevertheless, these flows are useful to assess the calibration found for the more suitable data sets.

5 Results and Analysis

This section describes the results of the data evaluation and their analysis. The log-law/half-power-law fit for a variety of mean-velocity profiles of the database is illustrated in Sect. 5.1. The robustness of the log law and the reduction of the extent of the log-law region in an APG are described in Sect. 5.2.

5.1 Mean-Velocity Profiles

This section illustrates the wall law and the results of the fitting method described in Sect. 4. First, two examples at moderately large values of $\Delta p_s^+$ are shown. The mean-velocity profile for the flow by Marusic & Perry Marusic and Perry (1995) at $x=3.08\,\mathrm {m}$, $\Delta p_s^+=7.55\times 10^{-3}$ and at moderately large $Re_\theta =19188$ and $Re_\tau =3406$ is shown in Fig.  7 (left). The profile for the flow by Perry at $\Delta p_s^+=7.85\times 10^{-3}$ and high values of $Re_\theta =73201$ and $Re_\tau =7926$ (ID 2907) is given in Fig.  7 (right).

Fig. 7

Left: Marusic & Perry at $\Delta p_s^+=7.17\times 10^{-3}$ and $Re_\tau =3406$. Right: Perry (ID 2907) at $\Delta p_s^+=7.89\times 10^{-3}$ and $Re_\tau =7926$

Subsequently, profiles at large values of $\Delta p_s^+$ are studied. For the equilibrium flow by Skare & Krogstad, the mean velocity profile at $\Delta p_s^+=0.012$, $Re_\theta =49107$ and $Re_\tau =5117$ is given in Fig.  8 (left). Finally, the mean-velocity profile for the DLR/UniBw experiment I for $U_\infty =12\mathrm {m/s}$ at $\Delta p_s^+=0.049$, $Re_\theta =20784$ and $Re_\tau =2376$ is shown in Fig.  8 (right).

Fig. 8

Left: Skare and Krogstad at station 4 at $\Delta p_s^+=0.012$ and $Re_\tau =5117$. Right: DLR/UniBw flow I for $U_\infty =12\mathrm {m/s}$ at $\Delta p_s^+=0.049$ and $Re_\tau =2376$

The log law in the mean velocity is found to be a robust feature for all flows. The region occupied by the log law is observed to be a large part of the inner layer for moderate values of $\Delta p_s^+$, but is found to be significantly smaller than $0.15\delta$ for $\Delta p_s^+>0.01$. For $y^+$-values above the log-law region, the mean velocity turns upward above the log law and can be fitted by a half-power law. The upward turn above the log law in the inner layer is found to be increasing with increasing values of $\Delta p_s^+$. The increase of the upward turn can be described by the half-power law and its dependency on $\Delta p_s^+$. In the following, these qualitative observations are studied in more detail.

5.2 Reduction of the Log-Law Region

The question is as to whether the log-law region extends up to $y/\delta =0.15$ as for ZPG. The results for $y_\mathrm {log,max}/\delta$ versus $\Delta p_s^+$ are shown in Fig.  9 (left). Error bars for the individual test cases are included, as described in Sect. 6.5. The log-law region extends up to $y/\delta =0.15$ only for the equilibrium flows in a mild APG by Bradshaw and Clauser (see Fig.  9 (left)). For the equilibrium flows in a larger APG by Bradshaw, Clauser, and Skare & Krogstad, $y_\mathrm {log,max}/\delta$ is found to be reduced already at the first measurement position in the APG region.

Next, consider the flows which evolve from a region of almost ZPG and then enter the APG region. These are the flow by Ludwieg and Tillmann in a mild APG, the flows B and E by Schubauer & Spangenberg, the flow by Marusic & Perry, and the flow by Schubauer & Klebanoff. For these flows, the outer edge of the log law is near $0.15\delta$ in the ZPG region, and a clear reduction is already found at the first measurement station in the APG region (see Fig.  9 (left)).

The DLR/UniBw experiment necessitates some additional comments. The flow passes a region of mild convex curvature and streamwise changing pressure gradient from favourable to adverse before entering the APG focus region, leading to a remarkably large reduction of the log-law region (see Figs. 13 and 14 in Knopp et al. 2021). Therefore, the low values found for $y_\mathrm {log,max}/\delta$ are supposed to be influenced by history effects.

Fig. 9

Reduction of the extent of the log-law region in an APG in two different scalings

To summarise, the values for $y_\mathrm {log,max}/\delta$ are found to be decreasing with increasing values of the pressure-gradient parameter, both in terms of $\Delta p_s^+$ and $\beta _\mathrm {RC}$. The overall observation is that $y_\mathrm {log,max}/\delta$ is below 0.11 for $\Delta p_s^+>0.005$ and $\beta _\mathrm {RC}>4.5$, and below 0.08 for $\Delta p_s^+>0.015$ and $\beta _\mathrm {RC}>12$.

6 Correlations for a Wall Law

Now the aim is to describe the empirical correlations of the wall law. The functional form of the correlations is described in 6.1. The correlations are described in Sects. 6.2 and 6.3. The analysis of the slope coefficient K of the half-power law (14) is given in Sect. 6.4. The uncertainties are estimated and discussed in Sect. 6.5.

6.1 Theoretical Considerations

The functional form of the correlations is prompted by two heuristic arguments, i.e., a similarity argument and a scaling argument.

6.1.1 Similarity Arguments

The first step is to find the basic functional dependency using arguments from the self-similarity analysis in Sect. 2.5. From this analysis, it is expected that $y^+_\mathrm {log,max}$ will depend on the Reynolds number and on the pressure-gradient parameter, in agreement with Yaglom (1979) and Klewicki et al. (2009). The first assumption is that $\beta _H$ is the most important parameter for the solution of (23). Consider the reduced Hartree parameter

$$\begin{aligned} -\beta _\mathrm {H,red} = \Delta p_s^+ \,Re_\tau ^2 \end{aligned}$$

(27)

based on (25). This neglects the influence of $u_\tau /U_e$. Note that $u_\tau /U_e$ is expected to be relevant for the outer layer as it determines the wake factor $\Pi$. For the inner layer, the influence of $u_\tau /U_e$ is assumed to be small at the moment. The functional dependency of the log law and the half-power law is irrespective of its formulation in terms of $u^+(y^+)$ and $f'(\eta )$. Then the following ansatz is made

$$\begin{aligned} \eta _\mathrm {log,max} =\frac{y_\mathrm {log,max}^+}{Re_\tau } = C\beta _{\mathrm {H,red}}^q = C Re_\tau ^{2q}\left( \Delta p_s^+\right) ^q \end{aligned}$$

(28)

with $q\in {\mathbb {R}}$ to be determined. The next idea is to determine the value of s (later being related to q) so that the plot of $y_\mathrm {log,max}^+/Re_\tau ^s$ versus $\Delta p_s^+$ gives the least amount of spreading among the flows at different $Re_\tau$ in the database. This prompts the assumption $y_\mathrm {log,max}^+\sim Re_\tau ^s$. Then q can be inferred from

$$\begin{aligned} \eta _\mathrm {log,max}^+=C Re_\tau ^{2q}\left( \Delta p_s^+\right) ^q= \frac{y_\mathrm {log,max}^+}{Re_\tau } \sim Re_\tau ^{s-1} \quad \Leftrightarrow \quad q=\frac{s-1}{2}\,. \end{aligned}$$

(29)

The least amount of spreading was found for $s=1/2$ (see Fig.  9 (right)), in agreement with the $Re_\tau$-dependency found in Klewicki et al. (2009), Romero et al. (2022). The intermediate result is

$$\begin{aligned} y_\mathrm {log,max}^+= C Re_\tau ^{2q+1}\, (\Delta p_s^+)^{q}\,,\quad \quad q=-\frac{1}{4}\,. \end{aligned}$$

(30)

6.1.2 Scaling Arguments

The simplification of using (27) neglects an additional Re-dependence involved in $u_\tau /U_e$. Therefore, (30) is revisited and modified using the ansatz

$$\begin{aligned} y_\mathrm {log,max}^+=C Re_\tau ^{2q'+1}\left( \Delta p_s^+\right) ^{q''} \end{aligned}$$

(31)

with $s=2q'+1$. A relation for $q''$ can be found from a scaling argument. Consider the boundary-layer parameters in the modified scaling for the inner layer (see Sect. 2.4) for the Reynolds number based on $u_\mathrm {T}$

$$\begin{aligned} \delta _\mathrm {T}^+=\frac{\delta u_\mathrm {T}}{\nu } = \delta ^+ \frac{u_\mathrm {T}}{u_\tau } \end{aligned}$$

(32)

and for the pressure-gradient parameter in the modified inner scaling

$$\begin{aligned} \Delta p_{s,\mathrm {T}}^+=\frac{\nu }{\rho u_\mathrm {T}^3}\frac{\mathrm {d}P_w}{\mathrm {d}s} = \Delta p_{s}^+\left( \frac{u_\tau }{u_\mathrm {T}}\right) ^3= \left( \frac{u_p}{u_\mathrm {T}}\right) ^3\,. \end{aligned}$$

(33)

When approaching separation, $\Delta p_{s,\mathrm {T}}^+\rightarrow 1/Re_c=1/12$ due to (20) and does not approach infinity. Similarly $\delta _\mathrm {T}^+\rightarrow Re_c^{1/3} \delta u_p/\nu$ does not go to zero. Written in modified inner scaling, relation (31) becomes

$$\begin{aligned} y_\mathrm {log,max,T}^+=C Re_\mathrm {T}^{2q'+1}(\Delta p_{s,\mathrm {T}}^+)^{q''}\left( \frac{u_\tau }{u_\mathrm {T}}\right) ^{2q'-3q''}\,. \end{aligned}$$

(34)

The explicit dependence on $u_\tau /u_\mathrm {T}$ disappears if $q''=2q'/3$. The choice $q'=-1/4$ based on $s=1/2$ leads to $q''=-1/6$. Note that the dependency on $(u_\mathrm {T}/u_\tau )^{-2q'+3q''}$ is only mild for $q''=-1/5$ (with $-2q'+3q''=-0.1)$ and $q''=-0.13$ (with $-2q'+3q''=0.11)$ found below.

6.2 The Extent of the Log-Law Region

Motivated by these heuristic arguments, we obtained the final calibration mainly from the data fit, which is shown in Fig.  9 (right)

$$\begin{aligned} y_\mathrm {log,max}^+= 1.78 Re_\tau ^{1/2}\, (\Delta p_s^+)^{-1/5}\,. \end{aligned}$$

(35)

Note the change of the correlation (35) compared to the prior work in Knopp (2016), due to a revised analysis of the database and accounting for Re-effects.

The variability of the data points and possible reasons for the deviation from (35) are discussed in Sects. 7.1, 7.2, and 7.3. The variability is due, on the one hand, to the uncertainty in the data and in the method used to determine the extent of the log-law region, and, on the other hand, to possible additional physical effects and parameters beyond $\Delta p_s^+$ and $Re_\tau$ unaccounted for in (35).

6.3 Variation of the Half-Power Law Region

The correlation for the beginning of the half-power law region is obtained in a similar manner to that employed for (35), using a data fit and guided by the heuristic arguments above. The same dependency on $Re_\tau$ as in (35) is used. The dependency on $\Delta p_s^+$ is a compromise due to the spreading in the data. The correlation becomes

$$\begin{aligned} y_\mathrm {sqrt,min}^+= 4.05 Re_\tau ^{1/2}\, (\Delta p_s^+)^{-0.13}\,. \end{aligned}$$

(36)

The result is shown in Fig.  10 (left). Large symbols are used to highlight the data sets used with the highest priority for the calibration. Additional data are needed for $\Delta p_s^+<0.002$ and $\Delta p_s^+>0.03$ at high Re.

Fig. 10

Variation of $y^+_\mathrm {sqrt,min}/(\delta ^+)^{1/2}$ (left) and results for K (right) using large filled symbols to highlight the data sets used for the calibration

6.4 The Slope Coefficient of the Half-Power Law

In the half-power law (14), the question is as to whether K can be described by a constant or follows a functional dependency, e.g., $K=f(\Delta p_s^+)$. For each profile of the database, the value for K was determined by a least-squares fit of (14) to the experimental data in the half-power law region. Note that K depends on the choice for $\alpha ^+$ in (14). As in all the present work, $\alpha ^+=\Delta p_s^+$ is used both for equilibrium flows and streamwise evolving flows. The results for K are shown in Fig.  10 (right). The data sets used for the calibration (SKr, SKl, MP, SJ, LT1) satisfy all criteria C1-C4 and are plotted using large filled symbols. The data sets by Perry and the DLR/UniBw experiments are considered at a lower priority, due to supposed history effects, and are plotted using small filled symbols. The other data sets not used for the calibration are plotted using open symbols. The values for K are found to scatter around a value of $K=0.45\pm 0.15$. The variability in K is assumed to be due, on the one hand, to an uncertainty in the data and in the method of determining K (see Sect.  6.5), and possibly, on the other hand, to differences in the flow characteristics (see Sects. 7.1-7.3).

For comparison, values reported in the literature for flows with non-zero skin friction are $K=0.48\pm 0.03$ in Townsend (1961), $K=0.48$ in Perry (1966), and values between 0.41 and 0.51 in Szablewski (1960). For large values of $\Delta p_s^+\delta ^+$, values reported are $K=0.447$ in Kader and Yaglom (1978) and $K=0.57$ in Afzal (2008). Note that the values obtained for K depend on the form of the half-power law, i.e., (14) or (15), and on the region used for the least-squares fit. For example, if the half-power law fit is applied above the log-law region, as proposed by Perry (1966), then smaller values are obtained than if the fit is applied to all data in the inner layer above the buffer layer, as used e.g. by Afzal (2008).

To summarise, a constant value for $K=0.45\pm 0.15$ is advocated, whose magnitude is congruent with previous findings in the literature.

6.5 Discussion of the Uncertainties

The variability of the results due to the uncertainty in the data and in the method for the data evaluation needs to be studied. First the uncertainties for $y^+_\mathrm {log,max}$ and $y^+_\mathrm {sqrt,min}$ are discussed. The first aspect is the uncertainty due to the distance $\Delta y^+$ between adjacent data points. The second aspect is the uncertainty due to the wiggles in each mean-velocity profile.

The results for the extent of the log-law region with the estimated uncertainty bars are shown in Fig. 9 (right). For each mean-velocity profile, the deviation of the most likely value for $y^+_\mathrm {log,max}$ from the minimum and maximum possible value was determined, yielding the basic uncertainty. Additional contributions to the error bars are an estimated relative uncertainty of $10\%$ in $\delta$, of $6\%$ in $u_\tau$, and of $1\%$ in $\nu$. The correlation is within or close to the uncertainty bars for most of the profiles except for the flows Br1, BrF, Cl1, DM2, and DM3. The results for the beginning of the half-power law region with the estimated error bars are shown in Fig.  10 (left). The deviations will be discussed below in Subsects. 7.1, 7.2, and 7.3.

Concerning the variability of K, two contributions are studied. The first aspect is the uncertainty of $\Delta p_s^+$, which affects the value inferred for K. A relative uncertainty for $\Delta p_s^+$ of $25\%$ was assumed, corresponding to an average relative uncertainty of $5\%$ in $\mathrm {d}P/\mathrm {d}s$, of $6\%$ in $u_\tau$ and of $1\%$ in $\rho$ and $\nu$. A Monte-Carlo type approach yields an uncertainty of up to $11\%$ for K. The second aspect is the lower and upper bound used for the half-power law fit. This was varied by adding and/or removing the first and/or the last data point in the half-power law region using a Monte-Carlo type approach. This uncertainty was found to become large for profiles having a small number of data points in the half-power law region and for profiles exhibiting discernible oscillations. The details of the uncertainty estimates are described in appendix A.

The values for K with the error bars are shown in Fig. 10 (right). The spreading of the data points for K is within the uncertainty bars. The values for the flow by Perry are found to be larger than $K=0.45$, whereas the values for the DLR/UniBw flows are smaller than for most of the other flows. This difference indicates that the value of K could be influenced by additional physical effects. This issue is discussed in Sects. 7.1 and 7.3.

To summarise: the spreading of the data around the correlations (35), (36) and around $K=0.45$ occurs mostly within the uncertainty bars.

7 Discussion of the Wall Law

Some aspects and issues of the wall law are worth discussing. The conjecture of a local wall law is discussed in Sect. 7.1. Higher-order local effects and history effects are studied in Sect. 7.2. The influence of the measurement accuracy improvement between the oldest and the more recent data and the comparison with data for low-Re flows are studied in Sect. 7.3. The question of the breakdown of the log law is discussed in Sect. 7.4.

7.1 Conjecture of a Local Wall Law

The main conjecture is the existence of a wall law for the mean velocity in the inner layer, which is governed mainly by local parameters and whose leading order effects can be described by $\Delta p_s^+$ and $Re_\tau$. Here $Re_\tau$ is considered as a local parameter, as it depends on the local value of $\delta$, albeit $\delta$ is not a quantity of the near-wall flow and depends on the flow history. The need for $Re_\tau$ is described in the work by Klewicki et al. (2009). Higher-order effects are assumed to slightly alter the wall law. Higher-order local effects are the mean flow acceleration described by the parameter $\Delta u_{\tau ,s}^+$, and the effects of an increasing or decreasing APG, described by $\Delta ^2 p_s^+$ based on $\mathrm {d}^2P/\mathrm {d}s^2$. The local flow parameters and their order of importance can be inferred from the models for the total shear stress (see Sect. 2.2). The first-order approximation is the linear stress distribution $\tau ^+=1+\Delta p_s^+y^+$, and $\Delta p_s^+$ appears as the leading order parameter. The relative importance of the mean-inertia term increases with increasing $y^+$. Therefore $\Delta u_{\tau ,s}^+$ is interpreted as a second-order parameter. Additional higher-order effects involve the parameter $\Delta ^2p_s^+$.

History and non-equilibrium effects can cause additional changes of the wall law. In streamwise evolving flows, the changing flow parameters can cause an imbalance between the different terms in the mean momentum equation. History effects are due to the finite response time of the flow to imbalancing effects (see Gungor et al. 2016). The response time of the mean flow is different in the different regions of the boundary layer, and the mean-velocity profile is the cumulative result of local conditions and history effects (see Gungor et al. 2016). An attempt to describe the response time of the local mean flow uses the eddy turn-over time $T_\mathrm {t.o.}=\kappa y / u^*$ (see Sillero et al. 2013). The eddy turn-over length $\delta _{\mathrm {t.o.}}=U T_\mathrm {t.o.}$ is the streamwise travelling distance of the local mean flow U(y) within $T_\mathrm {t.o.}$. By using $u^*=\tau ^{1/2}$ based on the total shear stress $\tau$ in conjunction with (10), the following estimate for $\delta _{\mathrm {t.o.}}$ as a multiple of $\delta$ at the wall-distance $\eta =y/\delta$ can be obtained

$$\begin{aligned} \frac{\delta _{\mathrm {t.o.}}^+(\eta )}{\delta ^+}=\frac{\kappa u^+\eta }{(1+\alpha ^+\eta \delta ^+)^{1/2}}\,. \end{aligned}$$

(37)

Following Sillero et al. (2013), the flow tends to relax to equilibrium within $2\tau _\mathrm {t.o.}$. The evaluation of $\delta _{\mathrm {t.o.}}/\delta$ using (37) leads to the estimate $2\delta _{\mathrm {t.o.}}\approx \delta$ for $\eta =0.1$ and $2\delta _{\mathrm {t.o.}}\approx 2\delta$ for $\eta =0.2$ for $\Delta p_s^+\gtrapprox 0.004$. This leads to the assumption that the flow in the inner layer relaxes rapidly, although not instantaneously. History effects are expected to be more relevant in the half-power law region than in the log-law region. The outer part of the inner layer can be influenced by history effects of the outer layer, given that the inner and outer layers are connected by an overlap region and that history effects are more prominent in the outer layer. In the outer layer, significant development distances are required for the large-scale turbulent motion to adjust to the local pressure-gradient conditions and for the mean flow to ”forget” perturbations (see Marusic et al. 2015), and the prior path of $\beta _\mathrm {RC}$-values was found to be relevant for the history effects (see Bobke et al. 2017 and Vila et al. 2017).

The conjecture of a local wall law, the systematic reduction of the log-law region, and the appearance of a half-power law above the log law for turbulent boundary-layer flows are seen to be in concurrence with the findings for Couette-Poiseuille (CP) flow by Telbany and Reynolds (1980), as described in the introduction. Note that CP flow is a self-similar flow in dynamic equilibrium within the meaning of Gungor et al. (2016). This supports the proposition that the wall law is a first-order effect of the pressure gradient and not a history effect, given the applicability of the ”moving-equilibrium” concept, as described in Sect. 7.2.

7.2 Discussion of Higher-Order Local and History Effects

The variability of $y_\mathrm {log,max}$, $y_\mathrm {sqrt,min}$ and K due to possible higher-order local effects depending on, e.g., $\Delta u_{\tau ,s}^+$ and $\Delta ^2p_s^+$, and history effects is discussed. The question is whether any systematic trends can be found.

For this purpose, the data of Fig.  9 (right) are depicted again in Fig.  11 using two highlighted groups of data for greater clarity. The equilibrium flows are highlighted in Fig.  11 (left) and the streamwise evolving flows are highlighted in Fig. 11 (right). The highlighted data sets are plotted using large symbols and include error bars, whereas the other data sets are plotted using small symbols and without error bars.

Fig. 11

Reduction of the log-law region highlighting in large symbols the equilibrium flows (left) and the streamwise evolving flows (right) for the data of Fig.  9 (right)

The variability of the extent of the log law is studied first. The equilibrium flows in a mild APG show slightly larger values for $y^+_\mathrm {log,max}/(\delta ^+)^{1/2}$ compared to the streamwise evolving flows in a mild APG (see Fig.  11 (left)). However, similar differences cannot be observed for $\Delta p_s^+>0.01$. Moreover, a clear effect of $\Delta ^2p_s^+$ cannot be identified from the flows by Perry and by Samuel & Joubert. For the variability of $y^+_\mathrm {sqrt,min}/(\delta ^+)^{1/2}$, similar observations can be made.

The significantly lower values found for $y^+_\mathrm {log,max}/(\delta ^+)^{1/2}$ for the two DLR/UniBw experiments are supposed to be due to history effects originating from a region of convex curvature and streamwise changing pressure gradient upstream of the APG region. Note that the ratio of $\delta$ to the radius of curvature was increased by a factor of two in the DLR/UniBw experiment II compared to the experiment I. This could explain the larger effects observed for the experiment II. The role of the measurement accuracy is discussed in Sect. 7.3.

The variability of K in Fig.  10 (right) is supposed to be attributed to both higher-order local and history effects. Both are expected to be increasing with increasing wall-distance. Equilibrium flows and streamwise evolving turbulent boundary-layer flows cannot be clearly distinguished. The largest values for K are found for the flow by Perry Perry (1966). The values at the first three stations (which are at the lowest $\Delta p_s^+$-values) could be influenced by history effects due to the flow acceleration upstream of the APG region. For the DLR/UniBw experiment, the relatively small values for K are supposedly due to history effects of the upstream region of streamwise convex curvature and streamwise changing pressure gradient.

To summarise, no systematic trends of the variability of $y_\mathrm {log,max}$, $y_\mathrm {sqrt,min}$ and K on higher-order local effects can be found. History is found to have an effect, but more data sets are needed to find systematic trends. This leads to the conclusion that a more refined model than (35), (36) cannot be found given the uncertainties of the present data sets.

7.3 Measurement Accuracy and Low-Re Effects

The values for $y^+_\mathrm {log,max}/(\delta ^+)^{1/2}$ for the DLR/UniBw data are found to be significantly lower than for the other flows. Although a physical explanation for this can be given, it is worthwhile to investigate as to whether, between the oldest and the more recent data, there is also an influence of the measurement accuracy improvement. For this purpose, the results of Figs.  10 and 11 are revisited. The more recent experimental data sets by Skare & Krogstad, Marusic & Perry, Samuel & Joubert and the DLR/UniBw flows are highlighted in Fig.  12 (left) using large symbols. Moreover, the DNS data by Coleman et al. (2018) and the experiment by Nagano et al. (1991) at low Re are included and highlighted. The dashed line is for the value $C=1.78$ found in (35). The dash-dotted line is for $C=1.68$, which is only a small modification to improve the agreement with the highlighted data. The first conclusion is that the correlation is useful over a large range of Re, as the low-Re data are close to the high-Re data. The second conclusion is the suggestion that the constant in (35) be changed to $C=1.68$.

Fig. 12

Influence of measurement accuracy on $y^+_\mathrm {log,max}/(\delta ^+)^{1/2}$ (left, some acronyms omitted in legend) and of small Re for $y^+_\mathrm {log,max}/(\delta ^+)^{1/2}$ (left) and $y^+_\mathrm {sqrt,min}/(\delta ^+)^{1/2}$ (right)

Now the role of the measurement accuracy and the details of the method to determine $y^+_\mathrm {log,max}$ are studied. On the one hand, the number of data points in the log-law region is increased for the more recent data. For example, Marusic & Perry achieved 13 data points in the log-law region below $y^+_\mathrm {log,max}=252$ at $\Delta p_s^+=7.5\times 10^{-3}$ compared to four points for Schubauer & Spangenberg (flow E) at a similar $\Delta p_s^+$. The larger number of data points gives a more critical view on the r.m.s. deviation between the $u^+$-profile and the log law. This can lead to smaller values for $y^+_\mathrm {log,max}$.

To illustrate, consider the DLR/UniBw flow II data for $U_\infty =36\,\mathrm {m/s}$. The results denoted by DM3v use an enlarged interval for the least-squares fit of $u^+$ to the log law up to $y^+=250$ (see Table 3). The idea is to emulate possible effects of the least-squares fit method used by Coles & Hirst. The increased interval yields larger values for $y^+_\mathrm {log,max}/(\delta ^+)^{1/2}$, reducing the deviation to the other flows. However, this is at the cost of a larger r.m.s. deviation and hence questionable. It is concluded that the measurement accuracy can explain in parts the deviation of the DLR/UniBw data. However, such cannot explain the full deviation, indicating that additional physical effects are causing the large bulk of the deviation.

It is worth commenting on the use of $\kappa =0.41$ and $B=5.0$ for the older flows. An indirect method for $u_\tau$ might mask the subtle changes of $\kappa$ and B in situations in which the mean velocity deviates from the universal log law (see Wei et al. 2005). Note that for the flows by Marusic & Perry and Samuel & Joubert, the agreement with the log law with $\kappa =0.41$ and $B=5.0$ is very good. For the flows by Skare & Krogstad and by Perry, an assessment is not possible due to the wiggles in the $u^+$-profile. The changes of $y^+_\mathrm {log,max}$ if fitted values for $\kappa$ and B are used, are well within the error bars. Moreover, for the old data, changes of $\kappa$ and B could be masked by near-wall measurement errors in the mean velocity using Pitot tubes, as recently revealed by Bailey et al. (2013).

The results for $y^+_\mathrm {sqrt,min}/(\delta ^+)^{1/2}$ for the low-Re flows are included in Fig.  12 (right). The data by Nagano and by Coleman et al. are highlighted using large symbols. They evince good agreement with the other data at moderate and high Re as well as with the correlation (36).

To summarise, the focus on the more recent data sets and the use of two flows at low Re confirm the results found in Sect. 6. As a minor change, the constant C in (35) is changed from 1.78 to 1.68.

7.4 On the Breakdown of the Log Law for $\Delta p_s^+>0.05$

The hypothesis of the breakdown of the log law, if $\Delta p_s^+$ exceeds some threshold, e.g., $\Delta p_s^+>0.05$ (see Alving and Fernholz 1995) is considered. The breakdown of the log law is understood here as the breakdown of a log-linear region $u^+\sim \log (y^+)$, and is distinguished from a change of $\kappa$ and B. Correlation (35) yields $y_\mathrm {log,max}^+=3.24(\delta ^+)^{1/2}$ for $\Delta p_s^+=0.05$. This implies that the log law extends up to $y^+=92$ for $Re_\tau =800$, indicating a rather thin region, whereas it extends up to around $y^+=162$ for $Re_\tau =2500$ reached in the DLR/UniBw experiment I. Here, it is noteworthy that the outer edge of the log law in an APG from (35) is even smaller than the widely believed start of the log-law region in ZPG flows (see Marusic et al. 2013). Thus (35) is seen to be in agreement with the previous work by Alving and Fernholz (1995).

8 Conclusion

An empirical wall law for the mean streamwise velocity for turbulent boundary-layer flows in an adverse pressure gradient is presented from a database analysis and from scaling and similarity arguments. The wall law describes the inner $20\%$ of the boundary layer and is composed of a log law and a half-power law above the log law. For the slope coefficient of the half-power law K, a value of $K=0.45\pm 0.15$ is found, in agreement with previous findings in the literature. An empirical correlation for the reduction of the log-law region in ratio to the boundary-layer thickness is proposed. The leading order parameters are the pressure-gradient parameter $\Delta p_s^+$ and $Re_\tau$. The results support the conjecture of the existence of a local wall law for the mean velocity and the moving equilibrium concept by Kader and Yaglom (1978). Systematic changes of the wall law due to higher-order local effects and significant differences between equilibrium flows and streamwise evolving flows cannot be identified, given the uncertainties in the data. History effects are larger in the half-power law region than in the log-law region and contribute to the variability observed for K.

The correlation proposed for the erosion of the log-law region in an adverse pressure gradient can describe the hypothesis of the breakdown of the log law, if $\Delta p_s^+$ exceeds some threshold, e.g., $\Delta p_s^+>0.05$, as described by Alving and Fernholz (1995). Moreover, the correlation implies that strict self-similarity of the mean-velocity profile in the inner layer cannot be expected, given the same value of the Rotta-Clauser pressure-gradient parameter $\beta _\mathrm {RC}$ alone, in agreement with the findings reported in Bobke et al. (2017) and Vila et al. (2017).

The correlation to describe the reduction of the log-law region in an adverse pressure gradient could also be of interest for experimental methods. The correlation could be used as an initial guess to identify the region of data points to which the Clauser-chart method can be applied.

Appendices

Uncertainty Estimation

The uncertainty estimation for the slope coefficient K of the half-power law (14) is summarised in Table 2. The sensitivity of K on $\Delta p_s^+$ is found to be increasing from around $9\,\%$ for $\Delta p_s^+=0.005$ to $11\,\%$ for $\Delta p_s^+=0.015$. The sensitivity of K on the lower and upper bound of the interval $I_\mathrm {sqrt}$ used for the half-power law fit was studied using a Monte-Carlo type approach, where $\epsilon (I_\mathrm {sqrt})=\Delta y_i^+$ denotes the variation of $I_\mathrm {sqrt}$ by adding and/or removing one measurement point at the lower and/or upper bound of $I_\mathrm {sqrt}$, as described in Sect. 6.5. The values found for the confidence intervals for the levels $60\%$, $80\%$, and $95\%$ are given in the table. The total uncertainty (denoted by $\epsilon _\mathrm {sum}$) is the sum of $\epsilon (\Delta p_s^+)$ and $\epsilon _{80}(I_\mathrm {sqrt})$. As an exception, $\epsilon _{95}(I_\mathrm {sqrt})$ is used for the flow by Marusic & Perry, due to the low values for this test case.

Table 2 Uncertainty estimation for the method to determine K of the half-power law (14)

Sensitivity Study of the Method for $y^+_\mathrm {log,max}$

The sensitivity study described in Sect. 4.2 for $y^+_\mathrm {log,max}$ for the DLR/UniBw experiment at $U_\infty =36\,\mathrm {m/s}$ is summarised in Table 3. The different values for $y^+_\mathrm {log,max}$ were obtained by a variation of the interval $(y^+_\mathrm {min},y^+_\mathrm {max})$ used to compute the least-square fit of the $u^+$-profile to the log law as described in Sect. 4.2. The results for $y^+_\mathrm {log,max}$ are given in the last column. The values obtained for $\kappa$ and B from the fit are also given in the table.

Table 3 Sensitivity study for $y^+_\mathrm {log,max}$ for the DLR/UniBw experiment at $U_\infty =36\,\mathrm {m/s}$

For $y^+_\mathrm {max}=185$ the r.m.s. deviation is relatively small and $u^+$ follows the log law up to significantly larger $y^+$-values ($y^+_\mathrm {log,max}$ up to 200) than used for the fit. For $y^+_\mathrm {max}$ up to 215, the changes of $y^+_\mathrm {log,max}$ are much smaller than the changes of $y^+_\mathrm {max}$. For $y^+_\mathrm {max}= 250$, the r.m.s. deviation becomes larger and the increased values for $y^+_\mathrm {log,max}$ are more questionable. The assessment of the r.m.s. deviation is possible only thanks to the large number of data points in the log-law region and the smoothness of the data. Note that such is not possible for most of the old data sets in the database. The changes of $y^+_\mathrm {log,max}$ are much smaller than the changes in $\kappa$ and B. The values for $\kappa$ and B are adversely affected by the lower resolution of the 2D PIV method, by a too large interval for $I_\mathrm {fit}$, and by the indirect method to determine $u_\tau$ (see Knopp et al. 2021). Note that the resolution of the 2D PIV method was too low in the log-law region for an accurate determination of $\kappa$ and B. If $u_\tau$ is determined from the CCM, then the $y^+_\mathrm {log,max}$-values are reduced by around $6\%$, due to the reduction of $u_\tau$ for the CCM compared to the direct method.