1 Introduction

Cycle-to-cycle variations (CCV) form a major uncertainty and obstacle for achieving better power and lower pollutant output from internal combustion engines, resulting in a high demand to further the understanding of their origin. It is expected that inhibiting or manipulating the variation of the mixture-quality and flame development could reduce the potential of misfire and abnormal combustion, as well as improve the overall combustion performance (Ozdor et al. 1994; Robert et al. 2015).

Multiple sources for CCV exist, including the in-cylinder flow processes, the formation of the mixture, the evolution of the early flame kernel and the flame propagation. The flame propagation was object of detailed experimental (Mansour et al. 2008; Aleiferis et al. 2000, 2004; Peterson et al. 2011) studies. Deviations in the early flame kernel development and flame propagation are considered to cause up to 50% of the CCV (Holmström and Denbratt 1996; Stone et al. 1996). The early flame kernel is sensitive towards the flow field, and different modes of combustion may appear, depending on the operating conditions of the engine (Peters 1988). Turbulence may be considered a crucial phenomenon driving CCV, not only by controlling the speed of combustion due to flame wrinkling, but also by introducing small-scale variations to the flow field, influencing the mixing-process and flame-propagation.

Three-dimensional Large Eddy Simulation (LES) forms a suitable and mature tool to complement the experimental analysis, especially in the context of CCV. High-fidelity LES was performed by Vermorel et al. (2007, 2009), Kazmouz et al. (2021), and Richard et al. (2007), as well as Goryntsev et al. (2009, 2013) demonstrating the suitability of LES for analyzing CCV in engine combustion.

In addition to classic pressure-based metrics, such as heat release analysis or multi-dimensional measures, further metrics were introduced in the recent years to characterize CCV relying on different data input. A bivariate 2D empirical-mode-decomposition was employed by Sadeghi et al. (2021) to identify CCV within the in-cylinder 2D flow fields. Jung et al. (2017) showed that the spark discharge energy and the in-cylinder turbulence level influence the combustion stability. Hanuschkin et al. (2021) followed a machine-learning based approach to predict high- and low-energy cycles by analyzing the shape and position of the early flame kernel. A joint evaluation of flow fields and heat-release data was performed by Zeng et al. (2019) to quantitatively compare the difference in flow and flame development between fast and slow burning cycles. The different approaches taken to investigate CCV are due to its complexity and suggest that both experimental and numerical techniques are required to further its understanding.

This work studies the CCV of the flame propagation in an optical research engine in a joint approach of experimental observations and simulation data. A port fuel-injection (PFI) strategy was used to allow for a high homogeneity of the fuel-air mixture. Thus, mixture effects on the flame may be neglected. This reduces the number of phenomena influencing the CCV. This study focuses on the turbulent effects on the early flame-propagation. In a first step, pressure traces and flame-radii will be analyzed to ensure a reliable basis. Then, the early evolution of the flame and the turbulence level in the cylinder will be investigated.

2 Methods

2.1 Experiments

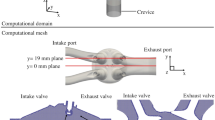
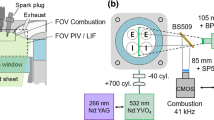
The measurements and simulations were conducted for an optically accessible four-stroke single-cylinder SI engine with port fuel-injection. The engine was operated at 1500 rpm, using iso-octane as fuel. Table 1 summarizes the operating conditions. Optical access is provided by a flat piston window and a quartz glass cylinder liner. In the experiments, to minimize the potential influence of residual gas on CCV and to decrease the thermal load, each fired cycle was followed by two motored cycles. Combining three subsequent measurements of 71 fired cycles lead to a data set of 213 cycles with short interruptions in between. The pressure was measured using a piezoelectric pressure sensor. A high-speed camera captured the line-of-sight integrated combustion luminosity (CH*) at a frame rate of 43 kHz. To extract the apparent burnt area the images were segmented by a predictor-corrector scheme (Shawal et al. 2016). Afterwards the equivalent flame radius was calculated (Aleiferis et al. 2000, 2004). With a field-of-view (FOV) of \(23\times 34\) mm, only the region around the spark plug was imaged, and the recording was performed from ignition timing at \(-20^\circ\)CA until \(+5^\circ\)CA.Footnote 1

Table 1 Engine operating conditions
Full size table

2.2 Simulation

Corresponding computations were carried out with the inhouse LES-solver PsiPhi. The Favre-filtered conservation equations for mass, momentum, total internal energy, flame-progress variable and mixture fraction were solved in a density-based framework. The finite volume method was used to discretize the equations on an isotropic equidistant grid of 0.39 mm size and a total of 38 Mio. cells. Convective fluxes were interpolated with an eighth-order central differencing scheme (CDS) supported by a tenth-order filter for momentum, at Mach numbers below 0.2. The CDS fluxes were blended linearly with a total variation diminishing (TVD) scheme with the non-linear CHARM limiter for \(0.1< \text {Ma} < 0.2\) and the full TVD fluxes were used for higher Mach numbers. Scalar fluxes were discretized using TVD. Time integration was performed with a low-storage third order Runge–Kutta scheme. The boundaries were treated using the Navier–Stokes Characteristic Boundary Conditions, supplied by pressure measurements inside the intake manifold and velocities obtained from GT-Power calculations for the corresponding target values. The extend of the ports included into the computational domain is shown in Fig. 1. All walls and moving parts of the engine follow a Lagrangian-Particle and immersed boundary-based framework first described by Nguyen et al. (2016). The Sigma model by Nicoud et al. (2011) with \(C_{\text {m}} = 1.5\) was employed to take into account the subfilter transport along with a turbulent Schmidt number of \(\text {Sc}_{\text {t}} = 0.7\). The simulation was performed over a total of 30 cycles for sampling, discarding the first two cycles to not include initial transient effects (different numbers of cycles for sampling can be found in literature, typically ranging between 10 and 30 (Vermorel et al. 2007; Goryntsev et al. 2013; Nguyen et al. 2016; Wadekar et al. 2019)). To reduce costs and reproduce the effect of the skip firing, the cycles were simulated consecutively without ignition. The fired results were obtained from restarting and running the simulation separately from short before ignition. Overall up to two cycles have been achieved on 1024 cores within 24 h, offering a good speed for an engine LES.

Fig. 1
figure 1

Computational domain included in the simulation. Top: flame kernel and image-normal velocity during early combustion phase (\(-17^\circ\)CA). Bottom: image-normal velocity component during intake stroke (\(-120^\circ\)CA)

Full size image

2.3 Combustion Modeling

The flame-surface density (FSD) approach is employed within this work. FSD models aim for the closure of the combined filtered laminar diffusion and reaction rate term using a transport equation for the reaction progress variable c. The reaction progress variable ranges between values of zero and unity, indicating fully unburnt mixture and completely burnt mixture, respectively. In this study, the Favre-filtered reaction progress variable c is transported using

$$\begin{aligned} \frac{\partial {\overline{\rho }} {\tilde{c}}}{\partial t} + \frac{\partial {\overline{\rho }} {\tilde{c}} {\tilde{u}}_{\text {j}}}{\partial x_{\text {j}}} + \frac{\partial {\overline{\rho }}\left( {\tilde{c}} {\tilde{u}}_{\text {j}}-\widetilde{c u_{\text {j}}}\right) }{\partial x_{\text {j}}} = \overline{\frac{\partial }{\partial x_{\text {j}}}\left( \rho D \frac{\partial c}{\partial x_{\text {j}}}\right) + {\dot{\omega }}_c} \end{aligned}$$
(1)

with the diffusivity D and the reaction rate \({\dot{\omega }}_c\). The Favre filtering of a general quantity Q is denoted as \({\tilde{Q}}\) and the LES filtering as \({\overline{Q}}\), respectively. The unclosed reaction and diffusion terms may be rewritten using the flame-surface density

$$\begin{aligned} \overline{\frac{\partial }{\partial x_{\text {j}}}\left( \rho D \frac{\partial c}{\partial x_{\text {j}}}\right) + {\dot{\omega }}_c} = \overline{\left( \rho _0 s_\text {d}\right) _\text {s}}\Sigma _{\text {gen}} \end{aligned}$$
(2)

where \(\rho _0\) indicates the unburnt density, \(s_\text {d}\) the flame displacement speed on the flame surface s and the generalized flame-surface density \(\Sigma _{\text {gen}}\), which combines the diffusion and source terms. A popular choice to calculate \(\Sigma _{\text {gen}}\) is a modified transport-equation based model by Colin and Truffin (2011), which takes into account the subgrid-behavior of the early flame kernel. The numerical framework used in the present study relies on the algebraic model by Muppala et al. (2005). Following this modeling philosophy, the flame-surface density may be approximated as

$$\begin{aligned} \overline{\left( \rho _0 s_\text {d}\right) _\text {s}}\Sigma _{\text {gen}} \approx \rho _{\text {u}} s_{\text {l}} \Xi |\nabla {\tilde{c}}| \end{aligned}$$
(3)

The model gives the wrinkling factor \(\Xi\) based on

$$\begin{aligned} \Xi = \left( 1+\frac{0.46}{\text {Le} }\text {Re}^{0.25}_\Delta \left( \frac{u'_\Delta }{s_{\text {l}}}\right) ^{0.3}\left( \frac{p}{p_0}\right) ^{0.2}\right) \end{aligned}$$
(4)

with the Lewis number \(\text {Le}\) assumed as unity, the laminar flame speed \(s_{\text {l}}\) and the pressure p. Here \(p_0\) represents the ambient pressure. \(\text {Re}_\Delta\) refers to the turbulent Reynolds number that can be rewritten using the turbulent lengthscale \(l_{\text {t}}\) and the laminar flame thickness \(\delta _{\text {l}}\) as \({\approx 4\left( l_{\text {t}} / \delta _{\text {l}}\right) \left( u'_\Delta /s_{\text {l}}\right) }\). The turbulent lengthscale in the context of LES is assumed as \({l_{\text {t}}=\Delta }\). The subfilter velocity fluctuations \(u'_\Delta\) are calculated using the OP1 formulation following Colin et al. (2000). The laminar flame speed \(s_{\text {l}}\) and flame thickness \(\delta _{\text {l}}\) are obtained from tabulation, which was generated using calculations of one-dimensional freely propagating flames with varying pressure, temperature and equivalence ratio in Cantera (Goodwin et al. 2009). The ignition was simulated by initializing a spherical kernel of burnt gas of 1.5 mm radius at the spark plug.

3 Results

3.1 Comparison of Experimental and Numerical Indicator Quantities

Figure 2 shows the experimental and numerical pressure traces over the crank angle interval of combustion. The overall agreement of the traces is good, even if the slowest cycles are not fully reproduced by the simulation. The crank angle of the maximum pressure shifts with the peak pressure-value, as indicated by the insert in Fig. 2. Linear regression lines were obtained by the least-squares method for the measured and simulated results and are displayed as lines. The scatter around the regression lines shows only little deviation, which was found to indicate stable combustion cycles (Matekunas 1983). The slope of the numerical data is slightly below that of the experiments. The lack of predictability of the slow cycles is a known topic in engine simulation. A common practice is the use of one-step chemistry for combustion modeling due to its robustness and efficiency, some works even applying sophisticated additional modeling for the capture of the spark and early flame development, that as a drawback have several sensitive calibration parameters. However, a shortcoming of these models is their incapability to capture the sensitive chemistry, in particular after ignition. It is possible that a spark model might improve the prediction of the slow cycles although even works including this philosophy revealed difficulties with this issue (Richard et al. 2007; Truffin et al. 2015; Wadekar et al. 2019).

Fig. 2
figure 2

Experimentally and numerically obtained pressure traces from all cycles. Averages are given by the colored lines. The insert shows the correlation between the peak pressure and the crank angle at which peak pressure occurs

Full size image
Fig. 3
figure 3

Experimentally and numerically obtained cumulative distribution function of peak pressures from all cycles

Full size image

In Fig. 3, the cumulative distribution function (CDF) for the experimental and numerical samples is presented. The CDF reveals that the simulation indeed manages to predict some of the weaker cycles. The agreement between the measured and simulated CDF may be seen as an indicator for the simulation to contain a sufficient amount of cycles to allow for a reasonable comparison with the experiment.

Fig. 4
figure 4

Experimentally and numerically obtained equivalent flame radii, calculated from the two-dimensional projection along the camera line-of-sight axis. The maximum flame radius produced by the simulation is indicated by the dashed line

Full size image

Figure 4 presents the values of the equivalent flame radius obtained from experiment and simulation. The experiments yield the line-of-sight integrated light emissions within the flame and the burnt gases. The projected area \(A_{\text {2D}}\) of the two-dimensional region was calculated, and the equivalent radius of a circle of the same area was computed as \({r = ( A_{\text {2D}}/\pi } )^{0.5}\). In the simulation, the progress variable field was projected in the same direction, and the resulting image was processed following the same procedure. The initial radii appear constant within the first crank angles. This is a consequence of the overexposure caused by the ignition spark and the size of the initialized flame-kernel in the simulation. After approximately four crank angle degrees—which may be interpreted as the time of the early flame kernel development—the flame radii increase but with substantial variation across the cycles. The spreading weakens as parts of the flame run into less turbulent regions closer to the cylinder wall. Eventually, the flame encounters the wall, where further growth is inhibited. The simulation exhibits somewhat stronger growth for the earlier crank angles and slower growth for the later crank angles compared to the experiment. The strong initial growth might be partially caused by the employed combustion model. A similar behavior was discussed by Colin and Truffin (2011), who proposed a modification to better consider the initial flame curvature in the context of transported FSD-type models.

Fig. 5
figure 5

Correlation between the equivalent flame radius \(r_{13}\) \(13^\circ\)CA after ignition and the crank angle \(\text {CA}_{10}\) of \(10\%\) percent fuel mass burnt for the experiment and the simulation

Full size image

In Fig. 5, the equivalent flame radius \(r_{13}\) \(13^\circ\)CA after ignition (calculated using the projected area in the imaging region as discussed in the previous paragraph) is plotted versus the crank angle \(\text {CA}_{10}\), at which ten percent of the fuel mass are burnt. The figure reveals a linear decrease of the flame radius and \(\text {CA}_{10}\) for experimental and numerical results. While the slope is similar, with a slight underprediction indicating smaller \(\text {CA}_{10}\), the numerical values are shifted towards lower radii, as also shown by the linear regression lines. This, in comparison with the experiment, may be interpreted as the simulation slightly underpredicting the flame speed. Considering the findings from Fig. 2, the correlation confirms that the simulation is struggling with reproducing the slowest cycles.

The metrics presented in Fig. 5 form the foundation for the classification of slow and fast cycles. The equivalent flame radius at \(13^\circ\)CA after ignition is an optically measured quantity, which indicates the quality of the combustion and correlates with the pressure. Both \(r_{13}\) and \(\text {CA}_{10}\) form a plausibility check for properly capturing the combustion physics in the experiment and simulation (Aleiferis et al. 2000, 2004). The value of \(\text {CA}_{10}\) is chosen to identify the slowest and fastest of the obtained cycles. As the propagation speed of the flame is crucial for the combustion of ten percent fuel mass, the terms slow and fast were chosen.

3.2 Flame Propagation and Kinetic Energy

Figure 6 shows the volume-rendered flame surface density \(\Sigma _{\text {gen}}\) projected along the cylinder axis and the camera line-of-sight. The figure shows the averages, which were obtained for the five fastest and slowest cycles. The images show crank angles until \(30^\circ\)CA to give insight into the progression of the flame through the cylinder. It can be seen that the flames in the fast cycles (columns two and four) are significantly faster than in the slow cycles (columns one and three), showing almost complete combustion at \(20^\circ\)CA already. The flames are initialized as a spherical kernel at the time of ignition. The flame then propagates and exhibits progressive wrinkling with increasing crank angle. The flames are not fully circular but oval-shaped, which causes the flame to take more time to reach the left side of the cylinder walls.

Fig. 6
figure 6

Average of the volume-rendered flame surface density \(\Sigma _{\text {gen}}\) projected along the cylinder axis (left column) and the camera line-of-sight (right column) for different crank angles visualizing the progress of combustion. The averaging was performed using slow and fast cycles separately

Full size image
Fig. 7
figure 7

Experimentally and numerically obtained centroids of the flame for crank angles up to \(10^\circ\)CA after TDC conditioned for slow and fast cycles

Full size image

Figure 7 presents the projections of the flame centroids obtained from experiment and simulation. The viewing direction is indicated by the insert in the bottom right corner. The location and size of the region shown in the figure is given by the rectangle within the insert. The coordinate axis are moved to give values of zero at the location of ignition. The experimental centroids are only found in the lower graph, due to lack of information about the third dimension. The mean for the centroids of the slowest and fastest cycles were obtained and are displayed by blue (slow) and red (fast) lines. The lines start at the spark plug and extend towards the left side, as also observed from Fig. 6. The centroids overall behave symmetrically in the z direction, only deviating by a millimeter. The flame centroids move in negative y direction. The flames of the slow cycles travel further to the left than the fast cycles. The slow cycles travel significantly further in the direction of negative x values than in the experiment. The difference between fast and slow cycles, however, is similar. In both experiment and simulation, the centroids of the weaker cycles traveled further. One should note, however, that the centroids are a sensitive and challenging quantity to assess. Overall, some deviations between the experiment and the simulation can be observed. Possible reasons for these deviations are the predicted flow field and the flame propagation as a result of the interaction of several numerical aspects including subgrid modeling, grid resolution, reaction modeling and discretization. Other potential causes are the precision of the experimental boundary conditions, the timing of ignition or the errors involved in the imaging of the flame kernel.

Fig. 8
figure 8

Simulated global kinetic energy \(k_{\text {g}}\) (dots) and turbulent kinetic energy \(k_{\text {t}}\) (crosses) during early combustion for all cycles, as well as averaged for fast and slow cycles based on different sampling methods: Conditioned for a progress variable \(Y_{\text {C}}\) of 1 and 0 for the whole domain (3D) as well as the central tumble plane (2D)

Full size image

Figure 8 shows the kinetic energies during the early combustion phase, using different sampling methods. The figure shows the volume-averaged global kinetic energy (GKE) \({k_{\text {g}} = \int {\tilde{u}}_{\text {i}}{\tilde{u}}_{\text {i}}/2\ dV/V}\) and the turbulent kinetic energy (TKE) \({k_{\text {t}} = \int {u^\prime }_{\text {i}}{u^\prime }_{\text {i}}/2 \ dV/V}\) with the velocity fluctuation \({{u^\prime }_{\text {i}} = {\tilde{u}}_{\text {i}} - \langle {\tilde{u}}_{\text {i}}\rangle }\) based on the instantaneous velocity \({\tilde{u}}_{\text {i}}\) and the phase-averaged velocity \(\langle {\tilde{u}}_{\text {i}}\rangle\), which were obtained using the entire three-dimensional domain (denoted 3D) and a two-dimensional slice in the central tumble plane of the cylinder (2D). The employed definition of TKE using the phase-average differs from the classical definition, as it may include coherent structures that vary from cycle to cycle. The energies were calculated with and without using the image-normal velocity component \(v_{\text {z}}\) (\(v_{\text {x,y,z}}\) and \(v_{\text {x,y}}\)). Also, the statistics are conditioned by using the energies in the fresh gas mixture \(Y_{\text {C}} = 0\) for the first set and the energies of the burnt gas \(Y_{\text {C}} = 1\) for the second set to perform the averaging. The colored values are the averages of the five fastest (red) and slowest (blue) cycles, the rest indicates the remaining cycles (grey). All values are obtained from the simulation.

Overall, the fast cycles exhibit higher TKE than the slow cycles, indicating stronger turbulence within the flow field, which potentially speeds up the flame propagation and causes the fast cycles. The slow cycles feature a higher separation between the GKE and TKE. This may be interpreted as a poorer distribution of the overall energy between the turbulent and large scale structures. As a result, the energy of the turbulent structures is comparably smaller, which leaves less turbulence to increase the flame speed than in the fast cycles. The GKE of the fast and slow cycles has similar values, revealing turbulence to be the main driver of the observed CCV. While few differences for the GKE between fast and slow cycles can be found, it is expected that a greater number of simulated cycles will reduce these differences further. Consideration of the image-normal velocity component only slightly increases the amplitudes of the shown energies without any change of the qualitative findings, as only minor transport can be expected along the tumble axis. This indicates that the typically two-dimensional experimental imaging techniques would capture similar physics without significant loss of information for this setup.

For the samples within the unburnt mixture, the energy values obtained from the 2D slice appear more scattered than for the 3D sampling. This results from the 3D sampling being based on more samples and including regions nearby walls, where the flow field energy is dampened. The decrease of GKE and TKE using the unburnt samples is low compared to the burnt samples, which is assumed to be a consequence of the high density and low viscosity. The GKE is overall decreasing until TDC for fast and slow cycles, which is assumed to be a result of the tumble collapse and the decay of directed flow as a consequence thereof. In the curves including the image-normal velocity component, the decrease between \(-15\) and \(-5^\circ\)CA is interrupted by a slight increase of GKE, which is assumed to be a consequence of the tumble collapse, leading to a less organized rotational but more unordered flow. The TKE of the slow cycles remains constant. The fast cycles reveal decreasing TKE with increasing crank angle. This might indicate that the fast cycles have experienced a stronger conversion of GKE to TKE during the tumble collapse, which is now dissipating.

The samples conditioned for the burnt mixture exhibit decreasing energies with increasing crank angle. This implies strong turbulence around the spark plug. The strong decay of energy is interpreted as a consequence of the ongoing tumble collapse. The separation between the GKE and TKE fades with increasing crank angle.

4 Conclusion

In the present study, the cyclical variation of the flame propagation in a port fuel-injected, spark-ignited engine was studied by experiment and simulation. The pressure traces revealed that both experiment and simulation are in good agreement for the peak pressure and its timing. The flame radii evolved at a similar rate. The burnt fuel fraction was used to classify slow and fast cycles.

The second part investigated the flame surface density terms for slow-burning and fast-burning cycles, revealing a notable difference in the flame speeds. The simulated flame was found to burn in an oval shape. Trajectories of the flame centroids showed that the flame is traveling towards intake ports. Interestingly, the flame moved further in the slow cycles, consistently in simulation and experiment. Finally, the global kinetic energy and turbulent kinetic energy was evaluated separately for slow and fast cycles, using samples of the unburnt and burnt mixture to examine if the turbulence affects the strength of a cycle. Negligible qualitative differences were observed between a two and three-dimensional sampling space, indicating that for this configuration the same findings can be made using either two or three-dimensional diagnostics. It was also found, that the differences between turbulent kinetic energy and global kinetic energy are larger for slow than for fast cycles. As expected, fast cycles were found to have higher turbulent kinetic energies than slow cycles. The kinetic energy conditioned on the burned state showed very high initial values, likely due to high turbulence levels at the spark plug.

In this work, the simulation assumed PFI to simply mean a perfectly homogeneous mixture. In reality, this is not the case, and slight mixture gradients occur that may influence CCV and might have caused some of the difference between experiment and simulation. Overall, the experiment and simulation have succeeded in demonstrating that much of the difference in cycle strength can be explained by the turbulence levels—within the two-dimensional tumble plane and outside of the plane.