Error Quantification for the Assessment of Data-Driven Turbulence Models

Abstract

Data-driven turbulence modelling is becoming common practice in the field of fluid mechanics. Complex machine learning methods are applied to large high fidelity data sets in an attempt to discover relationships between mean flow features and turbulence model parameters. However, a clear discrepancy is emerging between complex models that appear to fit the high fidelity data well a priori and simpler models which subsequently hold up in a posteriori testing through CFD simulations. With this in mind, a novel error quantification technique is proposed consisting of an upper and lower bound, against which data-driven turbulence models can be systematically assessed. At the lower bound is models that are linear in either the full set or a subset of the input features, where feature selection is used to determine the best model. Any machine learning technique must be able to improve on this performance for the extra complexity in training to be of practical use. The upper bound is found by the stable insertion of the high fidelity data for the Reynolds stresses into CFD simulation. Three machine learning methods, Gene Expression Programming, Deep Neural Networks and Gaussian Mixtures Models are presented and assessed on this error quantification technique. We further show that for the simple canonical cases often used to develop data-driven methods, lower bound linear models can provide very satisfactory accuracy and stability with limited scope for substantial improvement through more complex machine learning methods.

1 Introduction

Turbulence modelling has seen renewed interest over the past decade with the growing availability of high fidelity Direct Numerical and Large Eddy Simulation (DNS/LES) flow data (Durbin 2018). Models aim to provide predictions of turbulent flows by describing the unclosed statistical component of the turbulence in the Reynolds-Averaged Navier–Stokes (RANS) equations, in terms of mean flow variables. These predictions are computationally efficient as spatio-temporal fluctuations are not resolved, but classical models are well documented to suffer lower fidelity in many flow cases including those with large separation and streamline curvature (Wilcox 2006). In response, researchers are making use of machine learning methods to extract flow physics from the high fidelity data to develop data-driven models. These models are then used in RANS calculations to improve the fidelity of predictions, whilst maintaining computational efficiency.

Many data-driven turbulence models are currently developed and tested on a set of just a few canonical flow cases given the availability of validated high fidelity data for these cases. They include: (1) backward-facing step, (2) periodic hills, (3) curved backward-facing step, (4) converging diverging channel, (5) family of bumps, (6) square duct (Brener et al. 2021; Wu et al. 2018; Duraisamy et al. 2015). However, even in these simple test cases, a trend is appearing that models accurately fitting the high fidelity data a priori bare little correlation to improved velocity predictions a posteriori (Wu et al. 2017). Various solutions to this problem have been proposed. Zhao et al. (2020) for example, included CFD simulations in the optimisation loop, alleviating the discrepancy between a priori and a posteriori testing by removing the a priori component completely. This is made possible in their work by use of the Gene Expression Programming (GEP) algorithm which is gradient free and evolutionary in nature, so can work with any objective function. However, this method is practical only for low complexity flows where the computational effort of running RANS calculations in an optimisation loop is still feasible. Others, such as Schmelzer et al. (2020) have employed model-selection techniques to develop models which show promising characteristics a priori and subsequently check the performance of each model a posteriori. A common characteristic of these methods is penalising complex models where a simpler one yields the same performance (Huijing et al. 2021). The outcome is models that are rarely more complex than linear in the chosen set of input features.

Assessing the state-of-the-art in turbulence modelling gives light to numerous works, applying a wide range of machine learning techniques which show excellent improvement over a baseline model in the training case, and mixed performance when extrapolating models to predictive cases. Many of these works can be found in the review of Duraisamy et al. (2019). However, no clear method exists for unbiased comparison between models. With this in mind, this paper aims to present two clear advances:

• 1. An error quantification method for systematically assessing developed turbulence models, consisting of an upper and lower bound.

• 2. A computationally efficient model-selection procedure for generating data-driven models. The procedure is independent of the machine learning technique used and doesn’t rely on a priori predictions to guide model development.

The upper bound of the error quantification consists of a stable method for the insertion of the high fidelity Reynolds stresses into the RANS calculations which has been partially explored by Wu et al. (2019). This provides a stable approximation for the best reproduction of the high-fidelity velocity field available from the given high-fidelity dataset, when employing machine learning methods to enhance local RANS based closures by training models for the Reynolds stresses. However, it is only available for the training case as the Reynolds stresses are inserted via case specific static fields. At the lower bound, and arguably more important in assessing the performance of data-driven models, is models that are linear with respect to the chosen input features. It is highlighted that this linearity is not between the stress and strain as in classical turbulence models (which leads to a constant coefficient in the eddy viscosity). It is instead between the input features and the coefficients of the mean strain/rotation terms, which are the common subject of data-driven modelling. Given the successes of low complexity models in a posteriori testing on canonical flow cases, significant improvement over the baseline can be expected. It follows that machine learning techniques which aim to find complex nonlinear relationships, must be able to outperform a linear model in order to be considered worthwhile, rather than improving on the baseline alone.

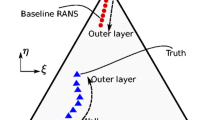
A secondary point of the lower bound is that it elucidates the scope to which machine learning techniques are necessary for a certain case. Take for example, a linear model that significantly improves on the baseline and is close to the upper bound. There would be limited scope for more complex data-driven methods to find further improvement on the linear model. If the linear model finds just a small improvement over the baseline however, and the upper bound is still close to the high fidelity data, then a case is found which demands the attention of nonlinear models and machine learning methods become justifiable. A schematic of the full process and the corresponding sections of the paper in which each step is presented is shown in Fig. 1.

This paper details both the error quantification technique and the model-selection procedure applied to the backward-facing step case of Le et al. (1997). Two established machine learning methods (Gene Expression Programming and Deep Neural Networks) and one new method (Gaussian Mixture Models) are then used to develop models with the model-selection procedure which are subsequently assessed against the error quantification bounds. The developed models are then applied to the periodic hills case to assess the viability of each technique in an unseen predictive case.

Fig. 1

Flow diagram showing steps in the error quantification process with the corresponding sections in which they are presented. DRS relates to Direct Reynolds Stress and LFA relates to Linear Feature Analysis

2 Governing Equations and Data Preparation

Before the bounds and data-driven models can be developed, the RANS equations into which the models will be substituted must be presented. The method for curating the high fidelity data, to a state in which it can be accepted into the data-driven framework is also presented in this section.

The steady, incompressible RANS equations comprising the continuity and momentum equations are given as

$$\begin{aligned} {\varvec{\nabla }} \cdot {\mathbf {U}}&= 0, \end{aligned}$$

(1)

$$\begin{aligned} ({\mathbf {U}} \cdot {\varvec{\nabla }}) {\mathbf {U}}&= {\varvec{\nabla }} \cdot \bigg [-\frac{1}{\rho }P{\mathbf {I}} + \nu ({\varvec{\nabla }}{\mathbf {U}} + {\varvec{\nabla }}^T{\mathbf {U}}) - {\varvec{\tau }}\bigg ], \end{aligned}$$

(2)

where ${\mathbf {U}}$ and P are the time averaged velocity and pressure fields, ${\mathbf {I}}$ is the identity matrix, $\rho$ is the fluid density and ${\varvec{\tau }}$ is the Reynolds stress tensor which is the subject of all turbulence modelling. The Reynolds stresses are typically decomposed into isotropic and anisotropic components

$$\begin{aligned} {\varvec{\tau }} = \frac{2}{3}k{\mathbf {I}} + 2k{\mathbf {a}}, \end{aligned}$$

(3)

where k is the turbulent kinetic energy and ${\mathbf {a}}$ is the nondimensional anisotropic component of the Reynolds stress (anisotropy). The isotropic component is incorporated into the pressure term by a redefinition of pressure as ${\overline{P}}=P/\rho + 2k/3$. It is the anisotropy (rather than the full Reynolds stresses) that is usually the target variable for classical and data-driven models alike. In classical turbulence modelling, the anisotropy is dealt with by assuming a linear relationship with the mean strain rate tensor such that $2k{\mathbf {a}}=-2\nu _t{\mathbf {S}}$ where $\nu _t$ is the scalar eddy (turbulent) viscosity. Many models exist for the computation of $\nu _t$ but here the one selected as baseline is the k-$\omega$ SST-2003 model. It consists of transport equations for the turbulent kinetic energy k and the specific turbulence dissipation rate $\omega$, which in steady form read

$$\begin{aligned} ({\mathbf {U}} \cdot {\varvec{\nabla }})k&= P_k - \beta ^*\omega k + {\varvec{\nabla }} \cdot [(\nu + \sigma _k\nu _t){\varvec{\nabla }}k], \end{aligned}$$

(4)

$$\begin{aligned} ({\mathbf {U}} \cdot {\varvec{\nabla }})\omega&= \frac{\gamma }{\nu _t}P_k - \beta \omega ^2 + {\varvec{\nabla }} \cdot [(\nu + \sigma _{\omega }\nu _t){\varvec{\nabla }}\omega ] + (1-F_1)CD_{k\omega }, \end{aligned}$$

(5)

where the eddy viscosity is then computed from

$$\begin{aligned} \nu _t = \frac{a_1k}{\mathrm {max}(a_1\omega ,SF_2)}, \end{aligned}$$

(6)

where $S=\sqrt{2{\mathbf {S}}:{\mathbf {S}}}$. Auxiliary expressions to complete the closure are given by the following

$$\begin{aligned} \begin{aligned} P_k&= \mathrm {min}(-2k{\mathbf {a}}:{\varvec{\nabla }}{\mathbf {U}},10\beta ^*\omega k), \\ F_1&= \mathrm {tanh}(\varGamma _1^4), \quad \varGamma _1 = \mathrm {min}\Bigg [\mathrm {max}\bigg (\frac{\sqrt{k}}{\beta ^*\omega y},\frac{500\nu }{y^2\omega }\bigg ),\frac{4\sigma _{\omega 2}k}{CD_{k\omega }y^2}\Bigg ], \\ CD_{k\omega }&= \mathrm {max}\bigg ( 2\sigma _{\omega 2}\frac{1}{\omega }{\varvec{\nabla }}k{\varvec{\nabla }}\omega ,10^{-10} \bigg ), \\ F_2&= \mathrm {tanh}(\varGamma _2^2), \quad \varGamma _2 = \mathrm {max}\bigg ( \frac{2\sqrt{k}}{\beta ^*\omega y}, \frac{500\nu }{y^2\omega } \bigg ). \end{aligned} \end{aligned}$$

(7)

Model constants are blended away from the wall from inner (1) to outer (2) by $\phi = F_1\phi _1 + (1-F_1)\phi _2$ and the full set of constants are

$$\begin{aligned} \begin{aligned} \gamma _1 = 5/9, \ \gamma _2&= 0.44, \ \sigma _{k1} = 0.85, \ \sigma _{k2} = 1.0, \ \sigma _{\omega 1} = 0.5, \ \sigma _{\omega 2} = 0.856, \\ \beta _1&=0.075, \ \beta _2=0.0828, \ \beta ^*=0.09, \ a_1=0.31. \end{aligned} \end{aligned}$$

(8)

We note that there are two locations where ${\mathbf {a}}$ is added to this full closed set of equations; through the momentum equations via the decomposition of ${\varvec{\tau }}$ in Eq. 3, and in the production term $P_k$, defined in the auxiliary expressions in Eq. 7 and entering the k and $\omega$ equations. Some works, such as that by Schmelzer et al. (2020), effectively discover separate models for ${\mathbf {a}}$ in each location. This approach is avoided here as it is the opinion of the authors that it moves away from the physics of the problem.

2.1 Data-Driven Closure Framework

In contrast to classical turbulence modelling where the anisotropy is modelled as linear with respect to the mean strain rate tensor, data-driven modelling often makes use of a nonlinear generalisation of the eddy viscosity hypothesis. First proposed by Pope (1975), the anisotropy is modelled as a function of strain rate tensor and rotation rate tensor such that ${\mathbf {a}}={\mathbf {a}}({\mathbf {s}},{\varvec{\omega }})$. Here ${\mathbf {s}}=\tau {\mathbf {S}}$ and ${\varvec{\omega }}=\tau {\varvec{\varOmega }}$ are non dimensional forms of the rate tensors found by a timescale $\tau$ (where the timescale $\tau$ is not to be confused with the Reynolds stress tensor ${\varvec{\tau }}$ and the specific dissipation rate $\omega$ is not to be confused with the nondimensional rotation rate tensor ${\varvec{\omega }}$). In many works this timescale is simply defined as $1/\omega$ but here, to maintain consistency with the baseline k-$\omega$ SST model the timescale is defined as $\tau = \nu _t/k = a_1/\mathrm {max}(a_1\omega ,SF_2)$ which accounts for the switch to a strain based timescale in regions where the ratio of production to dissipation of k is high (Menter 1994).

The most general form of the anisotropy in terms of the mean rate tensors is discovered by the Cayley–Hamilton theorem and can be expressed as

$$\begin{aligned} {\mathbf {a}}({\mathbf {s}},{\varvec{\omega }}) = \sum _{n=1}^{10} \beta _n(I_m){\mathbf {V}}^{(n)}, \quad \mathrm {where} \; m \in {\mathbb {Z}} \, \cap \, [1,5], \end{aligned}$$

(9)

which is the weighted sum of ten linearly independent tensor bases ${\mathbf {V}}^{(n)}$ with coefficients $\beta _n$ that can be described as functions of a set of five invariants $I_m$. In two-dimensional flows which will be considered herein, the first three terms alone form a linearly independent basis and only the first two invariants are non-zero and independent. These are given by

$$\begin{aligned} {\mathbf {V}}^{(1)} = {\mathbf {s}}, \quad {\mathbf {V}}^{(2)}&= {\mathbf {s}}{\varvec{\omega }} - {\varvec{\omega }}{\mathbf {s}}, \quad {\mathbf {V}}^{(3)} = {\mathbf {s}}^2 - \frac{1}{3}I_1{\mathbf {I}}, \end{aligned}$$

(10)

$$\begin{aligned} I_1&= \mathrm {tr}({\mathbf {s}}^2), \quad I_2 = \mathrm {tr}({\varvec{\omega }}^2). \end{aligned}$$

(11)

Whilst theoretically this framework should allow for a complete description of ${\mathbf {a}}$ (under the assumption that ${\mathbf {a}}$ is a function of local ${\mathbf {s}}$ and ${\varvec{\omega }}$ only), other works such as that by Wang et al. (2017) include an extended set of nondimensional flow features. In their case, these features are used to find regression functions for Reynolds stresses discrepancy fields. Some of these additional input features will also be considered here to augment the invariants in finding regression functions for the $\beta _n$ coefficients. We take the two features found to be the most important predictors by Wang et al. (2017) (turbulent kinetic energy and turbulent Reynolds no.) and add one additional feature which is the ratio of the eddy viscosity to the molecular viscosity. The complete set of input features ${\mathcal {I}}=\{q_p\}$, where $p \in {\mathbb {Z}} \, \cap \, [1,5]$ can now be defined in Table 1.

Table 1 Input feature set ${\mathcal {I}}$ used to find regression functions for the $\beta _n$ coefficients

2.2 Consistent Frozen RANS

To train regression functions of the $\beta _n$ coefficients and hence define models for ${\mathbf {a}}$, full field data of the variables $({\mathbf {U}}, {\varvec{\tau }}, k, \omega )$ is required from high fidelity simulation. From these base quantities the whole data set required for training (${\mathbf {a}}$, ${\mathbf {V}}^{(n)}$, $q_p$) can be calculated. Simple choices exist for ${\mathbf {U}}$ and ${\varvec{\tau }}$ as their high fidelity fields are consistent with the RANS fields we are trying to reconstruct. Less clear, and a point of difference in recent works (Weatheritt and Sandberg 2016; Schmelzer et al. 2020; Ling et al. 2016) is the choice of how to define k and $\omega$. To help distinguish between high fidelity and modelled turbulence variables in what follows, we denote high fidelity turbulent kinetic energy and specific dissipation rate as $k^*$ and $\omega ^*$ respectively and their modelled equivalents as $k^m$ and $\omega ^m$. It is widely recognized that using the $\omega ^*$ field calculated directly from high fidelity data is inconsistent with the $\omega ^m$ predicted by the RANS transport equation. This can impair the quality of results as the training environment is inconsistent with subsequent RANS calculations. To account for this, the frozen RANS approach was developed using ideas from Parneix et al. (1998). Here, the high fidelity data for ${\mathbf {U}}$, ${\varvec{\tau }}$ and $k^*$ are held constant and the $\omega$-equation solved for $\omega ^m$. The result is the $\omega ^m$ field that would be present given a RANS simulation that predicts the exact high fidelity velocity and Reynolds stress fields.

However, this approach relies on the high fidelity $k^*$ being consistent with the RANS predicted $k^m$, for which there is no guarantee. Schmelzer et al. (2020) suggested computation of the k-equation residual when inserting frozen $k^*$, alongside solving the $\omega$-equation. This residual then acts as an additional source or sink term depending on its sign and modifies $P_k$ accordingly. They then learn separate models for the discrepancy in the anisotropy and the k-equation residual in an attempt to match both the high fidelity ${\mathbf {U}}$ and $k^*$. Here, differences are accepted between the modelled $k^*$ and high fidelity $k^m$. To maintain consistency with subsequent RANS simulations, ${\mathbf {U}}$ and ${\varvec{\tau }}$ are both frozen and the k and $\omega$-equations solved simultaneously for $k^m$ and $\omega ^m$. It is important to note that ${\mathbf {a}}$, which enters the transport equations via the production term $P_k$, is calculated from its definition in Eq. 3 using $k^m$ obtained from solving the k-equation, rather than by using the high fidelity $k^*$ defined as $k^*=\frac{1}{2}\mathrm {tr}({\varvec{\tau }})$. This is because in subsequent RANS calculations only $k^m$ will be available to re-dimensionalise the anisotropy.

The result is an iterative procedure with steps following Algorithm 1. This algorithm ensures that modelled turbulence quantities $k^m$ and $\omega ^m$ are consistent with those that would be predicted in a RANS simulation that found the exact high fidelity velocity field, allowing a RANS consistent training set to be calculated. The transport equations are solved using linear upwinding for the divergence terms and central differencing for the diffusion. Turbulence quantities $k^m$ and $\omega ^m$ are initialised with fields predicted by a baseline k-$\omega$-SST and the residuals converged to $10^{-10}$. This process appears very robust and has shown strong convergence across all preliminary tests.

Fig. 2

Contour plots of input feature set calculated by consistent frozen RANS, shown over the full domain

Contour plots of the input features used can now be plotted for the backward-facing step case to visualise regions of the domain where each feature has importance. These are shown in Fig. 2. The shear layer is clearly visible in $q_1$ and $q_2$, in the incoming boundary layer and as the flow passes over the step. The turbulent viscosity given by $q_3$ is dominant in the turbulent wake region and the normalised kinetic energy $q_4$ effectively captures the recirculation region. Although the turbulent Reynolds number given by $q_5$ appears correlated to $q_3$ the near wall behaviour of both is very different and $q_5$ provides an effective feature to incorporate wall distance into data-driven models.

3 Upper Bound: Direct Reynolds Stress Approach

After defining a method for extracting (${\mathbf {a}}$, ${\mathbf {V}}^{(n)}$, $q_p$) from high fidelity simulations, it is important to set expectations of what can be achieved from the available data. This is found by uncovering optimal values for the $\beta _n$ coefficients and subsequently limiting them to ensure stability in RANS calculations. Two points are achieved here:

• 1. The stable upper bound in accuracy available from the high fidelity data set is found by substituting the limited basis coefficients into RANS. This substitution of the limited fields into RANS is termed the direct Reynolds stress approach.

• 2. A training data set promoting the stability of learned models can be uncovered. This is possible as potentially destabilising large magnitude values of the $\beta _n$ coefficients are removed, whilst ensuring that the limited coefficients are still capable of accurately reproducing the high fidelity mean flow fields.

3.1 Optimal Basis Coefficients

To introduce the Reynolds stresses to the RANS calculations in a stable manner that is consistent with the data-driven framework, we build on a method developed by Wu et al. (2019). They found a spatially varying optimal eddy viscosity which allowed the Reynolds stresses to be decomposed into a linear component with respect to the strain rate and the remaining nonlinear part. This is achieved by projecting the Reynolds stresses onto the strain rate tensor. The linear part can then be treated implicitly, improving the conditioning and thus the accuracy and convergence of the velocity fields compared to a fully explicit implementation. The approach is equivalent to obtaining the optimal $\beta _1$ coefficient and adding the component implicitly.

Here we extend the approach to find optimal values for each of the basis coefficients. This is achieved by vectorising each of the tensor bases and the anisotropy and forming a system of equations at each grid point

$$\begin{aligned} {\mathcal {V}}_n {\varvec{\beta }}_n = {\mathcal {A}}_n, \quad n=0,1,....,N \end{aligned}$$

(12)

where

$$\begin{aligned} \begin{aligned} {\mathcal {A}}_n&= \mathrm {vec}({\mathbf {a}}^{\mathrm {HF}}_n), \\ {\varvec{\beta }}_n&= [\beta _{1,n}, \; \beta _{2,n}, \; \beta _{3,n}]^T, \\ {\mathcal {V}}_n&= \big [\mathrm {vec}({\mathbf {V}}^{1,\mathrm {HF}}_n), \; \mathrm {vec}({\mathbf {V}}^{2,\mathrm {HF}}_n), \; \mathrm {vec}({\mathbf {V}}^{3,\mathrm {HF}}_n)\big ]. \end{aligned} \end{aligned}$$

(13)

${\mathcal {A}}_n$ and ${\mathcal {V}}_n$ have 3 independent components in two dimensional flows so this can be readily solved for ${\varvec{\beta }}_n$ at each point and yields ${\varvec{\beta }}^{\mathrm {opt}}_n=[\beta ^{\mathrm {opt}}_{1,n}, \; \beta ^{\mathrm {opt}}_{2,n}, \; \beta ^{\mathrm {opt}}_{3,n}]^T$. The spatially varying optimal basis coefficients can then be reconstructed as discretised fields. This process works well for statistically 2D flows, as the number of degrees of freedom of ${\mathcal {A}}_n$ is the same as the number of independent basis. However, for 3D flows ${\mathcal {A}}_n$ has 5 independent components (${\mathbf {a}}_{33}$ is related to the other diagonal entries by $\mathrm {tr}({\mathbf {a}})=0$), but there are 10 linearly independent basis. In this case, some additional thought is required to select 5 basis from the full set that show promise for a particular flow case, such that the coefficients may be solved for exactly. If no prior intuition exists as to which basis may be dominant for a certain flow class, one approach by which they could be uncovered is to project each basis onto the anisotropy field individually to obtain an optimal $\beta _n$ field for that basis. These terms could then be injected into separate RANS simulations to understand their contributions to the mean flow fields.

It is noted that considering a subset of the full set of basis restricts the functional relationships that can be represented. However, considering closures developed for specific classes of flow, which appears to be the direction of data-driven turbulence modelling in literature (Duraisamy et al. 2019), similar basis are likely to be dominant drivers of the mean flow fields. Taking a subset of the full basis therefore appears to be a reasonable approach and is one that has been chosen in many analytical and data-driven closure methods (Shih et al. 1995; Huijing et al. 2021). In this sense the basis, which are nonlinear in general, are treated as linear for specific classes of flow.

Extracting the optimal basis coefficients in this way fully decomposes the anisotropy tensor and elucidates the target variables for future data-driven methods. However, an interesting point of comparison between the method of Wu et al. (2019) and the present method is that extracting optimal coefficients of higher order basis can reintroduce instabilities into the CFD simulations. To inject $\beta ^\mathrm {opt}_n$, all fields are initialised to the frozen solution obtained in Sect. 2.2 and $\beta ^\mathrm {opt}_n$ are added as static fields. It may be expected that the RANS solver would stay at the frozen solution, but in practice there is inevitably a small initial transient. This may arise for a number of reasons but the authors believe it is likely due to: (1) the inability to obtain completely converged smooth high fidelity ${\mathbf {U}}$ and ${\varvec{\tau }}$ fields and (2) the introduction of the high fidelity pressure field p which is neglected through frozen training. These factors can both introduce small forcing on the flow as the variables adjust to the RANS momentum and continuity equations. This initial transient is enough to allow the extracted $\beta _n^{\mathrm {opt}}$ coefficients to drive the calculation to instability. Some manipulation of the data set prior to training is therefore necessary to ensure the data is not promoting inherent instability.

To explain this observation take a point in the flow at which the magnitude of the velocity gradient tensor approaches zero. This can trivially occur in the freestream, but more importantly at reattachment points. Here, the basis are nearly degenerate as they approach zero and the magnitudes of basis coefficients are forced to extremely large values to reconstruct the exact anisotropy. This is shown in Fig. 3 close to the wall around the reattachment point at $x \approx 5$. With small changes in the velocity field, these large coefficients may no longer occur in regions with small velocity gradient and ultimately drive the simulation to instability. This is confirmed for the backward-facing step, as introducing the $\beta _n^{\mathrm {opt}}$ coefficients directly yields oscillations in the solution stemming from the reattachment point.

Fig. 3

Large magnitudes of optimal beta coefficients local to reattachment point

3.2 Stabilising Basis Coefficients

It is apparent that if the $\beta _n^{\mathrm {opt}}$ coefficients, extracted directly from the high fidelity data set can lead to oscillatory CFD simulations without some prior manipulation, then data-driven models learned from this data are at risk of exhibiting the same behaviour. Many works condition the data on some metric and train models only on selected regions in the flow (Frey Marioni et al. 2021; Weatheritt et al. 2017) with the effect of removing regions in which large magnitude $\beta _n^{\mathrm {opt}}$ coefficients are present. Even in the case of non oscillatory solutions, the error metric used to find optimal models can be heavily skewed by large magnitude values and favour models which fit them better over the rest of the domain. As such, it is important that they are dealt with whilst pre-processing the high fidelity data.

Therefore, a conditioning approach is used to: (1) stabilise the RANS calculations by limiting the $\beta ^\mathrm {opt}$ fields across the domain to their maximum and minimum values within the conditioned region, and (2) define the region of the domain from which the training data set will be taken (Sect. 3.4). Until now, conditioning has been managed on an ad hoc basis with cross correlation of a posteriori performance necessary to check the selected training region is producing satisfactory models. By this method it is hard to fully separate the contributions of the training region and the model itself to overall performance. Now though, by directly limiting the $\beta _n^{\mathrm {opt}}$ fields and substituting them into RANS it is possible to ensure the high fidelity data itself is both accurate and convergent and will provide good training data, independent of any data-driven modelling.

The method adopted is to condition the domain based on the input feature set ${\mathcal {I}}$, to include only regions where the magnitude of the coefficients are small. Given the argument that large magnitude coefficients arise in regions of low velocity gradient, a natural choice is to condition where $q_1<q_1^{\mathrm {lim}}$. This removes most of the freestream and some of the recirculation region including the reattachment point. To remove the rest of the freestream, data is also excluded where $q_4<q_4^{\mathrm {lim}}$. Finally, to remove any outliers, the largest $1\%$ of points are also conditioned out. The limiting values of the input features found to give the best accuracy and stable convergence were $q_1^{\mathrm {lim}}=1.25 \times 10^{-2}$ and $q_4^{\mathrm {lim}}=1 \times 10^{-3}$. These values were chosen following a method of bisections approach. Emphasis was placed on stability in RANS calculations, whilst also checking that degradation of accuracy compared to the high fidelity velocity remained small. Maximum and minimum values of the $\beta _n$ coefficients are shown pre- and post-conditioning in Table 2 with results presented in the following section.

Table 2 Maximum and minimum values of $\beta _n$ pre- and post-conditioning

3.3 Basis Selection

As mentioned earlier, this analysis gives full decomposition of the anisotropy into basis components. This makes it possible to examine the contribution that each basis gives to the prediction of velocity and stress fields directly, without relying on a priori selection techniques such as in Weatheritt et al. (2019), which may or may not prove beneficial a posteriori. All combinations of tensor basis are run with the results shown in order of performance in Table 3. The basis ${\mathbf {V}}^{(1)}$ is used in all combinations as it corresponds to the linear component of the anisotropy and the implementation of ${\varvec{\tau }}$ becomes unstable without it.

Table 3 Results of direct Reynolds Stress approach for mean square errors $\epsilon (\cdot )$ and relative errors $\epsilon (\cdot )/\epsilon (\cdot ^0)$ where relative errors are presented with respect to the baseline k-$\omega$ SST

Using the linear component on its own although only giving a $13\%$ improvement in the Reynolds stress already provides a $68\%$ improvement in the velocity with respect to the baseline k-$\omega$ SST. Adding in the basis ${\mathbf {V}}^{(2)}$ then almost completely recovers the high fidelity velocity field with an improvement of $95\%$ and also significantly reduces the stress error with an improvement of $73\%$. Interestingly, we find that the basis ${\mathbf {V}}^{(3)}$ has an almost negligible effect on the velocity field. This result is explained considering the component $V_{12}^{(3)}$ is identically zero for 2D flows, so adds no contribution to $\tau _{12}$ which is the primary driver of the the velocity field in 2D. The observed improvement in the stress field comes only through the $\mathrm {diag}({\mathbf {V}}^{(3)})$ components. Including ${\mathbf {V}}^{(3)}$ also results in degradation of the residuals to which the RANS calculations converge. Given the potential destabilizing nature of the term and the negligible improvement in velocity prediction, we make the reasoned decision to exclude it from any data-driven models. This also serves as a good example of how the direct Reynolds stress approach can be used to dissect the high fidelity data in a controlled manner and analyse the stability and importance of each term individually.

3.4 Training Data Extraction

Given the success of the direct Reynolds stress approach at stabilising RANS calculations when the anisotropy is recast in a form consistent with the machine learning framework, the training data set can now be obtained with confidence that subsequent models will not learn coefficient magnitudes inherently promoting instability.

Fig. 4

Training region defined by conditioning on $q_1$ and $q_4$

Fig. 5

Optimal basis coefficients against each input feature for data within training region

The training data set comprises the variables $({\mathbf {a}},{\mathbf {V}}^{(n)},q_p)$ taken from the conditioned region of the domain defined by $q_1>q_1^\mathrm {lim}$ and $q_4>q_4^\mathrm {lim}$, shown in Fig. 4. The removal of the freestream and recirculation and reattachment regions are clear to see and the range of $\beta _1$ in this region is the same as the post-conditioning range in Table 2 as expected. The full set of training data can then be visualised in Fig. 5, where coefficients of the first two basis are plotted against the selected input features with respect to which they must be functions. The complexity of these mappings is immediately clear, highlighting the challenge facing data-driven turbulence models to find informative relationships from such a data set. One final pre-processing step is taken before passing the input features into any machine learning method. Namely, they are standardised to have zero mean and unit standard deviation. This helps accelerate training by providing the optimisation with features of similar magnitude. All subsequent models and plots are presented with respect to the standardised input features.

4 Model-Selection Procedure

In order to develop models independently of their a priori performance, and without resorting to implementing CFD within the optimisation loop, an efficient model-selection procedure needs to be proposed. The procedure presented here is agnostic of the machine learning technique used. It will be applied in discovering the lower bound via linear feature analysis in Sect. 5 and also in the development of models using machine learning techniques in Sect. 6.

To provide consistency across all data-driven methods the generalised architecture in Fig. 6 is used. First a subset of the input features are chosen for each basis coefficient and then separate machine learning units with a single output are deployed to find regression functions for these coefficients in terms of the chosen input features. This contrasts previous works by Ling et al. (2016) for example, where all input features enter one network with number of outputs equalling the number of coefficients to be modelled. Here more control is given to selecting which input features contribute to each coefficient. Inherent physical properties such as Galilean invariance are still preserved in the architecture by combining the coefficients and the tensor basis in the output layer. The general form of the models is then given by

$$\begin{aligned} {\mathbf {a}}^{\mathrm {pred}} = \sum _{n=1}^{10}\bigg ( \beta _n({\mathbf {X}}_n){\mathbf {V}}^{(n)}\bigg ), \end{aligned}$$

(14)

where ${\mathbf {X}}_n$ are the vectors of input features for the corresponding basis. Each vector ${\mathbf {X}}_n$ has elements $q_i$ such that $\{q_i\} \subseteq {\mathcal {I}}$ which is to say that any subset of the input features may be used in each feature vector ${\mathbf {X}}_n$.

Fig. 6

General architecture of data-driven models. Each ML unit is a completely general sub-architecture that finds a mapping of the chosen input features to the corresponding basis coefficient. This mapping can be generated by any available method, e.g., linear regression, symbolic regressions, neural networks or Gaussian processes

Models are regressed with the target of minimising the mean square error $\epsilon ({\mathbf {a}})$ between the high fidelity anisotropy and the predicted anisotropy

$$\begin{aligned} \epsilon ({\mathbf {a}}) = \frac{1}{N}\sum _{n=1}^N||{\mathbf {a}}^{\mathrm {hf}}_n-{\mathbf {a}}^{\mathrm {pred}}_n||^2. \end{aligned}$$

(15)

If the machine learning technique is gradient based, the full architecture is back propagated to calculate gradients. For gradient free techniques, the architecture simply governs the structure of the forward propagation.

The model-selection procedure then follows a similar direction to the direct Reynolds Stress approach. Models are built up from the selected basis iteratively. We start by considering just the basis ${\mathbf {V}}^{(1)}$, models are developed using each input feature from ${\mathcal {I}}$ individually and run in parallel in RANS calculations to determine their a posteriori performance. This gives an indication of the useful features for the current basis. Models using combinations of the top n performing features are then developed and again run in parallel in RANS to find the best combination of features for the basis which are then assigned to ${\mathbf {X}}_1$. The next basis is then added in and the process repeated until all selected basis have their features selected and the full model is developed. It is noted that although the set of input features used in the previous basis is now fixed, their weights are still trained. The procedure is outlined in Algorithm 2.

Table 4 Details of computational cost for the linear feature analysis

The computational resource required for this procedure is minimal. To highlight this, details of computational cost for the linear feature analysis (presented in the following section), are given in Table 4. The time taken in regression is negligible in comparison to running the RANS calculations, so the total time for each selected basis can be approximated in general as 2 RANS simulation times (one for each inner for loop), requiring m computational cores where m is equal to the size of whichever set ${\mathcal {I}}$ or ${\mathcal {C}}$ is larger. For the example of the linear feature analysis, it can be seen that $m=5$ and the total computational time is 3720 core-secs $\approx 1$ core-hr. Split between the 5 cores used, the entire procedure can therefore be run in around 12 minutes. Even in the limiting case considering 3D flows and using the full set of 10 basis, the computational time can be approximated to just 20 RANS calculations using m cores. Here, $m=26$ is the maximum value given the 5 input features used. This is in comparison to a CFD in the loop optimisation procedure which could evaluate $O(1 \times 10^{3})$ models per iteration over $O(1 \times 10^{3})$ iterations.

5 Lower Bound: Linear Feature Analysis

Given the production of an inherently stable training data set and a target performance for data-driven methods to aim at in Sect. 3, attention now turns to the lower limit of performance. Namely, what improvement can we get over the baseline simply modelling the $\beta _n$ coefficients as linear with respect to the input features. A data-driven method attempting to find complex nonlinear behaviour in the training data is of no practical use if it cannot improve on the performance of a linear regression which is easy to implement and inexpensive to perform.

This linear analysis is equivalent to setting each ML unit in the general architecture of Fig. 6 to a single node with a linear activation function, such that

$$\begin{aligned} \beta _n(\mathbf {X_n}) = {\mathbf {w}}_n \cdot {\mathbf {X}}_n + b_n. \end{aligned}$$

(16)

where ${\mathbf {w}}_n$ and $b_n$ are the set of weights and biases. Models are generated using the model-selection procedure outline in the previous section where the selected basis are ${\mathbf {V}}^{(1)}$ and ${\mathbf {V}}^{(2)}$. ${\mathbf {V}}^{(3)}$ is left out for the reasons detailed in Sect. 3.3.

The results of the linear feature analysis are illustrated in Fig. 7. The left hand column of Fig. 7a depicts the a priori error direct from linear regression and the second column depicts the a posteriori relative velocity error of each model with respect to the baseline k-$\omega$ SST. The top two rows give results of the model-selection for ${\mathbf {V}}^{(1)}$ alone, and the bottom two rows give the results for the second iteration when ${\mathbf {V}}^{(2)}$ is considered as well. The red dash dotted lines show the results from the direct Reynolds stress approach using initially just ${\mathbf {V}}^{(1)}$ in the first two rows and then using ${\mathbf {V}}^{(1)}$ and ${\mathbf {V}}^{(2)}$ in the next two rows. The grey dashed line shows the best performing linear feature model found for each of the basis combinations used.

Fig. 7

Results of linear feature analysis

The first point of note is confirmation that a model performing well a priori, does not necessarily carry over to a superior a posteriori performance. Here for example, $q_3$ and $q_5$ appear as promising features for regressing $\beta _2$, but manifest into worse predictors when tested in RANS. This is the observation that is often reported within data-driven turbulence modelling and is part of the motivation behind the computationally light, model-selection technique developed.

Turning attention to the a posteriori validation, it’s seen that for the first basis, the best model is found with $\beta _1$ simply a linear function of input feature $q_5$. This alone provides a $53\%$ improvement on the baseline in comparison to the maximum $68\%$ improvement available from the direct Reynolds stress approach. When adding in the second basis the best model is found where $\beta _2$ is a linear function of $q_1$ and $q_4$, however the improvement over using $q_1$ alone is just $0.5\%$ so this model is selected on account of its simplicity. The best model is then given by

$$\begin{aligned} {\mathbf {a}}^{\mathrm {pred}} = (-0.205q_5 - 1.027){\mathbf {V}}^{(1)} + (-0.085q_1 + 3.220){\mathbf {V}}^{(2)}. \end{aligned}$$

(17)

The percentage square errors for the basis coefficients $\epsilon (\beta _1)$ and $\epsilon (\beta _2)$ are plotted over the training domain at the top of Fig. 7b. The bottom plots show the linear regressions plotted against the high fidelity data where the left plot shows $\beta _1=\beta _1^L(q_5)$ and the right plot shows $\beta _2=\beta _2^L(q_1)$. Clearly the data is not fitted well over the full training domain with larger errors appearing further from the wall. However, with this simple model the improvement in velocity error over the baseline, is $77\%$. Whilst this is short of the direct Reynolds stress approach which improves over the baseline by $95\%$, for a stable model which is cheap to develop and compute, it may still be considered a very satisfactory improvement over the baseline k-$\omega$ SST.

The region between the grey dashed and red dash dotted lines can now be interpreted as the performance region in which any machine learning model should reside and they constitute the lower and upper bounds. Although applied only to the backward-facing step here, this can be applied generally to any case and gives a quantification of the expected errors. The performance of any developed model can then be interpreted within context of these bounds. In predictive cases the direct Reynolds stress approach will not be available (as it is case specific) but the linear model can still be applied to give a lower bound for the expected performance of a given model.

6 Assessment of Machine Learning Techniques

In the following section we assess the performance of several machine learning techniques against this error quantification region. To ensure each technique is tested fairly, the general architecture shown in Fig. 6 is maintained and the machine learning components are substituted into the relevant locations in the architecture.

The techniques assessed in this work are: (1) Gene Expression Programming (GEP); (2) Deep Neural Networks (DNN) and (3) a novel mixture model that regresses a sum of multivariate Gaussians, merging the gradient based optimisation of DNNs with the ability to obtain an explicit model, which is one of the key advantages of GEP.

6.1 Gene Expression Programming

The first technique assessed is gene expression programming (GEP). GEP is an evolutionary algorithm that performs symbolic regression given a set of input features and operators and some target variable to represent. It was introduced by Ferreira (2001) and has been primarily applied to turbulence modelling problems by Weatheritt and Sandberg (2016), the reader is referred to these work for full descriptions of the algorithm. One of the main arguments for GEP is that generating explicit models for the target variable is of practical use, and overcomes the often cited negative aspect of Neural Networks which is their inherent black box nature.

The standard implementation takes the basic set of arithmetic operators and regresses explicit expressions comprising of these operators and the chosen input features. It is thus capable of expressing multivariate polynomials of some predefined maximum length and order. Which terms are included within this skeleton however is left to GEP and so the form of the equation, to some extent, is generated by the algorithm itself.

Expression order and length are primarily controlled by two parameters. The order is related to the length h of each string of symbols (known as genes) and both h and the number of genes used to make an expression n controls the length. Preliminary tests found a suitable number of genes in each expression to be around $n=4$, which was not so large as to prohibit convergence but also allowed models enough freedom to reach lower values of the objective function $\epsilon ({\mathbf {a}})$. The length h is potentially a more sensitive parameter as it controls not just complexity but also to some extent the length of the expression. So, to avoid over constraining the algorithm by selecting all hyperparameters a priori, optimisations were run using 3 values $h=3,5,7$.

The results of the GEP optimisations are shown in Fig. 8 with the same set of plots presented in the results of the linear feature analysis. The only difference is that here, Fig. 8a plots three points for each combination of input features selected, relating to the values of h chosen above. As can be seen, the best GEP models perform very similarly to the linear feature analysis for both the initial feature selection of ${\mathbf {V}}^{(1)}$ and when ${\mathbf {V}}^{(2)}$ is added in as well. The best input feature set for $\beta _1$ is once again found to be just $q_5$ (including $q_4$ as well gives a $0.7\%$ improvement which is not considered significant enough to justify the additional term). All input feature combinations other than $q_3$ and $q_5$ perform similarly in modelling $\beta _2$ and it is highlighted that these input features don’t feature in the a posteriori results. The reason for this is that, although still convergent, they failed to produce smooth anisotropy field predictions and so have been left out of model selection. Once again there is a very small improvement of just $0.1\%$, to be found from including combinations of input features so the input feature set for $\beta _2$ is selected as the best performing individual input feature which here is $q_4$.

Fig. 8

Results of GEP analysis

There is also very little spread in the results of varying h and this, as well as the similarity in performance to the linear feature analysis is explained when considering Fig. 8b and the explicit form of the model which is given by

$$\begin{aligned} {\mathbf {a}}^{\mathrm {pred}} = (-0.002q_5^2 - 0.207q_5 - 1.028){\mathbf {V}}^{(1)} + (0.154q_4 + 3.188){\mathbf {V}}^{(2)}. \end{aligned}$$

(18)

The best model discovered by GEP is very close to linear, with the $q_5^2$ term having very little effect on the model due to it’s small magnitude coefficient. This explains why varying h had such little effect on the models generated as GEP struggled to find polynomials of higher order with significantly better fit to the data. The only noticeable difference between models is that GEP found $q_4$ to be the best coefficient for $\beta _2$ where the linear feature analysis found $q_1$, but the difference in velocity error for the two features is less than $0.5\%$ and cannot be considered significant.

Despite the potential for extra model complexity, it is interesting then that GEP has discovered a near linear model and doesn’t find significant improvement on this bound. It is suggested that this is most likely due to the adoption of a simple canonical flow case.

6.2 Deep Neural Networks

The next technique assessed is DNNs. They were first introduced to turbulent flow prediction in the current form by Ling et al. (2016) as a single corrective step. Here they are used as forward models to be inferenced with each iteration of the RANS solver.

The architecture used is again the one presented in Fig. 6. Each ML unit in this case consists of a number of densely connected layers with a variable number of inputs (depending on which features are chosen for each basis) and a single output that is the corresponding basis coefficient. This leads to 3 main hyperparameters which are the number of layers in each ML unit, the number of nodes in each layer and the activation function selected for each node. The $\tanh$ activation function was chosen in this work as it provides a smooth transfer function which is beneficial in RANS. Preliminary testing suggested that just 2 hidden layers were sufficient for good a priori prediction with more layers providing little further advantage. The number of nodes in each layer was varied to provide a larger search of the optimisation landscape and layers with $n=3,5,7$ nodes were tested.

Fig. 9

Results of DNN analysis

The results of the DNN optimisations are shown in Fig. 9 with the three sets of points for each input feature combination in Fig. 9a relating to the different number of nodes used in each hidden layer. When regressing just ${\mathbf {V}}^{(1)}$ the best model is found with the coefficient $\beta _1=\beta _1(q_3,q_4,q_5)$ and the performance improves on the lower bound and is just $1.7\%$ under the upper bound. This is a very encouraging result. However, when the ${\mathbf {V}}^{(2)}$ basis is included the improvement is not carried over to the same extent. Most of the models generated failed to produce smooth anisotropy fields when tested in RANS, so although convergent, are considered non physical and are not included here. Only $q_1$ and $q_2$ produced fully smooth models with $q_1$ marginally outperforming $q_2$. Although the explicit form of the final model cannot be presented, the best model found is of the form

$$\begin{aligned} {\mathbf {a}}^{\mathrm {pred}} = \beta _1(q_3,q_4,q_5){\mathbf {V}}^{(1)} + \beta _2(q_1){\mathbf {V}}^{(2)}. \end{aligned}$$

(19)

Figure 9b shows the a priori performance of this model. Clearly $\epsilon (\beta _1)$ is significantly reduced across the training domain and $\beta _1$ is no longer a linear function of the input features (it is plotted here as a point cloud for representation against $q_5$ as it has 3 input features so cannot be represented as a line or surface). $\epsilon (\beta _2)$ however is very similar again to the linear feature analysis and the linearity of $\beta _2$ with respect to $q_1$ is confirmed in the bottom right plot.

Overall, the best DNN model outperformed the lower bound by $7\%$ and falls short of the upper bound by $11\%$. Given the potential for more complex functional relationships than linear analysis and GEP, an improvement of just $7\%$ over these models appears underwhelming. However, it is remembered that this relates to an improvement of $84\%$ over the baseline k-$\omega$ SST, so we observe that this may be more testament to the performance of the linear feature analysis.

6.3 Mixtures Models

Having assessed two conventional machine learning techniques used in turbulence modelling, we now introduce a new method that blends the advantages of each. It is a gradient based approach like DNNs that allows an explicit form of the function to be read and manipulated as is the case for GEP. The method models the $\beta _n$ coefficients as a weighted sum of basis functions $\phi _{n,i}$ which are functions of the input feature vectors ${\mathbf {X}}_n$ such that $\phi _{n,i} = \phi _{n,i}({\mathbf {X}}_n)$ and ${\varvec{\phi }}_n$ is the vector of basis functions $\phi _{n,i}$. The weighted sum is combined with a weighted sum of the input feature vectors providing the linear performance and allowing the basis functions to focus on additional nonlinear behaviour. Each of these weighted sum units consitutes one ML unit in Fig. 6 such that the basis coefficients are modelled as

$$\begin{aligned} \beta _n = {\mathbf {w}}^b_n \cdot {\varvec{\phi }}_n({\mathbf {X}}_n) + {\mathbf {w}}^l_n \cdot {\mathbf {X}}_n + b_n, \end{aligned}$$

(20)

where ${\mathbf {w}}_n^b$ are the basis weights, ${\mathbf {w}}_n^l$ are the linear weights and $b_n$ are the biases. For large numbers of basis functions explicitly expressing resultant models quickly becomes impractical, so we aim to keep the number of basis functions small whilst capturing significant features in the data.

The choice of basis function is an interesting topic and a vast array of options present themselves including Fourier, Radial Basis Functions (RBFs) and polynomial basis such as Legendre and Hermite polynomials. Here however we select a basis of multivariate Gaussians. Multivariate Gaussians are selected over RBFs as their variance can vary in each input direction, theoretically allowing more complex function spaces can be mapped with fewer terms. They are also selected over Fourier or polynomial basis because of their well behaved nature at large values of the input feature space. While polynomials grow to large values and Fourier modes continue their periodicity, Gaussians reduce to zero at large values, so the mixture models will revert to a linear feature model in these regions. In predictive CFD cases, where the models must extrapolate to new regions of the input space this behaviour is more likely to maintain stability. The general form of the multivariate Gaussian used is given as

$$\begin{aligned} \phi ({\mathbf {X}}) = \exp ({\mathbf {X}}-\mu )^T\mathbf {\varSigma }^{-1}({\mathbf {X}}-\mu ) \end{aligned}$$

(21)

where $\mu$ is the mean and $\mathbf {\varSigma }$ is the covariance matrix. The prefactor in the standard multivariate Gaussian formula is simply incorporated in the basis weights.

Fig. 10

Results of GMM analysis

The results of the Gaussian mixture models (GMMs) are presented in Fig. 10. The main hyperparameter is the number of multivariate Gaussian terms used and here we test with $n=0,1,2$. It is noted that when $n=0$, the model reverts to being linear with respect to the input features. Analysing Fig. 10a the GMM finds the same combination of input features to best model $\beta _1$ as the DNN which is $\beta _1=\beta _1(q_3,q_4,q_5)$. A solution with just a single Gaussian is discovered, which improves on the lower bound by $9\%$ and is just $6\%$ short of the upper bound. Although inferior to the DNN, for a model with just one Gaussian term it is a promising result. Again, when including ${\mathbf {V}}^{(2)}$ it appears that more complex models introduce non smooth features in the anisotropy field and linear (or near linear) models give the best results. The best model overall improved over the baseline k-$\omega$ SST by $79\%$ which is just a $2\%$ improvement on the lower bound and $16\%$ below the direct Reynolds stress approach. This model is presented as

$$\begin{aligned} \begin{aligned} {\mathbf {a}}^{\mathrm {pred}} = \bigg [-0.883\exp \Big (({\mathbf {X}}_1 - \mu _1)\mathbf {\varSigma }_1^{-1}({\mathbf {X}}_1 - \mu _1)^T \Big ) + {\mathbf {w}}^l_1 \cdot {\mathbf {X}}_1 - 0.845\bigg ]&{\mathbf {V}}^{(1)} \\ + (0.027q_1 + 0.153q_2 + 3.231)&{\mathbf {V}}^{(2)}, \end{aligned} \end{aligned}$$

(22)

where

$$\begin{aligned} {\mathbf {X}}_1 = \begin{bmatrix} q_3 \\ q_4 \\ q_5 \end{bmatrix}, \mu _1 = \begin{bmatrix} -0.449 \\ 0.114 \\ -0.310 \end{bmatrix}, \mathbf {\varSigma }_1^{-1} = \begin{bmatrix} 0.614 &{} -1.508 &{} -0.021 \\ -1.508 &{} 4.566 &{} 0.497 \\ -0.021 &{} 0.497 &{} 0.232 \end{bmatrix}, {\mathbf {w}}^l_n = \begin{bmatrix} 0.006 \\ -0.020 \\ -0.242 \end{bmatrix}. \end{aligned}$$

(23)

Whilst the model is a clear step up in complexity from the linear analysis and GEP models, it consists of just 17 trainable parameters. Significantly fewer than the best DNN model which required 98 trainable parameters. The $\beta _n$ coefficient errors and function plots can be seen in Fig. 10b. The improvement of the modelling of $\beta _1$ over the linear and GEP is clear and again the difficulty of the technique to make significant improvements on the linear model for $\beta _2$ is observed.

6.4 Summary of Machine Learning Techniques

The pattern that modelling of $\beta _1$ allows for more complex models than the modelling of $\beta _2$ has emerged throughout the assessment of these machine learning techniques. The reason for this is likely twofold. Firstly, $\beta _1$ is negative across the training domain and thus acts as a purely viscous term, this combined with the fact that $\beta _1$ can be implemented implicitly in code make it very stable and accepting of complex models. Higher order coefficients, such as $\beta _2$ in this case, are not purely viscous and must be implemented explicitly. This allows additional model complexity to produce unexpected behaviour.

Table 5 Summary of the performance of the assessed machine learning techniques. Results are presented as a percentage improvement over the baseline k-$\omega$ SST model

Table 5 gives a summary of the performance of each of the techniques. The summary shows all models operate within the expected range between the lower bound linear feature analysis and the upper bound direct Reynolds stress approach. Whilst all models perform very well in comparison to the baseline k-$\omega$ SST, the results also show that for full models considering both basis, significant improvement over the lower bound can be hard to achieve.

7 Application to Periodic Hills

It is important now to asses how these models perform on out of sample predictive cases. To asses this performance each model is tested on the periodic hills geometry, which has become a standard test case for turbulence modelling problems due to it’s wide availability. It consists of a channel with periodic bumps in the lower wall of height H where the periodic domain has total height 3H and length 9H. The Reynolds number based on the bulk velocity and hill height is $Re=10595$. LES data is taken for comparison from the simulations run by Temmerman and Leschziner (2001). As mentioned previously, the upper bound is case specific so cannot be considered here but the lower bound can still be applied to test the predictive performance of the models. Previous work by Wu et al. (2019) and Schmelzer et al. (2020) however, has applied the high-fidelity Reynolds stresses in a frozen approach to the periodic hills case. Both reported good reproduction of the high-fidelity velocity field, so it is expected that upper bound for this case would be close to the LES data.

Fig. 11

Periodic hills velocity components a $U_1$ and b $U_2$

Fig. 12

Periodic hills normal stress components a $\tau _{11}$ and b $\tau _{22}$

Fig. 13

Periodic hills a shear stress $\tau _{12}$ and b turbulent kinetic energy k

The results are plotted in Figs. 11, 12 and 13. Figure 11 shows the $U_1$ and $U_2$ components of velocity at several streamwise locations along the periodic hills geometry. Plotted is the LES data of Temmerman and Leschziner (2001), the baseline k-$\omega$ SST model and then the results of running the models generated by the linear feature analysis (LFA), GEP, DNN and GMM. Figure 12 shows the normal components of Reynolds stress $\tau _{11}$ and $\tau _{22}$ and Fig. 13 plots the shear stress component $\tau _{12}$ and turbulent kinetic energy k. All models are seen to improve on the baseline k-$\omega$ SST predictions, most noticeably in the prediction of the recirculation region. For the $U_1$ and $U_2$ components of velocity, a much smaller degree of separation is predicted by the LES than by the baseline with the LES recovering its boundary layer profile much faster after the end of the hill. This feature is well predicted by the LFA, GEP and the GMM but interestingly the DNN fails to find the same improvements. None of the models manage to perform well along the top wall which occurs due to an under prediction of the turbulent mixing in the centre of the channel. This is likely because the backward-facing step case has a freestream upper wall boundary condition so the necessary physics is not present in the training case.

The same trend continues in the ${\varvec{\tau }}$ and k plots with the LFA, GEP and GMM all performing at a very similar level, and the DNN model not predicting as well. In fact, it is the lower bound LFA and GEP that provide the best models in the predictive case. Although the DNN was able to outperform other models on the case on which it was trained, it is likely that the model is over fit to the data from the backward-facing step. It is possible that the LFA emerges as the best predictor in the unseen case as it provides a simple description of the most important physical effects. GEP then also performs well as the technique has enough natural stiffness in the training phase to avoid over fitting the data.

8 Conclusions

A framework has been developed to provide error quantification of data-driven turbulence models. At the upper end of the quantification is the direct Reynolds stress approach, which inserts the high fidelity Reynolds stresses into RANS calculations in a stable manner. This is achieved through discovery of the exact basis coefficients, which are fully consistent with the data-driven framework. This direct Reynolds stress approach also allowed basis selection based on a posteriori results. At the lower end is a linear feature analysis, which models tensor basis coefficients as linear functions with respect to the chosen set of input features. Three machine learning techniques are then assessed based on these performance bounds, namely: (1) Gene Expression Programming, (2) Deep Neural Networks and (3) a novel Gaussian Mixture Model. It was found that these techniques struggled to improve substantially over the linear feature analysis with improvements over the baseline of $77\%$, $83\%$ and $79\%$ respectively in comparison to $77\%$ for the linear feature analysis. When tested on the periodic hills case which constitutes an out of sample test case for the models predictive performance, the linear models of the linear feature analysis and GEP performed best, with the DNN providing the least predictive performance. This result highlights the observation that data-driven turbulence models often benefit from finding simple relationships and overfitting a model to a specific case can have detrimental effects in predictive circumstances.

Whilst we are careful not to suggest that more complex machine learning methods are not useful in turbulence modelling, we have shown that they do not necessarily have to be used in cases where simple linear regressions provide satisfactory results. This is likely to be due to the selection of canonical flow cases. Assessment of data-driven methods on more complex flow cases is therefore required to discover if linear models still perform comparably, or, if when the physics of the problem is more complex, more complex data-driven methods are in fact required.